Abstract
In this paper, the uncertainty quantification and sensitivity analysis of a mathematical model of the SARS-CoV-2 virus transmission dynamics with mass vaccination strategy has been carried out. More specifically, a compartmental epidemic model has been considered, in which vaccination, social distance measures, and testing of susceptible individuals have been included. Since the application of these mitigation measures entails a degree of uncertainty, the effects of the uncertainty about the application of social distance actions and testing of susceptible individuals on the disease transmission have been quantified, under the assumption of a mass vaccination program deployment. A spectral approach has been employed, which allows the uncertainty propagation through the epidemic model to be represented by means of the polynomial chaos expansion of the output random variables. In particular, a statistical moment-based polynomial chaos expansion has been implemented, which provides a surrogate model for the compartments of the epidemic model, and allows the statistics, the probability distributions of the interesting output variables of the model at a given time instant to be estimated and the sensitivity analysis to be conducted. The purpose of the sensitivity analysis is to understand which uncertain parameters have most influence on a given output random variable of the model at a given time instant. Several numerical experiments have been conducted whose results show that the proposed spectral approach to uncertainty quantification and sensitivity analysis of epidemic models provides a useful tool to control and mitigate the effects of the COVID-19 pandemic, when it comes to healthcare resource planning.
1. Introduction
The recent approval of different COVID-19 highly effective vaccines by the U. K. Medicines and Healthcare Products Regulatory Agency (MHRA) [1], the U. S. Food and Drug Administration (FDA) [2], and the European Medicines Agency (EMA) [3], provides a determining pharmacological measure in the struggle against the COVID-19 pandemic, which opens the possibility to explore new scenarios that combine the effects of both non-pharmaceutical public health interventions and vaccination strategies.
In this paper, the uncertainty quantification and sensitivity analysis of a mathematical model of the SARS-CoV-2 virus transmission dynamics with mass vaccination strategy has been carried out. More specifically, a compartmental epidemic model has been considered, which also allows the possibility of social distance measures and testing of susceptible individuals to be included in the model. The introduction of uncertainties about the application of these non-pharmacological strategies results in a complex stochastic model which is difficult to solve. However, there exist inherent uncertainties about the sensitivity and specificity of COVID-19 tests, as well as about the degree of application of social distance measures that should be taken into account in order to obtain a more realistic model. Therefore, a surrogate model has been designed, which approximates the actual model with good precision and it is easier to solve. In particular, a Polynomial Chaos Expansion (PCE) [4] has been used to build this surrogate model. The PCE is a probabilistic method consisting in the projection of the model output on a basis of orthogonal stochastic polynomials in the random inputs. This stochastic projection provides a compact and efficient representation of the model output variability with respect to the inputs. Furthermore, the surrogate model provided by the PCE allows the statistical analysis of the output model to be conducted as a post-processing of the polynomial expansion coefficients.
Compartmental disease transmission models are characterized by the subdivision of the population into compartments and the assumptions that are made about the nature and time rate of transfer among them. Historically, these models have provided several key insights regarding the spread of communicable diseases, which could not be discerned from data and thus were missed by many public health and infectious disease experts. Indeed, for a long time, due to the lack of mathematical models, a significant number of experts thought that herd immunity threshold did not exist and thus believed that mass vaccination programs were bound to fail. Likewise, mathematical models have been decisive to understand that an epidemic ends because of the lack of new infected individuals and not because of the lack of susceptible individuals. Furthermore, compartmental models have contributed to increase the knowledge about some of the most common communicable diseases such as tuberculosis, influenza, AIDS, ebola, malaria, dengue, or zika [5].
The first mathematical model in epidemiology was presented in the seminal paper [6] and revisited in Dietz and Heesterbeek [7] as a susceptible-immune compartmental model, which estimated the impact of inoculation against smallpox. Later on, the foundations of the entire approach to epidemiology based on compartmental models were stablished in Kermack and McKendrick [8], where the Susceptible-Infected-Recovered (SIR) model was introduced. Ever since, a great deal of variants and extensions of the the SIR model have been proposed in the literature, which take into account both the geographical spread and the temporal evolution of the disease, such as the Susceptible-Exposed-Infected-Recovered (SEIR) model [9] or the delayed SIR epidemic model [10], [11].
Compartmental models have been crucial to study the evolution of several recent disease outbreaks including the SARS epidemic of 2002–2003 [12], the H5N1 influenza outbreak in 2005 [13], the H1N1 influenza pandemic of 2009 [14], and the ebola outbreak of 2014 [15]. Stochastic versions of these models have gained interest in the last years. For instance, in Allen [16], a stochastic SIR epidemic model has been formulated and a numerical simulation using a Markov chain approach has been conducted, whereas in Li et al. [17], the parameters in the transmission rate, based on a stochastic SIR epidemic model with media coverage, have been estimated by means of a maximum likelihood approach. A thorough treatment of stochastic epidemic models can be found in Britton and Pardoux [18].
In the last months, several research activities have been conducted to investigate different key aspects of the spread, control, and mitigation of the COVID-19 disease, which are based on compartmental-like epidemic models. In [19], a coarse taxonomy of models has been discussed, including the Imperial College model [20], and their significance in contributing to the analysis of COVID-19 has been explored. In [21], a theoretical framework to investigate the spread of COVID-19 within a community based on a SIR model has been presented, in which the total population is not defined or kept constant and the number of susceptible individuals does not decrease monotonically. In [22], a compartmental mathematical model for the spread of the COVID-19 disease, with special focus on the transmissibility of super-spreaders individuals, has been proposed, in which the sensitivity of the model with respect to the variation of each one of its parameters has also been investigated. In [23], a compartmental-like epidemic model has been proposed, which includes containment measures that are modeled by considering a time-dependent modulation of the bare infectivity and mimicking the combined effect of the asymptomatic onset of the disease, testing policies, and quarantine. In [24], an extended SEIR model has been proposed to estimate the size of the epidemic in Wuhan and forecast the extent of the domestic and global public health risks of epidemics, accounting for social and non-pharmaceutical prevention interventions. In [25], [26], a modified SEIR model devised to reproduce the realistic data of the World Health Organization (WHO) and to predict the effect of strategies used to flatten the power-law curves, has been proposed. In [27], a compartmental mathematical model with eight stages of infection that represent multiple population-wide strategies, including social distancing, testing, and contact tracing has been considered, whose simulation results have been compared with real data on the COVID-19 epidemic in Italy. In [28], three regional-scale models for forecasting and assessing the course of the COVID-19 pandemic have been presented, which are capable of measuring and forecasting the impacts of social distancing, highlighting the dangers of relaxing non-pharmaceutical public health interventions in the absence of a vaccine or antiviral therapies. In [29], the effect of major interventions, including lockdowns, across 11 European countries for the period from the start of the COVID-19 epidemic in February 2020 until 4 May 2020 has been studied using a model which calculates backwards from observed deaths to estimate transmission that occurred several weeks before, allowing for the time lag between infection and death. In [30], the effects of pharmacological measures have been studied, in particular, simulations have been conducted using a population pharmacokinetic model to predict plasma concentration-time profiles after a single and repeat fasted administration of ivermectin, a drug used in malaria spreading. In [31], a climate-dependent epidemic model has been developed, which simulates the COVID-19 pandemic by probing different scenarios based on known coronavirus biology in order to analyse whether climate may modulate the transmission of SARS-CoV-2.
As mentioned above, in this paper, the uncertainty quantification and sensitivity analysis of a mathematical model of the SARS-CoV-2 virus transmission dynamics with mass vaccination strategy, derived from the epidemic model introduced in Brugnago et al. [26], has been conducted. In the literature, there is a wide variety of approaches that allow uncertainty in mathematical systems to be quantified [32]. They include hierarchical models, Bayesian methods, or nonparametric techniques. In this paper, the spectral approach introduced in Xiu and Karniadakis [33] has been considered, which allows the uncertainity propagation through the epidemic model to be represented by means of its PCE. In particular, following [34], a statistical moment-based PCE has been implemented, which provides a surrogate model for the compartments of the epidemic model, in which a spectral expansion of the random output variables is employed that allows the probability distributions of the interesting output variables of the model to be efficiently estimated. Moreover, this approach yields a way to carry out both the computation of the main statistics of interest and a global sensitivity analysis of the model output variables based on the variance of the input random parameters, with the aim to understand which input parameters have more influence on the variability on the model outputs at a given time instant and with a very low computational cost. More specifically, under the assumption of a mass vaccination program deployment, the effects of the uncertainty about the application of social distance actions and testing of susceptible individuals on the disease transmission have been quantified. Several numerical experiments have been conducted whose numerical results show that the proposed spectral approach to the uncertainty quantification and sensitivity analysis of epidemic models provides a useful tool to control and mitigate the effects of the COVID-19 pandemic when it comes to healthcare resource planning. The obtained results have been validated using the Monte Carlo (MC) simulation method [35].
This paper is organized as follows. In Section 2, the mathematical model of the SARS-CoV-2 virus transmission dynamics with vaccination strategy is described. Then, the PCE technique used to model the propagation of the uncertainties through this epidemic model is introduced in Section 3. The methodology followed to quantify the uncertainty of the epidemic model is described in Section 4 and validated in Section 5, whereas a procedure to estimate the statistical distributions of the output, based on a surrogate model, is explained in Section 6. The technique employed for the global sensitivity analysis is presented in Section 7. Finally, in Section 8, some conclusions are drawn.
2. Mathematical model of COVID-19 transmission dynamics
Following [26], a modified SEIR model, designed to reproduce realistic data of the WHO [36], has been considered in this work. This model, denoted as SEIsIaQR, consists of 6 compartments: susceptible (), exposed (), symptomatic infectious (), asymptomatic infectious (), isolated (), and recovered () individuals. Besides, in the model considered in this paper, a vaccination term has been included. A schematic representation of this SEIsIaQR compartmental model with vaccination strategy is shown in Fig. 1 , which is represented by the following set of Ordinary Differential Equations (ODE):
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
| (1f) |
Fig. 1.
Schematic representation of the SEIsIaQR compartmental model with vaccination strategy [26].
The dynamic system (1) consist of 7 variables and 9 parameters. Two kind of parameters can be distinguished: parameters that do not depend on containment or mitigation strategies and parameters that represent the use of specific containment or mitigation strategies.
The meaning of the 7 variables involved in model (1) is the following:
-
•
Variable represents the number of individuals susceptible to infection.
-
•
Variable represents the number of exposed individuals, which remain latent until they are infected.
-
•
Variable represents the number of symptomatic individuals, which are included in the confirmed cases and assumed to show strong symptoms.
-
•
Variable represents the number of asymptomatic individuals, including the mild symptomatic cases.
-
•
Variable represents the number of infected individuals that have been isolated due to quarantine measures.
-
•
Variable represents the number of individuals which were infected but recovered and became immune. Deceased individuals are also included in this compartment.
-
•Variable represents the total population, which satisfies the condition
where denotes the final time of the period considered in the ODE system.
The parameters in model (1) that do not depend on containment or mitigation strategies are the following:
-
•
The mean serial time interval, which is the mean time between successive cases of transmission of the disease. According to [37], this parameter has been set to days.
-
•
The mean incubation period, which has been assumed to be equal to the latent time. The latent time, also called incubation time, is defined as the time interval the exposed individual remains infectious. According to [38], this parameter has been set to days.
-
•
The infectious period, which is calculated as .
-
•
The ratio between infectiousness of asymptomatic and symptomatic individuals, . According to [26], this parameter has been set to .
-
•
The population ratio that remains asymptomatic or mild symptomatic, . According to [36], this parameter has been set to .
The parameters in model (1) associated to the use of non-pharmacological containment or mitigation strategies are the following:
-
•
The replication factor, which is calculated as where denotes the proportion of interaction between individuals and represents the well-known basic reproduction number.
-
•
The isolation rate of symptomatic individuals, .
-
•
The identification and isolation rate of asymptomatic individuals, .
Finally, parameter denotes the daily vaccination rate, which ranges from 0 to 1 and has been assumed to be constant. Thus, the vaccination strategy in model (1) has been represented by the term .
Note that the cumulative number of confirmed cases of COVID-19, can be easily derived from the solution of (1) by solving the differential equation
Likewise, the cumulative number of symptomatic infectious cases, can be easily computed by solving the differential equation
In this paper, the coefficients and are considered as key parameters that represent non-pharmacological measures to struggle against the COVID-19. Likewise, analyzing parameters and is the main focus of the study presented in Brugnago et al. [26], where and are adjusted from the data provided in World Health Organization [36].
On the one hand, parameter is interpreted as the ratio between the average of the daily social interactions when social distancing actions are taken and the average of the daily social interactions when social distancing actions are not taken. Thus, larger social distance implies smaller values of . As shown in Brugnago et al. [26], values of over 4 correspond to very low degree of social distancing actions.
On the other hand, parameters and represent the rates of daily tests, which allow the infected symptomatic and asymptomatic individuals to be identified and isolated. Both coefficients range from 0 to 1. For instance, represents a daily rate of identification and isolation of 10% of all asymptomatic infected individuals, which means a great number of daily tests for countries with large population. Despite the availability of COVID-19 antigen rapid, portable tests, and tracking apps, the ideal situation represented by in which all asymptomatic infected people are identified and isolated every day, is, in general, not realistic. On the contrary, achieving high values of is easier since it entails testing and isolating only symptomatic individuals, which are easier to be identified in the population.
In this paper, assuming the availability of an effective vaccine, an immunization term has been added to the model proposed in Brugnago et al. [26], and the quantification of the effects of the uncertainty in the containment or mitigation strategies represented by parameters and on the disease transmission has been carried out. Besides, surrogate models for the compartments of the model (1) have been obtained, which allow the probability distributions of the output variables to be estimated. Moreover, a global sensitivity analysis has been carried out to identify the random input parameters that have most influence on the variability of the output variables.
3. Moment-based arbitrary polynomial chaos expansion
In this section, the statistical moment-based PCE technique used to study the propagation through the model (1) of the uncertainties about the application of the non-pharmacological strategies, represented by the parameters and is outlined. For a complete treatment of the subject, the reader is referred to [34].
Let denote a vector of independent random variables in a probability space where is the space of events, is a -algebra, and is a probability measure. Then, a multi-dimensional polynomial expansion dependent on the random input vector can be defined in order to represent a stochastic model output . In particular, the vector can be approximated by a linear combination of stochastic multivariate orthonormal polynomials as follows:
| (2) |
with deterministic coefficients which can be obtained as
| (3) |
In practice, integral (3) can be solved by means of Galerkin projection, collocation, or numerical integration, among others. In this paper, a Gaussian quadrature rule based on statistical moments has been employed. The generalized Polynomial Chaos (gPC) expansion techniques introduced in Xiu [4] provide the optimal choices for the nodes and weights of a great variety of parametric input distributions, as well as their corresponding orthogonal polynomials basis, which allow integral (3) to be numerically computed. However, the arbitrary Polynomial Chaos (aPC) expansion approach based on the statistical moments [39] provides a more general framework than the gPC, in which different kind of inputs can be considered, such as continuous Probability Density Functions (PDF), discrete Probability Mass Functions (PMF), and even data sets not characterized by a parametric probability distribution.
4. Statistics of the model output
Given a multi-dimensional polynomial expansion of the form (2) the statistics of the output such as mean, variance, skewness, or kurtosis can be evaluated directly in terms of the coefficients . For instance, the mean and variance of are given by the following simple expressions
| (4) |
Thus, in practice, the uncertainty quantification of an ODE system like (1) through the aPC expansion can be implemented as follows:
(i) Determine the set of nodes and weights using the Gaussian quadrature rule based on the statistical moments of the random inputs [34].
(ii) Substitute the nodes into the ODE system (1), which give deterministic ODE systems to be solved.
(iii) Solve each of the deterministic ODE systems using a numerical technique for the resolution of ODE systems, such as the Runge-Kutta method [40].
(iv) Compute the expansion coefficients using (3).
(v) Obtain the desired statistical properties such as mean and variance using (4).
4.1. Description of the numerical experiments
To study the effects of the uncertainty in the application of social distance actions and testing of susceptible individuals on the disease transmission, four different numerical simulations of the ODE system (1) have been carried out:
-
•
Experiment 1. Quantification of the effects of the uncertainty in the absence of non-pharmacological measures. This has been considered as the baseline experiment.
-
•
Experiment 2. Quantification of the effects of the uncertainty in testing individuals.
-
•
Experiment 3. Quantification of the effects of the uncertainty in the application of social distance actions.
-
•
Experiment 4. Quantification of the effects of different levels of vaccine efficacy.
In all the four experiments, a non-dimensionalized version of the system (1) has been considered, in which . Additionally, in the first three experiments, according to the reports [1], [2], [3], it has been assumed that two doses of vaccine are required to develop immunity and 95% vaccine efficacy with a daily vaccination rate of 0.0015, based on mass vaccination plans such as [41], [42], in which over 1 million vaccinations per week have been programmed. In the last experiment, under the same hypotheses as in Experiment 2, three different levels of vaccine efficacy, 50%, 75%, and 95%, have been considered.
In all these numerical experiments, the following initial conditions at time have been assumed:
The choice of these initial conditions has been based on the epidemiological situation reported by the Spanish Government at the end of the second transmission wave of COVID-19, in which it is pointed out that approximately 14.9% of immunized individuals and 0.1% of infected individuals have been detected in the population. Note that 4.9% of the immunized individuals are supposed to reach immunity through vaccination during the first stage of the Spanish vaccination plan in which 2.3 million individuals are assumed to be vaccinated during 12 weeks [41], [43].
4.2. Experiment 1. Quantification of the effects of the uncertainty in the absence of non-pharmacological measures
In the first experiment, the ODE system (1) has been solved assuming that the three non-pharmacological measures have been barely applied. In particular, according to [26], it has been hypothesized that the replication factor is a random variable centered at 3.5 and the rates of isolation and are random variables centered at 0.05. Since the replication factor takes nonnegative values, the random parameter has been modelled using a gamma distribution, whereas the random parameters and have been modelled using a beta distribution since isolation rates take values between 0 and 1. Thus, it has been supposed that follows a gamma distribution G(3500, 0.001) and and both follow a beta distribution B(10, 160), as shown in Fig. 2 . Then, an aPC expansion of order has been used to model these three random input parameters. The corresponding nodes are (3.3657, 3.4583, 3.5461, 3.6420) for parameter and (0.0321, 0.0552573, 0.0843, 0.1238) for parameters and as shown in Fig. 2.
Fig. 2.
Experiment 1: PDF of the random input parameters associated to the use of non-pharmacological containment or mitigation strategies.
The obtained solution is shown in Fig. 3 , in which the mean value of the variables that describe each compartment of the model have been represented together with a 95% confidence envelope, which have been calculated by means of the expansion coefficients using (4). As it can be seen in Fig. 3, this scenario corresponds to a huge outbreak of the infectious disease, with peaks of (0.95, 1.23)% of symptomatic infected individuals and (3.70, 5.05)% of asymptomatic infected individuals. This percentages would imply an overwhelmed healthcare system and a dramatic number of deaths during three months. Moreover, only (4.14, 4.90)% of the susceptible individuals would become immune through vaccination in this time period. Also, note the low dispersion in the results, which implies a high predictability of the model under these assumptions.
Fig. 3.
Experiment 1: mean values of the proportions of individuals in each compartment obtained in the solution together with the corresponding 95% confidence envelopes.
For the sake of comparison, the ODE system (1) has also been solved removing the vaccination term . The obtained results do not show significant differences neither in the mean values nor in the confidence envelopes of the compartment variables because of the low percentage of vaccinated population due to the uncontrolled outburst and the fast evolution of the disease.
4.3. Experiment 2. Quantification of the effects of the uncertainty in testing individuals
In the second experiment, the ODE system (1) has been solved assuming that the social distance actions have been barely applied and the number of daily tests allow both infected asymptomatic and symptomatic individuals to be identified and isolated. In particular, according to [26], it has been hypothesized that the replication factor is a random variable centered at 3.5 and the rates of isolation and are random variables centered at 0.95 and 0.5, respectively. Thus, it has been supposed that follows a gamma distribution G(3500, 0.001), follows a beta distribution B(160, 10), and follows a beta distribution B(160, 160), as shown in Fig. 4 . Again, an aPC expansion of order has been used to model these three random input parameters. The corresponding nodes are (3.3657, 3.4583, 3.5461, 3.6420) for parameter (0.8762, 0.9156, 0.9447, 0.9679) for parameter and (0.4353, 0.4794, 0.5206, 0.5647) for parameter as shown in Fig. 4.
Fig. 4.
Experiment 2: PDF of the random input parameters associated to the use of non-pharmacological containment or mitigation strategies.
The obtained solution is shown in Fig. 5 , in which the mean value of the variables that describe each compartment of the model have been represented together with a 95% confidence envelope. For the sake of comparison, the solution obtained removing the vaccination term from model (1) has also been included in light colors in Fig. 5.
Fig. 5.
Experiment 2: mean values of the proportions of individuals in each compartment obtained in the solution together with the corresponding 95% confidence envelopes.
Unlike Experiment 1, it can be seen that there are significant differences between the solutions obtained with and without the vaccination. For instance, in Table 1 , the 95% confidence intervals for the maximum percentages of individuals in the and compartments are given. They are the proportions of individuals in these compartments at the time instant corresponding to the maximum values of the respective curves. Note that, in the worst case, the percentage of symptomatic individuals in a single day would rise to which, although stressful, could be handled by a strong healthcare system. Moreover, in this solution, (15.79, 18.20)% of the susceptible individuals would become immune through vaccination in six months and the percentage of immunized individuals at the end of this time period would be . This percentage would be close but not reach 66.7%, which is the estimated threshold to reach herd immunity [44].
Table 1.
95% confidence intervals for the maximum percentages of individuals in the and compartments.
| Without vaccination | (1.25, 3.02)% | (0.03, 0.08)% | (0.19, 0.52)% | (1.11, 2.32)% |
| With vaccination | (0.59, 1.82)% | (0.01, 0.05)% | (0.08, 0.31)% | (0.50, 1.40)% |
4.4. Experiment 3. Quantification of the effects of the uncertainty in the application of social distance actions
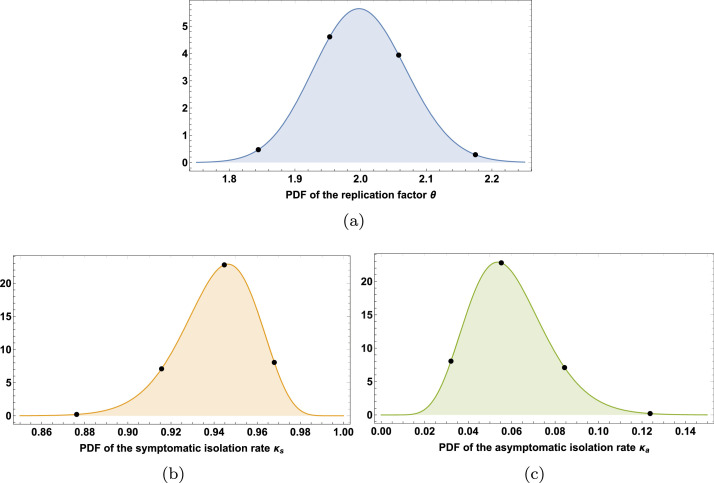
In the third experiment, the ODE system (1) has been solved assuming a moderate degree of social distance actions and supposing that the number of daily tests allow only the infected symptomatic individuals to be identified and isolated. In particular, according to [26], it has been hypothesized that the replication factor is a random variable centered at 2 and the rates of isolation and are random variables centered at 0.95 and 0.05, respectively. Thus, it has been assumed that follows a gamma distribution G(400, 0.005), follows a beta distribution B(160, 10), and follows a beta distribution B(10, 160), as shown in Fig. 6 . Once again, an aPC expansion of order has been used to model these three random input parameters. The corresponding nodes are (1.8442, 1.9529, 2.0580, 2.1749) for parameter (0.8762, 0.9156, 0.9447, 0.9679) for parameter and (0.0321, 0.0552573, 0.0843, 0.1238) for parameter as shown in Fig. 6.
Fig. 6.
Experiment 3: PDF of the random input parameters associated to the use of non-pharmacological containment or mitigation strategies.
The obtained solution is shown in Fig. 7 , in which the mean value of the variables that describe each compartment of the model have been represented together with a 95% confidence envelope. For the sake of comparison, the solution obtained removing the vaccination term from model (1) has also been included in light colors in Fig. 7.
Fig. 7.
Experiment 3: mean values of the proportions of individuals in each compartment obtained in the solution together with the corresponding 95% confidence envelopes.
As in Experiment 2, it can be seen that there are considerable differences between the solutions obtained with and without the vaccination. However, the dispersion of the envelopes for the compartment variables is larger when the uncertainty is due to de social distance measures, as shown in Fig. 8 , in which the proportion of individuals in compartments and obtained in the solutions of Experiment 2 and Experiment 3 are represented. In this figure, the curves corresponding to the effects of social distance measures are depicted in light color. Moreover, there is a significant difference in the evolution of the curve of asymptomatic individuals, in which the effects of testing and isolating asymptomatic individuals are apparent, which implies a greater control on the disease transmission.
Fig. 8.
Comparison between Experiment 2 and Experiment 3: mean values of the proportion of symptomatic and asymptomatic individuals together with the corresponding 95% confidence envelopes.
Note that, in the worst case, the percentage of symptomatic individuals in a single day for Experiment 3 would rise to . Besides, (15.69, 18.98)% of the susceptible individuals would become immune through vaccination during six months and the percentage of immunized individuals at the end of this time period would be which are similar estimates to the ones provided by the solution of Experiment 2.
4.5. Experiment 4. Quantification of the effects of different levels of vaccine efficacy
Since the variants of the SARS-CoV-2 virus could have a significant impact on the vaccine efficacy, in the forth experiment, under the same hypotheses as in Experiment 2, three solutions of the ODE system (1) have been computed using three different levels of vaccine efficacy. The mean value of the state variables that describe each compartment of the model obtained in these solutions have been represented in Fig. 9 together with a 95% confidence envelope. The curves for vaccine efficacy levels of 50%, 75%, and 95% are shown in red, blue, and green, respectively.
Fig. 9.
Experiment 4: mean values of the proportions of individuals in each compartment obtained in the solution together with the corresponding 95% confidence envelopes.
It can be seen in Fig. 9 that there are no significant differences neither in the mean values nor in the confidence envelopes of the compartment variables and whereas noticeable differences can be observed in the rest of the compartment variables. For instance, in the worst case, the percentage of symptomatic individuals in a single day would rise to 0.0658%, 0.0579%, and 0.0509%, for vaccine efficacy levels of 50%, 75%, and 95%, respectively. Thus, in Spain, the number of symptomatic individuals in a single day could increase by approximately 7000 individuals as the vaccine efficacy changes from 95% to 50%. Moreover, in these solutions (7.98, 9.38)%, (11.91, 13.87)%, and (15.79, 18.20)% of the susceptible individuals would become immune through vaccination in six months for vaccine efficacy levels 50%, 75%, and 95%, respectively.
5. Validation of the results
In order to validate the experimental results presented in the previous sections, the MC simulation method has been used [35]. More specifically, a comparison has been conducted between the solutions of the ODE system (1) computed using the aPC method with order and the MC method with several increasing samples sizes, .
In Fig. 10 , the mean values of the proportion of symptomatic individuals together with the corresponding 95% confidence envelopes in the solution of Experiment 2 are shown. The solution obtained using the aPC approach has been represented in green, whereas the solutions obtained using the MC simulations have been represented in red. It can be seen that, for both solutions are indistinguishable. Similar results have been obtained for the remaining variables and experiments. This demonstrates that, as expected [4], the PC expansion approach provides a method as accurate as the MC method at a lower computational cost.
Fig. 10.
Comparison between aPC (green) and MC (red): mean values of the proportion of symptomatic individuals together with the corresponding 95% confidence envelopes in the solution of Experiment 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
6. Distributions of the model output
The multi-dimensional polynomial expansion (2) provides a surrogate model, which can be used to estimate the PDF of the model output at a low computational cost. For instance, a data smoothing problem can be easily stated and a kernel density estimation approach [45] can be carried out, in which the data are derived from this surrogate model. Likewise, the Cumulative Density Function (CDF) of can be also estimated.
As a matter of example, consider variable shown in Fig. 11 , obtained by the solution of Experiment 2. It represents the proportion of symptomatic individuals provided by the solution of this experiment. The distributions, at time instants days, days, and days, of have been approximated using a Gaussian kernel estimator. The estimated PDF and CDF of these random variables are shown in Fig. 12 . They allow a wide variety of statistical analysis to be carried out. For instance, the probability that at time instant days, the percentage of symptomatic individuals exceeds of the population, which, in Spain, amounts to 23,500 individuals, is 0.0425 when the vaccination term is included in the model, whereas this same probability rise to 0.7012 if the vaccination term is omitted.
Fig. 11.
Slices at time instants days, days, and days of the curve of variable and the corresponding 95% confidence envelope in the solution of Experiment 2.
Fig. 12.
PDF and CDF of variable at time instants days (blue), days (orange), and days (green) in the solution of Experiment 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
In a similar way, multivariate analysis can be conducted. For instance, the estimated joint PDF and CDF of variable at time instants days and days are shown in Fig. 13 , while the correlation matrix for the distributions of symptomatic individuals at time instants days, days, and days, is
Note that there is a significant linear correlation among the three distributions despite their separation in time.
Fig. 13.
Joint PDF and CDF of variable obtained in the solution of Experiment 2 at time instants days and days.
7. Sensitivity analysis
The surrogate model provided by the multi-dimensional polynomial expansion (2) can be also used to carry out a global sensitivity analysis based on the variance of the model output at a low computational cost.
The objective of this analysis is to quantify of how much of the variance of an output variable of the model is due to the variance of each random input parameter, and relies on the computation of the so called Sobol’ indices, under the assumptions that the input random variables are independent and the output random variables are squared integrable [46], [47]. In particular, it is easy to see that the random parameters and are independent and the functions used to define the model (1) are squared integrable.
As in the case of the calculation of the statistics of the output based on the computation of its moments, Sobol’ indices can be derived from the coefficients of the aPC expansion (2). Following [48], the Sobol’ index for the th component of the input random variable can be obtained as
where is the variance computed in (4) and is the set of multi-indices such that the computation of only includes terms that depend on the random input variable that is,
In Fig. 14 , the Sobol’ indices of the variables of all the compartments obtained in the solution of Experiment 2 have been plotted as functions of time, where the indices calculated assuming that the ODE system (1) includes the vaccination strategy are represented with continuous lines and the indices calculated assuming that the system does not include the vaccination strategy are represented with dashed lines. The corresponding Sobol’ indices for the random parameters and are plotted in blue, orange, and green colors, respectively.
Fig. 14.
Sobol’ indices for Experiment 2 with (solid lines) and without (dashed lines) vaccination strategy, where the corresponding Sobol’ indices for the random parameters and are plotted in blue, orange, and green colors, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
It can be seen that, for the variables of all compartments, the uncertainty due to the variance of parameter is negligible, whereas, in general, between 60 and 80 percent of the variance is caused by the variance in the parameter . Besides, for variables and there are no significant differences between the Sobol’ indices computed from the models with and without vaccination. Moreover, for variables and the computed Sobol’ indices with and without vaccination show similar patterns. However, the fluctuations in the Sobol’ curves show a time delay of approximately 30–40 days when the vaccination term is included in the model.
A comparison of the Sobol’ indices computed for Experiment 2, in dashed lines, and Experiment 3, in solid lines, is presented in Fig. 15 , where the corresponding Sobol’ indices for the random parameters and are plotted in blue, orange, and green colors, respectively. Again, it can be seen that, for the variables of all compartments, the uncertainty due to the variance of parameter is negligible, whereas, in Experiment 2 the uncertainty caused by the parameter is between 20 and 60 percent higher than in Experiment 3. In particular, while in Experiment 3 the uncertainty in due to the magnitude of the variance of parameters and alternate along time, in Experiment 2 around 80% of the uncertainty is due to as it can be seen in Fig. 15d. Moreover, the relative magnitude of the uncertainties caused by the variance of parameters and on the variables and is reversed in experiments 2 and 3. For instance, as it can be seen in Fig. 15f, in Experiment 2, the uncertainties caused by the parameters and are around 30 and 70 percent, respectively, whereas these values turn into 60 and 40 percent in Experiment 3.
Fig. 15.
Sobol’ indices for Experiment 2 (dashed lines) and Experiment 3 (solid lines), where the corresponding Sobol’ indices for the random parameters and are plotted in blue, orange, and green colors, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
8. Conclusions
In this work, the uncertainty quantification and sensitivity analysis of a modified SEIR model of the SARS-CoV-2 virus transmission dynamics with mass vaccination strategy has been conducted. In particular, the effects of the uncertainty about the application of social distance actions and testing of susceptible individuals on the disease transmission have been studied by means of a spectral approach.
Assuming that two doses of vaccine are required to develop immunity and 95% vaccine efficacy, several numerical experiments have been conducted under different mitigation strategies. The statistical analysis of the numerical results show that, under the hypothesis of a mass vaccination program consisting of about 1 million vaccination per week during six months, (15, 18)% of the susceptible individuals would become immune through vaccination, and the percentage of immunized individuals at the end of this time period would be (46, 59)%, that is, the herd immunity threshold would not be reached yet. This scenario could be reached with the help of two strategies: testing of susceptible individuals or social distance actions. However, both strategies have some drawbacks. Indeed, to reach it through testing of susceptible individuals, it would be necessary a massive testing of the asymptomatic individuals, which would require the availability of COVID-19 antigen rapid, portable, tests and tracking apps. Similarly, the application of the required social distance actions to reach this scenario, would imply a large socio-economic impact.
There are significant differences between these two strategies. In general, the dispersion of the epidemic model outputs is larger when the application of social distance measures is assumed, which results in a less predictive epidemic model. Besides, testing and isolating asymptomatic individuals considerably reduces the peak in the curve of asymptomatic individuals, which implies a greater control on the disease transmission. There are also significant differences when several levels of vaccine efficacy are taken into account. Lower values of vaccine efficacy correspond to higher peaks of the curves of the exposed, symptomatic, asymptomatic, and isolated individuals.
The sensitivity analysis of the epidemic model shows that the uncertainty due to the variance related to the testing of the symptomatic individuals is negligible. Furthermore, this analysis shows that, when the application of social distance measures is assumed, the uncertainty due to the variance related to the testing of the symptomatic individuals and the application of social distance measures is almost the same, which results in a greater unpredictability about the evolution of the curve of asymptomatic individuals.
CRediT authorship contribution statement
Alberto Olivares: Conceptualization, Methodology, Software, Validation, Investigation, Formal analysis, Writing - original draft. Ernesto Staffetti: Investigation, Formal analysis, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.U. K. Medicines and Healthcare Products Regulatory Agency. Information for Healthcare Professionals on Pfizer/BioNTech COVID-19 vaccine. 2020. https://www.gov.uk/government/publications/regulatory-approval-of-pfizer-biontech-vaccine-for-covid-19/information-for-healthcare-professionals-on-pfizerbiontech-covid-19-vaccine.
- 2.U. S. Food and Drug Administration. Pfizer-Biontech COVID-19 Vaccine. Briefing Document. 2020. https://www.fda.gov/media/144246/download.
- 3.European Medicines Agency. COVID-19: latest updates. 2020. https://www.ema.europa.eu/en/human-regulatory/overview/public-health-threats/coronavirus-disease-covid-19/covid-19-latest-updates.
- 4.Xiu D. Princeton University Press; 2010. Numerical methods for stochastic computations. A spectral method approach. [Google Scholar]
- 5.Brauer F., Castillo-Chavez C., Feng Z. Vol. 69. Springer; 2019. Mathematical models in epidemiology. (Texts in Applied Mathematics). [Google Scholar]
- 6.Bernoulli D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir. Mem Math Phys Acad R Sci Paris. 1766:1–45. [Google Scholar]
- 7.Dietz K., Heesterbeek J.A.P. Daniel Bernoulli’s epidemiological model revisited. Math Biosci. 2002;180(1-2):1–21. doi: 10.1016/s0025-5564(02)00122-0. [DOI] [PubMed] [Google Scholar]
- 8.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A. 1927;115(772):700–721. [Google Scholar]
- 9.Brauer F., van den Driessche P., Wu J. Springer; 2008. Mathematical epidemiology. [Google Scholar]
- 10.Naresh R., Tripathi A., Tchuenchec J.M., Sharma D. Stability analysis of a time delayed SIR epidemic model with nonlinear incidence rate. Comput Math Appl. 2009;58(2):348–359. [Google Scholar]
- 11.Hattaf K., Al Lashari A., Louartassi Y., Yousfi N. A delayed SIR epidemic model with a general incidence rate. Electron J Qual Theory Differ Equ. 2013;3:1–9. [Google Scholar]
- 12.Chowell G., Fenimore P.W., Castillo-Garsow M.A., Castillo-Chavez C. SARS outbreaks in Ontario, Hong Kong and Singapore: the role of diagnosis and isolation as a control mechanism. J Theor Biol. 2003;224:1–8. doi: 10.1016/S0022-5193(03)00228-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kilpatrick A., Chmura A.A., Gibbons D.W., Fleischer R.C., Marra P.P., Daszak P. Predicting the global spread of H5N1 avian influenza. Proc Natl Acad Sci. 2006;103:19368–19373. doi: 10.1073/pnas.0609227103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Prosper O., Saucedo O., Thompson D., Castillo-Chavez C. Modeling control strategies for concurrent epidemics of seasonal and pandemic H1N1 influenza. Math Biosci Eng. 2011;8(1):141–170. doi: 10.3934/mbe.2011.8.141. [DOI] [PubMed] [Google Scholar]
- 15.Feng Z., Zheng Z., Hernandez-Ceron N., Glasser J.W., Hill A.N. Mathematical models of Ebola—Consequences of underlying assumptions. Math Biosci. 2016;277:89–107. doi: 10.1016/j.mbs.2016.04.002. [DOI] [PubMed] [Google Scholar]
- 16.Allen L.J.S. A primer on stochastic epidemic models: eormulation, numerical simulation, and analysis. Infect Dis Model. 2017;2(2):128–142. doi: 10.1016/j.idm.2017.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li C., Pei Y., Zhu M., Deng Y. Parameter estimation on a stochastic SIR model with media coverage. Discrete Dyn Nat Soc. 2018;2018:3187807. [Google Scholar]
- 18.Britton T., Pardoux E. Springer; 2019. Stochastic epidemic models with inference. [Google Scholar]
- 19.Eubank S., Eckstrand I., Lewis B., Venkatramanan S., Marathe M., Barrett C.L. Commentary on Ferguson, et al., “Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand”. Bull Math Biol. 2020;82(52):1–7. doi: 10.1007/s11538-020-00726-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Imperial College COVID-19 Response Team. Report 9: Impact of Non-Pharmaceutical Interventions (NPIS) to reduce COVID-19 mortality and healthcare demand. 2020. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf. [DOI] [PMC free article] [PubMed]
- 21.Cooper I., Mondal A., Antonopoulos C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals. 2020;139:110057. doi: 10.1016/j.chaos.2020.110057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ndaïrou F., Area I., Nieto J.J., Torres D.F. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals. 2020;135:109846. doi: 10.1016/j.chaos.2020.109846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bianconi G., Krapivsky P.L. Epidemics with containment measures. Phys Rev E. 2020;102:032305. doi: 10.1103/PhysRevE.102.032305. [DOI] [PubMed] [Google Scholar]
- 24.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Manchein C., Brugnago E.L., da Silva R.M., Mendes C.F.O., Beims M.W. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies. Chaos. 2020;30:041102. doi: 10.1063/5.0009454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brugnago E.L., da Silva R.M., Manchein C., Beims M.W. How relevant is the decision of containment measures against COVID-19 applied ahead of time? Chaos Solitons Fractals. 2020;140:110164. doi: 10.1016/j.chaos.2020.110164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med. 2020;26:855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bertozzi A.L., Franco E., Mohler G., Short M.B., Sledge D. The challenges of modeling and forecasting the spread of COVID-19. PNAS. 2020;117(29):16732–16738. doi: 10.1073/pnas.2006520117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nat Res. 2020;584:257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- 30.Schmith V.D., Zhou J., Lohmer L.R.L. The approved dose of ivermectin alone is not the ideal dose for the treatment of COVID-19. Clin Pharmacol Ther. 2020;108(4):762–765. doi: 10.1002/cpt.1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baker R.E., Yang W., Vecchi G.A., Metcalf C.J.E., Grenfell B.T. Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic. Science. 2020;369:315–319. doi: 10.1126/science.abc2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ghanem R., Higdon D., Owhadi H. Springer; 2017. Handbook of uncertainty quantification. [Google Scholar]
- 33.Xiu D., Karniadakis G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput. 2002;24(2):619–644. [Google Scholar]
- 34.Ahlfeld R., Belkouchi B., Montomoli F. SAMBA: sparse approximation of moment-based arbitrary polynomial chaos. J Comput Phys. 2016;320(529):1–16. [Google Scholar]
- 35.Rubinstein R.Y., Kroese D.P. Wiley; 2017. Simulation and the Monte Carlo method. [Google Scholar]
- 36.World Health Organization. Coronavirus disease (COVID-2019) situation reports. 2020. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/.
- 37.Li Q., et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Oladyshkin S., Nowak W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab Eng Syst Saf. 2012;106:179–190. [Google Scholar]
- 40.Griffiths D., Higham D.J. Springer; 2010. Numerical methods for ordinary differential equations. [Google Scholar]
- 41.Spanish Healthcare Ministry. Spanish Government COVID-19 Vaccination Plan. 2020a. https://www.mscbs.gob.es/en/profesionales/saludPublica/prevPromocion/vacunaciones/covid19/vacunasCovid19.htm.
- 42.British Medical Association. COVID-19 vaccination programme. 2020. https://www.bma.org.uk/advice-and-support/covid-19/gp-practices/covid-19-vaccination-programme.
- 43.Spanish Healthcare Ministry. ENE-Covid: Spanish Government Seroprevalence Study. 2020b. https://www.mscbs.gob.es/ciudadanos/ene-covid/home.htm.
- 44.Fontanet A., Cauchemez S. COVID-19 herd immunity: where are we? Nat Rev Immunol. 2020;20:583–584. doi: 10.1038/s41577-020-00451-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gramacki A. Springer; 2018. Nonparametric kernel density estimation and its computational aspects. [Google Scholar]
- 46.Sobol I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math Comput Simul. 2001;55(1-3):271–280. [Google Scholar]
- 47.Saltelli A., Ratto M., Andres T., Campolongo F., Cariboni J., Gatelli D., et al. John Wiley & Sons; 2008. Global sensitivity analysis. The primer. [Google Scholar]
- 48.Trucchia A., Egorova V., Pagnini G., Rochoux M. On the merits of sparse surrogates for global sensitivity analysis of multi-scale nonlinear problems: application to turbulence and fire-spotting model in wildland fire simulators. Commun Nonlinear Sci Numer Simul. 2019;73:120–145. [Google Scholar]