Prevention schemes for future pandemic cases: mathematical model and experience of interurban multi-agent COVID-19 epidemic prevention

Abstract

To enhance the effectiveness of epidemic prevention (EP) in urban sustainability transformation, joint prevention and control mechanism should be established to prevent and control the COVID-19 epidemic. The interurban multi-agent EP strategy, as a key component of this mechanism, includes the spontaneous EP model, the superior leading EP model, and the collaborative EP model. In this study, firstly, the theoretical mechanism of the interurban multi-agent EP strategy was analyzed. Then, we proposed a three-party differential game model including factors such as the risk coefficient for the virus infection and EP experience teaching. Finally, prevention strategies, prevention efficiency, and prevention losses were compared under the three models based on theoretical analysis and numerical analysis. The results of this study are as follows. COVID-19 EP should be guided by a model of central government (CG) leadership, interurban collaboration, and social participation. The CG and urban governments (UGs) should comprehensively carry out COVID-19 EP from various aspects, including EP experience teaching, mass EP comfort, the utilization rate of EP funds, and the ability to implement strategies. During the course of the COVID-19 EP, when the CG and UGs transition from spontaneous EP model to a higher-level EP model, the UG’s EP efforts will be enhanced. Under the collaborative EP model, the CG and UGs undergo the highest levels of EP effort. Compared with spontaneous EP model, the superior leading EP model can promote a Pareto improvement for all parties. From the perspective of total loss, the collaborative EP model is superior to the other two EP models. This study not only provides practical guidance for coordinating interurban relationships and enabling multi-agents to fully form joint forces, but also provides theoretical support for the establishment of an interurban joint EP mechanism under unified leadership.

Introduction

Since the first reported case of COVID-19 in December 2019, the COVID-19 virus and its prevention and control have received widespread attention in countries around the world [1]. The World Health Organization (WHO) designated COVID-19 as an “International Public Health Emergency” on 31 January 2020. The global risk from the transmission and impact of the COVID-19 outbreak was raised from “High” to “Very High” on 28 February 2020. On 11 March 2020, the WHO identified the COVID-19 outbreak as “Characteristically a Pandemic”. The COVID-19 outbreak has now been underway for eight months, which may seem like a short period of time, but it is a once-in-a-century health crisis [2]. On 31 July 2020, the WHO reported that the impact of the epidemic would be felt for decades to come, and it released COVID-19 outbreak Report No. 193. According to the report, as of 10:00 a.m. CEST on 31 October 2020, the number of confirmed cases of COVID-19 worldwide had increased by nearly 300,000 (292,527 new cases) from the previous day, and the number of confirmed cases globally had exceeded 17.1 million, reaching 17,106,007. Globally, 668,910 deaths had been reported, an increase of 6812 from the previous day. It has been shown that COVID-19 virus, a new highly pathogenic virus, has broken out and spread globally, bringing great damage and impact to human society. Globally, as of 3:17 p.m. CEST, 6 August 2020, 18,614,177 confirmed cases of COVID-19, including 702,642 deaths, had been reported to the WHO [3].

As the first country to be affected and hit by COVID-19, China has played an important role in the global fight against COVID-19. China’s strength, speed, wisdom, and confidence in the fight against COVID-19 have provided valuable experience for countries around the world to build mechanisms to deal with the epidemic [4]. China’s experience in fighting COVID-19 includes strategic decision-making, policy implementation and action, social mobilization, regional coordination, resource allocation, incentive mechanisms, and international cooperation [4, 5]. Their successful epidemic prevention (EP) practices show that it is impossible to bring the COVID-19 epidemic under control by only relying on individuals, civil organizations, and the urban government (UG) [6]. To comprehensively promote COVID-19 EP and control, leading institutions with a strategic vision, overall awareness, a rapid response, efficient decision-making, and centralized coordination are required to enhance strategic decision-making and coordination functions [7–9]. To make up for the shortage of anti-epidemic materials in key areas, the central government (CG) has fully allocated national resources to achieve the overall distribution of anti-epidemic materials nationwide. The CG has strengthened people’s determination and confidence to fight against the epidemic through the support of large-scale medical workers in many regions and the supply of medical resources as well as anti-epidemic materials [7]. The CG has also encouraged the division of labor and cooperation between different regions and between the epidemic and non-epidemic areas, thus fostering a spirit of regional cooperation [8]. In addition, the CG has established effective connections and complementary advantages between urban hospitals and national medical resources to form a large-scale and networked response [9].

As the main battlefield for sustainable human development in the future [10], urban areas only account for 3% of the Earth’s land area but contribute about 70% of the global economic aggregate. Since January 2020, the COVID-19 outbreak has put many cities under unprecedented public health pressure [11. In particular, urban areas such as Beijing, Shanghai, Shenzhen, and Guangzhou have faced greater levels of risk due to the large number of migrants and great mobility of the populations that reside there. COVID-19, as a major public health emergency, is unprecedented in terms of its speed of spread, scope of infection, and difficult prevention and control. It has therefore been a major test of the urban governance system and capacity [11, 12]. The dense populations, narrow spaces, and heavy traffic volumes in urban areas drive rapid economic development and provide an excellent infection chain for the human-to-human transmission of COVID-19 [11–13]. As urban transformation is accelerating, 70% of the world’s population will live in urban areas by 2050, requiring an additional 400 urban areas. Based on the characteristics of COVID-19 transmission, urban areas with high population densities may be at high risk of outbreaks [12, 14]. The main methods for COVID-19 EP and control are early detection, early reporting, early isolation, early diagnosis, and early treatment [15]. The precondition is having a rapid response and efficient operation by the urban area’s response institution and response mechanism, necessitating significant urban governance health emergency management department capacity [16]. However, most of the special urban safety plans that have been developed focus on earthquakes, fires, floods, geological disasters, and other disasters and rarely involve public health. It is imperative to improve the urban governance capacity for EP.

The concept of urban governance emphasizes two representative features: government as the center and comprehensive mobilizer of diverse participation of social organizations, markets, and the public [17]. Efficient decision-making and coordination are necessary for urban emergency management. In the face of COVID-19, on the one hand, urban areas must keep abreast of the spread of the epidemic and progress in prevention and control efforts while making timely and effective emergency decisions [¹¹,¹²]. On the other hand, social resources should be mobilized quickly to provide a solid foundation for the COVID-19 EP [18]. If coordination of the EP command system is not sound, social disorder can easily result, which may even have a negative impact on the management of COVID-19. In this context, resilience is a necessary condition for sustainable urban transformation. It is important to consider how urban areas will respond to epidemics [19] and what the emergency mechanisms to help urban areas get back to normal as soon as possible will be [20]. The UG should undergo a positive sustainable transformation to enhance the urban resilience of the public health emergency response [¹⁹]. However, at present, most urban areas only build an emergency management framework and lack effective coordination of the responsibility mechanism of various EP subjects. The urban area is a complex system with multiple levels and centers. Under the current level of EP, in some urban areas, the epidemic situation has escalated into a regional risk with significant negative impacts. In addition, urban areas lack public health systems that are deeply rooted at the grassroots level. Therefore, the effectiveness of the EP system should be strengthened to fully mobilize the enthusiasm of all kinds of EP subjects through the multi-agent coordinated EP method. Coordination among government, social organizations, enterprises, and other EP subjects is the key to achieving a sufficient COVID-19 EP in urban areas.

In the response to COVID-19, interurban relations are an important way to improve the effectiveness of sustainable prevention in urban areas [21]. The interurban relationships involved in the COVID-19 response include vertical relationships between the CG and UGs, and horizontal relationships among UGs. Poor interurban communication channels are prone to the island phenomenon, resulting in difficult information exchange, blockage, and closure [22]. The existence of information islands is not only a problem of the system but also a problem of with technology. As an important mechanism for COVID-19 EP and control, a strategy involving joint prevention and control can be used to respond to institutional and technical issues [23]. The mechanism emphasizes coordination and interaction and achieves organic interactions among multiple departments and urban areas to build a three-dimensional and standardized EP system [23]. Determining how to coordinate EP actions among EP subjects so that they can form joint forces for EP that work in a comprehensive, efficient, and orderly manner is the key to the prevention and control of public health emergencies.

At present, many scholars are devoting themselves to research on the prediction and prevention of the COVID-19 epidemic, and mathematical models and statistical methods have been widely used in research related to the COVID-19 epidemic. These models of infectious diseases based on mathematical models and statistical methods mainly study epidemic problems such as prediction of the number of infected people, simulation of the transmission process, the effectiveness of prevention and control measures, and factors related to susceptibility.

Many researchers have also used susceptible, exposed, infectious, recovered (SEIR)-type infectious disease dynamic models to analyze, predict, and control the spread of COVID-19. Wu et al. [24] considered the total traffic flow from Wuhan to major cities in China using the SEIR model and forecasted the domestic extent of the epidemic. Huang and Qi [25] adopted a comprehensive SEIR model to fit the obtained clinical progressive data of COVID-19 in Spain and studied the risk of easing the control measures. Using the improved SEIQR model, Liu et al. [26] divided the population into five subregions—susceptible, exposed, infected, isolated, and removed—and used a set of delayed integral equations to describe the system dynamics. He et al. [27] established the SEIR epidemic model of COVID-19 and used the particle swarm optimization algorithm to estimate the parameters of the COVID-19 EP system. Kwuimy et al. [28] used a nonlinear COVID-19 SEIR model and added government policy dynamics. They used a genetic algorithm technique and COVID-19 data from South Korea to reveal the conditions under which a pandemic would continue to occur. Mandal et al. [29] developed the SEQIR model in which isolation categories and government interventions were considered to mitigate disease transmission. Qun et al. [30] collected information on the demographic characteristics of pneumonia and estimated the time taken to double the strength of the epidemic and the number of births. Wan et al. [31] studied data from “Fengcheng” in Wuhan and predicted the peak number of infected people in Wuhan based on the SEIR modeling method. Joseph et al. [32] predicted the public health risk and drug prevention interventions related to COVID-19 both domestically and worldwide. Smirnova et al. [33] compared regularization algorithms and modified truncated singular value decomposition to determine the most effective stabilization strategy with finite data to be used for predictions. Ivanov et al. [34] studied two SEIR models, one described by ordinary differential equations and the other by a discrete model of a first-order difference equation, which predicted the peak day of the epidemic and the maximum number of infections. Yang et al. [35] used the improved SEIR model to derive a COVID-19 prevalence curve and used artificial intelligence methods to predict the spread of the epidemic. Guerrero-Nancuante et al. [36] analyzed the spread of COVID-19 in Hubei, Wuhan, Beijing, and Shanghai through the generalized SEIR model and determined the main prevention and control measures through a sensitivity analysis. In addition, the least-squares method, ant colony algorithm, and branching process model have been introduced into COVID-19 EP research models. Bentout et al. [37] used the least-squares method and the method of minimizing the sum of squares of residuals to fit the data and estimated the epidemiological parameters and the basic reproductive number. Yu et al. [38] proposed a compartment model based on the least-squares method to study the development of COVID-19 in India after relaxing control. Hellewell et al. [39] used the branching process model to analyze the effects of a simulation involving isolating patients and tracking close contacts. Furthermore, Kucharski et al. [40] proposed a stochastic transmission model combined with data and investigated the transmission of COVID-19 in Wuhan with new internationally exported cases. Shao et al. [41] made use of the time-delay convolution model and discrete convolution model of stochastic dynamics to fit the development trend of COVID-19 in Wuhan and Shanghai. Cui et al. [42] optimized a transmission dynamics model of emerging infectious diseases and applied it to predict the peak of COVID-19 transmission in Guangzhou and Wuhan. Zhang et al. [43] proposed a new stochastic dynamics model based on the transmission mechanism and prevention and control characteristics of COVID-19 and predicted the relevant timelines and characteristics of the development of overseas epidemics.

These studies have made important contributions to research on the COVID-19 EP in different aspects. However, there are still some shortcomings. On the one hand, in the above research, the epidemic situation of COVID-19 in an urban area or region has been taken as the research object, and the research goal has been to realize effective EP of COVID-19 in an urban area or region. On the other hand, the establishment and use of mathematical models have been based on past data, leading to a big difference between the predicted results and the actual situation. Moreover, in the process of model construction, the important model parameters have not been fully analyzed and discussed. The overall and systematic defense systems have not been fully integrated into urban or interurban pandemic preparedness systems. In addition, there have been some common defects in model construction, mainly including the following points: First of all, there is a basic assumption that the exposure probability of all kinds of people in these studies is exactly the same, meaning that the randomness of the transmission process between cities has not been considered. Second, the apparent infectivity of COVID-19 during incubation has not been fully considered.

To enhance the effectiveness of interurban EP, this study theoretically revealed the mechanism of the interurban multi-agent EP strategy and proposed a three-party differential game led by government and non-governmental organizations. In terms of prevention schemes for future pandemic cases, three COVID-19 EP models were studied to reveal an appropriate interurban multi-agent EP mechanism. Finally, COVID-19 EP strategies, EP efficiency, and EP losses under the three models were compared. The study not only provides practical guidance for coordinating interurban relations and enabling multi-agents to fully form joint forces for epidemic control, it also provides theoretical support for the establishment of a joint interurban prevention and control mechanism under unified leadership.

The research structure of this paper is as follows: Sect. 2 describes and constructs the theoretical mechanism and game model for the interurban multi-agent EP strategy. The spontaneous EP model, the superior leading EP model, and the collaborative EP model are displayed in Sects. 3, 4, and 5, respectively. In Sect. 6, the effectiveness of the three EP models is further studied based on theoretical analysis and numerical analysis. The conclusions and implications are presented in Sect. 7.

Theoretical mechanism and game model

The theoretical mechanism behind the interurban multi-agent EP strategy

Urban governance is increasingly becoming concerned with multi-agent participation across borders [44]. In the context of COVID-19, EP involves different urban areas and departments within the government system as well as other organizations outside the government system. The urban COVID-19 EP requires the pooling and mobilization of multiple national and social forces. A cooperative, coupled, and stable EP mechanism involving mutual assistance is formed among the subjects by means of an ownership relationship, contract, or agreement [45]. According to the different scope of the EP process, the EP unit includes the EP leader and the EP participant [46]. The government is the main commander and decision maker for the EP and maintains overall social order using public power to the safeguard EP. Enterprises, care organization, charities, volunteers, media, and other subjects are participants in EP [⁴⁶]. COVID-19 poses a general threat to many urban areas. The COVID-19 EP requires communication and cooperation between different urban areas horizontally and coordination of government organizations at different levels vertically. The process involves cooperation in social and public security, ecological environment, finance, real economy, and other fields.

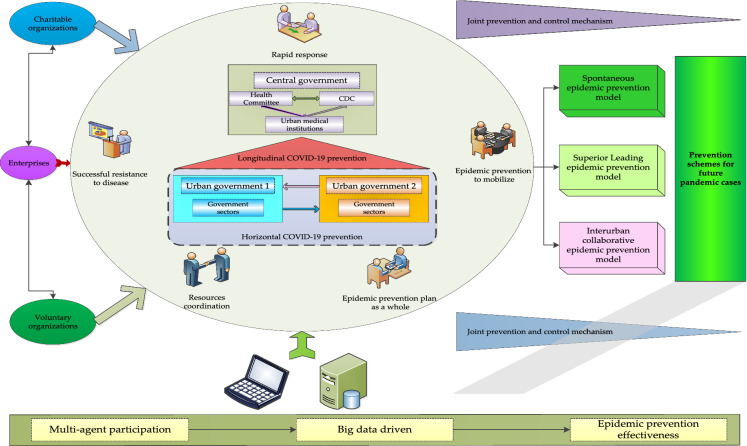
Under COVID-19, social mobilization has broken boundaries between urban areas, between individuals and organizations, between local and central areas, and between governmental and non-governmental organizations, achieving collaborative interactions between multi-agent actors [²³]. The development of social mobilization has mainly manifested in the systematic operation and effective combination of multiple subjects [47]. At the same time, multi-level and multi-dimensional coordination among the main subjects has prevented the spread of the epidemic to the greatest extent and reduced the infection rate. The urban COVID-19 EP is divided into prevention decisions and prevention losses. In terms of EP decisions, the urban EP can quickly respond to EP needs, doubling the efficiency of EP. Coordination among stakeholders is essential to minimize the extent of epidemic losses. Based on the above analysis, the theoretical mechanism behind the interurban multi-agent EP strategy is shown in Fig. 1.

Fig. 1.

Theoretical mechanism behind the interurban multi-agent EP strategy

As shown in Fig. 1, interurban EP involves a process of responding to public health emergencies, such as COVID-19, through both vertical and horizontal coordination between governments.

Vertical relationships

Public health events such as COVID-19 occur in urban areas and are characterized by multiple levels, from local to national. In the prevention and control of COVID-19, it is necessary to coordinate relationships between the CG and UGs[23]. The CG is authoritative and plays a leading role in COVID-19 EP and control. The UGs obey the commands and leadership of the CG and accept the supervision of the CG [48]. When COVID-19 expands beyond the capacity of urban areas to respond, active involvement of superiors to provide necessary support and even direct commands is necessary. However, interventions by superiors will further widen the distance between EP decision points and the COVID-19 epidemic, and the asymmetry in the transmission of epidemic information will easily lead to errors in EP decision-making. This is also a disadvantage of using vertical relationships to deal with the COVID-19 epidemic.

The relationship between the CG and UGs is mainly reflected in the transmission of epidemic information, EP financial support, and the placement of patients [49]. The CG should subsidize resources for urban areas appropriately to promote active responses by UGs to the EP. The interaction between the CG and UGs in response to COVID-19 EP is an extension of the government-to-government relationship. The key to an interactive relationship is determining how to transform the disordered non-cooperative game into a relatively ordered cooperative game [50]. When implementing specific anti-epidemic measures, the CG usually pays attention to the overall and long-term interests, while the UGs pay attention to local and current interests. Governments at all levels are inclined to choose COVID-19 EP behaviors requiring a low level of investment to maximize their own interests.

Horizontal relationships

In COVID-19 EP, horizontal relationships are those between municipal governments at the same level. Horizontal coordination between UGs is important to relieve pressure and maintain the stability of the vertical structure [51]. Cross-sectional relationships are mainly influenced by the sudden and stubborn nature of COVID-19, the self-interest and dependence of lower governments, and the great pressure of higher governments. COVID-19 EP and control enables geographically dispersed departments to work together to respond to COVID-19 through organizational communication and disciplinary incentives.

During the course of COVID-19 EP, the UG is the direct provider of urban public EP resources. Departmentalism leads some urban areas pursuing local interests even at the expense of overall interests. Due to the high infectivity rate of the COVID-19 virus, its adverse effects tend to spread to neighboring urban areas, and the active governance of UGs will also have spillover effects for neighboring urban areas. UGs may also adopt free-rider strategies to maximize local interests. During the course of COVID-19 EP, an interurban EP system needs to be built in a coordinated manner to promote sound communication between governments at the same level and optimize resource allocation [52].

Multi-agent collaboration

Multi-agent collaboration is a big data-driven, multi-agent system to provide an early warning and anti-epidemic COVID-19 response [23, 47].

First, the design and coupling of multi-agent collaborative EP policies between UG departments is necessary. Subsequently, the UG and enterprise groups coordinate and integrate EP resources to guarantee the provision of EP services. Finally, media, residents, and other subjects participate in EP, and all subjects form a consensus on the value of EP. Having a rapid response, mobilization of the EP, the EP plan as a whole, resource coordination, and successful resistance to disease are important parts of the process of multi-agent collaboration EP. The purpose of multi-agent collaboration is to achieve symbiotic value through multi-agent capacity building for EP and to gradually achieve the goal of large-scale participation in the COVID-19 EP. In terms of resource allocation activities, enterprises demonstrate efficient advantages through economic mechanisms such as price and competition and can quickly realize optimal allocation of human resources, financial resources, materials, and information related to the fight against the epidemic and disaster relief [53]. For example, Jiuzhou Tong Pharmaceutical Group Co., Ltd. made full use of its mature level of experience in medical circulation operation and quickly achieved efficient allocation of donated materials. Social organizations and communities are important external stakeholders in the operation of enterprises. These non-governmental organizations can facilitate smooth operation of the governance mechanism by filling the EP space between the government and enterprises [54]. For example, during the construction of Huoshenshan hospital, the smooth docking and participation of social forces, including the community, charity organizations, and volunteer groups, achieved a self-consistent and inclusive the EP management system.

Game model of the interurban multi-agent EP strategy

COVID-19 EP requires multi-agent collaboration including both horizontal and vertical relationships. In this study, vertical relationships are simplified as relationships between the CG and UGs, and horizontal relationships are simplified as relationships between two UGs. The interurban multi-agent EP system is simplified as a system consisting of two UGs and a CG. The UGs and the CG are low-level and high-level anti-epidemic agencies, respectively. During the course of COVID-19 EP, vertical EP units go from UGs to the CG, and horizontal EP units go from a single urban area to multiple urban areas. On this basis, multi-agent cooperation can achieve interurban multi-agent interactions for EP.

To enhance the effectiveness of the interurban multi-agent EP strategy, interurban multi-agent EP game models were constructed. In these models, the COVID-19 multi-agent EP system consists of the CG $G$, the UG $X$_, and another UG $Y$. In the event of a COVID-19 outbreak, UGs with high medical standards and complete EP systems can quickly and promptly formulate and implement scientific, effective EP strategies to minimize the losses caused by COVID-19[23]. The efforts of UG $X$ and UG $Y$ to respond to COVID-19 are represented by $E_X\left(t\right)$ and $E_Y\left(t\right)$. The CG’s efforts to address COVID-19 are represented by $E_{\mathit{XG}}\left(t\right)$ and $E_{\mathit{YG}}\left(t\right)$. The input costs of the CG $G$, UG $X$ and UG $Y$ for multi-agent coordination, financial subsidies, and the procurement of EP materials for COVID-19 EP are represented by $C_G\left(t\right)$, $C_X\left(t\right)$, and $C_Y\left(t\right)$, respectively. The investment in COVID-19 EP is proportional to the efforts of all parties. As the effort increases, the cost of further EP will also increase. ${\mu }_G$, ${\mu }_X$, and ${\mu }_Y$ represent cost factors for COVID-19 EP for the CG and UGs, respectively. The cost of COVID-19 EP can be expressed as follows:

$$\left\{\begin{array}{c}{C}_G\left(t\right)=\frac{{\mu }_G}{2}\left[E_{\mathit{XG}}^2\left(t\right)+E_{\mathit{YG}}^2\left(t\right)\right]\\ C_X\left(t\right)=\frac{{\mu }_X}{2}{E}_X^2\left(t\right)\\ C_Y\left(t\right)=\frac{{\mu }_Y}{2}{E}_Y^2\left(t\right)\\ \end{array}\right)$$ 1

$P_X\left(t\right)$ and $P_Y\left(t\right)$ represent the effectiveness of COVID-19 EP for UG $X$ and UG $Y$ at time $t$. The effectiveness of EP for UG comes from the joint efforts of the CG and the UGs. With the continuous implementation of joint prevention and control, the risk of COVID-19 infection gradually decreases [55]. The COVID-19 risk factor ${\kappa }_i$ is closely related to the effectiveness of EP. The COVID-19 EP effectiveness shows a natural attenuation to a degree of ${\iota }_i$. Due to the transboundary nature of COVID-19 and the externality of urban EP, the improvement in EP effectiveness has a certain spillover effect. Assuming that UG $X$ has a higher level of EP medical treatment than UG $Y$, $\phi$ represents the influence coefficient for the UGs’ EP medical levels. The stochastic differential equation for the COVID-19 EP effectiveness of UG $X$ and UG $Y$ can be expressed over time as follows:

$$\left\{\begin{array}{c}\frac{\text{d}{P}_X\left(t\right)}{\text{d}t}={\alpha }_X{E}_{\mathit{XG}}\left(t\right)+{\beta }_X{E}_X\left(t\right)-{\kappa }_X{P}_X\left(t\right)-{\iota }_X{P}_X\left(t\right)\\ \frac{\text{d}{P}_Y\left(t\right)}{\text{d}t}=\phi \frac{\text{d}{P}_X\left(t\right)}{\text{d}t}+{\alpha }_Y{E}_{\mathit{YG}}\left(t\right)+{\beta }_Y{E}_Y\left(t\right)-{\kappa }_Y{P}_Y\left(t\right)-{\iota }_Y{P}_Y\left(t\right)\\ \end{array}\right)$$ 2

where ${\alpha }_i$ and ${\beta }_i$ represent the extent of the effect of the efforts of the CG and the UGs on the effectiveness of COVID-19 EP, respectively.

$L_G\left(t\right)$, $L_X\left(t\right)$, and $L_Y\left(t\right)$ represent the loss caused by COVID-19 at time $t$ for the CG, UG $X$_, and UG $Y$, respectively. During the course of COVID-19 EP, both the CG and UGs will make efforts to prevent COVID-19 [56]. In addition, urban enterprises, care organizations, charities, volunteers, media, and other entities play indispensable roles in COVID-19 EP [57]. Assuming that ${\eta }_i$ is the coefficient of the effect of non-governmental organizations on urban losses, it should be emphasized that UG $X$’s EP experience will be taught to UG $Y$ EP centers through artificial intelligence, 5G, and other information integration technologies during the EP process [58]. Experience in EP is a powerful tool for the rapid and effective treatment of COVID-19. $\psi$ is the impact coefficient of EP experience teaching on the loss of UG $Y$. Therefore, at time $t$, the losses of UG $X$ and UG $Y$ caused by COVID-19 can be expressed as follows:

$$\left\{\begin{array}{c}{L}_X\left(t\right)=M_X\left(t\right)-{\tau }_X{E}_{\mathit{XG}}\left(t\right)-{\upsilon }_X{E}_X\left(t\right)-{\eta }_X{E}_X\left(t\right)-{\zeta }_X{R}_X\left(t\right)\\ L_Y\left(t\right)=M_Y\left(t\right)-{\tau }_Y{E}_{\mathit{YG}}\left(t\right)-{\upsilon }_Y{E}_Y\left(t\right)-{\eta }_Y{E}_Y\left(t\right)-\psi E_Y\left(t\right)-{\zeta }_Y{R}_Y\left(t\right)\\ \end{array}\right)$$ 3

where $M_X$ and $M_Y$ represent the maximum loss degree of UG $X$ and UG $Y$, respectively. ${\tau }_i$ and ${\upsilon }_i$ represent the extent to which the CG’s and UGs’ efforts have contributed to a reduction in COVID-19 cases. ${\zeta }_i$ is the effect of EP on the loss caused by COVID-19.

Compared with open-loop control, feedback control, which is widely applied in the analysis of game models, performs better in terms of control [59].

The spontaneous EP model of the interurban multi-agent strategy

The spontaneous EP model of the interurban multi-agent strategy is based on the natural division of labor, and the information sharing of interurban COVID-19 EP is very limited. Although there is a certain amount of information exchange between urban areas with gradual strengthening of the power of UGs, negative cooperation and interactions between inter-UGs are common [60].UG $X$ and UG $Y$ spontaneously carry out COVID-19 EP and control, and the three parties play a non-cooperative game. With the goal of minimizing their own losses caused by COVID-19, all parties choose the best level of effort to carry out multi-agent joint prevention and control.

Under the current system, the losses caused by COVID-19 are shared between the CG and UGs. The loss that the CG bears is ${\omega }_i\left(0\le {\omega }_i\le 1\right)$, and the loss that each UG bears is $1-{\omega }_i$. All three have the same positive discount rate $r$. $T_G\left(t\right)$, $T_X\left(t\right)$_, and $T_Y\left(t\right)$ represent the losses of the three subjects caused by COVID-19 over time $0-t$, respectively.

The EP objective functions of UG $X$_, UG $Y$_, and CG $G$ can be expressed as follows:

$$\left\{\begin{array}{c}{T}_X={\int }_0^{\infty }{e}^{-rt}\left\{(1-{\omega }_X)L_X\left(t\right)+C_X\left(t\right)\right\}\text{d}t\\ T_Y={\int }_0^{\infty }{e}^{-rt}\left\{(1-{\omega }_Y)L_Y\left(t\right)+C_Y\left(t\right)\right\}\text{d}t\\ T_G={\int }_0^{\infty }{e}^{-rt}\left\{{\omega }_X{L}_X\left(t\right)+{\omega }_Y{L}_Y\left(t\right)+C_G\left(t\right)\right\}\text{d}t\\ \end{array}\right).$$ 4

The control variables for the model include $E_{\mathit{XG}}\left(t\right)$, $E_{\mathit{YG}}\left(t\right)$, $E_X\left(t\right)$, and $E_Y\left(t\right)$, and the state variables include $P_X\left(t\right)$ and $P_Y\left(t\right)$.

Prevention strategies for the spontaneous EP model

Each EP subject conducts its own COVID-19 EP for an unlimited period of time. The prevention strategy for the spontaneous EP model is static feedback equilibrium.

Proposition 1

Under the non-cooperative game between the CG, UG $X$_, and UG $Y$, the spontaneous EP model COVID-19 EP strategies can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X^{\ast }=\frac{1-{\omega }_X}{{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)\\ E_Y^{\ast }=\frac{1-{\omega }_Y}{{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\\ \end{array}\right)$$ 5

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}^{\ast }=\frac{{\omega }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{{\mu }_G\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ E_{\mathit{YG}}^{\ast }=\frac{{\omega }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\\ \end{array}\right).$$ 6

Proof

To obtain the EP strategy for the non-cooperative game, namely, the Markov refined Nash equilibrium, assume that the loss function $V_i\left(P_X,P_Y\right)$ caused by COVID-19 is a continuously bounded differential function. This function satisfies the Hamilton–Jacobi–Bellman (HJB) equation. The loss function can be expressed as follows:

$$r·V_X\left(P_X,P_Y\right)=\underset{E_X\ge 0}{min}\left\{\begin{array}{c}\left(1-{\omega }_X\right)\left(M_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X\right)+\frac{{\mu }_X}{2}{E}_X^2\\ -\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)-\\ \frac{\partial V_X}{\partial P_Y}\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\upsilon }_Y+{\eta }_Y\right)P_Y\right)\\ \end{array}\right\}$$ 7

$$r·V_Y\left(P_X,P_Y\right)=\underset{E_Y\ge 0}{min}\left\{\begin{array}{c}\left(1-{\omega }_Y\right)\left(M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y\right)+\frac{{\mu }_Y}{2}{E}_Y^2\\ -\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\kappa }_Y+{\iota }_Y\right)P_Y\right)\\ -\frac{\partial V_Y}{\partial P_X}\left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)\\ \end{array}\right\}$$ 8

$$r·V_G\left(P_X,P_Y\right)=\underset{E_{\mathit{XG}}\ge 0,E_{\mathit{YG}}\ge 0}{min}\left\{\begin{array}{c}{\omega }_X\left(M_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X\right)+\\ {\omega }_Y\left(M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y\right)+\\ \frac{{\mu }_X}{2}{E}_X^2+\frac{{\mu }_Y}{2}{E}_Y^2-\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\\ \left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)-\\ \frac{\partial V_G}{\partial P_Y}\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\kappa }_Y+{\iota }_Y\right)P_Y\right)\\ \end{array}\right\}.$$ 9

$\square$

The first partial derivatives with respect to $E_X$ and $E_Y$ at the right end of Eqs. (7) and 8) are obtained, respectively. The first partial derivative of $E_{\mathit{XG}}$ and $E_{\mathit{YG}}$ is taken with respect to Eq. (9) and set equal to zero. The results can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X=\frac{\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\eta \frac{\partial V_X}{\partial P_Y}\right)}{{\mu }_X}\\ E_Y=\frac{\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}}{{\mu }_Y}\\ \end{array}\right)$$ 10

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}=\frac{{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\eta \frac{\partial V_G}{\partial P_Y}\right)}{{\mu }_G}\\ E_{\mathit{YG}}=\frac{{\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}}{{\mu }_Y}\\ \end{array}\right).$$ 11

Equations (10) and (11) are substituted into Eqs. (7)–(9), and the results can be expressed as follows:

$$\begin{array}{cc}\hfill r·V_X& =\left[\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)-\left(1-{\omega }_X\right){\zeta }_X\right]P_X+\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_X}{\partial P_Y}{P}_Y\hfill \\ \hfill & -\frac{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]\left[\left(1-{\omega }_X\right){\tau }_X+{\alpha }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]-{\alpha }_Y\frac{\partial V_X}{\partial P_Y}\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)}{{\mu }_G}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]}^2}{2{\mu }_X}\hfill \\ \hfill & -\frac{{\beta }_Y\frac{\partial V_X}{\partial P_Y}\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]}{2{\mu }_Y}+\left(1-{\omega }_X\right)M_X\hfill \\ \hfill \end{array}$$ 12

$$\begin{array}{cc}\hfill r·V_Y& =\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_Y}{\partial P_Y}-\left(1-{\omega }_Y\right){\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)\left[\left(1-{\omega }_Y\right){\tau }_Y+{\alpha }_Y\frac{\partial V_Y}{\partial P_Y}\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\alpha }_X\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\beta }_X\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]}{2{\mu }_X}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]}^2}{2{\mu }_Y}+\left(1-{\omega }_Y\right)M_Y\hfill \\ \hfill \end{array}$$ 13

$$\begin{array}{cc}\hfill r·V_G& =\left[\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)-{\omega }_X{\zeta }_X\right]P_X+\left(\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_G}{\partial P_Y}-{\omega }_Y{\zeta }_Y\right)P_Y\hfill \\ \hfill & -\frac{{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}^2-{\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}{{\mu }_X}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]\left({\omega }_Y\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_G}{\partial P_Y}\right)}{{\mu }_Y}+{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 14

As shown by Eqs. (12)–(14), the linear optimal function of $P_X$ and $P_Y$ is the solution to the HJB equation. The results can be expressed as follows:

$$\left\{\begin{array}{c}{V}_X\left(P_X,P_Y\right)=p_X{P}_X+q_X{P}_Y+u_X\\ V_Y\left(P_X,P_Y\right)=p_Y{P}_X+q_Y{P}_Y+u_Y\\ V_G\left(P_X,P_Y\right)=p_G{P}_X+q_G{P}_Y+u_G\\ \end{array}\right)$$ 15

where $p_i$ and $q_i$ are constants.

The derivative of Eq. (15) is substituted into Eqs. (12)–(14), and the result can be expressed as follows:

$$\begin{array}{cc}\hfill r\left(p_X{P}_X+q_X{P}_Y+u_X\right)& =\left[\left({\kappa }_X+{\iota }_X\right)\left(p_X+\phi q_X\right)-\left(1-{\omega }_X\right){\zeta }_X\right]P_X+\left({\kappa }_Y+{\iota }_Y\right)q_X{P}_Y\hfill \\ \hfill & -\frac{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]\left[\left(1-{\omega }_X\right){\tau }_X+{\alpha }_X\left(p_X+\phi q_X\right)\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\alpha }_Y{q}_X\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)}{{\mu }_G}-\frac{{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_X+\phi q_X\right)\right]}^2}{2{\mu }_X}\hfill \\ \hfill & -\frac{{\beta }_Y{q}_X\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_Y\right]}{2{\mu }_Y}+\left(1-{\omega }_X\right)M_X\hfill \\ \hfill \end{array}$$ 16

$$\begin{array}{cc}\hfill r\left(p_Y{P}_X+q_Y{P}_Y+u_Y\right)& =\left({\kappa }_X+{\iota }_X\right)\left(p_Y+\phi q_Y\right)P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)q_Y-\left(1-{\omega }_Y\right){\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)\left[\left(1-{\omega }_Y\right){\tau }_Y+{\alpha }_Y{q}_Y\right]}{{\mu }_G}-\frac{{\alpha }_Y\left(p_Y+\phi q_Y\right)\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\beta }_X\left(p_Y+\phi q_Y\right)\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_X+\phi q_X\right)\right]}{2{\mu }_X}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_Y\right]}^2}{2{\mu }_Y}+\left(1-{\omega }_Y\right)M_Y\hfill \\ \hfill \end{array}$$ 17

$$\begin{array}{cc}\hfill r\left(p_G{P}_X+q_G{P}_Y+u_G\right)& =\left[\left({\kappa }_X+{\iota }_X\right)\left(p_G+\phi q_G\right)-{\omega }_X{\zeta }_X\right]P_X+\left(\left({\kappa }_Y+{\iota }_Y\right)q_G-{\omega }_Y{\zeta }_Y\right)P_Y\hfill \\ \hfill & -\frac{{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]}^2-{\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_X+\phi q_X\right)\right]\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_G+\phi q_G\right)\right]}{{\mu }_X}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_Y\right]\left({\omega }_Y\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_G\right)}{{\mu }_Y}\hfill \\ \hfill & +{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 18

If Eqs. (16)–(18) satisfy $P_X\ge 0$ and $P_Y\ge 0$, the result can be expressed as follows:

$$\left\{\begin{array}{c}{p}_X=-\frac{\left(1-{\omega }_X\right){\zeta }_X}{r+{\kappa }_X+{\iota }_X}\\ p_X=0\\ u_X=-\frac{\left(1-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\\ -\frac{{\left(1-{\omega }_X\right)}^2{\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}^2}{2{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}+\frac{\left(1-{\omega }_X\right)M_X}{r}\\ \end{array}\right)$$ 19

$$\left\{\begin{array}{c}{p}_Y=\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ q_Y=-\frac{\left(1-{\omega }_Y\right){\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\\ u_Y=-\frac{\phi {\alpha }_X\left(1-{\omega }_Y\right){\zeta }_Y\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_G{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\\ -\frac{\phi {\beta }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ -\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}+\frac{\left(1-{\omega }_Y\right)M_Y}{r}\\ \end{array}\right)$$ 20

$$\left\{\begin{array}{cc}\hfill p_G& =\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\hfill \\ \hfill q_G& =-\frac{{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\hfill \\ \hfill u_G& =-\frac{{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}^2}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\omega }_Y^2{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}+\frac{{\omega }_X{M}_X+{\omega }_Y{M}_Y}{r}\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]\left\{{\omega }_X\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}\right)$$ 21

Loss of the spontaneous EP model

Equations (19)–(21) are substituted into Eq. (15). The loss functions caused by the minimum COVID-19 responses of UG $X$ and UG $Y$ and the CG can be expressed as follows:

$$\begin{array}{cc}\hfill V_X^{\ast }& =\frac{\left(1-{\omega }_X\right)M_X}{r}-\frac{\left(1-{\omega }_X\right){\zeta }_X}{r+{\kappa }_X+{\iota }_X}{P}_X-\frac{{\left(1-{\omega }_X\right)}^2{\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill \end{array}$$ 22

$$\begin{array}{cc}\hfill V_Y^{\ast }& =\frac{\left(1-{\omega }_Y\right)M_Y}{r}+\frac{\phi {\gamma }_X\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}{P}_X-\frac{\left(1-{\omega }_Y\right){\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\phi {\alpha }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{{\mu }_G{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\phi {\beta }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 23

$$\begin{array}{cc}\hfill V_G^{\ast }& =\frac{{\omega }_X{M}_X+{\omega }_Y{M}_Y}{r}+\left[\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right]P_X-\frac{{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\omega }_Y^2{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]\left\{{\omega }_X\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\gamma }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{{\mu }_{Y}r{\left(r+{\gamma }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 24

Based on the above analysis, the total loss caused by COVID-19 can be expressed as follows:

$$\begin{array}{cc}\hfill V^{\ast }\left(P_X,P_Y\right)& =V_X^{\ast }+V_Y^{\ast }+V_G^{\ast }\hfill \\ \hfill & =\frac{M_X+M_Y}{r}+\left[\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right]P_X-\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}\left\{\left(2-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\omega }_Y\left(2-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]\left\{\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{2{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 25

Effectiveness of the spontaneous EP model

Equations (22)–(24) are substituted into Eq. (15) after obtaining the partial derivative. It is easy to obtain Eqs. (5) and (6). Under the Nash non-cooperative equilibrium, the effectiveness of COVID-19 EP for UG $X$ can be expressed as follows:

$$\left\{\begin{array}{c}{P}_X^{\ast }\left(t\right)=\frac{1}{{\kappa }_X+{\iota }_X}\left[\frac{{\omega }_X{\alpha }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\left(1-{\omega }_X\right){\beta }_X}{{\mu }_G}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_Y+{\iota }_Y}\right)-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\right]\\ P_X^{\ast }\left(0\right)=P_X\\ \end{array}\right\}$$ 26

The effectiveness of COVID-19 EP for UG $Y$ can be expressed as follows:

$$\left\{\begin{array}{c}{P}_Y^{\ast }\left(t\right)=\frac{\phi }{{\kappa }_Y+{\iota }_Y}\left[\frac{{\omega }_X{\alpha }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\left(1-{\omega }_X\right){\beta }_X}{{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\right]\\ +\frac{1}{{\kappa }_Y+{\iota }_Y}\left[\frac{{\omega }_Y{\alpha }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)+\frac{\left(1-{\omega }_Y\right){\beta }_Y}{{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)-e^{-\left({\kappa }_Y+{\iota }_Y\right)t+H_Y}\right]\\ P_Y^{\ast }\left(0\right)=P_Y\\ e^{H_X}=\frac{{\omega }_X{\alpha }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\left(1-{\omega }_X\right){\beta }_X}{{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)-\left({\kappa }_X+{\iota }_X\right)P_X\\ \end{array}\right\}$$ 27

where $H_X$ and $H_Y$ are arbitrary constants.

Analysis of the spontaneous EP model

Equations (5) indicate that under the spontaneous EP model of the interurban multi-agent strategy, the level of each UG’s COVID-19 EP efforts is negatively correlated with the risk coefficient for viral infection, the EP cost coefficient, the attenuation coefficient of the EP effect, the discount rate, and the loss sharing ratio. The level of EP effort by each UG is positively correlated with the coefficient of non-governmental organizations, the coefficient of EP experience transfer, the coefficient of impact of UG efforts on loss, and the coefficient of impact of EP effectiveness on a reduction in COVID-19 cases.

According to Eq. (6), in the spontaneous EP model, the efforts of the CG to prevent COVID-19 spread are negatively correlated with the EP cost coefficient, the risk coefficient of viral infection, the attenuation coefficient of the EP effect, and the discount rate. The level of the CG’s EP effort is positively correlated with the proportion of losses caused by COVID-19, the impact coefficient of the CG’s efforts on the losses caused by COVID-19, and the effectiveness of EP.

The above results indicate that the CG and UGs should comprehensively respond to COVID-19 EP and control from various aspects, such as COVID-19 EP effectiveness, EP experience teaching, mass EP comfort, the EP fund utilization rate, the government’s influence capacity, and the implementation capacity, thereby reducing losses caused by COVID-19.

Under the spontaneous EP model, the CG and UGs act as relatively independent COVID-19 EP subjects. Governments of all parties choose the optimal level of COVID-19 EP based on minimization of their own losses caused by COVID-19, without considering the overall interests related to EP. In this model, the UGs have obvious EP subjectivity characteristics, which is helpful as it brings into play the initiative of multi-agent coordinated EP system construction. However, using this system of joint prevention and control, it is difficult to effectively address public health events such as COVID-19 EP. This model is not an effective response to COVID-19 outbreaks in multiple urban areas.

The superior leading EP model of the interurban multi-agent strategy

In the context of COVID-19 EP, masks, goggles, and other resources are very important. However, in the early stages of the outbreak, the lack of these resources not only alarmed the public but seriously hindered the COVID-19 response. In order to improve the allocation efficiency of EP resources, the CG can provide policy guidance through special fiscal measures, departmental coordination, and matchmaking support [61]. In this process, the CG shares a certain proportion of the cost of COVID-19 EP for UG $X$ and UG $Y$ through EP efforts ${\nu }_X\left(t\right)$ and ${\nu }_Y\left(t\right)$. The CG first determines the intensity of EP for UG $X$ and UG $Y$. The UGs choose the appropriate level of effort after the CG’s EP strategy. The CG is the leader in COVID-19 EP, and the UGs are the followers.

The objective functions for EP of UG $X$_, UG $Y$, and the CG $G$ can be expressed as follows:

$$\left\{\begin{array}{c}{T}_X={\int }_0^{\infty }{e}^{-rt}\left\{(1-{\omega }_X)L_X\left(t\right)+\left(1-{\nu }_X\right)C_X\left(t\right)\right\}dt\\ T_Y={\int }_0^{\infty }{e}^{-rt}\left\{(1-{\omega }_Y)L_Y\left(t\right)+\left(1-{\nu }_Y\right)C_Y\left(t\right)\right\}dt\\ T_G={\int }_0^{\infty }{e}^{-rt}\left\{{\omega }_X{L}_X\left(t\right)+{\omega }_Y{L}_Y\left(t\right)+C_G\left(t\right)+\frac{1}{2}({\mu }_X{\nu }_X{E}_X^2+{\mu }_Y{\nu }_Y{E}_Y^2)\right\}dt\\ \end{array}\right)$$ 28

Prevention strategies under the superior leading EP model

Proposition 2

Under the superior leading EP model, the COVID-19 EP strategies of UG $X$_, UG $Y$, and the CG can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X^{\ast \ast }=\frac{1+{\omega }_X}{2{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{{\mu }_X\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ E_Y^{\ast \ast }=\frac{1+{\omega }_Y}{2{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\\ \end{array}\right)$$ 29

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}^{\ast \ast }=\frac{{\omega }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{{\mu }_G\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ E_{\mathit{YG}}^{\ast \ast }=\frac{{\omega }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\\ \end{array}\right)$$ 30

$${\lambda }_X^{\ast \ast }=\left\{\begin{array}{c}0,\left(0\le {\omega }_X\le \frac{1}{3}\right)\\ \frac{\left(3{\omega }_X-1\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}}{\left({\omega }_X+1\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}},\left(\frac{1}{3}\le {\omega }_X\le 1\right)\\ \end{array}\right)$$ 31

$${\lambda }_Y^{\ast \ast }=\left\{\begin{array}{c}0,\left(0\le {\omega }_Y\le \frac{1}{3}\right)\\ \frac{3{\omega }_Y-1}{{\omega }_Y+1},\left(\frac{1}{3}<{\omega }_Y\le 1\right)\\ \end{array}\right)$$ 32

Proof

To obtain the Starberg equilibrium, the inverse induction method is used to solve the equation. Assuming that the loss function $V_i\left(P_X,P_Y\right)$ caused by COVID-19 is a continuously bounded differential function, this differential function satisfies the following HJB equation:

$$r·V_X\left(P_X,P_Y\right)=\underset{E_X\ge 0}{min}\left\{\begin{array}{c}\left(1-{\omega }_X\right)\left(M_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X\right)+\frac{{\mu }_X}{2}\left(1-{\nu }_X\right)E_X^2\\ -\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)-\\ \frac{\partial V_X}{\partial P_Y}\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\upsilon }_Y+{\eta }_Y\right)P_Y\right)\\ \end{array}\right\}$$ 33

$$r·V_Y\left(P_X,P_Y\right)=\underset{E_Y\ge 0}{min}\left\{\begin{array}{c}\left(1-{\omega }_Y\right)\left(M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y\right)+\frac{{\mu }_Y}{2}\left(1-{\nu }_Y\right)E_Y^2\\ -\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\kappa }_Y+{\iota }_Y\right)P_Y\right)\\ -\frac{\partial V_Y}{\partial P_X}\left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)\\ \end{array}\right\}.$$ 34

$\square$

The first partial derivatives of Eqs. (33) and (34) with respect to effort degrees $E_a$ and $E_b$ are obtained and set to zero. The results can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X=\frac{\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\eta \frac{\partial V_X}{\partial P_Y}\right)}{{\mu }_X\left(1-{\nu }_X\right)}\\ E_Y=\frac{\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}}{{\mu }_Y\left(1-{\nu }_Y\right)}\\ \end{array}\right).$$ 35

The CG can be familiar with UG $X$ and UG $Y$ and chooses its effort function according to the above equation. The CG determines its own level of assistance based on the rational responses of UG $X$ and UG $Y$. The HJB equation for the CG can be expressed as follows:

$$r·V_G\left(P_X,P_Y\right)=\underset{E_{\mathit{XG}}\ge 0,E_{\mathit{YG}}\ge 0}{min}\left\{\begin{array}{c}{\omega }_X\left(M_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X\right)+\\ {\omega }_Y\left(M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y\right)+\\ \frac{{\nu }_X{\mu }_X}{2}{E}_X^2+\frac{{\nu }_Y{\mu }_Y}{2}{E}_Y^2+\frac{{\mu }_G}{2}\left(E_{\mathit{XG}}^2+E_{\mathit{YG}}^2\right)-\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\\ \left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)-\\ \frac{\partial V_G}{\partial P_Y}\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\kappa }_Y+{\iota }_Y\right)P_Y\right)\\ \end{array}\right\}.$$ 36

Equations (35) are substituted into Eq. (36), and the right part of the equation is solved. To maximize that, the first partial derivative of $E_{\mathit{XG}}$ and $E_{\mathit{YG}}$ is set equal to zero. The results can be expressed as follows:

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}=\frac{{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\eta \frac{\partial V_G}{\partial P_Y}\right)}{{\mu }_G}\\ E_{\mathit{YG}}=\frac{{\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}}{{\mu }_Y}\\ \end{array}\right)$$ 37

$$\left\{\begin{array}{c}{\nu }_X=\frac{\left(3{\omega }_X-1\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left[2\left(\frac{\partial V_G}{\partial R_X}+\phi \frac{\partial V_G}{\partial R_Y}\right)-\left(\frac{\partial V_X}{\partial R_X}+\phi \frac{\partial V_X}{\partial R_Y}\right)\right]}{\left({\omega }_X+1\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left[2\left(\frac{\partial V_G}{\partial R_X}+\phi \frac{\partial V_G}{\partial R_Y}\right)+\left(\frac{\partial V_X}{\partial R_X}+\phi \frac{\partial V_X}{\partial R_Y}\right)\right]}\\ {\lambda }_Y=\frac{\left(3{\omega }_Y-1\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(2\frac{\partial V_G}{\partial P_Y}-\frac{\partial V_Y}{\partial P_Y}\right)}{\left({\omega }_Y+1\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(2\frac{\partial V_G}{\partial P_Y}+\frac{\partial V_Y}{\partial P_Y}\right)}\\ \end{array}\right).$$ 38

Equations (35) and (37)–(49) are substituted into Eqs. (33), (34), and (36), and the results can be expressed as follows:

$$\begin{array}{cc}\hfill r·V_X& =\left[\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)-\left(1-{\omega }_X\right){\zeta }_X\right]P_X+\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_X}{\partial P_Y}{P}_Y\hfill \\ \hfill & -\frac{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]\left[\left(1-{\omega }_X\right){\tau }_X+{\alpha }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]-{\alpha }_Y\frac{\partial V_X}{\partial P_Y}\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)}{{\mu }_G}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]}{4{\mu }_X}\hfill \\ \hfill & -\frac{\left\{\left(1+{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left[2\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)+\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]\right\}}{4{\mu }_X}\hfill \\ \hfill & -\frac{{\beta }_Y\frac{\partial V_X}{\partial P_Y}\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]}{2{\mu }_Y}+\left(1-{\omega }_X\right)M_X\hfill \\ \hfill \end{array}$$ 39

$$\begin{array}{cc}\hfill r·V_Y& =\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_Y}{\partial P_Y}-\left(1-{\omega }_Y\right){\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)\left[\left(1-{\omega }_Y\right){\tau }_Y+{\alpha }_Y\frac{\partial V_Y}{\partial P_Y}\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\alpha }_X\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\beta }_X\left(\frac{\partial V_Y}{\partial P_X}+\phi \frac{\partial V_Y}{\partial P_Y}\right)\left[\left(1+{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left[2\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)+\left(\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]\right]}{2{\mu }_X}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]\left[\left(1+{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(2\frac{\partial V_G}{\partial R_Y}+\phi \frac{\partial V_Y}{\partial R_Y}\right)\right]}{4{\mu }_Y}+\left(1-{\omega }_Y\right)M_Y\hfill \\ \hfill \end{array}$$ 40

$$\begin{array}{cc}\hfill r·V_G& =\left[\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)-{\omega }_X{\zeta }_X\right]P_X+\left(\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V_G}{\partial P_Y}-{\omega }_Y{\zeta }_Y\right)P_Y\hfill \\ \hfill & -\frac{{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}^2-{\left({\omega }_Y{\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}+\frac{\partial V_X}{\partial P_X}+\phi \frac{\partial V_X}{\partial P_Y}\right)\right]}{{\mu }_X}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(\frac{\partial V_X}{\partial R_X}+\phi \frac{\partial V_X}{\partial R_Y}\right)\right]}^2}{8{\mu }_X}\hfill \\ \hfill & -\frac{\left[{\omega }_Y\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]\left({\upsilon }_Y+{\eta }_Y+\psi +{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right)}{{\mu }_Y}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\frac{\partial V_Y}{\partial P_Y}\right]}{8{\mu }_Y}+{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 41

Using Eqs. (39)–(41), the linear optimal function of $P_X$ and $P_Y$ is the solution to the HJB equation. The results can be expressed as follows:

$$\left\{\begin{array}{c}{V}_X\left(P_X,P_Y\right)=p_X{P}_X+q_X{P}_Y+u_X\\ V_Y\left(P_X,P_Y\right)=p_Y{P}_X+q_Y{P}_Y+u_Y\\ V_G\left(P_X,P_Y\right)=p_G{P}_X+q_G{P}_Y+u_G\\ \end{array}\right)$$ 42

where $p_i$ and $q_i$ are constants.

The derivative of Eqs. (42) is substituted into Eqs. (39)–(41), and the results can be expressed as follows:

$$\begin{array}{cc}\hfill r\left(p_X{P}_X+q_X{P}_Y+u_X\right)& =\left[\left({\kappa }_X+{\iota }_X\right)\left(p_X+\phi q_X\right)-\left(1-{\omega }_X\right){\zeta }_X\right]P_X+\left({\kappa }_Y+{\iota }_Y\right)q_X{P}_Y\hfill \\ \hfill & -\frac{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]\left[\left(1-{\omega }_X\right){\tau }_X+{\alpha }_X\left(p_X+\phi q_X\right)\right]}{{\mu }_G}-\frac{{\alpha }_Y{q}_X\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)}{{\mu }_G}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_X+\phi q_X\right)\right]}{4{\mu }_a}\otimes \left\{\left(1+{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left[2\left(p_G+\phi q_G\right)+\left(p_X+\phi q_X\right)\right]\right\}\hfill \\ \hfill & -\frac{{\beta }_Y{q}_X\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_Y\right]}{2{\mu }_Y}+\left(1-{\omega }_X\right)M_X\hfill \\ \hfill \end{array}$$ 43

$$\begin{array}{cc}\hfill r\left(p_Y{P}_X+q_Y{P}_Y+u_Y\right)& =\left({\kappa }_X+{\iota }_X\right)\left(p_Y+\phi q_Y\right)P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)q_Y-\left(1-{\omega }_Y\right){\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)\left[\left(1-{\omega }_Y\right){\tau }_Y+{\alpha }_Y{q}_Y\right]}{{\mu }_G}-\frac{{\alpha }_X\left(p_Y+\phi q_Y\right)\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]}{{\mu }_G}\hfill \\ \hfill & -\frac{{\beta }_X\left(p_Y+\phi q_Y\right)\left\{\left(1+{\omega }_X\right)\left({\nu }_X+{\eta }_X\right)+{\beta }_X\left[2\left(p_G+\phi q_G\right)+\left(p_X+\phi q_X\right)\right]\right\}}{2{\mu }_X}\hfill \\ \hfill & -\frac{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_Y\right]\left[\left(1+{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(2q_G+q_Y\right)\right]}{4{\mu }_Y}\hfill \\ \hfill & +\left(1-{\omega }_Y\right)M_Y\hfill \\ \hfill \end{array}$$ 44

$$\begin{array}{cc}\hfill r\left(p_G{P}_X+q_G{P}_Y+u_G\right)& =\left[\left({\kappa }_X+{\iota }_X\right)\left(p_G+\phi q_G\right)-{\omega }_X{\zeta }_X\right]P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)q_G-{\omega }_Y{\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{{\left[{\omega }_X{\tau }_X+{\alpha }_X\left(p_G+\phi q_G\right)\right]}^2}{2{\mu }_G}-\frac{{\left({\omega }_Y{\tau }_Y+{\alpha }_Y{q}_G\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_G+\phi q_G\right)\right]\left[{\omega }_X\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_G+\phi q_G+p_X+\phi q_X\right)\right]}{2{\mu }_X}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X\right)+{\beta }_X\left(p_G+\phi q_G\right)\right]}^2}{8{\mu }_X}\hfill \\ \hfill & -\frac{\left[{\omega }_Y\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y{q}_G\right]\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(q_Y+q_G\right)\right]}{2{\mu }_Y}\hfill \\ \hfill & -\frac{{\left[\left(1-{\omega }_Y\right)\left({\upsilon }_Y+{\eta }_Y+\psi \right)+{\beta }_Y\left(p_X+\phi q_X\right)\right]}^2}{8{\mu }_Y}+{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 45

If Eqs. (43)–(45) satisfy $P_X\ge 0$ and $P_Y\ge 0$, the result can be expressed as follows:

$$\left\{\begin{array}{c}{p}_X=-\frac{{\zeta }_X\left(1-{\omega }_X\right)}{r+{\kappa }_X+{\iota }_X}\\ p_X=0\\ u_X=-\frac{\left(1-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\\ -\frac{{\left(1-{\omega }_X\right)}^2\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{4{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\otimes \\ \left\{\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}\\ +\frac{\left(1-{\omega }_X\right)M_X}{r}\\ \end{array}\right)$$ 46

$$\left\{\begin{array}{cc}\hfill p_Y& =\frac{{\zeta }_Y\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right)}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill q_Y& =-\frac{{\zeta }_Y\left(1-{\omega }_Y\right)}{r+{\kappa }_Y+{\iota }_Y}\hfill \\ \hfill u_Y& =-\frac{\phi {\alpha }_X\left(1-{\omega }_Y\right){\zeta }_Y\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_G{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\phi {\beta }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left\{\left[\left(1+{\omega }_X\right)\left(\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right)\right]+\frac{2\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{2{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{4{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}+\frac{\left(1-{\omega }_Y\right)M_Y}{r}\hfill \\ \hfill \end{array}\right)$$ 47

$$\left\{\begin{array}{cc}\hfill p_G& =\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\hfill \\ \hfill q_G& =-\frac{{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\hfill \\ \hfill u_G& =-\frac{{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}^2}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\omega }_Y^2{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}+\frac{{\omega }_X{M}_X+{\omega }_Y{M}_Y}{r}\hfill \\ \hfill & -\frac{\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}}{8{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\left(1+{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{8{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}\right).$$ 48

The loss of the superior leading EP model

Equations (46)–(48) are substituted into Eqs. (42). The loss functions caused by COVID-19 in UG $X$ and UG $Y$ and the CG can be expressed as follows:

$$\begin{array}{cc}\hfill V_X^{\ast \ast }& =\frac{\left(1-{\omega }_X\right)M_X}{r}-\frac{\left(1-{\omega }_X\right){\zeta }_X}{r+{\kappa }_X+{\iota }_X}{P}_X\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{4{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & \otimes \left\{\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}\hfill \\ \hfill & -\frac{\left(1-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_Y+{\iota }_Y\right)}\right\}}{{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill \end{array}$$ 49

$$\begin{array}{cc}\hfill V_Y^{\ast \ast }& =\frac{\left(1-{\omega }_Y\right)M_Y}{r}+\frac{\phi {\zeta }_Y\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right)}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}{P}_X-\frac{\left(1-{\omega }_Y\right){\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\phi {\alpha }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{{\mu }_G{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\omega }_Y\left(1-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\phi {\beta }_X{\zeta }_Y\left(1-{\omega }_Y\right)\left[\left(1-{\omega }_X\right)\left(\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right)+\frac{2\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}{2{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & -\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{4{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 50

$$\begin{array}{cc}\hfill V_G^{\ast \ast }& =\frac{{\omega }_X{M}_X+{\omega }_Y{M}_Y}{r}+\left[\frac{\left({\kappa }_X+{\iota }_X\right)\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right]P_X-\frac{{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\omega }_Y^2{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{{\left[\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}^2}{8{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & -\frac{{\left(1+{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{8{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 51

Based on the above analysis, the total loss caused by COVID-19 can be expressed as follows:

$$\begin{array}{cc}\hfill V^{\ast \ast }\left(P_X,P_Y\right)& =V_X^{\ast \ast }+V_Y^{\ast \ast }+V_G^{\ast \ast }\hfill \\ \hfill & =\frac{M_X+M_Y}{r}+\left[\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right]P_X-\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{\left\{{\omega }_X\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & \otimes \left\{\left(2-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X{\zeta }_Y\left(2-{\omega }_Y\right)}{r+{\kappa }_Y+{\iota }_Y}\right\}\hfill \\ \hfill & -\frac{{\omega }_Y\left(2-{\omega }_Y\right){\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\left(3-{\omega }_Y\right)\left(1+{\omega }_Y\right){\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{8{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{\left\{\left(1+{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}{8{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & \otimes \left\{\left(3-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\zeta }_Y\left(2-{\omega }_Y\right)}{r+{\kappa }_Y+{\iota }_Y}\right\}\hfill \\ \hfill \end{array}$$ 52

EP effectiveness of the superior leading EP model

Equations (49)–(52) are substituted into Eqs. (35) and (36)–(38) after the partial derivative is obtained, and it is easy to obtain Eqs. (29)–(32). Under the superior leading EP model, the COVID-19 EP effectiveness of the UG $X$ can be expressed as follows:

$$\left\{\begin{array}{c}{P}_X^{\ast \ast }\left(t\right)=\frac{1}{{\kappa }_X+{\iota }_X}\left\{\begin{array}{c}\frac{{\alpha }_X}{{\mu }_G}\left[{\omega }_X\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{{\beta }_X}{{\mu }_X}\left[\frac{1+{\omega }_X}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_Y+{\iota }_Y}\right)+\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\\ \end{array}\right\}\\ P_X^{\ast \ast }\left(0\right)=P_X\\ \end{array}\right)$$ 53

The COVID-19 EP effectiveness of the UG $Y$ can be expressed as follows:

$$\left\{\begin{array}{c}{P}_Y^{\ast \ast }\left(t\right)=\frac{\phi }{{\kappa }_Y+{\iota }_Y}\left\{\begin{array}{c}\frac{{\alpha }_X}{{\mu }_G}\left[{\omega }_X\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{{\beta }_X}{{\mu }_X}\left[\frac{1+{\omega }_X}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\\ \end{array}\right\}\\ +\frac{1}{{\kappa }_Y+{\iota }_Y}\left[\frac{{\omega }_Y{\alpha }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)+\frac{\left(1+{\omega }_Y\right){\beta }_Y}{{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)-e^{-\left({\kappa }_Y+{\iota }_Y\right)t+H_Y}\right]\\ P_Y^{\ast \ast }\left(0\right)=P_Y\\ e^{H_X}=\frac{{\alpha }_X}{{\mu }_G}\left[{\omega }_X\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{{\beta }_X}{{\mu }_X}\left[\frac{1+{\omega }_X}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]-\left({\kappa }_X+{\iota }_X\right)P_X\\ \end{array}\right)$$ 54

Analysis of the superior leading EP model

Equations (5) and (29) were, respectively, compared. Under the superior leading EP model, the level of COVID-19 EP efforts of the UG was found to be positively correlated with the proportion of loss sharing, but the impact was less than that of the non-cooperative model. The level of EP efforts of UG was positively correlated with the coefficient of non-governmental organizations, the coefficient of EP experience transfer, the coefficient of the effect of UG efforts on the loss, and the coefficient of impact of the effect of EP on the loss caused by COVID-19. The EP efforts of UGs were found to be negatively correlated with the risk coefficient of viral infection, the cost coefficient of EP, the attenuation coefficient of EP effectiveness, and the discount rate.

Equations (6) and (30) were compared. Under the superior leading EP model, the efforts of the CG were found to be negatively correlated with the EP cost coefficient, the risk coefficient of viral infection, the attenuation coefficient of the EP effect, and the discount rate. The level of the CG’s EP effort was found to be positively correlated with the proportion of losses caused by COVID-19, the impact coefficient of the CG’s efforts on the losses caused by COVID-19, and the EP effect.

The above results indicate that the CG should comprehensively carry out prevention and control of COVID-19 from the following aspects: the COVID-19 EP effect, EP experience teaching, mass EP comfort, the rate of utilizing EP funds, the government’s influence ability, and the implementation ability.

Equations (31) and (32) show that the proportion of COVID-19 assistance from the CG depends on the proportion borne by urban areas. When the proportion of the CG’s EP assistance is less than one-third, the cost will not be shared through the EP funding mechanism. When an UG is unable to cope with COVID-19, the CG will invest extensively in special EP projects and coordinate corresponding EP measures to improve the effect of the urban EP. The phenomenon reflects the “economic man” characteristics of the CG.

Under the superior leading EP model, interventions by the CG can effectively contain the continued development of COVID-19 epidemic. The CG’s EP measures can reduce the uncertainty of intergovernmental EP behavior and lay the foundation for the realization of a joint prevention and control mechanism.

The collaborative EP model of interurban multi-agent strategy

In addition to the CG-led model, UGs can proactively respond to COVID-19 outbreaks [62]. The CG works with UG $X$ and UG $Y$ to determine optimal strategies to improve COVID-19 preparedness and reduce COVID-19 losses.

Prevention strategies in the collaborative EP model

Proposition 3

Under the collaborative EP model, the COVID-19 EP strategies for UG $X$_, UG $Y$, and the CG can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X^{\ast \ast \ast }=\frac{1}{{\mu }_X}\left[{\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\beta }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ E_Y^{\ast \ast \ast }=\frac{1}{{\mu }_Y}({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y})\\ \end{array}\right)$$ 55

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}^{\ast \ast \ast }=\frac{1}{{\mu }_G}\left[{\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{{\mu }_G\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ E_{\mathit{YG}}^{\ast \ast }=\frac{1}{{\mu }_G}({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y})\\ \end{array}\right).$$ 56

Proof

When the relationship between the CG, UG $X$ and UG $Y$ is transformed from superior leadership to cooperation, the three parties aim to minimize the loss caused by COVID-19 and jointly determine optimal $E_X$, $E_Y$, $E_{\mathit{XG}}$ and $E_{\mathit{YG}}$ values. The total loss caused by COVID-19 can be expressed as follows:

$$T={\int }_0^{\infty }{e}^{-rt}\left\{\begin{array}{c}{M}_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X+M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y\\ +\frac{1}{2}({\mu }_X{E}_X^2+{\mu }_Y{E}_Y^2+{\mu }_G{E}_{\mathit{XG}}^2+{\mu }_G{E}_{\mathit{YG}}^2)\\ \end{array}\right\}dt$$ 57

$\square$

Assuming that $V\left(P_X,P_Y\right)$ is the differential function of loss caused by continuously bounded COVID-19, the differential function satisfies the following HJB equation:

$$r·V\left(P_X,P_Y\right)=\underset{\begin{array}{c}{E}_{\mathit{XG}}\ge 0;E_X\ge 0\hfill \\ E_{\mathit{YG}}\ge 0;E_Y\ge 0\hfill \end{array}}{min}\left\{\begin{array}{c}{M}_X-{\tau }_X{E}_{\mathit{XG}}-\left({\upsilon }_X+{\eta }_X\right)E_X-{\zeta }_X{P}_X+\frac{{\mu }_G}{2}{E}_{\mathit{XG}}^2+\frac{{\mu }_X}{2}{E}_X^2\\ M_Y-{\tau }_Y{E}_{\mathit{YG}}-\left({\upsilon }_Y+{\eta }_Y+\psi \right)E_Y-{\zeta }_Y{P}_Y+\frac{{\mu }_G}{2}{E}_{\mathit{YG}}^2+\frac{{\mu }_Y}{2}{E}_Y^2\\ -\left(\frac{\partial V}{\partial L_X}+\phi \frac{\partial V}{\partial L_Y}\right)\left({\alpha }_X{E}_{\mathit{XG}}+{\beta }_X{E}_X-\left({\kappa }_X+{\iota }_X\right)P_X\right)\\ -\frac{\partial V}{\partial L_Y}\left({\alpha }_Y{E}_{\mathit{YG}}+{\beta }_Y{E}_Y-\left({\kappa }_Y+{\iota }_Y\right)P_Y\right)\\ \end{array}\right\}$$ 58

The first partial derivative of the above equation with respect to $E_X$, $E_Y$, $E_{\mathit{XG}}$_, and $E_{\mathit{YG}}$ is set to 0. The results can be expressed as follows:

$$\left\{\begin{array}{c}{E}_X=\frac{{\upsilon }_X+{\eta }_X+{\beta }_X\left(\frac{\partial V}{\partial P_X}+\phi \frac{\partial V}{\partial P_Y}\right)}{{\mu }_X}\\ E_Y=\frac{{\upsilon }_Y+{\eta }_Y+\psi +{\beta }_Y\frac{\partial V}{\partial P_Y}}{{\mu }_Y}\\ \end{array}\right)$$ 59

$$\left\{\begin{array}{c}{E}_{\mathit{XG}}=\frac{{\tau }_X+{\alpha }_X\left(\frac{\partial V}{\partial P_X}+\phi \frac{\partial V}{\partial P_Y}\right)}{{\mu }_G}\\ E_{\mathit{YG}}=\frac{{\tau }_Y+{\alpha }_Y\frac{\partial V}{\partial P_Y}}{{\mu }_Y}\\ \end{array}\right).$$ 60

Equations (59) and (60) are substituted into (58), and the results can be expressed as follows:

$$\begin{array}{cc}\hfill r·V& =\left[\left({\kappa }_X+{\iota }_X\right)\left(\frac{\partial V}{\partial P_X}+\phi \frac{\partial V}{\partial P_Y}\right)-{\zeta }_X\right]P_X+\left(\left({\kappa }_Y+{\iota }_Y\right)\frac{\partial V}{\partial P_Y}-{\zeta }_Y\right)P_Y\hfill \\ \hfill & -\frac{{\left[{\tau }_X+{\alpha }_X\left(\frac{\partial V_G}{\partial P_X}+\phi \frac{\partial V_G}{\partial P_Y}\right)\right]}^2}{2{\mu }_G}-\frac{{\left({\tau }_Y+{\alpha }_Y\frac{\partial V_G}{\partial P_Y}\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{{\left[{\upsilon }_X+{\eta }_X+{\beta }_X\left(\frac{\partial V}{\partial P_X}+\phi \frac{\partial V}{\partial P_Y}\right)\right]}^2}{2{\mu }_X}-\frac{{\left({\upsilon }_Y+{\eta }_Y+\psi +{\beta }_Y\frac{\partial V}{\partial P_Y}\right)}^2}{2{\mu }_Y}+{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 61

Equation (61) shows that the linear minimum disaster loss function of $P_X$ and $P_Y$ is the solution to the HJB equation. The results can be expressed as follows:

$$V\left(P_X,P_Y\right)=p{P}_X+q{P}_Y+u$$ 62

where $p_i$, $q_i$, and $u$ are constants.

The derivative of Eqs. (62) is substituted into Eq. (61), and the results can be expressed as follows:

$$\begin{array}{cc}\hfill r\left(p{P}_X+q{P}_Y+u\right)& =\left[\left({\kappa }_X+{\iota }_Y\right)\left(p+\phi q\right)-{\zeta }_X\right]P_X+\left[\left({\kappa }_Y+{\iota }_Y\right)q-{\zeta }_Y\right]P_Y\hfill \\ \hfill & -\frac{{\left[{\tau }_X+{\alpha }_X\left(p+\phi q\right)\right]}^2}{2{\mu }_G}-\frac{{\left({\tau }_Y+{\alpha }_{Y}q\right)}^2}{2{\mu }_G}\hfill \\ \hfill & -\frac{{\left[{\upsilon }_X+{\eta }_X+{\beta }_X\left(p+\phi q\right)\right]}^2}{2{\mu }_X}-\frac{{\left({\upsilon }_Y+{\eta }_Y+\psi +{\beta }_{Y}q\right)}^2}{2{\mu }_Y}+{\omega }_X{M}_X+{\omega }_Y{M}_Y\hfill \\ \hfill \end{array}$$ 63

$$\left\{\begin{array}{cc}\hfill p_G& =\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}-\frac{{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\hfill \\ \hfill q_G& =-\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\hfill \\ \hfill u_G& =-\frac{{\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X+\frac{\phi r{\alpha }_X{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{{\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X+\frac{\phi r{\beta }_X{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}^2}{2{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & +\frac{{\omega }_X{M}_X+{\omega }_Y{M}_Y}{r}\hfill \\ \hfill \end{array}\right).$$ 64

The loss of the collaborative EP model

Equation (64) is substituted into Eq. (62). The minimum loss function caused by COVID-19 can be expressed as follows:

$$\begin{array}{cc}\hfill V^{\ast \ast \ast }\left(P_X,P_Y\right)& =\frac{M_X+M_Y}{r}-\left[\frac{{\zeta }_X}{r+{\kappa }_X+{\iota }_X}-\frac{{\zeta }_Y\left({\kappa }_X+{\iota }_X\right)}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]P_X-\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}{P}_Y\hfill \\ \hfill & -\frac{{\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X+\frac{\phi r{\alpha }_X{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_{G}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill & -\frac{{\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X+\frac{\phi r{\beta }_X{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right]}^2}{2{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}-\frac{{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\hfill \\ \hfill \end{array}$$ 65

The partial derivatives of the above equations are obtained with respect to $P_X$ and $P_Y$, respectively, and then substituted into Eqs. (59) and (60) to obtain Eqs. (55) and (56).

EP effectiveness of the collaborative EP model

Under the collaborative EP model, the COVID-19 EP effectiveness of the UG $X$ can be expressed as follows:

$$\left\{\begin{array}{c}{R}_X^{\ast \ast \ast }\left(t\right)=\frac{1}{{\kappa }_X+{\iota }_X}\left\{\begin{array}{c}\frac{{\alpha }_X}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right)\\ +\frac{{\beta }_X}{{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_Y+{\iota }_Y}+\frac{\phi r{\beta }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right)-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\\ \end{array}\right\}\\ P_X^{\ast \ast \ast }\left(0\right)=P_X\\ \end{array}\right)$$ 66

The COVID-19 EP effectiveness of UG $Y$ can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill P_Y^{\ast \ast \ast }\left(t\right)& =\frac{\phi }{{\kappa }_Y+{\iota }_Y}\left\{\begin{array}{c}\frac{{\alpha }_X}{{\mu }_G}\left[{\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{{\beta }_X}{{\mu }_X}\left[{\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]-e^{-\left({\kappa }_X+{\iota }_X\right)t+H_X}\\ \end{array}\right\}\hfill \\ \hfill & +\frac{1}{{\kappa }_Y+{\iota }_Y}\left[\frac{{\alpha }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)+\frac{{\beta }_Y}{{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)-e^{-\left({\kappa }_Y+{\iota }_Y\right)t+H_Y}\right]\hfill \\ \hfill P_Y^{\ast \ast \ast }\left(0\right)& =P_Y\hfill \\ \hfill e^{H_X}& =\frac{{\alpha }_X}{{\mu }_G}\left[{\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\hfill \\ \hfill & +\frac{{\beta }_X}{{\mu }_X}\left[{\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]-\left({\kappa }_X+{\iota }_X\right)P_X\hfill \\ \hfill \end{array}\right)$$ 67

Analysis of the collaborative EP model

According to Eqs. (55) and (56), under the interurban collaborative EP model, the optimal levels of COVID-19 EP effort by the CG and UGs are independent of the loss sharing ratio. The factors influencing EP efforts are consistent with those of the above two models. China’s EP experience shows that the integrated application of emerging information technologies such as 5G, the Internet of Things, big data, cloud computing, wireless communication networks, and artificial intelligence has been widely applied to respond to COVID-19. These integrated technologies break institutional and organizational constraints [63]. Having interurban multi-agent collaborative EP enhances the scientific nature of COVID-19 EP and the transparency of multi-agent collaboration.

The effectiveness and discussion of EP models

In the previous section, three COVID-19 EP models were proposed to enhance the effectiveness of interurban multi-agent EP. To reveal the related mechanisms, EP strategies, EP efficiency, and losses caused by COVID-19 were compared under the three models. This helped us to analyze whether different urban COVID-19 response models can effectively promote the construction of an interurban multi-agent COVID-19 EP system.

Theoretical analysis of EP models

Theoretical analysis of COVID-19 EP strategies

COVID-19 EP strategies of the CG and UGs were compared under the spontaneous EP model, the superior leading EP model, and the collaborative EP model.

Proposition 4

When $\frac{1}{3}<\omega \le 1$, the following scenario holds: (i) The level of COVID-19 EP effort by UG $X$ is $E_X^{\ast }<E_X^{\ast \ast }\le E_X^{\ast \ast \ast }$. (ii) The level of COVID-19 EP effort by UG $Y$ is $E_Y^{\ast }<E_Y^{\ast \ast }\le E_Y^{\ast \ast \ast }$. (iii) The level of COVID-19 EP effort by the CG is represented by $E_{\mathit{XG}}^{\ast }=E_{\mathit{XG}}^{\ast \ast }\le E_{\mathit{XG}}^{\ast \ast \ast }$ and $E_{\mathit{YG}}^{\ast }=E_{\mathit{YG}}^{\ast \ast }\le E_{\mathit{YG}}^{\ast \ast \ast }$. (iv) The level of CG support to the UGs for COVID-19 EP is represented by ${\lambda }_X^{\ast \ast }=\frac{E_X^{\ast \ast }-E_X^{\ast }}{E_X^{\ast \ast }}$ and ${\lambda }_Y^{\ast \ast }=\frac{E_Y^{\ast \ast }-E_Y^{\ast }}{E_Y^{\ast \ast }}$.

Proof

(i) Using Eqs. (5), (29), and (55), the results can be expressed as follows:

$$E_X^{\ast \ast }-E_X^{\ast }=\frac{3{\omega }_X-1}{2{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{{\mu }_X\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}>0$$ 68

$$\begin{array}{c}{E}_X^{\ast \ast \ast }-E_X^{\ast \ast }=\frac{1-{\omega }_X}{2{\mu }_X}\left[{\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\beta }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{\phi r{\beta }_X\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\ge 0,\\ \end{array}$$ 69

$\square$

so $E_X^{\ast }<E_X^{\ast \ast }\le E_X^{\ast \ast \ast }$ is true.

(ii) Using Eqs. (5), (29) and (55), the results can be expressed as follows:

$$E_Y^{\ast \ast }-E_Y^{\ast }=\frac{3{\omega }_Y-1}{2{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)>0$$ 70

$$\begin{array}{c}{E}_Y^{\ast \ast \ast }-E_Y^{\ast \ast }=\frac{1-{\omega }_Y}{2{\mu }_Y}\left[{\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}+\frac{\phi r{\beta }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{\phi r{\beta }_Y\left(1-{\omega }_Y\right){\zeta }_Y}{{\mu }_Y\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\ge 0,\\ \end{array}$$ 71

so $E_Y^{\ast }<E_Y^{\ast \ast }\le E_Y^{\ast \ast \ast }$ is true.

(iii) Using Eqs. (6), (30)m and (56), the results can be expressed as follows:

$$E_{\mathit{XG}}^{\ast }=E_{\mathit{XG}}^{\ast \ast }$$ 72

$$E_{\mathit{XG}}^{\ast \ast \ast }-E_{\mathit{XG}}^{\ast \ast }=\frac{1-{\omega }_X}{{\mu }_G}\left[{\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\ge 0,$$ 73

so $E_{\mathit{XG}}^{\ast }=E_{\mathit{XG}}^{\ast \ast }\le E_{\mathit{XG}}^{\ast \ast \ast }$ is true.

Using Eqs. (6), (30), and (56), the results can be expressed as follows:

$$E_{\mathit{YG}}^{\ast }=E_{\mathit{YG}}^{\ast \ast }$$ 74

$$E_{\mathit{YG}}^{\ast \ast \ast }-E_{\mathit{YG}}^{\ast \ast }=\frac{1-{\omega }_Y}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\ge 0,$$ 75

so $E_{\mathit{YG}}^{\ast }=E_{\mathit{YG}}^{\ast \ast }\le E_{\mathit{YG}}^{\ast \ast \ast }$ is true.

(iv) Using Eqs. (5), (29), and (31), the results can be expressed as follows:

$$\begin{array}{c}{E}_X^{\ast \ast }-E_X^{\ast }=\frac{3{\omega }_X-1}{2{\mu }_X}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)\\ +\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{{\mu }_X\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}=E_X^{\ast \ast }·{\nu }_X^{\ast \ast }>0.\\ \end{array}$$ 76

Using Eqs. (5), (29) and (32), the results can be expressed as follows:

$$\begin{array}{c}{E}_Y^{\ast \ast }-E_Y^{\ast }=\frac{1-{\omega }_Y}{2{\mu }_Y}\left[{\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}+\frac{\phi r{\beta }_X{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ +\frac{\phi r{\beta }_Y\left(1-{\omega }_Y\right){\zeta }_Y}{{\mu }_Y\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}=E_Y^{\ast \ast }·{\nu }_Y^{\ast \ast }\\ \end{array}$$ 77

Proposition 4 shows that under the collaborative EP model, the CG and UGs have the highest level of EP effort. Intervention by the CG releases a positive signal, promoting the construction of the urban COVID-19 EP system, which will help the UG to actively implement the construction of the prevention system. The CG effectively coordinates the allocation of urban public health resources through policy levers.

Theoretical analysis of COVID-19 EP efficiency

The COVID-19 EP efficiency by the CG and UGs was compared under the spontaneous EP model, the superior leading EP model, and the collaborative EP model.

Proposition 5

When $\frac{1}{3}<\omega \le 1$, the following scenario holds: (i) The efficiency of COVID-19 EP of UG $X$ is $P_X^{\ast }\le P_X^{\ast \ast }\le P_X^{\ast \ast \ast }$. (ii) The efficiency of COVID-19 EP of UG $Y$ is $P_Y^{\ast }\le P_Y^{\ast \ast }\le P_Y^{\ast \ast \ast }$.

Proof

1. According to Eqs. (26), (31), and (66), the results can be expressed as follows:

$$\left\{\begin{array}{c}{P}_X^{\ast \ast }\left(t\right)-P_X^{\ast }\left(t\right)=\frac{(1-e^{-\left({\kappa }_X+{\iota }_X\right)t}){\beta }_X}{\left({\kappa }_X+{\iota }_X\right){\mu }_X}\left[\begin{array}{c}\frac{3{\omega }_X-1}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_Y+{\iota }_Y}\right)\\ +\frac{\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ \end{array}\right]\ge 0\\ P_X^{\ast }\left(0\right)=P_X^{\ast \ast }\left(0\right)\\ \end{array}\right)$$ 78

$$\left\{\begin{array}{c}{P}_X^{\ast \ast \ast }\left(t\right)-P_X^{\ast \ast }\left(t\right)=\frac{1-e^{-\left({\kappa }_X+{\iota }_X\right)t}}{{\kappa }_X+{\iota }_X}\left\{\left\{\frac{{\alpha }_X}{{\mu }_G}\left(1-{\omega }_X\right)\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{{\beta }_X}{2{\mu }_X}\left[\begin{array}{c}\left(1-{\omega }_X\right)\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_Y+{\iota }_Y}\right)\\ +\frac{\phi r{\beta }_X\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\\ \end{array}\right]\right)\right\}\\ P_X^{\ast \ast }\left(0\right)=P_X^{\ast \ast \ast }\left(0\right)\\ \end{array}\right)\ge 0$$ 79

$\square$

so $P_X^{\ast }\le P_X^{\ast \ast }\le P_X^{\ast \ast \ast }$ is true.

• 2.According to Eqs. (21), (54), and (67), the results can be expressed as follows:

$$\left\{\begin{array}{c}{P}_Y^{\ast \ast }\left(t\right)-P_Y^{\ast }\left(t\right)=\frac{1}{{\kappa }_Y+{\iota }_Y}\left\{\begin{array}{c}\frac{\phi {\beta }_X\left(1-e^{-\left({\kappa }_X+{\iota }_X\right)t}\right)}{{\mu }_X}\left[\frac{3{\omega }_X-1}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\theta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]+\\ \frac{\left(1+{\omega }_Y\right){\beta }_Y\left(1-e^{-\left({\kappa }_Y+{\iota }_Y\right)t}\right)}{2{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\\ \end{array}\right\}\ge 0\\ P_Y^{\ast }\left(0\right)=P_Y^{\ast \ast }\left(0\right)\\ \end{array}\right)$$ 80

$$\left\{\begin{array}{c}{P}_Y^{\ast \ast \ast }\left(t\right)-P_Y^{\ast \ast }\left(t\right)\\ =\frac{\phi \left(1-e^{-\left({\kappa }_X+{\iota }_X\right)t}\right)}{{\kappa }_Y+{\iota }_Y}\left\{\begin{array}{c}\left[\frac{{\alpha }_X\left(1-{\omega }_X\right)}{{\mu }_G}\left({\tau }_X+\frac{{\alpha }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X{\omega }_Y{\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]+\\ \frac{{\beta }_X}{{\mu }_X}\left[\frac{1-{\omega }_X}{2}\left({\upsilon }_X+{\eta }_X+\frac{{\beta }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}\right)+\frac{\phi r{\alpha }_X\left(1-{\omega }_Y\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\\ \end{array}\right\}\\ +\frac{1-e^{-\left({\kappa }_Y+{\iota }_Y\right)t}}{{\kappa }_Y+{\iota }_Y}\left[\frac{{\alpha }_Y\left(1-{\omega }_Y\right)}{{\mu }_G}\left({\tau }_Y+\frac{{\alpha }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)+\frac{{\beta }_Y\left(1-{\omega }_Y\right)}{2{\mu }_Y}\left({\upsilon }_Y+{\eta }_Y+\psi +\frac{{\beta }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right)\right]\ge 0\\ P_Y^{\ast \ast }\left(0\right)=P_Y^{\ast \ast \ast }\left(0\right)\\ \end{array}\right)$$ 81

so $P_Y^{\ast }\le P_Y^{\ast \ast }\le P_Y^{\ast \ast \ast }$ is true.

Proposition 5 shows that for the UGs, a superior response model can improve the effectiveness of COVID-19 EP compared with the spontaneous response model.

Theoretical analysis of losses caused by COVID-19

Losses caused by COVID-19 in the CG and UGs were compared under the spontaneous EP model, the superior leading EP model, and the collaborative EP model.

Proposition 6

When $P_X\ge 0$, $P_Y\ge 0$ and $\frac{1}{3}<\omega \le 1$, the following scenario holds: (i) The minimum loss caused by COVID-19 of UG $X$ is $V_X^{\ast }\left(P_X,P_Y\right)\ge V_X^{\ast \ast }\left(P_X,P_Y\right)$, (ii) the minimum loss caused by COVID-19 of UG $Y$ is $V_Y^{\ast }\left(P_X,P_Y\right)\ge V_Y^{\ast \ast }\left(P_X,P_Y\right)$, (iii) the minimum loss caused by COVID-19 of the CG is $V_G^{\ast }\left(P_X,P_Y\right)\ge V_G^{\ast \ast }\left(P_X,P_Y\right)$; and (iv) the minimum total loss caused by COVID-19 is $V^{\ast }\left(P_X,P_Y\right)\ge V^{\ast \ast }\left(P_X,P_Y\right)\ge V^{\ast \ast \ast }\left(P_X,P_Y\right)$.

Proof

1. Using Eqs. (22) and (49), the results can be expressed as follows:

$$\begin{array}{c}{V}_X^{\ast }\left(P_X,P_Y\right)-V_X^{\ast \ast }\left(P_X,P_Y\right)\\ =\left[\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}-\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\left(P_X^{\ast \ast }-P_X^{\ast }\right)+\frac{{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\left(P_Y^{\ast \ast }-P_Y^{\ast }\right)\\ +\frac{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{4{\mu }_{X}r{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\\ \otimes \left\{\left(3{\omega }_X-1\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}\ge 0\\ \end{array}$$ 82

so $V_X^{\ast }\left(P_X,P_Y\right)\ge V_X^{\ast \ast }\left(P_X,P_Y\right)$ is true.

• 2.Using Eqs. (23) and (50), the results can be expressed as follows:

$$\begin{array}{cc}\hfill V_Y^{\ast }\left(P_X,P_Y\right)-V_Y^{\ast \ast }\left(P_X,P_Y\right)& =\left[\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}-\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\left(R_X^{\ast \ast }-R_X^{\ast }\right)\hfill \\ \hfill & +\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\left(P_Y^{\ast \ast }-P_Y^{\ast }\right)\hfill \\ \hfill & +\frac{\phi {\beta }_X\left(1-{\omega }_Y\right)\left(3{\omega }_X-1\right){\zeta }_Y\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]}{2{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & +\frac{{\phi }^{2}r{\alpha }_X{\beta }_X{\omega }_Y\left(1-{\omega }_Y\right){\zeta }_Y^2}{{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & +\frac{\left(1-{\omega }_Y\right)\left(3{\omega }_Y-1\right){\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{4{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\ge 0\hfill \\ \hfill \end{array}$$ 83

so $V_Y^{\ast }\left(P_X,P_Y\right)\ge V_Y^{\ast \ast }\left(P_X,P_Y\right)$ is true.

• 3.Using Eqs. (24) and (51), the results can be expressed as follows:

$$\begin{array}{cc}\hfill V_G^{\ast }\left(P_X,P_Y\right)-V_G^{\ast \ast }\left(P_X,P_Y\right)& =\left[\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}-\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\left(R_X^{\ast \ast }-R_X^{\ast }\right)\hfill \\ \hfill & +\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\left(P_Y^{\ast \ast }-P_Y^{\ast }\right)\hfill \\ \hfill & +\frac{{\left\{\left(3{\omega }_X-1\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X{\omega }_Y{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}^2}{2{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & +\frac{{\left(3{\omega }_Y-1\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{8{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}>0\hfill \\ \hfill \end{array}$$ 84

so $V_G^{\ast }\left(P_X,P_Y\right)\ge V_G^{\ast \ast }\left(P_X,P_Y\right)$ is true.

• 4.Using Eqs. (25) and (65), the results can be expressed as follows:

$$\begin{array}{cc}\hfill V^{\ast \ast }\left(P_X,P_Y\right)-V^{\ast \ast \ast }\left(P_X,P_Y\right)& =\left[\frac{{\omega }_X{\zeta }_X}{r+{\kappa }_X+{\iota }_X}-\frac{\left({\kappa }_X+{\iota }_X\right){\zeta }_Y}{\left(r+{\kappa }_X+{\iota }_X\right)\left(r+{\kappa }_Y+{\iota }_Y\right)}\right]\left(R_X^{\ast \ast \ast }-R_X^{\ast \ast }\right)\hfill \\ \hfill & +\frac{{\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\left(P_Y^{\ast \ast \ast }-P_Y^{\ast \ast }\right)\hfill \\ \hfill & +\frac{{\left\{\left(1-{\omega }_X\right)\left[{\tau }_X\left(r+{\kappa }_X+{\iota }_X\right)+{\alpha }_X{\zeta }_X\right]+\frac{\phi r{\alpha }_X\left(1-{\omega }_Y\right){\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}^2}{2{\mu }_G{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & +\frac{{\left(1-{\omega }_Y\right)}^2{\left[{\tau }_Y\left(r+{\kappa }_Y+{\iota }_Y\right)+{\alpha }_Y{\zeta }_Y\right]}^2}{2{\mu }_G\left(r+{\kappa }_Y+{\iota }_Y\right)}\hfill \\ \hfill & +\frac{{\left\{\left(1-{\omega }_X\right)\left[\left({\upsilon }_X+{\eta }_X\right)\left(r+{\kappa }_X+{\iota }_X\right)+{\beta }_X{\zeta }_X\right]+\frac{2\phi r{\beta }_X\left(1-{\omega }_Y\right){\zeta }_Y}{r+{\kappa }_Y+{\iota }_Y}\right\}}^2}{8{\mu }_X{\left(r+{\kappa }_X+{\iota }_X\right)}^2}\hfill \\ \hfill & +\frac{{\left(1-{\omega }_Y\right)}^2{\left[\left({\upsilon }_Y+{\eta }_Y+\psi \right)\left(r+{\kappa }_Y+{\iota }_Y\right)+{\beta }_Y{\zeta }_Y\right]}^2}{2{\mu }_{Y}r{\left(r+{\kappa }_Y+{\iota }_Y\right)}^2}\ge 0\hfill \\ \hfill \end{array}$$ 85

so $V^{\ast }\left(P_X,P_Y\right)\ge V^{\ast \ast }\left(P_X,P_Y\right)\ge V^{\ast \ast \ast }\left(P_X,P_Y\right)$ is true.

Numerical analysis of EP models

Data fitting

As a typical form of interurban cooperation, cooperation in metropolitan areas is characterized by a dense population, industrial agglomeration, frequent cross-border commuting and material transportation, and the heavy pressure and task of EP and control. Under the background of sporadic outbreaks of COVID-19, multiple urban areas strengthened interurban cooperation and jointly prevented and fought the epidemic according to the deployment of the CG, which achieved positive results for coordinated interurban EP. Coordinated EP measures shall be taken among cities in terms of EP information exchange, quarantine results mutual recognition, material supply guarantee, emergency material transportation, commuter transportation, labor demand guarantee, and resumption of work and production. Shanghai and Suzhou have one station each for inspection and control. A communication mechanism has been established between the Xiamen–Zhangzhou–Quanzhou levels and the health departments to inform each urban area of the epidemic situation in a timely manner. Beijing associates with Langfang to ensure convenient cross-border commuting by issuing letters of certification, filling in body temperature monitoring cards, and having residential community entry cards. Chengdu, together with Deyang, Meishan, and Ziyang, has implemented the mutual recognition of health certificates and coordinated service control for personnel returning to work and production at different levels. All cities in the Shenzhen metropolitan area have set up specialized logistics and distribution teams to coordinate and solve problems with production and sales not being connected as well as addressing cross-regional transportation difficulties. Beijing has coordinated efforts to promote the resumption of production of upstream and downstream supporting enterprises in the supply chain of Mercedes-Benz, Xiaomi, and BOE in Tianjin-Hebei.

At present, the situation of EP and control remains grim and complex. According to statistics, the numbers of new confirmed cases and new severe cases are still increasing, and the early achievements in EP and control need to be consolidated. At the same time, major central cities, especially first-tier cities, are about to welcome a flood of returnees, thereby facing a transition from an import period to a diffusion period. In the face of real pressure from large population movement, interurban screening and treatment of patients must still be the top priorities to further reduce the numbers of confirmed and suspected cases. To win the battle in EP and control, effective prevention measures should be taken in metropolitan areas to reduce the risks from hidden infections and cross-infections.

In this study, UG $X$, UG $Y$ and the CG all rely on the selection of parameters in the model under three models: COVID-19 EP strategies, COVID-19 EP efficiency, and the loss caused by COVID-19. Due to limited epidemic conditions, it is difficult to obtain data related to COVID-19 EP between cities. First, we studied the basic way in which simulation parameters were set in references [25–28] in detail. The parameter setting simulation was based on the parameter setting methods used in these studies. Second, we interviewed and consulted experts focusing on simulations in urban management, emergency management, health event management, and other fields. Third, we took the Shanghai and Suzhou, Beijing and Langfang, and Shenzhen metropolitan area as objects of investigation and conducted interviews to set parameters related to EP in different cities.

During the course of the survey, we referred to relevant domestic and foreign literature and combined this information with a mature interview design method. In the study, university experts, government departments, and enterprises serving urban operations with cooperative relationships with the research group and related fields of urban EP were selected as the research objects. These interviews were divided into two stages. In the first stage, the interviewees included experts in urban management and other fields as well as managers of provincial government departments. In the second stage, the interview objects were experts and scholars in fields related to emergency management and health events as well as managers of enterprises related to urban operation. The main contents of the first interview stage were as follows: What policies did the government promulgate to prevent epidemic disease using coordination between cities? What do you think are the factors that affect coordinated EP among cities? What do you think about the impacts of independent EP, leading EP and collaborative EP on interurban collaborative EP? The main contents of the second stage of the interview were as follows. Will EP experience transmission, populace comfort, fund utilization rate, and government influence the ability promote interurban collaborative EP? In the process of interurban EP, which means do you prefer to strengthen interurban EP cooperation? With the deepening of interurban collaborative EP, simulation parameters were designed due to the difficulty in obtaining data on the epidemic situation and EP, do you think the simulation values of basic parameters, such as the viral infection risk coefficient, EP cost coefficient, EP effect attenuation coefficient, EP experience transmission coefficient, and UG effort degree are reasonable? What are the appropriate simulation value ranges for these parameters? We sorted out the interview results and constructed a table to show the simulation parameter settings. After integrating the first interview, the new simulation parameter setting table was returned to the experts to develop the second settings. After multiple rounds of comprehensive feedback and expert setting, the final simulation parameter settings for interurban EP tended to be consistent, as shown in Table 1.

Table 1.

Fitting results of epidemic prevention (EP) parameters based on survey interviews

Parameter	Value	Source	Parameter	Value	Source
$\text{r}$	0.10	Fitted	${\upsilon }_{\text{y}}$	0.40	Fitted
${\varpi }_x$	1.00	Fitted	${\eta }_{\text{x}}$	1.00	Fitted
${\varpi }_y$	0.50	Fitted	${\eta }_{\text{y}}$	0.40	Fitted
${\kappa }_x$	0.25	Fitted	$\psi$	0.20	Fitted
${\kappa }_{\text{y}}$	0.15	Fitted	${\alpha }_{\text{x}}$	3.00	Fitted
${\iota }_{\text{x}}$	0.05	Fitted	${\alpha }_{\text{y}}$	1.00	Fitted
${\iota }_{\text{y}}$	0.05	Fitted	${\beta }_{\text{x}}$	3.00	Fitted
${\mu }_{\text{x}}$	3.00	Fitted	${\beta }_{\text{y}}$	1.00	Fitted
${\mu }_{\text{y}}$	3.00	Fitted	${\zeta }_{\text{x}}$	3.00	Fitted
${\mu }_{\text{G}}$	5.00	Fitted	${\zeta }_{\text{y}}$	2.00	Fitted
${\upsilon }_{\text{x}}$	1.00	Fitted	$\phi$	0.20	Fitted

Numerical analysis of COVID-19 EP strategies

COVID-19 EP strategies for the CG and UGs were compared using the spontaneous EP model, the superior leading EP model, and the collaborative EP model. The COVID-19 EP strategies of the CG and UGs under the three interurban EP models are shown in Table 2.

Table 2.

The COVID-19 EP strategies for the CG and UGs under the three EP models

EP models	EX	EY	EXG	EYG
Spontaneous EP model	1.63	1.28	4.50	1.17
Superior leading EP model	7.52	1.92	4.50	1.17
Collaborative EP model	8.50	2.56	5.50	2.33
Order	$E_X^{\ast }<E_X^{\ast \ast }\le E_X^{\ast \ast \ast }$	$E_Y^{\ast }<E_Y^{\ast \ast }\le E_Y^{\ast \ast \ast }$	$E_{\mathit{XG}}^{\ast }=E_{\mathit{XG}}^{\ast \ast }\le E_{\mathit{XG}}^{\ast \ast \ast }$	$E_{\mathit{YG}}^{\ast }=E_{\mathit{YG}}^{\ast \ast }\le E_{\mathit{YG}}^{\ast \ast \ast }$

In the urban COVID-19 EP spontaneous management model, the efforts of the central and local governments are always the lowest. In the superior model of urban COVID-19 EP, the efforts of the CG are consistent with the efforts of the spontaneous governance model. The degree of local government effort is higher than that of spontaneous governance. In the urban COVID-19 EP cooperative cooperation model, the efforts of all parties in the game significantly improve and reach the highest state. These conclusions from the numerical analysis are consistent with Proposition 4. When the CG and UGs move from a spontaneous EP model to a higher-level model, the level of preparedness of the CG remains the same and the level of preparedness of the UGs increases. The improvement in the COVID-19 EP effort of UGs is related to the intensity of the prevention effort by the CG.

Numerical analysis of COVID-19 EP efficiency

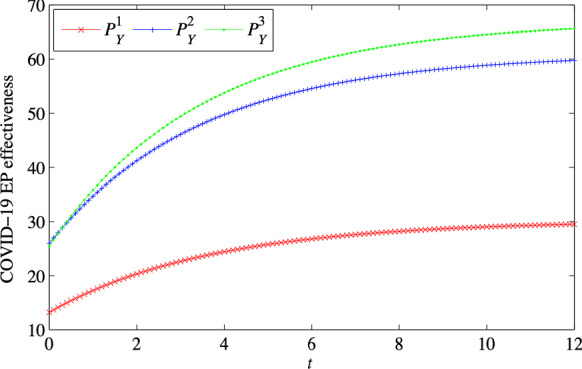
Under the spontaneous EP model, the COVID-19 EP effectiveness of UG $X$ is $P_X^{\ast }\left(t\right)=P_X^1\left(t\right)=56.33-40{\text{.33e}}^{-0.3t}$, and the COVID-19 EP effectiveness of UG $Y$ is $P_Y^{\ast }\left(t\right)=P_Y^1\left(t\right)=30.32-12.1{\text{e}}^{-0.3t}-5{\text{e}}^{-0.2t}$. Under the superior leading EP model, the COVID-19 EP effectiveness of UG $X$ is $P_X^{\ast \ast }\left(t\right)=P_X^2\left(t\right)=120.17-100{\text{.17e}}^{-0.3t}$, and the COVID-19 EP effectiveness of UG $Y$ is $P_Y^{\ast \ast }\left(t\right)=P_Y^2\left(t\right)=61.05-30.05{\text{e}}^{-0.3t}-5{\text{e}}^{-0.2t}$. Under the collaborative EP model, the COVID-19 EP effectiveness of UG $X$ is $P_X^{\ast \ast \ast }\left(t\right)=P_X^3\left(t\right)=142-122{\text{e}}^{-0.3t}$, and the COVID-19 EP effectiveness of UG $Y$ is $P_Y^{\ast \ast \ast }\left(t\right)=P_Y^3\left(t\right)=67.05-36{\text{.6e}}^{-0.3t}-5{\text{e}}^{-0.2t}$. The trends for the COVID-19 EP effectiveness of UG $X$ and UG $Y$ over time are shown in Figs. 2 and 3, respectively.

Fig. 2.

The COVID-19 EP effectiveness of UG $X$ under the three EP models

Fig. 3.

The COVID-19 EP effectiveness of UG $Y$ under the three EP models

Figure 2 shows the COVID-19 EP effectiveness of UG $X$ under the three EP models. Compared with the spontaneous EP model, the COVID-19 EP effectiveness of UG $X$ is higher in the superior leading EP model and the cooperative EP model. The COVID-19 EP effectiveness of UG $X$ in the superior leading EP model is 2 times that in the spontaneous EP model. The COVID-19 EP effectiveness of UG $X$ in the collaborative EP model is higher than that in the superior dominant EP model.

Figure 3 shows the COVID-19 EP effectiveness of UG $Y$ under the three EP models. Compared with the spontaneous EP model, the COVID-19 EP effectiveness of UG $Y$ is higher in the superior leading EP model and the cooperative EP model. The COVID-19 EP effectiveness of UG $Y$ in the superior leading EP model is 2 times that in the spontaneous EP model. The COVID-19 EP effectiveness of UG $Y$ in the collaborative EP model is higher than that in the superior dominant EP model.

Based on the comparative analysis, Figs. 2 and 3 show that the improvement in COVID-19 EP effectiveness tends to be stable over time under the three EP models. The COVID-19 EP effectiveness of UG is the lowest in the spontaneous EP model. Using the superior EP model, the improvement of the COVID-19 EP effectiveness improves to some extent. In the collaborative EP model, the improvement of the COVID-19 EP effectiveness is always higher than with the first two models. This analysis is consistent with the conclusion of Proposition 5. Before the improvement in the COVID-19 EP effectiveness levels off, the rate of improvement in COVID-19 EP effectiveness is the slowest under the spontaneous management model. The rate of improvement in COVID-19 EP effectiveness in the superior EP model is in the middle. The COVID-19 EP effectiveness improves the fastest in the collaborative EP model. As the CG and UGs make maximum efforts in EP, the effectiveness of the multi-agent collaborative EP model also reaches the optimal state. Interurban multi-agent collaborative EP is an effective mechanism to improve urban COVID-19 EP. In the context of the development of COVID-19, governments should cooperate with each other to achieve large-scale EP to obtain the spillover effects of EP policies.

Numerical analysis of losses caused by COVID-19

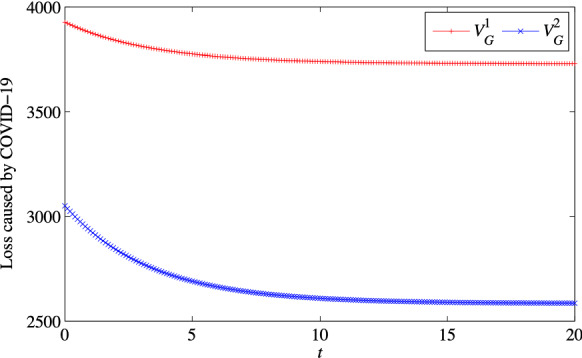
Under the spontaneous EP model, the loss caused by COVID-19 in UG $X$ is $V_X^{\ast }=V_X^1=528.69-1.5P_X$. The loss caused by COVID-19 in UG $Y$ is $V_Y^{\ast }=V_Y^1=880.87+0.5P_X-3.3P_Y$. The loss caused by COVID-19 in CG is $V_G^{\ast }=V_G^1=4027.12-3.5P_X-3.3P_Y$. The loss caused by COVID-19 across cities is $V^{\ast }=V^1=5012.02-2.5P_X-6.67P_Y$. Under the superior leading EP model, the loss caused by COVID-19 in UG $X$ is $V_X^{\ast \ast }=V_X^2=368.34-1.5P_X$. The loss caused by COVID-19 in UG $Y$ is $V_Y^{\ast \ast }=V_Y^2=\begin{array}{c}\hfill 879.79\end{array}+0.5P_X-3.3P_Y$. The loss caused by COVID-19 in the CG is $V_G^{\ast \ast }=V_G^2=3207\text{.11}-3.5P_X-3.3P_Y$. The loss caused by COVID-19 across cities is $V^{\ast \ast }=V^2=4434.24-2.5P_X-6.67P_Y$. Under the collaborative EP model, the loss caused by COVID-19 across cities is $V^{\ast \ast \ast }=V^3=3869.93-2.5P_X-6.67P_Y$. Under the three EP models, the trends in the loss caused by COVID-19 for UG $X$, UG $Y$, the CG, and the interurban area as a whole over time are shown in Figs. 4, 5, 6, and 7.

Fig. 4.

The loss caused by COVID-19 in UG $X$

Fig. 5.

The loss caused by COVID-19 in UG $Y$

Fig. 6.

The loss caused by COVID-19 in the CG

Fig. 7.

The loss caused by COVID-19 across cities

As shown in Figs. 4, 5, 6, and 7, the loss caused by COVID-19 for UG $X$, UG $Y$, and the CG tend to be stable over time under the superior EP model. The loss caused by COVID-19 is consistently lower than that for the spontaneous EP model for UG $X$, UG $Y$, and the CG. The loss caused by COVID-19 under the interurban collaborative EP model is consistently lower than the loss under the spontaneous EP model and the superior leading EP model. This conclusion is consistent with the conclusion of Proposition 6. For UG and CG, the superior leadership model promotes a Pareto improvement in all parties as compared with the spontaneous EP model. In this case, the loss caused by COVID-19 is reduced, and the superior EP model is superior to the spontaneous EP model. From the perspective of total loss, if a reasonable urban COVID-19 EP commitment plan can be formulated, the interurban multi-agent collaborative EP model is superior to the other two EP models. Based on the above analysis, under the spontaneous EP model, the main characteristics of UGs are obvious. Despite the high level of enthusiasm for COVID-19 EP in urban areas, the effectiveness of multi-agent prevention in urban areas is almost negligible. Under the superior leading EP model, the CG intervenes to some extent to optimize the allocation of EP resources. The interurban multi-agent collaborative EP model, which aims to minimize the total loss caused by COVID-19, is the optimal model for the CG and UGs in the response to COVID-19 and can effectively control the loss caused by COVID-19. Interurban multi-agent collaborative EP is a continuous process that can maximize the integration of multi-agent EP advantages.

In terms of examples, in the face of the sudden Covid-19 epidemic, the Yangtze River Delta demonstration areas (Shanghai, Suzhou, and Jiaxing) used cross-regional collaborative EP as an important part of the integrated system innovation for joint EP and control. The three cities gave full control to the coordination advantages of the CG to deepen the joint prevention and control of the epidemic, and the specific joint prevention and control, mass prevention, and control work experience were summarized. Three cities—Shanghai, Suzhou, and Jiaxing—jointly established an integrated cooperation mechanism. These three cities should strengthen their cooperation through a joint defense mechanism, public opinion publicity, and legal protection to achieve information sharing, work interaction, mutual assistance of resources, and coordination of forces. Six integrated joint prevention and control working mechanisms have been jointly established, including dynamic information exchange and mutual learning, mutual recognition and mutual communication of personnel flow, co-guarantee of the passage of material transport vehicles, merging of border points near bayonets, mutual assistance with emergency supplies, and joint management of social security. The WeChat public account platform has been used and strengthened to provide a strong guarantee for the prevention and control of the epidemic. In these three cities, the governments have strengthened the coordination and allocation of transregional supplies for important medical and EP purposes, production and living, and improvements to people's livelihoods. The three cities have established mechanisms for the mutual recognition of prevention and control measures and the mutual recognition of passenger and vehicle passes in response to repeated cross-regional inspections, inconvenient commuting, and rush hour congestion during EP and control. The three cities will jointly study and promote the construction of public service projects in the demonstration area, with public security, emergency management, and public health capacity building being the key directions. At present, the three cities continue to deepen the guidance of the CG and promote the integration of EP and control.

Conclusions and implications

The highly infectious and asymptomatic characteristics of the COVID-19 virus make the related epidemic crisis much more difficult to manage, which has caused great damage to and impacts on human society. The COVID-19 epidemic is a major test of urban governance systems and capacities. The dense populations, narrow spaces, and heavy traffic volumes in cities provide an excellent chain of infection for the human-to-human transmission of COVID-19. It is imperative to improve the urban governance capacity for EP. Interurban relationships, including the vertical relationships between the CG and UGs, as well as horizontal relationships among UGs at the same level, are important factors in producing sustained EP. Joint EP and control mechanisms have been set up in key urban areas and regions such as the Yangtze river delta, the Beijing–Tianjin–Hebei region, the Guangdong–Hong Kong–Macao greater bay area, and Hubei province. Determining how to coordinate EP actions among EP subjects so that they can form joint forces for EP in a comprehensive, efficient, and orderly manner is the key to the prevention and control of public health emergencies. Therefore, this study revealed the mechanism behind the interurban multi-agent EP strategy and proposed a three-party differential game strategy with government leading and non-governmental organizations participating. COVID-19 EP strategies, prevention efficiency, and prevention losses were compared under the three models.

The results of this study are as follows:

1. COVID-19 EP efforts are negatively correlated with the risk of viral infection, the cost of prevention, the attenuation of prevention effectiveness, and the discount rate. The level of COVID-19 EP effort is positively correlated with the coefficient of non-governmental organizations, the coefficient of experience transfer, the coefficient of the impact of UG efforts on loss, and the coefficient of the impact of prevention effectiveness on the reduction of COVID-19 cases. Under the spontaneous EP model, the level of COVID-19 EP effort by UGs is negatively correlated with the proportion of loss sharing. Under the superior EP model, the level of COVID-19 EP effort by the UGs is positively correlated with the proportion of loss sharing, but the impact is less than that in the spontaneous EP model. Under the collaborative EP model, the levels of COVID-19 EP effort of the CG and UGs are not related to the loss sharing ratio. The above results indicate that the CG and UGs should comprehensively address the prevention and control of COVID-19 from various aspects, such as the EP effect, EP experience teaching, mass EP comfort, the EP fund utilization rate, the government’s influence ability, and the execution ability.

2. During the course of COVID-19 EP, when the CG and UGs transition from the spontaneous EP model to the superior EP model, the UGs’ EP effort will be enhanced. Under the collaborative EP model, the CG and UGs have the highest levels of EP effort. Compared with the spontaneous EP model, the superior leading EP model promotes a Pareto improvement for all parties. In this case, the superior leading EP model is superior to the spontaneous EP model. From the perspective of total loss, the collaborative EP model is superior to the other two models.

3. In the spontaneous EP model, although the initiative of COVID-19 EP in urban areas is somewhat high, the effect of multi-agent collaborative EP in urban areas can be almost ignored. Under the superior leading EP model, the CG intervenes to some extent to optimize the allocation of EP resources. The collaborative EP model is the optimal model for the CG and UGs to deal with COVID-19, as it can effectively control the losses caused by COVID-19. Interurban multi-agent collaborative EP can maximize the integration of multi-agent EP advantages.

The contribution of this study is that it addresses the lack of interurban multi-agent collaborative response to public health events, which has important theoretical and practical significance. The study provides theoretical support for the establishment of an interurban joint prevention and control mechanism under unified leadership. The study lays a theoretical foundation for transformation of the vertical relationships between governments, the relationships between governments and social organizations, the relationships between governments and market organizations, and the relationships between governments and citizens after the COVID-19 epidemic. The study also provides practical guidance for EP in order to coordinate interurban relationships and enable multiple actors to fully undertake joint efforts in epidemic control.

The implications of this study are as follows:

1. Cooperation between government organizations and non-governmental organizations in response to COVID-19 is the only way to prevent and control the epidemic. In response to COVID-19, governments should move away from the use of unprofessional and inefficient public services and join hands with market-based and socialized professionals. COVID-19 EP, in particular, requires the introduction of central leadership, interurban coordination, and social participation. This model can be widely used to respond to public health events in the process of urban sustainability transformation.

2. An extensive interurban EP and control mechanism should be established. Interurban areas should discuss major EP and control decisions and share the latest epidemic information in a timely manner. The joint prevention and control mechanism should involve building a high-level, multi-framework, all-dimensional, and well-connected communication and liaison network. Interurban exchanges on case information, treatment plans, EP and control measures, and port docking at regular intervals should be conducted.

3. The government plays an important role in the promulgation and implementation of relevant policies, the mobilization of social forces, the organization and rescue of crises, and the pacification of people’s emotions. Government sectors should establish credibility and authority in the community. The establishment of a service-oriented government is conducive to the establishment of the government in the hearts of the people and the community image. As COVID-19 develops, unified government deployment may be needed to improve the effectiveness of the COVID-19 EP.

Although this study achieved the goal of addressing interurban multi-agent collaborative EP, it still had some deficiencies. Non-governmental organizations were integrated into this study as a whole, but the roles of enterprises, charities, community groups, and other non-governmental organizations in the interurban multi-agent collaborative EP should be further revealed. In addition, determining how to coordinate multi-agents and optimize an interurban joint prevention and control network in different stages of COVID-19 EP should be further studied.

Declarations

Conflict of interest

The authors declare no conflicts of interest.