Abstract
Motivation
Protein structure refinement is an important step of protein structure prediction. Existing approaches have generally used a single scoring function combined with Monte Carlo method or Molecular Dynamics algorithm. The one-dimension optimization of a single energy function may take the structure too far away without a constraint. The basic motivation of our study is to reduce the bias problem caused by minimizing only a single energy function due to the very diversity of different protein structures.
Results
We report a new Artificial Intelligence-based protein structure Refinement method called AIR. Its fundamental idea is to use multiple energy functions as multi-objectives in an effort to correct the potential inaccuracy from a single function. A multi-objective particle swarm optimization algorithm-based structure refinement is designed, where each structure is considered as a particle in the protocol. With the refinement iterations, the particles move around. The quality of particles in each iteration is evaluated by three energy functions, and the non-dominated particles are put into a set called Pareto set. After enough iteration times, particles from the Pareto set are screened and part of the top solutions are outputted as the final refined structures. The multi-objective energy function optimization strategy designed in the AIR protocol provides a different constraint view of the structure, by extending the one-dimension optimization to a new three-dimension space optimization driven by the multi-objective particle swarm optimization engine. Experimental results on CASP11, CASP12 refinement targets and blind tests in CASP 13 turn to be promising.
Availability and implementation
The AIR is available online at: www.csbio.sjtu.edu.cn/bioinf/AIR/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The 3D structure of a protein is of great significance for understanding its biological functions and is the base for new drug development. Due to the heavy cost of the experimental methods to determine the structure, many popular automatic protein structure prediction methods, such as Rosetta (Leaver-Fay et al., 2011), I-TASSER (Yang et al., 2015), MULTICOM (Cao et al., 2016) and QUARK (Xu and Zhang, 2012), have been developed. These predictors only require a 1D amino acid sequence as their input from which a 3D structure model is finally predicted. Due to their rapid prediction speed, existing structure predictors have significantly narrowed the gap between the fast sequencing and relatively slow wet-lab structural solution experiments. Although different predictors vary in the core algorithms, they generally include two stages: initial model generation and refinement. For different protein targets, the initial models can be generated in different routines. When searching the query sequence against the Protein Data Bank (PDB) database, if we find reliable homology deposited structures, then the template-based algorithms (He et al., 2015; Hegler et al., 2009; Leaver-Fay et al., 2011; Yang et al., 2015) can be applied. For the hard targets, which do not have homology structures in PDB, the ab-initio algorithms (Bradley et al., 2005; Kihara et al., 2001; Klepeis et al., 2004; Xu and Zhang, 2012) are usually used to generate initial models.
After we have the initial models, the refinement is the next important procedure to narrow the gap between the final prediction and the native structure (Della Corte et al., 2016). This is a blind optimization problem, where no benchmark is available as guidance. Results of the refinement assessment category in recent CASP (Critical Assessment of Structure Prediction) competitions have shown that the refinement of an initial model toward the experimental structure is challenging. Very slow progresses have been achieved according to the earlier results of CASP competitions (Moult et al., 2016), where most of the algorithms developed by different groups degrade the starting model more often than they improve it. On the other hand, in the last two CASPs, we have seen sustained progress of a few groups that showed consistent improvements compared to the original models. However, the improvement is small, where for most of the targets, the TM-score (Zhang and Skolnick, 2004) increases only by 0.01 even for the best group as per the CASP12 Target Refinement Assessment report (http://predictioncenter.org/casp12/doc/presentations/CASP12_TR_final.pdf). This indicates that the structure refinement remains a significant problem until now.
Protein structure refinement is often achieved by an optimization framework, where two issues are of crucial importance. The first is the precise energy function to describe the protein structure. Generally speaking, a common hypothesis is that the conformation corresponding to the lowest energy is the closest to the native structure. In such a hypothesis, the accuracy of the energy function will ultimately determine whether better structures will be predicted. Considering its importance, many energy functions, such as the Rosetta energy function (Rohl et al., 2003), DFIRE (Zhou and Zhou, 2009), CHARMM force field (Brooks et al., 1983), UNRES force field (Oldziej et al., 2005) and Amber force field (Case et al., 2005), were proposed in this field. However, as the length of the protein increases, the conformation of the protein turns out to be more complex, and thus it becomes extremely difficult to precisely describe the atomic interactions. Therefore, even though several physics-based force fields (Brooks et al., 1983; Cornell et al., 1995; Mayo et al., 1990) or knowledge-based energy functions (Leaver-Fay et al., 2011; Zhang and Zhang, 2010) have been developed, neither of them is universally the best on all targets. For instance, the parameters of knowledge-based energy functions are derived almost exclusively from protein structures, which ignore the physical chemistry of inter-atomic interactions and would lead to considerable double counting of the same interactions (Song et al., 2011). This is probably the reason that in the CASP experiments, the performance of the participating groups often varies with the targets. This interesting phenomenon also indicates that different energy functions have their own merits and the shortcomings simultaneously, highlighting that using multiple energy functions in protein structure refinement can be more effective than using a single one.
The second key point in efficiently performing the conformational search in a huge space is an appropriate optimization algorithm. One of the most widely used optimization methods in protein structure refinement is the molecular dynamics (MD) simulation (Fan and Mark, 2004), which can track very detailed information of the conformational changes by using Newton’s law to guide the movement of every atom. However, the accuracy of the final result from the simulation is largely dependent on the accuracy of the physical force field, and reliable development of that is challenging due to the complexity of protein structures. Computational complexity is another challenging problem for MD-based refinement, especially in the case of large proteins with hundreds of residues that lead to extremely long simulation time to obtain the stable final structures. Many attempts have been made to overcome these difficulties in the past years. For instance, a common approach to improve the efficiency of MD-based conformational search is replica exchange molecular dynamics (REMD) (Yeh et al., 2008). Through the application of parallel simulation, different temperature is assigned for each replica during the simulation for speeding up the conformational sampling process. Furthermore, Hansmann and coworkers implemented an adaptive replica-exchange molecular dynamics, which allows the temperature set to be dynamically adapted in the temperature space (Trebst et al., 2006). Raval et.al incorporated the contact-based restraints in MD simulation to accelerate the determination of the final structure (Raval et al., 2016). Zhang et al. incorporated contact and distance restraints extracted from analogous fragments in the PDB to enhance the convergence of MD-based structural refinement simulations (Zhang et al., 2011).
Monte Carlo (MC) simulation has also been widely used in the protein structure refinement field (Rohl et al., 2003) that utilizes the Boltzmann law to sample the possible conformations in energy landscape and search for the optimal structure with minimum energy through the iteration sampling. In each iteration, a new conformation is attempted with the acceptance decided by the Metropolis protocol. One limitation of traditional Monte Carlo approach is that the conformation tends to get trapped in local minima at low temperatures, and thus it often takes too long time to reach convergence. Several variants have been developed to overcome this issue. For instance, Liang et al. proposed an evolutionary Monte Carlo (EMC) simulation approach (Liang and Wong, 2001), which expends the searching space by incorporating the Genetic Algorithm (GA) (Morris et al., 1998). Another variant called entropy sampling Monte Carlo, which is described by Lee (Lee, 1993) and later employed in other studies (Kolinski et al., 1998; Scheraga and Hao, 2007), incorporated an entropy-based distribution of the conformations of proteins in the Monte Carlo simulation process. A more universal method is the replica exchange Monte Carlo (Thachuk et al., 2007), in which multiple copies of the conformations are simulated in parallel, and the replicas move not only in the conformation space but also at different temperatures. Although Monte Carlo simulation is quite efficient in conformational search with many improved variants proposed, the successful application in structure refinement relies on proper energy functions and sufficient search through the huge conformation space remains very time-consuming.
Based on the above discussions, it is evident that protein structure refinement is still a long-term challenging task in protein structure prediction after decades of efforts due to its difficulty. Therefore, assessing the progress of the methodology development of structure refinement is one of the core tasks in recent CASP experiments. By retrieving the past CASPs, it can be found that an overwhelming majority of the reported refinement methods are either MD- or MC-based. However, very few of them can make consistent improvement of the initial structures. One important reason could be that existing approaches are conducted mostly based on a single force field or scoring function. Considering the complexity of the inter-atomic forces and the limited coverage and preference of a particular force field or scoring function, the general performance of such single-objective-based methods should have significant room to improve. Meanwhile, since the conformational space of protein structure is huge and the priori knowledge we obtained on it is limited, optimal conformational search is another critical issue need to explore.
Motivated by the two above unsolved problems and aiming to develop a new structure refinement protocol, we proposed an artificial intelligence-based multi-objective protein structure refinement method (AIR) in this study. In the AIR framework, we have designed a new multi-objective particle swarm optimization (PSO) structure refinement protocol. The basic idea is to use multiple energy functions as multi-objectives instead of one for correcting the potential bias problem caused by minimizing only a single energy function. The PSO algorithm has found its significant usefulness in the computational intelligence field and demonstrated advantages in both fast global convergence and high solution quality. This multi-objective optimization idea is expected to be an efficient solution for the very diversity protein conformation space search as have been demonstrated by a few previous studies, such as the combination of global and local optimization-based 3D structure reconstruction from the 2D contact map (Chen and Shen, 2012), and the application of multi-objective evolutionary algorithms in protein folding (Olson and Shehu, 2014). With swarm intelligence and the information sharing mechanism between the particles in PSO, it has the potential to achieve optimal search when huge conformation spaces are needed. The data reported in this study showed that as a new protocol, which is fundamentally different from the existing MD- and MC-based methods, represents a promising approach to the high-resolution protein structure refinement problem.
2 Materials and methods
2.1 Dataset
We benchmarked our proposed new refinement protocol, AIR, based on CASP11 and CASP12 refinement targets (Table 1). There are 37 refinement targets in CASP11, where 6 of them do not have their structures in PDB and hence are not incorporated in this study. The rest 31 targets can be divided into three groups based on their lengths: (i) small-size group comprising 19 proteins whose lengths are less than 150 amino acids, (ii) medium-size group that consists of 11 proteins with length in the range of [150, 300) and (iii) big-size group of 1 protein that have more than or equal 300 amino acids. For CASP12 targets, we consider 25 proteins, whose structures are currently available in the PDB. Table 1 summarizes the dataset used and the distribution of different sizes of proteins in the dataset.
Table 1.
Dataset used for validating and comparing different refinement methods
Proteins of sequence length <150 amino acids.
Proteins of sequence length∈[150, 300) amino acids.
Proteins of sequence length ≥300 amino acids.
2.2 Methods
To solve the potential bias problem caused by minimizing only a single energy function, we use three different energy functions as multi-objectives in the proposed AIR approach to evaluate the search conformations. In the approach, Rosetta energy function (Rohl et al., 2003) is used as objective 1, the RWplus potential (Zhang and Zhang, 2010) is used as objective 2, and the CHARMM force field (Brooks et al., 1983) is used as the objective 3. An immediate change of the conformation evaluation is from 1-D (single objective) to 3-D (3 objectives). To perform an efficient multi-objective search to solve the difficulty of huge searching space and the randomness in protein structure conformation search process, we applied PSO, an artificial intelligence-based swarm intelligence algorithm, in the AIR to search for the optimal solution.
The PSO, proposed in 1995 (Kennedy, 2011), is a typical population-based computational optimization algorithm, which works by iteratively trying to improve a candidate solution with the quality evaluation and control. The populations in PSO are called particles (structure conformations in this study). Each individual particle has the searching behavior, which will move around in the search-space by updating its velocity and position. The PSO approach has the memory function, which can remember ever-best known position of every particle through the evaluation process and remember the global ever-best known position. By communicating with other particles on their positions found, a typical particle will update its position to a better solution. Iteratively, it is expected that the whole swarm will move toward the global best solutions. The PSO algorithm and its variants are popular in fields like system control, neural network training and other artificial intelligence fields due to its faster global convergence, higher solution quality and stronger robustness (Cheung and Shen, 2014). To the best of our knowledge, it has never been explored in protein atomic structure refinement field to investigate the capability of such artificial intelligence-based PSO optimization algorithm on this complicated problem. Considering the characteristics of parallelism and search memory, the PSO algorithm is expected to find optimal solutions from the huge structure conformation space efficiently, and can provide an alternative solution to existing MD- and MC-based optimization methods.
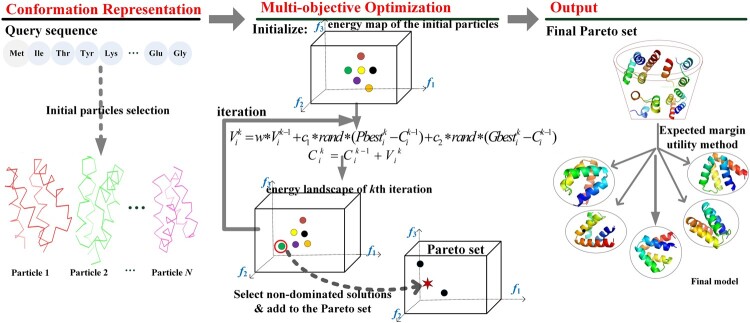
Figure 1 shows the protocol of AIR algorithm, which can be divided into three steps. The first step is initial particles (structures) collection, the second step is the main cycle of the multi-objective PSO simulation, and the third step is for final structure selection.
Fig. 1.
Flowchart of AIR, an artificial intelligence-based protein structure refinement method. The f1, f2, f3 in the landscape represent the 3 objective energy functions respectively: Rosetta energy function, RWplus potential and CHARMM force field
Step 1-Initialization : The AIR searches for the optimal solution by the movement and communication of a swarm of N particles. Each particle is defined as the conformation of the ith model in the kth iteration. Thus the swarm of initial particles can be described as , where N is the number of initial particles in the experiment.
Step 2-Optimization and searching : In the second step, the main optimization iterations are performed, where Rosetta energy function, RWplus potential and CHARMM force field are designed as three fitness functions in the AIR protocol. Each iteration cycle includes two parts: (i) update the position of the particles through movement operation, i.e. update the conformation of the structures , and (ii) evaluate the particles by the above three fitness functions, and then select those equivalently efficient solutions as for the three fitness functions (also named non-dominated solutions) into the Pareto sets (Coello et al., 2004), which is a collection of the output for multi-objective optimization problem.
Step 3-Solution ranking : In the third step, we rank all the Pareto optimal particles in the Pareto set according to the expected utility rule, where the top final structures will be selected.
2.3 Generation of initial particles
In general, the protein structure refinement method is to obtain an initial model and optimize the structure of this initial model. However, in the AIR protocol we use initial particles generated by multiple initial models to ensure particle diversity. The specific operation is as follows: Firstly, different protein structures from ab-initio protein prediction software is obtained as a candidate set of the initial model; After that, the protein structure of the candidate set was scored by Pcons (Wallner and Elofsson, 2005; Wallner et al., 2003) software, and the top three protein structures were selected as the initial models. Finally, each initial model structure is given different random perturbations to produce different protein structures as initial particles, each initial model producing approximately the same number of initial particles.
2.4 Representation of protein conformations
In AIR, considering the planarity of the peptide bond and the reduced number of variables to optimize (Borguesan et al., 2015), we represent the conformation of the protein backbone by a list of main-chain torsion angles in the internal coordinates: (phi), (psi) and (Supplementary Fig. S1 of Supporting Information). So the conformation of a sequence with L amino acids can be represented as a dimensional vector ():
| (1) |
where is the three torsion angles of the ith amino acid.
During the iteration, conformation modification occurs in torsion space firstly, where the torsion angles are fixed at the value of 180 according to the properties of the amide plane, while the angles and of every amino acid change according to the particle updating rules (stated below). Meanwhile, we utilize the Cartesian coordinates in the process of simulation (Zhang and Kavraki, 2002), where the corresponding 3D coordinates of each backbone atom are calculated from the torsional angel system based on Denavit and Hartenberg (DH) method from robotic field. The Cartesian system is convenient to calculate some energy terms of the conformations such as the bond length term and other terms that rely on the 3D coordinates of all atoms.
In robotics field, the parameters of link twist and link length are constant. For a revolute joint is the joint variable and is constant, while for a prismatic joint is variable, is constant and . However, when applying DH-Method to the transformation of protein structure (Craig, 1989; Zhang and Kavraki, 2002), there are some differences. Firstly, in this DH-Cartesian coordinate space, each atom equals to a joint and the chemical bonds between atoms can be considered as the links between two neighboring joint axes (Supplementary Fig. S2 of Supporting Information). Secondly, during the evolution iterations in our algorithm, the parameter atom angle is constant but covalent bond twist is a variable which will keep changing according to MOPSO algorithm.
2.5 Multi-objective energy functions
The Energy function is used for the evaluation of the conformations generated during the simulation. In the AIR protocol, for a given conformation, every energy function will return an evaluation score. One basic hypothesis here is that the lower the energy value, the better should be the conformation, which is in fact widely adopted in the protein structure prediction field (Zhang, 2008). Thus, a precise energy function is crucial for the structure prediction and refinement, and it is a long-term interesting topic for improving the energy functions in the community (Leaver-Fay et al., 2013).
Widely used physics-based force fields are designed on the basis of all kinds of interactions at the atomic and molecular level, and the calculation involves many parameters, and the approximate values of these parameters are obtained from experiments, which may generate certain bias in a complex molecule.
Different from the physics-based force fields, the knowledge-based energy functions are derived from statistical analysis and computation based on known structures (Li and Liang, 2007). The merits of this type of energy functions is that they are simple to construct and easy to utilize. However, they are strongly dependent on the structure dataset used for the statistics that may limit the accuracy of the energy functions on specific targets, which are not covered by the existing structure databases (Zhang et al., 2005).
Majority of the existing programs for protein structure refinement use a single energy function of any of the two types. Therefore, the quality of the final structure is significantly affected by the merits and shortcomings of the specific energy function. In order to take advantages of both types of energy functions, we choose two typical knowledge-based scoring functions, Rosetta energy function (Rosetta Score12) (Rohl et al., 2003) and RWplus potential function (Zhang and Zhang, 2010), and one physical-based scoring function, CHARMM (The Chemistry at Harvard Macromolecular Mechanics) force field (Brooks et al., 1983), in our method (see supporting information for details). These three fitness functions are used as the three objectives in our multi-objective optimization protocol for evaluating a particle in a 3D space instead of the traditional 1D space derived by a single function.
2.6 Multi-objective optimization
We now have three different energy functions, and thus we formulate the protein structure refinement in a multi-objective optimization problem, i.e. detecting the best conformation solution through the co-constraints of the multi-objectives. Mathematical statement for the multi-objective protein structure refinement problem can be formulated as:
| (2) |
where is the 1st Objective, is the 2nd Objective, is the 3rd Objective, is the conformation of particle i updated in the kth iteration, and is the overall conformational searching space.
Different from the single objective optimization problem, multi-objective optimization cannot obtain a unique optimal solution, which has the best performance in all the objectives. That means, in multi-objective optimization, a solution (a conformation) may have the best performance in one objective while it will perform relatively poorly in another objective. This makes sense when considering the complexity of the protein structure space as well as the diversity of energy functions used in the community. Hence, the concept of Pareto dominance can be applied to the evaluation of the solutions.
For two solutions and , we can define their fitness vectors in terms of the given m objectives:
| (3) |
where is said to dominate (denoted as ), i.e. the conformation is better than the conformation , if and only if both of the two following conditions are satisfied:
| (4) |
When there is no other solution that dominates , then it becomes a non-dominated solution and is selected into Pareto set. Through the utilization of Pareto dominance, all the conformations generated during the refinement process can be classified into two groups: dominated conformations and non-dominated conformations. All the non-dominated solutions compose the Pareto optimal set . Our goal now is generating the Pareto optimal set and selecting final conformations from it.
2.7 Detecting Pareto optimal set with multi-objective particle swarm optimization
The PSO algorithm was proposed according to the simulation of groups of birds, which utilizes the collaboration between individuals and the information sharing mechanism to find the optimal solution. As a kind of swarm intelligence optimization algorithm, PSO has many advantages in terms of the computational speed and precision. The traditional PSO evaluates the quality of the particles through a single objective function. However, due to the utilization of multiple objectives, there are some major differences in its main cycle from the traditional single-objective PSO in terms of the evaluation of the particles and the selection of the parameters.
The basic idea of multi-objective PSO (Coello et al., 2004) is to select the global best position and the best position every swarm has had by use of the dominance relationship of swarms, and then update the position of all swarms so that the swarm move towards the optimal direction. In our specific problem of protein structure refinement, a particle represents a structure conformation, and the searching space comprises all conformations represented by all possible and angles. At the beginning of the initialization, all particles are different initial structures, each of which is represented as . Then, their positions in the space are updated to get the optimal conformation from the main cycle of the simulation. In the kth iteration, the new conformation of particle i is updated according to the velocity updating equation (Eq. 5) and the position updating equation (Eq. 6). The newly updated conformations are then evaluated based on the fitness functions.
| (5) |
| (6) |
Here, is the velocity of particle i in the kth iteration, which means the change of the angles, (Eq.1) is the new conformation of particle i in the kth iteration. w is the inertia weight and we make it linearly decrease from 1.3 to 0.7 with the iteration processing in our protocol according to our local test and recommended empirical value (Tripathi et al., 2007). and are the cognitive parameter and social parameter, respectively, and the values for these parameters are set as two (Parsopoulos and Vrahatis, 2002). is a uniformly generate random value that range [0, 1] to introduce perturbation. The is the best conformation of particle i in the previous iteration, and it is selected by the use of the dominance relationship of swarms:
| (7) |
where is all the historical conformations of particle i. The in Eq.5 is randomly selected from the Pareto set in the current iteration, and it can be either from the ith particle or from other particles, reflecting the communication in the swarm.
After the conformation update, the non-dominated ones will be selected based on the three objectives and stored in the Pareto set . In the movement process, the velocity of particle is important. If it is too big, the particle may miss some searching space and hence miss the optimal solution. On the other hand, if it is too small, less searching space will be reached accordingly in the limited iterations. In order to balance the searching accuracy and speed, we limit the velocity to a reasonable value according to the length of the sequence. According to our local tests, the following velocity restraint rule is applied:
| (8) |
where is a threshold. Our local tests have shown that is related with the size of the protein. With the increase of the length of the sequence, the same value of the velocity causes a bigger change of the entire conformation. Considering this, we have applied a decreasing threshold strategy, where when the length of the protein < 150, for the protein with length [150, 250] and for the bigger proteins of length larger than 250. Supplementary Figure S3 (Supporting Information) shows the pseudo code for AIR program.
2.8 MOPSO with the square root distance
In original single-objective PSO, there are only one global best particle, which is called ‘global leader’, which can be found by comparing the single function value and also called ‘Gbest’. However, in MOPSO, there may be a lot of particles in the ‘global leader archive’. Each of them can’t dominate any other particle in the archive. Therefore, it’s important to find an algorithm for a specific particle to find its own most appropriate global leader (). In MOPSO-SRD (Leung et al., 2014), each particle can freely choose its own leader, but not a single global best particle, by using the square root distance calculation. Due to its flexibility, we used this strategy in our AIR prototol.
2.9 Final model selection
After the iteration terminates, we clustered the structure of the non-dominated solution set before sorting. We calculate the TM-score score of the protein structure between each candidate in solution set and the initial model. In this way we can project all the candidates into a three-dimensional space, where the coordinates represent the corresponding TM-score value between candidates and three initial templates. Through the three-dimensional scatter plot, we can clearly find out that there are different number of clusters in final candidate sets (see Fig. 2 for three cases of final clusters).
Fig. 2.

Three cases of different number of clusters in final Pareto candidate sets. (a) One cluster case example of R0989D1’s non-dominated solution. (b) Two clusters case example of R0993s2’s non-dominated solution. (c) Three clusters case example of R0996D4’s non-dominated solution
After the iteration terminates, we will get nrep non-dominated conformations, and we can represent the Pareto set as: . Considering the three objective functions in our method, the energy map of the non-dominated conformations can be calculated, which is also called the Pareto front (Tripathi et al., 2007) and described as:
| (9) |
where , and are from the Rosetta, RWplus and CHARMM energy functions, respectively.
Since we have nrep non-dominated solutions in , we need to formulate a decision-making rule to rank the solutions of Pareto sets and hence get the final refined structures of the protein. Although there is no a perfect ranking method till now, we find that there are some special solutions called ‘knees’ in the Pareto front (see Supplementary Fig. S4 for an example) through observing the energy distribution of the non-dominated particles. In such ‘knees’ solutions, it shows the phenomena that a small depravation in one objective causes large improvement in other objectives. In order to recognize the more important ‘knees’ solutions in the Pareto front , we adopted an margin utility-based method (Branke et al., 2004), where bigger margin utilities of the solutions indicate more important solutions. The expected margin utility is used to measure the importance of the solutions in the Pareto set (Branke et al., 2004), and the margin utility can be defined as:
| (10) |
where C is the non-dominated solution in the Pareto set, and is the weight variants. The expectation of this utility for each solution in the Pareto set can find ‘knee’ solutions to some extents, because the ‘knee’ solutions have the characteristic of decreasing slightly in one objective while increasing largely in other objectives that lead to a distinct increment in the expected margin utility. This expected margin utility assumes the linear utility functions being equally likely with all possible . Therefore, when calculating the for an individual in Pareto set, we sampled a number of utilities randomly and set their average value as the expected . Finally, we rank the solutions according to the expected margin utility .
First, the expected margin utility can be approximated by random sampling of . Through sampling, we get plenty of different utility values for an individual solution , where s is the number of sampling. Then, we take the average utility as the expected margin utility of this solution, i.e. . To get a stable expectation, the sampling time needs to be big enough. In this study, s is set to 20 000. After calculating the expected margin utility of each conformation in the Pareto set, we can rank the conformation by their expected margin utilities and get the high-ranked solutions as the final output.
3 Experimental results
As mentioned in Section 2, we have 56 targets for the refinement 31 targets from CASP 11 and 25 targets from CASP 12 in our experiments. We set the parameter N = 50, i.e. for each target, we use 3 initial models as the input to AIR. We collected 20 predicted models that were submitted by the top 4 predictors (5 models each), BAKER-ROSETTA (Leaver-Fay et al., 2011), RaptorX-DeepModeller (Peng and Xu, 2011), QUARK(Xu and Zhang, 2012) and Zhang-Server (Yang et al., 2015), in the CASP experiments. Then, the top two models of the 20 prediction models ranked by Pcons software and the initial model provided by the CASP server are used as the original models. Additionally, we made small changes of the angles based on these three original models to produce 47 new decoy structures. Together these 50 models are considered as initial particles and inputted to the AIR. The other parameter, the maximum iteration times in the main searching cycle, is set to 3000. For a fair comparison with CASP refiners, we also output 5 models for each target from the Pareto set in the AIR protocol, where the model 1 and the best model are evaluated and compared.
3.1 Asynchronous optimization objectives
One important reason for better performance of the multi-objective search compared to a single objective optimization is that different objectives provide distinct evaluation of the object. Generally, the typical characteristic of multi-objective optimization problem is that the objectives are asynchronous. To intuitively show the dynamic changes of the 3 energy functions, Supplementary Figure S5 (Supporting Information) shows the track of the refinement process for target TR829 (PDB id: 4rgi). Supplementary Figure S5(a), (b) and (c) show the change of the three objectives during the iterations, where three objectives tend to converge with the increase of the iterations. In addition, the three energy functions are unsynchronized and even reverse at some iteration times, indicating their evaluations are complementary to each other.
3.2 AIR’s performance on the test set
As mentioned before, we tested our method on the refined protein targets from CASP 11 and CASP 12. In Supplementary Table S1 of Supporting Information, the refinement results for each target are summarized, where the template modeling score (TM-score), global distance test high accuracy score (GDT_TS score) (Cozzetto et al., 2009) and RSMD are used as the assessment criteria of the refinement quality. We compared the best model and the model 1 from our output with the initial released model for each target protein. From the perspective of the best model generated by AIR, in all the 56 targets, 52 initial models are improved (93%) to some degree after being refined in terms of TM-score. Based on GDT_TS score and RSMD score, 48(86%) and 51(91%) targets show improvement. For the model 1, 89%, 80% and 91% targets are improved in terms of TM-score, GFT-TS and RSMD respectively.
Figure 3 shows the overall comparison of the refined models and the initial input models. Comparing TM-score, GDT_TS and RSMD between the best model and model 1, it is evident that the model 1 is not always the best model in the output. Besides, more targets show improvement in terms of TM-score and RSMD compared to GDT_TS score.
Fig. 3.
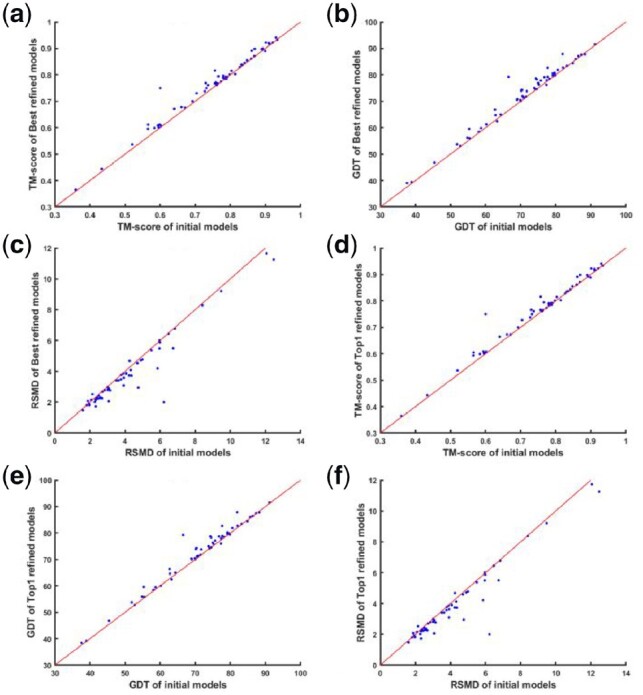
The comparison of AIR’s refined models with the initial models. The comparison of the best model refined by AIR and the initial model in terms of TM-score, GDT_TS and RSMD are shown in (a), (b) and (c), respectively. On the other hand, the comparison of the AIR refined model 1 and the initial model in terms of TM-score, GDT_TS and RSMD are presented in (d), (e) and (f) respectively
The refinement gained by running AIR on the initial structures varies on the protein size and the initial model quality. Figure 4(a–c) illustrate the gains of AIR on targets of different size groups. As can be seen from these figures, when the length of the target is smaller than 150, the average TM-score is improved by 0.018 (best model), the GDT_TS is improved by 1.95 and the RSMD is improved by −0.40. However, for the group of targets with length > 250, the TM-score, GDT_TS and RSMD gain is decreased to 0.007, 0.78 and −0.20, respectively. With the length of amino acids increases, the possible conformation space for the protein gets much larger and it is more difficult to search for the near-native structures in the same iterations.
Fig. 4.
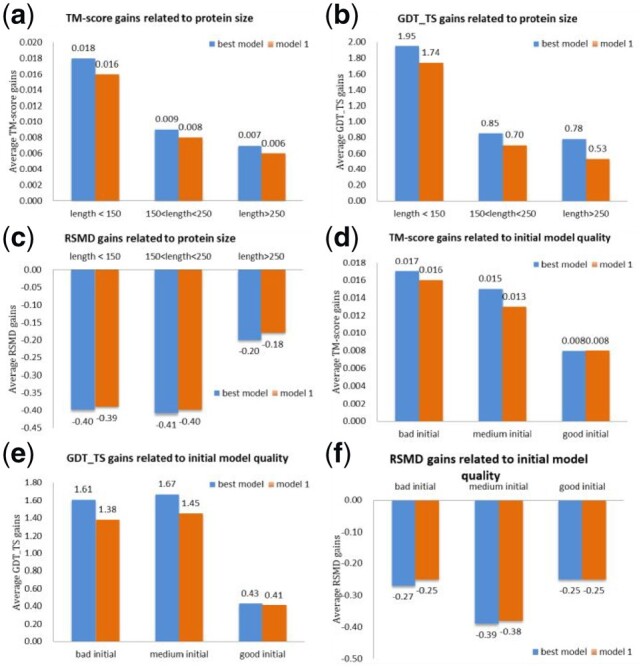
AIR’s refinement gains on different target groups. (a) Average TM-score gains, (b) average GDT_TS gains and (c) Average RSMD gains on three target groups of different sizes. (d), (e) and (f) show the average TM-score, GDT-TS and RMSD gains for three types (bad, medium and good) of initial models
We have also found that the AIR’s refinement gain is also related with the initial model quality. In general, bigger improvements are observed on relatively bad initial models. As shown in Figure 4(d–f), we classify all the targets into three groups according to the quality of initial models: the bad group consists of targets whose initial models have TM-score ≤ 0.6, the medium group comprises targets that have initial models of 0.6 < TM-score < 0.9, and the TM-score of the good group is larger than 0.9. Figure 4(d–f) shows AIR has a better refinement performance on the targets with bad and medium initial models compared to the targets with good initial models. For instance, for bad initial models, there is an average gain of 0.017 in terms TM-score as shown in Figure 4(d), while for good initial models, only an average gain of 0.007 can be viewed. A potential reason is that when the initial model quality is already very high, the improvement space is limited. These results also indicate that our method has the potential to explore more conformation spaces, and has more possibilities to search the good conformation when the initial structure is not so good.
3.3 Performance comparison between AIR with state-of-the-art refinement methods
We compare our algorithm AIR with the algorithms that have achieved good results in CASP12, including Seok (Ko et al., 2012), Baker (Dimaio et al., 2009) and Zhang-refinement(Zhang et al., 2011). Seok is the best group for the overall evaluation of CASP12 on the refinement project. Baker and Zhang-refinement are also well-known groups in the field of protein structure prediction, and have also achieved excellent results in the CASP12 competition. The test data includes 12 targets in the real structure of the PDB in the refinement project of CASP12. The comparison results of each target are shown in Table 2 below. Overall, on the 7 targets out of 12 targets, our AIR algorithm produces a model that is better than the other three algorithms. Four structures have better performance with BAKER than AIR. These results also indicate that using multiple objectives does not guarantee reach a better solution. Multiple objective functions are a type of balance between different evaluations. On some targets, one specific energy function would be more suitable, and the other external energy functions may have deviations in the evaluation of protein structure. In such cases, more energy functions will make our output results fall into a bad local optimal solution in stead.
Table 2.
Performance comparison between AIR with other refinement methods on GDT_TS
| Target/Method | Initial | AIR | BAKER | Zhang | Seok |
|---|---|---|---|---|---|
| TR520 | 79.13 | 79.70 | 75.39 | 78.82 | 77.57 |
| TR594 | 55.34 | 60.94 | 67.98 | N/A | 53.09 |
| TR869 | 38.94 | 39.18 | 38.22 | 38.94 | 38.94 |
| TR879 | 79.20 | 79.77 | 77.84 | 79.32 | 79.32 |
| TR891 | 91.20 | 91.52 | 91.30 | 91.07 | 90.18 |
| TR893 | 87.28 | 87.57 | 85.36 | 86.09 | 87.43 |
| TR894 | 74.54 | 78.30 | 81.02 | N/A | 74.54 |
| TR895 | 70.21 | 73.93 | 72.92 | N/A | 71.67 |
| TR920 | 79.68 | 79.91 | 82.76 | 79.80 | 81.51 |
| TR921 | 69.02 | 70.44 | 68.84 | 69.02 | 69.56 |
| TR928 | 63.27 | 63.42 | 67.30 | N/A | 63.42 |
| TR944 | 74.11 | 74.41 | 72.33 | N/A | 74.90 |
| Avgerage Z-score | 0.38 | 0.54 | 0.53 | 0.42 | 0.47 |
Note: The significance of bold is shown the better GDT_TS score for each target between different groups.
Table 2 shows the average Z-score on the test targets, where for AIR is 0.54, and 0.53, 0.42 and 0.47 for Baker, Zhang and Seok groups respectively. To further test whether there is significant difference among the tested approaches, we performed the student’s t-test on the 12 targets’ GDT_TS scores of the 4 methods. Our results show that the P-values are 0.8504 for AIR & Baker, 0.0498 for AIR & Seok, and 0.0139 for AIR & Zhang. These results are consistent with the average Z-score comparison.
3.4 Complementary benefits of multiple initial models
Unlike other refinement methods, we used three different protein structures as the initial models. In addition to the role of expanding the search space for particles and reducing the reliance on the accuracy of a single template, an obvious complementary benefit is that through the learning process of particle swarm optimization, particles are expected to be able to assemble each initial model’s advantage. The interactive learning in the iterative process combines the high accurate structural parts of templates from different initial models to obtain a better output structure, which is very hard to be achieved by a single template. For example, Figure 5 (a–c) shows a comparison of the three initial models of TR829 with the real structure, and Figure 5(d) is a comparison of the best output model with the real structure. From the Figure 5, the structure model 1 circled by the yellow ellipse is better than the model 2, and the final output model adopts the structure of the model 1 part. In the same way, the final structure also adopts the better partial structure of model 2 with a blue ellipse circle and the better partial structure of model 3 circled by a green ellipse. After absorbing the high accurate partial structure of each of the three templates, the final output model is significantly improved on the TM-score and GDT_TS compared to the initial models.
Fig. 5.
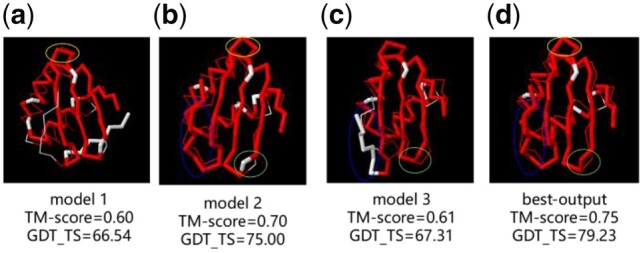
Comparison of different models of TR829 and real structure (a) initial model 1, (b) initial model 2, (c) initial model 3 and (d) best-output model. Residues with d < 5Å in red and residues with d > 5Å in white. (Color version of this figure is available at Bioinformatics online.)
3.5 The importance of cluster-based final model selection
After obtaining the candidate structures, we need to select the best five candidate structures as the output model. We first use the clustering algorithm to divide the candidate structures, and then use the Knee algorithm to classify the candidate structures in each cluster. Figure 6(a) represents the distribution of the output model of the R1016 candidate structure after clustering using the Knee algorithm in the TM-score space; Figure 6(b) represents the distribution of the output model of the candidate structure of R1016 directly using the Knee algorithm in the TM-score space. As shown in the Figure 6(b), all the five output models directly selected using the Knee algorithm belong to one small cluster, but the output model that best matches the real structure belongs to another cluster. Intuitively, this method has space to improve. Through clustering, we select the top three structures from the large cluster and the top two structures in the small cluster as the final output model. Interestingly, one of the selected models in the large cluster is very close to the best model. Therefore, the method of clustering and reordering can diversify the structure of the output model and increase the possibility of selecting the best model. In Supplementary Figure S6 of Supporting Information, the TM-score space for each target’s candidate structures are summarized.
Fig. 6.
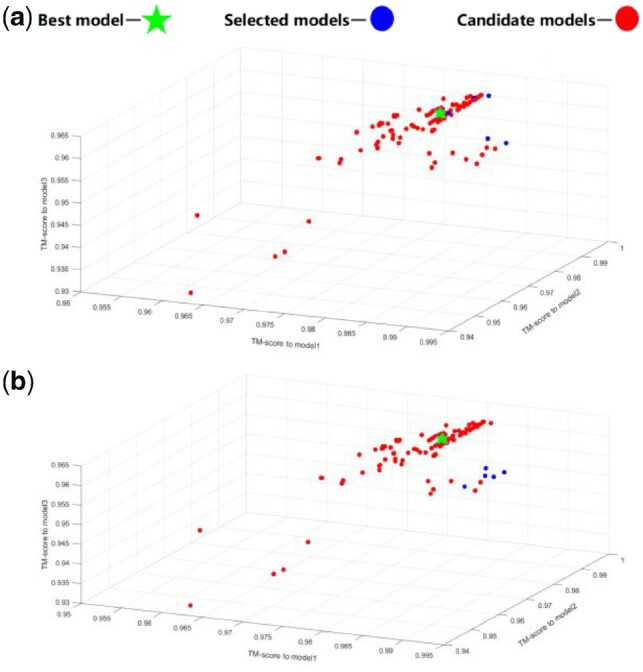
Case study of selecting the five final models from candidates of R1016 (target in CASP 13) in the TM-score space: (a) the final selection through combination of clustering and knee approach, (b) the final selection without clustering, i.e. only knee approach
3.6 Advantages of DH-based molecular conformations representation
Compared to traditional coordinate transformation methods, such as Rodriguez rotation (Rodriguez, 1840), the DH method (Zhang and Kavraki, 2002) can effectively eliminate the cumulative error. Under Rodriguez's rotation framework, the coordinates of the amino acid backbone atoms depend on the atomic coordinates of the previous amino acid backbone, and the numerical error caused by the previous coordinate is passed to the new position to form the error accumulation. Therefore, the anchor atom at the end of the molecular chain will have a large error at the other end, and the longer the length of the amino acid chain, the bigger the cumulative error. However, the DH method combines multiple rotations into one rotation to obtain a rotation matrix. The atomic coordinates of the amino acid do not depend on the previous atomic coordinates, therefore no accumulated error occurs. Schematic diagram of comparison of two coordinate conversion methods is shown in Figure 7.
Fig. 7.
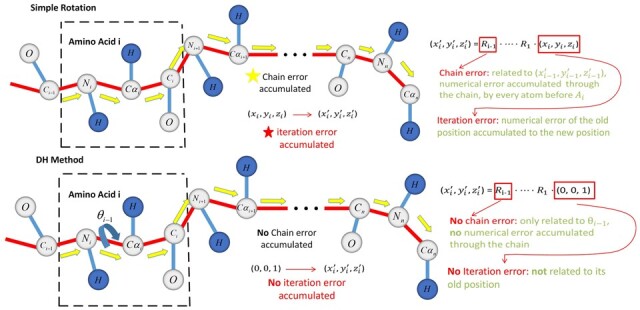
Schematic diagram of error transfer reduction of DH coordinate transformation modes
We selected 10 targets of different lengths as the test set on CASP12, and used the Rodrigues rotation and DH Method in the AIR algorithm to compare the effects of two different coordinate transformation methods. The comparison results of each target are shown in Table 3. Overall, for the targets with an amino acid sequence length less than 100 (TR594, TR894), the two coordinate transformation methods have little effect on refinement. For targets with an amino acid sequence length greater than 200 (TR879, TR920, TR928, TR944), the DH Method has a significant improvement in the effect of refinement compared to Rodriguez rotation. This phenomenon corresponds to the traditional coordinate transformation method with the increase of the accumulated error of the chain length.
Table 3.
Performance comparison between DH Methods with Rodrigues rotation on GDT_TS
| Target/Method | Length | Initial | Best model of Rodrigues | Top 1 model of Rodrigues | Best model of DH Method | Top 1 model of DH Method |
|---|---|---|---|---|---|---|
| TR520 | 321 | 79.13 | 78.71 | 77.41 | 79.70 | 78.90 |
| TR594 | 89 | 55.34 | 60.94 | 60.11 | 59.55 | 59.55 |
| TR879 | 220 | 79.20 | 76.05 | 75.35 | 79.65 | 79.65 |
| TR891 | 112 | 91.20 | 91.07 | 90.63 | 91.52 | 91.29 |
| TR893 | 169 | 87.28 | 83.73 | 83.73 | 87.57 | 87.57 |
| TR894 | 54 | 74.54 | 78.30 | 77.36 | 78.30 | 77.36 |
| TR920 | 219 | 79.68 | 73.95 | 73.95 | 80.70 | 79.91 |
| TR921 | 138 | 69.02 | 70.24 | 69.94 | 70.83 | 70.44 |
| TR928 | 341 | 63.27 | 56.14 | 56.14 | 63.42 | 63.42 |
| TR944 | 253 | 71.74 | 71.25 | 72.33 | 74.60 | 74.41 |
Note: The significance of bold is shown the better GDT_TS score for each target between the DH Methods with Rodrigues rotation.
3.7 Case study in CASP13
As a case study of the performance in the most recent CASP13 experiment, we examine the models of AIR on R0979 (http://predictioncenter.org/casp13/results.cgi?view=tables&target=R0979&model=1&groups_id=) in Figure 8, which has the best TM-align (0.80) (Zhang and Skolnick, 2005) and MAMMOTH (6.85) (Ortiz et al., 2009) scores among all models from different groups. Both of these indicators are based on the comparison of similarity of the models independent of the sequence, and our algorithm has a good effect in this respect.
Fig. 8.

Comparison of different models of R0979 and the experimental structure. (a) initial model 1, (b) initial model 2, (c) initial model 3 and (d) AIR first model. Residues with d < 5Å in red and residues with d > 5Å in white. (Color version of this figure is available at Bioinformatics online.)
R0979 is a homo-trimer complex, where each monomer represents an artificially engineered protein made by fusing residue 18–54 of an uncharacterized protein (http://www.uniprot.org/uniprot/A0A0G1XU35) with residue 250–277 of GCN4 protein from yeast (www.uniprot.org/uniprot/P03069) repeated twice in the terminals; it has an overall long-helix fold but tilted in the middle due to the fusion of the middle segment. AIR started with three monomer models provided by CASP, where one has a GDT_TS (70.65) much higher than other two (49.73 and 45.56, respectively). Despite the poor quality of the other two initial models, the alternative orientations provide complementary information on the fusion segment. As AIR uses a multi-objective optimization procedure, these helped AIR to create the first refined model that has a much-improved quality with the GDT_TS 2.99 units higher than the best initial model (Fig. 8). The success of this case highlights the advantage of PSO in refining protein structures of frustrating energy landscape, as characterized by multiple energy basins due to the complementary energy components and initial models.
4 Discussions
We proposed a novel protein structure refinement protocol, AIR, built on the principle of multi-objective optimization, in which each protein structure is treated as a particle moving through the energy landscape guided by multiple and complementary energy force fields. The success of AIR can be attributed to three main aspects: The first is the anisotropy of multiple templates, which can expand the search space of particles and reduce the dependence of algorithm performance on the accuracy of a single template. The second is the complementarity of multi-objective energy functions that partly alleviates the inaccuracy of the single energy function; the third is the swarm intelligence of the PSO algorithm, which helps to effectively search for the good solutions.
4.1 Combination of multiple energy functions
The proposed AIR program features by a flexible capability of fusing multiple energy functions to evaluate a model solution. In current protocol, three objective functions, CHARMM, Rosetta and RWplus, have been used in the multi-objective optimization process; but it is straightforward to incorporate other efficient energy functions. To compare the relative importance of these three energy functions in our protocol, we have performed the backward elimination-based tests, which were performed on 50 protein targets using three different combinations of two energy functions and results are shown in Supplementary Table S3. According to the results, we can see that if the Rosetta energy function is not used, the improvement will be affected at the most, indicating it is the most important energy term in current AIR protocol, followed by the CHARMM and the RWplus energy function with similar analysis.
Our experiments also suggest that it’s not guaranteed better by fusing the above three energy functions on some specific targets. In our algorithm’s future development, on one hand, we will keep updating new versions of the three energy functions used in our program. For example, we will systematically test the new CHARMM version of CHARMM36m (Huang et al., 2017) in our AIR framework. On the other hand, we will keep expanding our energy functions pool to include more new energy functions. One potential direction for us to explore future is to try to design a personal-mode objective functions combination for specific protein targets, including global fold evaluation and local structure refinement dynamically.
4.2 The influence of the number of iterations
We set the number of iterations for each target to 3000. Theoretically, the larger number of iterations allows the algorithm to perform a more detailed search on the search space, which can improve the quality of the output models. We also tried to set the number of iterations to 6000 and 12 000 and found that only some of the target's output models have a slight improvement on GDT_TS and TM-score. At the same time, the number of iterations is positively related to the running time of the algorithm. When the number of iterations is 6000 and 12 000, the running time of the algorithm is 2 times and 4 times. To balance the effect of the algorithm and the running time of the algorithm, we finally set the iteration parameter to 3000 in current AIR.
4.3 The influence of the number of initial models
In current AIR, we use three different initial structures as the original template to generate particles. To test whether the number of original templates has an effect on the algorithm's performance, we also performed related experiments on three targets in CASP 13, whose experimental structures are known till now for benchmark purpose, i.e. R0968s1, R0968s2 and R1016. We have compared the AIR refinement with only 1 single initial template model input, 3 initial models template as the input and another well-established single-template-based refinement approach 3Drefine (Bhattacharya et al., 2016). Supplementary Table S4 has given the results.
The merit of the multiple model templates is it can increase the energy landscape exploration, as structural diversities from different templates will expand the particle searching space. This can be clearly observed in Supplementary Figure S7, which compares the searching space sizes of single input and multiple inputs at both the 1st iteration and the 3000th iterations at the end. In terms of the TM-score and GDT-TS criteria, on the R0968s1 refinement target, the AIR with three templates is the best among the three compared methods. It’s interesting to find that on the target of R0968s2, the three-templates-based AIR is inferior to the single-template-based AIR and 3Drefine. The reason is that the quality of the other two templates is quite different from the initial template, which will accordingly affect the search space. On the R1016, 3Drefine is better and the three templates-based AIR, which achieves the same TM-score and comparable GDT-TS score. These results suggest that the performance of AIR depends on the qualities of the multiple initial templates. When all the input model templates are good, they will all contribute positively to the final refinement output. However, when some of the initial templates are not good enough, the risk of falling into the bad solution will increase at the case of multiple template inputs. We also implemented the AIR with 4 or 2 initial inputs, and the overall effect of the algorithm is not as good as the three original templates. In the future, we will go on to find a better mechanism for picking initial multiple input models to AIR.
4.4 On ranking criteria
In current AIR, we only restrict the velocity of the dihedral angles in each iteration to a reasonable range for balancing the accuracy and the searching conformation. However, there are still some unreasonable solutions in the Pareto set. Considering the usage of both internal coordinates and Cartesian coordinates in the optimization process, we will further attempt to utilize the contact map in order to make the dihedral angle of each residue limited to the reasonable value in the future. Additionally, the final step in our method, which ranks the structures in Pareto set, needs more studies. Although the method of sorting after clustering can achieve better results than the method of directly sorting all candidate structures, there is still a gap between the model 1 and the best model. Typically, more accurate ranking criteria will lead to better quality of final structures. Overall, with the encouraging initial results in both benchmark and blind tests, we expect that the further development of AIR along these lines will help build it towards a very promising approach to the extremely important protein structure refinement problem, complementary to the current state-of-the-art of the field.
Supplementary Material
Acknowledgements
We thank Dr. S. M. Golam Mortuza for critical reading through the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (No. 2018YFC0910500), National Natural Science Foundation of China (No. 61725302, 61671288, 61603161), Science and Technology Commission of Shanghai Municipality (No. 16JC1404300, 17JC1403500, 16ZR1448700) and National Institute of General Medical Sciences (GM083107, GM116960).
Conflict of Interest: none declared.
Contributor Information
Di Wang, Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, and Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China.
Ling Geng, Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, and Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China.
Yu-Jun Zhao, Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, and Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China.
Yang Yang, Department of Computer Science, Shanghai Jiao Tong University, Shanghai 200240, China.
Yan Huang, State Key Laboratory of Infrared Physics, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China.
Yang Zhang, Department of Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor, MI 48109, USA.
Hong-Bin Shen, Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, and Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China; Department of Computer Science, Shanghai Jiao Tong University, Shanghai 200240, China.
References
- Bhattacharya D. et al. (2016) 3Drefine: an interactive web server for efficient protein structure refinement. Nucleic Acids Res., 44, W406–W409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borguesan B. et al. (2015) APL: an angle probability list to improve knowledge-based metaheuristics for the three-dimensional protein structure prediction. Comput. Biol. Chem., 59, 142–157. [DOI] [PubMed] [Google Scholar]
- Bradley P. et al. (2005) Toward high-resolution de novo structure prediction for small proteins. Science, 309, 1868–1871. [DOI] [PubMed] [Google Scholar]
- Branke J. et al. (2004) Finding knees in multi-objective optimization. In: International Conference on Parallel Problem Solving from Nature.
- Brooks B.R. et al. (1983) CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem., 4, 187–217. [Google Scholar]
- Cao R. et al. (2016) Massive integration of diverse protein quality assessment methods to improve template based modeling in CASP11. Proteins, 84, 247–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case D.A. et al. (2005) The Amber biomolecular simulation programs. J. Comput. Chem., 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Shen H.B. (2012) Glocal: reconstructing protein 3D structure from 2D contact map by combining global and local optimization schemes. Curr. Bioinf., 7, 116–124. [Google Scholar]
- Cheung N.J., Shen H.B. (2014) Hierarchical particle swarm optimizer for minimizing the non-convex potential energy of molecular structure. J. Mol. Graph. Modell., 54, 114–122. [DOI] [PubMed] [Google Scholar]
- Coello C.A.C. et al. (2004) Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput., 8, 256–279. [Google Scholar]
- Cornell W.D. et al. (1995) A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- Cozzetto D. et al. (2009) Evaluation of template-based models in CASP8 with standard measures. Proteins, 77, 18–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig J.J. (1989) Introduction to Robotics: Mechanics and Control. Addison-Wesley, Reading, MA. [Google Scholar]
- Della Corte D. et al. (2016) Protein structure refinement with adaptively restrained homologous replicas. Proteins, 84, 302–313. [DOI] [PubMed] [Google Scholar]
- Dimaio F. et al. (2009) Refinement of protein structures into low-resolution density maps using Rosetta. J. Mol. Biol., 392, 181–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan H., Mark A.E. (2004) Refinement of homology-based protein structures by molecular dynamics simulation techniques. Protein Sci., 13, 211–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y. et al. (2015) Alternative approach to protein structure prediction based on sequential similarity of physical properties. Proc. Natl. Acad. Sci. USA, 112, 5029–5032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegler J.A. et al. (2009) Restriction versus guidance in protein structure prediction. Proc. Natl. Acad. Sci. USA, 106, 15302–15307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J. et al. (2017) CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy J. (2011) Particle swarm optimization. In: Sammut,C. and Webb,G.I. (eds.) Encyclopedia of Machine Learning. Springer. pp. 760–766. [Google Scholar]
- Kihara D. et al. (2001) TOUCHSTONE: an ab initio protein structure prediction method that uses threading-based tertiary restraints. Proc. Natl. Acad. Sci. USA, 98, 10125–10130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klepeis J.L. et al. (2004) Ab initio prediction of the three-dimensional structure of a de novo designed protein: a double-blind case study. Proteins, 58, 560–570. [DOI] [PubMed] [Google Scholar]
- Ko J. et al. (2012) GalaxyWEB server for protein structure prediction and refinement. Nucleic Acids Res., 40, W294–W297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinski A. et al. (1998) Monte Carlo studies of the thermodynamics and kinetics of reduced protein models: application to small helical, β, and α/β proteins. J. Chem. Phys., 108, 2608–2617. [Google Scholar]
- Leaver-Fay A. et al. (2013) Scientific benchmarks for guiding macromolecular energy function improvement. Methods Enzymol., 523, 109–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leaver-Fay A. et al. (2011) Chapter nineteen—Rosetta 3: an object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol., 487, 545–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J. (1993) New Monte Carlo algorithm: entropic sampling. Phys. Rev. Lett., 71, 211–214. [DOI] [PubMed] [Google Scholar]
- Leung M.F. et al. (2014) A new strategy for finding good local guides in MOPSO. In: 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing. pp. 1990–1997.
- Li X., Liang J. (2007) Knowledge-based energy functions for computational studies of proteins. Biol. Med. Phys. Biomed. Eng., 1, 71–123. [Google Scholar]
- Liang F., Wong W.H. (2001) Evolutionary Monte Carlo for protein folding simulations. J. Chem. Phys., 115, 3374–3380. [Google Scholar]
- Mayo S.L. et al. (1990) DREIDING: a generic force field for molecular simulations. J. Phys. Chem., 94, 8897–8909. [Google Scholar]
- Morris G.M. et al. (1998) Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem., 19, 1639–1662. [Google Scholar]
- Moult J. et al. (2016) Critical assessment of methods of protein structure prediction: progress and new directions in round XI. Proteins, 84, 4–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldziej S. et al. (2005) Physics-based protein-structure prediction using a hierarchical protocol based on the UNRES force field: assessment in two blind tests. Proc. Natl. Acad. Sci. USA, 102, 7547–7552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson B., Shehu A. (2014) Multi-objective optimization techniques for conformational sampling in template-free protein structure prediction. In: International Conference on Bioinformatics and Computational Biology (BICoB), Las Vegas, NV.
- Ortiz A.R. et al. (2009) MAMMOTH (Matching molecular models obtained from theory): an automated method for model comparison. Protein Sci., 11, 2606–2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsopoulos K.E., Vrahatis M.N. (2002) Particle swarm optimization method in multiobjective problems. In: Proceedings of the 2002 ACM Symposium on Applied Computing. ACM, Madrid, Spain, pp. 603–607. [Google Scholar]
- Peng J., Xu J. (2011) RaptorX: exploiting structure information for protein alignment by statistical inference. Proteins Struct. Funct. Bioinf., 79, 161–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raval A. et al. (2016) Assessment of the utility of contact-based restraints in accelerating the prediction of protein structure using molecular dynamics simulations. Protein Sci., 25, 19–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez O. (1840) Des lois geometriques qui regissent les desplacements d’un systeme solide dans l’espace et de la variation des coordonnees provenant de deplacements consideres independamment des causes qui peuvent les produire. J. Mathematiques Pures Appliquees, 5, 380–440. [Google Scholar]
- Rohl C.A. et al. (2003) Protein structure prediction using Rosetta. Methods Enzymol., 383, 66. [DOI] [PubMed] [Google Scholar]
- Scheraga H.A., Hao M.H. (2007) Entropy Sampling Monte Carlo for Polypeptides and Proteins. In: Prigogine,I. and Rice,S.A. (eds.) Advances in Chemical Physics. Wiley, New York.
- Song Y. et al. (2011) Structure-guided forcefield optimization. Proteins, 79, 1898–1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thachuk C. et al. (2007) A replica exchange Monte Carlo algorithm for protein folding in the HP model. BMC Bioinformatics, 8, 342.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trebst S. et al. (2006) Optimized parallel tempering simulations of proteins. J. Chem. Phys., 124, 174903.. [DOI] [PubMed] [Google Scholar]
- Tripathi P.K. et al. (2007) Multi-Objective Particle Swarm Optimization with time variant inertia and acceleration coefficients. Inf. Sci., 177, 5033–5049. [Google Scholar]
- Wallner B., Elofsson A. (2005) Pcons5: combining consensus, structural evaluation and fold recognition scores. Bioinformatics, 21, 4248–4254. [DOI] [PubMed] [Google Scholar]
- Wallner B. et al. (2003) Automatic consensus-based fold recognition using Pcons, ProQ, and Pmodeller. Proteins, 53, 534–541. [DOI] [PubMed] [Google Scholar]
- Xu D., Zhang Y. (2012) Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins Struct. Funct. Bioinf., 80, 1715–1735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J. et al. (2015) The I-TASSER Suite: protein structure and function prediction. Nat. Methods, 12, 7–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh I.C. et al. (2008) Calculation of protein heat capacity from replica-exchange molecular dynamics simulations with different implicit solvent models. J. Phys. Chem. B, 112, 15064–15073. [DOI] [PubMed] [Google Scholar]
- Zhang C. et al. (2005) A knowledge-based energy function for protein–ligand, protein–protein, and protein–DNA complexes. J. Med. Chem., 48, 2325–2335. [DOI] [PubMed] [Google Scholar]
- Zhang J. et al. (2011) Atomic-level protein structure refinement using fragment-guided molecular dynamics conformation sampling. Structure, 19, 1784–1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J., Zhang Y. (2010) A novel side-chain orientation dependent potential derived from random-walk reference state for protein fold selection and structure prediction. PLoS One, 5, e15386.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M., Kavraki L.E. (2002) A new method for fast and accurate derivation of molecular conformations. J. Chem. Inf. Comput. Sci., 42, 64–70. [DOI] [PubMed] [Google Scholar]
- Zhang Y. (2008) Progress and challenges in protein structure prediction. Curr. Opin. Struct. Biol., 18, 342–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2004) Scoring function for automated assessment of protein structure template quality. Proteins, 57, 702–710. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2005) TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res., 33, 2302–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H., Zhou Y. (2009) Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci., 11, 2714–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.