Abstract
Vaccination is one of the most effective methods to prevent the spread of infectious diseases, but due to limitations in vaccines’ availability, especially when faced with a new disease such as COVID-19, not all individuals in the community can be vaccinated. A limited number of candidates should be selected when the supply of vaccines is limited. In this paper, a method is introduced to prioritize the individuals for vaccination in order to achieve the best results in preventing the spread of COVID-19. We divide this problem into two steps: vaccine allocation and targeted vaccination. In vaccine allocation, vaccines are allocated among different population. An algorithm is proposed by defining the maximization of the total immunity among populations as an optimization problem. The aim of the targeted vaccination step is to select the individuals in each population that when vaccinated, create the greatest reduction in the transmission paths of the disease. The contact tracing data for this step is obtained from wireless communication networks and is modeled using graph theory. A metric is presented for selection of the candidates, based on centrality metrics. Simulations indicate that a 30% drop in infection rate could be achieved compared to random vaccination.
Keywords: Targeted vaccination, Vaccine allocation, COVID-19, Centrality metrics, SIR model
1. Introduction
COVID-19 (SARS-CoV-2) is an infectious disease that was first diagnosed in December 2019 in Wuhan, China. The World Health Organization declared the COVID-19 as a public health emergency of international concern on January, 2020, and a global pandemic on March 2020.
Many solutions have been proposed to mitigate the effects of the global pandemic, based on the concept of sustainable cities and environments. These include city management (Zhou, Qiu, Pu, Huang, & Ge, 2020), lockdown management (Rahman et al., 2020), and case prediction (Zivkovic et al., 2021). In the same framework of sustainability, the effects of urban environments on the spread of the disease (Kim, 2021, Kutela et al., 2021, Li et al., 2021, Shokouhyar et al., 2021) have been explored.
Another way to leverage the concept of sustainable cities to mitigate the effects of the pandemic is to utilize the wireless communications infrastructure to gather information, and various machine learning and optimization methods to use this information to stop the transmission chain of the virus, e.g. by performing targeted vaccination. Various methods could be employed to collect this information. These including Bluetooth signals to detect proximity and duration of contacts (Leith & Farrell, 2020), base station antennas to determine the locations of users (cell tower triangulation), the GPS system to locate and track users, network of drones connected to a central system (Saeed, Bader, Al-Naffouri, & Alouini, 2020), wireless sensor networks in the form of mobile and stationary sensors to monitor individuals (Sun, Lu, Zhang, Salathé, & Cao, 2016), and scanning QR codes with mobile phones and storing the contact information of the individuals (Sharma et al., 2020).
Vaccination is one of the most effective methods to prevent the spread of diseases in the community. But due to the limited resources currently available, public vaccination is not possible in short term. On the other hand, due to the high prevalence, if a vaccine is approved, a fair and optimal distribution of it will be a very important issue, since it will take a long time to produce enough doses of the vaccine to vaccinate the entire society. As a result, a limited number of people should be selected in such a way that vaccinating them would be most effective in disrupting the transmission chain of the disease.
The authors of [13] prioritize the target individuals from the community at large by dividing the community into smaller groups and analyzing them, without examining individuals. The method used in [3] is based on the analysis of the eigenvalues of the community graph matrix to vaccinate the nodes that maximize these eigenvalues. In [14], digital communication activities of individuals have been utilized for finding target individuals for vaccination. Information is collected from several sources, such as Facebook friendships, Facebook activity/feeds, call records and Bluetooth for measure in person-to-person contacts; and individuals are selected on the basis of their closeness centrality within cyber networks. Sun et al. in Sun et al., 2015, Sun et al., 2016 have deployed contact tracing in a high school using a wireless sensor system. Each student is given a mobile unit to carry in all times, to record their movements and interactions. The gathered information is modeled as a graph, and vaccination candidates are selected using centrality metrics. The authors of [12] propose a new algorithm based on both intra-central and inter-central criteria for describing nodes in societies. Several heuristics methods are proposed in [15] to distribute a fixed amount of resources throughout the nodes of a network such that the infection rate is minimized. In [4], targeted vaccination has been investigated in scale-free synthetic networks, assuming a simple disease model with variable disease rates. An equal graph partitioning strategy is presented in [2] to immunize a network with limited resources. The authors of [25] propose a model where users in a network are first divided into clusters, and then either all users in each cluster receive a security software pack to counter the effects of the virus, or none of them does.
In this paper, a method is introduced to find suitable candidates for vaccination to achieve the best results in preventing the spread of COVID-19. This method is comprised of two steps: vaccine allocation and targeted vaccination. In the vaccine allocation phase, available vaccines are distributed among different population communities (e.g. different cities) depending on the conditions of each area, and in the targeted vaccination phase, the best candidates for vaccinate in each community are determined.
The candidates for vaccination in the targeted vaccination phase could be determined by different methods and criteria, including random vaccination, vaccination based on number of daily contacts with other people, and vaccination based on predefined protocols. Another contribution of this paper is proposing a combined metric, based on a number of centrality metrics in graph theory, to find the optimal candidates for vaccination.
The rest of the paper is organized as follows; Mathematical modeling of the epidemic is discussed in Section 2. The problem of vaccine allocation is defined in Section 3. The targeted vaccination problem and the metrics utilized to solve it are examined in Section 4, and the simulations and their results are provided in Section 5. The conclusions are provided in Section 6.
2. System and epidemic model
2.1. System model
There are two general types of vaccination strategies; Static and dynamic methods. In the static strategy, specific protocols are designed by different countries on the basis of their national priorities and guidelines. By contrast, in the dynamic strategy, protocols are designed based on mathematical modeling of infectious diseases. In this paper, a dynamic strategy is proposed to model social contacts and the vaccination process.
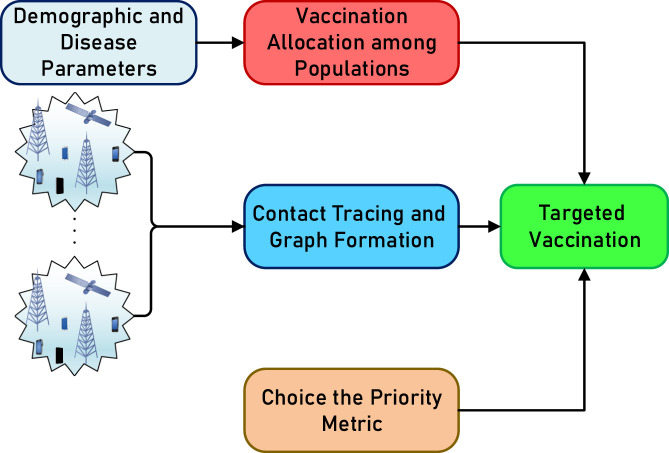
The proposed system model and vaccination strategy are presented in Fig. 1. The vaccines are first distributed among different populations based on demographics and disease parameters, and then administered to the individual candidates proposed by applying predefined criteria (e.g. number of contacts with other individuals) using the contact tracing graph model, which is in turn obtained from wireless network data.
Fig. 1.
The proposed system model.
2.2. Mathematical modeling of the spread of the disease
Compartmental models are mathematical models that divide the community into a number of “compartments”, and move individuals between them at certain rates. These models are described using systems of ordinary differential equations, and solution of these equations describes the number of individuals in each compartment over time and shows how the disease behaves (Keeling and Rohani, 2011, Kiss et al., 2017).
2.3. SIR model
The “SIR” model is a simple compartmental model where the individuals is divided into three groups: Susceptible, Infected, and Recovered. The susceptible group includes individuals who are susceptible to the disease and if they come in contact with an infected person they may contract the disease. The infected group comprises of individuals who have the disease, and the recovered group contains individuals who recover from the disease, are vaccinated, or die (Hethcote, 2000, Westerink-Duijzer, 2017).
Suppose that is a set of populations, and , and represent the fractions of the susceptible, infected, and recovered individuals in population at time , respectively. Denoting the number of people in population by , and the number of susceptible, infected and recovered individuals of this population at time is by , and , respectively, It is obvious that . With these definitions, , and . Afterwards with respect to these relationships:
| (1) |
The SIR model is described by following systems of ordinary differential equations (Keeling and Rohani, 2011, Kiss et al., 2017):
Where and represent the disease transmission rate and recovery rate, respectively. (2a) states that the change of susceptible individuals is related to the population of the susceptible group and the number of infected people. (2c) expresses the relationship between changes in recovered and infected Individuals. (2b) can be obtained from the (2a), (1), (2c). The SIR model described by (2a), (2b), (2c) is shown in Fig. 2. It is usually assumed that the initial conditions are given, i.e. the values , and are known.
Fig. 2.
The SIR model.
2.4. SEIR model
This model is similar to the SIR model, with the addition of a fourth exposed compartment . The individuals in this compartment are infected but cannot transmit the infection yet. The system of ordinary differential equations describing this model is forumlated as follows:
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where is the rate of exposure.
3. Vaccine allocation
The goal of this optimization problem is to distribute a limited number of vaccines among different population communities. The solution determines the number of vaccines allocated to each community.
3.1. Vaccination and immunity
Vaccination decreases the number of susceptible individuals and thus reduces the number of individuals who will be infected. In this problem, the objective function is defined as the total number of individuals who do not get infected. Vaccination increases these individuals in two ways. The first case is for susceptible individuals who have been vaccinated, which is called the direct method, and the second case is for individuals who are not vaccinated but will be less exposed to the disease when other people are vaccinated, which is called the indirect method.
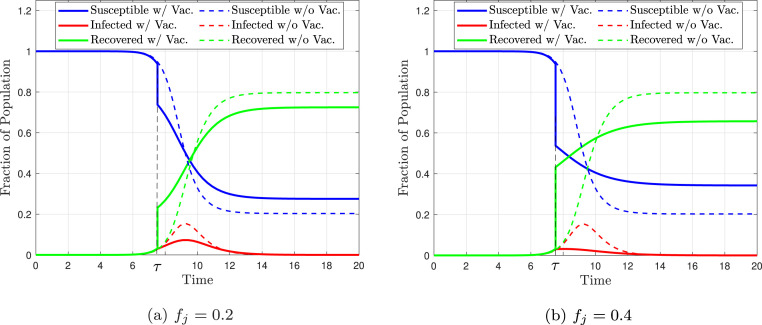
Suppose a fraction of the population is vaccinated at time . This fraction is denoted by and it cannot be greater than the fraction of the susceptible individuals at the time of vaccination, so . The state of the disease at time and exactly before vaccination can be expressed by . Assuming that everyone is immune immediately after vaccination, the state of the disease changes to instantly after vaccination. That is, at the time of vaccination, the vaccination fraction is subtracted from the susceptible individuals fraction and added to the recovered individuals fraction (Westerink-Duijzer, 2017). Fig. 3 shows the solution of the Eqs. (2) of the SIR model with vaccination. It is noteworthy that the system of equations is solved twice, and the initial values of the second solution are the final value of the first solution. In this figure, the dashed lines are for the unvaccinated case and the solid lines are for the vaccinated case. It can be seen that at the time of vaccination , the fraction of susceptible individuals and the fraction of recovered individuals exhibit a sudden change equal to the value of . In Fig. 3, Fig. 3, it is assumed that is equal to 0.2 and 0.4, respectively. As evident in these figures, with vaccination, the fraction of infected people is lower compared to the case without vaccination (dashed line) and it also has a smaller peak. It is also clear that with a greater vaccination fraction (more people vaccinated), the curve is suppressed further.
Fig. 3.
The value of the three compartments of the SIR model, with vaccination occurring at time for population . Solid lines represent the vaccinated case and dashed lines represent the unvaccinated case. It is assumed that vaccination occurs when 2.5% of the population is infected and assumed that , , , and .
Note that the behavior of the curve depends on the number of vaccines available and vaccination time . The number of susceptible individuals who have not been infected is a suitable metric for comparing different methods of vaccine allocation. To this end, the final state of the system must be considered. Since , this state is also called the disease-free state. Function is defined as the final fraction of susceptible individuals while fraction of susceptible individuals is vaccinated at time in the population . Formally,
| (4) |
where and .
The immunity of individuals in the susceptible group can be achieved in several ways. People who receive the vaccine or recover from the disease will have immunity. Susceptible individuals whose contact with others is confined to a sufficient number of vaccinated or cured people are also immune to the disease. This type of immunity is called herd immunity. The part of the population that not get the disease due to herd immunity is called herd effect. In fact, the herd effect is equal to the fraction of individuals who are still susceptible to the disease when the disease dies out (Westerink-Duijzer, 2017). Therefore, measures the herd effect on the population , according to (4) and it is appropriate to study this function in more detail.
3.2. The herd effect
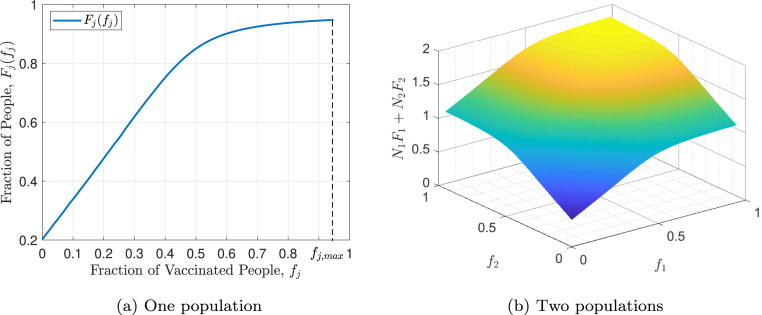
In this subsection, the general structure of , which measures the herd effect, is examined. There is no explicit expression for and it should be calculated numerically. For convenience, the cases of fixed vaccination fraction and fixed vaccination time are considered and are denoted by and respectively.
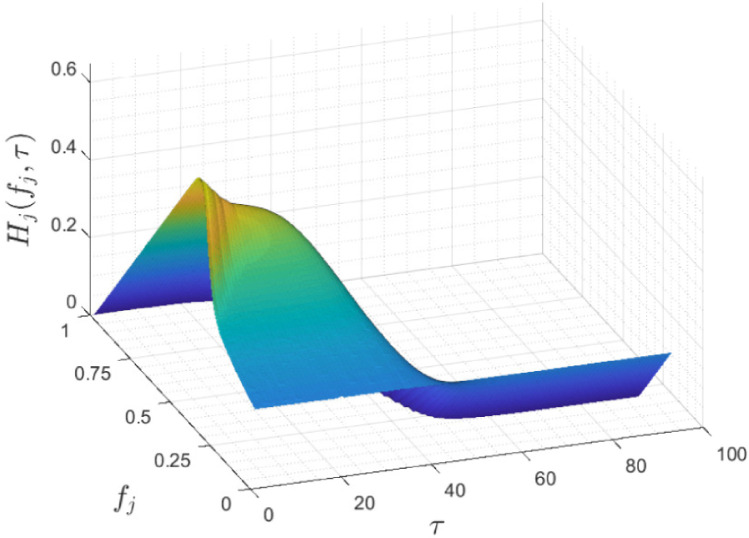
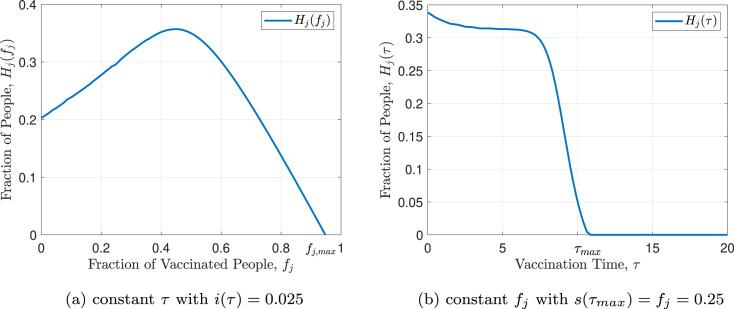
Fig. 4 shows as a function of vaccination fraction and vaccination time. As it can be seen in the figure, this function is decreasing with respect to time of vaccination and first increasing and then decreasing with respect to the vaccination fraction . For a closer look, Fig. 5 represents and . As evident in Eq. (4) and proven in [23], has one maximum point and one inflection point. Also it is monotonically increasing up to the maximum point and monotonically decreasing after that. By evaluating the function in terms of different and ’s, it can be concluded that the general structure of the function does not depend on these variables and has a specified shape. As evident in Fig. 5(b), is strictly decreasing and its maximum occurs at . By increasing the vaccination time, more individuals become infected, so the final susceptible individuals fraction, , decreases. It can be concluded that the best time for vaccination is at the beginning of the outbreak of the disease and if the vaccine is not available at that time, vaccination should be performed as soon as possible and immediately after the vaccine is produced. Note that, like , The general structure of is not dependent on and ’s values.
Fig. 4.
Herd effect with respect to the fraction of vaccination and the time of vaccination.
Fig. 5.
Herd effect function.
3.3. Vaccine allocation problem formulation
Assuming that is the number of available vaccines, the objective is to maximize the total number of people in different populations who do not get infected. Considering the optimization variable , The optimization problem can be formulated as follows (Westerink-Duijzer, 2017):
The first and second terms in (5a) represent the direct and indirect (herd) effects of vaccination, respectively. (5b) states that the total number of vaccines distributed among different populations should not exceed the number of available vaccines. (5c) states that the vaccination fraction of one population cannot be negative and should at most be equal to the fraction of susceptible individuals in the population at the time of vaccination.
The function is defined as the total effect of vaccinating a fraction of the population . This total effect is resulted from direct and indirect (herd effect) methods and can be written as follows:
| (6) |
where the first and second terms represent the direct and indirect (herd effect) methods of vaccination, respectively. It should be noted that the objective function in (5) is equal to . The function corresponding to the function in Fig. 5(a) is shown in Fig. 6(a). As can be seen, is a monotonically increasing function, i.e. more immunity is achieved when more susceptible individuals are vaccinated in a population and it is better to allocate all available vaccines to the population. The maximum value of this function occurs in , which is equal to the fraction of susceptible individuals in the population at the time of vaccination, i.e. . It should be noted that usually, due to the lack of vaccines, not all susceptible individuals can be vaccinated at the time of vaccination, i.e. usually , but should be as large as possible. It is also noteworthy that extensions of the SIR model, such as the SIR model with demography, the MSIR model, and the SEIR model yield very similar results, which can be verified easily.
Fig. 6.
The Total Effect of Vaccination.
Assuming that there are two populations , the objective function can be written as . Fig. 6(b), represents this function assuming and . In fact, , and the initial values of the two populations are assumed to be identical. The objective function does not depend on the values of and , but on their ratio. It is also evident that this function is monotonically increasing with respect to both and .
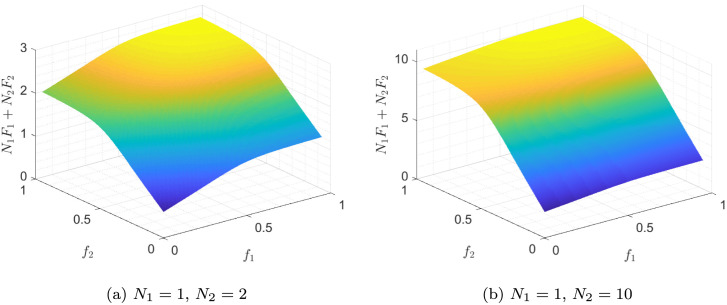
In Fig. 7, the objective function is drawn for , and , . As it can be seen, by increasing , the sensitivity of the objective function to decreases. Compared to the case of , the value of changes less with . This is a result of the fact that smaller populations have fewer individuals and their immunity has less overall impact than larger populations.
Fig. 7.
The objective function of (5), assuming to have two populations and .
3.4. Solution of the vaccine allocation problem
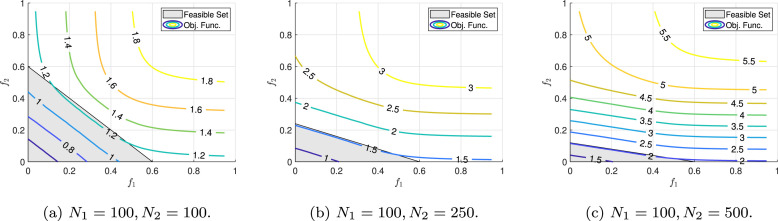
So far we have only examined the objective function of the optimization problem (5), and have not analyzed the constraints. In this examination, it was concluded that the objective function is strictly increasing with respect to and and reaches its maximum value at point (assuming ). It should be noted that this value violates constraint (5b), and as a result, is not in the feasible set. Assuming that there are two populations, constraint (5b) represents the half-plane at the bottom of the line. This line intersects the axes and at points and , respectively. Also, constraint (5c) describes a rectangle with two opposite vertices and . Assuming and (if any of these two inequality does not hold, the feasible set would become smaller) the contour plots of the objective function and the feasible set are presented in Fig. 8 for different values of and . , , and the initial values of the populations are assumed to be identical.
Fig. 8.
Contour plot of the objective function and the feasible set of the optimization problem (5) for different values of and . It is assumed that .
Two observations can be seen on this figure. First, by increasing , the objective function becomes more sensitive to changes in , and less sensitive to changes in . Second, by increasing , the value of , which is the point of intersection of the line with the axis, decreases, and large values cannot be chosen for . As already mentioned, constraint (5) must be active, therefore in Fig. 8 the feasible points must reside on the line passing through the points and , and the two dimensional feasible set is reduced to a line segment (to a dimensional hyper-plane in general). According to this perceptive, by observing Fig. 8, by increasing the value of , the values of the objective function that on the line passing through the two points and , which are less sensitive to and and have an almost constant value.
To solve this optimization problem numerically, given the concave structure of the objective function, an algorithm inspired by the gradient descent method can be utilized. For the two-variable optimization problem (), an arbitrary point on the line is selected, and is iteratively moved on the line in the direction that the value of the objective function increases, in order to reach the maximum point. The pseudo code of proposed algorithm is represents in Algorithm 1. To solve a problem with larger dimensions, we can proceed like a two-variable problem, except that the feasible points have higher dimensions (one less than the dimensions of the problem variable). Another method is to find the vaccination fraction ratio for both populations using Algorithm 1 and finally distribute the vaccines based on these ratios.
4. Targeted vaccination
In this section, the disease propagation graph is first introduced, and then a targeted vaccination algorithm is presented to control the pandemic.
4.1. Disease propagation graph
Since the disease can spread via physical contact between infected and susceptible individuals, we could utilize a graph to model the transmission of the disease, where the nodes represent individuals and the edges represent the existence of contact between two people. This graph is called the disease propagation graph (Sun et al., 2016), and it is defined as where is the set of graph nodes (individuals in the community) and is the set of graph edges (possibility of transmission between people) with weights assigned to the edges. and represent the number of people in the study population and the number of connections between them, respectively. The elements of set are ordered pairs; In other words, for , there exists an edge if and only if there is a connection between and . Since the disease can be transmitted in both directions, this graph is undirected. The weight of each edge in the disease propagation graph indicates the probability of disease transmission between the two nodes. These weights depend on the frequency of contacts between the people and their locations (indoors or outdoors).
4.2. Metrics
The importance of each node in the spread of the disease can be measured by metrics such as degree centrality, betweenness centrality, and closeness centrality (Brandes, 2001, Sun et al., 2015, Sun et al., 2016) A new metric called connectivity centrality is defined as follows:
| (7) |
where is equal to if there exists a path between nodes and and to zero if there are no paths between nodes and , is weight of the edge between and nodes; and indicates the number of paths from node to node . It should be noted that after calculating the values of each centrality metric for nodes in the graph, the nodes that have the highest value for each metric are not necessarily candidates for vaccination, since some nodes might be infected and it is pointless to vaccinate infected people.
4.2.1. Infection susceptibility and infecting ability metrics
The centrality metrics determine the vertices that impact the greatest number of nodes. To find the best vaccination candidates, proximity to infected nodes should also be taken into account. Infecting ability, and infection susceptibility metrics are defined for this purpose. Infecting ability is defined as the ability of each individual to infect other people in the community, and infection susceptibility is defined as the probability of getting infected for each node.
The set of all infected nodes is denoted by . To calculate the infecting ability metric, it should be noted that, no one can infect a node that is already infected and the impact of any given node on other nodes that are close to infected nodes is negligible. Infecting ability is then defined as follows (Sun et al., 2016):
| (8) |
And infection susceptibility is defined as follows:
| (9) |
where is degree centrality. (9) is a recursive model, and the linear equations system should be solved in order to obtain infection susceptibilities. To more accurately assess the eligibility of the nodes for vaccination, both infecting ability and infection susceptibility should be taken into account. To achieve this, these two metrics could be combined as in a new metric, which we call combined susceptibility metric (Sun et al., 2016):
| (10) |
where .
In the targeted vaccination algorithm, the candidate nodes for vaccination are selected and vaccinated based on an appropriate metric. After calculating the metric for all nodes, the node with the highest value is vaccinated if it is susceptible to the disease. The vaccinated node is then removed from the graph, and the graph is updated. This process is then repeated until all available vaccines are administered.
5. Simulation and results
The proposed method has been simulated using “Primary school - cumulated networks” dataset (Stehlé et al., 2011), which is a contact tracing network, representing a weighted graph of daily face-to-face contacts among 242 individuals.
The SIR model has been utilized in simulating the spread of the disease. On the first day, 1% of the nodes are randomly infected, and the rest of the nodes are considered susceptible to infection, and the infection spreads among the individuals. After the number of infected nodes exceeds (where controls the vaccination time), vaccines are administered to the nodes obtained from the proposed method (where is the fraction of the population that is vaccinated). The disease continues to spread after vaccination, until no infected nodes remain, and the disease is eradicated.
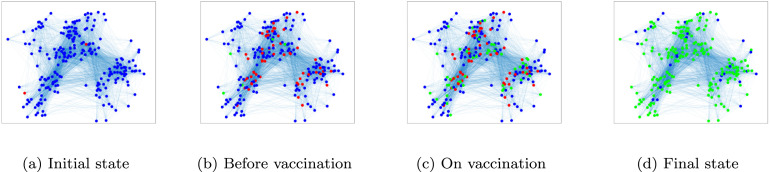
The graph of susceptible, infected, and recovered individuals are plotted in Fig. 9. In this figure, blue, red and green nodes represent the susceptible, infected, and recovered individuals, respectively. This figure shows the spread of the disease and the administration of the vaccine. In Fig. 9(a), before the disease begins spreading, 1% of the nodes are considered infected and the rest are susceptible to the disease. Also, and are both assumed to be equal to 0.2. Fig. 9(b) shows the status of graph right before vaccination. Immediately after vaccination, the status of graph changes to Fig. 9(c). Then the disease continues spreading, until finally, in Fig. 9(d) it dies out and the graph reaches its steady state.
Fig. 9.
An example of the spread of the disease and vaccination. The blue, red, and green nodes indicate susceptible, infected, and recovered individuals, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
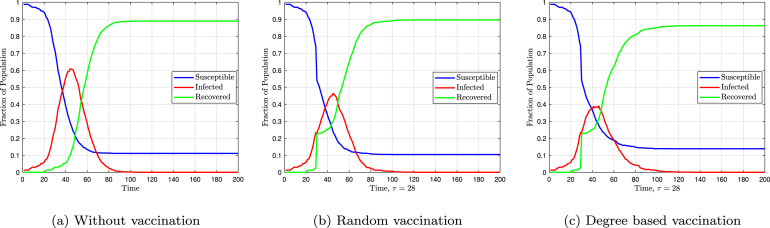
Fig. 10 shows the fractions of susceptible, infected, and recovered individuals over time. Vaccination is not performed in Fig. 10(a), and the disease dies out due to the herd effect. In Fig. 10, Fig. 10, vaccination is performed randomly and based on degree centrality, respectively. In these two figures, the fractions of susceptible and infected individuals abruptly change by a value equal to the vaccination fraction. It is obvious that targeted vaccination reduces the maximum fractions of infected individuals.
Fig. 10.
Fraction of susceptible, infected and recovered individuals assuming .
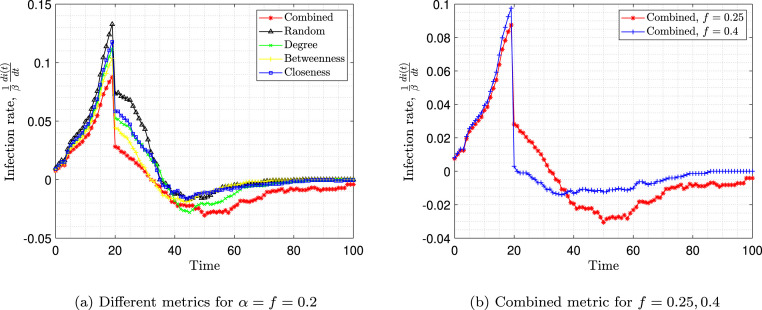
Fig. 11(a) represents the infection slope normalized to beta over time. The infection slope is defined as . This slope represents the derivative of the red curve in Fig. 10. As expected, when the number of susceptible individuals is large, the infection slope is high. After vaccination, the infection slope decreases but remains positive until the number of infected individuals reaches its peak and the slope reaches zero. After that, the infection slope becomes negative and finally, due to the herd effect, the disease dies out and the infection slope reaches zero again. It is observed that targeted vaccination using any metric can reduce the infection rate after vaccination and bring it down to zero. However, as the figure suggests, using the combined metric results in an immediate reduction in the rate of infection after vaccination, and keeping the infection rate lower (more negative) in comparison to other metrics. Immediately after vaccination, the infection rate in the case of vaccination using the combined metric is about 30% lower than the random vaccination.
Fig. 11.
Infection rates over time.
Fig. 11(b) shows the infection rate when using the combined metric for vaccination of two different populations. As it is expected, when the number of vaccinated individuals increases, the disease is better controlled. The figure also shows that the infection rate after vaccination is much lower for and reaches zero slope (eradication of the disease) faster than .
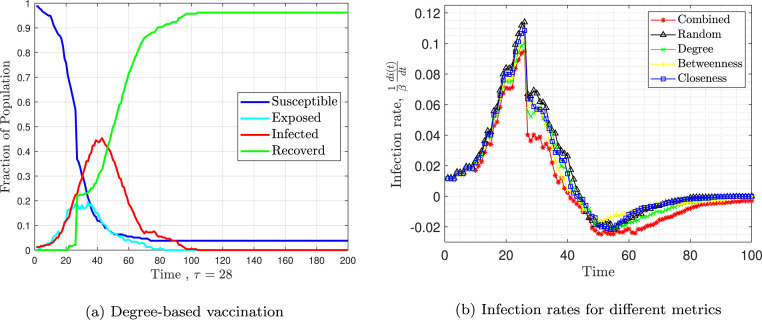
Fig. 12 presents the results of SEIR model. Fig. 12, Fig. 12 are similar to Fig. 10(c) and Fig. 11(a). Fig. 12(a) shows the fraction of susceptible, exposed, infected, and recovered individuals over time. Fig. 12(b) shows the infection rate over time. The combined metric outperforms the others.
Fig. 12.
Simulation of the SEIR model assuming .
6. Conclusion
In this paper, a vaccination strategy was proposed to allocate a limited number of vaccines among different populations, and to vaccinate the most effective candidates in disrupting the transmission chain of the disease in each population. The proposed vaccination strategy is divided into two parts: vaccine allocation and targeted vaccination. In vaccine allocation, all available vaccines are allocated among populations so that total immunity is maximized. Then in targeted vaccination, individuals are prioritized according to an appropriate predefined metric. To facilitate the prioritization of the individuals, graph-based methods and contact tracing data obtained from wireless communication networks are used. By investigating different metrics, such as, degree centrality, and connectivity centrality, a combined metric was proposed to model infecting ability and infection susceptibility. The results of the simulations indicate that this combined susceptibility metric can control the spread of the disease faster than any other metric on its own, and achieve a 30% drop in infection rate immediately after vaccination compared to random vaccination.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The support of the Hatam research fund of Amirkabir University of Technology is gratefully acknowledged.
References
- Brandes U. A faster algorithm for betweenness centrality. Journal of Mathematical Sociology. 2001;25(2):163–177. [Google Scholar]
- Chen Y., Paul G., Havlin S., Liljeros F., Stanley H.E. Finding a better immunization strategy. Physical Review Letters. 2008;101(5) doi: 10.1103/PhysRevLett.101.058701. [DOI] [PubMed] [Google Scholar]
- Cohen R., Havlin S., Ben-Avraham D. Efficient immunization strategies for computer networks and populations. Physical Review Letters. 2003;91(24) doi: 10.1103/PhysRevLett.91.247901. [DOI] [PubMed] [Google Scholar]
- Fu X., Small M., Walker D.M., Zhang H. Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Physical Review E. 2008;77(3) doi: 10.1103/PhysRevE.77.036113. [DOI] [PubMed] [Google Scholar]
- Hethcote H.W. The mathematics of infectious diseases. SIAM Review. 2000;42(4):599–653. [Google Scholar]
- Keeling M.J., Rohani P. Princeton University Press; 2011. Modeling infectious diseases in humans and animals. [Google Scholar]
- Kim D. Exploratory study on the spatial relationship between emerging infectious diseases and urban characteristics: Cases from Korea. Sustainable Cities and Society. 2021;66 doi: 10.1016/j.scs.2020.102672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss I.Z., Miller J.C., Simon P.L., et al. Springer; Cham: 2017. Mathematics of epidemics on networks. [Google Scholar]
- Kutela B., Novat N., Langa N. Exploring geographical distribution of transportation research themes related to COVID-19 using text network approach. Sustainable Cities and Society. 2021 doi: 10.1016/j.scs.2021.102729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leith D.J., Farrell S. 2020. Coronavirus contact tracing: Evaluating the potential of using bluetooth received signal strength for proximity detection. [Google Scholar]
- Li B., Peng Y., He H., Wang M., Feng T. Built environment and early infection of COVID-19 in urban districts: A case study of Huangzhou. Sustainable Cities and Society. 2021;66 doi: 10.1016/j.scs.2020.102685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z., Sun X., Wen Y., Cao G., La Porta T. Algorithms and applications for community detection in weighted networks. IEEE Transactions on Parallel and Distributed Systems. 2014;26(11):2916–2926. [Google Scholar]
- Lu Z., Wen Y., Cao G. 2013 IEEE international conference on pervasive computing and communications (PerCom) IEEE; 2013. Community detection in weighted networks: Algorithms and applications; pp. 179–184. [Google Scholar]
- Mones E., Stopczynski A., Pentland A.S., Hupert N., Lehmann S. Optimizing targeted vaccination across cyber–physical networks: an empirically based mathematical simulation study. Journal of the Royal Society Interface. 2018;15(138) doi: 10.1098/rsif.2017.0783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash B.A., Adamic L., Iwashyna T., Tong H., Faloutsos C. Proceedings of the 2013 SIAM international conference on data mining. SIAM; 2013. Fractional immunization in networks; pp. 659–667. [Google Scholar]
- Rahman M.A., Zaman N., Asyhari A.T., Al-Turjman F., Bhuiyan M.Z.A., Zolkipli M. Data-driven dynamic clustering framework for mitigating the adverse economic impact of Covid-19 lockdown practices. Sustainable Cities and Society. 2020;62 doi: 10.1016/j.scs.2020.102372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saeed N., Bader A., Al-Naffouri T.Y., Alouini M.-S. 2020. When wireless communication faces COVID-19: Combating the pandemic and saving the economy. arXiv preprint arXiv:2005.06637. [Google Scholar]
- Sharma S., Singh G., Sharma R., Jones P., Kraus S., Dwivedi Y.K. Digital health innovation: exploring adoption of COVID-19 digital contact tracing apps. IEEE Transactions on Engineering Management. 2020 [Google Scholar]
- Shokouhyar S., Shokoohyar S., Sobhani A., Gorizi A.J. Shared mobility in post-COVID era: New challenges and opportunities. Sustainable Cities and Society. 2021 doi: 10.1016/j.scs.2021.102714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stehlé J., Voirin N., Barrat A., Cattuto C., Isella L., Pinton J.-F., et al. High-resolution measurements of face-to-face contact patterns in a primary school. PLoS One. 2011;6(8) doi: 10.1371/journal.pone.0023176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X., Lu Z., Zhang X., Salathé M., Cao G. 2015 IEEE international conference on pervasive computing and communications (PerCom) IEEE; 2015. Targeted vaccination based on a wireless sensor system; pp. 215–220. [Google Scholar]
- Sun X., Lu Z., Zhang X., Salathé M., Cao G. Infectious disease containment based on a wireless sensor system. Ieee Access. 2016;4:1558–1569. doi: 10.1109/ACCESS.2016.2551199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerink-Duijzer E. 2017. Mathematical optimization in vaccine allocation. [Google Scholar]
- Zhou Z.-J., Qiu Y., Pu Y., Huang X., Ge X.-Y. BioAider: An efficient tool for viral genome analysis and its application in tracing SARS-CoV-2 transmission. Sustainable Cities and Society. 2020;63 doi: 10.1016/j.scs.2020.102466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Z., Cao G., Zhu S., Ranjan S., Nucci A. Handbook of optimization in complex networks. Springer; 2012. A social network based patching scheme for worm containment in cellular networks; pp. 505–533. [Google Scholar]
- Zivkovic M., Bacanin N., Venkatachalam K., Nayyar A., Djordjevic A., Strumberger I., et al. COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach. Sustainable Cities and Society. 2021;66 doi: 10.1016/j.scs.2020.102669. [DOI] [PMC free article] [PubMed] [Google Scholar]