Rules of contact inhibition of locomotion for cells on suspended nanofibers

Significance

When cells heal a wound or invade a new area, they coordinate their motion. Coordination is often studied by looking at what happens after pairs of cells collide. Postcollision, cells often exhibit contact inhibition of locomotion—they turn around and crawl away from the point where they touched. Past knowledge of repolarization on contact comes from studies on flat surfaces, unlike cells in the body, which crawl along fibers. We discover that cells on single fibers walk past one another, but cells in contact with multiple fibers stick to one another and move as pairs. This outcome changes to walk past after cell division. Our experiments and models reveal how the environment regulates cell–cell coordination after contact.

Abstract

Contact inhibition of locomotion (CIL), in which cells repolarize and move away from contact, is now established as a fundamental driving force in development, repair, and disease biology. Much of what we know of CIL stems from studies on two-dimensional (2D) substrates that do not provide an essential biophysical cue—the curvature of extracellular matrix fibers. We discover rules controlling outcomes of cell–cell collisions on suspended nanofibers and show them to be profoundly different from the stereotyped CIL behavior on 2D substrates. Two approaching cells attached to a single fiber do not repolarize upon contact but rather usually migrate past one another. Fiber geometry modulates this behavior; when cells attach to two fibers, reducing their freedom to reorient, only one cell repolarizes on contact, leading to the cell pair migrating as a single unit. CIL outcomes also change when one cell has recently divided and moves with high speed—cells more frequently walk past each other. Our computational model of CIL in fiber geometries reproduces the core qualitative results of the experiments robustly to model parameters. Our model shows that the increased speed of postdivision cells may be sufficient to explain their increased walk-past rate. We also identify cell–cell adhesion as a key mediator of collision outcomes. Our results suggest that characterizing cell–cell interactions on flat substrates, channels, or micropatterns is not sufficient to predict interactions in a matrix—the geometry of the fiber can generate entirely new behaviors.

Cell migration is an essential component of various physiological processes such as morphogenesis, wound healing, and metastasis (1). Cell–cell interactions in which cell–cell contact reorients cell polarity are necessary for the correct function of many developmental events (2). One of the earliest such interactions known was termed “contact inhibition of locomotion” (CIL) by Abercombie and Heaysman over five decades ago in chick fibroblasts cultured on flat two-dimensional (2D) substrates (2–4). In CIL, two approaching cells isolated from the rest of the cell population first make contact, followed by protrusion inhibition at the site of contact, which leads to cell repolarization through formation of new protrusions away from the site of contact. Subsequently, cells migrate away from each other in the direction of newly formed protrusions (1). This sequence can, however, be altered in specific conditions such as metastasis in which a loss of CIL allows malignant cells to invade fibroblast cultures—this is a loss of CIL between different cell types (heterotypic CIL) (4, 5). Recent work has also begun to identify the molecular players that initiate and regulate CIL, including Rac activity, microtubules, Eph/Ephrin binding, and E- and N-cadherin expression (6–10).

CIL is most commonly studied and analyzed on flat 2D substrates using several invasion and collision assays (2, 3, 11). By contrast, cells traveling in matrix in vivo are constrained to move along narrow fibers. A common shortcoming in featureless 2D assays is thus the inability to study CIL under natural constraints (11–13). Recently, micropatterned substrates have been used to understand restricted motility, developing one-dimensional (1D) collision assays where cell migration is constrained to straight lines, allowing for a greater occurrence of cell–cell collisions to quantify rates and outcomes of different types of cell–cell interactions (11, 13–15). These interactions do not necessarily resemble the stereotyped CIL behavior. Broadly, experiments and simulations (16–18) have observed the following: 1) the classical stereotype of CIL with two cells contacting head-on, with both cells repolarizing (referred to as “reversal” or “mutual CIL”); 2) after a head-on collision, only one cell reverses (“training” or “nonmutual CIL”); and 3) cells manage to crawl past or over one another, exchanging positions (“walk past” or “sliding”). Within the well-studied neural-crest cell explants, walk past is extremely rare (11), but it can occur in epithelial cells, especially in those that have been metastatically transformed or that have decreased E-cadherin expression (15).

Both 2D substrates and micropatterned stripes provide controllable and reproducible environments but neither fully models the details of in vivo native cellular environments, which consist of extracellular matrices (ECM) of fibrous proteins, with these fibers having different radii. Our earlier in vitro recapitulation of the effects of fiber curvature showed that both protrusive and migratory behavior is sensitive to fiber diameter (19–21). Furthermore, we have shown that suspended, flat 2D ribbons do not capture the protrusive behavior observed on suspended round fibers (19); thus, we wanted to inquire if the CIL rules developed on 1D collision and 2D assays extend to contextually relevant fibrous environments. To understand CIL in fibrous environments that mimic native ECM, we use suspended and aligned nanofiber networks to study CIL behavior in NIH/3T3 fibroblast cell–cell pairs exhibiting two distinct elongated morphologies: spindle, attached to a single fiber and parallel cuboidal, attached to two fibers (22). We further investigate the effect of cell division on CIL by studying the encounters of cells that have recently divided (daughter cells) with other cells; these recently divided cells are much faster, consistent with earlier work (23). Our work allows us to determine the types and rates of cell–cell contact outcomes—the “rules of CIL”—in a biologically relevant system with a controlled geometry. These rules are radically different from the known stereotypical behavior in 2D assays, but the essential features of these rules emerge robustly from a minimal computational model of CIL in confined geometries.

Results

Fiber Spacing and Diameter Control Cell Shape; Cell Division Controls Speed.

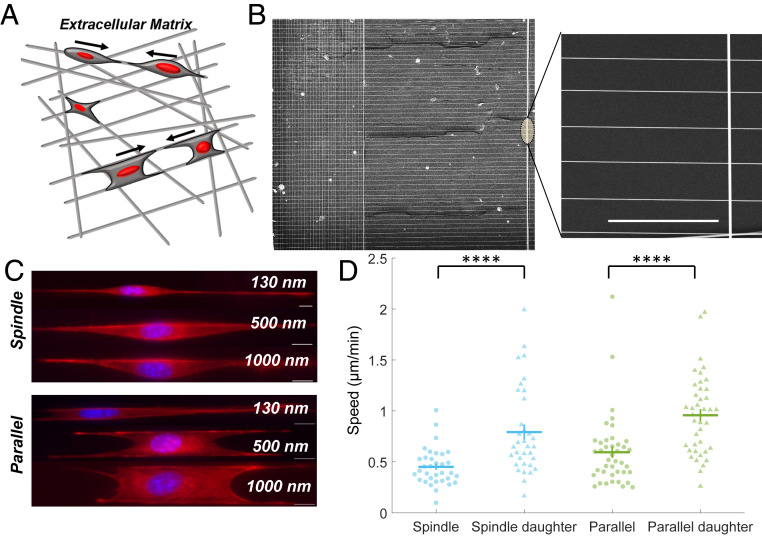
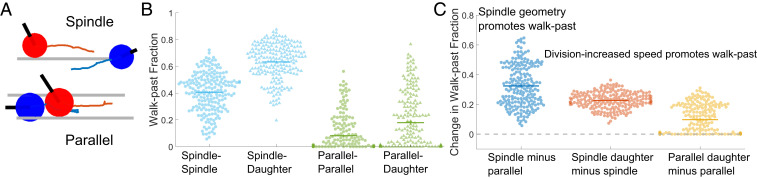
To develop the rules of CIL in fibrous environments mimicking native ECM, as shown schematically in Fig. 1A (24), we must first specify a controllable geometry. We cultured cells on suspended fibers of four diameters: 130, 150, 500, and 1,000 nm, which we created using the previously reported nonelectrospinning spinneret-based tunable engineered parameters (STEP) method (Fig. 1B) (25–27). We observed that cells on these fiber networks were generally found in a “spindle” geometry when placed on fibers with spacing ∼20 µm where cells are only in contact with one fiber and elongate along that fiber, or in a “parallel-cuboidal” geometry, spanning two fibers (Fig. 1C), when on fibers with spacing ∼10 µm. We observed that cells on ∼130 and 150 nm fibers exhibited dynamic plasticity in shape changes leading to shedding of cellular fragments from longer protrusions during migration (Movie S1, Fig. 1C, and SI Appendix, Fig. S1). Furthermore, on these diameters, cell contractility led to parallel fibers being pulled inward toward the cell—parallel-cuboidal geometry cells quickly become spindle geometry cells. Protrusions formed on 1,000 nm diameter fibers were of similar lengths as those observed on 500 nm diameter fibers but at times difficult to optically discern (Movie S2). Thus, we selected our ∼500 nm diameter fibers as the central model system. We also immediately observed that cells underwent mitotic division, and daughter cells subsequently migrated with a large increase in speed in both spindle and parallel-cuboidal configurations (Fig. 1D).

Fig. 1.

Cell motility on nanofiber network. (A) Depiction of a cell’s in vivo ECM environment with ECM fibers. (B) SEM image of aligned parallel fibers (500 nm) manufactured using the STEP method and used for CIL experiments. (Scale bar, 50 μm.) (C) Spindle and parallel-cuboidal cell morphologies on fibers of three diameters stained for actin (red) and nucleus (blue). Cells on 130 and 150 nm diameter fibers form long protrusions (SI Appendix, Fig. S1), shown here only for 130 nm. (D) Daughter cells have significantly increased speed compared to cells that have not recently divided (n = 34 and 41 for each spindle and parallel case on 500 nm fibers, respectively). Error bars show SE.

CIL Collision Outcomes in Two Approaching Spindle Cells.

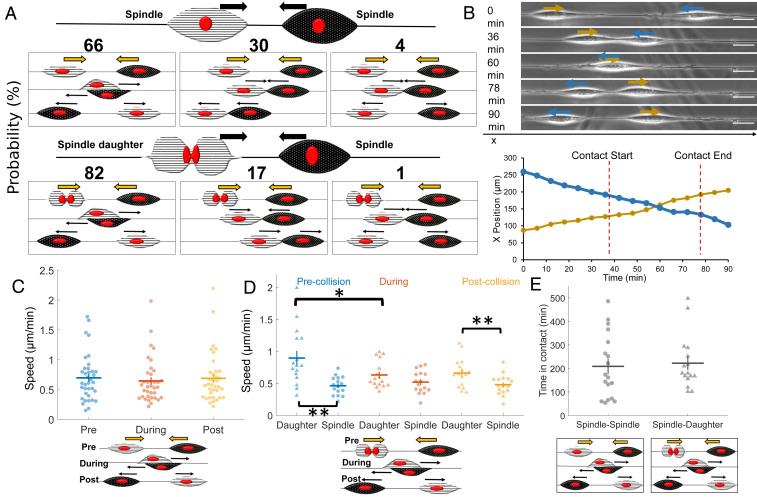
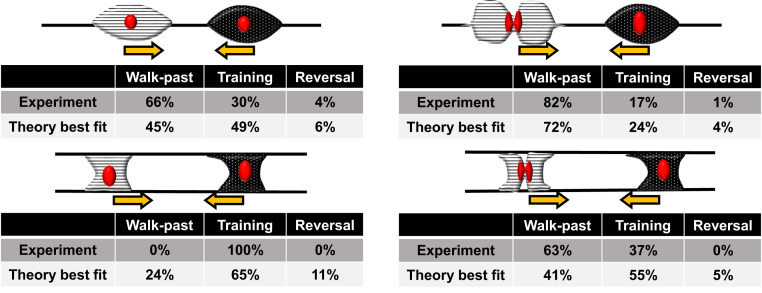
Next, we wanted to observe and quantify the outcomes of spindle-cell CIL interactions. We looked at 47 randomly selected approaching spindle-cell–cell collisions without cell division from 40 experiments. We found that spindle cells approaching each other mostly walked past each other without repolarizing (66%, Fig. 2A and Movies S3 and S4). Since spindle cells on fibers form focal adhesions at the poles (22), they can shift position around the fiber, thus allowing them to walk past one another. We also observed nonmutual CIL (30%) where upon contact only one spindle repolarized, and both cells continued to migrate as a cohesive unit (“train”) in the new migration direction (Movie S5). Very rarely, 4% of the time, we see a mutual CIL response wherein upon contact, both spindle cells experience protrusion inhibition at the site of contact and repolarize away from one another—the stereotype of CIL on 2D substrates (Movie S6). In a separate set of collisions, in which one of the colliding cells had recently divided (n = 98), we observed increased occurrence of walk-past behavior (82%, Movies S7 and S8) and a decrease in both nonmutual CIL (17%, Movies S9 and S10) and mutual CIL (1%). Similar behavior was observed on fibers of 150 nm or 1,000 nm diameters (SI Appendix, Fig. S4). We also tracked the cell position over time for approaching spindles with and without cell division (Fig. 2B). The cell tracking revealed that in the scenario without cell division, there is no significant deviation in cell speed throughout the walk past, though in the presence of cell division, the daughter cell slows down upon contact with the approaching spindle (Fig. 2 C and D). Division increases the speed of daughter cells and also increases the rate of cells walking past each other—does the increased cell speed of daughter cells also lead to walk-past events that are shorter in duration? Surprisingly, we found almost no difference in the time in contact between spindle–spindle and spindle–daughter walk-past events (Fig. 2E). Similarly, we do not find a large effect of division on the time for repolarization in nonmutual CIL (SI Appendix, Fig. S2).

Fig. 2.

Spindle cell CIL. (A) Outcomes of two approaching spindle cells in the absence (n = 47) and presence (n = 98) of cell division. Walk past is the dominant mode, followed by nonmutual (training) and mutual (reversal) CIL. (B) Cell position and phase images over time for a walk-past event without division. (Scale bar, 50 μm.) (C) Average speed pre-, during, and postcontact for spindle cells undergoing walk past (n = 18 collisions). (D) Average speed pre-, during, and postcontact for spindle and daughter cells undergoing walk past (n = 16 collisions). (E) Time in contact for spindle walk past without and with cell division are similar (P = 0.76) (n = 18,16). Error bars show SE.

Parallel-Cuboidal Cell CIL Outcomes.

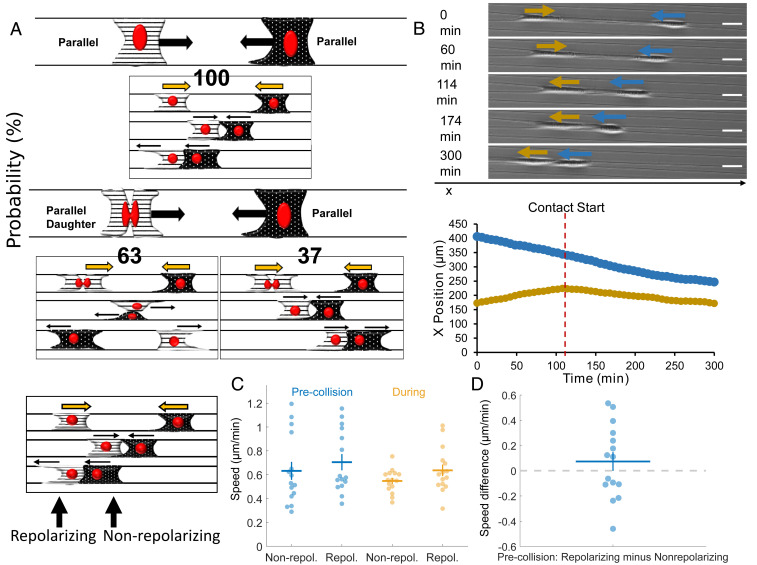
Next, we wanted to explore the outcomes of the collisions of cell pairs with both in the parallel geometry—attached to two fibers. We observed 28 randomly selected cell collisions without division from 41 independent experiments (Fig. 3A). In the absence of cell division, CIL outcomes were strikingly different from in the spindle geometry: two approaching parallel cells always resulted in nonmutual CIL (100% in 28 randomly selected movies, Movies S11 and S12). One of the cells would repolarize, and subsequently, both cells would move in the new migration direction as a cohesive unit (training). In some instances, we observed that after the initial training phase, the repolarized cell would move faster leading to both cells separating but moving in the same direction (Movie S13), and in rare instances, one or both cells would repolarize (Movie S14). We have counted these outcomes as training as long as the initial motion lasted for at least one cell length. By contrast, in the presence of cell division, from 59 randomly selected cell collisions, we observed two outcomes: walk past (Movies S15 and S16) and nonmutual CIL (Movie S17). The dominant outcome of collision between a daughter cell and a normal cell was walk past (63%). During these walk-past events, we often observed that the daughter cell changed shape to a spindle cell (attached to one fiber) during the contact period. Postcontact, the daughter regained its original parallel shape in most of the cases observed. We tracked cell positions for both collisions involving recent postdivision cells and those without division (Fig. 3B). In the absence of cell division—when the only outcome is a train of cells being formed—cell speeds before and during contact were similar in both cells (Fig. 3C). In the presence of division (SI Appendix, Fig. S3A), we find cell speeds to be similar throughout the process of walk past for both dividing and nondividing cells. We emphasize that, though cells can be briefly stalled during a collision, the speed may not drop to zero, because speed measured as changes in both x and y centroids over a time of 6 min can reflect changes in cell shape as well as motility. Can variability in speed predict the outcome of repolarization, as observed in epithelial cells (28)? We found no evidence that the cell that repolarized was slower than the cell that did not (Fig. 3D). As in spindle cells, we found no strong dependence of the repolarization time of nonmutual CIL on the presence of cell division (SI Appendix, Fig. S3B).

Fig. 3.

Parallel cell CIL. (A) Outcomes of two approaching parallel cells in the absence and presence of cell division. Nonmutual CIL is the dominant mode in the absence of cell division—100% of approaching parallel cells result in one cell repolarizing and altering its migration direction for at least one cell length (n = 28). With cell division, walk-past behavior is the most likely to occur followed by nonmutual CIL (n = 59). (B) Cell position and phase images over time for parallel cells exhibiting nonmutual CIL (training). (Scale bar, 50 μm.) (C) Average cell speeds pre- and during contact for parallel nonmutual CIL for the cell that repolarizes and the nonrepolarizing cell. (D) No strong evidence that the cell that repolarizes has a slower or faster speed than the cell that does not (P = 0.3). Error bars indicate the SE.

In collisions with daughter cells, a rare subset of the nonmutual CIL had, unexpectedly, an apparent cell “push,” wherein a daughter cell that collides with a normal parallel-cuboidal cell leads to the nondaughter cell moving, even before the nondaughter parallel cell repolarizes and makes new protrusions (Movies S18 and S19). This suggests that it is the physical force exerted by one cell literally pushing the other, overcoming any resistance from cell-fiber adhesion.

Leading–Trailing Spindle- and Parallel-Cell Collisions.

In addition to leading–leading or head–head collisions, we also observed instances where the leading edge of one cell would contact the trailing edge of another cell, and both cells would continue to migrate (both in spindle–spindle and parallel–parallel). This behavior was previously reported in collisions on micropatterns (13) and suggests that there may be an asymmetry in the signals cells receive in contact with another cell’s tail or head. Recent experiments describing “contact following of locomotion” also support the idea of an asymmetry of interactions (29).

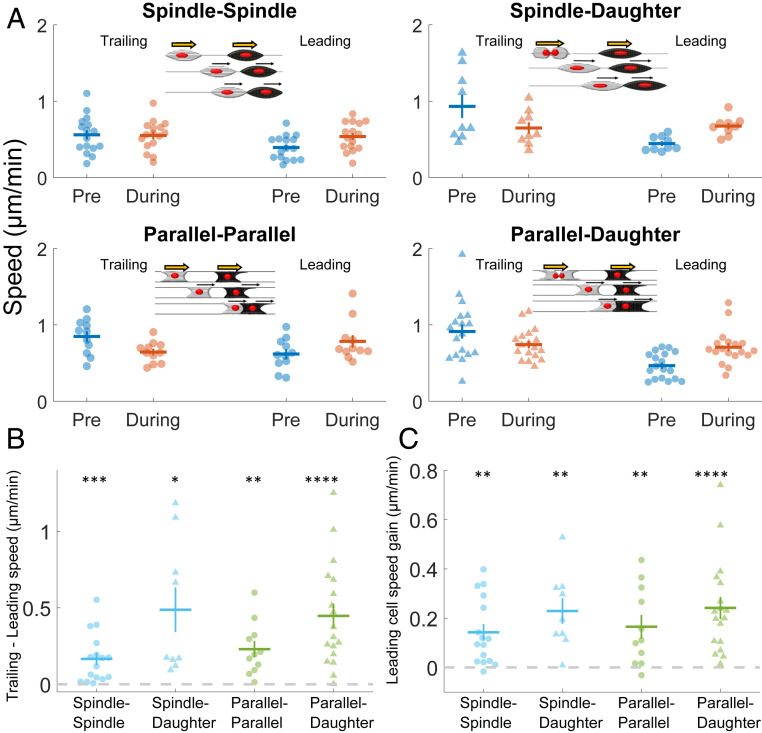
We show the speeds of the trailing and leading cells prior to the collision and then during the contact in Fig. 4A for all of the collision types (spindle–spindle: Movie S20, spindle–daughter: Movie S21, parallel–parallel: Movie S22, and parallel–daughter: Movie S23). Because of the variability of cell speeds, some information is not apparent in this data but is only clear in paired comparisons. For instance, we show in Fig. 4B that the trailing cell always has a higher speed than the leading cell—which is necessary for the trailing cell to catch up. Interestingly, the primary effect of a trailing cell catching up with a leading cell is that the leading cell gains speed during contact (Fig. 4C). This effect is consistent over all the collision types we studied.

Fig. 4.

Leading–trailing CIL. (A) Average speeds for cells before and during a trailing–leading contact. Four cases are shown: 1) spindle–spindle collisions, 2) spindle–daughter spindle collisions, 3) parallel–parallel collisions, and 4) parallel–daughter parallel collisions. (B) Speeds of trailing cells precollision are always larger than that of leading cells, allowing them to catch up, across all types of collisions 1 through 4 in A. (C) Leading cells robustly gain speed once they are in contact with the faster trailing cell across all types of collisions 1 through 4 in A. Statistical tests, which test if the mean speed change is significantly different from zero, are only performed on the pairwise comparison data shown in B and C.

A Simple Simulation Framework Captures CIL Outcomes.

Our experimental results show three broad qualitative features which differ from classical results in 2D CIL: 1) spindle–spindle collisions commonly lead to walk past; 2) the parallel fiber geometry suppresses this walk-past behavior; and 3) cells that have recently divided, which move more quickly, are more likely to walk past another cell—even within the parallel geometry. Altering the adhesive environment of a cell can regulate many processes (30), while cell division also can alter the localization of receptors on the cell surface and ability to respond to signals (31), motility, and the extent of contact guidance (23). We want to understand to what extent our observed CIL features can arise solely from the change in geometry and the observed change in speed of recently divided cells. To address this question, we developed a theoretical framework for our fiber CIL by extending our previously reported 2D CIL model (32). This model describes cells with positions r_i and polarities p_i. The polarity is a vector indicating the direction a cell is traveling—its magnitude is the speed the cell would have in the absence of other forces acting on it. Cells are modeled as self-propelled particles, with forces attaching them to each of the fibers. Between the two cells are adhesive forces representing cadherin-mediated attachment and forces of repulsion to represent elastic deformation of cells when they begin to contact. In addition, we include two key biochemical processes affecting the cell’s polarity: 1) contact guidance, in that cells tend to polarize along the fibers; and 2) CIL, in which cells tend to polarize away from contact with the fronts of other cells. In addition, we include stochastic fluctuations in polarity. Cell division is modeled solely by increasing the initial polarization (speed) of the cell. Model equations are shown in the Materials and Methods, with additional details and parameters in SI Appendix.

We used our model to simulate cell–cell collisions (Fig. 5A) and characterized three outcomes: 1) walk past, where cells crawled past each other, exchanging positions, and then separated; 2) reversal, where cells contacted each other, repolarized, and separated without exchanging positions (“mutual CIL”); and 3) training, where the two cells failed to separate and generally had one repolarizing cell following the other (“nonmutual CIL”).

Fig. 5.

Model reproduces key qualitative experimental outcomes robustly to parameters. (A) Illustration of model for cells on single fiber (spindle geometry) and attached to two fibers (parallel geometry). Black lines indicate cell polarity p and gray lines indicate fibers. The red and blue lines indicate the past trajectory of the cells. A walk-past event is shown for the spindle configuration, and a training event is shown for the parallel configuration. (B) The fraction of walk-past events is shown for parameters randomly sampled from plausible values (SI Appendix); each dot is a different parameter set. Though changing parameters affects the overall fraction of walk past, walk past is common. (C) Comparisons between walk-past levels. Holding other parameters fixed, we change one element of the model and show the change in walk past for different parameters, with one point representing one parameter set, as in B. We see the spindle geometry always has more walk past than the parallel. Collisions where division occurs always have an increase in walk past for spindle and never have a decrease in walk-past behavior in parallel geometry.

In the spindle geometry, simulated cells can walk past each other (Fig. 5B and Movies S24 and S25). In large part, this reflects that cells can freely rotate around the fiber and that they can therefore either rotate after contact or, if the cells start at different angles, only come in glancing contact. The details of the cell–cell contact and possible rotation are difficult to distinguish in microscopy, but from videos it is clear that cells can have their bodies distributed to one side of the fiber and can shift their body to the other side during migration. When simulated cells are attached to two fibers, cell body distribution around the sides of the fiber is strongly suppressed, and walk past occurs less frequently (Fig. 5C and Movies S26 and S27). This behavior is generic and is true across many parameters: we show in Fig. 5C and SI Appendix, Fig. S12 that, sweeping across 200 independent parameter sets spanning the plausible range, fewer cells walk past one another in the parallel geometry than in the spindle geometry. Similarly, we see that when one cell has recently divided (modeled as having a higher initial polarization in the x direction, SI Appendix), walk past is always increased in the spindle case and never decreases in the parallel case. Some parameter sets for parallel geometries with very high attachment to the fiber have zero change in walk-past rate due to division, because walk past is effectively impossible due to the tight constraints. We thus find that, at a qualitative level, matching behavior of cell–cell collision outcomes seen in our experiments and simulations are robust, showing that geometric confinement alone is sufficient to alter outcomes of CIL. In addition, our simulations show that in silico, it is sufficient to merely increase a cell’s speed in order to increase walk past.

Our central results are robust to many model parameters, but the quantitative values vary with the specific parameters chosen (Fig. 5). We fit our model to the experiment by varying the five parameters in which we do not have preexisting values (strength of CIL, β, cell–cell adhesion strength, α, cell-fiber attachment strength, κ, cell stiffness, κ_cell, and variation in cell velocity, σ) over plausible ranges and choose the best fit. How outcome statistics depend on these parameters and others are shown in SI Appendix, Figs. S8–S10. Our model is in excellent agreement with experimental observations of spindle head–head collisions and reasonably good agreement with the parallel fiber category (Fig. 6), thus allowing us to qualitatively describe rules in CIL outcomes on suspended fibers.

Fig. 6.

Summary of comparison between experiment and best-fit theory. Theory values are for the best-fit parameters provided in SI Appendix and are generated from statistics of n = 500 collisions.

Characterizing the Role of Division and Cell–Cell Adhesion in Walk Past.

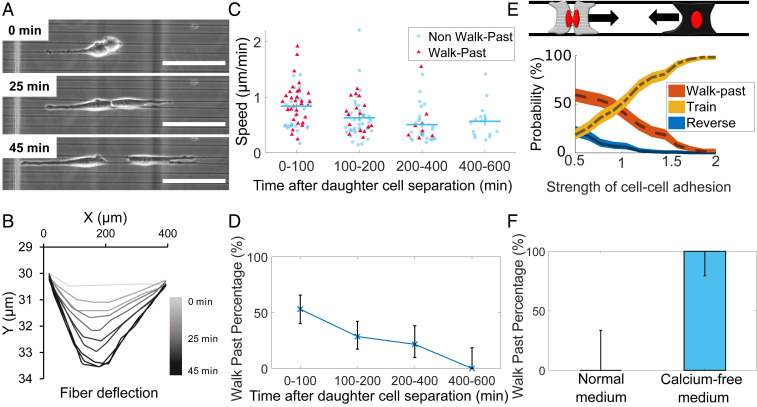
We have discovered that cell division can qualitatively alter cell–cell collisions, leading to high rates of walk past and absence of traditional CIL. Cell division alters many elements of cell migration, including cell speed (our results and ref. 23), decisions at branches in confined migration (33), cell-substrate adhesion (34), and cortex tension (35). Our simulations show that increased cell polarization postdivision is sufficient to lead to increased walk past, but other factors could also potentially alter walk past upon division. We explore several of these factors. First, we study cell-substrate adhesion by determining fiber displacements, to indicate the traction forces exerted (36, 37) (Movie S29). Fiber displacements saturate (reach maximum displacement) typically 35 to 45 min after the daughter cells begin to spread postdivision. A typical example is shown in Fig. 7 A and B, and others are shown in SI Appendix, Fig. S5. Traction forces reach their saturation point when the two daughter cells separate, suggesting that in a collision between a recently divided daughter cell and a nondividing cell, both cells should have very similar levels of cell-fiber adhesion. We have argued that one of the critical differences in recently divided cells is cell speed. We show cell speed as a function of time post cell-cell separation in Fig. 7C; note that daughter-cell separation takes typically 45 to 60 min past division time (t = 0 in Fig. 7 A and B). We observe that cell speed decreases as a function of time past daughter-cell separation. The fraction of collisions that lead to walk past also decreases systematically as a function of time past separation (Fig. 7D). This is consistent with the idea that increased polarization and speed could drive increased walk past. However, these parameters do not fully describe the CIL outcomes. First, we see that cells that walk past each other are not necessarily the faster cells (Fig. 7C, see coloring of the symbols: red triangles for walk past and round blue for nonmutual CIL). This might not be surprising as cell speed is a dynamic and fluctuating quantity, and so the instantaneous speed may not reflect the extent to which the cell is polarized. Second, we find that cells that collide 200 to 400 min after division and those that collide 400 to 600 min after division have indistinguishable mean speeds, but we observe walk past in the 200 to 400 category but not the 400 to 600 (Fig. 7D). This suggests that cell speed postdivision, though identified by our simulations as sufficient to create walk past, is not the sole origin of the postdivision walk past. Within our simulations, cell–cell adhesion is one of the significant controlling factors of collision outcomes (Fig. 7E), suggesting that the division’s effect on collision outcomes could potentially be through modification of cell–cell adhesion. To test these predictions, we studied cell collisions in low-calcium media, which is known to significantly reduce cell–cell adhesion (38). We found that in low-calcium media, surprisingly, all nondividing cells in the parallel geometry walked past each other, in contrast with our results of no nondividing cells exhibiting walk past in regular media (Fig. 7F). We found the morphology of cells undergoing walk past to be similar between the dividing daughter cells in regular media and the nondividing cells in low-calcium media cells (Movie S30). Overall, our findings suggest that the effect of cell–cell division may arise from decreased cell–cell adhesion in addition to altered speed.

Fig. 7.

Effects of cell division and cell–cell adhesion. (A) Cells create fiber deformations postdivision. (Scale bar, 50 μm.) (B) Measurement of fiber deflection over time shows these tractions quickly stabilize; time shown is time after cell division. Other examples are shown in SI Appendix, Fig. S5. (C) Cell speed and (D) walk past both decrease with time after division. (E) Our model suggests that decreasing cell–cell adhesion promotes walk past (see also SI Appendix, Fig. S8A). (F) Cells in low-calcium media show walk past in parallel geometry robustly even in the absence of division. Error bars in D and F indicate 95% confidence intervals, determined via the Clopper–Pearson method. n = 9 (normal), n = 16 (calcium-free).

Discussion

In this paper, we present a combined experimental-theoretical platform to quantify outcomes of cell–cell collisions and CIL in fibers analogous to in vivo ECM. Using suspended fibers in aligned patterns, we investigated CIL decisions of two fibroblasts approaching each other in two elongated shapes: spindle cells attached to single fibers, and parallel-cuboidal cells attached to two fibers (Fig. 1). Two approaching spindle cells most commonly do not repolarize but rather walk past one another and continue along their respective directions (Fig. 2). We attribute this behavior to spindle cells being able to shift their position around the fiber axis, as they are primarily attached to the fibers at the poles, as demonstrated by a gentle push to a spindle cell using an external probe (Movie S28). Spindle walk-past behavior is similar to a rare walk past observed in neural crest cells on micropatterned lines where the cells also pass by one another without repolarization (11), though notably, this walk-past behavior was extremely rare (under 2% of collisions of wild-type cells, and about 10% when CIL was suppressed). Milano et al. (15) have also observed a similar “sliding” behavior—though they find that it is only present at high rates (∼50%) in metastatic MDA-MB-231 cells, and the rates of sliding can be increased by down-regulation of E-cadherin in noncancerous MCF-10A. By contrast to both results, our experiments show that on suspended fibers, walk past can be the majority outcome even in normal 3T3 cells. We can also regulate this behavior by changing the local geometry: when two parallel cells approach one another, upon contact, one cell will repolarize, switch its migration direction, and continue to move as a unit with the other—nonmutual CIL or train formation (Fig. 3). These behaviors differ from the traditional CIL definition as both cells do not inhibit their protrusive behavior and alter their migration path as seen in initial studies (4), though similar behavior has been captured before both in vitro (13) and in vivo (39). Our simulations (Figs. 5 and 6) suggest that the transition from high walk past to high train formation can be generated solely by changing the geometry of the ECM from a single to two parallel fibers. Importantly, we hold all other model parameters constant—we do not assume that the changed matrix geometry alters CIL strength explicitly. Cell division has significant influences on both spindle and parallel CIL. Both spindle and parallel daughter cells migrate faster postdivision than a nondaughter cell, and when a daughter cell contacts another cell, walk past occurs more often—in both parallel and spindle geometries. Our simulations suggest that the increased speed of daughter cells alone may be sufficient to explain the increased rate of walk past—within our model, walk-past rates robustly increase when one cell’s initial polarization (speed) is increased. Cell division will likely also affect the degree of cell adhesion, and prior work has emphasized that cues from mitosis can override chemical signals, suggesting that division may have independent effects on CIL (31). To extend our understanding of how cell division alters cell–cell interaction outcomes, we observed the timeline of how cell-fiber forces, cell speed, and outcomes change after division (Fig. 7). Our model suggests that speed is sufficient to generate increased walk past, but experimental changes in walk past postdivision are larger than those seen in our model (Fig. 6), suggesting division may affect more than speed. Our data shows that altered cell–cell adhesion levels postdivision are consistent with our experimental results. Interestingly, we find that cell-fiber adhesion is likely not the controlling factor in cell–cell interaction outcomes.

We also note an important effect of head–tail collisions of cells in changing cell speed, in which a trailing cell catches up with a leading cell. When a trailing cell—which must be moving faster than the leading cell to catch it—contacts the leading cell, the leading cell almost always speeds up (Fig. 4C). This effect would be anticipated from simple models of cells as self-propelled particles, which suggest that the velocity of a cluster of cells is the average of the velocity they would have if they were separated (32).

While our model, robustly to parameters, reproduces the key qualitative outcomes (Fig. 5), our best fit to the observed quantitative rates does not perfectly match experimental outcomes (Fig. 6). Because we have not modeled cell shape changes or addressed cell-to-cell variability (17), we should not expect a perfect result. Nevertheless, we get a reasonable best fit. The most challenging outcomes to predict with a single, consistent set of parameters are the experimental observations that 0% of cells walk past in the parallel geometry without division while 63% of them walk past when division occurs. We can choose parameters so that parallel cells cannot walk past (Fig. 5B) but when this is done, the increase in speed alone is insufficient to create walk past in the parallel geometry (zeros in Fig. 5C). We suspect that this difficulty in fitting reflects our assumption that cells remain connected to both fibers, while in our experiments, parallel walk past often occurs with one cell becoming disconnected from one fiber and becoming more spindle-like. To provide insight into the roles of different model parameters, we take these fitting parameters as our “wild type” and show how the outcomes depend on key parameters like cell–cell adhesion (SI Appendix, Figs. S8–S10). Our model also provides insight into other factors, like fiber size. Because we do not explicitly resolve the fiber diameter in our model, changing fiber diameter would only be reflected in, for example, changes in effective speed and adhesion level; our central results are robust to these variations.

Within the range of parameters we have considered, our model robustly produces results qualitatively consistent with our experimental data (Fig. 5). To what extent would we expect this to generalize to other cell types? If other cell types are best described by different parameters, for example, cells that do not speed up on division (M = 1 in our model), we would not expect division to alter walk past—unless division also alters adhesion, as we hypothesize because of our results in Fig. 7. However, we expect that walk past will exist in spindle geometries but be reduced in parallel geometries, as we have seen this in all parameter sets we have studied.

In conclusion, in this paper, we present a platform to demonstrate how CIL depends on ECM geometry and cell geometry in a system closely analogous to ECM fibers. Our results are strikingly different from prior studies on CIL, observing that even healthy, noninvasive cells are able to walk past one another. We show, using computational modeling, that this can be explained solely as a function of the different fiber configuration we expose cells to. Our studies suggest that, even given our in-depth understanding of 2D CIL and CIL on micropatterned lines, even if no new biochemical processes are triggered by the nanofiber geometry, understanding and predicting the behavior of in vivo cell–cell interactions in ECM may be difficult and require computational modeling and validation. This has implications beyond our initial focus on homotypic interactions between two fibroblast cells. Loss of heterotypic CIL is viewed as a signature of cancerous cells, allowing cancerous cells to invade the healthy population (14, 40); neural crest cells also maintain homotypic CIL among themselves while lacking a heterotypic CIL response allowing them to invade the mesoderm layer and other tissues (1). Our rules of CIL in cells on suspended and aligned fibers imply that earlier CIL findings from use of flat 2D substrates, microprinted lines, and confined channels, for both homotypic and heterotypic cell–cell interactions, may need to be reexamined in order to better understand the role of ECM geometry.

Materials and Methods

Nanofiber Network Manufacturing.

A 10% by weight solution was made by dissolving polystyrene (molecular weight: 2,000,000 g ⋅ mol⁻¹) in xylene. Migration networks of nanofibers with ∼500 nm diameters with 15 micron or 30 micron spacing were created using the nonelectrospinning STEP method. After formation, the nanofibers were fused by exposure to tetrahydrofuran utilizing a custom fusing chamber. Fibers were deposited at two spacings: ∼20 µm to achieve spindle cells that attached to single fibers, and ∼10 µm to achieve parallel-cuboidal cells attached to two fibers.

Cell Culturing, Seeding, and Imaging.

The nanofiber networks were placed in individual wells of a six-well plate and sterilized before coating with 4µg/mL fibronectin for approximately 1 h. NIH 3T3 fibroblasts were cultured in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% Fetal Calf Serum (FCS) at 37 °C and 5% CO₂ in T-25 flasks. For the low calcium experiments, NIH 3T3 fibroblasts were cultured in calcium-free DMEM with 10% FCS. The cells were seeded at a low concentration onto the nanofiber networks after removal of the fibronectin and were subsequently left to attach for 1 h prior to flooding each well with 3 mL media. Time-lapse imaging for migration was executed for 12 to 24 h with an imaging interval ranging from 1, 2, or 3 min using a 10× or 20× objective.

Cell Migration Analysis.

Time-lapse videos were created with spindle and parallel-cuboidal cells prior to contact, during contact, and for some cases postcontact. Image J was used to outline cells, track cell centroids every 6 min, and obtain an average migration rate (µm/min). Cells are tracked individually, and the curvature of the edges of the cells are used as a guide for tracing (Movie S31). As cells come into contact, it becomes difficult to distinguish each cell. When cells were completely overlapping, both cells were treated as one cell until the curvature of each cell became apparent as cells separated. The x and y coordinates of cell centroid were measured at each time point, and the 2D speed was determined by (V_x² + V_y²)^1/2. Only clean cell–cell collisions (those where only two cells interacted) were used for analysis in order to avoid multiple cell interferences.

Statistical Analysis.

Throughout the paper, unless otherwise indicated, we show error bars corresponding to the SE (SD of the mean). Statistical tests are indicated by ****P < 0.0001, ***P < 0.001, **P < 0.01, and *P < 0.05. In Fig. 2 C and D, statistical tests are t tests computed on the difference in speeds between two cases, that is, on paired differences. Figs. 2E, 3D, and 4 B and C show statistical tests that are t tests with a null hypothesis that the difference is zero. Full P values and details of tests are included in the provided analysis code.

Computational Model.

Cells are characterized by position r_i and polarity vector p_i. The vector p_i reflects the degree of biochemical polarization of cell i. In the absence of additional forces on the cell, cell i travels with velocity p_i:

$$\begin{array}{c}\frac{d{\mathit{r}}_i}{dt}={\mathit{p}}_i+\mu {\mathit{F}}_{\text{i}}\hspace{1em}\end{array}.$$ [1]

Here, F_i is the force exerted on cell i by other cells and the environment, for example, cell–cell adhesion and cell-fiber attachment. The cell’s mobility is μ, which relates forces F exerted onto the cell to its resulting velocity. The polarity evolves by the following stochastic differential equation:

$$\begin{array}{c}\frac{d{\mathit{p}}_i}{dt}=-\frac{1}{\tau }\left({\mathit{p}}_i-v_{cg}\hspace{0.17em}\widehat{\mathit{x}}\hspace{0.17em}sign\left[{\mathit{p}}_i\cdot \widehat{\mathit{x}}\right]\right)+\hspace{1em}\beta {\mathit{\nu }}_{\text{i}}+\sigma {\mathit{\xi }}_{\mathit{i}}\left(t\right)\end{array}.$$ [2]

The first term in this equation models a tendency to polarize along the fiber with a time scale τ, reaching a speed ν_cg (contact guidance), the second models CIL with strength β, and the third is a stochastic noise. Detailed explanation of the terms in these equations, additional computational details, parameter values, etc., are available in the SI Appendix.

Data Availability

Analysis and simulation code data have been deposited in Zenodo (https://doi.org/10.5281/zenodo.4584099) (41).