Modulation of a protein-folding landscape revealed by AFM-based force spectroscopy notwithstanding instrumental limitations

Significance

Atomic force microscopy (AFM) is widely applied to unfold proteins. Using advanced cantilevers in a commercial AFM to improve stability and precision, we unfolded and then refolded an individual fast-folding, mechanically labile protein—a technically challenging sample—thousands of times. To address concerns that the measured dynamics of such proteins are dominated by the AFM assay, we modulated the protein’s folding rate using pH. Kinetic analysis demonstrated changes in free-energy landscape parameters with pH, despite the reconstructed landscape being dominated by the assay. Hence, AFM using advanced cantilevers can yield biophysical insight into proteins, even if they unfold at low force.

Abstract

Single-molecule force spectroscopy is a powerful tool for studying protein folding. Over the last decade, a key question has emerged: how are changes in intrinsic biomolecular dynamics altered by attachment to μm-scale force probes via flexible linkers? Here, we studied the folding/unfolding of α₃D using atomic force microscopy (AFM)–based force spectroscopy. α₃D offers an unusual opportunity as a prior single-molecule fluorescence resonance energy transfer (smFRET) study showed α₃D’s configurational diffusion constant within the context of Kramers theory varies with pH. The resulting pH dependence provides a test for AFM-based force spectroscopy’s ability to track intrinsic changes in protein folding dynamics. Experimentally, however, α₃D is challenging. It unfolds at low force (<15 pN) and exhibits fast-folding kinetics. We therefore used focused ion beam–modified cantilevers that combine exceptional force precision, stability, and temporal resolution to detect state occupancies as brief as 1 ms. Notably, equilibrium and nonequilibrium force spectroscopy data recapitulated the pH dependence measured using smFRET, despite differences in destabilization mechanism. We reconstructed a one-dimensional free-energy landscape from dynamic data via an inverse Weierstrass transform. At both neutral and low pH, the resulting constant-force landscapes showed minimal differences (∼0.2 to 0.5 k_BT) in transition state height. These landscapes were essentially equal to the predicted entropic barrier and symmetric. In contrast, force-dependent rates showed that the distance to the unfolding transition state increased as pH decreased and thereby contributed to the accelerated kinetics at low pH. More broadly, this precise characterization of a fast-folding, mechanically labile protein enables future AFM-based studies of subtle transitions in mechanoresponsive proteins.

Single-molecule force spectroscopy (SMFS) has been remarkably successful across broad classes of biological molecules (RNA, DNA, and proteins) (1–5). A particularly fruitful data acquisition regime probes multiple back-and-forth folding/unfolding transitions at near-equilibrium and equilibrium conditions (6–9). This methodology efficiently yields numerous transitions and therefore a wealth of kinetic data, one-dimensional (1D) free-energy landscape parameters, and even a full 1D projection of the free-energy landscape along the stretching axis (10, 11). The standard SMFS assay has the molecule of interest tethered via a flexible linker to the force probe, such as an optically trapped bead or an atomic force microscopy (AFM) cantilever (Fig. 1A). These micrometer-sized force probes are the primary measurement (x_meas) but have finite response time and are therefore coupled to, but do not precisely track, molecular dynamics (x_prot) (Fig. 1B) (12–14). Additionally, the flexible linker’s compliance modifies this coupling between the molecule and the force probe. Linkers stretched at a finite force (F) can even create an entropic barrier not present in the absence of applied force (15, 16). More generally, there is an expanding set of theoretical and experimental studies (12–30) investigating how such instrumental and assay parameters affect the underlying biomolecular dynamics and whether the measured dynamics are dominated by the instrument used to measure them.

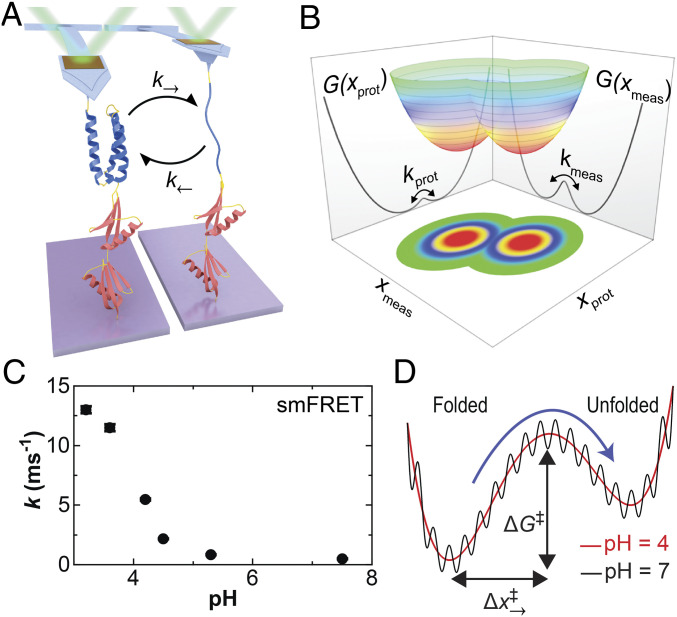
Fig. 1.

Probing the folding and unfolding dynamics of a globular protein by SMFS. (A) Cartoon showing a polyprotein consisting of a single copy of α₃D (blue) and two copies of NuG2 (red) stretched with an atomic force microscope. At low forces, the mechanically labile α₃D repeatedly unfolds and refolds as detected by a change in cantilever deflection. (B) A conceptual two-dimensional free-energy landscape shows the underlying protein extension (x_prot) and the experimentally measured extension (x_meas). The macroscopic force probe has finite temporal resolution, and the application of force can introduce an entropic barrier between resolved states. (C) The sum of the equilibrium folding and unfolding rates for α₃D in a strong denaturant (5 to 6 M urea) as a function of pH as determined in a prior smFRET study (37). (D) A conceptual sketch of α₃D’s 1D free-energy landscape deduced by a combination of smFRET and molecular dynamics studies based on Ref. 37. The dramatic increase in α₃D’s kinetics at low pH shown in panel C was explained as increased configurational diffusion along a smooth rather than a rough energy landscape.

AFM characterization of proteins is widely used (1–5) and therefore is an important experimental regime to explore, distinct from numerous studies investigating instrumental effects on nucleic acid hairpins measured with optical traps (17, 18, 23, 24, 26, 31). Historically, limited force precision and stability coupled with the slow response of the force probe has made it challenging to perform AFM-based equilibrium and near-equilibrium studies (32) and thereby difficult to quantify the role of instrumental artifacts. Recent work using a standard gold-coated cantilever concluded that the equilibrium dynamics of the fast-folding protein gpW were dominated by the dynamics of the cantilever diffusing on a force-induced entropic barrier (29). Such results raise significant concerns about interpreting rates or landscapes measured in AFM studies of globular protein folding and thereby motivate the following question: How do variations in intrinsic protein folding dynamics manifest in AFM-based studies, particularly in an experimental regime dominated by an instrument-induced entropic barrier?

Here, we address this question by directly modulating a globular protein’s underlying folding dynamics without significantly changing the height of the barrier or the free-energy difference between the states. To do so, we studied α₃D using AFM-based force spectroscopy (Fig. 1A). The dynamics and energetics of α₃D, a computationally designed, fast-folding three-helix bundle of 73 amino acids (33, 34), have been studied by traditional ensemble (33) and single-molecule fluorescence resonance energy transfer (smFRET) (35–39) assays. Equilibrium smFRET studies in chemical denaturants showed accelerated folding/unfolding kinetics as pH was reduced (35). A subsequent landmark paper (37) combined state-of-the-art smFRET and microsecond-long, all-atom molecular dynamics simulations to show that this acceleration resulted from suppression of nonnative contacts changing the local roughness of the 1D landscape (Fig. 1 C and D) rather than a change in the height or the overall shape of the barrier between states. In the context of Kramers theory (40), this roughness manifests as a change in D, the conformational diffusion coefficient along the 1D landscape. The authors concluded that most, if not all, of the 14-fold change in folding kinetics came from an increase in D. This pH-dependent change in kinetics serves as a benchmark of α₃D’s dynamics in the absence of the force probe and associated linker. In other words, we will leverage conditions known to modulate the rate of folding along the molecular coordinate (x_prot) while measuring the consequence of that change on the measured coordinate (x_meas) (Fig. 1B).

While α₃D provides a conceptually attractive means to modulate intrinsic molecular dynamics, it presents significant experimental challenges. Like gpW (28, 29), α₃D unfolds at a low force (< 15 pN) by AFM standards (2, 3, 41) and exhibits even faster folding kinetics under force. Thus, spatiotemporal resolution is critical, and instrumentation limitations are expected to be even more pronounced. Force drift is also a critical issue, particularly for extended assays (>1 to 100 s) because standard gold-coated cantilevers exhibit significant force drift (42); yet, equilibrium assays of structured RNA (6) and proteins (9) are sensitive to sub-pN changes in F. We therefore used focused ion beam (FIB)–modified cantilevers (32, 43) that combine sub-pN stability over 100 s (43, 44) with a ∼13-fold improvement in spatiotemporal precision compared with the standard cantilever used in the aforementioned AFM study characterizing gpW (29). This stability in conjunction with a newly designed polyprotein construct allowed us to measure an individual α₃D unfold and fold over 5,000 times and for periods up to 1 h using both constant velocity (v) and equilibrium (v = 0) data acquisition protocols. Rates derived from both the equilibrium and dynamic data recapitulated α₃D’s pH-dependent kinetics from smFRET. However, the reconstructed 1D folding-energy landscape was consistent with the predicted entropic barrier and therefore encodes no information about α₃D’s folding landscape beyond ΔG₀, the thermodynamic stability of α₃D. Importantly, rate analysis yielded the expected asymmetric distance to the transition state from the folded and unfolded state and revealed a significant increase in the distance to the unfolding transition state as pH was lowered. These studies demonstrate that AFM-force spectroscopy can track changes in intrinsic protein dynamics with high precision, even in mechanically labile, fast-folding systems.

Results

A Precise, High-Bandwidth Force-Spectroscopy Assay for α₃D.

To characterize the pH-dependent rate of α₃D folding, we developed a polyprotein construct featuring a site-specific covalent attachment to a PEG-coated glass coverslip and a mechanically strong but reversible attachment to a PEG-coated cantilever (Fig. 2A). The PEG coating suppressed nonspecific adhesion and allowed clear detection of α₃D at low extensions (45). Surface coupling used a short 11-amino-acid ybbR tag (46) at the polyprotein’s N terminus that was enzymatically coupled to coenzyme-A (CoA)-PEG–derivatized glass (47). After testing biotin–streptavidin and the mechanically stronger Fgβ-SdrG (48) at low pH (<5), we ultimately used dockerin (III) at the C terminus, which forms a strong, noncovalent interaction with cohesin [F_rupture ∼300 pN at 100 nm/s (49)]. This strong, specific interaction was critical to achieving long-lived attachments for extended study of single molecules at low pH. A pair of NuG2 domains, a protein well characterized by AFM (50–52), served as markers to allow us to verify single-molecule attachment.

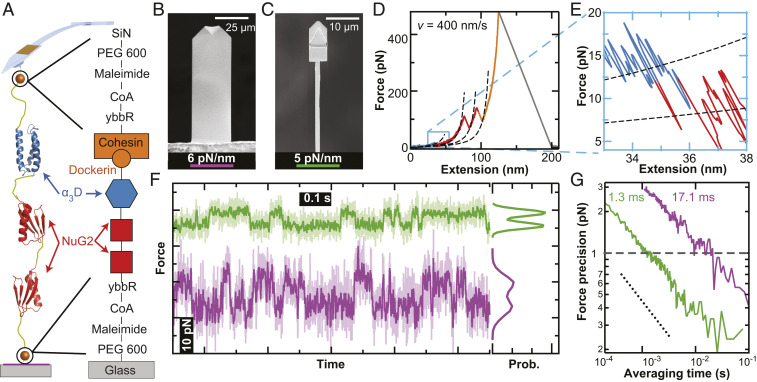
Fig. 2.

High-precision characterization of α₃D with modified AFM cantilevers. (A) Schematic showing the site-specific coupling of the polyprotein to a PEG-coated glass coverslip via a ybbR–CoA bond and to a PEG-coated cantilever via the mechanically strong but reversible cohesin–dockerin receptor–ligand interaction. SiN denotes silicon nitride. (B) SEM image of an uncoated long BioLever (L = 100 µm; k = 6 pN/nm). (C) SEM image of a FIB-modified BioLever Mini in a Warhammer geometry (L = 40 µm; k = 5 pN/nm). (D) Force-extension curve shows α₃D (blue) unfolding at low force followed by two NuG2 marker domains (red) at moderate forces and then the rupture of the mechanically robust cohesin–dockerin interaction (orange) at high force. Dashed lines represent worm-like chain model fits that deviate at higher force due to a structural isomerization in the PEG linkers (57). (E) High-resolution force-extension curve detailing the unfolding of α₃D. (F) Force-versus-time plot showing equilibrium folding/unfolding of α₃D at constant height of the cantilever base using traditional (purple) and modified (green) cantilevers. Traces were smoothed to 1 kHz (light colors) and 200 Hz (dark colors). (G) Force precision plotted as a function of averaging time for the BioLever Long (purple) and Warhammer (green) shows that the modified cantilever achieves 1 pN force precision with 13-fold less smoothing than the BioLever Long cantilever. The dotted line serves as a reference and has a slope consistent with averaging Brownian motion.

Our goal of characterizing the rapid folding and unfolding dynamics of a mechanically labile protein is challenging for AFM-based force spectroscopy. The handful of successful AFM-based equilibrium assays of globular proteins (28, 29, 53) have employed long, soft AFM cantilevers (L = 100 μm; k_nom = 6 pN/nm [Olympus BioLever Long]) (Fig. 2B). While such longer cantilevers can achieve sub-pN stability over 100 s when their gold coating is removed (42), they have moderate temporal response (∼400 μs) and force precision due to their size (43). To circumvent these limitations, we used shorter cantilevers (L = 40 μm [Olympus BioLever Mini]) that were FIB modified in a “Warhammer” geometry (Fig. 2C) (44). These cantilevers offered an exceptional combination of force precision, stability, and temporal resolution by reducing stiffness and hydrodynamic drag. Here, we further optimized this cantilever geometry for force stability, critical in equilibrium studies (6), by making them quite soft (∼5 pN/nm) at the cost of a slight reduction in temporal resolution compared with prior work (44).

To characterize α₃D’s kinetics with high precision, we leveraged our assay’s stability and long-lived tip attachment strategy to repeatedly unfold and refold the same individual molecule. To do so we used an advanced data acquisition protocol. First, we aligned the surface attachment point directly underneath the attachment to the cantilever’s tip to improve the precision and accuracy of our assay (54). We then repeatedly stretched and relaxed the polyprotein at multiple velocities (v) and acquired equilibrium data at v = 0. Using this assay, we could measure a single molecule for an extended period (∼10 to 60 min) (SI Appendix, Fig. S1).

The improved spatiotemporal resolution of our assay produced high-precision records of the unfolding of the polyprotein. A full force-extension curve contained the unfolding of α₃D at low force followed by the two NuG2 marker domains at a higher force and finally the rupture of the cohesin–dockerin interface at >400 pN (Fig. 2D). The low-force unfolding of α₃D is more clearly visualized when plotted in a restricted force range (Fig. 2E). Segments of the force-extension curve were generally well described by a worm-like chain model (55, 56) at forces below 100 pN, the threshold for a force-induced change in PEG (57). Such analysis yielded a change in contour length (ΔL₀) consistent with the number of amino acids in α₃D [ΔL₀ ≈ 23 nm (45)] and NuG2 [ΔL₀ ≈ 18 nm (50)]. The modified cantilevers also resolved near-equilibrium dynamics when pulling at 400 nm/s (Fig. 2E) whereas near-equilibrium dynamics of calmodulin (58) and ankyrin (59) were previously observed at v ≈ 1 to 10 nm/s when using the standard BioLever Long.

Equilibrium dynamics of α₃D transitions at pH 6.2 were significantly better resolved using FIB-modified cantilevers than with uncoated BioLever Long cantilevers (Fig. 2F, green versus purple, respectively). When using FIB-modified cantilevers, the probability distribution of force records smoothed to 200 Hz showed a significant dip between two well-defined peaks (dark green). This dip and two peaks were not well resolved when using an uncoated BioLever Long of similar stiffness (dark purple). Hence, modified cantilevers were much better at distinguishing the folded and unfolded states. More quantitatively, we found that during an equilibrium assay, a FIB-modified cantilever achieved a force precision of 1 pN at an averaging time of 1 ms calculated using the Allan deviation; an uncoated BioLever Long required ∼13-fold more smoothing to achieve this same resolution (Fig. 2G).

pH-Dependent Equilibrium Dynamics of α₃D.

Having established a precise, high-bandwidth AFM assay, we next investigated α₃D’s equilibrium dynamics as a function of pH. This pH dependence was efficiently mapped using a temperature-controlled, closed fluidic cell to exchange buffers in our AFM without having to dewet and rewet the sample and the cantilever. After the initial measurements at pH 6.2 (Fig. 3A, green), we dropped the pH to 4.2 (red) before raising it incrementally to pH 4.5 (orange), pH 5.0 (purple), pH 5.5 (blue), and finally back to pH 6.2. These records showed numerous, small (<5 pN) folding/unfolding transitions. To improve precision, we acquired this full data set with a single cantilever, similar to prior works (47, 48). Force stability was confirmed by observing consistent state occupancy when individual 5-s records were subdivided into thirds (SI Appendix, Fig. S2) (60).

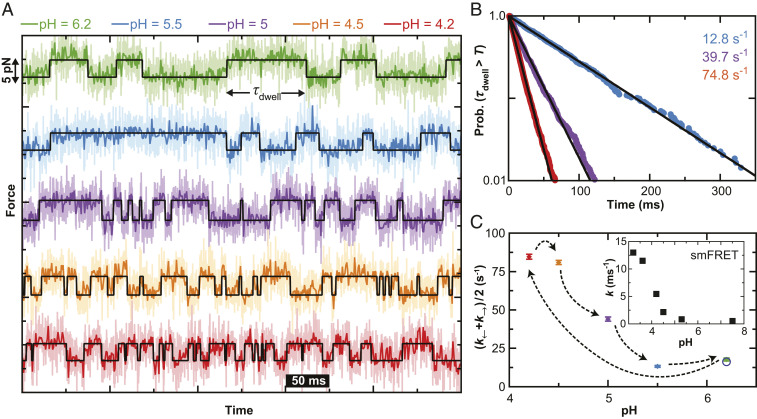
Fig. 3.

Equilibrium folding dynamics of α₃D as a function of pH. (A) Force-versus-time traces showing α₃D repeatedly folding and unfolding at different pH values (as denoted by color). The base of the cantilever was held for 5 s at a constant position such that the populations of folded and unfolded states were approximately equal. State lifetimes determined by a hidden Markov model analysis (black line). (B) Normalized cumulative distribution functions at different pH values computed by combining the folded and unfolded state lifetimes across multiple molecules (pH 5.5 [blue; N_mol = 3; N_transitions = 494], pH 5.0 [purple; N_mol = 3; N_transitions = 1170], and pH 4.2 [red; N_mol = 3; N_transitions = 2782]). Lifetimes determined by an exponential fit (line). (C) The average of the folding and unfolding rates as determined from the inverse of the mean lifetimes for each trace at each pH. Error bars represent SEM. (Inset) α₃D folding rates determined by smFRET (37).

To quantify α₃D’s kinetics, we analyzed individual records that had approximately equal occupancy of each state (44 to 56%) using a hidden Markov model to determine the dwell time (τ_dwell) for each state occupancy (Fig. 3A, black line). To calculate a rate constant from different molecules, we combined all τ_dwell for folded and unfolded state occupancies at each pH (494, 1170, and 2782 dwell times for pH 5.5, 5.0, and 4.2, respectively). We next computed the cumulative probability distribution for observing a state longer than a specified time. As shown in Fig. 3B, this distribution was linear on a log-linear plot and therefore fit well to an exponential decay (black line). The resulting decay constant decreased as the pH was lowered. Traditional histogram analysis also showed an exponential distribution at each pH value measured (SI Appendix, Fig. S3). To account for molecule-to-molecule variation, we calculated an average inverse lifetime for each trace after correcting for missing events due to limited temporal resolution (61) and report the average and the standard error in the mean as a function of pH in Fig. 3C. Overall, this analysis shows AFM-based SMFS equilibrium records recapitulate the observed acceleration in α₃D’s kinetics measured by smFRET (Fig. 3C, Inset) (37), albeit with differences in the percentage acceleration at each pH (see Discussion).

Rate Maps Derived from Nonequilibrium Dynamics Show pH Dependence.

Rate maps, k(F) versus F, are a powerful means to deduce free-energy landscape parameters governing biomolecular folding (62) via the Bell (63) or the more advanced Dudko (64) models. Rate maps are easily calculated from equilibrium data at constant force (6), though the range of forces probed is limited to values near F_1/2, the force at which both the folded and unfolded state are equally populated. In 2013, Zhang and Dudko introduced a new analysis method to calculate rate maps from constant velocity records showing near-equilibrium dynamics, offering the opportunity to explore a wider range of forces.

We applied a variant of Zhang–Dudko analysis that accounted for finite temporal resolution (61) to deduce rate maps for α₃D at two different values of pH. To do so, we repeatedly stretched and relaxed an individual polyprotein at fixed velocity by moving the base of the cantilever. The total number of cycles per trace varied from five to 80 depending on the pulling velocity to maintain trace durations below 100 s. Several such traces were sequentially collected at each pulling velocity, and we performed this dynamic assay at four different velocities (v = 20, 50, 100, and 400 nm/s). The range of cantilever motion was chosen so that α₃D unfolded and refolded in each cycle, but the NuG2 marker proteins remained folded (Fig. 4A). This protocol assured the compliance of the construct did not vary due to additional unstructured amino acids from an unfolded NuG2 domain. After each stretching and relaxing cycle, the cantilever was held at a constant height just above the surface for ∼0.2 s to embed a zero-force measurement into longer records. The resulting force-extension curves showed multiple near-equilibrium folding/unfolding transitions in each 20 nm/s cycle at pH 6.2 (Fig. 4B), similar to the pioneering optical trapping studies of an RNA hairpin (6). The overlap in the pair of force-extension curves derived from a retraction and approach cycle implies minimal force drift over the time to complete a cycle, which was ∼5 s at the slowest velocity (20 nm/s). The unfolding pattern of the polyprotein did not change when the pH was lowered to pH 4.2, and the overlap between force-extension curves at pH 4.2 and 6.2 indicates no detectable change in the persistence length of the unstructured linker (SI Appendix, Fig. S4).

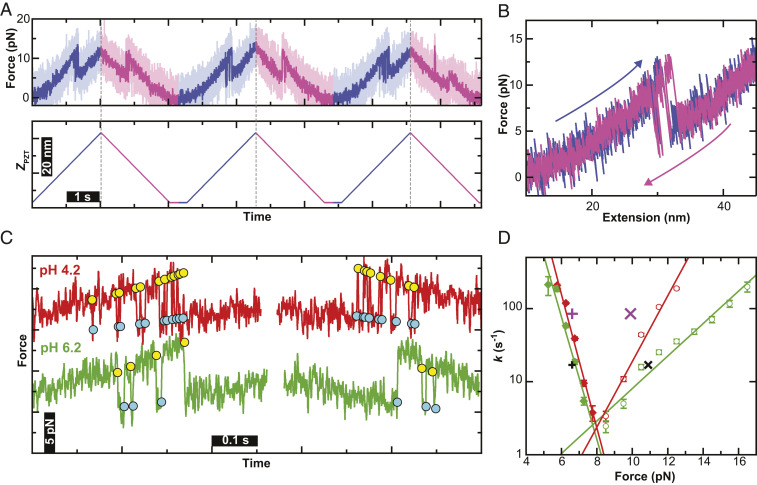
Fig. 4.

Characterization of the near-equilibrium folding of α₃D in a dynamic assay. (A) Force-versus-time record (Upper) driven by repeated cycles of cantilever retraction and approach (Lower: blue and magenta, respectively) at ν = 20 nm/s. Traces were smoothed to 1 kHz (light colors) and 100 Hz (dark colors). (B) Force-extension curve derived from a single cycle of cantilever retraction (blue) and approach (magenta). (C) Force-versus-time graphs of a stretching and relaxing cycle performed at pH 6.2 (green) and pH 4.2 (red). Unfolding (yellow) and folding (cyan) transitions are marked by circles. Smoothing in panels B and C 200 Hz. (D) Force-dependent rates for the folding (filled diamond) and unfolding (open circle) transitions of a representative single molecule measured at pH 6.2 (green) and another at pH 4.2 (red). Error bars represent the SEM. Unfolding and folding rates determined from 5 s long equilibrium records are indicated by × and + symbols respectively (pH 6.2 [black], pH 4.2 [purple]); the width of these symbol represents the SEM of the force.

As with the equilibrium data, we observed a significant increase in the folding rates at pH 4.2 compared with pH 6.2 (Fig. 4C, red versus green, respectively). To analyze these information-rich records, we first identified each transition using a semiautomated protocol (SI Appendix). With this process and the underlying data quality, we identified state occupancies as short as ∼1 ms (SI Appendix, Fig. S5). Rates were then computed using a variation on the Zhang–Dudko analysis (61) and subsequently corrected for missing events due to limited effective temporal resolution (61). Rate maps for the same individual molecule—but at different pulling velocities—showed concurrence (SI Appendix, Fig. S6). We therefore combined data at different pulling velocities on an individual molecule to yield a rate map over a broader range of forces (Fig. 4D).

The most notable aspect of the representative rate maps is the significant difference in slope of the unfolding branch between the two pH values, while the slope of the folding branch is approximately the same (Fig. 4D, open circles versus closed diamonds, respectively). We analyzed individual rate maps using the Bell model with $k\left(F\right)=k_0\exp \left(F\mathrm{\Delta }{x}^{‡}/k_{\text{B}}T\right)$ where k₀ is the zero-force transition rate, k_BT is the thermal energy, and Δx^‡ is the distance to the folding $\left(\mathrm{\Delta }{x}_{\leftarrow }^{‡}\right)$ or unfolding $\left(\mathrm{\Delta }{x}_{\to }^{‡}\right)$ transition state (SI Appendix, Fig. S7). Averaging over multiple molecules at pH 6.2 and pH 4.2 yielded an average distance to the unfolding transition state $\left(\mathrm{\Delta }{x}_{\to }^{‡}\right)$ of 2.0 ± 0.2 nm (mean ± SEM; n = 6) and 3.5 ± 0.3 nm (n = 5), respectively. The same analysis on the folding branch yielded the average distance to the folding transition state $\left(\mathrm{\Delta }{x}_{\leftarrow }^{‡}\right)$ of −8.3 ± 0.4 nm (n = 6) and −8.1 ± 0.3 nm (n = 5). We note that the Bell model yields $\mathrm{\Delta }{x}^{‡}$ calculated at zero applied force, and the implications of these very large $\mathrm{\Delta }{x}_{\to }^{‡}$ will be addressed below in Discussion. As a consistency check, we also plotted the average folding and unfolding rates determined from equilibrium data (Fig. 4D, + and × symbols, respectively). For pH 6.2, the equilibrium data falls very close to the Bell model best-fit lines (Fig. 4D, black). The pH 4.2 equilibrium folding rate is equally close to the best-fit line, while the corresponding data point on the unfolding branch is at a slightly lower force (Fig. 4D, purple). Considering the difficulty in achieving a 1-pN level of accuracy between distinct AFM records, we describe this comparison as excellent by AFM standards (2, 3, 41) and one that relied upon our efforts to maintain force stability.

1D Free-Energy Landscapes Derived from Dynamic Data Approximately Equal Entropic Barrier.

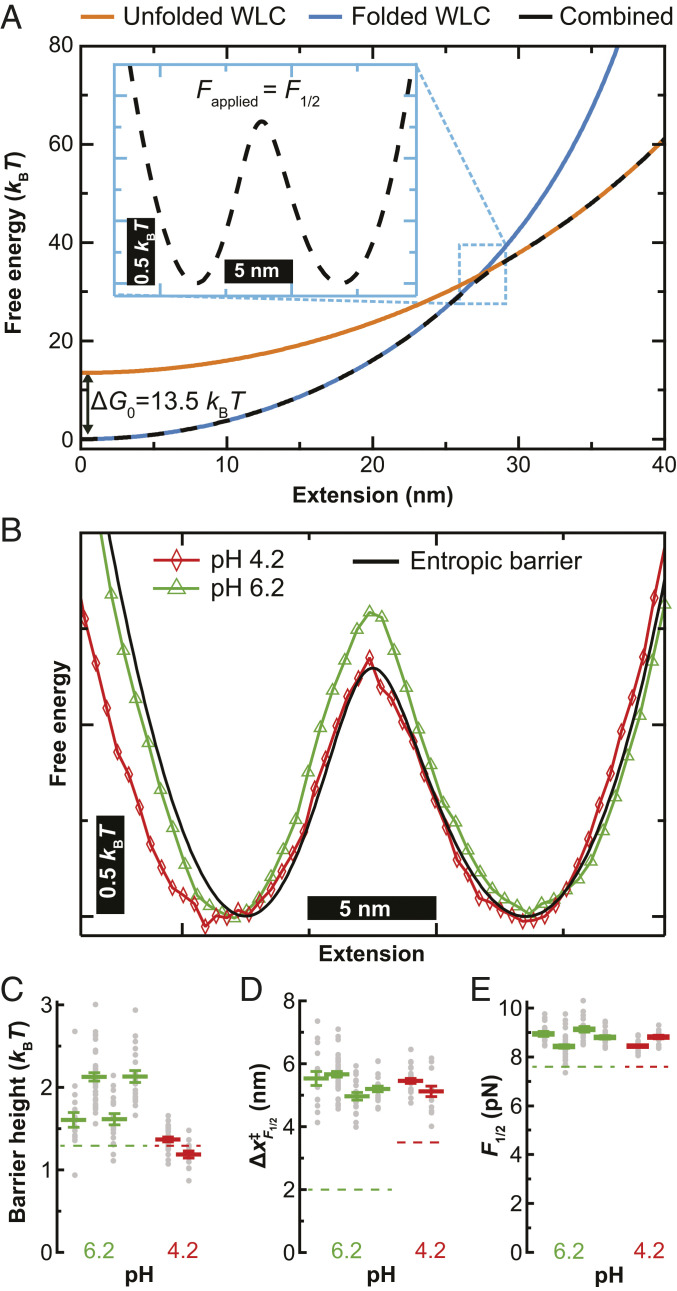
Experimentally reconstructed 1D energy landscapes are necessarily derived from properties of the target molecule in the context of the entire assay, including the force probe and the flexible linkers (10, 65). The contribution to the free-energy landscape from the linkers was easily calculated from a simple model (16). This landscape is calculated by combining the energy associated with the folded structure (Fig. 5A, blue) and from the unfolded structure (Fig. 5A, orange). The free energy of the two states was calculated using a worm-like chain model with linker lengths deduced by fits to a representative force-extension curve. The free-energy landscape of the unfolded state was shifted upward by ΔG₀ (13.5 k_BT). This ΔG₀ was calculated from an average of the equilibrium data of three molecules at pH 4.2 and five molecules at pH 6.2. The resulting free-energy profile does not show a barrier (Fig. 5A, black dashed curve). However, when a constant force of F_1/2 is applied, a small entropic barrier (∼1.3 k_BT) separating the folded and unfolded states is introduced (Fig. 5 A, Inset) (15). Note that, in this simple calculation, the observed landscape contains no information about, or contribution from, the folding landscape of α₃D but only the entropic barrier arising from stretching flexible linkers due to an applied force and ΔG₀ between the folded and unfolded states.

Fig. 5.

Reconstruction of the free-energy landscape of α₃D. (A) The free-energy landscape at zero force for entropic stretching of the polypeptide chain (black dashed curve) calculated from the energetic contributions of the folded (blue) and unfolded (orange) states offset by the free energy of folding (ΔG₀). (Inset) The landscape tilted to F_1/2 = 8.9 pN. (B) Free-energy landscapes at F_1/2 reconstructed from IWT for α₃D at pH 4.2 (red) and pH 6.2 (green). The landscape for entropic stretching of the polypeptide chain from panel A is overlaid (black). (C–E) For four individual molecules at pH 6.2 (green) and two at pH 4.2 (red), the average value (colored line) of barrier height at F_1/2 (C), distance to unfolding transition state at F_1/2 (D), and F_1/2 (E). Measurements from individual sets of force-extension curves acquired at a constant velocity are shown as gray dots. Error bars are SEM. The dashed lines represent in C the barrier height from the entropic limit, in (D) the distance to the transition state from Bell model analysis, and in (E) the F_1/2 from the rate map analysis.

We experimentally reconstructed 1D energy landscapes from dynamic stretching and relaxing data using an inverse Weierstrass transform (IWT) of the Jarzynski equality (16). The IWT determines landscapes from nonequilibrium data efficiently (66) and is particularly well suited to AFM data given the higher stiffness of AFM cantilevers (67). We note that there are alternative landscape reconstruction techniques best suited to soft probes (k << 4 pN/nm) (68). Importantly, landscapes reconstructed by IWT have the contribution from the force probe subtracted out, but not the linkers. Our IWT-based reconstructions used dynamic data of the same type as used to generate rate maps (SI Appendix, Fig. S7). Specifically, we generated a free-energy landscape as a function of molecular extension by combining the stretching and relaxing records at a given velocity. To facilitate comparison, we tilted the resulting landscape by a constant applied force (F_1/2), such that the minima corresponding to the folded and unfolded states were equally populated. The resulting constant-force landscapes reconstructed from 20 nm/s data were highly symmetric and showed a small barrier of ∼1.6 k_BT at pH 6.2 (Fig. 5B, green). The landscape reconstructed from pH 4.2 data yielded a similarly shaped landscape with a marginal decrease in the barrier height at F_1/2 (Fig. 5B, red). We also plot the landscape arising from just the entropic barrier (Fig. 5B, black) which generally overlapped with the pH 4.2 landscape. As discussed more fully below, the similarity of the reconstructed landscapes at both pH values and their concurrence with the entropic barrier induced by the assay does not provide insight into the measured change in kinetics with pH. Rather, these results reflect that α₃D is mechanically labile, and the elastic properties of the linkers do not change with pH.

Repeated measurements of the same molecule at different speeds led to consistent reconstructed landscapes (SI Appendix, Fig. S8). Specifically, we reconstructed a set of landscapes at four velocities (20, 50, 100, and 400 nm/s) for each molecule and then calculated a trio of landscape parameters: the height of the barrier at $F_{1/2}\hspace{0.17em}(\mathrm{\Delta }{G}_{F_{1/2}}^{‡})$, the distance to the unfolding transition state at $F_{1/2}\hspace{0.17em}(\mathrm{\Delta }{x}_{F_{1/2}}^{‡})$, and F_1/2 (Fig. 5 C–E, respectively). Although individual reconstructions varied, we obtained consistent estimates of $\mathrm{\Delta }{G}_{F_{1/2}}^{‡}$ (1.5 to 2.1 k_BT) at pH 6.2 and 1 to 1.3 k_BT at pH 4.2. However, the differences in barrier heights are small, and we caution against overinterpreting a fraction of a k_BT change in $\mathrm{\Delta }{G}_{F_{1/2}}^{‡}$. We similarly found $\mathrm{\Delta }{x}_{F_{1/2}}^{‡}$ to be ∼5 nm (Fig. 5D), consistent with a barrier halfway between the unfolded and folded state. Finally, F_1/2 derived from landscape analysis was just slightly (∼1 pN) higher than the F_1/2 derived from the rate maps shown in Fig. 4D (Fig. 5E, points versus dashed line, respectively). In summary, our reconstructed landscapes were consistent with and dominated by the entropic barrier arising from the flexible linkers used to attach α₃D to the coverslip and the cantilever (15).

Discussion

Comparing Folding Rates Determined by AFM with smFRET.

The central idea explored in the present work was to control the rate of folding along the molecular coordinate (x_prot) while measuring the consequence of that change on the measured coordinate (x_meas) in a force-spectroscopy assay (Fig. 1B). To do so, we sought to directly vary Kramer’s diffusion coefficient (D) by investigating α₃D as a function of pH. This interpretation was based on a prior work investigating the dynamics of individual α₃D molecules using a global denaturant (5 to 6 M urea) in a state-of-the-art smFRET assay and elevated temperature in molecular dynamics simulations. In contrast, our present study combined a more physiologically relevant buffer and temperature with applied force as a well-controlled, mechanical denaturant.

Notwithstanding these differences in denaturants, our force-spectroscopy records mirrored the smFRET data: the folding rate increased as the pH was decreased (Fig. 3C). This acceleration began at pH 5, which is consistent with the smFRET and molecular dynamics study (37). While we note the overall acceleration differed between assays for AFM (fivefold), smFRET (14-fold), and molecular dynamics (twofold), the measurements were made with differences in the denaturant, the temperature of the assay, and/or the unfolding pathway. The observed pH dependence in rates seen across all three platforms supports the conclusion that changes in dynamics measured by AFM (x_meas) reflect a controlled modulation of dynamics of the protein (x_prot) and not an instrumental artifact. However, we note that this agreement does not exclude the possibility that different protein folding pathways are explored in the three assays, and future computational studies can more fully investigate these issues.

Considerations for Landscape Reconstruction of Mechanically Labile Proteins by AFM.

While reconstruction of folding-energy landscapes by AFM from nonequilibrium (69, 70) and equilibrium (71) data were initially demonstrated for the membrane protein bacteriorhodopsin, it has also been recently achieved using equilibrium data for a short RNA hairpin (60) and the mechanically labile, fast-folding protein gpW (28, 29). Here, we reconstructed the full 1D energy landscape of α₃D, another mechanically labile, fast-folding protein (33). In contrast to gpW, α₃D’s reconstructed landscape matched the predicted entropic barrier within a fraction of a k_BT. Although such a landscape encodes limited information about α₃D, studying α₃D in this regime serves as an excellent means to probe if changes in intrinsic protein folding dynamics can be observed despite using an AFM-based assay dominated by the entropic barrier.

As diagramed in Fig. 5A, the entropic landscape accounts only for the energetics of stretching the polyprotein construct in its folded and unfolded states (16) and ΔG₀. The size of the resulting barrier decreases for longer linkers. However, longer linkers also decrease the resolution of the assay as they increase compliance. We demonstrated this by comparing our typical attachments with an attachment with an exceptionally short linker and a construct lengthened by the insertion of elastin-like polypeptide (ELP), an unstructured protein sequence (72). The data confirmed that longer linkers significantly reduced both the folding and unfolding signals and the force-induced barrier in the reconstructed landscape (SI Appendix, Fig. S9). This result further supports our conclusion that the IWT reconstructions were dominated by the entropic barrier. As a result, variations in tether lengths may contribute to observed molecule-to-molecule variations in the barrier height, even when using a very short PEG (MW = 600 D). Similarly, variations in tether lengths introduce an uncertainty to our calculation of ΔG₀ (SI Appendix).

While we determined a landscape reconstruction for α₃D using an IWT from dynamic data, reconstructing landscapes from equilibrium data using inverse Boltzmann analysis has been the gold standard for the field (10, 24) and often the point of comparison for other reconstruction techniques, like the IWT (66). We therefore attempted to reconstruct the landscape for α₃D using inverse Boltzmann analysis from equilibrium data. Note that any smoothing—whether it be intentional or by acquiring the data at limited bandwidth—alters the underlying variance of the data and the reconstructed landscape. In the absence of smoothing, the full 500-kHz acquisition bandwidth data lacked a minimum in the probability distribution of x_meas [P(x_meas)] or, indeed, any modulation away from a Gaussian distribution (SI Appendix, Fig. S10). Therefore, inverse Boltzmann analysis did not yield a barrier between states (SI Appendix, Fig. S10). Smoothing data to at least 500 Hz was necessary to observe a barrier in the reconstructed landscape. This barrier allowed us to calculate ΔG^‡, the curvature at the barrier (κ_barrier), and the well (κ_well). However, these values varied systematically and substantially with the degree of smoothing, making any analysis and interpretation unreliable. Finally, we note that deconvolution can be used to sharpen a barrier (10), but it was not tractable in our hands in the absence of a significant modulation in P(x_meas) away from a Gaussian distribution.

In contrast, the IWT using dynamic data reconstructed a landscape from 50-kHz data, and therefore, our conclusion that our reconstructed landscape along x_meas matched the entropic barrier did not require a modulation in P(x_meas) (SI Appendix, Fig. S10). The IWT is based on the Jarzynski equality (73), a fluctuation theorem. It therefore calculates landscapes from an ensemble of N force-extension curves using so-called work-weighted ensemble statistics (16). We note that in the present study we combined both forward and reverse records to more efficiently calculate the landscape, and convergence was more rapid because the underlying data were close to equilibrium (74). Indeed, we found as few as five stretching and relaxation cycles at 20 nm/s generated reproducible landscapes. While these landscapes were consistent with the entropically limited landscape, this demonstration sets the stage for using AFM-based IWT to investigate a wide array of globular proteins, including more mechanically robust ones.

Estimating Rates Limited by Instrumental Apparatus.

We next show that our measured rates reflect protein-folding dynamics and are not dominated by the instrument. To do so, we follow the formalism put forth by Cossio and colleagues to calculate the transition rate that would be attributed purely to the apparatus (k_A) (13). If k_A is significantly faster than the measured rate, we have confidence that the observed dynamics are not dominated by the instrument. To calculate k_A, one needs a set of curvatures that describe the 1D landscape and an effective diffusion coefficient based on the instrument, labeled D_meas here. For the landscape, we used the one derived from the IWT, which was at the entropic limit. One then applies Kramer’s formula (40),

$$k_{\text{A}}=\frac{1}{2\pi k_{\text{B}}T}\sqrt{{\kappa }_{\text{barrier}}{\kappa }_{\text{well}}}{D}_{\text{meas}}\exp -\left(\frac{\mathrm{\Delta }{G}^{‡}}{k_{\text{B}}T}\right),$$ [1]

to determine the rate limited by an apparatus composed of the force probe and linkers.

We calculated D_meas using $D_{\text{meas}}=\langle \partial x_{\text{meas}}^2\rangle /\tau$ in which $\partial x_{\text{meas}}^2$ is the variance in x_meas in the folded and unfolded state and τ is the autocorrelation time of x_meas in each state. While the exact value varies between different molecules and cantilevers, a typical value for D_meas for our assay was 2.3 × 10⁴ nm²/s (SI Appendix, Fig. S11). This value is ∼10- to 20-fold slower than a prior state-of-the-art optical trapping study (31) but ∼50- to 100-fold higher than a pair of estimates from AFM data using traditional commercial cantilevers (29, 75). Our data suggested a 13-fold difference in spatiotemporal resolution between a BioLever Long and our modified cantilever (Fig. 2G). Therefore, we also calculated D_meas for an uncoated BioLever Long using our 50 kHz data. This calculation yielded 3.1 × 10³ nm²/s, about 10-fold larger than a prior report using a BioLever Long (29). However, we note that batch-to-batch variations in cantilevers can lead to measurable variations. For instance, the present BioLever Long had an approximately twofold faster response time than a prior characterization by our group (43).

With this estimate for D_meas, we calculated an average k_A of 179 s⁻¹ using κ_barrier = 1.9 pN/nm, κ_well = 0.76 pN/nm, and ΔG^‡ = 1.8 k_BT derived from the IWT landscape. This value for k_A is an order of magnitude faster than the dynamics observed during equilibrium unfolding k_meas = 17 s⁻¹. k_A is still more than twofold higher than the measured rates at pH 4.2 (85 s⁻¹). The stiffness of the linkers was ∼0.8 pN/nm at the unfolding transition, and a table is supplied reporting the various stiffnesses of our system (SI Appendix, Table S1). We note that this calculation is not in the large barrier limit (ΔG^‡ >> k_BT) as often assumed, but the application of transition state theory is supported because the observed distribution in τ_dwell is exponential (SI Appendix, Fig. S3) (33). A further caveat is that this calculation was done based on landscapes tilted to F_1/2. However, our equilibrium assay was not done under constant force, but rather at constant cantilever base height. This leads to a significant acceleration in the observed rates (60), as illustrated by the equilibrium rates plotted on Fig. 4D (squares). The effective rate at F_1/2, as determined by the intersection of the two Bell fits, was significantly slower, which further separates constant force rates from k_A. To summarize, our measured rates for α₃D dynamics were slower than that predicted by the reconstructed landscape when using a diffusion coefficient describing the instrumentation, particularly at pH 6.2. This disagreement is expected and indeed required to demonstrate that our assay provides biophysical insight from analyzing the measured rates. Finally, we note that Cossio et al. also provide analytic calculations to correct measured rates for instrumental artifacts (13). However, application of these corrections was not tractable for our work as we lack access to experimentally determined, deconvolved energy landscapes such as were obtained in studies of DNA hairpins by optical traps (31).

Rate Maps Yield Biophysical Insight Hidden from Reconstructed Landscapes.

The most striking result from reconstructing the landscape from the dynamic data is that landscapes measured at pH 6.2 and 4.2 both essentially match the calculated entropic landscape despite a measured increase in rates at low pH. In isolation, this lack of pH dependence appears to confirm our central motivation for studying α₃D. Namely, there would be no change in landscape shape, and an acceleration in the observed rate of folding would originate from a change in the roughness of the energy landscape, albeit perhaps on an unobserved coordinate (Fig. 1B).

However, the rate maps showed the acceleration is not constant across all forces, suggesting that changes in landscape roughness alone may not explain the acceleration in the force spectroscopy assay. We first note that the overall acceleration near F_1/2 of the representative rate map appears small (Fig. 4D). However, averaged across multiple molecules, the average rates at F_1/2 increased twofold between pH 6.2 and 4.2, as determined from the Bell model fits across the full range of the rate maps (SI Appendix, Fig. S7). Further, closer inspection suggests that this extrapolation may overestimate the rate at F_1/2, as the unfolding arm of the pH 6.2 rate map shows curvature for four of the six molecules fully characterized. This issue is clearly visible for the rates at the lowest three characterized forces (e.g., Fig. 4D, open green circles).

Bell model analysis of the rate maps yielded additional information: the acceleration in observed kinetics at low pH arose, in part, from a change in $\mathrm{\Delta }{x}_{\to }^{‡}$. We first note that the differing slopes of the folding and unfolding branches yield an asymmetry in $\mathrm{\Delta }{x}_{\to }^{‡}$ and $\mathrm{\Delta }{x}_{\leftarrow }^{‡}$ in Bell analysis. This asymmetry is not reflected in the reconstructed landscape, but asymmetry is expected because typical values of $\mathrm{\Delta }{x}_{\to }^{‡}$ for globular proteins range from 0.2 to 2 nm (41). A significant increase in $\mathrm{\Delta }{x}_{\to }^{‡}$ to 3.5 ± 0.3 nm (mean ± SEM) was consistently observed at pH 4.2 in our rates map of individual molecules (SI Appendix, Fig. S7). Therefore, at low pH, the unfolding rates increased much faster with increasing force, resulting in more rapid dynamics. These rate maps are supported by our equilibrium data (Fig. 4D, + and ×) which were not acquired at a constant force near F_1/2. Note that we avoided performing measurements at constant force because active feedback loops affect the measured kinetic rates, especially in assays with short lifetimes (20) such as those observed for α₃D. Instead, our equilibrium measurements occur at constant cantilever height but at two different forces on the unfolding and folding arms of the rate map where rates were approximately equal because the applied force changed upon folding/unfolding (60).

In summation, we attribute approximately half of the observed fivefold acceleration in measured kinetics (Fig. 3C) to the change in $\mathrm{\Delta }{x}_{\to }^{‡}$ with pH. The remaining portion of the change in kinetics could therefore arise from a change in the diffusion coefficient (or, potentially, an undetected change in the height of the barrier along x_prot). As stated above, our measured fivefold acceleration in folding kinetics at low pH places our results between the 14-fold change in folding rate measured by smFRET in a chemical denaturant (5 to 6 M urea) and the twofold change reported in the accompanying all atom simulations at elevated temperature (∼97 °C) (37).

More generally, this result of $\mathrm{\Delta }{x}_{\to }^{‡}=3.5\pm 0.3\hspace{0.17em}\mathrm{nm}$ at pH 4.2 reveals α₃D at low pH to be an exceptionally mechanically compliant globular protein (41). Despite this compliance, prior work showed that α₃D remained well folded at pH 2.2 using infrared and circular dichroism spectroscopy (33). Moreover, this result reinforces an earlier mutational study that showed α₃D, a computationally designed protein, had a particularly compliant core relative to most natural, natively folded proteins (76). Finally, inspection of the all-atom simulation analysis (37) showed a previously undiscussed increase in $\mathrm{\Delta }{x}_{\to }^{‡}$ of ∼50%, at low pH. This result is similar to the 75% increase in $\mathrm{\Delta }{x}_{\to }^{‡}$ observed in the present study notwithstanding any differences between the thermally induced and the force-induced unfolding pathways.

Our success in deriving biophysical insight from a rate map was anticipated by Hummer and Szabo (16). They stated that the measured molecular rates reflect the underlying landscape along x_prot by encoding rates of transition along this unobserved coordinate into the measured rates. This process occurs by a transition occurring along x_prot and the system then relaxing along x_meas, a process they term surface hopping along x_prot. Such a thermally activated process across a barrier is consistent with our equilibrium data, which shows exponential distributions in τ_dwell at all pH values explored (Fig. 2B and SI Appendix, Fig. S3).

We did observe an acceleration in the folding rates as pH was lowered (Fig. 4D, green versus red, respectively), though the extent of this effect varied from molecule to molecule in our study. This acceleration would be consistent with a modest increase in D arising from a decrease in the roughness in the landscape as described in the smFRET data (37). However, quantifying the degree of contribution is beyond the current precision of our assay, as such analysis requires aligning rate maps with sub-pN absolute accuracy.

We note that the Bell model analysis yielded a median zero-force unfolding rate constant (k₀) that was approximately sixfold slower at pH 4.2 than at 6.2. This analysis relies upon extrapolating the measured rate to a 50- to 500-fold lower value at zero force, and significant molecule-to-molecule variation was observed in the extrapolated rates. Physically more realistic force-spectroscopy models show the unfolding transition state moving closer to the folded state as force is increased (64). Therefore, we expect there should be some curvature in the rate map and such curvature significantly affects the extrapolation to zero force. This limitation of the Bell model is well documented (62, 64, 65). As mentioned previously, both Fig. 4D and the individual unfolding branches for most of the molecules quantified (SI Appendix, Fig. S7) show a small amount of the expected curvature. The degree of this curvature and its reproducibility, however, is not yet sufficient for us to reliably apply the Dudko model (64) and thereby constrain the height of the barrier (ΔG^‡). Therefore, more accurate analysis of rate maps with the Dudko model remains a future goal, requiring further enhancement of experimental techniques, discussed in detail below. That said, this small degree of curvature and the large degree of extrapolation needed did hinder reliable interpretation of k₀. Thus, we concur with prior work (64, 65) that cautions against overinterpreting such extrapolated values, as they may be unreliable.

Our study also highlights an advantage of repeated back and forth stretching of a polyprotein in conjunction with the Zhang and Dudko formulism (77) as compared with the traditional AFM assay and analysis. In the traditional assay, the cantilever is retracted at a constant velocity, and a single rupture force is measured. Tens to hundreds of such records must then be combined to yield median rupture force or, in more advanced analyses, rupture force distributions, typically interpreted using the Bell–Evans analysis (78). Even if near-equilibrium dynamics were observed, standard analysis requires only the first rupture to be included in subsequent analysis. Here, by applying the Zhang and Dudko formalism that explicitly includes refolding, the many near-equilibrium transitions seen in our traces (Fig. 4C) contributed to calculating the rate map (Fig. 4D) deduced from hundreds to thousands of transitions. Moreover, the stiffness of the cantilever accelerates these transitions in comparison with a constant force assay (60), another popular force spectroscopy modality. Finally, by moving the cantilever’s base at different velocities, we expand the force range of the rate map compared with holding the cantilever’s base at a fixed height in an equilibrium assay.

Current Limitations and Opportunities in AFM-Based SMFS of Globular Proteins.

Our study of α₃D, a fast-folding and mechanically labile protein, revealed several ongoing challenges and opportunities when studying globular proteins by AFM. For example, by observing thousands of transitions per molecule, we observed kinetic variation between individual molecules (SI Appendix, Fig. S7). Given each molecule was centered under the tip to assure a vertical pulling geometry (54), we attribute much of this variation to polydispersity in the length of PEG linkers rather than variation in the tethering geometry. Therefore, employing more homogeneous linkers for tethering of proteins between the AFM cantilever and glass coverslip should reduce molecule-to-molecule variation in the rate map analysis. As discussed above, replacing PEG with ELPs provides for genetically controlled, monodisperse linkers (72) and therefore offers an advantage beyond avoiding the well-known force-induced structural transition in PEG at ∼100 to 200 pN (57).

In our assay, the energy landscape reconstructed via IWT encoded limited information about α₃D, namely the free-energy change upon unfolding (ΔG₀). Extending the linker length decreased the entropic barrier along x_meas to ∼1/2 k_BT; yet, two-state behavior was still resolved albeit at reduced signal-to-noise ratio (SI Appendix, Fig. S9). Further theoretical work is necessary to investigate this low-barrier regime in the context of two-dimensional landscapes (Fig. 1B), as a significant amount of SMFS theory explicitly or implicitly assumes the existence of a significant (≫1 k_BT) folding barrier.

Looking forward, for more typical globular proteins that are not fast-folding with minimal ΔG^‡, we expect that AFM-based landscape reconstruction is now positioned to yield additional information about the protein’s folding landscape, as has been done using dual-beam optical traps, including a leucine zipper (11) and PrP (79). Note, both the leucine zipper and PrP have uncharacteristically large Δx^‡ (∼8 and ∼10 nm, respectively). For typical globular proteins [Δx^‡ < 2 nm (41)], AFM-based reconstructions are likely to employ IWT using only unidirectional data (i.e., stretching) as such proteins are unlikely to refold quickly, except at the lowest pulling rates (52). Therefore, to acquire a sufficiently extensive set of unidirectional data, cantilevers with further improvements in force stability are needed. Our work with FIB-modified cantilevers have empirically shown cantilevers with lower stiffness yield better force stability (32, 43, 44, 80). To date, we have been limited to ∼4 pN/nm; softer cantilevers often irreversibly fold when passing through the air–liquid interface. A final point on landscape reconstruction is that we urge caution when applying an inverse Boltzmann reconstruction to AFM data unless both a clear modulation of probability density is observed in the absence of intentional or accidental filtering (SI Appendix, Fig. S10) and sub-pN force stability is demonstrated over the duration of the record (SI Appendix, Fig. S2). Both effects can lead to biased conclusions.

Rate map analysis (Fig. 4D) will also benefit from improved force stability, as subtle sub-pN shifts in the data alter F_1/2. As discussed, our α₃D rate maps show a small degree of the expected curvatures when depicted on a log-linear plot. This curvature hinders determination of F_1/2 based off linear Bell model fits to the data (Fig. 4D, lines). Yet, the degree and reproducibility of curvature is not yet sufficient to reliably apply more realistic models, such as the Dudko model that accounts for such curvature by adding ΔG^‡ as a fitting parameter (64). Merging further advances in modified cantilevers with lower hydrodynamic drag (32), very high stretching velocities (81), and repeated stretching and relaxing of the target molecule (60) provide means to extend AFM-based rate map analysis over a broader force regime to facilitate resolving such curvature and thereby experimentally constraining ΔG^‡ (64).

Absolute comparison between α₃D dynamics measured via smFRET in a chemical denaturant and the dynamics measured by AFM remains challenging. On occasion, such comparisons have proven successful for specific proteins (82) and have therefore been used to infer a similar folding pathway. However, such comparison is technically challenging and may not succeed for a variety of reasons. For instance, it requires projecting both measurements to a common reference state, zero force and zero denaturant. It is generally accepted that extrapolating rate map data over several orders of magnitude in rate can be problematic (64, 65). Moreover, many studies have used the standard Bell model (6, 8, 65, 81, 82), while others used a more physically descriptive models that incorporate curvature (83). Expanding the dynamic range of rate maps, as discussed immediately above, will facilitate extrapolating force spectroscopy determined rates to zero force.

Conclusions

In summary, we studied the folding dynamics and landscape reconstruction of α₃D. Our AFM-based SMFS measurements captured the acceleration in folding rates below pH 5, similar to previous smFRET work (37). The IWT-reconstructed landscape along x_meas was dominated by the energetic contribution of stretching the flexible linkers and therefore contained limited information about α₃D. However, rate map analysis showed a significant increase in $\mathrm{\Delta }{x}_{\to }^{‡}$ not seen in the reconstructed landscape, which accelerated the unfolding rate at low pH. Moreover, based on $\mathrm{\Delta }{x}_{\to }^{‡}$, α₃D at low pH is remarkably mechanically compliant compared with other standard globular proteins (41). This biophysical insight highlights that AFM-based force spectroscopy can be sensitive to underlying protein dynamics and landscapes along x_prot despite being in a regime where reconstructed landscapes are dominated by a force-induced entropic barrier. This success relied upon the exceptional capability of the FIB-modified cantilevers to resolve state lifetimes of just 1 ms at low forces (SI Appendix, Fig. S5). The present work also presents a framework for leveraging the higher stiffness of AFM cantilevers in landscape reconstruction for globular proteins based on IWT and evaluating when such landscapes are above the entropic limit. More broadly, resolving the dynamics of a fast-folding, mechanically labile protein opens the door to studying more subtle transitions in mechanoresponsive proteins, such as focal adhesion kinase (84), that have been challenging to study by AFM.

Materials and Methods

Sample Preparation.

The polyprotein tethered to the surface consisted of ybbR-6xHisTag–NuG2–NuG2–α₃D–dockerin (III). The DNA template was constructed via Gibson assembly (85) and confirmed by sequencing. The DNA encoding the dockerin, including the associated Xmod domain as well as a plasmid for expression of the cohesin–ybbR for tip functionalization, was kindly provided by Prof. Hermann Gaub’s laboratory (49). Plasmids were transformed into commercially available Escherichia coli BL21 cells, overexpressed during growth in autoinduction media (86), and purified over a packed His-column (HisPure, Thermo Fisher).

Cantilever and Coverslip Preparation.

We used commercially available BioLever Mini cantilevers (Olympus) that were modified using an FIB, as previously described (44, 87). The resulting cantilevers were individually calibrated in air using the thermal method (88). Glass coverslips and cantilevers were functionalized following established protocols (45). Briefly, we functionalized both coverslips and cantilevers with a silane-PEG-maleimide (MW_PEG = 600 D, Nanocs) which was then reacted with CoA (C3019, Sigma-Aldrich). On the day of the assay, we covalently coupled ybbR-tagged cohesin to the cantilever and ybbR-tagged polyprotein to the coverslip using a 1-h deposition in the presence of the enzyme Sfp (46). ybbR is a short 11-amino-acid genetically encoded tag previously used in force spectroscopy assays (89).

AFM Assay.

We used a commercial AFM (Cypher ES, Asylum Research) featuring a temperature-controlled (T = 25 °C), closed fluidic flow cell and a custom-built laser module that generated a ∼3 μm spot size for detecting FIB-modified AFM cantilevers (80). Experiments were performed in 50 mM citric acid/sodium citrate buffer with 150 mM NaCl + 1 mM CaCl₂ added to promote the stability of the cohesin on the cantilever. We tuned the pH from 6.2 to 4.2 by varying the ratio of citric acid to sodium citrate and fine-tuned it by addition of NaOH. The volume of the perfusion fluid chamber enclosing the cantilever, and the sample was ∼200 μL. We therefore flushed the chamber with >5 mL of buffer during each buffer exchange and then let the instrument equilibrate for >30 min before restarting the single-molecule assay.

After letting the sample settle, we initiated the assay by gently (≤100 pN) pressing the cantilever tip into the surface for ∼0.1 s. We then retracted the cantilever at a moderate velocity (e.g., v = 400 nm/s) until the AFM reached a minimum force and extension threshold that fully unfolded the α₃D and NuG2 but does not rupture the cohesin–dockerin bond (e.g., F > 40 pN @ x_meas > 120 nm). This real-time trigger indicated a molecular attachment, and the cantilever was returned to the surface. If this first retraction showed a single attachment based on visual inspection of the force-extension curve, an automated centering routine was run to improve the force precision and accuracy (54). This routine positioned the surface attachment point directly below the tip attachment point to correct for lateral offset (SI Appendix) (54). We typically acquired dynamic data by performing several series of multiple back-and-forth cycles lasting ∼100 s at each of four velocities (v = 20, 50, 100, and 400 nm/s). Equilibrium data were generated by a semiautomated process which moved the cantilever to a height with near equal populations of folded and unfolded extensions and recorded cantilever deflection for 5 s (60). Cantilever deflection data were sampled at 50 kHz, with 500 kHz data often sampled concurrently.

Data Analysis.

We analyzed the collected data in Igor Pro (WaveMetrics) using both Asylum Research software as well as custom analysis code. All force-extension curves were corrected for an optical interference artifact often seen when using small cantilevers (80, 81). Data displayed was digitized at 50 kHz unless noted and smoothed using a second order Savitzky–Golay filter. We report smoothing values based on $f_{\text{smooth}}=\frac{50\text{kHz}}{n_{\text{pnts}}}$ in which n_pnts is the number of points smoothed. To analyze force-extension curves, we used an improved WLC approximation (56). IWT was performed using previously developed python code (67) and is available on GitHub (https://github.com/prheenan/AppIWT).

To identify states and state lifetimes, we analyzed equilibrium records using the free python package hmmlearn (https://hmmlearn.readthedocs.io/en/latest/) and visually reviewed the results to ensure reliable state identification. To do so, the 50 kHz data were smoothed by 21 points and decimated by a factor of 10 to eliminate high frequency peaks in the resulting HMM analysis.

To determine a rate map, the transition rate was calculated for a series of force bins. The force-dependent transition rate k_ij from state i to state j was calculated using

$$k_{\text{ij}}\left(F\right)=\frac{N_{\text{ij}}\left(F\right)}{t_{\text{i}}\left(F\right)},$$ [2]

where N_ij(F) is the number of transitions from i to j at F, and t_i(F) is the total time spent in state i in the force bin F (61). These rates were corrected to account for finite temporal response of the instrument by ignoring state lifetimes less than 1 ms and applying an analytic correction (61). We discarded extrema points in the rate map containing fewer than five to 10 rupture events and those occurring above 250 s⁻¹. We did not include data collected at 400 nm/s in our final rate map analysis as the analytic correction led to nonphysical corrections at the lowest rates. We do note that uncorrected data at v = 400 nm/s were consistent with the corrected rates at other pulling velocities.

Data Availability

The data presented in this paper, including supplementary figures, are available via Dryad (https://doi.org/10.5061/dryad.rxwdbrv7n).