Tricuspid valve leaflet strains in the beating ovine heart

Abstract

The tricuspid leaflets coapt during systole to facilitate proper valve function and, thus, ensure efficient transport of deoxygenated blood to the lungs. Between their open state and closed state, the leaflets undergo large deformations. Quantification of these deformations is important for our basic scientific understanding of tricuspid valve function and for diagnostic or prognostic purposes. To date, tricuspid valve leaflet strains have never been directly quantified in vivo. To fill this gap in our knowledge, we implanted four sonomicrometry crystals per tricuspid leaflet and six crystals along the tricuspid annulus in a total of five sheep. In the beating ovine hearts, we recorded crystal coordinates alongside hemodynamic data. Once recorded, we used a finite strain kinematic framework to compute the temporal evolutions of area strain, radial strain, and circumferential strain for each leaflet. We found that leaflet strains were larger in the anterior leaflet than the posterior and septal leaflets. Additionally, we found that radial strains were larger than circumferential strains. Area strains were as large as 97% in the anterior leaflet, 31% in the posterior leaflet, and 31% in the septal leaflet. These data suggest that tricuspid valve leaflet strains are significantly larger than those in the mitral valve. Should our findings be confirmed they could suggest either that the mechanobiological equilibrium of tricuspid valve resident cells is different than that of mitral valve resident cells or that the mechanotransductive apparatus between the two varies. Either phenomenon may have important implications for the development of tricuspid valve-specific surgical techniques and medical devices.

1. Introduction

The tricuspid valve leaflets coapt during systole and thereby enable successful valve closure. In this role, they prevent regurgitant blood flow and ensure efficient transport of deoxygenated blood to the lungs (Silver et al. 1971). During their motion from the opened to the closed state, the tricuspid leaflets undergo large deformations that are driven by the transvalvular blood pressure. Additionally, the tricuspid valve leaflets are subject to forces due to the contracting peri-annular myocardium and indirectly, via the chordae tendineae, due to contraction of the subvalvular myocardium (Sacks and Yoganathan 2007; Weinberg et al. 2010). Normal leaflet motion throughout the cardiac cycle is therefore indicative not only of healthy leaflet tissue, but also of proper ventricular function and of a well-orchestrated valvulo-ventricular coupling. Thus, quantification of leaflet strains is of interest to basic science, of diagnostic importance, and possibly of therapeutic relevance. This is particularly true given that resident valvular cells in other heart valves, such as mitral valve interstitial cells, are mechanically sensitive and continuously remodeling their host tissue to maintain mechanobiological equilibrium (Grande-Allen and Liao 2011). In those valves, alterations in the mechanical environment of the leaflets due to disease or surgery lead to microstructural and macrostructural changes that can worsen symptoms or contribute to repair failure (Chaput et al. 2009; Rausch et al. 2012; Pierlot et al. 2014; Dal-Bianco and Levine 2015). Hence, abnormalities in deformational patterns in the mitral valve are indicative of disease and a predictor for future disease. Although yet to be shown, the same could be true for the tricuspid valve, thus further motivating the study of tricuspid valve leaflet deformation.

Toward quantifying the mechanics of the tricuspid valve leaflets, Kong et al. (2018) have used an indirect approach. Based on CT images from patients and mechanical properties derived from unmatched patients, they developed a complex finite element framework to estimate both stresses and strains in the normal tricuspid leaflets of three patients. Others have also computed strains in the tricuspid valve leaflets using the finite element method, but used less comprehensive data sets than Kong et al. (Stevanella et al. 2010; Kamensky et al. 2018). On the other hand, Khoiy et al. (2016) quantified strains of the septal tricuspid valve leaflet in an ex vivo beating porcine heart model, while Spinner et al. (2012) quantified leaflet strains in isolated valves connected to a right heart simulator. While these studies took critical steps toward an improved understanding of the deformation of tricuspid valve leaflets, each is subject to significant limitations. To date, the in vivo deformation of the tricuspid valve leaflets has never been directly measured.

The objective of our work is to fill this gap. To this end, we combine a well-established, fiduciary marker-based imaging modality with a large deformation kinematic framework that we have successfully applied to the mitral valve and to quantify the kinematics of the right ventricular epicardial surface (Rausch et al. 2011; Meador et al. 2018).

2. Materials and methods

2.1. Surgical procedure

We performed all surgical and experimental procedures according to the Principles of Laboratory Animal Care, formulated by the National Society for Medical Research, and the Guide for Care and Use of Laboratory Animals prepared by the National Academy of Science and published by the National Institutes of Health. This protocol was also approved by the local Institutional Animal Care and Use Committee (IACUC #:18–01).

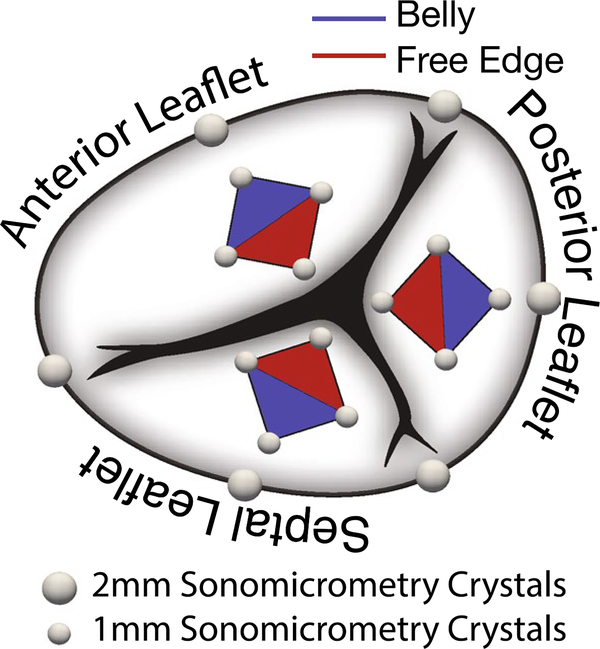
We described the animal procedure and all medications that were administered in detail in our previous work (Malinowski et al. 2016a, b). In short, we pre-medicated the sheep, intravenously anesthetized them, intubated and ventilated them mechanically. To gain access to the heart, we performed a median sternotomy and subsequently prepared the animals for cardiopulmonary bypass. For an unrelated study, we surgically implanted 14, 2-mm sonomicrometry crystals to the epicardial surface of the right ventricle (Sonometrics Corporation, London, ON, Canada). Once we initiated bypass, we opened the right atrium and, with the heart beating, surgically placed six, 2-mm sonomicrometry crystals around the tricuspid annulus as per Fig. 1. Additionally, we sutured 12, 1-mm sonomicrometry crystals on the tricuspid leaflets (four crystals per leaflet, in a diamond pattern), see Fig. 1. Subsequently, we exteriorized the valvular crystal wires through a right atriotomy and placed pressure transducers (PA4.5-X6; Konigsberg Instruments, Inc., Pasadena, CA, USA) in the right atrium and through the apex in the left and right ventricles. Finally, we closed the atriotomy. After weaning the animals from cardiopulmonary bypass, we waited until hemodynamics stabilized and were normal. Subsequently, we collected crystal data (at 128 Hz sampling frequency) under open-chest, open-pericardium conditions for three consecutive cardiac cycles. At the end of the experiments, we euthanized all animals and visually confirmed proper crystal placements.

Fig. 1.

Anatomy of the tricuspid valve with sonomicrometry crystal placement. We implanted six, 2-mm crystals along the annulus with three crystals at the commissures and the other three crystals bisecting the resulting annular regions. To determine strains in the leaflet belly (blue) and the leaflet free edge (red), we implanted additional four, 1-mm crystals in a diamond shape on each leaflet for a total of 12 leaflet crystals and 18 valvular crystals

2.2. Mean surface reconstruction

To approximate the mean shape of the tricuspid valve leaflets from the crystal coordinates, we chose an approach described in our previous work (Rausch et al. 2011; Meador et al. 2018). First, we computed a mean data set based on five animals. Toward this end, we divided the cardiac cycle of each animal into four segments: (1) end-diastole (ED) to end-isovolumic contraction (EIVC), (2) EIVC to end-systole (ES), (3) ES to end-isovolumic relaxation (EIVR), and (4) EIVR to ED of the next cardiac cycle. Next, we linearly interpolated all crystal positions segment-wise throughout the cardiac cycle to then average the resampled data between all animals.

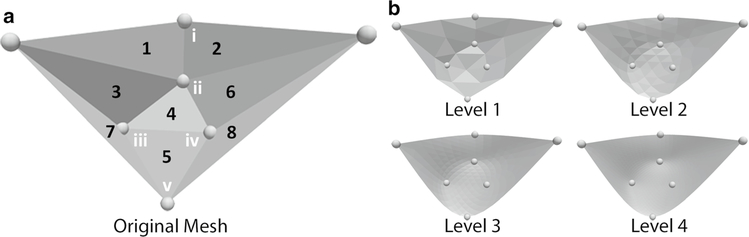
Subsequently, we combined manual crystal triangulation, a triangular surface subdivision algorithm (Loop 1987; Cirak et al. 2000; Göktepe et al. 2010), and an iterative optimization procedure (Rausch et al. 2017a) to create C²-continuous approximations to the native leaflet surfaces that interpolate the actual crystal coordinates. Figure 2 illustrates the result of this process for the anterior leaflet starting with the original mesh in Fig. 2a and four different levels of subdivision in Fig. 2b. Note, we used the subdivided surfaces primarily to ease visualization, but performed all quantitative analyses on the original mesh.

Fig. 2.

Anterior leaflet crystal locations and mesh triangulation of a the original mesh with region designation (Arabic numerals) used in Table 3 and marker designations (Roman numerals) used in Fig. 3, b the smoothed, subdivided surfaces. Subsequently, we refer to regions 4 and 5, which are defined solely by 1-mm crystals, as leaflet “belly” and “free edge”, respectively. We computed the leaflet surfaces of Levels 1–4 by combining a subdivision surface algorithm with an iterative optimization scheme to ensure that the smoothened surfaces interpolate the original crystal locations

2.3. Leaflet motion

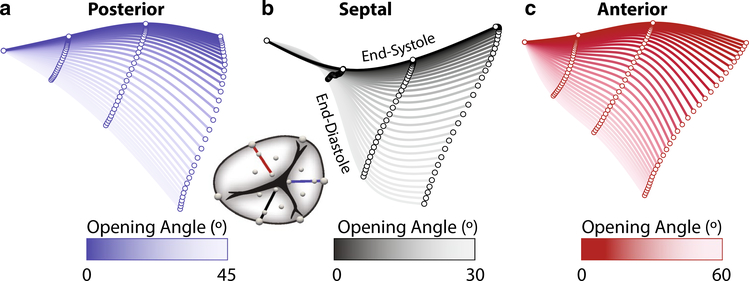
To illustrate the basic motion of the tricuspid valve leaflets, we first reduced the full crystal data set to only a central radial line; see insert of Fig. 3a. Specifically, we identified the mid annular segment crystal (i, in Fig. 2a), mid-belly crystal (ii), free edge crystals (v), and averaged the two lateral crystal locations (iii, iv), for each leaflet. To quantify the opening and closing angles, we fit a line to those markers in a least-squares sense. Subsequently, we computed the angle between this line and the least-squares plane fit to the annular markers for each time point and each leaflet. Moreover, we based our calculation of the opening and closing angular velocities on a finite difference scheme for those same data. Finally, to qualitatively depict the motion of the leaflets during systole, we projected the averages between all animals of those same four crystals on their least-squares plane and fit a cubic spline to interpolate the inter-crystal space.

Fig. 3.

Kinematics of the radial centerline for the a posterior, b septal, c anterior leaflet during systole. We show the leaflet crystal coordinates after averaging between animals and after projecting them onto a least-squares plane. Each centerline is computed as a least-squares cubic spline and colored according to its angle relative to the center line at end-diastole. We calculated this angle using least-squares line fits to the crystals coordinates at each time point

2.4. Leaflet strain computation

To compute tricuspid leaflet strain in the beating ovine heart, we used an approach as described in (Bothe et al. 2011b; Rausch et al. 2012). Specifically, for both the original triangular mesh and for the smoothed mesh, we interpolated each triangular element via linear shape functions in terms of the local curvilinear coordinates θ^α, with α= 1, 2; see Eq. (1). Here, X(θ¹, θ²) are the interpolated coordinates in the reference configuration, for which we chose ED because it is likely the time at which the leaflets are the least strained and therefore closest to a stress-free reference configuration. While this state is probably not entirely stress-free (Amini et al. 2012; Rausch and Kuhl 2013; Rausch et al. 2013), we have previously shown in the mitral valve that leaflet strains are relatively insensitive to the choice of reference configuration (Rausch et al. 2011). On the other hand, x(θ¹, θ²) represents the interpolated coordinates in the spatial configuration, which varies throughout the cardiac cycle.

$$\mathit{X}\left({\theta }^1,{\theta }^2\right)=\mathbf{\sum }_{i=1}^n{N}_i\left({\theta }^1,{\theta }^2\right){\mathit{X}}_i\text{and}\mathit{x}\left({\theta }^1,{\theta }^2\right)=\mathbf{\sum }_{i=1}^n{N}_i\left({\theta }^1,{\theta }^2\right){\mathit{x}}_i,$$ (1)

Furthermore, N_i(θ¹, θ²) are aforementioned linear shape functions, and X_i and x_i are the crystal coordinates in the reference configuration and spatial configuration, respectively. Based on the partial derivatives of the shape functions, we next computed the covariant base vectors in both configurations,

$${\mathit{G}}_{\alpha }\left({\theta }^1,{\theta }^2\right)=\mathbf{\sum }_{i=1}^n\partial N_i/\partial {\theta }^{\alpha }{\mathit{X}}_i\text{and}{\mathit{g}}_{\alpha }\left({\theta }^1,{\theta }^2\right)=\mathbf{\sum }_{i=1}^n\partial N_i/\partial {\theta }^{\alpha }{\mathit{x}}_i,$$ (2)

while we determined the contravariant counterparts to the above bases via the covariant surface metric in the reference configuration G_αβ =G_α · G_β, i.e.,

$${\mathit{G}}^{\alpha }=G^{\alpha \beta }{\mathit{G}}_{\beta },\text{where}{G}^{\alpha \beta }=G_{\alpha \beta }^{-1},\text{with}\alpha ,\beta =1,2$$ (3)

and via the covariant surface metric in the current configuration g_αβ =g_α · g_β, i.e.,

$${\mathit{g}}^{\alpha }=g^{\alpha \beta }{\mathit{g}}_{\beta },\text{where}{g}^{\alpha \beta }=g_{\alpha \beta }^{-1}$$ (4)

Moreover, we computed the Green–Lagrange strain tensor as,

$$\mathit{E}=E_{\alpha \beta }{\mathit{G}}^{\alpha }\otimes {\mathit{G}}^{\beta },\text{where}{E}_{\alpha \beta }=\frac{1}{2}\left[g_{\alpha \beta }-G_{\alpha \beta }\right].$$ (5)

To determine circumferential and radial strains, E_c and E_r, we projected the full strain tensor onto the circumferential and radial direction vectors, n_c and n_r, respectively, which we calculated for each triangular element, i.e.,

$$E_c={\mathit{n}}_c\cdot \mathit{E}{\mathit{n}}_c,\text{and}{E}_r={\mathit{n}}_r\cdot \mathit{E}{\mathit{n}}_r.$$ (6)

In detail, for each triangular element, we calculated n_r as the vector connecting the triangular element’s centroid with the leaflet free edge crystal and projected this vector onto the triangular element’s surface before normalizing. The circumferential vector followed from the cross-product of the surface normal vector and the radial direction vector n_r. Finally, we computed the area strain, E_a, as the ratio between each triangular element’s surface area in the current configuration and the reference configuration. To compute maximum principal strains, we solved the eigenvalue problem for the full strain tensors of Eq. (5) and reported the tensor’s largest eigenvalue.

2.5. Statistics

We compared differences in peak strains across the three leaflets, two leaflet regions, and two directions (i.e., radial vs. circumferential) using a three-way ANOVA as implemented in MATLAB R2017b (MathWorks, Natick, MA, USA), where we considered subject ID as a random effect. To compare individual groups, we performed a Tukey post hoc analysis. Similarly, to compare opening/closing angles as well as their velocities, we performed a one-way ANOVA in MATLAB. For all tests, we considered a p value of 0.05 as statistically significant.

3. Results

All five animals included in our study showed stable hemodynamics, and we were able to confirm secure crystal implantation in all animals postmortem. The hemodynamic data are listed in Table 1.

Table 1.

Hemodynamic data for all sheep included in our study

HR (bpm)	116.0	±4.2
LVP MAX (mmHg)	94.5	±8.0
LVPED (mmHg)	12.1	±2.7
RVPMAX (mmHg)	28.6	±3.2
RVPED (mmHg)	4.5	±2.8
RAPMAX (mmHg)	14.0	±1.5
RAPED (mmHg)	8.6	±0.9
RVVED (ml)	116.2	±20.4
RVVES (ml)	86.2	±10.4

HR heart rate, LVP left ventricular pressure, RVP right ventricular pressure, RAP right atrial pressure, RVV right ventricular volume, ED end-diastole, ES end-systole

The average shapes of the three leaflets are depicted in Fig. 3. Specifically, we show the radial center line of each leaflet throughout systole, i.e., during valve closure. During the closing motion, the posterior leaflet maintains a convex shape between ED and ES, while the septal leaflet changes its shape from convex near the annulus and concave near the tip during diastole, to a fully concave shape at ES. Finally, the anterior is shaped the opposite from the septal leaflet at ED. In its open state, the shape of anterior leaflet is dominated by a concave curvature at the annulus, but a convex curvature near the free edge. This pattern remains throughout systole. Moreover, in Table 2 we quantitatively compare the maximum and minimum opening angle as well as their velocities to describe leaflet kinematics. Among the three leaflets, the septal leaflet had the smallest opening angle when compared to the posterior leaflet (p < 0.001) and the anterior leaflet (p = 0.005). Moreover, the septal leaflet underwent a smaller range of motion than the anterior leaflet (p = 0.008). Finally, the septal leaflet had a slower closing velocity than the anterior leaflet (p = 0.008). We found no differences between the anterior and posterior leaflets.

Table 2.

Average maximum and minimum angles measured relative to the annular plane as well as maximum and minimum angular velocities ± 1 standard deviation for each leaflet. Negative angular velocities indicate closure, while positive angular velocities indicate opening. p values in table are determined via 1-way ANOVA

	AngleMAX (°)		AngleMIN (°)		AngleREL (°)		VelocityMAX(°/ms)		VelocityMIN (°/ms)
Posterior	80.4	±6.8	34.3	±14.3	46.1	±16.0	0.97	±0.45	−1.02	±0.41
Septal	52.0	±7.2	22.8	±7.5	*29.2	±7.0	0.63	±0.14	*−0.71	±0.23
Anterior	73.4	±6.6	14.3	±4.2	59.1	±4.2	1.22	±0.28	−1.61	±0.29
p	0.005		0.058		0.050		0.058		0.010

^*Different from anterior leaflet (p < 0.05)

^#different from posterior leaflet (p < 0.05) per Tukey post hoc

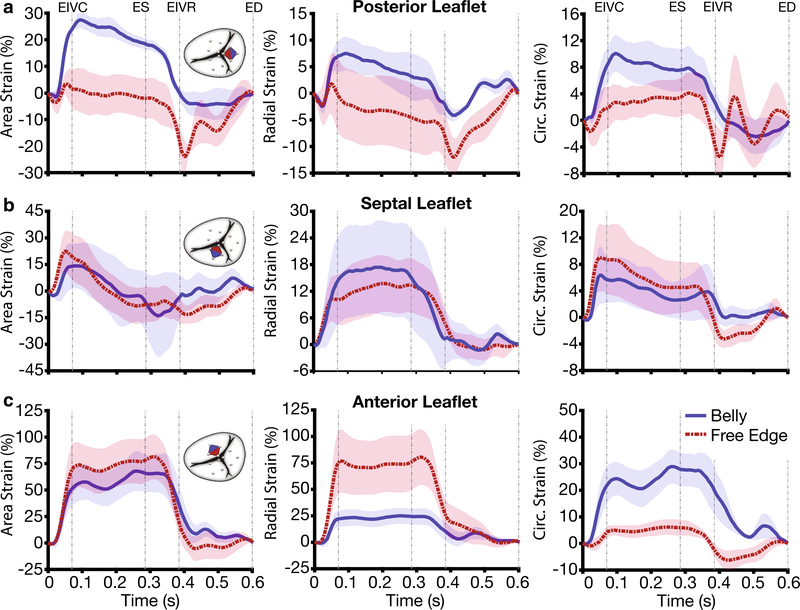
Strains of the belly region and the free edge region over time are depicted in Fig. 4. Specifically, Fig. 4a illustrates the evolutions of area strain, radial strain, and circumferential strain for the posterior leaflet throughout the cardiac cycle. We observed that mean belly strains appeared generally larger than mean free edge strains. Additionally, strains in the two regions behaved qualitatively different. While belly strains were positive throughout systole and deviated marginally from zero during diastole, free edge strains were either small (area and circumferential strain) or negative (radial strain) during systole. During diastole, all free edge strains showed significant negative deviations. On the other hand, free edge and belly strain in the septal leaflet showed qualitatively and quantitatively very similar behavior, Fig. 4b. Both, belly strains and free edge strains, rose during isovolumetric contraction. However, area strains and circumferential strains began decaying immediately after EIVC to approach zero at around EIVR. In contrast, radial strains maintained almost constant levels between EIVC and ES, before returning to zero. Finally, belly and free edge strains in the anterior leaflet behaved qualitatively very similarly Fig. 4c. Both strains, again, rose during isovolumetric contraction and maintained constant levels during systole before decaying shortly after ES to reach approximately zero strain at EIVR where they stayed for the remainder of diastole. However, quantitatively, they differed. While they appeared to have similar mean area strains, free edge strains were larger on average in the radial direction, while mean belly strains were larger in the circumferential direction.

Fig. 4.

Temporal evolutions of strains in the belly region (blue) and free edge (red) region of the a posterior, b septal, c anterior tricuspid valve leaflet. Based only on the 1-mm leaflet crystals, we computed area strain, radial strain, and circumferential strain throughout the cardiac cycle. We calculated averages and standard errors between animals by dividing the cardiac cycle of each animal into four segments, averaging strains between animals for each segment, and re-assembling the data. Abbreviations in figure: end-diastole (ED), end-isovolumetric contraction (EIVC), end-systole (ES), end-isovolumetric relaxation (EIVR)

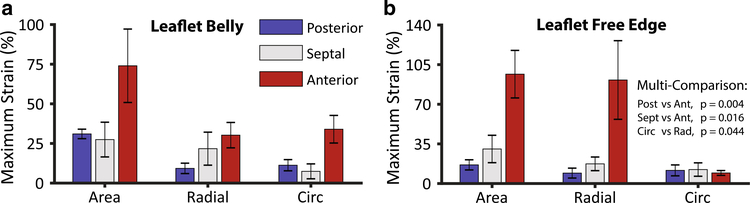
We compare types of strains between leaflets and leaflet regions quantitatively in Fig. 5 in terms of maximum strain, i.e., the largest strain throughout the cardiac cycle. Statistically, we found that there is no significant difference between strains in the leaflet belly and free edge (p = 0.411). However, we did find that there is a difference in strains between leaflets (p < 0.003). Specifically, the anterior leaflet underwent larger strains than the posterior (p = 0.004) and the septal leaflet (p = 0.016). There was no significant difference between the posterior and septal leaflet. Moreover, we found that radial strains were larger than circumferential strains (p = 0.044). To supplement Fig. 5, we also provide numerical data on maximum strains for all leaflet regions in Table 3 including maximum principal strains; see Fig. 2a for regional designations.

Fig. 5.

Maximum area strain, radial strain, and circumferential strain per leaflet in a the leaflets’ bellies and b the leaflets’ free edges. We computed strains as the largest strains throughout the cardiac cycle for each animal on the non-subdivided, original leaflet triangulations. We performed the multi-comparison per Tukey post hoc

Table 3.

Average maximum area strain, radial strain, circumferential strain (Circ), and maximum principal (Max) strain ± 1 standard deviation for each leaflet and leaflet region (see Fig. 2a for regional designations)

	Area (%)		Radial (%)		Circ (%)		Max (%)
Region 1
Posterior	57.84	±68.33	14.13	±23.05	81.98	±117.28	106.12	±139.70
Septal	20.72	±15.03	3.84	±3.15	6.03	±2.23	26.97	±17.24
Anterior	20.61	±7.58	20.76	±10.10	5.12	±4.93	29.74	±8.11
Region 2
Posterior	29.12	±34.26	15.80	±31.01	20.12	±18.54	56.89	±51.28
Septal	22.57	±10.40	13.88	±14.39	5.47	±3.26	28.35	±19.19
Anterior	17.92	±10.26	16.34	±9.12	8.23	±8.29	28.19	±11.78
	Region 3
Posterior	12.17	±7.14	9.73	±6.71	4.04	±3.88	16.46	±7.84
Septal	15.10	±10.12	14.49	±8.66	1.44	±1.46	27.71	±21.35
Anterior	34.52	±45.32	44.79	±49.59	11.22	±22.99	64.70	±68.46
Region 4
Posterior	31.01	±6.69	9.28	±7.34	11.28	±7.89	31.94	±12.97
Septal	27.45	±24.50	21.72	±23.28	7.41	±10.51	40.50	±30.53
Anterior	74.00	±51.79	30.24	±17.91	33.98	±19.47	81.85	±32.04
Region 5
Posterior	16.48	±10.02	9.22	±9.79	11.61	±10.79	28.26	±10.08
Septal	30.51	±27.08	17.39	±13.49	12.35	±13.24	37.57	±24.74
Anterior	96.58	±46.96	91.43	±77.64	9.33	±4.75	119.91	±58.76
Region 6
Posterior	19.02	±20.38	4.69	±2.51	12.23	±13.88	46.11	±28.68
Septal	15.16	±20.20	6.29	±3.43	8.37	±14.75	24.89	±26.48
Anterior	17.37	±9.63	17.78	±9.95	21.57	±25.48	63.68	±27.53

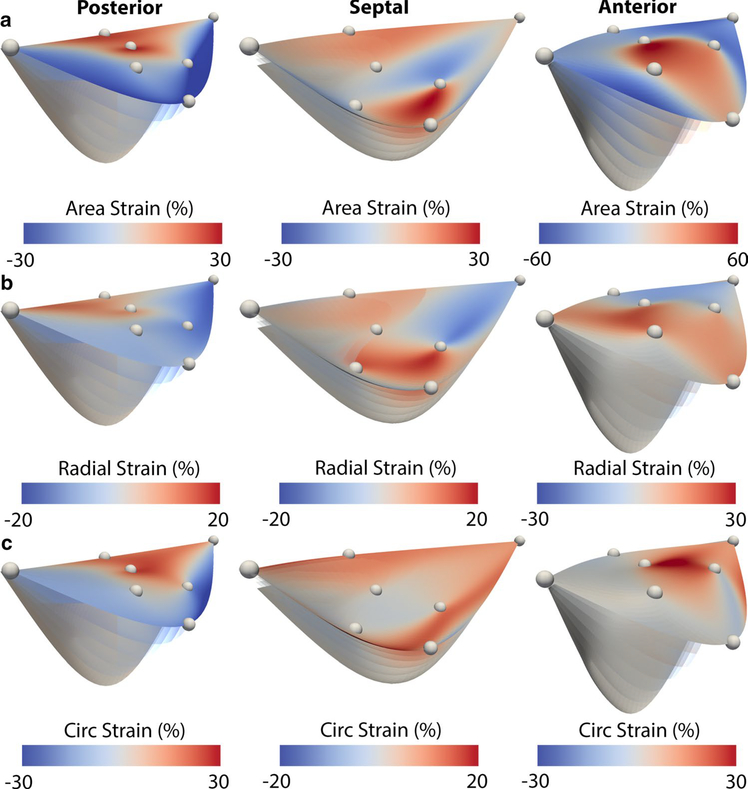
We further illustrate the leaflet motion between ED and EIVC in Fig. 6 and show the full strain maps of each leaflet at EIVC. Specifically, we show area, radial, and circumferential strains, which demonstrated large degrees of heterogeneity across the leaflet surfaces. Between the leaflets, we were not able to discern a common strain pattern. While the posterior leaflet was governed by large positive strains in the annular area and negative strains at the leaflet edges, the septal leaflet showed significant positive strains in both the annular region and the free edge. The anterior leaflet in contrast showed strain predominantly in the belly and the free edge. Between radial strain and circumferential strain no particular pattern seemed to emerge either. While in the posterior leaflet both strains were mostly co-localized, in the septal leaflet and anterior leaflet, both strains appeared complimentary. The kinematics of the tricuspid leaflets are further displayed in three supplementary videos.

Fig. 6.

Complete maps of a area strain, b radial strain, and c circumferential strain across the posterior, septal, and anterior leaflet surfaces from end-diastole to end-isovolumetric contraction. We computed strains for each leaflet relative to end-diastole based on a Level 4 subdivided mesh of an averaged data set between all animals

4. Discussion

The tricuspid valve has long been considered less important than its left-sided counterpart, the mitral valve (Mascherbauer and Maurer 2010). This oversight has led to a sparsity in data on tricuspid valve mechanics. Consequently, knowledge of the mitral valve was frequently extrapolated to the tricuspid valve, which is not only futile because of their differing gross anatomy (Madukauwa-David et al. 2018), but also because the tissues’ resident cells show different phenotypes (Taylor et al. 2003; Merryman et al. 2006). Fortunately, the tricuspid valve has recently received increased interest (Bouleti et al. 2016), which has greatly improved our understanding of tricuspid valve mechanics. This interest is largely driven by our evolving understanding of tricuspid valve pathophysiology and its role to cardiovascular function. Specifically, tricuspid valve regurgitation, or leakage of the tricuspid valve, was historically considered tolerable (Braunwald et al. 1967). Today, it is established that tricuspid valve regurgitation is a significant predictor of patient morbidity and mortality (Ton-Nu et al. 2006). Now, surgeons take a more aggressive approach, and it is recommended to repair tricuspid valves during concomitant mitral surgery if they have more than moderate regurgitation and/or are dilated more than 40 mm (Benedetto et al. 2012; Bertrand et al. 2014). With a higher frequency of surgery comes a need for a better understanding of normal valve function, e.g., to determine appropriate surgical targets. Moreover, following the general trend toward minimally invasive treatment, medical device companies are actively developing trans-catheter repair technologies targeted at tricuspid valve surgeries (Taramasso et al. 2017; Singh-Gryzbon et al. 2019). They, too, require a better understanding of normal valve function.

Toward a deepened understanding of tricuspid valve mechanics, we have rigorously studied and quantified tricuspid annular dynamics in sheep (Rausch et al. 2017b, 2018) and ex vivo beating human heart preparations (Malinowski et al. 2018). Additionally, we have used very similar techniques as described in this work to study right ventricular epicardial strains, also in sheep (Meador et al. 2018). Now, we are extending our analysis to the tricuspid valve leaflets. Our data contribute to the recent progress that has been made in this area through studies of in vitro and in silico specimen. To this end, we have determined area strain, radial strain, and circumferential strain in all three leaflets in beating ovine hearts as well as basic metrics of valve kinematics, such as opening angles and velocities. We found that strain magnitudes and patterns vary between leaflets, but, because of large deviations, could not confirm statistically that they vary between locations. However, we did confirm that strains are larger in the radial direction than in the circumferential direction, i.e., strains are anisotropic. Because there are currently no other accounts of in vivo data on tricuspid leaflet strain, we compare our results to three sets of data that were not directly collected in vivo: (1) an in vitro study on the anterior and posterior leaflets of isolated tricuspid valves (Spinner et al. 2012), (2) an in vitro beating heart study of the septal tricuspid valve leaflet (Khoiy et al. 2016), and (3) an in silico study of the full tricuspid valve complex (Kong et al. 2018). In all three studies, time-varying transvalvular pressure gradients were synthetically imposed. Therefore, we do not compare our temporal evolutions to those obtained in studies by Khoiy et al., Spinner et al., and Kong et al. In terms of maximum strain values, we found that our average values for area strains in any leaflets agree poorly with those measured by Spinner et al. and Khoiy et al. in their in vitro studies. Specifically, Spinner et al. reported area strains in the posterior leaflet of 52% exceeding our values of 31% and 16% in the belly and free edge, respectively. On the other hand, their area strains reported for the anterior leaflet of 21% fall below our values of 74% and 97%, again, in the belly and free edge regions, respectively. Similarly, our area strains of 29% in the septal leaflet exceed the ~ 10% area strain reported by Khoiy et al. In contrast, our data compares better to the results of Kong et al. who presented strain maps across all three human leaflets in three patients based on inverse finite element analyses. Although they do not provide quantitative data, images of their strain fields imply maximum strains in radial and circumferential direction of up to ~ 50%, with largest strains consistently in the anterior leaflet. However, their data imply anisotropy with strains being larger in circumferential direction than in radial direction, thus disagreeing with our findings. Potential sources for inconsistencies are plentiful. First of all, none of the other studies were performed in sheep. Spinner et al. and Khoiy et al. studied porcine valves, while Kong et al. studied human valves. Additionally, the methodologies for strain measurements varied between studies. Spinner et al. used biplane photogrammetry, while Kong et al. combined in vivo CT data with a complex nonlinear finite element framework. Only the work by Khoiy et al. was performed using sonomicrometry as in our study. Also, as mentioned earlier, none of the studies other than ours were direct in vivo measurements. Given these large inconsistencies, clearly more work is needed to paint a complete and confident picture of the deformation of the tricuspid valve leaflets. Among future studies, we plan on performing similar experiments on a larger cohort of animals to reduce uncertainty. Moreover, comparative studies between species should be performed in vivo, in silico, and in vitro.

Should our findings be confirmed, they imply that the tricuspid valve leaflets undergo much larger deformations than the mitral valve leaflets. Specifically, we and others have previously reported that in vivo area strains in the anterior mitral valve leaflet do not exceed ~ 15% under normal conditions. These findings are consistent between different in vivo methodologies (Sacks et al. 2006; Bothe et al. 2011a; Rausch et al. 2011) and in silico studies (Rausch et al. 2013). However, here too, discrepancies are found with in vitro studies (Sacks et al. 2002). Given that leaflet morphology and structure are driven and maintained by resident synthetic cells, ostensibly valvular interstitial cells, one possible implication could be that tricuspid valve leaflet resident cells have different mechanobiological homeostatic targets (Taylor et al. 2003). Thus, our findings could be supported by in vitro studies of cultured tricuspid leaflet valvular interstitial cells and their mechanobiological response to various stretch profiles. In turn, such findings may be relevant to our understanding of tricuspid valve remodeling. Although, to date, there is no evidence of the tricuspid valve leaflets actively responding to patho-mechanical stimuli, it is fully appreciated that the mitral valve has the capacity to remodel in response to disease-induced strains suggesting that the tricuspid valve may as well (Chaput et al. 2009; Beaudoin et al. 2013; Dal-Bianco and Levine 2015). Obviously, if the valves had different mechanobiological targets, the valves’ response to disease-induced mechanical stimuli would differ also. Hence, valve repair techniques and technologies should be sensitive to these possible differences.

Naturally, our data are subject to a number of limitations. First, our experiments were performed on sheep, not on humans. Although sheep have been established as good models of cardiovascular physiology and pathophysiology, care must be taken when extrapolating our data to patients. This is particularly true given the large inconsistencies between species and methodologies revealed in our discussion. Methodologically, the largest limitation is that our data were collected under open-chest, open-pericardium conditions. Hence, without the physical constraint of the pericardium and the chest wall, cardiac deformation may be exaggerated. Additionally, while our methodology of combining sonomicrometry with a large deformation kinematic framework allows for accurate spatial tracking of crystal coordinates and thus high fidelity strain computations, the crystals themselves may affect leaflet dynamics. Specifically, the crystals have finite weight and are attached to wires of finite bending stiffness. Together, these deleterious forces likely induce deviations from normal leaflet motion, which lead to errors in our results. To minimize these errors, we chose small, 1-mm crystals for the leaflets that are lighter and their wires have a smaller bending stiffness than the 2-mm crystals. The technical challenge of suturing these markers to the very thin and anatomically complex leaflets may have also added to the general inter-subject variability present when working with biological tissues. Additionally, all animals were under anesthesia during data collection, which affects cardiac function and may therefore also affect leaflet motion (Jazwiec et al. 2018). Finally, because of the sparse distribution of sonomicrometry crystals across the leaflets, our methodology is insensitive to potential leaflet folding and unfolding in the inter-crystal spaces. We believe that large deviations in leaflet regions other than the belly and free edge may, at least in part, result from such effects. Because we believe those deleterious effects to be significant in regions 7 and 8, we excluded those from Table 3.

5. Conclusion

For the first time, we reported in vivo strains in the tricuspid valve leaflets. Combining sonomicrometry with a finite strain kinematic framework, we computed area, radial, and circumferential strains across the entire leaflet surfaces and throughout the full cardiac cycle. We found that strains were significantly larger in the anterior leaflet than in the posterior or septal leaflets and that radial strains were larger than circumferential strains, i.e., leaflet strains are anisotropic. Unfortunately, because of large deviations in strains across the leaflet surfaces, we failed to demonstrate any statistically significant heterogeneities in strains. Moreover, we found significant inconsistencies between data on leaflet strains obtained through in vivo, in vitro, and in silico studies, which warrants more work on tricuspid valve leaflet mechanics. If our findings were confirmed, however, they would imply that the deformations in the tricuspid valve are significantly larger than those in the mitral valve. This revelation could have important implications about the leaflets’ resident cells and the mechanobiological homeostasis they maintain. Thus, we believe our work is another important step toward a deepened understanding of the tricuspid valve leaflets, which will aid our basic scientific understanding of the valve itself and better inform future surgical and technological strategies toward tricuspid valve repair.