Conductance selectivity of Na⁺ across the K⁺ channel via Na⁺ trapped in a tortuous trajectory

Significance

Ion selectivity is a fundamental property of ion channels. Potassium channels exhibit an unusual selectivity, allowing passage of larger K⁺ ions (ionic radius of 1.3 Å) over smaller Na⁺ ions (1.0 Å); the mechanism underlying the small ion rejecting selectivity remains unknown. Here, we applied Na⁺ as a probe for examining the pore of a prototypical potassium channel and found slight Na⁺ conduction across the pore. Na⁺ traced a tortuous trajectory in the narrow pore, with multiple Na⁺ ions trapped here and there, leading to slow elution. Contrarily, K⁺ passed straight, with three ions moving together rapidly. Na⁺ and K⁺ take different paths and interactions in the pore, which creates dramatic contrast in the conduction rates of Na⁺ and K⁺.

Abstract

Ion selectivity of the potassium channel is crucial for regulating electrical activity in living cells; however, the mechanism underlying the potassium channel selectivity that favors large K⁺ over small Na⁺ remains unclear. Generally, Na⁺ is not completely excluded from permeation through potassium channels. Herein, the distinct nature of Na⁺ conduction through the prototypical KcsA potassium channel was examined. Single-channel current recordings revealed that, at a high Na⁺ concentration (200 mM), the channel was blocked by Na⁺, and this blocking was relieved at high membrane potentials, suggesting the passage of Na⁺ across the channel. At a 2,000 mM Na⁺ concentration, single-channel Na⁺ conductance was measured as one-eightieth of the K⁺ conductance, indicating that the selectivity filter allows substantial conduit of Na⁺. Molecular dynamics simulations revealed unprecedented atomic trajectories of Na⁺ permeation. In the selectivity filter having a series of carbonyl oxygen rings, a smaller Na⁺ was distributed off-center in eight carbonyl oxygen-coordinated sites as well as on-center in four carbonyl oxygen-coordinated sites. This amphipathic nature of Na⁺ coordination yielded a continuous but tortuous path along the filter. Trapping of Na⁺ in many deep free energy wells in the filter caused slow elution. Conversely, K⁺ is conducted via a straight path, and as the number of occupied K⁺ ions increased to three, the concerted conduction was accelerated dramatically, generating the conductance selectivity ratio of up to 80. The selectivity filter allows accommodation of different ion species, but the ion coordination and interactions between ions render contrast conduction rates, constituting the potassium channel conductance selectivity.

Ion selectivity is a fundamental property of ion channels that generate the physiological functions of the cell membrane. Ion selectivity determines the direction of net currents through a channel under a given ionic composition of intracellular and extracellular solutions (1). Potassium channels carry outward K⁺ currents even in the presence of abundant Na⁺ ions in the extracellular solution. The selective passage of large K⁺ ions (ionic radius of 1.3 Å) over smaller Na⁺ ions (1.0 Å) (2–5) is a feature of the potassium channel that distinguishes it from other channels. The molecular mechanisms underlying this selectivity have been studied extensively for decades (2, 4, 6–8) but remain to be fully elucidated (6, 9–11). To examine the selectivity mechanism, the KcsA potassium channel has been applied as a prototypical channel; a broad spectrum of data related to ion permeation and selectivity has been accumulated (8, 12–17). The crystal structure of the KcsA channel revealed that its selectivity filter is narrow (3 Å in diameter) and short (12 Å in length), which is common for all potassium channels.

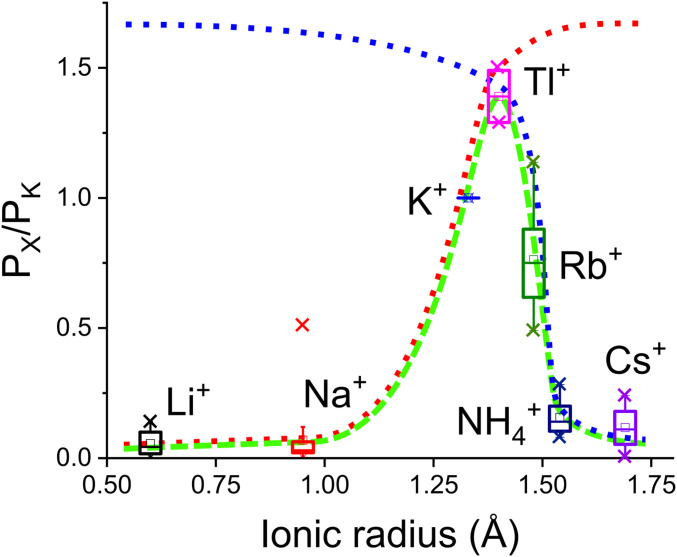
Generally, potassium channels share a typical selectivity feature for monovalent cations, and the permeability ratio relative to K⁺, which is the most frequently used parameter for the ion selectivity, is plotted here as a function of the ionic radius of the relevant ion species (Fig. 1) (1, 4). The channel allows the permeation of ionic species in a limited window with respect to ion size. Ionic species, with ionic radii ranging from 0.9 to 1.7 Å, including K⁺, Tl⁺, Rb⁺, and Na⁺ as a limiting case, are permissible for conduction; however, larger and even a smaller ion (Li⁺) are rejected from permeation. This feature of the potassium channel has been explained by the classical and static concept of the snug fit (3, 18), wherein an ion species within a limited ion size is selected through matching to the cavity size in the pore via formation of a host-guest complex (19). However, molecular dynamics (MD) simulation has demonstrated that the filter structure of the potassium channel is intrinsically flexible, dismissing the strict cavity size (14). Moreover, the crystal structure revealed that even the nonconducting Li⁺ is bound in the selectivity filter (12). A more dynamic picture of the cavity, such as that based on the concept of strain energy, was proposed (10, 14, 19).

Fig. 1.

Ion selectivity of potassium channels. Permeability ratios of monovalent cations relative to K⁺ as a function of ionic radius are shown for various types of potassium channels. The data were collected from literature (SI Appendix, Table S1) and are presented as a box plot, where the box covers the 25th to 75th percentiles, with the center line indicating the median. The potassium channel selectivity is characterized as a band-pass filter with a limited ion-size window (broken green line). The band-pass is arbitrarily decomposed into plausible small-pass (or low-pass; broken blue line) and large-pass (or high-pass; broken red line) filters. The lines do not have physical meanings.

In the selectivity filter, K⁺ is coordinated to eight carbonyl oxygens (cage configuration), whereas Na⁺ is coordinated to four carbonyl oxygens (plane configuration) (9, 12, 20–24). High-affinity K⁺ binding to the filter deduced from the equilibrium crystal structure and spectroscopy has been interpreted as the basis for strict K⁺ selectivity (25–28). However, a comparison between the affinity and conductance revealed that the high affinity of an ion is not a determinant of its selectivity (11, 29). Recently, data supporting the low-affinity binding of K⁺ to the filter have been accumulated (30–32), and a dynamic principle has been proposed as an alternative mechanism for the selectivity (20, 33). Simulation studies revealed differential conduction of K⁺ and Na⁺ under different energy profiles, and Burykin et al. demonstrated that a different effective charge–charge dielectric for the Na⁺ and K⁺ was a unifying idea of the origin of the selectivity (34–36). The distinct nature of Na⁺ from that of K⁺ under the collective dynamics of ions and water within the selectivity filter has been studied extensively (9, 12, 20, 21, 33, 37–40) (see references in the following review articles: refs. 6, 9–11, 33, 37).

Here, we consider that the selectivity arises dynamically and that traveling ions undergo multiple selection steps along the passage of the entire pore. To delineate these selectivity processes, we describe the unique selectivity of potassium channels as a feature of a band-pass filter. The band-pass filter is an electrical device, allowing the passage of signals within a limited frequency range by rejecting low- and high-frequency signals (41). By analogy, potassium channel selectivity is featured as a band-pass filter with respect to the ion size (broken green line, Fig. 1). Generally, a band-pass filter is fabricated from a combination of low- and high-pass filters. Accordingly, the band-pass feature of ion selectivity can be deconvoluted into two types of successive filtering processes along the pore. As small-pass (low-pass) filters (broken blue line, Fig. 1), potassium channels allow the passage of small ionic species with a size cutoff of ∼1.7 Å. The working principle of the small-pass filter is shared with that of other types of channels and is determined by the geometrical pore size (1, 42). Simultaneously, potassium channels impose a unique large-pass (high-pass) filter (broken red line, Fig. 1) that rejects small ions; this is the main issue addressed and studied herein.

Na⁺ is a small ion that can serve as a signature ion to characterize the features of conduction through potassium channels. Consequently, in this study, Na⁺ conduction was examined using single-channel current recordings and MD simulations for the KcsA potassium channel. To characterize the selectivity, the permeability ratio obtained from experimentally measured reversal potentials has frequently been used, as in Fig. 1. Although it is an experimentally feasible parameter, the underlying Nernst–Planck equation assumes independent ion diffusion across a homogeneous membrane phase rather than through a structured pore (1, 43). The reversal potential for calculating the permeability ratio is simply the membrane potential at which inward currents and outward currents are balanced (zero-current potential). Alternatively, the single-channel conductance ratio at a specific membrane potential for different ion species is more straightforward and contrasts the integrated permeation kinetics of different ion species through the pore (4). However, the single-channel conductance of Na⁺ through the potassium channel has not been measured (12, 20, 33) due to experimental difficulty. Instead, indirect evidence of Na⁺ conduction through a potassium channel at the single-channel level has been reported as a punchthrough (12, 13). In the previous simulation, Na⁺ and K⁺ conduction through the KcsA channel was performed, and the conductance ratio was theoretically predicted (34).

In the present study, the intracellular Na⁺ concentration was increased, exceeding the physiological concentration range, and the distinct Na⁺ processes in the pore, which involved blocking and a single-channel Na⁺ current through the potassium channel, were resolved. MD simulations revealed an intricate process of Na⁺ conductance at an atomic scale across the channel. Accordingly, critical permeation processes of the large-pass filter for Na⁺ conduction have been highlighted here.

Results

Single-Channel Behavior of the E71A Mutant Channel under Bi-Ionic Conditions.

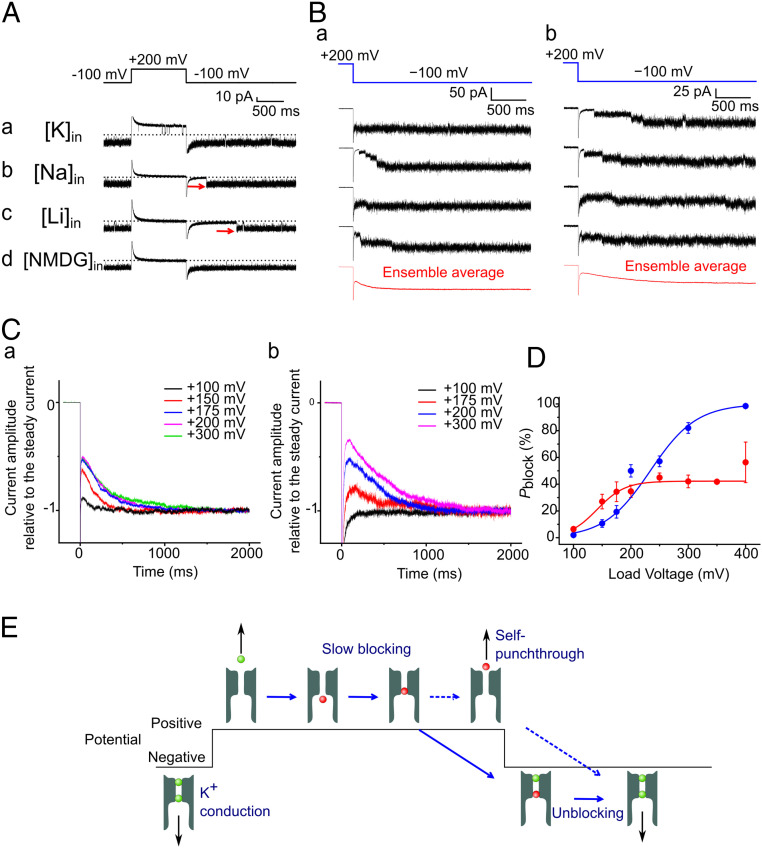
The single-channel current of the KcsA channel in the presence of Na⁺ in the intracellular solution was examined. The KcsA channel was reconstituted into a lipid bilayer using the contact bubble bilayer method (44–46). The acidic pH of one of the compartments (intracellular side) allowed current measurement from functionally oriented channels (see SI Appendix, Supplementary Information Methods). Experiments were performed using a Na⁺ solution (200 mM) with no other cations on the intracellular side. The presence of K⁺ ions on the extracellular side (200 mM) allowed the detection of the single-channel current at negative membrane potentials. Throughout the study, the noninactivating E71A mutant of the KcsA channel was adopted for elucidating Na⁺ permeation through the open filter structure, and all experiments were performed under single-channel current-resolvable conditions to exclude anomalous E71A channel activity (13).

An outward current carried by Na⁺ at +200 mV was not detected upon a positive voltage jump (Fig. 2Ab). In a reference experiment with pure K⁺ ions contained in both the intracellular and extracellular solutions (200 mM; Fig. 2Aa), signature single-channel currents of the E71A-mutant KcsA channel (nearly 100% open probability under all voltages and flicker currents at negative potentials) were observed. Similar to Na⁺, outward currents were not detected for Li⁺ and N-methyl-D-glucamine (NMDG⁺) (Fig. 2Ac and d).

Fig. 2.

Voltage-dependent blocking by Na⁺ and Li⁺. (A) Single-channel current recordings from the E71A mutant of the KcsA channel in different intracellular cationic solutions. The single-channel currents were measured using a pulse protocol (+200 mV) of 1-s duration followed by a negative potential (−100 mV; holding potential was −100 mV). The extracellular solution contained 200 mM K⁺, and the intracellular solution contained 200 mM K⁺ (a), Na⁺ (b), Li⁺ (c), and NMDG⁺ (d). In the symmetric K⁺ solution (A), signature E71A currents were recorded, such as the single-channel current amplitude of 17.7 pA at a positive potential, flickering currents at the negative potential, and the open probability of almost 100% at both −100 mV and +200 mV. (B) Delayed openings at negative potentials in Na⁺ (a) and Li⁺ (b) solutions. A repeated pulse protocol similar to that mentioned in A was applied to the membrane containing a few channels, and the representative current traces are shown. The ensemble current trace (red) obtained from 100 raw traces is shown. (C) Voltage-dependent blocking for Na⁺ (a) and Li⁺ (b). The ensemble current traces for different positive potentials for Na⁺ (a) and Li⁺ (b) are shown. (D) Steady-state blocking probability (P_block) of the channel by Na⁺ (red) or Li⁺ (blue) ions as a function of the membrane potential. P_block was evaluated as the instantaneous current level at the negative potential relative to the steady-state current amplitude. The error bars represent SEM (n = 3 to 30 for Na⁺ and 3 to 26 for Li⁺). The data are fitted with the Boltzmann function (see SI Appendix) with the parameter z = 0.62 ± 0.12 for Li⁺. For Na⁺, the blocking model and fitted parameters are shown in SI Appendix, Fig. S13. (E) Schematic for the slow Na⁺ (red) blocking. The channel remains either blocked or unblocked at positive potentials, and unblocking occurs by self-punchthrough (broken arrow). Upon a negative jump, the blocked channel is unblocked, leading to a delayed opening with inward K⁺ (green) conduction. The unblocked channel allows inward K⁺ conduction from the beginning of the negative jump.

For the [NMDG⁺]_i/[K⁺]_o solution (i = inner solution and o = outer solution), an inward K⁺ current similar to that noted for the symmetric K⁺ solution was observed when the membrane potential was returned negative (−100 mV, Fig. 2Ad). In contrast, in the [Li⁺]_i/[K⁺]_o and [Na⁺]_i/[K⁺]_o solutions, the channel opened after a delay upon a negative jump (Fig. 2A b and c, red arrows). This result indicates that Li⁺ and Na⁺, but not NMDG⁺, enter the pore at positive potentials; they are then released back to the intracellular solution from the pore after a delay at a negative potential. This behavior represents a typical slow blocking, such that Na⁺ and Li⁺ ions travel halfway through the pore into the filter where they are trapped until delayed release occurs at a negative potential. The delay time for the opening at negative potentials indicates a high energy barrier for returning to the conductive state. This slow blocking was observed when the membrane potential was above +100 mV.

The blocking time was examined using similar pulse protocols with increasing pulse durations and determined as 147.1 ± 21.8 ms (n = 3 to 16) at +200 mV (SI Appendix, Fig. S1). For unblocking at negative potentials, the unblocking time was obtained by ensemble averaging of the current traces (SI Appendix, Fig. S2). This kinetic behavior is typical for channel blocking, and the time constants of blocking and unblocking were ∼100 ms for both Na⁺ (unblocking time constant at −200 mV = 165.6 ± 33.5 ms, n = 5) and Li⁺ (blocking time constant at +200 mV = 112.7 ± 36.3 ms, n = 4 to 27, and unblocking time constant at −200 mV = 324.2 ± 32.5 ms, n = 11). Accordingly, at low positive potentials below +100 mV, Na⁺ and Li⁺ were effectively excluded from entering the filter, but they remained in the filter once they entered at high potentials until intracellular release at negative potentials. This process is schematically illustrated using solid blue arrows (Fig. 2E).

Invisible Na⁺ Conduction across the Channel.

The slow blocking of Na⁺ and Li⁺ at positive potentials was not visible, but the blocking probability was evaluated based on the delayed opening at negative potentials (Fig. 2B). To attain steady-state blocking, the duration of the positive pulse was set to 1 s, which is much longer than the blocking time (SI Appendix, Fig. S1). Upon the negative jump to −100 mV, a few channels in the membrane were opened successively with distinct delay times for [Na⁺]_i/[K⁺]_o (Fig. 2Ba) and [Li⁺]_i/[K⁺]_o (Fig. 2Bb) solutions. The number of open channels at the beginning of the negative potential jump provides a rough estimate of the blocked probability at the positive potential (P_block). Ensemble averaging of the single-channel current traces was performed, and P_block was evaluated using the peaks of the “tail” currents. This ensemble protocol was performed for different positive potentials, while the return potential was fixed at −100 mV (Fig. 2C). The voltage-dependence of the steady-state P_block at the positive potentials was evaluated for Na⁺ (red) and Li⁺ (blue) ions (Fig. 2D).

In the case of Li⁺ blocking, P_block increased monotonously as the membrane potential became more positive, demonstrating a typical sigmoidal shape. The Boltzmann fit was performed for Li⁺ blocking, providing a good fit. The electrical distance for Li⁺ blocking was 0.62 ± 0.12 (n = 3 to 26, see SI Appendix, Fig. S3 and Supplementary Information Methods for the definition), suggesting that Li⁺ reached the selectivity filter by overcoming a high energy barrier. For Na⁺ blocking, P_block increased as the membrane potential became more positive but remained nearly unchanged at ∼40% for +200 mV; this value was observed up to +400 mV. This insufficient blocking of Na⁺ relative to the full blocking of Li⁺ is reminiscent of the previously reported release of blocked Na⁺ to the extracellular space in fast blocking (13) as shown in the next section.

Na⁺ blocking in the presence of K⁺ was examined previously for the KcsA channel (13), and we repeated the experiment (SI Appendix, Fig. S3). A single-channel K⁺ current at an intracellular K⁺ concentration of 180 mM was measured, and the outward current amplitude was depressed with an intracellular Na⁺ concentration of 20 mM in a voltage-dependent manner. This showed a typical fast blocking of Na⁺ at the cavity, but the blocking was alleviated above +200 mV (SI Appendix, Fig. S3 A and B). The relief of fast blocking at a high positive potential was called the punchthrough and indicated that the blocked Na⁺ was released extracellularly, driven by the entering K⁺ ions (13). Our repeated experiment reproduced the punchthrough for Na⁺ but not for Li⁺ (SI Appendix, Fig. S3 A and B).

The fact that the complete block for Li⁺ and the incomplete block for Na⁺ appeared to be in parallel with fast and slow blocking at low and high ion concentrations suggests that the selectivity filter allows Na⁺ conduction under pushing by either K⁺ or Na⁺, which will be further studied in the next section (Fig. 3A). For Li⁺, on the contrary, the punchthrough phenomenon was not discernible, indicating that Li⁺ was immobilized and remained in the filter even under a large outward driving force.

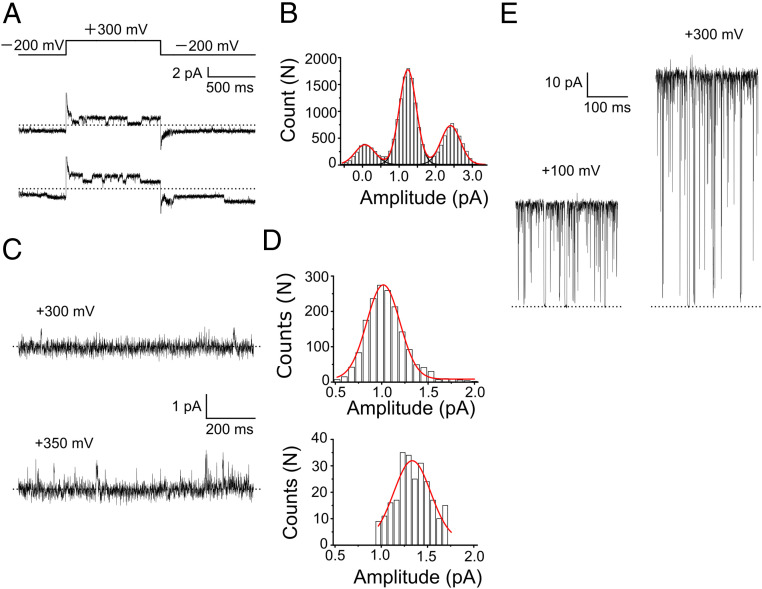
Fig. 3.

Single-channel Na⁺ currents of the KcsA channel. (A) Representative Na⁺ current traces of the E71A mutant with a positive pulse of +300 mV (2 M NaCl intracellular solution and 0.1 M KCl with 1.9 M Tris⁺ extracellular solution). The currents were low-pass filtered at 800 Hz. (B) Single-channel current histogram at +300 mV (all-points amplitude histogram). The membrane contains two channels, and the histogram is fitted with a binomial distribution, which gives an open probability of ∼50%. The single-channel current amplitude was 1.2 ± 0.4 pA (n = 3) at +300 mV. (C) Representative single-channel current traces of the WT channel at +300 (Upper) and +350 mV (Lower). The dashed line represents the zero-current level. The same solutions as those for the E71A experiments were used. The currents were low-pass filtered at 800 Hz. (D) Single-channel amplitude histogram of the WT channel at +300 mV (Upper) and +350 mV (Lower). For the low-open probability channel, rare opening events were detected with an event-detecting algorithm (66) in which the amplitudes of current jumps upon openings were used to construct a histogram. The single-channel current amplitude was 1.02 ± 0.01 (n = 3) at +300 mV and 1.33 ± 0.02 pA (n = 3) at +350 mV. (E) Representative single-channel K⁺ current traces of the E71A mutant. These were recorded in a symmetric 2 M KCl solution at +100 and +300 mV. The single-channel current amplitude was 41.9 ± 1.1 (n = 3) at +100 mV and 94.4 ± 1.8 pA (n = 3) at +300 mV. The dashed line represents the zero-current level.

The single-channel results indicate that at lower positive potentials below +100 mV, Na⁺ and Li⁺ rarely interfere with the KcsA channel (Fig. 2D), indicating that both Na⁺ and Li⁺ are mostly not allowed to enter the filter. At over +100 mV, both Na⁺ and Li⁺ enter the selectivity filter. Thus, the membrane potential is a crucial factor to focus the distinct process of selective permeation.

Single-Channel Na⁺ Currents through the KcsA Channel.

To examine Na⁺ conduction directly using the single-channel current recordings, which was not possible at the concentration of 200 mM, the intracellular Na⁺ concentration was increased to 2,000 mM (described in SI Appendix, Supplementary Information Methods). The presence of 100 mM K⁺ in the external solution allows the evaluation of the number of channels incorporated into the membrane using inward potassium currents at negative potentials (Fig. 3A). The outward single-channel Na⁺ current at +300 mV was successfully recorded in the first direct observation of the single-channel Na⁺ current through a selective potassium channel. The single-channel current was 1.2 ± 0.4 pA in amplitude (n = 3) (Fig. 3B; all-point histogram) and exhibited open–closed transitions. Herein, single-channel Na⁺ conduction through the wild-type (WT) KcsA channel was also measured (Fig. 3C). In the case of the WT channel, the channel current was recorded at steady membrane potentials as the open probability is much lower than that of the E71A mutant. Thus, the event-detecting algorithm was applied to identify the current amplitude of the open state (Fig. 3D; histograms are drawn for the open events; see SI Appendix, Supplementary Information Methods for details). The single-channel current was 1.02 ± 0.01 pA at +300 mV (n = 3), which is similar to that of the E71A mutant.

As a reference, the single-channel K⁺ current was recorded under similar experimental conditions (intracellular K⁺ concentration of 2000 mM). The single-channel K⁺ amplitude was 94.4 ± 1.8 pA (n = 3) at +300 mV (Fig. 3E), and the conductance (γ) ratio, or γ_Na/γ_K value, was 1/78.3. The average residency time of Na⁺ in the pore was calculated as ∼133 ns from the single-channel current amplitude. Compared with those for K⁺ (∼1.7 ns), the rate-limiting energy barriers for K⁺ and Na⁺ permeation differed by 2.6 kcal/mol. This represents an overall quantification of the large-pass filter at +300 mV.

As the single-channel behavior of the E71A mutant at a positive potential was visible, the underlying events of the hitherto invisible slow blocking were discernible. At the positive potential, the Na⁺ conducting channel underwent on-and-off current transitions, and the apparently nonconducting level of the current trace (Fig. 3A) represented the slow blocked state. The blocking probability of ∼50% and the closed time of ∼100 ms in this current trace corresponded to the P_block value and the unblocking time constant deduced from the invisible blocking, respectively (Fig. 2D and SI Appendix, Fig. S2). The opening of the channel from the blocked state at the positive potential indicated that blocked Na⁺ was released into the extracellular space under a strong outward driving force, followed by continuous Na⁺ flow through the unblocked open channel. The detailed mechanism of slow blocking is discussed in SI Appendix, Figs. S4 and S13.

MD Simulation of Na⁺ Permeation through the KcsA Channel.

MD simulation allows understanding of the Na⁺ conduction process through the KcsA channel at an atomic scale (31, 47). The WT KcsA channel without the cytoplasmic domain was embedded in a lipid bilayer phosphatidylcholine (PC) membrane (Fig. 4A) (48), and the simulation was performed in either a pure K⁺ or a pure Na⁺ solution with a concentration of 1,000 mM. A membrane potential of +350 mV, similar to that of the experiments (Fig. 3), was applied, and the outward ion fluxes were examined. Over a simulation time of 4 μs, 137 K⁺ ions permeated the KcsA channel, while only four Na⁺ ions permeated the channel under 4.5 μs. This value corresponds to the K⁺ conductance of 5.5 pA (15.7 pS), which is reasonable for the PC membrane (49). The conductance ratio (γ_Na/γ_K) of 38.5 also corresponds to the experimental value (78.3) as well as the early simulation (34).

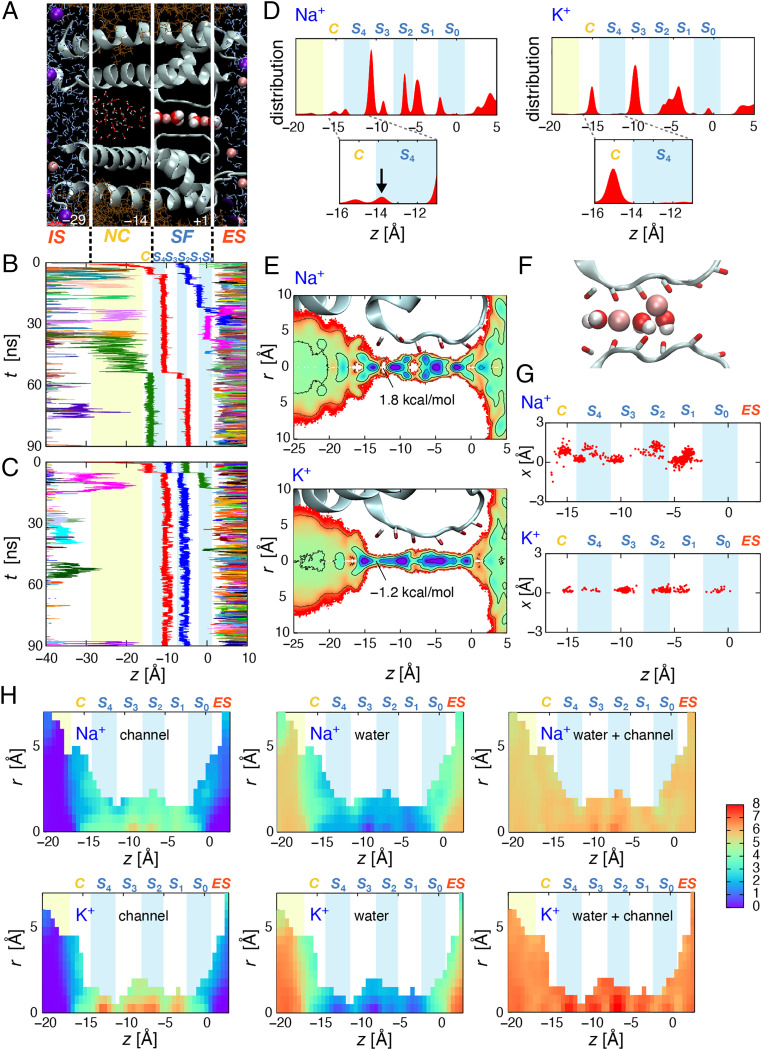
Fig. 4.

MD simulation of Na⁺ permeation through the KcsA channel. (A) KcsA channel embedded in the PC membrane. The names of the permeation pathways are as follows. IS, intracellular space; NC, (nano-)cavity; SF, selectivity filter; and ES, extracellular space. The site in the NC that is closest to the filter is termed as the C-site. Light red spheres corresponding to Na⁺, purple spheres indicate Cl⁻, and red and white spheres indicate water molecules. (B) Representative Na⁺ trajectory. The time course of the movement of Na⁺ ions along the z-axis (z = 0 at the S0 site) is shown. Each color represents an individual trajectory of Na⁺. The light blue and white stripes are bound by the carbonyl oxygens of the filter backbone; these are the five cage sites for K⁺ binding, named S0 to S4. Na⁺ enters the NC frequently but returns to the IS. In the SF, Na⁺ ions occupy either plane or cage sites. The Na⁺ concentration was 1 M, and the membrane potential was +350 mV. (C) The additional trajectory involves three Na⁺ ions moving in concert. (D) Distribution of Na⁺ and K⁺ ions across the pore. In the cavity, Na⁺ ions are present at the entrance of the filter (C-site, arrow), wherein the K⁺ ions are not (Inset). In the filter, Na⁺ ions are present either at the cage (represented by integers, such as S2) or the plane (represented by real numbers, such as S3.5) sites, while K⁺ ions are mostly distributed at the cage sites. The vertical scale corresponds to 1.5 Å⁻¹. (E) Two-dimensional (z- and r-axis) free energy distribution of Na⁺ (Upper) and K⁺ (Lower) around the selectivity filter. Each contour line corresponds to a free energy difference of 1 kcal/mol. At the cage site, Na⁺ distribution is split into two peaks away from the central pore axis, whereas K⁺ distribution remains centered across the filter. (F) Snapshot of Na⁺ ions in the filter. Two Na⁺ ions occupy S3.5 and S2. The on-center Na⁺ in the S3.5 plane site (Left) is flanked by two water molecules. The off-center Na⁺ in the S2 cage site (Right) is solvated by the carbonyl oxygens of two adjacent rings as well as water molecules. (G) Superimposed locations of permeating Na⁺ and K⁺ ions in two-dimensional coordinates of the filter. (H) The coordination numbers at z and r positions. The coordination number was calculated for water (Middle), atoms having less than −0.5e charges (including carbonyl oxygens, Left), and the sum of these atoms (Right) in the range within 3.2 Å for Na⁺ (Upper) and 3.5 Å for K⁺ (Lower). In the cage sites, K⁺ is coordinated by seven carbonyls, while Na⁺ is coordinated by up to five carbonyls.

The representative trajectories of Na⁺ permeation along the z-axis (the pore axis) are shown in Fig. 4 B and C. As seen in Fig. 4B, two Na⁺ ions occupy S3.5 to S0.5 (rational numbers, such as S3.5, represent the occupancy at the plane site, while integers, such as S2, represent the cage site), and other Na⁺ ions frequently enter the cavity but fail to reach the selectivity filter. Once a Na⁺ ion reaches the entrance of the filter, the Na⁺ at S3.5 moves S2 and S1.5 successively. In Fig. 4C, two ions occupy S3.5 (blue) and S1.5 (green) at the beginning, and one ion (red) moves from the cavity to the entrance site. These three Na⁺ ions, moving in concert, reach the S3.5, S2, and S0.5 sites, and the outermost ion (green) leaves the channel. These sequences of events result in net Na⁺ conduction (other trajectories are shown in SI Appendix, Fig. S5).

Fig. 4D shows the positional distributions of Na⁺ (Left) and K⁺ (Right) ions accumulated along the z-axis over the entire simulation time. The overall distributions along the pore differ substantially for Na⁺ and K⁺, with more peaks observed for Na⁺ conduction. In the cavity, K⁺ is predominantly present at the center of the cavity, while Na⁺ has an additional site at the entrance of the filter (C-site, Fig. 4D, inset arrow). The integral of probability distribution in the center of the cavity is much higher for K⁺ (0.42) than for Na⁺ (0.07). This indicates that Na⁺ is less accessible to the cavity (13) and that the large-pass filter is operative at the cavity, supporting earlier reports (13, 50).

The Amphipathic Nature of Na⁺.

In the selectivity filter, Na⁺ ions are predominantly present at the plane sites (S3.5, S1.5, and S0.5), in agreement with the crystal data (33). However, Na⁺ ions are also present at the cage sites, such as S3 and S2. The ability of Na⁺ to occupy either a plane or a cage site in the selectivity filter is herein referred to as the amphipathic nature of Na⁺ binding. The position of Na⁺ fluctuates frequently between the plane and cage sites (Fig. 4C). Moreover, the amphipathic nature of Na⁺ allows varieties of configurations for multiple Na⁺ ions in the filter, such as S3.5-S2-S0.5 and S3-S1.5-S0.

The distribution of Na⁺ was further examined using the two-dimensional free energy profile (Fig. 4E). Along the pore, a high energy barrier for Na⁺ ions was observed between the entrance of the selectivity filter and the S3.5 site. Surprisingly, in the filter, Na⁺ ions occupying the cage sites were off-center. This is in contrast to the on-axis occupancy of Na⁺ ions in the plane sites and the exclusive on-axis occupancy of K⁺ ions throughout the filter. A snapshot revealed that the small Na⁺ ion accesses a site near the carbonyl oxygens of the adjacent carbonyl rings of S1.5 and S2.5 and is therefore off-center (Fig. 4F). Fig. 4G shows the superimposed locations of the permeating Na⁺ and K⁺ ions, contrasting the off-center location of Na⁺ at the cage sites. The occupancy in the off-center cage sites allows the ready transfer of Na⁺ between the cage and plane sites, which creates a continuous conduit across the selectivity filter. Accordingly, the pathway of Na⁺ along the selectivity filter was tortuous rather than the straight on-axis pathway of K⁺ ions. Moreover, the amphipathic binding to the on-center plane and off-center cage provides more degrees of freedom for different configurations of multiple Na⁺ ions in the filter.

To understand the environment of Na⁺ and K⁺ in the pore, the coordination numbers for Na⁺ (Upper) and K⁺ (Lower) were examined. The coordination numbers for water molecules (Middle), carbonyl oxygens, and others (Left; see figure legends for detail) and the sum of these numbers (Right) are presented separately in a two-dimensional profile (Fig. 4H). In the cavity continuous to the intracellular bulk solution, fully hydrated K⁺ and Na⁺ with coordination numbers of 5.87 and 6.94, respectively, diffuse down to the filter entrance and shed most of their hydration water. The water coordination number decreased to 1 to 2 in the filter for both K⁺ and Na⁺, and carbonyl oxygens replaced the solvation with a coordination number of 4 for Na⁺ and up to 7 for K⁺.

We found that the total coordination number (right) was nearly uniform along the pore for Na⁺, indicating that the selectivity filter accommodates Na⁺ with a similar environment to that of the bulk solution in terms of the coordination number. For K⁺, the coordination number was also nearly uniform, but there were four sites in the filter having a carbonyl coordination of 7 to 8 (at −12, −9, −6, and −3 Å sites, right), which correspond to the cage sites. The binding energy of Na⁺ to one carbonyl group in the selectivity filter was very close to that of one water molecule, and this is also the case for K⁺ (SI Appendix, Fig. S6). This explains the invariance of the total coordination number along the pore.

A Mesoscopic Conduction Model and the Conduction Rates.

The distinct binding sites and the coordination numbers for Na⁺ and K⁺ along the pore are crucial for elucidating conduction. However, knowing the residency time of each ion in each site is not sufficient to describe conduction and selectivity (9) because, as is evident from the MD trajectories (Fig. 4 B and C), multiple Na⁺ ions participate in conduction. For example, flickery transitions between plane and cage sites (Fig. 4C) do not yield net conduction. Here, we introduce a previously developed mesoscopic model (31) for characterizing the conduction of Na⁺ ensembles.

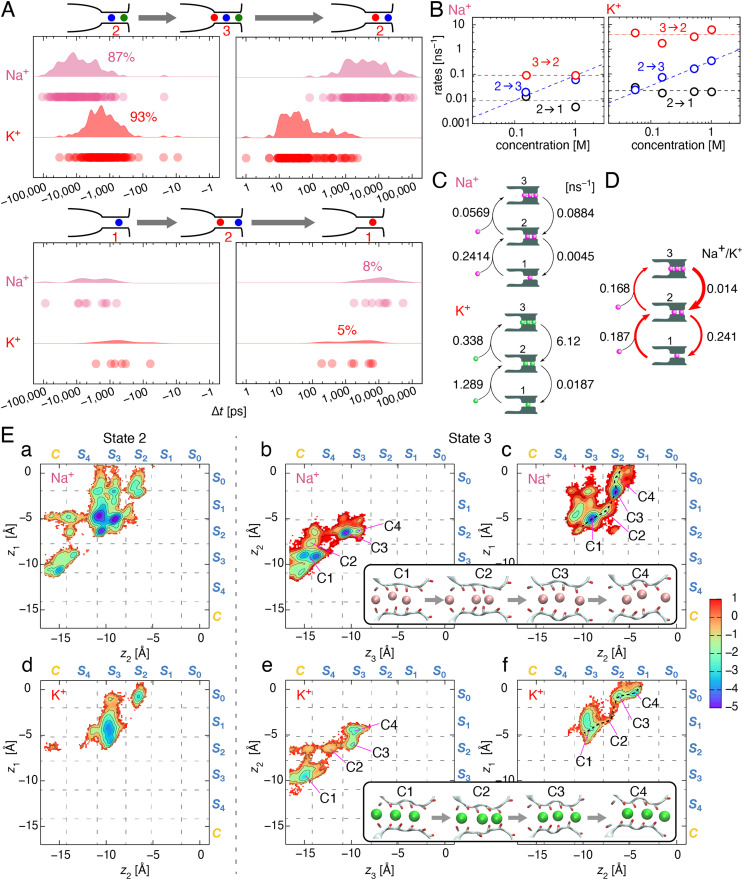
Various configurations of ions in the filter are categorized into a few states by the number of occupied ions in the filter (discrete random variables, see SI Appendix, Fig. S12). For example, ion configurations in the plane and cage sites, such as S4-S2.5-S1 and S3.5-S2-S0.5, with three ions in the filter are consolidated into the three–ion-occupied state (State 3; Fig. 5C) (22, 31). For the transition from the two–ion-occupied state (State 2) to the three–ion-occupied state (State 3), an ion is supplied from the cavity side. Subsequently, the outer ion exits to the extracellular space through transitions from State 3 to State 2 via the single-file nature of ion conduction (2, 22). By completing a cyclic transition around State 2 and State 3, a net ion is transferred across the pore (Fig. 5C and SI Appendix, Fig. S13). The same is true for State 1 and State 2. The different ion-occupied states are integrated into a cyclic model, in which a States 1 to 2 cycle and a States 2 to 3 cycle are merged at State 2; this is called a 1-2-3 model [Fig. 5C; also known as the queueing model (31)]. The simple 1-2-3 model allows the quantitative comparison of Na⁺ and K⁺ conduction.

Fig. 5.

Conductance rates of Na⁺ and K⁺ through the KcsA channel. (A) The residency time of Na⁺ and K⁺ for each ion-occupied state. Up to three ions can occupy the filter (States 1 to 3). The net ion flux occurs through transitions between less–ion-occupied states and more–ion-occupied states, such as State 2 and State 3 (Upper). Completing a cycle yields a net ion flux across the channel. The residency time of each ion-occupied state is shown (Upper Left, State 2; Upper Right, State 3; Lower Left, State1; Lower Right, State 2). The residency time sampled from the MD simulation data are expressed as a dot (raw data), from which the distributions of the residency time are derived based on kernel density estimations (31, 67). In this condition (1 M, +1,000 mV), conduction occurs predominantly through transitions between State 2 and 3 for both Na⁺ and K⁺. The residency time of State 3 for Na⁺ is prolonged 100 times relative to that for K⁺, which is responsible for the slow elution of Na⁺. (B) Concentration dependency of the rates of Na⁺ and K⁺ conduction. The transition rates were derived from the residency times and the number of the transitions (see SI Methods). The rates of transition for State 3 → 2 (red), State 2 → 1 (black), and State 2 → 3 (blue) are shown. The blue dashed line represents a linear fit for the State 2 → 3 rate (= [K⁺] · 0.33 ns⁻¹), and the red dashed line is a constant rate for State 3 → 2 (3.89 ns⁻¹). For Na⁺, the blue dashed line represents the State 2 → 3 rate (= [Na⁺] · 0.088 ns⁻¹), and the red dashed line is a constant rate for State 3 → 2 (0.091 ns⁻¹). (C) The simple permeation models for Na⁺ and K⁺ conduction involving State 1 to 3 (1-2-3 model) at 1.0 M (31). The continuous ion permeation process is coarse grained with a set of the occupied ion numbers (discrete random variables), and the probability and transitions among them yield the net ion flux (SI Appendix) (68, 69). The transition rates between states for Na⁺ were deduced from B. (D) Comparison of the rates for Na⁺ and K⁺. The thickness of the arrows (red) represents the transition rate of Na⁺ relative to K⁺, with the thicker ones indicating more attenuation. All rates are depressed for Na⁺ conduction, but the State 3 → 2 rate is the most prominently depressed, leading to the low Na⁺ conductance. (E) Two-dimensional free energy surfaces for a pair of Na⁺ (a, b, c) and K⁺ (d, e, f) ions in the filter at 1.0 M and 1,000 mV. The left column (a, d) is for State 2 and the middle (b, e) and right (c, f) columns are for State 3. The x- and y-axes represent the z coordinates of ions: z₁ for Na⁺-1, z₂ for Na⁺-2, and z₃ for Na⁺-3, respectively. Snapshots are shown for different ion configurations (C1, C2, …, etc.), and each configuration was assigned on the energy surface. Most likely paths are shown by black dashed lines. The color bar at the right indicates the free energy in kcal/mol relative to that at the exit, and contour lines correspond to an energy interval of 1 kcal/mol. Free energy (F(z₁, z₂)) was evaluated by the following equation: F(z₁, z₂) = −k_BT ln(P(z₁, z₂)), where k_B, T, and P are the Boltzmann constant, temperature, and the probability of finding two ions at z₁ and z₂, respectively.

The MD trajectory was obtained at a membrane potential of +1,000 mV for better sampling (SI Appendix, Fig. S7 for 1.0 M and SI Appendix, Fig. S8 for 0.15 M). At 1.0 M for 5.75 μs of simulation, 96 Na⁺ ions permeated, and 44 Na⁺ ions permeated through the KcsA channel at 0.15 M in the 6 μs simulation time. The patterns of the trajectories were similar to those at +350 mV (Fig. 4B versus SI Appendix, Fig. S7). For example, at 1.0 M, two or three Na⁺ occupied the selectivity filter, predominantly at S3.5 and S1.5 sites. At 0.15 M, two Na⁺ often occupied S3.5 and S1.5 sites, and one ion was sometimes located at S1.5. The same was observed for the K⁺ conduction (31).

The residency times of Na⁺ and K⁺ at 1.0 M for State 1 to State 3 are shown as a distribution (Fig. 5A; the residency times at 0.15 M are shown in SI Appendix, Fig. S9). The average residency time of State 3 (Fig. 5A, Upper) was exceedingly short (0.16 ns) for K⁺ (31), whereas that for Na⁺ was prolonged by a factor of ∼70 (11.3 ns) relative to that of K⁺. This indicates that Na⁺ binds to the filter with a higher affinity.

The transition rates (or rate constants) of these states are derived from the residency time and the number of the transitions (Fig. 5B, see SI Appendix, Supplementary Information Methods) (31), which are shown for Na⁺ and K⁺ in Fig. 5C. All rate constants for Na⁺ exhibited a roughly four to fivefold depression relative to those of K⁺. Among them, the transition from State 3 to State 2 (3 → 2) for Na⁺ was the most prominently depressed (1/70). In Fig. 5D, the depressing ratios of the transition rates for Na⁺ over K⁺ are shown, emphasizing the smallest value (0.014) for 3 → 2 that is responsible for the slow elution of Na⁺.

For both ion species, the ion entering rate for 2 → 3 was more depressed than that for 1 → 2 and can likely be ascribed to the electric repulsion from the ions in the filter. Both Na⁺ entering rates (1 → 2 and 2 → 3) were depressed in parallel, relative to those of K⁺. The Na⁺/K⁺ ratios for entering an ion (1 → 2 [0.187] and 2 → 3 [0.168]) were nearly constant. This suggests that the relative free energy for Na⁺ over K⁺ (ΔF = 1.1 kcal/mol)—likely due to dehydration—is invariable, even though the number of ions occupying the filter differs.

The 3 → 2 rate for both ion species was accelerated substantially relative to the 2 → 1 rate. These transitions involve movements of ions in the filter, followed by the exit of one ion toward the extracellular space. The rehydration process upon exit is common for both the 3 → 2 and 2 → 1 processes. Thus, the differences in the rates can be attributed to the moving process in the filter for the different ion numbers. In the case of Na⁺, the 3 → 2 rate was accelerated 20 times relative to the 2 → 1 rate (0.0884 ns⁻¹/0.0045 ns⁻¹) in which electric repulsion among more ions in the filter is likely involved. In the case of K⁺, the acceleration was as high as 300 times (6.12 ns⁻¹/0.0187 ns⁻¹). The dramatic acceleration for K⁺ has been referred to the “knock-on” mechanism. Underlying mechanisms for such a significant difference between the K⁺ and Na⁺ ions are examined in the next section.

Mechanism Underlying the Contrast Conduction of Na⁺ and K⁺.

To understand distinct ion conduction processes, the number of water molecules intercalated between the ions in the filter was examined; it was found to be 1.26 for K⁺ and 1.11 for Na⁺. The number for K⁺ is in accordance with the previous experimental data of the water–ion coupling ratio of one at high K⁺ concentration (51–53), indicating the occurrence of the classical or soft knock-on, rather than the direct knock-on (31).

The two-dimensional free energy surfaces for Na⁺ and K⁺ in and around the filter were examined (Fig. 5E; also see SI Appendix, Fig. S10 for one-dimensional free energy profiles along the most likely paths). Here, the free energy surfaces for State 2 and State 3 are separately demonstrated for Na⁺ (Fig. 5E, Upper) and for K⁺ (Lower), respectively. In State 2 for Na⁺ (Fig. 5 Ea), numerous energy wells were distributed all over the map along the filter, owing to the amphipathic nature of Na⁺ bindings. Moreover, the wells were separated from each other by substantial barriers. Accordingly, a Na⁺ pair moves successively: when the upstream Na⁺ (Na⁺-2) enters the filter, the downstream Na⁺ (Na⁺-1) moves from S3.5 to S1.5 via S3 and S2, followed by the movement of Na⁺-2 to S3.5. These inchworm movements continue until Na⁺-1 exits to the extracellular space, leading to the transition to State 1; at the exit of Na⁺-1, high energy barriers are seen (red contour), retarding the ion exit. In contrast, the distribution of K⁺ was highly localized (Fig. 5Ed), mostly in the cage sites; the upstream K⁺ (K⁺-2) is located at S3, and the downstream K⁺ (K⁺-1) progresses from S1.5 to S1. Following this, the pair jumped to S2 and S0.

For State 3 (Fig. 5E), three ions were separated into two pairs (upstream [Na⁺-3]–middle [Na⁺-2] pair [Middle] and middle [Na⁺-2]–downstream [Na⁺-1] pair [Right]), and the two-dimensional free energy surface for each pair is displayed (Fig. 5E, Upper for Na⁺ and Lower for K⁺). Accordingly, the free energy of the three-ion ensemble with each ion located at a specific site is readily identified. For Na⁺, one can superimpose the State 3 surface to the State 2 surface, from which it is evident that the overall picture is similar; Na⁺-3 enters the filter, and Na⁺-2 moves from S3.5 to S3, while Na⁺-1 stays at S1.5 (snapshot C1). As Na⁺-3 moves to S3.5, Na⁺-2 moves to S2, and Na⁺-1 moves to S0.5 (snapshot C3). Then, as Na⁺-2 remains at S2, Na⁺-1 exits from S0.5 to the extracellular space (snapshot C4). The inchworm movements of Na⁺ encounter high energy barriers for the exit of Na⁺-1. In these trajectories, ion ensembles are trapped; the high barriers between wells and toward the extracellular space via S0 (C3 → C4) induced slow elution.

For K⁺, on the other hand, a dramatic difference in the free energy surfaces appeared for State 3. The K⁺-3–K⁺-2 pair exhibited a distinct and defined surface, with the surface of the K⁺-2–K⁺-1 pair being similar to that for State 2. When K⁺-3 enters the filter, K⁺-2 stays at S3, and K⁺-1 stays at S1 (snapshot C1). As K⁺-3 moves to S3, K⁺-2 advances to S1, and K⁺-1 moves to S0 (snapshot C4). In State 3, we unexpectedly found that a few distinct energy wells are connected with narrow grooves, which were absent in State 2. These narrow grooves attenuate the barrier heights and allow ready transfers between the wells, permitting rapid K⁺ conduction, reminiscent of the knock-on process.

The two-dimensional free energy surfaces for State 2 and State 3 elucidated the trajectories of multiple ions and their positional relations exclusively. Na⁺ is conducted through the filter in an inchworm-like manner by frequently being trapped in the deep wells separated by high barriers, leading to a slow exit toward the extracellular space. This conduction mode is not qualitatively changed by the number of occupied ions. Contrastingly, for K⁺ conduction, narrow grooves are created exclusively in State 3 between the distinct and well-defined wells, permitting rapid jumps of the ion ensemble between wells. Accordingly, as far as the filter bears two ions at very low ion concentrations, the conductance of Na⁺ and K⁺ is comparable, being only four times faster for K⁺ (Fig. 5C). In contrast, in the three–ion-occupied state, which prevails in a wide K⁺ concentration range, dramatic acceleration occurs exclusively for K⁺ conduction. This induces a sharp contrast of the 3 → 2 rates of K⁺ over that of Na⁺ (Fig. 5D), leading to the distinct Na⁺ versus K⁺ conductance selectivity over 70 folds.

In addition to the process in the filter, the entrance barrier to the filter was examined by decomposing the free energy into energy and entropy (54), which was applied to the one-dimensional free energy profile along the Na⁺ permeation (SI Appendix, Fig. S11). The largest free energy barrier at the entrance (at S4) solely arose from the energy barrier (not entropy) (54, 55). The two-dimensional coordination plot (Fig. 4H) shows that the hydration number abruptly changed from 4 to 2 at the site, indicating that the dehydration process is completed here. Therefore, the rejection of Na⁺ by the free energy barrier at the filter entrance likely arises from the dehydration. This profile also proves that S3.5, S2, and S0.5 sites are energetically favored for Na⁺.

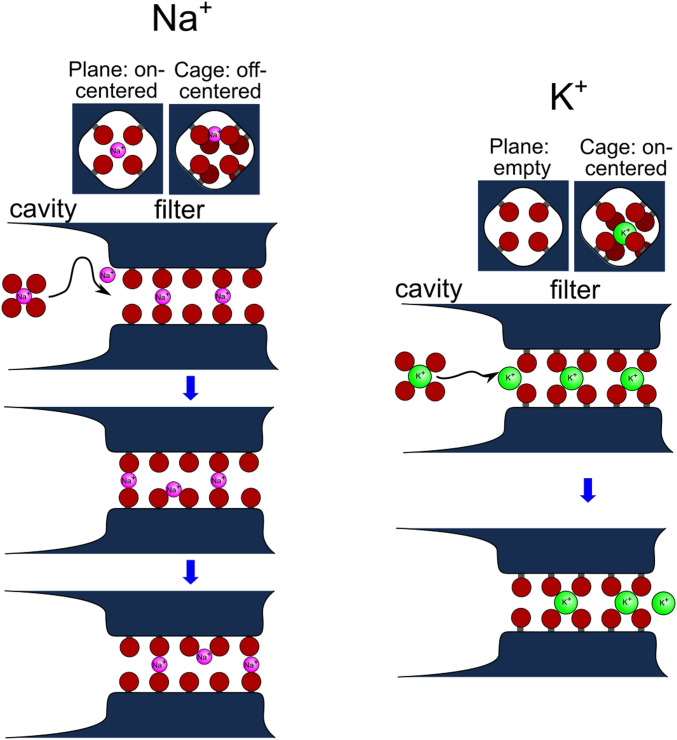
The results in this study indicate that the selectivity filter structure provides a characteristic space for Na⁺ and K⁺. Conducting Na⁺ and K⁺ participate bindings with different coordination numbers (greater than seven for Na⁺ versus four for K⁺) and with different configuration types (amphipathic versus exclusive cage). The amphipathic nature of Na⁺ in binding to either the on-center plane or off-center cage site allows the formation of a continuous and tortuous path (Fig. 4G), wherein the total coordination number is retained across the pore. The filter structure accommodates the Na⁺, allowing for more degrees of freedom in their configurations; however, the free energy wells are separated by high energy barriers, yielding slow elution. In contrast, the filter serves as a specific environment likely optimized for K⁺ in which K⁺ ions are distributed at a few distinct sites; the free energy wells are readily connected when the number of K⁺ ions increases to three, rendering rapid transfer via concerted movements. Accordingly, as a definition of the ion selectivity, the conductance ratio characterizes the large-pass filter via the dynamic nature of the distinct conduction features between Na⁺ and K⁺. Meanwhile, equilibrium binding suits nonconductive Li⁺.

Discussion

In this study, the ion selectivity of the potassium channel was characterized by examining dynamic conduction processes rather than those at equilibrium. The conductance selectivity is adopted as a straightforward measure of selectivity for which the single-channel current amplitude is measured at a defined membrane potential in the presence of a single ion species upstream. The conductance ratio reflects the integrated permeation processes along the pore for different ion species. To corroborate the use of conductance selectivity, the concept of the band-pass filter is introduced. This filter illustrates the unusual nature of the potassium channel selectivity, which allows the permeation of ionic species having a limited range of ion sizes (Fig. 1). The band-pass filter concept permits the deconvolution of the selectivity process into kinetic processes of small- and large-pass filters. The large-pass filter is a prominent feature of the potassium channel, and herein, the kinetic mechanisms underlying the large-pass filter were examined by studying the conduction process across the KcsA potassium channel, as probed using small Na⁺ and Li⁺ (Fig. 2). Examinations of the single-channel current recordings (Fig. 3) as well as atomistic trajectories (Figs. 4 and 5) clarified the broad range of the kinetic spectrum of Na⁺ conduction processes in the KcsA channel.

For decomposing the conduction processes, the membrane potential provides an avenue for focusing on a specific step of conduction and selectivity. At a low positive potential below +100 mV, Na⁺ and Li⁺ hardly affect the outward K⁺ conduction because Na⁺ and Li⁺ do not reach the filter entrance (Fig. 2D and SI Appendix, Fig. S3). Over +100 mV, Na⁺ and Li⁺ reach the high energy barrier at the filter entrance where they interfere with K⁺ permeation (SI Appendix, Fig. S3A). At a high positive potential, this barrier is overcome nearly equally for Na⁺ and Li⁺ (Fig. 2 and SI Appendix, Figs. S1 and S2), indicating the involvement of a dehydration process (Fig. 4H) (1). Henceforth, Na⁺ and Li⁺ exhibit contrasting behaviors. Distinct single-channel Na⁺ conductance was recorded for the first time at a high intracellular Na⁺ concentration (2,000 mM, Fig. 3A), from which the γ_Na/γ_K value of 1/78.3 was obtained. This value is a benchmark for the kinetic characterization of Na⁺ conduction. By changing the membrane potential from low to high, critical steps occurring at the cavity, the filter’s entrance, and in the filter were gradually highlighted, finally yielding the net Na⁺ conduction, therefore rationalizing the use of the conductance ratio as a measure of the ion selectivity.

The MD simulations show a net Na⁺ flux across the pore and reproduce the experimentally obtained conductance and its ratio over K⁺ with the γ_Na/γ_K value of 1/38.5 (Fig. 4), which is comparable to the experimental data. The selectivity filter provides a series of periodic carbonyl oxygen rings (Fig. 6), and permeation is expressed with the 1-2-3 model in which variable ion configurations are lumped together by the number of occupied ions in the filter (31). At high K⁺ concentrations, as in this study, three K⁺ ions in the filter are intercalated by water molecules (21, 31, 56, 57), which are expressed with the upper cycle (via State 2 and 3) of the 1-2-3 model (Fig. 5C). At low K⁺, K⁺ permeation via less K⁺ occupancy in the filter has been shown (31), representing lower cycle contributions. Less occupied ions relate to more water molecules in the single-file nature of the selectivity filter, containing up to five permeants of either ion or water molecules. This is in accord with the experimental data of the water–ion coupling ratio toward three at low K⁺ concentrations (three water molecules and one K⁺) (51–53). The 1-2-3 model covers the permeation process in a wide concentration range by using different cycles and serves as a platform to examine conductance selectivity (31).

Fig. 6.

Distinct conductance features of Na⁺ and K⁺ through the KcsA channel filter via the large-pass filter. The origin of the large-pass filter is schematically shown. Na⁺ (pink) and K⁺ (green) in the cavity (fully hydrated) and the selectivity filter (cross-sectional view of the plane site [Upper Left] and the cage site [Upper Right]; Lower: longitudinal view) are shown. The dark red spheres represent the oxygen atoms of the water molecules (in the cavity), carbonyl, and hydroxyl groups of threonine (in the filter). Upon entering the filter, a much higher dehydration energy barrier was imposed for Na⁺, as deduced from the slow blockings. In the filter, K⁺ was on-center, while Na⁺ was off-center at the cage sites and on-center at the plane sites, leading to tortuous trajectories for Na⁺. An off-center Na⁺ interacts with the carbonyl oxygens of the adjacent rings (Right Upper), whereas an on-center Na⁺ interacts with the carbonyl oxygens of a ring (plane site). These affinities to multiple sites and high barriers between them are integrated into the longer residency time of multiple Na⁺ ions in the filter, leading to slow elution.

Recently, Köpfer et al. proposed the direct knock-on mechanism (58) and showed that the conductance ratio of K⁺ over Na⁺ was only 6.7 at 220 mV in 300 mM concentration (28), which is unrealistically low relative to the present experimental and simulated values. Moreover, the direct knock-on mechanism failed to reproduce the water–ion coupling ratio measured experimentally (51–53), which was reproduced in the present MD simulation. In their MD simulation, the electric field was applied by introducing charge imbalance in the intracellular and extracellular solutions, while we used the conventional method, applying the constant forces to mimic the voltage clamp condition. The force field was almost similar between their study and ours. Accordingly, their method for applying the membrane potential remains fine-tuned.

Here, single-channel experiments and MD simulation were integrated to understand the conductance selectivity. The MD simulation demonstrated that Na⁺ can bind to either the plane or the cage site (Fig. 4). This is in accordance with our previous observations deduced from the static distribution of ions along the pore (59, 60), indicating that Na⁺ binds in an amphipathic (either plane or cage) manner, while Li⁺ exclusively binds to the plane sites (SI Appendix, Fig. S12) (12, 59). The gaps between the plane sites lead to poor transfer of Li⁺ across the filter, reflecting no punchthrough (Fig. 2D). The present simulation reveals that Na⁺ in the cage sites are located off-center (Fig. 4). Thus, the amphipathic nature of Na⁺ binding to the filter is doubled; plane versus cage and on-center versus off-center. These features underpin the tortuous trajectories across the selectivity filter, which provide nearly contiguous pathways for Na⁺ passage. Permeating Na⁺ ions regard the filter as a tortuous pathway in the long range, where multiple ions reside. On the other hand, each permeating Na⁺ is subject to transfer between nearby on-center plane sites and off-center cage sites via the short-range flexibility of the filter. However, the free energy surface shows many deep energy wells along the filter separated by high energy barriers (Fig. 5E), which leads to a long residency time: the residency time of State 3 reached 11.3 ns, which is 70 times longer than that of State 3 for K⁺ conduction (0.16 ns) (Fig. 5A). Accordingly, the tortuosity of the path reconciles the ready conductivity and the high barrier for Na⁺ ensembles, leading to slow elution. This is the kinetic feature of the conductance selectivity of the Na⁺ side for the large-pass characteristics.

In parallel, conductance features of K⁺ are crucial for the high ion selectivity. Exclusive binding of K⁺ to cage sites yields only a few free energy wells (Fig. 5E). Binding of three K⁺ ions reshapes the free energy surface having narrow grooves between these wells, leading to rapid concerted movement (61). Even though the filter serves an accommodated space for Na⁺, the filter structure is specially designed, such that the configuration of three K⁺ ions is optimized for generating effective electrostatic repulsion. Accordingly, State 3 steps up the conduction rate dramatically (3 → 2) relative to the 2 → 1 rate, rendering further contrast of K⁺ conduction over Na⁺ conduction. The strict selectivity for K⁺ as high as 80 times over Na⁺ occurs when the conduction via State 3 is dominant (knock-on mode). We predict that in the absence of the knock-on mode at very low K⁺ concentrations, the selectivity should be attenuated only several times, although this is experimentally unfeasible.

In conclusion, we decomposed the broad spectrum of the kinetic phenomena of Na⁺ across the pore into multiple critical steps to examine the conductance selectivity of the potassium channel. The entrance barrier of the selectivity filter provides an initial and effective large-pass filter for dehydration that prefers large K⁺ ions over small Na⁺ and Li⁺ ions (Fig. 2 and SI Appendix, Fig. S11). Simultaneously, the cutoff radius of 1.7 Å for the filter leads to a small-pass filter for size exclusion. Once ions enter the selectivity filter, the filter structure provided a space for different configurations for each ion species (Fig. 4). The ions are eluted at differential rates, with K⁺ exhibiting fast passage via concerted movements, while the flow of small Na⁺ ions is retarded (Figs. 3 and 5), owing to close interactions with both the plane and cage sites (Fig. 6). These Na⁺ ions are thereby trapped to many deep wells separated by high energy barriers, and Li⁺ remained blocked (SI Appendix, Fig. S9). Thus, the barriers at the filter entrance and those in the processes inside the filter are the origin of the large-pass filter. This kinetic differentiation mechanism can be applied to understand other types of ion channels.

From the contrasting features of Na⁺ and Li⁺, we learned that the small conduction of Na⁺ through the potassium channel is physiologically meaningful. Once it enters the filter by chance, Li⁺ is scarcely released from the blocked channel except by returning to the cavity, although the channel needs not to be optimized for physiologically nonexisting Li⁺. Contrarily, the substantial conductivity of Na⁺ allows the recovery of the channel function. Thus, the high-affinity regime for characterizing the selectivity is relevant to channel blocking. Alternatively, defining the selectivity by differences in conductance is relevant to channel functionality.

Materials and Methods

Sample Preparation.

The expression, purification, and reconstitution of KcsA channels into liposomes have been previously described (SI Appendix, Supplementary Information Methods) (62).

Single-Channel Current Recording.

Single-channel current recordings were performed using a lipid bilayer technique, the contact bubble bilayer, at room temperature (25 °C) according to a previously described method (SI Appendix, Supplementary Information Methods) (44, 63).

MD Simulations.

MD simulations were performed on the transmembrane domain of the KcsA potassium channel, which was embedded in a PC membrane and bathed in a solution of 1 M NaCl. MD simulations were performed using the AMBER11 package (64). The following empirical potentials were used: the TIP3P model for water, ff94 force field for the channel, and those developed by Smith and Dang (65) for Na⁺. Other detailed simulation conditions have been described in SI Appendix, Supplementary Information Methods (31, 48).

The 1-2-3 Model and Rate Constants among Them.

The ion permeation process was described coarse grained with the number of occupied ions in the filter, the 1-2-3 model (SI Appendix, Fig. S13) (31). The rate constants were calculated using the residency time and the number of transition events, which were derived from the MD simulation data (SI Appendix).

Data Availability

All study data are included in the article and/or SI Appendix.