Abstract
The study presents a complete one-dimensional model to evaluate the parameters that describe the operation of a Proton Exchange Membrane (PEM) electrolyzer and PEM fuel cell. The mathematical modeling is implemented in Matlab/Simulink® software to evaluate the influence of parameters such as temperature, pressure, and overpotentials on the overall performance. The models are further merged into an integrated electrolyzer-fuel cell system for electrical power generation. The operational description of the integrated system focuses on estimating the overall efficiency as a novel indicator. Additionally, the study presents an economic assessment to evaluate the cost-effectiveness based on different economic metrics such as capital cost, electricity cost, and payback period. The parametric analysis showed that as the temperature rises from 30 to 70 °C in both devices, the efficiency is improved between 5-20%. In contrast, pressure differences feature less relevance on the overall performance. Ohmic and activation overpotentials are highlighted for the highest impact on the generated and required voltage. Overall, the current density exhibited an inverse relation with the efficiency of both devices. The economic evaluation revealed that the integrated system can operate at variable load conditions while maintaining an electricity cost between 0.3-0.45 $/kWh. Also, the capital cost can be reduced up to 25% while operating at a low current density and maximum temperature. The payback period varies between 6-10 years for an operational temperature of 70 °C, which reinforces the viability of the system. Overall, hydrogen-powered systems stand as a promising technology to overcome energy transition as they provide robust operation from both energetic and economic viewpoints.
Keywords: Electrolyzer, Fuel cell, Economic assessment, Proton exchange membrane, Electric power generation
Electrolyzer; Fuel cell; Economic assessment; Proton exchange membrane; Electric power generation
1. Introduction
The unprecedented growth of the population rate is leading to a dramatic increase in global energy demand. This socio-economic matter generates a significant impact on energy consumption, which is significantly fossil fuel-dependent. Moreover, aspects such as energy market price fluctuations and elevated greenhouse emissions foster uncertainty for sustainable development. Hence, clean energy sources stand as a promising solution for the harmful effects of conventional energy production and industry practices [1, 2]. The combined efforts of investigators and different stakeholders have created a new path for cost-effective and environmentally friendly energy sources such as water electrolysis and fuel cells [3]. However, water electrolyzers only account for 4% of the worldwide hydrogen production [4], which highlights the importance of research in this area. As a short-term alternative, this green hydrogen source can be implemented for partial fuel substitution in internal combustion engines or turbines to improve the overall performance while reducing the pollutant emissions [5, 6, 7]. Cells construction is categorized by their electrolyte in alkaline, molten carbonate, solid oxide, and Proton Exchange Membrane (PEM); however, PEM type stands as a suitable technology in energy applications due to significant advantages such as compactness, operation flexibility, large production rates, hydrogen purity, and high effectiveness [8]. Moreover, PEM technology is very versatile and can be used in sectors such as agriculture, automotive, oil industry, and even aerospace applications [9, 10]. For this type of device, the main focus is to identify the operational parameters that influence the overall performance, such as pressure, temperature, current intensity, voltage, reagents, and product flows.
Mathematical modeling facilitates a comprehensive analysis of the overall behavior of PEM electrolyzers and PEM fuel cells while unraveling the influence of operational parameters on the overall performance. Specifically, in PEM Fuel Cells (PEMFC), sophisticated models have been developed to characterize the electrochemical and flow transport phenomena. Accordingly, Abdollahzadeh et al. [11] proposed a novel transient multi-dimensional, non-isothermal, and multi-phase model. The latter accurately captured the steady polarization curves of PEMFCs that contained different amounts of and The results showed that the concentration in the anode leads to considerable degradation of the PEMFC as the overall performance is negatively affected. A PEMFC multi-dimensional model was also introduced by Sahraoui et al. [12] to characterize liquid water transport effects on the overall performance. This study determined the water content in the electrodes at different temperatures to enable a wider spectrum for calculations while exposing the influence of liquid water on the operation. Although multi-dimensional models feature robustness and high predictability [13], less complex methodologies offered by one-dimensional models are reliable and effective for practical applications on fuel-cells performance evaluation [14]. A one-dimensional model implemented in Matlab/Simulink® environment was proposed by Abdin et al. [15], where despite some simplifications, the model accurately describes the influence of pressure, temperature, humidification, and reactant partial pressure on PEMFC performance. A similar study was presented by Chavan and Talange [16], which proposed a simplified model of a PEMFC computed in Matlab/Simulink® software to evaluate the cell performance under different operating conditions. The simulation results were validated experimentally, highlighting the accuracy of the model.
For PEM Electrolyzers, Yigit et al. [17] developed a model to describe the main features of PEM electrolysis behavior. Again, Matlab/Simulink® was implemented as the computational software to compute the simulations. The results stated that the current drawn by the stack decreases as the voltage increments as a result of the pressure rise. This model was further compared with experimental data, obtaining a consistent comparison of the polarization curves. A similar model was proposed by Abdin et al. [18]; this model predicts the influence of temperature, pressure, and water content on PEM electrolyzer efficiency. On the other hand, Han et al. [19] studied the electrochemical influence of different overpotentials in the electrolyzer voltage. The implementation of the model helps to estimate the total ohmic losses. For instance, a representative current density of 1.5 A/cm2 represents 31.8% of the total ohmic loss due to the interfacial resistance between the membrane and the electrode.
The economic evaluation of an energy system is the most suitable tool to evaluate feasibility from a techno-economic perspective [20]. Renewable energy systems are designed to be competitive with electricity market prices while maintaining robust operation at minimal emissions [21, 22]. PEMFC and PEM electrolyzer have been evaluated via economic analysis focusing on the relation of performance efficiency and overall cost. Frangopoulos and Nakos [23] proposed a complete model to obtain fuel cells' economic indicators for marine applications. In the study, an optimization methodology based on parameters such as current density, operational temperature, lifetime, and mass production demonstrated a significant reduction of the electricity cost by around 0.15–0.208 $/kWh. On the other hand, the electrolyzer economics centers on the hydrogen cost, which is driven to be competitive with other hydrogen production routes. AlZahrani and Dincer [24] proposed an experimental test bench to evaluate the hydrogen cost of a standalone solid oxide electrolyzer in a 1MWe plant. The results showed that the hydrogen cost varies between 3-9 $/kg, demonstrating competitiveness with the hydrogen market. The study incorporates exergo-economic analysis to optimize hydrogen production. Similarly, Taner et al. [25], evaluated the economic performance of a PEM electrolyzer, demonstrating that the proposed system of Cr-C coated SS304 bipolar plates is 3–4 times more efficient than hydrogen gas production while operating with no emissions. Overall, significant contributions have been established to independently perform a cost estimation procedure of both fuel cell and electrolyzer. However, a combined economic model of the aforementioned components is rarely found in the literature. Most of the studies agreed that the cost estimation depends on variables such as the number of stacks, mass production, material type, dimensions, among others [23, 24, 25, 26].
Nowadays, renewable energy systems such as solar panels and wind turbines integrate hydrogen-powered devices to promote energy recovery [22]. The parametric study and modeling of integrated energy systems are becoming the central motivation for both researchers and industry that lead the energy transition commitment. Therefore, some pilot projects of green hydrogen generation have been developed. For instance, HYSOLAR [27] is a long-term German-Saudi Arabian cooperative program for research, development, and testing of solar-hydrogen production as well as the utilization of hydrogen as an energy carrier. The integration of hydrogen-powered components offers a practical solution for over-demand, and energy fluctuations in the grid as the fuel cell can maintain a stable and reliable energy supply to overcome the system's needs [28].
The current status of hydrogen production is considerably inclined to fossil-fuel gasification via hydrocarbon reforming, methane steam reforming, coal gasification, or pyrolysis technologies [29]. The imminent dominance and attractiveness of gas reforming technologies can be attributed to the reduced production cost and large-scale production rate. However, the utilization of fossil fuels as feedstock for hydrogen production led to a significant carbon footprint, which triggers a pressing need to consolidate non-pollutant technologies that facilitate greenhouse emissions reduction [30]. Moreover, there is an increased concern about global warming from governmental and international entities that leads to strict energy policies and regulations to decelerate global emissions from conventional energy practices, which further extends an open path for the penetration, development, and competitiveness of green-hydrogen technologies [31]. Specifically, hydrogen production from non-fossil feedstock mainly comprises biomass and water-splitting technologies. The latter is becoming of increasing interest due to the continuous advances and developments of water electrolysis. So far, PEMFCs and PEM electrolyzers stand as mature technologies that have been extensively implemented in different applications demonstrating reliability and appropriate performance [19]. Nowadays, there are systematic methodologies to evaluate PEM components' overall performance independently based on operational parameters [15, 17]. However, the incorporation of performance metrics to evaluate the integration of PEMFCs and PEM electrolyzers in a compound system for electric power generation has not drawn much attention from researchers. The latter takes relevance considering that hydrogen technologies could be envisioned as a supplementary system for large-scale renewable energy systems to combine energy-to-fuel (electrolyzer) and zero-emissions electricity (fuel cell) conceptualizations. A recent survey [29] outlines the significance of incorporating economic evaluation of hydrogen technologies as a robust tool to foster commercialization and massive penetration of hydrogen-powered devices in residential, commercial, and industrial contexts.
The main contribution of this investigation is to evaluate the electrochemical performance of both PEMFC and PEM electrolyzer independently and when integrated, based on operational parameters such as current density, temperature, pressure, and overpotentials. The significance of this work relies on the performance characterization of the integrated system (PEMFC and PEM electrolyzer) while proposing a novel indicator for the overall efficiency in a multivariate context. Moreover, the study incorporates an economical approach to relate electric power generation perspectives as a differential factor from former research, which elucidates its feasibility and attractiveness compared to other hydrogen production technologies. Therefore, this investigation contributes to close the knowledge gap regarding PEMFC and PEM electrolyzer integration while describing the main operational parameters that describe the overall performance and economic indicators. The paper is organized as follows: Section 2 describes the mathematical formulation to evaluate the electrochemical performance of the PEMFC and PEM electrolyzer at a component level; also, the validation and economic modeling are illustrated in this section. Afterward, Section 3 outlines the main results of the performance evaluation, economic features, and general discussions. Finally, Section 4 provides the concluding statements, limitations, and future developments.
2. Materials and methods
This section describes the procedure followed to implement the models of the PEMFC and the PEM electrolyzer. A complete characterization of the assumptions, parameters, and limitations of each subsystem computed in Matlab/Simulink® is reviewed.
2.1. Parameters, considerations, and general limitations of the models for the PEM electrolyzer and PEMFC
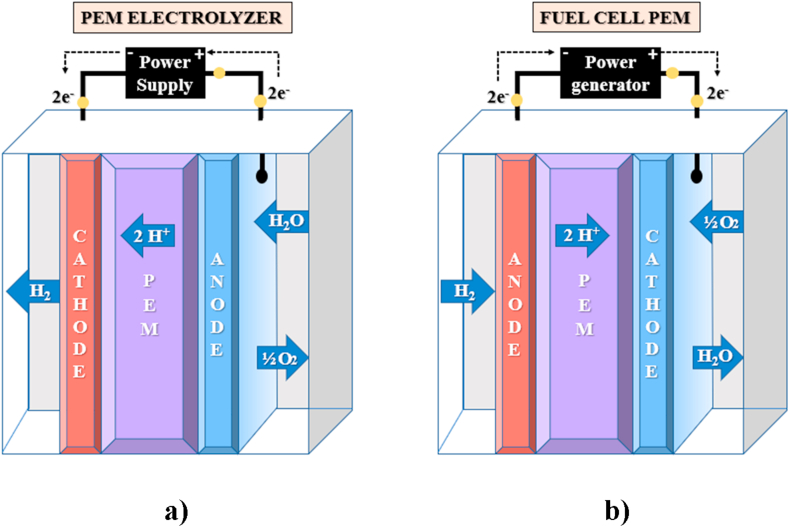
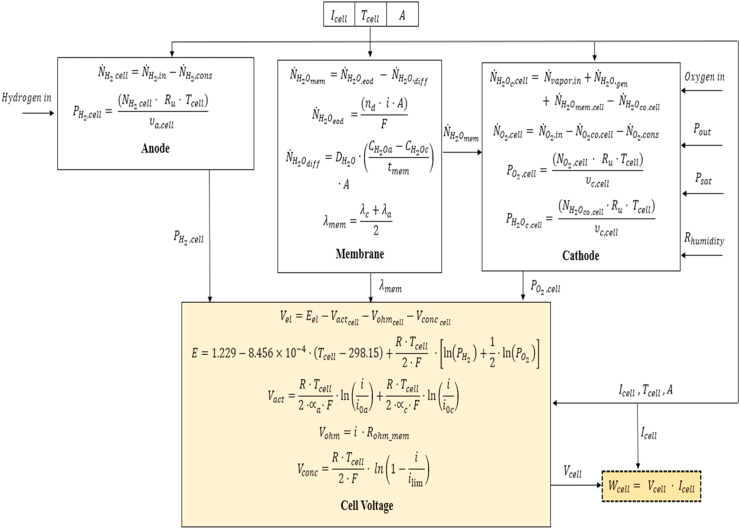
The approach to describe the electrolyzer and the fuel cell performance relies on the description of the main subsystems: anode, membrane, and cathode. Both systems are shown in Figure 1. These models are based on the electrochemical and flow balance equations.
Figure 1.
Illustrative diagram of the main subsystems. a) PEM electrolyzer and b) PEMFC.
When implementing the characteristic equations that describe the behavior of the devices, some considerations and limitations are required to reduce complexity while maintaining the robustness of the numerical modeling [32]. The general assumptions for both models are described as follows:
-
▪
The model is one-dimensional. Therefore, the current and the reagents are uniformly distributed inside the devices.
-
▪
The only interacting gases considered are hydrogen, oxygen, and water vapor.
-
▪
Water activity is uniform across the membrane and is in equilibrium with the water activity at the cathode and anode catalyst layer.
-
▪
In the case of the fuel cell, water is present as vapor at the membrane-electrode interface. Therefore, the effect of cathode flooding when the partial water pressure exceeds the saturation vapor pressure is not quantitatively predicted. This assumption is reasonable for fuel cells operating at moderately elevated temperatures. This is most likely to be the case in real installations, as the cell temperature is higher than the coolant temperature, which is also higher than the ambient temperature [15, 33].
-
▪
The electrodes and membrane are at the same temperature. This assumption is valid considering that devices such as controllers and cooling systems are responsible for heat dissipation from the stack.
-
▪
There are no pressure gradients between the electrodes, and only diffusion and electro-osmotic drag for reagents and product transport are considered. Additionally, partial pressures of the reagents and products were calculated through the law of ideal gases. These considerations are consistent with other studies in the literature [15, 17, 18, 34].
2.2. Mole balance models for electrolyzer and fuel cell
This section aims to explain the characteristics that describe the nature of the process developed for each module. In addition, a separate computational model is presented to estimate the molar flow rate through the anode, membrane, and cathode.
2.2.1. Mole balance sub-models for anode
For the fuel cell, humidified hydrogen enters the anode, which implies two reagents inside the electrode. In the majority of systems composed of one or more coupled cells (stack), the management of water flow in liquid and gaseous phase (steam) inside the anode is neglected, especially if it is considered that processes such as water production and purge of the system occur at the cathode [34, 35]. In other words, these considerations rule out the presence of water interaction inside the anode; thus, the molar flow balance in this module only considers the hydrogen entering and the one consumed, as presented in Eq. (1):
| (1) |
The flow of consumed hydrogen () is defined by Faraday's law [34]:
| (2) |
where is the number of cells in the stack, is the current intensity through the cell, and is Faraday's constant.
The hydrogen inlet flow () can be expressed as the product of the consumed hydrogen flow and a factor that express the stoichiometric ratio () [15]:
| (3) |
On the other hand, the partial pressure of hydrogen ( in the cell can be obtained through the ideal gas law [34]:
| (4) |
where is the universal gas constant, and and are the temperature and volume of the fuel cell's anode, respectively.
In the electrolyzer, the liquid water entrance and its dissociation into its two constituent elements (hydrogen and oxygen) take place inside the anode. However, the only reactants present in the anode are oxygen and water in two phases (liquid and gaseous). The analysis for the oxygen flow balance focuses on the ratio of generated oxygen and the flow of oxygen exiting to the underlying systems (storage):
| (5) |
where the ratio of generated oxygen ( is given by Faraday's law:
| (6) |
The flow balance analysis for the water inside the anode takes into account the liquid water inlet flow ( and the water outlet flow through the membrane () and the underlying system ():
| (7) |
The water consumption ratio ( is defined as follows [36]:
| (8) |
The partial pressures inside the electrolyzer's anode can be expressed as:
| (9) |
| (10) |
where and are the temperature and volume in the anode of the electrolyzer, respectively. The sum of the partial pressures of oxygen and water yields the total pressure inside the anode:
| (11) |
The molar fraction for oxygen can be calculated as:
| (12) |
The output flows are then obtained using the following expressions:
| (13) |
| (14) |
| (15) |
| (16) |
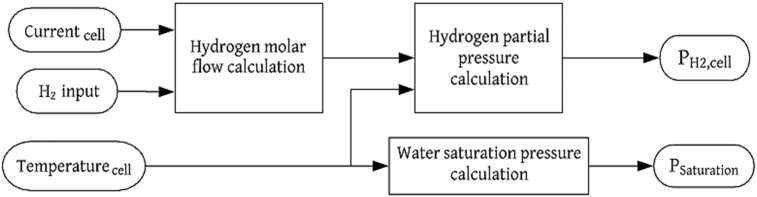
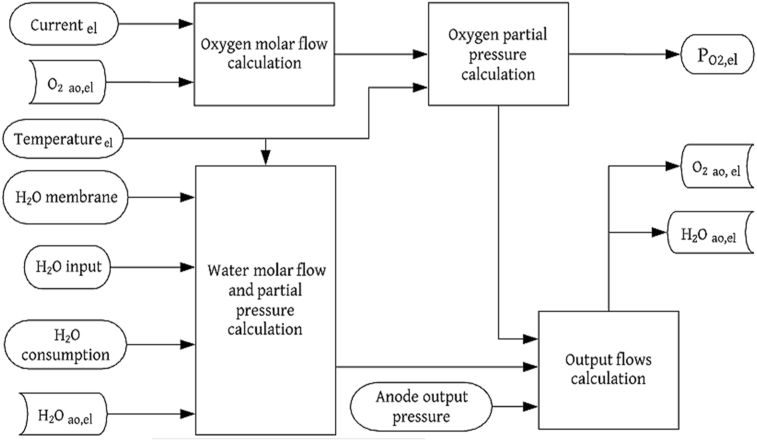
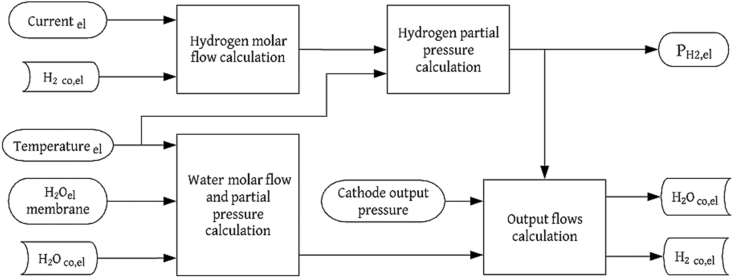
The anode's output flow in the electrolyzer ( depends on several factors such as the valve opening, geometry of the device, the output diameters, among others [24, 26]. The effect of the previously mentioned parameters can be incorporated by an output flow coefficient (), which is considered as a fitting parameter [38]. Note that, and are the inlet and outlet pressure of the anode, respectively. Figures 2 and 3 show the flow balance diagrams for the subsystems of the PEMFC and the PEM electrolyzer anodes, respectively.
Figure 2.
Flow balance diagram for the PEMFC anode.
Figure 3.
Flow balance diagram for the PEM electrolyzer anode.
2.2.2. Flow balance sub-models for cathode
In the case of the PEMFC, humidified oxygen enters the cathode, which implies the presence of two reagents (oxygen and water) inside the electrode. The cathode analysis requires a broad perspective as it is necessary to account for the effects of incoming water with oxygen, the water flow from the membrane , and the water production as a result of the reaction between oxygen and hydrogen coming from the anode. The flow balance analysis for the water inside the cathode is expressed as follows:
| (17) |
where the water entering in gas phase (vapor) can be defined as [15]:
| (18) |
is the excess factor or stoichiometric ratio for oxygen, is the relative humidity of the cathode, and is the output pressure of the cathode. The saturation pressure () can be expressed as a function of temperature [17] as:
| (19) |
The ratio of generated water ( ) is defined as:
| (20) |
On the other hand, the oxygen flow balance analysis focuses on the incoming oxygen ratio (), the flow of consumed oxygen (), and the flow ratio that escapes by purging the system (), as expressed by Eq. (21):
| (21) |
The oxygen flow entering the cathode can be calculated as:
| (22) |
The oxygen consumed is expressed as:
| (23) |
The partial pressures inside the fuel cell cathode are defined as:
| (24) |
| (25) |
The total cathode pressure is calculated as:
| (26) |
The molar fraction of oxygen is:
| (27) |
Analogously, the output flows for the fuel cell cathode can be summarized as:
| (28) |
| (29) |
| (30) |
| (31) |
where is the total output flow of the cell cathode, relates the output flow coefficient, and and are the total and outlet pressure of the cathode in the fuel cell, respectively.
In the case of the electrolyzer, water and hydrogen interact inside the cathode. The analysis for the water flow balance focuses on the water inlet from the membrane () and the water outlet to the adjacent systems ():
| (32) |
On the other hand, the analysis for hydrogen flow balance is expressed as:
| (33) |
where is the outcoming hydrogen, and accounts for hydrogen generated which is defined as:
| (34) |
The partial pressures of the reagents (hydrogen and water) inside the cathode of the electrolyzer can be expressed as:
| (35) |
| (36) |
where is the volume of the cathode in the electrolyzer. The sum of the partial pressures of the reagents yields the total pressure inside the cathode:
| (37) |
The molar fraction for hydrogen can be calculated as:
| (38) |
The output flows are then summarized as follows:
| (39) |
| (40) |
| (41) |
| (42) |
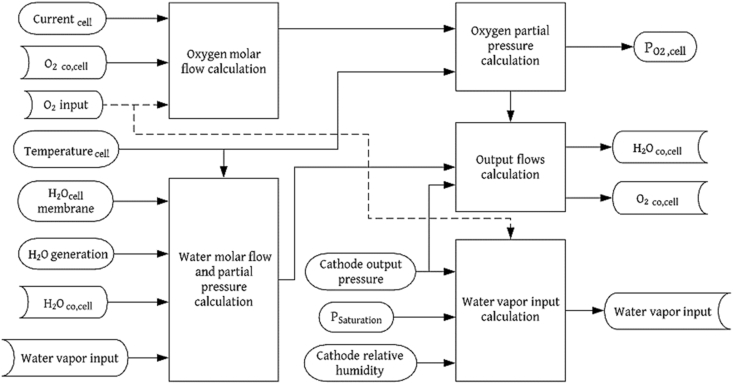
where is the flow outlet of the cathode in the electrolyzer. On the other hand, and are the total and output pressure of the cathode, respectively. Figures 4 and 5 display the flow balance diagrams for the subsystems of the fuel cell and electrolyzer cathodes, respectively.
Figure 4.
Flow balance diagram for the PEMFC cathode.
Figure 5.
Flow balance diagram for the PEM electrolyzer cathode.
2.2.3. Flow balance sub-models for membrane
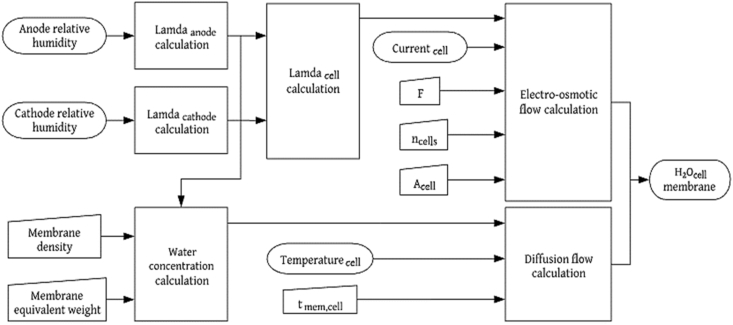
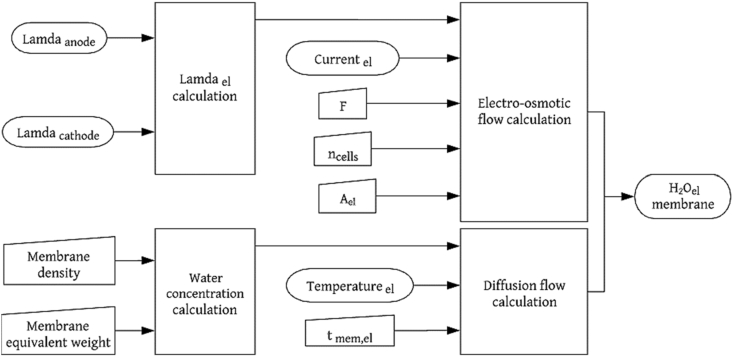
The PEM is not electrically conductive, and it is impervious to neutral reactive gases. Therefore, there are no internal currents or losses due to fuel crossing. The membrane is the place where hydrogen ions and water can be transported. Accordingly, water transportation through the membrane occurs through four different processes: electro-osmotic entrainment, diffusion, pressure gradients, and thermo-osmosis. When analyzing a membrane under constant temperature and pressure conditions, the flows induced by pressure and temperature gradients are ignored because their contribution to the balance is negligible compared to the flows caused by the electro-osmosis drag () and diffusion (), which are the dominant mechanisms [18]. For both the electrolyzer and the fuel cell, the water flow balance is expressed as follows:
| (43) |
where the electro-osmotic drag flow is given by [37]:
| (44) |
and are the current density and the active area, respectively. On the other hand, is the electro-osmotic drag coefficient, which can be calculated as [37]:
| (45) |
where the water content through the membrane () is given by:
| (46) |
In a fully humidified state (100% relative humidity, water content balanced in steam), a maximum value of can be accomplished. In practice, however, decreases with temperature rise. The absorption of Nafion® with liquid water is much higher, i.e., [18]. This difference between the equilibrium conditions of liquid water and vapor results from the Schroeder paradox [39, 40]. In the case of PEM water electrolyzers, it can be considered that the entire membrane is fully hydrated since the water reaches the anode section in large quantities. Typically, in these cases, is considered to be in the range of 14–21 [41]. In this study, for the electrolyzer, the water contents of the two electrodes ( and ) are directly defined as input variables according to parameters obtained from the literature. In contrast, for the fuel cell, the water content of the electrodes is defined by:
| (47) |
| (48) |
| (49) |
| (50) |
where and are the ratios of the partial pressure and the saturation pressure of the water inside the electrodes, respectively. For this model, these two parameters are chosen as input variables that subsequently define the cell membrane content by linearity.
On the other hand, the diffusion flow of water through the membrane is given by Fick's first diffusion law [42]:
| (51) |
where is the membrane thickness. and are the concentrations of water on the surface of the membrane at the interface of the cathode and the anode, respectively. These concentrations can be expressed as:
| (52) |
| (53) |
where and are the density and the equivalent dry weight of the membrane, respectively. Both are physical properties of the material used in the manufacture of the PEM membrane, which is considered a key component in PEMFC. Nafion®, among perfluorinated polymers, is the most widely used electrolyte in PEMFC due to its chemical and electrochemical stability, as well as the high proton conductivity [43].
Finally, the water diffusion coefficient () is defined as:
| (54) |
where,
| (55) |
| (56) |
| (57) |
| (58) |
Figures 6 and 7 show the flow balance diagrams for the PEMFC and the PEM electrolyzer membranes, respectively.
Figure 6.
Flow balance diagram for the PEMFC membrane.
Figure 7.
Flow balance diagram for the PEM electrolyzer membrane.
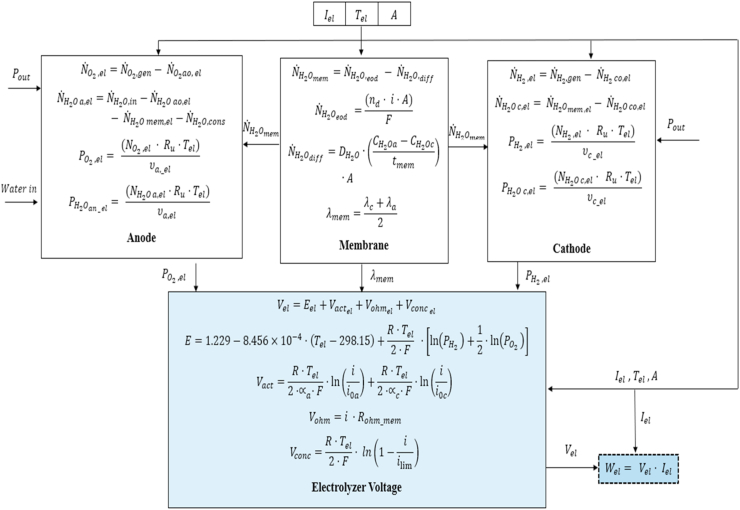
2.3. Electrochemical model for the electrolyzer and the fuel cell
The electrochemical models were developed to define the overall performance of the components based on the operational conditions. This is achieved considering the interactions between various subsystems that describe the flow at the anodes, cathodes, and membranes with the required or generated voltage module for the PEM electrolyzer and the PEMFC.
The performance of the fuel cell and the electrolyzer as functions of the voltage are given by Eqs. (59) and (60), respectively:
| (59) |
| (60) |
The reversible voltage calculation () is given by Nernst's equation, which considers the stoichiometry of the reaction, as follows:
| (61) |
The activation overpotential () is expressed as:
| (62) |
The current exchange densities, and , have a substantial impact on the activation overpotential, and depend mainly on factors such as the material and porosity of the electrodes, concentration, distribution, size of the catalyst particles, and the operating temperature. Due to the complexity of predicting their values, they are often considered fitting parameters in the model [44, 45]. For Pt-based electrodes, the current exchange densities for oxygen reduction and hydrogen oxidation reactions range between [46] and [47], respectively. On the other hand, the values of the charge transfer coefficient for anodes and cathodes ( and ) vary between 0-1 and 0–2, respectively [48]. In this study, the variables , , , and are considered fitting parameters that vary within the reported ranges.
The definition of the ohmic overpotential () in the models does not contemplate the resistance imposed by the cell and electrolyzer's components, such as collector plates or connection cables, which have a small magnitude and can be neglected. Therefore, the ohmic overpotential can be calculated as:
| (63) |
The membrane resistance () is defined as:
| (64) |
where is the membrane conductivity, which is calculated as [49]:
| (65) |
The overpotential concentration () is given by:
| (66) |
where is the maximum current density allowed for each device. Figures 8 and 9 show simplified diagrams of the calculation process for the integrated subsystems of the electrolyzer and fuel cell, respectively.
Figure 8.
Subsystems of the PEM electrolyzer.
Figure 9.
Subsystems of the PEMFC.
For most electrolyzers available in the market, their operation is set to “current mode,” which means that the current entering the electrolyzer is controlled to provide a steady-state hydrogen production, while the power supply must meet the required operating voltage [18]. In this study, this approach is used to develop the PEM electrolyzer model, defining the voltage required to generate a required rate of reagent (hydrogen or oxygen) as a function of the physical variables and parameters of the device. On the other hand, the hydrogen generation system is intrinsic to the electrolyzer cathode module. In the fuel cell, the approach proposed for the model describes the generated voltage as a function of an imposed external load, which is related to the current needed to overcome the resistance of the load.
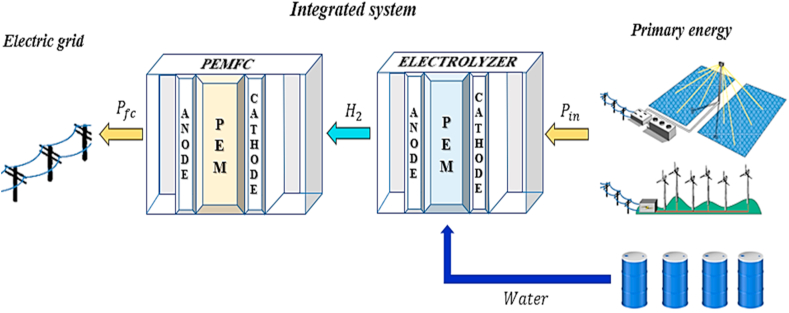
2.4. Integrated electrolyzer- fuel cell model
The integrated Electrolyzer-Fuel Cell model describes the interaction between both devices. This analysis stands as a unique factor as these two devices are not generally connected in energy generation systems directly. Hence, the study aims to relate each component's efficiency to evaluate the performance of the integration while examining the variation of the main operational conditions (current density, pressure, temperature). Note that physical and geometric parameters such as density, equivalent weight of the membrane, active area, thickness of the membrane, and number of stack cells have been set identical for both devices. Table 1 lists the parameters fixed for the integrated model.
Table 1.
Physical and geometric parameters of the integrated model.
| Parameter | Value |
|---|---|
| [ | |
| [kg/mol] | |
| [cm] | |
| A [ | |
| n |
The fuel cell efficiency is defined as the ratio between the electricity produced and hydrogen consumed [50].
| (67) |
Electricity generation is simply defined as the product between voltage and current, as follows:
| (68) |
where is the current in amperes, and is the cell potential in Volts. The energy related to hydrogen consumption is defined as:
| (69) |
where is the enthalpy change, which relates the amount of energy necessary to build/break up a bond for a chemical reaction, and is defined according to Faraday's Law [34]. The term can be expressed in terms of the Higher Heating Value (HHV) or the Lower Heating Value (LHV). The difference relies on the heat of the water content that might present in the product as either liquid or vapor [50]. However, for a low-temperature fuel cell or electrolyzer, the HHV () should be used for efficiency calculations [51]. Combining Eqs. (2) and (69), the following expression can be obtained:
| (70) |
The term is set to , which corresponds to the so-called thermoneutral potential [17]. Therefore, the fuel cell efficiency () can be obtained by rearranging Eq. (67) [52]:
| (71) |
On the other hand, the electrolyzer's efficiency () is the reverse of the fuel cell's, and thus it can be calculated as follows [53]:
| (72) |
Lastly, the product between these two efficiencies (fuel cell and electrolyzer) can be defined as the overall efficiency of the system:
| (73) |
In this study, the overall efficiency () of the integrated system emerges as a novel and significant indicator to evaluate the performance of both components combination, while the model proposed helps to predict the electrochemical interactions in the context of a multivariate parametric analysis. It is worth mentioning that the conceptualization of this model is to operate as a support system to withstand energy fluctuations and over-demand circumstances in a primary energy system (e.g., wind turbines and photovoltaic panels) that is model as a black box. Therefore, the study of the integrated system centers on the electrical power generation in the PEMFC, which is powered by the electrolyzer that is respectively driven by the primary energy source. Notice that the study does not address the incorporation of hydrogen storage, as it assumes that all the hydrogen produced is used by the PEMFC to generate electricity. In this sense, the analysis focuses on the performance evaluation that uses the power-to-fuel concept (electrolyzer) to produce zero-emission electricity (PEMFC). Nonetheless, in future studies, a complete characterization of hydrogen storage is required to provide a wider perspective of this proposal, which can be accompanied by an hourly-based operation assessment that measures the fluctuations of the primary energy source and dynamic operation of the integrated model. It can be mentioned that hydrogen storage can be done through different techniques such as high-pressure gas cylinders, adsorbed materials, cryogenic tanks, among others [54]. Therefore, a clear selection criterion must be considered to determine the most suitable technology based on the techno-economic perspectives of a specific application. The economic model of the integrated system presented in this investigation serves as an initial step for the implementation of such a comprehensive framework. Figure 10 illustrates the integrated model's characteristics.
Figure 10.
Diagram for Integrated Electrolyzer-fuel cell model.
2.5. Mathematical model validation
The proposed models aim to obtain the polarization curves as the main verification tool for the accurate prediction of the physical-chemical processes inside the electrolyzer and the PEMFC. The selected polarization curves were introduced from the results by Yigit et al. [17] and Abdin et al. [15], which were obtained from experimental data for the electrolyzer and fuel cell, respectively. Table 2 shows the operational parameters found in the aforementioned investigations.
Table 2.
| PEM electrolyzer | ||||||
| PEM fuel cell |
Table 3 displays the fitting parameters used in the validation procedure, which corresponds to the operational conditions settled in the studies.
Table 3.
Fitting parameters for PEM electrolyzer and PEMFC models.
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|
| PEM electrolyzer | |||||||
| PEM Fuel cell | 0.7 | 2 |
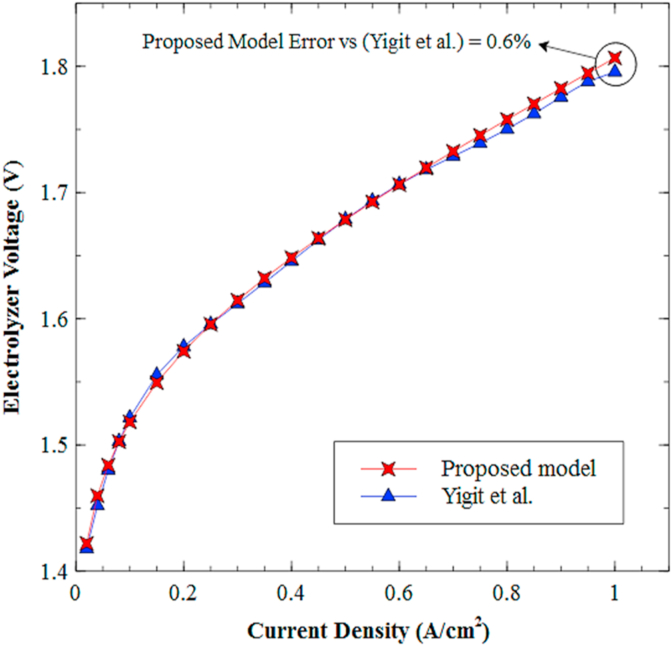
Figure 11 shows the comparison between the polarization curve obtained by the proposed PEM electrolyzer model and the one obtained by Yigit et al. [17], under the operating conditions listed in Table 2. According to the results, it can be verified that the relative error between both models is not greater than 0.6% within the entire range of current density. Therefore, it can be assured that the proposed model will guarantee an appropriate behavior description for the required voltage of the PEM electrolyzer, which relates to the interactions of the reagents and subsequent elements.
Figure 11.
Comparison between polarization curves for the proposed PEM Electrolyzer model and Yigit et al. model [17].
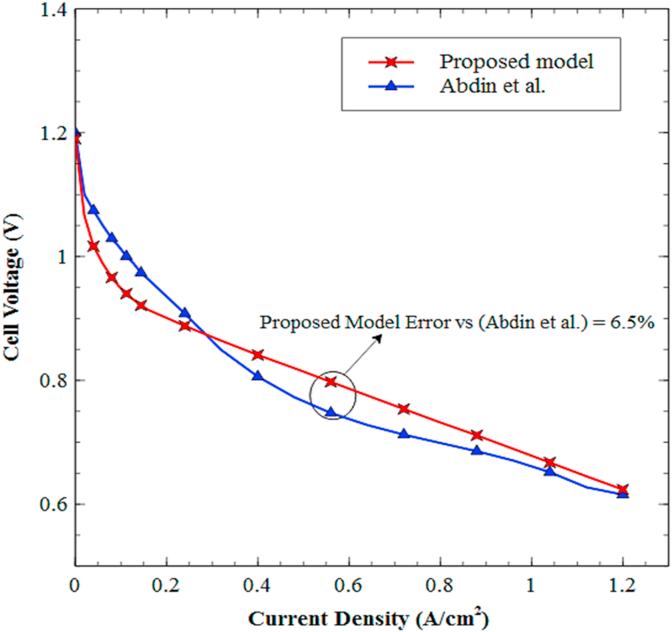
Figure 12 displays the comparison between the polarization curve obtained by the PEMFC model developed in this work and that obtained by Abdin et al. [15]. Notice that the validation results exhibit similar behavior throughout the current density range with the reference author, presenting the most significant differences for current densities between 0-0.2 A/cm2. Such deviation corresponds to an apparent late response of the model in the initial operation period, which might be related to the influence of the activation overpotential in the startup of the cell. However, the model's response improves as the current density increases, featuring clear similarity for the voltage output results within a range of current density between 0.9-1.25 A/cm2.
Figure 12.
Comparison between polarization curves for the proposed PEMFC model and Abdin et al. model [15].
Overall, the simulation results for both models demonstrated acceptable matching with the reference authors. Thus, it can be concluded that the models provide a simplified mathematical approach while maintaining robustness to describe the performance of the PEMFC and the PEM electrolyzer.
2.6. Economic analysis
Economic considerations become vital to evaluate an energy system's feasibility while providing a clear, cost-effective criterion. Thus, the economic assessment incorporates different tools to estimate the main economic features of the integrated system of the PEM electrolyzer and PEMFC. Notice that both devices feature similar construction and manufacturing as they correspond to PEM type. Therefore, the cost estimation for both components is similar, and the system considerations will be determined by each functionality (electric generation and hydrogen production). For this specific model, the economic approach centers on estimating of the electricity cost and the overall cost of the integrated system. Note that the cost associated with hydrogen is not determined directly, and the pricing assumptions were made based on available literature [24, 55]. The economic methodology proposed is based on the Annualized Cost of the System (ACS) perspective [56]. Overall, the total cost of the system () can be divided into capital cost (), fuel cost (), and operation & maintenance cost () as presented in Eq. (74):
| (74) |
The contribution of the O&M cost will be assumed constant throughout the system's lifetime, and it is related by the maintenance factor (φ) as a percentage of the total cost [56]. The total cost of electricity can be defined as follows [55]:
| (75) |
where, is the cost of electricity in $/kWh, is the annual capital cost in $/year, relates the annual fuel cost in $/year, is the maintenance cost in $/year, and accounts for the annual electricity production in kWh/yr.
Note that all the cost terms in Eq. (75) should be annualized to account for depreciation and time value of money. First, the Capital Recovery Factor (CRF) presented in Eq. (77) helps to annualize the capital cost () for each component as follows:
| (76) |
where CRF is defined as:
| (77) |
where is the interest rate, and is the system's lifetime. The total capital cost () mainly considers the cell stack cost for each component (PEMFC and PEM electrolyzer):
| (78) |
where, is the stack fixed cost in $/stack, accounts for the cost of each component in $/cell, and represents the number of cells in the stack. Note that the fixed cost comprises the cost of testing, assembly, and those stack components that are independent of the number of cells, namely, end plates, bus plates, fluid connectors, among others [55, 57]. Moreover, the number of cells in the stack is calculated as a function of nominal power output/input (), operational voltage (V) and current density (i), and cell-active area (A) as follows:
| (79) |
The electricity produced by the fuel cell yearly () is calculated as a function of the load profile:
| (80) |
where H is the number of operating hours per year, and is the electricity generation in the fuel cell. The Capacity Factor (CF) relates the ratio between the actual energy produced and the energy that can be produced while maintaining a full-rated power throughout the operation time. This parameter takes relevance in the integrated system to evaluate different operation scenarios. Moreover, the annualized fuel cost () of the systems is calculated as follows:
| (81) |
where is the hydrogen cost in $/kWh, and is the average annual efficiency of the integrated system. Hydrogen cost plays an important role in the economic evaluation of the model and for proper positioning of the proposed technology. A critical comparison of different production routes requires contemplating aspects such as production scale, Levelized Cost of Hydrogen (LCOH), and Technology Readiness Level (TRL), as presented in Table 4.
Table 4.
Comparison schemes of different hydrogen production routes [29].
| Technology | TRL | Production scale | LCOH ($/kg) |
|---|---|---|---|
| Steam methane reforming | 9 | Large | 0.77 |
| Coal gasification | 9 | Large | 0.92–2.83 |
| Steam reforming | 8 | Small | 1.83–2.35 |
| Gasification | 7 | Mid-size | 1.21–3.5 |
| Pyrolysis | 7 | Mid-size | 1.21–2.57 |
| Water electrolysis | 9 | Small | 2.35–4.80 |
| Biomass | 2–4 | Under research | 2.57–4 |
Based on Table 4, the low cost associated with steam reforming and gasification technologies is a direct consequence of the development level (TRL 9), low cost of feedstock, and large production scale that significantly reduces the production cost. However, this technology faces significant challenges regarding the environmental impact due to inherent CO2 emissions during the process, which forces the implementation of Carbon Capture and Storage (CCS) technologies that increase the investment cost [58]. On the other hand, water electrolysis features high LCOH despite being in the advanced development stage (TRL 9). The latter can be explained considering that electrical consumption represents a significant share of the operational cost in the electrolyzer, predominantly when renewable energy is implemented [29, 58]. Several studies predict that the hydrogen production cost of electrolyzers will significantly drop in the future, fostering the massive penetration and large-scale commercialization of this technology [30, 31, 58]. Moreover, the imminent intermittence or over-supply of renewable energy sources (e.g., wind turbines, solar panels) extend the possibility to integrate hydrogen-power devices.
Lastly, the average annual efficiency is calculated as follows:
| (82) |
where is the cell potential at a given power level, and accounts for the portion of time that the component operates at a power level of . The Payback Period (PBP) is incorporated within the analysis to determine the investment return time based on the economic indicators. The PBP can be calculated as follows [59]:
| (83) |
where accounts for the annual profitability cash flow in the system's lifetime. Table 5 summarizes the main assumptions for the economic model of the integrated system.
Table 5.
Economic Parameters.
3. Results and discussions
Based on the results from the models' validation for both devices independently, it is possible to perform a sensitivity analysis considering different scenarios for the PEM electrolyzer, PEMFC, and the integrated system. This section aims to describe the behavior of all the proposed models while expanding the operational conditions of the analysis. The temperature and pressure for both components vary between 30-70 °C and 1–10 atm, respectively, which in accordance with the common operational range in PEM type equipment [15, 17]. It must be clarified that intermediate conditioning devices such as humidifiers, heat exchangers, dryers, gas separators, among others, guarantee the correct operation of the system as described within the electrochemical model. The latter takes relevance since it guarantees that the reactants enter the given conditions to ratify the results reported.
3.1. PEMFC and PEM electrolyzer performance
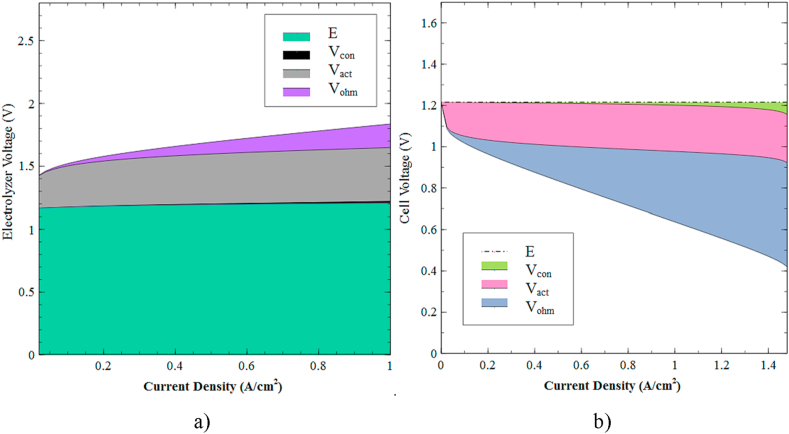
First, Figure 13a shows the contribution of each overpotential to the voltage required for the electrolysis process. It can be noticed that the activation overpotential features the greatest voltage restriction due to the resistance imposed by water dissociation. The second greatest contributor is the ohmic overpotential. Finally, the one that contributes the least is the concentration overpotential, which increases with respect to the current intensity.
Figure 13.
Contribution of overpotentials to the polarization curve. a) PEM electrolyzer, and b) PEM fuel cell.
Similarly, Figure 13b displays the contribution of overpotentials to the polarization curve of the fuel cell. According to the results, the most significant contributions are attributed to the ohmic and activation overpotentials; these findings are associated with the slow kinetics of chemical reductions in the electrode and the ions transfer restrictions. Finally, the concentration overpotential has the smallest impact on cell polarization.
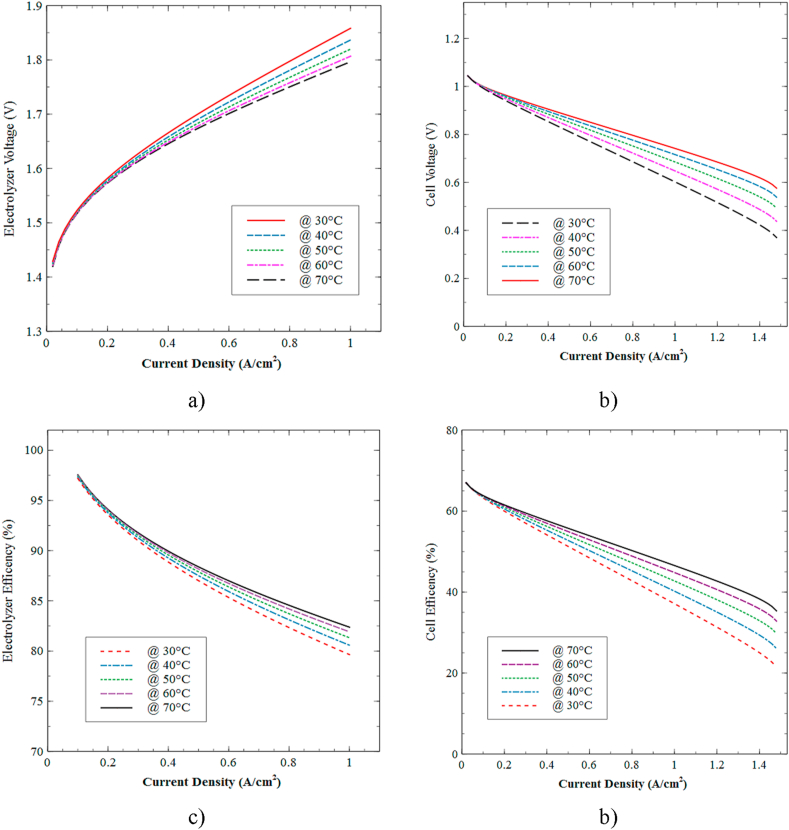
Figure 14 shows the effect of temperature on the PEMFC and PEM electrolyzer operation for a temperature range between 30 and 70 °C at atmospheric pressure conditions. The polarization curves for the electrolyzer in Figure 14a exhibit an inverse relationship between the operating temperature and the voltage required for the appropriate operation. In other words, increasing the temperature reduces the energy necessary to dissociate the water, producing a better transfer reaction between the electrode-membrane interface. This phenomenon is characterized by the activation resistance imposed by the electrolyzer.
Figure 14.
Effect of temperature on voltage and efficiency. a) and c) PEM electrolyzer, b) and d) PEM fuel cell.
Analogously, Figure 14b shows that a temperature rise produces an acceleration of the electrochemical reaction related to the molecular binding of the incoming reagents in the PEMFC. The positive effects on the voltage generated in the cell can be explained by the lower incidence of losses as the operating temperature increases. In general, Figures 14a, b show that for different temperatures at low ranges of current density, the required and generated voltage values appear to be ideal due to the limited overpotential resistance imposed by the system. Finally, Figures 14b, c prove that higher operating temperatures improve the efficiency of both devices, a pattern that supports the results of the polarization curves.
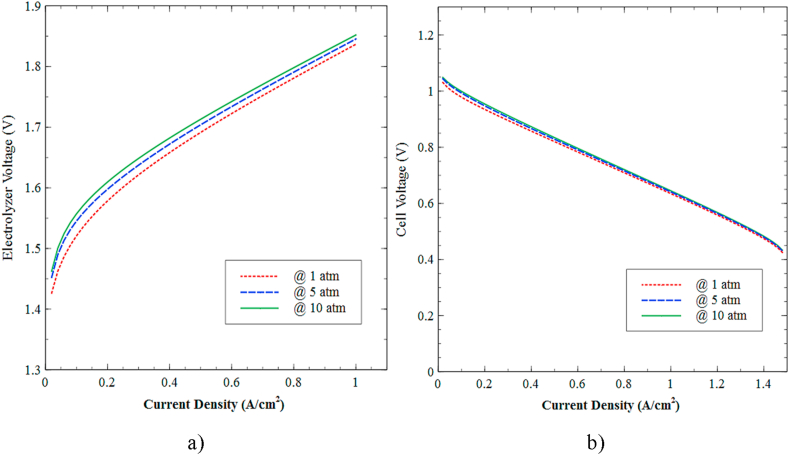
Subsequently, Figure 15 shows the effect of pressure on both devices' performance for a range between 1 to 10 atm at a temperature of 40 °C. The polarization curves presented in Figure 15a experience a proportional relationship between the electrolyzer's pressure and the voltage required to maintain operation at a given current density range.
Figure 15.
Effect of pressure on performance in polarization curves. a) PEM electrolyzer, and b) PEMFC.
Figure 15b shows that the polarization curve of the PEMFC experiences a decreasing trend as the current density increases while the operating pressure shows a direct relation to the voltage generation. The last pattern can be justified since outlet pressure on both sides of the electrodes imposed a notable resistance to the reagents' output, allowing a greater part of the reagent to be used, and therefore a higher voltage is obtained. Overall, the results indicate that the required and generated voltage increment due to higher pressures on the cathodic and anode side, which produce, in turn, back pressure to the capillary pressure of the membrane, narrowing the ion channels and preventing a suitable ion transfer reaction. This reduces the water content in the channels and hence the conduction of protons through the diffusion mechanism.
3.2. Integrated system
Figure 16 shows the overall efficiency of the integrated system proposed in the study as a function of current density. Notice that the system operates at atmospheric pressure conditions, and the same geometric parameters (active area, membrane thickness, and estimated electrode volumes) have been set for both devices.
Figure 16.
Effect of temperature on the overall efficiency of the integrated electrolyzer-fuel cell model.
Based on the results, the integrated system's efficiency experiences a decreasing trend in relation to the current density, whereas temperature increments boost the overall efficiency. The last behavior can be explained since temperature rise benefits both dissociative and power generation performances in the electrolyzer and the fuel cell, respectively. Hence, the indirect interaction between these two devices is greatly improved by the ratio between the consumed and generated voltage.
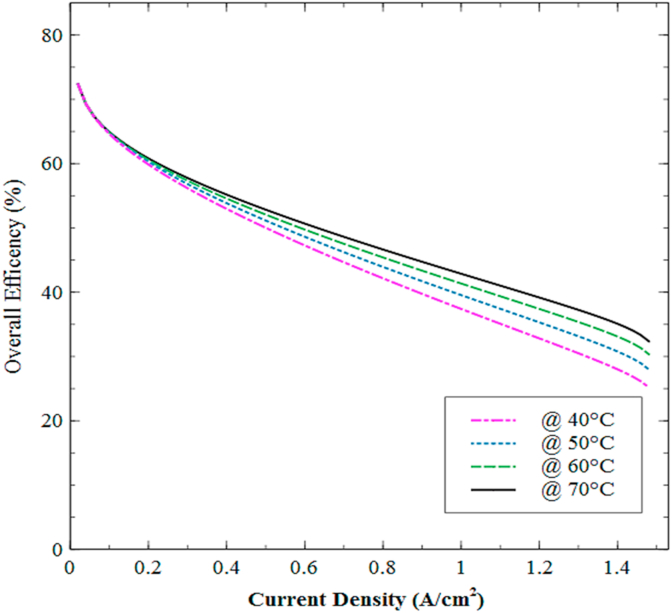
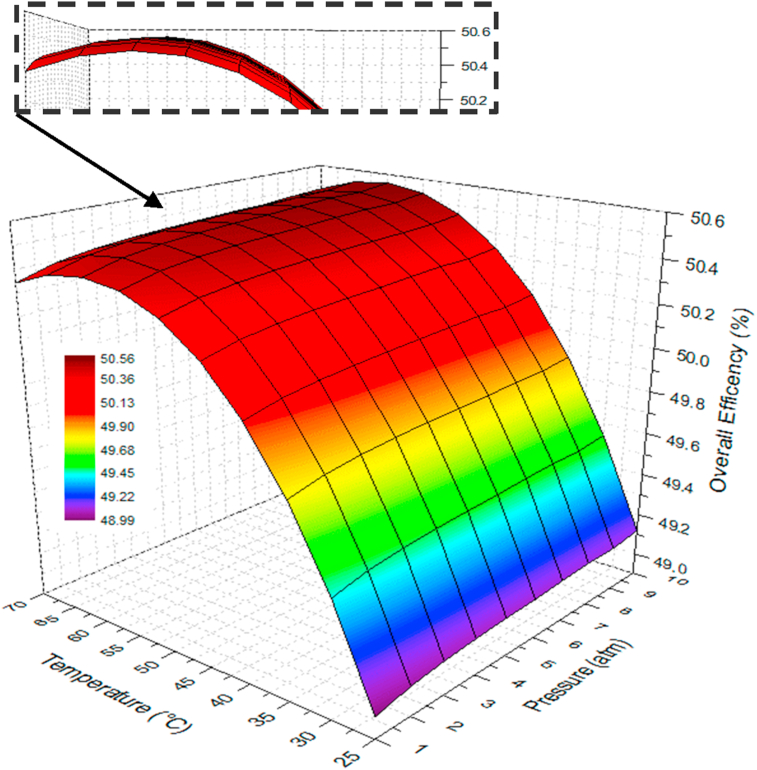
Figure 17 shows the combined effect of temperature and pressure on the integrated system's efficiency for a current density condition of 0.5 A/cm2.
Figure 17.
Effect of temperature and pressure on the overall efficiency of the integrated electrolyzer-fuel cell model.
According to the outcomes, it can be verified that temperature features the greatest incidence on the integrated system's performance. At high temperatures, better performance can be achieved for both devices since the kinetics of the transfer reaction improves at the membrane-electrode interface, a phenomenon related to the activation overpotential. On the other hand, the conductivity of the PEM is favored, resulting in a decrement of the ohmic overpotential.
This sensitivity assessment takes relevance as the influence of temperature and pressure on the overall efficiency is not quite intuitive. For instance, the minimum efficiency is recorded for the lowest pressure and temperature (1 atm and 25 °C). However, the maximum efficiency does not correspond to the highest pressure and temperature (10 atm and 70 °C). Indeed, the highest efficiency range is presented for the combination of temperatures between 55 °C and 60 °C and pressures between 3 atm and 7 atm.
It is worth mentioning that the efficiency differential across the temperature range is not higher than 1.3%. However, the economic analysis presented in the next section will reveal the economic impact of such an enhancement through the analysis of different financial indicators. Considering that efficiency improvements in hydrogen-power devices have been relatively slow in the last decade, the outcomes reported in this section are promising. For instance, in other applications, extensive proposals have been implemented to improve the overall efficiency in combustion engines by 1–4% [60, 61]. In practice, the overall efficiency can be optimized by analyzing different membrane parameters such as construction materials, thickness, porosity, permeability, among others, which can be integrated into a multi-objective optimization methodology [62].
3.3. Economic perspectives
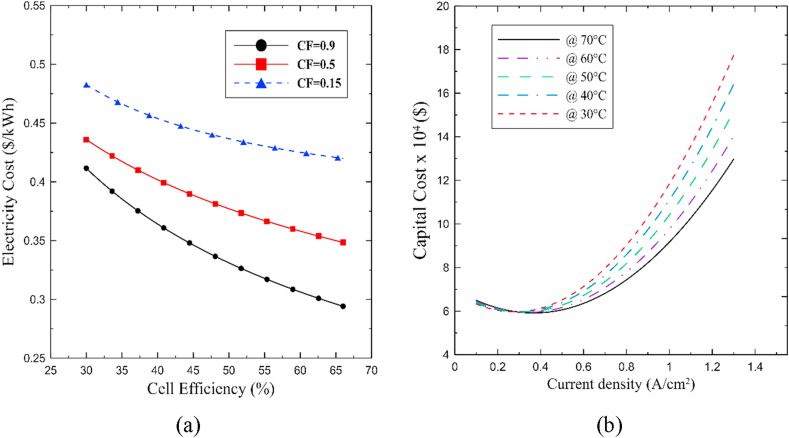
This section aims to reveal the results of the economic assessment of the integrated system. First, Figure 18a shows the electricity cost () for different capacity factors (CF) scenarios. This relation becomes vital to examine the cost-effective performance of the integrated system as the CF accounts for the operation mode. Thus, this value can be fixed to 0.9 for steady load conditions, whereas it can reach 0.5 or even 0.15 for variable or intermittent load operation. On the other hand, Figure 18b displays the capital cost of the integrated system as a function of current density and operational temperature.
Figure 18.
Economic results for the (a) electricity cost and (b) capital cost.
According to the results, Figure 18a shows that the overall trend of the electricity cost features an inverse relation concerning the system's efficiency. The results are in agreement with the common behavior of this variable in hydrogen-power systems [23, 55, 56]. Moreover, the steady-state condition operation (CF = 0.9) presents the lowest energy generation cost-share obtaining a minimum value of 0.296 $/kWh, which represents an idealistic scenario in the economic analysis considering the functionality of the integrated system. Therefore, a more precise comparison can be made while accounting for the operation's intermittence (CF = 0.5), which displays values between 0.37-0.45 $/kWh. The results obtained prove that the electricity selling price of the proposed system is not competitive with the average industrial selling price in the US (0.05–0.2 $/kWh) [63], but it is close to non-conventional energy systems in remote areas (0.25–0.3 $/kWh) [56, 59]. Note that the results reported in the economic perspectives disregard the incorporation of hydrogen storage in the overall cost, which will be determined by the specific application and indisputably boost the capital cost. Particularly, in some applications, the PEM electrolyzer's output pressure is enough to eliminate compression in storage, elucidating a significant advantage from this technology. In a general sense, analyzing a concrete scenario of a small-scale carbon-free hydrogen production plant for electric power generation that characterized the primary energy source, control devices, heat exchangers, and PEMFC-PEM electrolyzer will contribute to providing a wider perspective of the proposed system from a techno-economic perspective.
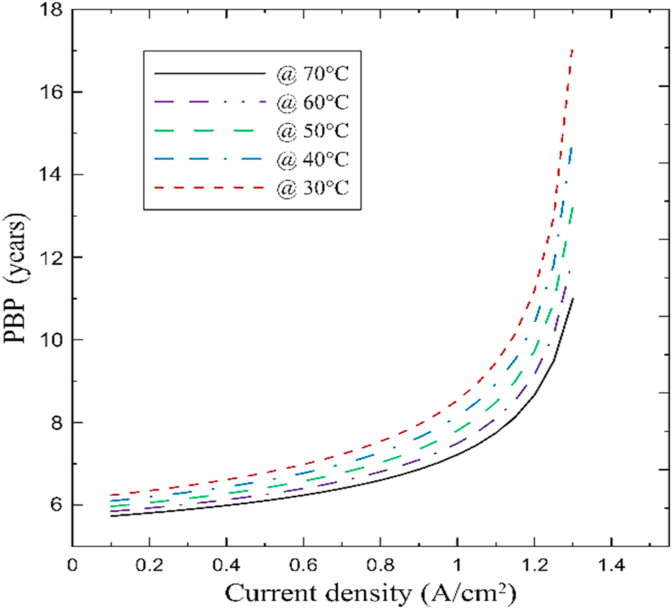
On the other hand, Figure 18b shows that higher temperatures foster lower capital cost in the system; similarly, low current density values contribute to reducing the overall investment cost. The overall behavior demonstrates that between 0.1 to 0.65 A/cm2, the differences between capital costs are not significant. However, the temperature plays an important role in the overall cost as the current density increases. Higher temperatures, namely 70 °C, are strongly recommended as they facilitate reasonable capital costs between $ 6–10 × 104, which is reasonably high compared to other technologies. The cost estimation agreed with the overall cost expectations settled by similar studies on a similar scale [23, 55, 57]. Notice that PEM technology possesses a pressing need to reduce the overall cost since it reaches values of $ 4–8x106 for high-scale plants [29]. Lastly, Figure 19 presents the influence of temperature operation and current density on the PBP of the system.
Figure 19.
Payback period (PBP) of the integrated system.
Based on the results, reasonable investment return periods can be obtained through the operation range. It is evident that low current densities and high temperatures enable higher efficiencies and minimal cost; thus, the PBP is significantly reduced. For most of the operative range, the PBP varies between 6-10 years, which reinforces the proposed model's feasibility and contributes to engaging commercialization of these technologies.
4. Conclusions
A complete model was developed to assess the overall behavior of a PEM electrolyzer and a PEM fuel cell individually and when integrated. Also, an economic methodology is proposed to evaluate the integrated system from a cost-effective perspective. The characterization of the integrated system and performance conceptualization from both electrochemical and economic aspects was found to be the unique contribution of the present investigation. The mathematical description was implemented in Matlab/Simulink® to reveal the impact of parameters such as temperature, pressure, overpotentials, humidity ratio, voltage, and design parameters on the overall performance.
The models were developed based on the equations that characterize the subsystems of each device, namely, anode, cathode, and membrane. The study incorporated physical and geometric patterns that reduce the complexity of the phenomena.
Simulation scenarios were assessed for temperature ranges from 30 to 70 °C and pressure between 1 to 10 atm. Also, current density varies from 0.1 to 1.33 A/cm2. Based on the individual model results, the activation and ohmic overpotentials had the greatest effect on PEM electrolyzer and PEMFC performance. Furthermore, temperature rise improves the performance of both devices up to 10%. Specifically, higher temperatures improve the dissociation of water molecules in the electrolyzer, thus, producing better ion exchange in the electrode interface-membrane. In contrast, the enhanced performance on the fuel cell is associated with the acceleration of the electrochemical reactions related to the molecular union of incoming reagents. The effect of pressure was found to be only substantial on the PEMFC performance but in a minor proportion (2–5%) compared to the temperature.
The evaluation of the overall efficiency in the integrated system stands as a novel performance criterion. The overall efficiency ranged between 25 to 75%, whereas temperature rises facilitate efficient operation. Moreover, the combined effect of pressure and temperature on the overall efficiency revealed that for the combination of temperatures between 55 °C and 60 °C and pressures between 2atm and 7atm, the overall efficiency features peak values.
The economic assessment of the integrated system demonstrated that operation at constant load conditions represented by a high-capacity factor can provide the lowest electricity cost between 0.28 to 0.45 $/kWh. These findings support the importance of PEMFC and PEM electrolyzer integration as it prevents intermittent operation (low-capacity factor). The capital cost can be minimized up to 25% while maintaining steady operating at a low current density and a maximum temperature of 70 °C. The influence of temperature on the overall cost is not significant at low current density values (0.1–0.6 A/cm2). However, when the current gets higher, the effect of temperature increases dramatically, featuring differences between $2- 4 × 104. The payback period varies between 6-17 years, while the most efficient scenario (highest temperature) reduces to 6–10 years.
Overall, the proposed integrated model demonstrated reliability to stand operation as a complementary system for power generation and further contributes to reducing greenhouse emissions; the parameters that contribute the most to the overall efficiency were identified. Also, the economic assessment stands as a robust tool to foster the commercialization of hydrogen-powered systems.
The study features some limitations related to the neglection of hydrogen storage for the integrated system performance and economic perspectives. Moreover, in-depth analysis is required to relate realistic operational conditions within the modeling. In future studies, there is an open path for further investigation regarding the identification of optimal operation ranges via advanced optimization methodologies and the complete characterization of a primary energy source. Also, there is a pressing need to minimize the capital cost and extend the lifetime of components to reduce the electricity and hydrogen cost while promoting a competitive scenario compared to conventional energy sources.
Declarations
Author contribution statement
Rony Escobar Yonoff & Daniel Maestre-Cambronel: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data.
Sebastián Charry: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Adriana Rincón Montenegro & Ivan Portnoy: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This work was supported by COLCIENCIAS and Gobernación del Atlántico (Grant No. 673 (2014) and Grant 727 (2015)).
Data availability statement
The data that has been used is confidential.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors thank UNIVERSIDAD DEL NORTE, UNIVERSIDAD DE LA COSTA, the industrial instrumentation and thermal machines laboratory (LIMTER) at UNIVERSIDAD DEL ATLÁNTICO, and SPHERE ENERGY Company.
References
- 1.Abu-Rumman G., Khdair A.I., Khdair S.I. Current status and future investment potential in renewable energy in Jordan: an overview. Heliyon. 2020;6(2) doi: 10.1016/j.heliyon.2020.e03346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ochoa G.V., Isaza-Roldan C., Duarte Forero J. Economic and exergo-advance analysis of a waste heat recovery system based on regenerative organic rankine cycle under organic fluids with low global warming potential. Energies. 2020;13(6):1317. [Google Scholar]
- 3.Ursúa A., Sanchis P. Static–dynamic modelling of the electrical behaviour of a commercial advanced alkaline water electrolyser. Int. J. Hydrogen Energy. 2012;37(24):18598–18614. [Google Scholar]
- 4.Zeng K., Zhang D. Recent progress in alkaline water electrolysis for hydrogen production and applications. Prog. Energy Combust. Sci. 2010;36(3):307–326. [Google Scholar]
- 5.Amador G. Characteristics of auto-ignition in internal combustion engines operated with gaseous fuels of variable methane number. J. Energy Resour. Technol. 2017;139 [Google Scholar]
- 6.Duarte Forero J., Valencia Ochoa G., Piero Rojas J. Effect of the geometric profile of top ring on the tribological characteristics of a low-displacement diesel engine. Lubricants. 2020;8(8):83. [Google Scholar]
- 7.Valencia G., Peñaloza C., Forero J. Thermo-economic assessment of a gas microturbine-absorption chiller trigeneration system under different compressor inlet air temperatures. Energies. 2019;12:4643. [Google Scholar]
- 8.Gutiérrez-Martín F., Amodio L., Pagano M. Hydrogen production by water electrolysis and off-grid solar PV. Int. J. Hydrogen Energy. 2020;xxxx [Google Scholar]
- 9.Bargal M.H.S., Abdelkareem M.A.A., Tao Q., Li J., Shi J., Wang Y. Liquid cooling techniques in proton exchange membrane fuel cell stacks: a detailed survey. Alexandria Eng. J. 2020;59(2):635–655. [Google Scholar]
- 10.Yonoff R.E., Ochoa G.V., Cardenas-Escorcia Y., Silva-Ortega J.I., Meriño-Stand L. Research trends in proton exchange membrane fuel cells during 2008–2018: a bibliometric analysis. Heliyon. 2019;5(5) doi: 10.1016/j.heliyon.2019.e01724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abdollahzadeh M., Ribeirinha P., Boaventura M., Mendes A. Three-dimensional modeling of PEMFC with contaminated anode fuel. Energy. 2018;152:939–959. [Google Scholar]
- 12.Sahraoui M., Bichiou Y., Halouani K. Three-dimensional modeling of water transport in PEMFC. Int. J. Hydrogen Energy. 2012;38 [Google Scholar]
- 13.Kone J.-P., Zhang X., Yan Y., Hu G., Ahmadi G. Three-dimensional multiphase flow computational fluid dynamics models for proton exchange membrane fuel cell: a theoretical development. J. Comput. Multiph. Flows. 2017;9 1757482X1769234. [Google Scholar]
- 14.Shekhar K. 2013. An Investigation into the Minimum Dimensionality Required for Accurate Simulation of Proton Exchange Membrane Fuel Cells by the Comparison between 1- and 3-dimension Models. [Google Scholar]
- 15.Abdin Z., Webb C.J., Gray E.M. PEM fuel cell model and simulation in Matlab–Simulink based on physical parameters. Energy. 2016;116:1131–1144. [Google Scholar]
- 16.Chavan S.L., Talange D.B. Modeling and performance evaluation of PEM fuel cell by controlling its input parameters. Energy. 2017;138:437–445. [Google Scholar]
- 17.Yigit T., Selamet O.F. Mathematical modeling and dynamic Simulink simulation of high-pressure PEM electrolyzer system. Int. J. Hydrogen Energy. 2016;41(32):13901–13914. [Google Scholar]
- 18.Abdin Z., Webb C.J., Gray E.M. Modelling and simulation of an alkaline electrolyser cell. Energy. 2017;138:316–331. [Google Scholar]
- 19.Han B., Steen S.M., Mo J., Zhang F.-Y. Electrochemical performance modeling of a proton exchange membrane electrolyzer cell for hydrogen energy. Int. J. Hydrogen Energy. 2015;40(22):7006–7016. [Google Scholar]
- 20.Alibaba M., Pourdarbani R., Manesh M.H.K., Ochoa G.V., Forero J.D. Thermodynamic, exergo-economic and exergo-environmental analysis of hybrid geothermal-solar power plant based on ORC cycle using emergy concept. Heliyon. 2020;6(4) doi: 10.1016/j.heliyon.2020.e03758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Moorthy K., Patwa N., Gupta Y. Breaking barriers in deployment of renewable energy. Heliyon. 2019;5(1) doi: 10.1016/j.heliyon.2019.e01166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alshehri F., Suárez V.G., Rueda Torres J.L., Perilla A., van der Meijden M.A.M.M. Modelling and evaluation of PEM hydrogen technologies for frequency ancillary services in future multi-energy sustainable power systems. Heliyon. 2019;5(4) doi: 10.1016/j.heliyon.2019.e01396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Frangopoulos C.A., Nakos L.G. Development of a model for thermoeconomic design and operation optimization of a PEM fuel cell system. Energy. 2006;31(10–11):1501–1519. [Google Scholar]
- 24.AlZahrani A.A., Dincer I. Exergoeconomic analysis of hydrogen production using a standalone high-temperature electrolyzer. Int. J. Hydrogen Energy. 2020;xxxx [Google Scholar]
- 25.Taner T., Naqvi S.A.H., Ozkaymak M. Techno-economic analysis of a more efficient hydrogen generation system prototype: a case study of PEM electrolyzer with Cr-C coated SS304 bipolar plates. Fuel Cells. 2019;19(1):19–26. [Google Scholar]
- 26.Zoulias E.I., Lymberopoulos N. Techno-economic analysis of the integration of hydrogen energy technologies in renewable energy-based stand-alone power systems. Renew. Energy. 2007;32(4):680–696. [Google Scholar]
- 27.Thema M., Bauer F., Sterner M. Power-to-Gas: electrolysis and methanation status review. Renew. Sustain. Energy Rev. Sep-2019;112:775–787. Elsevier Ltd. [Google Scholar]
- 28.Steeb H., Seeger W., Aba Oud H. Hysolar: an overview on the German-Saudi Arabian programme on solar hydrogen. Int. J. Hydrogen Energy. 1994;19(8):683–686. [Google Scholar]
- 29.Lepage T., Kammoun M., Schmetz Q., Richel A. Biomass-to-hydrogen: a review of main routes production, processes evaluation and techno-economical assessment. Biomass Bioenergy. Jan-2021;144:105920. Elsevier Ltd. [Google Scholar]
- 30.Milani D., Kiani A., McNaughton R. Renewable-powered hydrogen economy from Australia’s perspective. Int. J. Hydrogen Energy. 2020;45(46):24125–24145. [Google Scholar]
- 31.Dincer I., Acar C. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrogen Energy. 2014;40(34):11094–11111. [Google Scholar]
- 32.Thanapalan K.K.T., Williams J.G., Liu G.P., Rees D. Modelling OF a PEM fuel cell system. IFAC Proc. Vol. 2008;41(2):4636–4641. [Google Scholar]
- 33.Mennola T. Mass transport in the cathode of a free-breathing polymer electrolyte membrane fuel cell. J. Appl. Electrochem. 2003;33(11):979–987. [Google Scholar]
- 34.Pukrushpan H., Jay T., Stefanopoulou Anna G., Peng . Springer; 2004. Control of Fuel Cell Power Systems. [Google Scholar]
- 35.Nam J.H., Kaviany M. Effective diffusivity and water-saturation distribution in single- and two-layer PEMFC diffusion medium. Int. J. Heat Mass Tran. 2003;46(24):4595–4611. [Google Scholar]
- 36.García-Valverde R., Espinosa N., Urbina A. Simple PEM water electrolyser model and experimental validation. Int. J. Hydrogen Energy. 2012;37(2):1927–1938. [Google Scholar]
- 37.Görgün H. Dynamic modelling of a proton exchange membrane (PEM) electrolyzer. Int. J. Hydrogen Energy. 2006;31(1):29–38. [Google Scholar]
- 38.V Santhanam K.S., Press R.J., Miri M.J., V Bailey A., Takacs G.A. Wiley; 2017. Introduction to Hydrogen Technology. [Google Scholar]
- 39.Vallieres C., Winkelmann D., Roizard D., Favre E., Scharfer P., Kind M. On Schroeder’s paradox. J. Membr. Sci. 2006;278(1):357–364. [Google Scholar]
- 40.Onishi L., Prausnitz J. Water−Nafion equilibria. Absence of Schroeder’s paradox. J. Phys. Chem. B. 2007;111:10166–10173. doi: 10.1021/jp073242v. [DOI] [PubMed] [Google Scholar]
- 41.Zawodzinski T.A., Neeman M., Sillerud L.O., Gottesfeld S. Determination of water diffusion coefficients in perfluorosulfonate ionomeric membranes. J. Phys. Chem. 1991;95(15):6040–6044. [Google Scholar]
- 42.Marangio F., Santarelli M., Calì M. Theoretical model and experimental analysis of a high pressure PEM water electrolyser for hydrogen production. Int. J. Hydrogen Energy. 2009;34(3):1143–1158. [Google Scholar]
- 43.Kim D.J., Jo M.J., Nam S.Y. A review of polymer–nanocomposite electrolyte membranes for fuel cell application. J. Ind. Eng. Chem. 2015;21:36–52. [Google Scholar]
- 44.Qi J., Zhai Y., St-Pierre J. Effect of contaminant mixtures in air on proton exchange membrane fuel cell performance. J. Power Sources. 2019;413:86–97. [Google Scholar]
- 45.Milewski J., Guandalini G., Campanari S. Modeling an alkaline electrolysis cell through reduced-order and loss-estimate approaches. J. Power Sources. 2014;269:203–211. [Google Scholar]
- 46.Beattie P.D., Basura V.I., Holdcroft S. Temperature and pressure dependence of O2 reduction at Pt∣Nafion® 117 and Pt∣BAM® 407 interfaces. J. Electroanal. Chem. 1999;468(2):180–192. [Google Scholar]
- 47.Marković N.M., Grgur B.N., Ross P.N. Temperature-dependent hydrogen electrochemistry on platinum low-index single-crystal surfaces in acid solutions. J. Phys. Chem. B. 1997;101(27):5405–5413. [Google Scholar]
- 48.Santarelli M.G., Torchio M.F., Cochis P. Parameters estimation of a PEM fuel cell polarization curve and analysis of their behavior with temperature. J. Power Sources. 2006;159(2):824–835. [Google Scholar]
- 49.Springer T.E., Zawodzinski T.A., Gottesfeld S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991;138(8):2334–2342. [Google Scholar]
- 50.Barbir F. PEM Fuel Cells: Theory and Practice. Academic Press; Burlington: 2005. Fuel cell electrochemistry; pp. 33–72. [Google Scholar]
- 51.Dell R.M., Moseley P.T., Rand D.A.J. Towards sustainable road transport. Academic Press; Boston: 2014. Hydrogen, fuel cells and fuel cell vehicles; pp. 260–295. [Google Scholar]
- 52.Barbir F., Gómez T. Efficiency and economics of proton exchange membrane (PEM) fuel cells. Int. J. Hydrogen Energy. 1997;22(10–11):1027–1037. [Google Scholar]
- 53.Barbir F. Fuel cell applications. In: Barbir F., editor. PEM Fuel Cells. second ed. Academic Press; Boston: 2013. pp. 373–434. [Google Scholar]
- 54.Zhou L. Progress and problems in hydrogen storage methods. Renew. Sustain. Energy Rev. Aug-2005;9(4):395–408. Elsevier Ltd. [Google Scholar]
- 55.Kamarudin S.K., Daud W.R.W., Som A. Md., Takriff M.S., Mohammad A.W. Technical design and economic evaluation of a PEM fuel cell system. J. Power Sources. 2006;157(2):641–649. [Google Scholar]
- 56.Rahimi S., Meratizaman M., Monadizadeh S., Amidpour M. Techno-economic analysis of wind turbine-PEM (polymer electrolyte membrane) fuel cell hybrid system in standalone area. Energy. 2014;67:381–396. [Google Scholar]
- 57.Mayyas A. Manufacturing cost analysis for proton exchange membrane water electrolyzers manufacturing cost analysis for proton exchange membrane water electrolyzers. Natl. Renew. Energy Lab. 2019:65. August. [Google Scholar]
- 58.Yukesh Kannah R. Techno-economic assessment of various hydrogen production methods – A review. Bioresour. Technol. Jan-2021;319:124175. doi: 10.1016/j.biortech.2020.124175. Elsevier Ltd. [DOI] [PubMed] [Google Scholar]
- 59.Valencia Ochoa G., Acevedo Peñaloza C., Duarte Forero J. Thermoeconomic optimization with PSO algorithm of waste heat recovery systems based on organic rankine cycle system for a natural gas engine. Energies. 2019;12(21):4165. [Google Scholar]
- 60.Consuegra F., Bula A., Guillín W., Sánchez J., Duarte Forero J. Instantaneous in-cylinder volume considering deformation and clearance due to lubricating film in reciprocating internal combustion engines. Energies. 2019;12(8):1437. [Google Scholar]
- 61.Valencia Ochoa G., Cárdenas Gutierrez J., Duarte Forero J. Exergy, economic, and life-cycle assessment of ORC system for waste heat recovery in a natural gas internal combustion engine. Resources. 2020;9(1):2. [Google Scholar]
- 62.Zhang Z., Wang X., Zhang X., Jia L. Optimizing the performance of a single PEM fuel cell. J. Fuel Cell Sci. Technol. 2008;5(3) [Google Scholar]
- 63.Fontalvo A., Solano J., Pedraza C., Bula A., Gonzalez Quiroga A., Vasquez Padilla R. Energy, exergy and economic evaluation comparison of small-scale single and dual pressure organic rankine cycles integrated with low-grade heat sources. Entropy. 2017;19(10):476. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.