Approaches for the Integrated Analysis of Structure, Function and Connectivity of the Human Brain

Abstract

Understanding the organization of the human brain is the fundamental prerequisite for appreciating the neural dysfunctions underlying neurological or psychiatric disorders. One major challenge in this context is the presence of multiple organizational aspects, in particular the regional differentiation in structure and function on one hand and the integration by inter-regional connectivity on the other. We here review these fundamental distinctions and introduce current methods for mapping regional specialization. The main focus of this review is to provide an overview over the different concepts and methods for assessing connections and interactions in the brain, in particular anatomical, functional and effective connectivity. In this context, we focus less on technical details and more on the comparative description of strengths and weaknesses of different aspects of connectivity as well as different methods for examining a particular aspect. This overview closes by raising several open questions on the conceptual and empirical relationship between different approaches towards understanding brain structure, function and connectivity.

PRINCIPLES OF BRAIN ORGANIZATION

One of the eminent long-term goals in systems neuroscience research is to elucidate the neural dysfunctions underlying neurological or psychiatric disorders. Evidently, however, understanding the pathophysiology of complex disorders such as schizophrenia or Parkinson’s disease will remain futile without a concept of psychological brain organization. In other words, in order to appreciate the brain’s pathologies, we first need to understand its normal organization in healthy subjects.

The mammalian brain is governed by two fundamental principles of organization, i.e., functional segregation and functional integration.¹ The former refers to the fact, that the brain, in particular the cerebral cortex, is not a homogenous entity but can be subdivided into regionally distinct modules (cortical areas or subcortical nuclei) based on both functional and microstructural properties. The concept of functional integration, on the other hand, highlights that no brain region is by itself sufficient to perform a particular cognitive, sensory or motor process. Further, all of these mental capacities or “tasks” have to rely on a dynamic interplay and exchange of information between different regions. However, functional integration is not in contrast with the aforementioned principle of functional segregation, as it can be conceptualized as the interaction between specialized regions, each performing a distinct computational sub-process.^1,2

How to define a specialized module

Research in non-human primates has indicated that regional specialization, i.e., the cognitive or sensory processes served by particular cortical location, is determined by its intrinsic (structure) and extrinsic (connectivity) properties.^3-8 Although closely related to the fundamental distinction between functional segregation and functional integration described above, the latter view provides a slightly different focus. In particular, specialization for a specific function is not regarded as an intrinsic property of a region that is independent of its connectivity. However, the functional specialization of a cortical region results from the local anatomical and neurochemical features but does not necessarily map on psychological concepts of mental processes or operations. Moreover, the computational processes only become specialized operations through the patterns of input and output, i.e., connectivity. In that sense, a module of functional specialization may not be defined independent of its connectivity but is also given by the intersection of regionally specific architecture and connectivity patterns. Each cognitive, sensory or motor task or mental capacity relies on the coordinated activity and interaction of many of such modules.

Structure - function - connectivity

We here suggest that brain organization and the pathophysiology underlying neurological and psychiatric disorders can only be understood at a sufficient level if considering (i) the anatomical differentiation of the cerebral cortex into micro-structurally distinct areas, (ii) its response properties or, more general, its pattern of recruitment by various mental operations and finally (iii) its interaction with other brain regions. Such multi-modal analyses should then help the understanding of how mental capacities emerge from a network of specialized but interacting regions. Research in non-human primates has a long tradition of integrated analysis of regional brain organization.^9-12 Here, functional properties of a microstructurally distinct area (e.g., as determined by cyto- or myeloarchitectonic examinations) may be probed by recording single cells or local field potentials. Axonal connectivity of the very same location may then be revealed by injection of a tracing dye that is transported to interconnected brain regions. Such analyses have repeatedly demonstrated the close correspondence of brain structure, function and connectivity, and provided most of our current knowledge on organizational principles of the brain. Unfortunately, however, all of these techniques are invasive in nature and ultimately entail sacrificing the examined animal. This evidently makes them unfeasible for advancing our understanding of the human brain. Consequently, knowledge of the organization of the human brain has lagged for many decades behind that on non-human primates. Over the last two decades, however, several new methods and technologies have become available, which may enable a similarly precise and multi-modal assessment of the human brain.

FUNCTIONAL NEUROIMAGING

Regional functional specialization

Functional neuroimaging by positron emission tomography (PET) and functional magnetic resonance imaging (fMRI) enables the in-vivo investigation of functional specialization in the human brain.^13-19 Based on local changes in cerebral blood flow, glucose or oxygen metabolism, these techniques allow the identification of regionally specific increases in neural activation under a certain motor, sensory or cognitive task across the whole brain simultaneously. The spatial resolution in single subject data lies within the range of a few millimeters. However, when considering the much more frequent case of group activation studies, the precision of the spatial localization is reduced by factors such as inter-individual variability, averaging effects and technical confounds such as variance introduced by different normalization approaches.²⁰ For example, in fMRI group data, spatial uncertainty is equivalent to a Gaussian distribution of about 10 mm FWHM.²⁰ While functional neuroimaging has led to a wealth of information on the neural correlates of various processes, it has a predominantly confirmatory role in the context of differentiating cortical modules. That is, using appropriate experimental designs, fMRI is a powerful tool for testing hypotheses about, e.g., a functional differentiation between two regions or a dichotomy between the neural correlates of two processes. Neuroimaging is, however, intrinsically less well suited to delineate the organization of a particular brain region. A prime reason for this drawback is that in most instances the tasks that would differentiate different modules in a region of interest are unknown so that experiments cannot be specifically designed to reveal a functional distinction.

Regional structural specialization

The structural examination of the human brain by histological mapping has a long tradition.^21-25 Similar to anatomical studies in monkeys, these analyses rely on the investigation of post-mortem tissue, where cell bodies, myelinated fibers or the presence of specific molecules may be visualized using staining, radioactive labeling or in-situ hybridization.^26,27 Recent advances in high field imaging methods also allow assessing the microstructural properties of the human brain in-vivo.²⁸ Currently, however, no in-vivo imaging approach seems capable of providing a similarly rich amount of ultrastructural information as histological post-mortem data. As noted above, fMRI and PET are excellent tools to identify the regions recruited by a mental operation but cannot distinct the borders of cortical modules. Therefore, combining functional imaging and histological maps may lead to an integrated description of regional segregation. However, while neuroimaging produces volume-datasets of group results, anatomical mapping yields slice-wise individual information on the borders of microstructural areas. Therefore, the current approach for analyzing the correspondence between brain structure and function is to perform both analyses separately (evidently in two groups of subjects) and then to integrate them by means of probabilistic brain atlases in electronic formats.^29-31 Such probabilistic atlases can be generated on the basis of automated analyses of histological sections, e.g., by means of image analyzer algorithms detecting laminar changes in cell body densities along the cerebral cortex in micrometer resolution.³² Cytoarchitectonic parcelations performed in a number of brains can then be warped to an anatomical reference brain in order to describe the location and variability of cortical areas on the group level in standard stereotaxic space. This is not only in clear contrast to classical anatomical brain atlases that present observer-dependent parcelations of one or a few brains as schematic surface views. But, it also allows the direct and quantitative assessment of structure-function correlations in the same reference space, supporting the notion that functional differentiation indeed corresponds to microstructural differentiation.²⁹

Regional structure-function relationships

These advances in the mapping of regional specialization led to the description of mental processes that recruit a specific, structurally defined, area. There are now plenty of studies, which demonstrated that anatomical borders indeed constrain functional specialization.^33,34 However, this “localization approach” seems insufficient to describe brain function, as a number of studies indicated that a single region can be “specialized” for a broad range of mental operations. For example, the inferior frontal gyrus hosts a distinct cytoarchitectonic area which Korbinian Brodmann termed “area 44”.²² Pierre-Paul Broca already noticed in the middle of the 19th century that this part of the brain is strongly engaged in language production.³⁵ However, a number of neuroimaging studies clearly showed that this region is not language-specific but gets recruited by a broad variety of different tasks, ranging from speech to working memory and motor production.³⁶ Does this contradict the fundamental idea of functional specialization? Not necessarily. We can assume that BA 44 is specialized to perform computations at a very basic level rather than being specialized to sustain any particular (psychologically defined) mental operations. However, these basic computations, which may be sequencing, temporo-spatial updating or even more fundamental processes, would then be integral parts of many different task-specifically recruited networks. Therefore, without taking an explicit network-perspective, that is consideration of integration as the second major organizational principle in the brain, physiological and pathological roles of probably most brain regions will remain elusive.

The elusive concept of brain connectivity

The concept of brain connectivity in itself has remained somewhat enigmatic. First, there is no such thing as “the” connectivity of an area, as several conceptually different aspects of brain connectivity may be distinguished. The following overview shall outline the major concepts and approaches that have been employed to capture different aspects of brain connectivity but importantly also point to their strength and drawbacks.

ANATOMICAL CONNECTIVITY

Classical approaches to anatomical connectivity

Anatomical connectivity denotes the presence of fiber connections between two areas in the brain, or — more specifically — between neurons. Early investigations of anatomical connectivity in the human brain were limited to the use of post-mortem dissection techniques, which only allow the description of the location and direction of major fiber pathways on a macroscopic level.^37,38 With the advent of appropriate myelin staining techniques, also microscopical examinations of white matter bundles also became feasible.³⁹ Such myeloarchitectonic techniques, however, barely allow the researcher to assess the three-dimensional course of a particular fiber tract. Therefore, until the end of the last century knowledge on the anatomical connectivity of the human brain was mostly limited to the course of major fiber bundles such as the cortico-spinal tract or the arcuate fasciculus. In contrast, invasive tract-tracing studies in non-human primates have provided detailed information on axonal connections with high spatial precision and specificity.⁴⁰ Since the tracers are injected into locations that are usually defined based on electrophysiological properties of histologically distinct regions, connectivity patterns may be obtained for specific cortical areas and directly related to particular functions. Importantly, invasive tracing relies on either antero- or retrograde axonal transport of a particular tracer.⁴⁰ It thus entails a high degree of confidence that the obtained results indeed reflect true axonal connections between two areas which in turn is a necessary prerequisite for any functional interaction between regions. Moreover, afferent and efferent connections can be distinguished due to the direction of axonal transport, which is something fundamentally impossible by those techniques applicable to humans that primarily identify the location and direction of fiber bundles. This long-standing discrepancy between highly precise and specific anatomical connectivity measures in non-human primates on one hand and the relatively coarse and limited methods available for the investigation of the human brain may explain why in particular anatomical connectivity of the human brain is often compared and referenced against that in non-human primates.

Diffusion weighted imaging and tractography

The advent of diffusion-weighted imaging (DWI) and the development of tractography approaches over the last decade have considerably changed this situation by opening the possibility of in-vivo explorations of anatomical connectivity in the human brain.^41-44 DWI may be tuned sensitive to random motion of water molecules along a diffusion-encoding direction in a pulsed field gradient.⁴¹ By measuring diffusion along many different directions, it becomes possible to characterize the diffusion properties within a voxel (usually at an isotropic resolution of about 2 mm), most commonly reflected as a three-dimensional Gaussian process. Importantly, diffusion in the brain is not isotropic along different spatial directions. In tissue with a high degree of directional organization such as the brain’s white matter where all axons along a fiber bundle are organized in parallel, diffusion is more hindered in some directions than others (Figure 1A), leading to a “diffusion ellipsoid”.⁴² The diffusion characteristics of a particular voxel, i.e., the shape of the diffusion ellipsoid, may be described by two main properties. The first is the direction of its principal axis, which corresponds to the direction of greatest diffusion (the principal diffusion direction, PDD). In white matter, where diffusion is almost not restricted if water molecules follow the direction of the axons, and most limited perpendicular to the fibers due to the presence of myelin sheath and cell membranes, the PDD corresponds well with the dominant orientation of fibers within a voxel. The second important feature of the diffusion ellipsoid is its anisotropy, which corresponds to the preponderance of diffusion to follow the PDD relative to all other directions. This anisotropy thus reflects the degree of homogeneous organization within a voxel that may be brought upon by several fiber orientations, non-directional tissue and other factors. From the fiber orientation directions in each voxel (Figure 1B-1E) in combination with measures about diffusion uncertainty, it is possible to infer the course of a particular fiber tract in the brain. Such tractography may be deterministic (following the principal diffusion direction at each voxel) or probabilistic (by repeated sampling of the possible diffusion directions in each voxel as reflected by the uncertainty or complex orientation distributions, Figure 1F). Given the dynamic of the field and the constantly evolving methods and modeling approaches, the reader may be referred to the methodological papers describing the various methods for modeling diffusion directions and performing tractography.^45-49

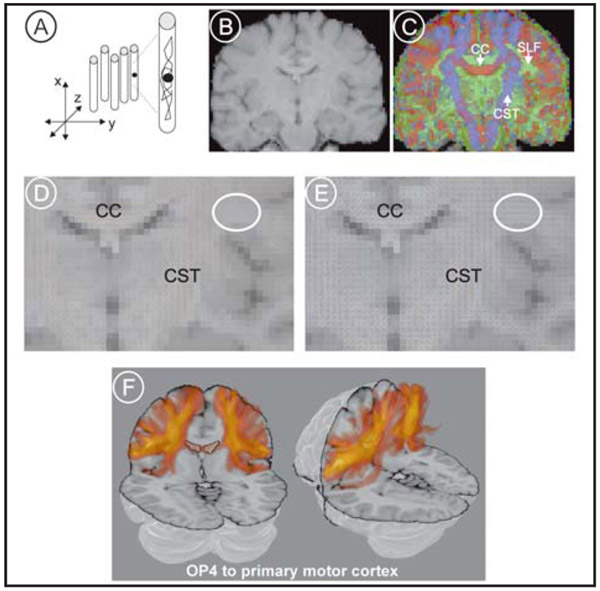
Figure 1.

Diffusion Tensor Imaging (DTI). (A) Restricted diffusion in white matter. (B) T1 weighted coronal section. (C) Diffusion tensor image of the same coronal section as in (B). The direction of fiber orientation is color-coded in blue (dorso-ventral direction, e.g., the corticospinal tract, CST), red (medio-lateral direction, e.g., the corpus callosum, CC) and green (antero-posterior direction, e.g., the superior longitudinal fascicle, SLF). (D) Detail of diffusion tensors of the principal diffusion direction. (E) Detail of the diffusion tensors of “crossing fibers” representing higher order models of fiber orientation per voxel. (F) Probabilistic tractography between the parietal operculum (area OP 4) and the primary motor cortex.

Limitations of diffusion tractography

In spite of recent advances allowing for modeling different fiber orientations within a voxel, the reliability of diffusion tractography to define paths considerably depends on anisotropy. While large pathways in deep white matter may be well-defined, reliability strongly decreases in regions closer to the cortical surface due to a higher degree of fiber divergence as these fan out to cortical targets. In other words, while it is well possible to map the course of larger white matter pathways, assessing the anatomical connectivity between two locations in the grey matter is much less reliable. Furthermore, tractography studies always face the problem of false positives and false negatives due to limitations in resolution which could cause tractography traces to “join” bigger fiber tracts like the superior longitudinal or the arcuate fasciculus, thereby impeding the delineation of the precise connectivity between two locations connected with less prominent fiber bundles.

Given the symmetry of random water diffusion along a particular direction and the absence of any physiological characterization of axonal directions, tractography does not allow inference on the direction of a fiber tract and hence differentiation between afferent and efferent projections. Therefore, DWI based tractography primarily yields qualitative information on the presence and course of fibers that could provide an anatomical connection between two regions. Assessment of, e.g., the number of samples in probabilistic tractography that reached a particular target from a specific seed region, is not a valid approach for quantifying the strength of a fiber bundle. Such parameters also reflect the probability of how likely it is to reach that particular target in a random journey along the principle diffusion directions relative to all other possible locations that could be reached.

Problems in cross-species validation

Given the current limitations of diffusion weighted tractography for the delineation of regionally specific anatomical connectivity, it is common practice to reference the results of DWI tractography against the wealth of literature on anatomical connections available from invasive tracing studies in non-human primates. This may, in the most extreme cases, lead to the problematic view that connections that have not been found in monkeys are regarded as false positives in human DWI data while connections obtained in tracer studies that are not replicated are regarded as false negatives. In other words, axonal tracing is seen as the ground truth that tractography has to verify in order to be accepted. There are, however, plenty of reasons why results from invasive tracing studies and tractographic analyses may diverge. First, axonal tracing also does not have perfect reliability. Likewise, the choice of the particular tracer dye used, and in particular the selection and definition of the injection sites, may strongly influence the results.⁴⁰ Moreover, sample size is usually limited to only a small number of animals (often less than five) so that inter-individual differences may further obscure inference on connection patterns. In light of these drawbacks, it is not surprising that axonal tracing studies investigating the connectivity of the same brain region may yield different results, which evidently poses the question, which of these actually reflects the “ground truth” that tractography has to match. Along the same line, while diffusion based connectivity analysis certainly suffers from limited spatial resolution (in the range of millimeters), it does have the considerable advantage of whole brain coverage in contrast to invasive tract tracing studies where axon terminals have to be delineated by histological preparation of sections through the brain. Thus, only if continuous sections through the entire brain are assessed, which is not always feasible or even attempted, whole brain connectivity may be inferred in invasive tract tracing studies. Finally, and maybe most importantly, any attempt to use cross-species comparison as an unconditioned validation of data obtained in humans runs into the danger of disregarding evolutionary changes. While there is plenty of evidence, that the brains of macaque monkeys and humans are homologous in many aspects, it would be a fallacy to assume that their organization should match completely.⁵⁰ In particular in regions showing considerable expansion and potentially re-organization during the divergent courses of evolution, such as the frontal or temporal lobes, discrepancies between species may reflect true differences in connection patterns rather than methodological problems.

What can we learn from anatomical connectivity?

Performing tractography from micro-structurally defined regions may open the exciting perspective of evaluating one of the major conceptual questions: what constitutes a cortical module? Does a cortical area have a distinct histological architecture, connectivity and function? Or may a particular histologically defined area have multiple zones of differential connectivity within it, with functional specialization arising from the intersection of the architectonic and connectivity-defined boundaries? On the practical level, however, one faces the same problem as that from the use of group activations from functional imaging studies, i.e., added noise by the fact that the subject-specific borders of a particular area are highly variable and hence unknown. Previous attempts to delineate the anatomical connectivity of histologically defined areas have thus focused on the “centers” of the respective areas, i.e., those locations where the confidence to be indeed within the particular area is highest. Using such approaches, connection patterns of structurally defined areas may be reliably identified, though more specific questions on topographic relationships between histological borders and changes in connectivity patterns probably remain to be addressed. Finally, even if the potential drawbacks of diffusion tractography outlined above may be overcome by advancing imaging and analysis technology, it is worth remembering the fundamental limitations of anatomical connectivity information. In particular, the presence of an anatomical connection, even at the axonal level, does not predicate any functional interaction along this path. Coupling between areas is dynamic and context-dependent.⁵¹ A given anatomical connection may thus be employed only in a specific context or at a specific time. It may convey many different kinds of information such as inputs for computation, feedback or bidirectional exchange for parallel processing. A weak anatomical connection may be crucial for the functional interaction, e.g., if one area provides the “go signal” for the second. On the other hand, a strong connection may have little relevance for a particular context. This is particularly true in brain systems that follow a topical organization, i.e., sensory cortices. For example, many somatotopically organized fiber bundles connect different areas of the somatosensory cortex, however, only a small subset of these may be relevant for any particular task at hand.

In summary, anatomical connectivity represents the structural scaffold, on which any functional interaction may be realized. It also represents a truly independent aspect of inter-regional integration and brain networks that is not confounded by using the same source of data as investigations into functional specialization. Anatomical connectivity studies, however, do not allow any inference on information transfer and dynamics within the hereby defined networks.

FUNCTIONAL CONNECTIVITY

Definition and electrophysiological application

Functional connectivity is defined as the temporal coincidence of spatially distant neurophysiological events.² The assumption behind this connectivity approach is that areas are presumed to be components of the same network if their time courses are consistently correlated. This definition already clearly reveals two main aspects that need to be considered when dealing with functional connectivity analyses.

First, functional connectivity is primarily correlative in nature. That is, two regions show significant functional connectivity, if increased activity in the first site is associated above chance with activity at the second site. As always with correlations, however, this does not imply any causal relationship or even any sort of direct connection between these two regions. Correlated activity in two regions may be mediated via additional structures relaying information from the first area to the second. Such relay processes could moreover be transmitted through cascades of several intermediates or via cortical-subcortical loops involving, e.g., the basal ganglia or the cerebellum. It is also possible that a third area induces correlated activation between regions that do not have any form of direct interaction. Therefore, functional connectivity may be driven by an external source inducing concurrent activity in both areas. An example of such situation would be the feed-forward of stimulus-driven activity in early sensory areas that is forwarded to parietal sensory areas for perceptual analysis and, in parallel, to premotor cortex for response preparation. In this case, functional connectivity may be seen between the parietal and the premotor cortex which, however, does not necessarily imply that their activity is directly related to each other.

Second, the notion of functional connectivity may pertain to any form of neurophysiological events, i.e., is not limited to the currently most popular analysis of resting state patterns or even fMRI time-series analyses. Additionally, functional connectivity may also be realized as correlated spiking patterns or field potentials. This application of functional connectivity analysis is commonly found in electrophysiological experiments in non-human species, where direct recordings of individual cells or multi-unit activity may be correlated among different recording sites.⁵² It may, however, also be applied to direct recordings during deep brain stimulation, across sites or with peripheral signals.⁵³ Another non-fMRI application of functional connectivity analyses is the delineation of correlations or coherence between EEG sensors, which due to the high temporal resolution of EEG may be computed as broad band correlations or specific for particular frequency bands. In these instances, functional connectivity analyses indicate coherent oscillations,i.e., neuronal mass activity, between different regions of the brain reflecting synchronous activity.^54-57

Functional connectivity MRI

Probably the current most widely applied strategy for the examination of functional connectivity is based on the assessment of correlated signal changes in fMRI time-series.^57-60 Given the richness of fMRI data, which usually consists of several hundred time-points of voxel-wise data across the brain, this approach has the perspective to yield information on the functional connectivity at the level of the entire brain. The idea underlying “functional connectivity MRI” confines to the same fundamental approach as outlined above for other applications of functional connectivity analyses, i.e., correlation of signals between different brain areas.¹ While functional connectivity MRI is still a developing field and concepts are continuously evolving, several key concepts and approaches seem to be emerging.

Analyses of functional connectivity by the correlation of regional BOLD signal intensities may be performed on fMRI time-series obtained in the task-state, i.e., while subjects are engaged in a particular cognitive or perceptual experiment. In these cases, however, the major predicament is the immanent presence of task-driven correlations. That is, all those regions that are activated by the particular task at hand will necessarily show functional connectivity due to common stimulus-evoked modulations. Importantly, these effects may not be discarded as spurious, as they reflect the functional connectivity during that task. Such common recruitment by a particular task in fact follows precisely the idea of functional connectivity as the coincidence of neurophysiological events. Nevertheless, it is often regarded as not adding substantial new information above the observation of jointly activated regions in a conventional fMRI analysis. However, functional connectivity analysis by correlation of voxel- or region-wise fMRI time series obtained during the performance of an experimental paradigm that entails multiple conditions may indeed add new insight into how closely different regions interact during the assessed tasks. Here the correlation of time-series fluctuations may be regarded as a quantification of the similarity in response or recruitment characteristics. In other words, in the context of complex tasks consisting of multiple contextual sets, functional connectivity describes to which degree two regions are commonly recruited. It thus represents an interesting though little employed tool for the further characterization of the relationship between different regions (jointly) activated in functional imaging experiments.

fMRI “resting state” functional connectivity

Currently, however, the main application of functional connectivity analysis pertains to the assessment of “resting state” images.^60,61 Here, fMRI time series are obtained while the subjects are lying in the scanner without being challenged by a particular task. An important issue in the assessment of functional connectivity in this context is that raw MRI signal time courses are noisy due to scanner artifacts, motion-induced effects, and physiological sources such as cardiac and respiratory cycles. Consequently, there is an important need to reduce spurious correlations by multiple processing steps such as spatial and temporal filtering as well as removal of signal contributions from motion, physiological noise and global signal fluctuations. This application has led to the observation that even in the absence of a structured external task, distant brain regions often show strong correlations in their activity levels (Figure 2), which are particularly expressed at lower frequencies (<0.1 Hz). A large number of different studies have used data-driven approaches, in particular independent component analysis (ICA), to delineate large-scale systems of coherent MRI signal changes with a considerable degree of consistency between datasets.⁶² These studies have thus presented converging evidence for the existence of several distinct components (i.e., functional networks) in fMRI datasets obtained during a task-free, “resting” state. Moreover most of these “resting state networks” closely resemble networks that are commonly engaged in task-based fMRI studies.⁶² This has led to the intuitive but little validated notion that virtually any functional system is reflected in what has been termed resting state networks (RSNs). It has also contributed to the now widely established but confusing labeling of these components as “dorsal attention network”, “visual network”, “auditory network”, “sensorimotor network”, “central-executive network”, “core network” and so on. The relation of components defined by ICA decomposition of resting state data to such task-related networks, however, certainly warrants further examination as intuitive associations may be premature.

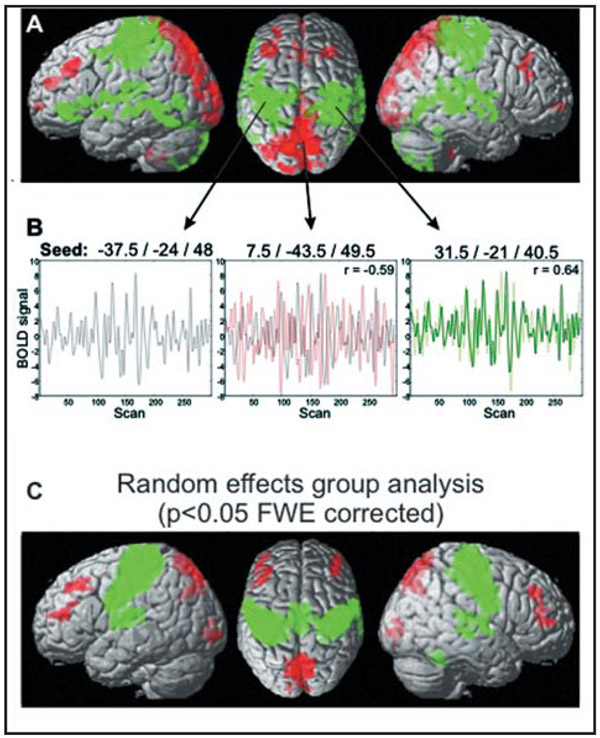
Figure 2.

Functional connectivity in resting state fMRI data. (A) Single subject data of correlated activity with a seed voxel situated in left primary motor cortex (M1). Positive correlations are colored in green, negative correlations in red . (B) Time series information from voxels in left M1 (left panel, seed), precuneus (middle panel) and right M1 (right panel) illustrate the underlying correlations. r = Pearson correlation coefficients with seed voxel in left M1. (C) Group data of correlated activity with left M1 (n = 100, random effects analysis, p < 0.01, FWE corrected on the voxel level).

Regardless of the precise relationship between RSNs and networks recruited by specific tasks, these observations have raised an ongoing debate on the physiological basis of such correlations. It was suggested that these fluctuations are driven by intrinsic activity events constrained by anatomical connections between the respective areas.^61,63 In this concept, functional connectivity may be regarded to be largely a reflection of the anatomical connectivity between different brain regions in the absence of an external task. Supporting this view simulation studies show that one may generate patterns similar to resting state fluctuations by injecting stochastic activity in structural networks defined by anatomical connectivity information.⁵⁷ On the other hand, some patterns of functional “resting state” connectivity exist, which cannot be explained by anatomical connections. Moreover, it remains unresolved what drives these interactions in a physiological sense, i.e., why there should be fluctuations of sufficient magnitude to propagate along anatomical connections.⁶⁴ This has motivated a modified view on the physiology of the “resting state networks”, which de-emphasizes the “resting” aspect.^65-67 However, it is assumed that the brain is never at rest. There is a large amount of ongoing activity composed of a vast variety of mental functions. These range from bodily perception and somatosensation to memories and reflections, emotions and feeling as well as explicit cognitive reasoning and planning including inner speech. When lying in an MRI scanner without a specific task we are not thus resting but instead performing all sorts of mental operations in succession or parallel. The correlation in the MR signal time course between two regions should thus reflect the degree to which these jointly participate in the various networks engaged in the absence of an externally pre-set task. “Resting state” activity would hence consist of a, more or less random, sampling of all the different task-related networks that the brain is capable of, with a certain preponderance for introspective and inter-personal aspects. This view not only presents a plausible explanation for the apparent presence of networks resembling those seen in task-based fMRI but also reconciles the psychological experience of “rest” with the hypothesis of coordinated stochastic fluctuations in brain activity. It has thus been proposed to avoid the term “resting state” in favor of “task-free functional connectivity” or “functional connectivity in the absence of an externally structured task set”.^65-67

Task-based functional connectivity and co-activations

The notion of functional connectivity in the absence of an externally structured task set easily leads to the complementary aspect of task-based or task-dependent functional connectivity. As noted above, task-based functional connectivity may be inferred from correlation analysis between time series from different brain regions during the performance of a particular task. In this case, however, inference is limited to the task at hand or — more precisely — to the particular experimental implementation of a given task. While such an approach may reveal new insight into functional connectivity networks, it does not allow answering the core question about task based functional connectivity: With which other regions does a particular area in question work? In other words, if a particular area is activated, which other brain regions are co-activated over and above chance? If such a question may be answered comprehensively by considering a large number of different tasks and implementations, it would allow inference on jointly activated and hence most likely interacting areas. Ideally, however, such a data-driven definition of brain networks should cover a broad range of functional domains in order to reveal associations between regions beyond a particular mental function. A possible solution to this problem has emerged from the advent of large scale databases on functional neuroimaging results (Figure 3). These enabled completely new approaches to task-based functional connectivity analysis.^68-70 Such resources, like the BrainMap (http://brainmap.org/) or Caret database (http://brainvis.wustl.edu/wiki/index.php/), contain a summary of the results of several thousands of functional neuroimaging experiments. Given the high standardization of neuroimaging data reports and in particular the ubiquitous adherence to standard coordinate systems (such as the MNI system), the results reported in these studies can be readily compared with each other with respect to the spatial location of significant neural activity. Using such broad pools of neuroimaging data functional connectivity may be assessed by testing for co-activation probabilities between different areas. In practice, functional connectivity of a given region is established by retrieving all experiments from a database that feature at least one focus of activation within this seed region of interest.^71,72 Coordinate based meta-analysis is then performed over all activation foci reported in these experiments in order to test for significant convergence (Figure 3C). As the experiments entered into such an analysis are selected based on the presence of an activation in a given seed region, any significant convergence of coordinates outside that seed would reflect above-chance co-activation. Importantly, such meta-analytic connectivity mapping (MACM) does not differentiate between different experimental paradigms or other factors, but is solely based on the likelihood of observing activation in a target region (or voxel).^73-75 Note that MACM follows exactly the definition of functional connectivity by testing for coincidences of neurophysiological events. In MACM, however, time-scales are very distinct from other approaches as the unit of observation is not a specific point in an acquired time-series but a particular neuroimaging experiment. Thus functional connectivity is not expressed as coherent fluctuation across time but as coherent activation across experiments.

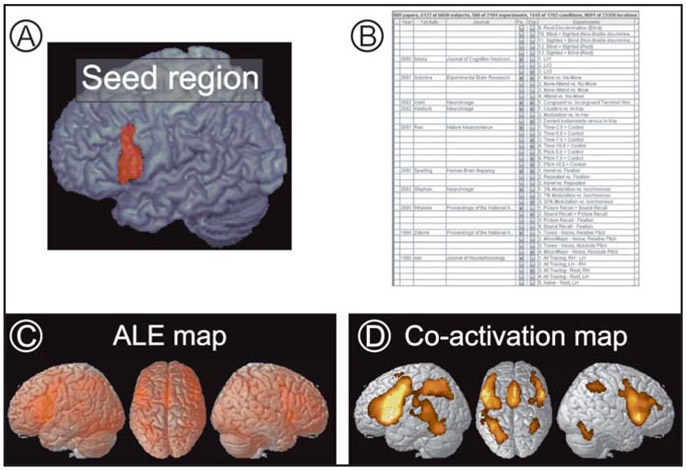
Figure 3.

Task-based functional connectivity and co-activations. (A) Seed region in left BA 44 according to the SPM Anatomy toolbox.²⁹ (B) Excerpt from the list of experiments from the BrainMap database that feature at least one focus of activation within this seed region of interest. (C) Activation likelihood estimation (ALE) map quantifying the degree of convergence across the activations reported in these experiments (cf. B). Thresholding the ALE map at p<0.05 (corrected for multiple comparisons) reveals those regions, where experiments activating BA 44 show significant above-chance co-activation, i.e., the functional connectivity of the seed region.

Task-based vs. task-free functional connectivity

Compared to task-free functional connectivity measures, the advantage of task-based functional connectivity analysis by MACM is twofold. First, MACM delineates networks that are conjointly recruited by a broad range of tasks and should hence reflect robust (i.e., meaningful) patterns of coordinated activity in response to an external challenge. Secondly, the MACM approach can also be used to investigate what kinds of experiments yield co-activation between two regions allowing the establishment of a link between functional connectivity and particular mental operations. In contrast, as MACM analyses are based on task-related neural activity, spontaneous networks related to self-initiated behavior and thought will be largely missed in MACM analyses.

Hence, a comprehensive assessment of the functional connectivity patterns of a particular seed region may consist of performing a meta-analysis identifying significant co-activation in all experiments activating that seed region (MACM) as well as identifying all voxels in the brain whose time-series in a task-free state (resting state) show significant correlation with the reference time-course extracted from that seed. In a comparison of both functional connectivity maps, two situations may arise. First, regions are congruently implicated as functionally connected with the seed in both analyses. Such convergent evidence across fundamentally different states (presence or absence of a preset task) may be regarded as a very strong indication of a functional coupling with the seed. Second, strong but non-matching evidence obtained from both analyses, however, may relate to the fundamental differences between two states. It is well conceivable that a seed region of interest interacts with a particular set of areas (related, e.g., to planning and internal goals) during spontaneous, self-initiated mental operations and with other distinct set areas (related, e.g., to sensory processing) during the performance of an externally presented task. Both convergence and divergence of results may hence contribute to our understanding of functionally connected networks in the brain. While there has been little to no research along these lines, the prospect of differentiating internally and externally driven functional connectivity networks by such a comparison may hold an important potential for understanding the physiology of the two main states of brain function, reaction to the external world and reflection on our inner states.

Relation to regional specialization

In contrast to the assessment of anatomical connectivity, which is closely related to the regional differentiation of brain (micro-) structure, functional connectivity is conceptually much closer related to the regional specialization of brain function. As noted above, there is growing consensus that functional connectivity in the task-free state reflects, similar to task-based functional connectivity, the degree to which different brain regions are involved in the same functional networks. The role of a particular network is evidently to fulfill a particular mental function. However, conjoint contribution to a particular function does not imply that different regions within the respective network feature similar functional specializations but also sustain different computational processes that need to interact for task performance. Nevertheless, if two areas show a highly similar profile of “network-participation” we may thus assume that the functional specialization realized in these modules are closely linked to each other indicating that the computational processes sustained by these modules are often used together. Regions that are obtained from a conjunction analysis over “resting state” correlations and MACM co-activations may thus be regarded as robustly connected with the seed due to the incorporation in similar networks and the engagement by, potentially, the same mental operations. This approach thus allows delineation of functional specialization in the brain based on the location of significantly coupled regions. This perspective is much sharpened, if multiple seed regions are employed. Hereby the triangulation of brain networks may allow a detailed mapping of regional specialization in other parts of the brain. Especially when we have a good notion about the seeds and their respective roles, this opens the perspective to connectivity based mapping allowing identification of brain regions not based on activation in a specific task or their structural properties but on their connectivity with a set of seed regions. Functional connectivity may also be assessed for cortical modules or areas as defined by functional or structural criteria. In this case, a histologically defined cortical area or the region activated by a particular functional task would represent the seed for the functional connectivity analysis. By delineating distant brain regions showing task-free and task-based functional connectivity with this module, one may then describe the network which interacts most closely with that particular region. In the case of a functionally defined seed area, such an approach enables the generalization of inference beyond the current task-set. That is, while a particular experiment may show that right area 44 is activated in the same contrast as, e.g., the bilateral intraparietal sulcus and the dorsolateral prefrontal cortex, functional connectivity analyses may test whether this association is consistently expressed over many tasks (MACM) or whether it is also present in the task-free, i.e., self-reflexive state. Functional connectivity analyses seeding from a histologically defined region of interest may already provide, albeit indirect, evidence for its functional role by delineating those regions of the brain which interact with the area in question. This inference is considerably strengthened by assessing the functional properties of experiments that activate the particular area in a large database. Hereby it becomes possible to draw conclusions about the functional role and network-interactions of a purely structurally defined regional specialization.

What can we learn from functional connectivity?

The fact that functional connectivity analyses are fundamentally correlative in nature represents both their major strength and mostly severe drawback. As outlined from the opposite perspective in the discussion on anatomical connectivity, a correlation between the neuroimaging signals on any scale may arise not only from direct interaction but may be induced by a third area or mediated via relays and loops. Moreover, given the absence of a specific model on the nature of the interactions, functional connectivity analyses tend to be susceptible to confounding factors such as global signal changes and physiological artifacts in task-free analyses, or activation corresponding to task-elements generic to most imaging experiments such as remembering the instruction and paying attention in MACM. The fact that functional connectivity analysis does not depend on a specific model of interactions but describes the strength of coupling, i.e., the similarity in network participation between regions, however, also represents a major advantage. Being a hypothesis-free approach, minimal assumptions have to enter into functional connectivity analyses rendering them largely unbiased in the mapping of interacting networks. Functional connectivity studies, however, do not allow any inference on the causal nature, context-dependency or directionality of the respective interactions.

EFFECTIVE CONNECTIVITY

One concept, many approaches

Effective connectivity in the brain is defined as the causal influence one area exerts over another.² In contrast to measures of anatomical connectivity aiming at identifying fiber pathways or functional connectivity analyses identifying coupled networks by correlated signal changes, effective connectivity analyses thus strive to understand how different brain regions affect another. Importantly, effective connectivity measurements are based on explicit models, how influences between brain regions are mediated. Model parameters are then fitted using the measured fMRI (or electrophysiological) signal.

In spite of the considerable differences between methods and concepts for effective connectivity modeling, all approaches allow inference on directed influences. This has led to the common custom of representing effective connectivity analyses as directed graphs, where nodes represent the individual brain regions that were either included in the analysis or inferred from it. ^56,76 The directed edges of the graph then express the causal influences of one region on another, i.e., effective connectivity. The dependency on an explicit model of interactions between areas is the major advantage of effective connectivity analyses. Since models reflect hypotheses about functional integration in the brain, the comparison of different models allows the comparison of competing hypotheses. Models of effective connectivity are thus hypothesis-driven investigations of how data are propagated and processed in and between different areas of the brain. However, the reliance on the explicit and implicit assumptions going into a particular model and its parameter estimation scheme has also been voiced as the most fundamental limitation of effective connectivity modeling. In particular, while model-and hypothesis-based analyses enable a mechanistic assessment of interaction processes, any inference drawn from these analyses crucially depends on the validity of the modeling assumptions.

Above this fundamental commonality to all approaches for assessing effective connectivity, there are also major lines of conceptual and practical distinctions between them. Some methods such as psycho-physiological interactions (PPI) or Granger Causality Mapping (GCM) enable spatial inference.^77,78 That is, given a particular seed region or a set of seed regions, regions showing effective connectivity with these, either by influencing the seed or being influenced by it, may be delineated. Other approaches, for example Dynamic Causal Modeling (DCM) or Structural Equation Modeling (SEM) do not aim at localizing effects but also model the interactions within a pre-defined network or regions.^51,79,80 Models of effective connectivity also differ in whether external perturbations of a system are explicitly incorporated in a model, assumed to be stochastic or in equilibrium. Examples for the former would be PPIs and DCM, the probably prime example for the latter is SEM. Finally, modeling schemes may also differ with respect to the level of hemodynamic modeling involved.^81-83 All of the approaches discussed here estimate effective connectivity from fMRI time series, which presents a challenge to the estimation of effective connectivity, since fMRI measurements do not reflect any neuronal signal directly but clearly after its convolution with a hemodynamic response function (HRF).⁸⁴ Evidently, interactions in the brain should be expressed at the neuronal level instead of at the (measureable) level of hemodynamic responses. Consequently, there is a growing consensus that models of neuronal interactions, i.e., effective connectivity, should be based on a constrained approximation or inference of neuronal responses based on the measured time-series instead of on the hemodynamic observation.⁸³

Psycho-physiological interactions

Analyses of effective connectivity via psycho-physiological interactions (PPI)⁷⁷ are conceptually closely related to functional connectivity analyses, in particular task-based correlations with a seed-region. An important assumption underlying PPI is that if activity in one brain area is regressed on the time series of another area, the slope of this regression should reflect the dependency of the first area on the second, i.e., the influence of the latter on the former. Functional connectivity analyses in turn usually assess correlation between two time-series as a bidirectional estimate of coupling but follow the same concept. What makes PPI a measure of effective connectivity? The basic distinction of PPI from functional connectivity analyses is that it addresses contextual modulations of these influences. PPI analyses are conditioned on at least two distinct mental states being present in an experiment. The slope obtained from regressing the activity measured in the first area on the activity measured in the second area is then compared between the images obtained under the different psychological contexts. Any change in slope, i.e., any change in the influence that the second area exerts over the first within the experimental context represents a PPI. Importantly, locations where the PPI becomes significant may actually be interpreted twofold. Either the effective influence (connectivity) of the seed region to this particular area of the brain is modulated by the experimental manipulation. Or the response of that particular region to the experimental manipulation is modulated by the influence (connectivity) of the seed. That is, either term may be ascribed the role of the effector and modulator, respectively. While there is no statistical approach to disentangle this ambiguity, it has to be remembered that both main effects are also specified in the design-matrix as confound regressors and can therefore be used to identify the relationship of the interaction with the respective main effects.

In practice, PPI analysis does not require performance of separate regression analyses. The explanatory variable used to predict the activation time-series in any other location of the brain is given by the interaction-effect (point-wise multiplication) between a standard experimental design regressor (presence / absence of a particular context or stimulus) and the response time-series from another part of the brain (the seed). In this context, however, it needs to be remembered, that interactions in the brain should be expressed at the neuronal level, and not at the level of hemodynamic responses which are slow and regionally variable.^51,83 This constraint to effective connectivity analyses implicates that the simple interaction between a psychological factor and a delayed hemodynamic response does not precisely reflect the object of inference. It has been suggested to first de-convolve the time-series of the seed region, hereby estimating its neuronal states.^85,86 The interaction term between the de-convolved physiological regressor and the psychological factor is then again convolved with a canonical hemodynamic response function to represent a more faithful predictor of a PPI effect. The observed signal time-series in each voxel of the brain is regressed on this interaction term as well as on the physiological (time-series of the seed) and psychological (experimental context) time-series used as confound regressors. Inclusion of these latter regressors of no interest is crucial to remove the main effects of either factor from the variance explained by the PPI regressor and thus remove confounding, e.g., stimulus-locked effects. This general linear model, testing for the presence of a differential influence from the seed region, is applied to every voxel in the brain. Hence, the PPI approach can be used in an exploratory fashion enabling inference on regional specialization based on differences in context-specific functional integration. This is an important difference to other network-based models of effective connectivity and renders PPI analyses again close to context-dependent functional connectivity models. However, as only pair-wise interactions between the seed region and all other voxels are considered, PPIs have limited capacity to represent complex neural systems.⁸⁰

Granger Causality Mapping

Granger causality mapping (GCM) is another exploratory approach for assessing effective connectivity.⁷⁸ It was originally developed in the field of econometrics for the analysis of directed dependencies in time-series data.⁸⁷ The application of GCM in the context of effective connectivity analyses taps into what many would describe as our common-sense description of causality, i.e., temporal precedence. Simply speaking, any effect that is present in structured time-series data may only be explained by the history of that time-series, not by other observations made at the same time or even the future. That means that if region X has an influence on the activity in region Y, region X has to activate earlier than Y. On the other hand, however, if these two brain regions would activate at the same time, fulfilling the definition of functional connectivity, then the common cause must lie in the past. Examples for such earlier causes may be activity in a third area driving both areas. Apart from temporal precedence, the second fundamental assumption in GCM is predictability. Together, precedence and predictability define what has been termed “Granger causal” or g-causal as follows: If there is a causal influence of one area on a second, then knowledge of the time-series history of the first region should improve the prediction of further values of the latter.⁷⁸ This means that effective connectivity is assumed when the current value of the target area is better predicted by the past values of this area as well as the ones from the seed area as compared to using only the past values of the target area itself. Given this asymmetrical definition it becomes evident that GCM enables delineation of the directionality in the interaction of two regions. If the activation history of region X helps to predict the current values of Y but not vice versa, X has an influence on Y. Conversely, if Y helps to predict X but not the other way around, Y has an influence on X. What, however, happens if both past time series help predicting each other? One of the most discussed aspects of GCM is the fundamental assumption that fMRI data contains enough temporal information to enable a delineation of directed influences in a data-driven fashion based only on temporal precedence in the measured BOLD data. It has been argued, that due to physiological variations in the hemodynamic response function, scanner noise, and most importantly sparse sampling, i.e., limited temporal resolution, many short-lagged influences may remain unresolved.^83,88,89 These would then get absorbed in an instantaneous influence term, which essentially describes the correlations within the two time-series. While such instantaneous influences, under steady state assumptions, are elementary to SEM as discussed below, they are usually not of specific interest in GCM analyses. Notably, however, these instantaneous influences, which may not be attributed to any directed influence at the given temporal resolution, confine precisely with the notion of functional connectivity as discussed in the previous section. GCM may thus be regarded as a temporal expansion of functional connectivity analyses that uses temporal precedence in the time-series to ascribe directionality to functional interactions.

GCM is usually applied as a seed-region based analysis of every other voxel in the brain. Similar to seed correlations or PPI analyses, a particular location in the brain is chosen as the reference region, whose effective connectivity is of interest. A vector autoregressive model is then fitted at each voxel of the brain, assessing the degree to which prior information from the reference region improve predictability of the current target voxel and vice versa.⁷⁸ In contrast to PPI analyses, which are only concerned with the influence of the seed on the rest of the brain, GCM thus enables delineation of regions influenced by the seeds as well as those regions that in turn influence the seed region. It must be noted though that direct and directed influences may only be inferred in a situation where the seed or reference region and the current target, or more general any two areas of the brain, may be regarded as the only relevant sources of influence. Indirect influence, e.g., mediated by a third region that drives both the reference region and the current target voxel, will wrongly appear as direct influence unless their time series is likewise added to the model. Given the observation, that at any given time a large number of regions in the brain is concurrently active (since most brain networks are composed of multiple areas) the assumption of “exclusive” influences may evidently be rarely upheld. In most cases regions of confounding influences are usually not known a priori, although in cases were a strong hypothesis on a particular confound exists it may be added. Since on the other hand inclusion of all other regions in the brain is computationally difficult, a possible solution to overcome this problem is to compute an influence difference term.⁷⁸ This influence difference term is given by the difference of the estimated influence of the reference region on the current target and vice versa, thereby mapping of influence to and from the reference region over the brain.

Similar to PPI analyses, GCM may also be used to test for context-dependent differences in the effective connectivity between conditions. Unlike the situation in PPI, where the interaction is computed from a single time-series, however, GCM difference analyses are based on two separate functional imaging time series obtained under different conditions. Influences to and from the reference region are then delineated based on the time-series obtained for each condition and contrasted with each other. Such contrast analysis has been advocated as a remedy for the most crucial problem associated with the application of GCM to fMRI data, namely the inter-regional variability of the hemodynamic response function.^83,88 It is easily conceivable that in a scenario of two perfectly synchronous neuronal responses GCM on the BOLD time-series would indicate strong directed influences if one area would show a more sluggish, i.e., later hemodynamic response. That is, the key caveat in analyses of an indirect signal that are based on temporal precedence is that differences in hemodynamic latencies may be misinterpreted as effective connectivity.

Structural equation models

Structural Equation Models (SEM) also have a long tradition in the fields of econometrics and social sciences and were introduced in the field of effective connectivity analysis of neuroimaging data (initially PET) in the early 1990s.^79,81,90 The basic idea behind SEM is to model the interactions within a pre-defined set of areas based on an a priori hypothesis about their interactions. These interactions are specified as directed connections in the model that represent the causal relationship between the examined areas. The model is tested against the data obtained in fMRI time-series or PET scans from individual subjects. The model parameters, i.e., path coefficients representing connection strengths, are then optimized such as the discrepancy between the covariance-structure of the measured data and that implied by the model is minimal. In this context, three aspects deserve special attention when SEM is applied to fMRI rather than, as originally proposed, PET data. SEM path coefficients reflect instantaneous correlations between measured variables. On one hand, this requires the temporal dynamics in the system to be negligible and the system to be in equilibrium. These assumptions certainly met the case in PET images which are usually acquired over the course of several minutes while the subjects are constantly engaged in a particular task, but are more difficult to ascertain in fMRI time-series. On the other hand, the model parameters are fitted to represent the covariance structure of the measured (hemodynamic or metabolic) data, not the underlying neuronal activity. SEM thus has to rely on the tenuous assumption that the mapping from neuronal to measured activity is invariant across areas. Finally, SEM does not allow the direct modeling of modulatory effects of experimental manipulations on effective connectivity. If separate imaging datasets are obtained for the different conditions, as in PET, this problem is easily circumvented by fitting separate SEMs to the data obtained under the various conditions and inferring changes in effective connectivity from the differences between the obtained path coefficients. In the case of a single time-series in which measurements pertaining to a particular condition are not clearly separable but part of the same time-series, however, inference on context-dependent effective connectivity may be limited.

A drawback that is shared between SEM and all other network-based analyses of effective connectivity is the strong reliance on a priori assumptions. Model-based confirmatory analyses have major advantages over exploratory strategies, as they represent an approach to explicitly test hypotheses about interactions in neuronal systems. They may, however, give rise to potential biases in effective connectivity modeling. Given the large number of areas commonly engaged in a particular mental process, testing for all possible models of how these may interact by separate models is rarely a viable option (if there was only a binary choice of modeling a connection or not, the number of possible models grows as an exponential of 2 with the number of theoretical connections, which in turn raise as a second-order power of the number of regions). In most cases, even including all regions that may participate in this particular function may exceed the model capacity. Virtually all applied models must hence be constrained by specific hypotheses about the underlying network architecture. This aspect is crucial for the validity of the subsequent inference. Typically, assumptions are based on anatomical connectivity information obtained in non-human primates, observations or hypotheses on the physiological “function” of an area from previous neuroimaging experiments or functional connectivity analyses. Furthermore, Bayesian approaches allow for testing multiple network models against each other in order to identify the optimal model structure. However, even prior information and model selection cannot completely alleviate the problem of experimenter-induced bias in a network model. This leads to the uncomfortable situation that on one hand hypothesis-based modeling is highly needed in a field still dominated by exploratory analyses. On the other hand, the motivation for (not) including a particular area or connection into the assessed model space may always be questioned as deteriorating the validity of the entire model.

Dynamic causal modeling

In contrast to SEM or GCM, which are rooted in non-brain imaging applications, dynamic causal modeling (DCM) represents an approach to effective connectivity modeling that has been specifically designed for the analysis of fMRI time-series.⁵¹ The idea behind DCM is to consider the brain as a nonlinear dynamic system in which external perturbations (inputs) cause changes in neuronal activity or inter-regional coupling strength, i.e., connectivity (Figure 4). The ensuing changes in neuronal activity states in turn cause changes in the blood oxygen level-dependent (BOLD) signal observable with fMRI. Importantly, the hidden neuronal dynamics (neuronal states) are driven by the experimental inputs (sensory stimulation or contextual influences such as task settings). These neuronal dynamics then give rise to externally assessable outputs such as BOLD signal changes which are explicitly modeled in DCM by a set of differential equations. The effective connectivity within the assessed dynamic system is thus expressed in terms of coupling between unobservable brain states (e.g., the modeled neuronal activity in the different regions comprised in the model), and being inferred directly from the measured time-series data. The modeled neuronal dynamics are then linked to the observable changes in the BOLD response via a biophysically validated hemodynamic forward model translating neuronal states into predicted measurements.⁵¹ In DCM, effective connectivity within a given brain network is inferred from the coupling parameters computed for the hidden neuronal states. Estimation of these in turn is based on perturbing the system through experimental manipulation, e.g., by engaging the subjects with different tasks while measuring the evoked effects on the BOLD time-series of the regions included in the model. The parameters of the model that best translate the input functions based on the experimental design into the measured time-series may be estimated by Bayesian inversion. The aspect of perturbation is especially important in the classical formulation of DCM,⁵¹ as here the modeled neuronal network is considered completely deterministic and only driven by external inputs. Without such driving input, however, the system would stay and remain at rest. More recent developments, however, have added stochastic behaviour and may thus alleviate the strong dependency of DCM analyses on the experimental manipulation and the assumption that neural population dynamics may be correctly captured from the modeled inputs.⁹¹ In spite of these revisions, the mainstay of DCM analyses is still the modeling of task-specific contextual influences aiming at an interpretation of functional neuroimaging data in terms of the underlying connectivity patterns. DCM may thus be seen primarily as a tool providing an additional layer of insight into the causes of regionally specific activation patterns rather than revealing information about functional connectivity patterns that go beyond the particular experiment. In other words, stemming from general systems theory, DCM represents the most confirmative modeling approach currently available for effective connectivity modeling in healthy subjects and patients suffering from neurological or psychiatric disease.^{81,85,86,92,93}

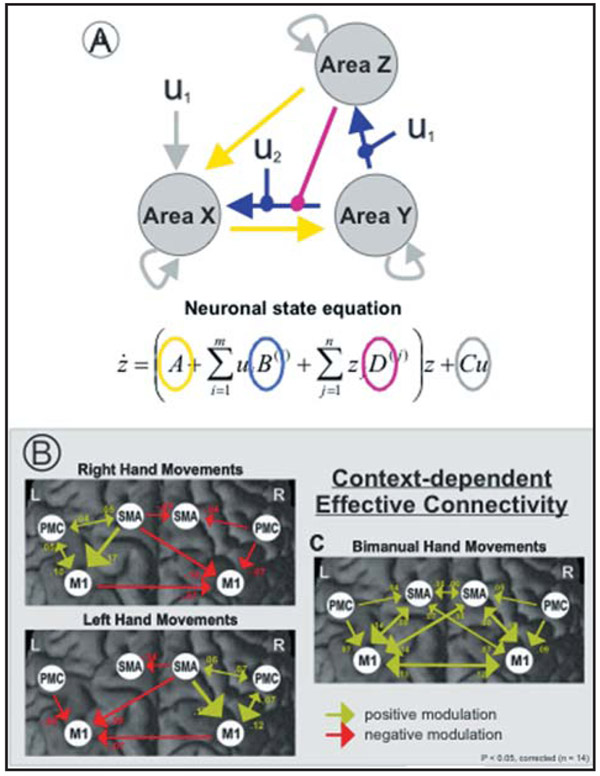
Figure 4.

Effective connectivity as established with dynamic causal modeling (DCM). (A) Simplified network model of three interacting regions (Area X, Y, Z) receiving context-independent (yellow arrows), context-dependent (blue arrows) and nonlinear (purple arrows) inputs. Direct influences of an experimental condition (i.e., u1) on activity (e.g., of area X) are coded with grey arrows. (B) Context-dependent connectivity (DCM B-matrix) within key areas of the motor system for rhythmic fist closures performed with the right hand (upper left panel), left hand (lower left panel), and with both hands in-phase (right panel). Coupling parameters (rate constants in 1/s [Hertz]) indicate connection strength, which is also coded in the size and color of the arrows representing effective connectivity. Positive (green) values refer to facilitation of neural activity. Negative (red) values denote inhibitory influences on neuronal activity. (Adopted from Grefkes et al. [2008],⁹⁸ with permissions).

Bayesian model inversion does not only provide estimates (posterior densities) for the model parameters, but also an approximation to the log evidence of the model for the observed data. This log evidence can be used to compare alternative DCMs of the same data, i.e., to decide between alternative hypotheses on the architecture of the neuronal interactions underlying an observed pattern of activation.^94,95 This formal approach to comparing different hypotheses on the model structure has been conceptualized as one of the major advantages of DCM over other approaches to effective connectivity.

At present, DCM is certainly the most specific and biologically informed tool for modeling neuronal networks. As outlined above, confirmatory models of connectivity like DCM strongly depend on a priori assumptions. This dependency on a priori assumptions spans several aspects of DCM analyses, starting with the definition of regions to be included in the model. Given the context-dependency regions going into the model should be based on task-specific effects. But there are usually many of these while DCM analyses are currently limited to eight regions for any given model due to computational constraints. The definition which areas among the set of activated regions are deemed crucial to the model may thus be a matter of conjecture. Moreover, although model selection may allow to identify the most likely model given the measured data, inference is evidently limited to the models included into the comparison which may only reflect a small proportion of the potential full model space. Finally, Bayesian inversion of the model and estimation of the neuronal and hemodynamic parameters is only feasible by constraining these estimates using priors on each parameter. For the neuronal interactions, these priors are (conservative) shrinkage priors.⁵¹ The hemodynamic priors reflect biological constraints on the nature of the BOLD response.⁹⁶ Evidently, all of these assumptions have considerable influence on the ensuing models of effective connectivity. As an example, given that hemodynamic priors are generally more relaxed than neuronal ones, a delayed influence may be absorbed by the former instead of being interpreted as effective connectivity. Consequently, DCM currently allows the most specific modeling of effective connectivity in neuronal systems but this specificity comes at the cost of a high dependency on prior information and assumptions going into the model.

The notion of causality

The fundamental definition of effective connectivity relates to the influence of one area over another.² Consequently, effective connectivity is commonly framed in terms of (implicit or explicit) causality, e.g., “area X inhibits area Y”. It is important to note, however, that strictly speaking true causality cannot be assessed by pure observation of a system from a theoretical point of view. To illustrate the point, when observing that the street is wet in the morning after hearing a storm at night, do we know that this was caused by rain (and not by a cleaner who drove by in the early morning or a malfunctioning sewer)? Inference on causality, if philosophically acceptable at all, requires the intervention and manipulation of a system. Thus, while all approaches to effective connectivity analysis evoke a notion of causality, these differ between the different analysis concepts.

In PPI, causality is understood as the contribution of another area to the local signal time-course and is thus inferred from dependencies revealed by context-dependent regression of a regional time-series on the activity in another brain region.

In GCM causality is framed as predictability and temporal precedence, and parameterized in an increased predictability of current activity in area X by adding information about the history of a distant area Y to the history of X. The distant area Y would hence have effective influences on X.

In SEM causal relationships are derived from the direction of the connections that are included in the fitted model. A directed connection between two areas hence equate to the assumption of a causal influence whose strength would be reflected in the estimated path coefficients.

In DCM, effects are deemed causal in the sense of control theory, describing how dynamics in one neuronal population cause dynamics in another and how such interactions are modulated by contextual manipulations.

Relation to regional specialization

Effective connectivity models may be separated into those that have localizing power by assessing the effective connectivity with a seed region in every voxel of the brain and into those representing network-based models of interactions within a predefined set of regions. The former (PPI, GCM) may be described as exploratory methods, the latter (SEM, DCM) as confirmatory, although this distinction is blurry given cross-validation and model selection procedures, respectively. Regarding their relationship with the fundamental concept of regional specialization in the brain, most that has been said for functional connectivity analyses also holds true for voxel-based effective connectivity models. Analyses such as PPI allow the identification of regionally specific effects. In contrast to functional neuroimaging or histological examinations, however, these effects are not referring to response properties or structural features. In other words, the property of interest, whose regional distribution and specificity is examined, relates to the (context-specific) influences of a distant area. Like functional connectivity analyses, PPI and GCM use connectivity to provide regionally specific properties (“where is something connected to the seed”), adding context-specificity to these (“and under which circumstances”).

On the other hand, graph-based approaches such as SEM and DCM have a very distinct relationship with analyses of regional specialization, as they are not aimed at identifying locations that show a particular effect. Their focus is to model interactions between a set of regions defined by other methods of structural or functional brain mapping. This renders network-based effective connectivity analyses highly complementary to studies on regional differentiation using, e.g., fMRI analyses of task-related activity. It should be noted that “complementary” does by no means imply independence. In virtually all cases, the networks in which effective connectivity is modeled as well as the task-specific effects representing the experimental perturbations to the system will be derived from a particular functional mapping study. Analysis on regional differentiation and functional integration is thus performed on the same dataset. From a more system-based perspective, functional mapping reveals the nodes, and effective connectivity modeling the edges of a brain network. Despite the potential influence of various priors and assumptions, effective connectivity models allow unrivaled insight into the processes and mechanisms of functional integration and may hence be a powerful complement to any analysis that identifies regionally specific effects.

What can we learn from effective connectivity?

The strength and drawbacks of effective connectivity modeling are largely the mirror reverses of those discussed for functional connectivity analyses. Certainly the major advantage of assessing effective connectivity is that it allows inference on the directed, context-specific influences between cortical areas. Models of effective connectivity thus represent an approach to mechanically understand the dynamics within brain networks. Evidently, the precise nature of transmitted information remains obscure, but context dependency of promoting or inhibitory influence often enables to ascribe more specific functional roles to a particular area as would have been possible from the pure observation of task specific activations. Thereby, effective connectivity analyses offer the opportunity to disentangle the relative contribution of areas conjointly activated in a particular task as well as to delineate the flow of information through a particular network.

There is, however, the implicit problem of potential misspecifications in the model. This is particularly relevant to confirmatory network-based approaches where, e.g., misguided choices of not including a particular region may compromise the validity of the entire model. Seed region based approaches also specify a particular model, e.g., by assuming that a particular region should show differential connectivity with other areas in the context of two experimental states. Most approaches additionally evoke choices on model parameters ranging from the order of a multivariate autoregression to a particular hemodynamic model.^80,89 On the deepest level, the various approaches available for modeling effective connectivity also differ in their concepts about brain dynamics. For example, DCM assumes that interactions between brain regions may be sufficiently described with bi-linear influences and time-invariant quadratic effects. In contrast, GCM is based on the belief that in spite of regionally variable hemodynamic low-pass filtering the originally neuronal signal interactions may be inferred from temporal precedence and predictability. Extensive simulation analyses have attempted to verify or challenge the assumptions of various effective connectivity analyses,⁸³ but it has to be remembered that simulations themselves are reflections of assumptions about some underlying truth.

SUMMARY AND OPEN QUESTIONS

Although far from exhaustive, we hope that this synopsis has provided an overview on the different concepts and approaches to study regional specialization and functional integration in the brain. As discussed above, there is no optimal tool or model for understanding the organization of the human brain.⁹⁷ Both regional specialization and integration may be expressed in many different facets. Regional specialization comprises microstructural and functional aspects, with the latter closely related to regionally specific differences in the interaction with other parts of the brain. Inter-regional integration, i.e., brain connectivity, may be described along various lines such as anatomical connections, participation of distant areas in the same networks during a task-based or task-free state and effective influences within these networks. While each approach has its particular strength and allows statements not possible by any other method, they all come with their particular associated drawbacks as well. Importantly, however, strengths and weaknesses of these different approaches to understand the human brain are often complementary to each other. For example, functional connectivity analyses may inform models of effective connectivity by pointing to important nodes in a network. Histologically defined areas of the brain may provide seed points for anatomical connectivity analyses using probabilistic tractography.

Using a modular and highly interconnected structure, our brain is able to fulfill the large array of cognitive, affective and sensory-motor capacities. Given this complexity, a deeper understanding of how the brain is organized thus calls for an integrated multi-modal and multimethod analysis of structure, function and connectivity. Such integration of information on different aspects of brain organization will without doubt enable more new insight into the neurobiological basis of mental capacities and disturbances thereof in the diseased brain.¹⁷

We would thus like to conclude this overview with a dozen questions all being located at the junction between methodological considerations and neurobiological challenges. This is in particular to point to the issue that conceptual knowledge of the organization of the human brain and an improved understanding of what the different methods actually reflect are closely linked to each other. In other words, understanding how different aspects of structure, function and connectivity relate to each other may actually guide us to the fundamental principles underlying human brain organization.

1. Do borders of microstructure and anatomical connectivity patterns coincide? Or do intersecting mosaics represent the constraints on functional specialization?

2. Are structural features such as histology and anatomical connectivity patterns sufficient for functional specialization or may functional differentiation exist if these are homogeneous?

3. Which are the modules of brain function that form the unit of functional specialization? And how do they relate to our concepts of mental functions or psychological ontology?

4. What is the explanation of the involvement of some regions in many different tasks? If connectivity, what is the explanation of the presence of similar networks in many different tasks then?

5. Is there a difference between functional specialization in task-based fMRI and specialization of functional or effective connectivity patterns assessed by seed-voxel based methods?

6. To what degree are functional connectivity patterns in a task-free “resting” state a reflection of anatomical connectivity? To what degree are they a reflection of functional specialization?

7. How does one quantify connection strength in exploratory seed-based analyses of anatomical and functional connectivity in a way that is comparable across methods?

8. Do task-based and task-free functional connectivity correspond to each other? Are differences only a reflection of the different “tasks” engaged in during experiments or free thought?

9. Can anatomical and functional connectivity inform and hence improve effective connectivity models? If not, are we missing or messing information?

10. Could a combination of different exploratory approaches to functional and effective connectivity analyses render them confirmatory?

11. How do results from different approaches towards effective connectivity analyses relate to each other under the same context?

12. Which information on structure, function and connectivity are actually congruent and may be used for cross-validation? If none, how much overlap is there to drive converging evidence?