Pangenome graphs

Abstract

Low-cost whole genome assembly has enabled the collection of haplotype-resolved pangenomes for numerous organisms. In turn, this technological change is encouraging the development of methods that can precisely address the sequence and variation described in large collections of related genomes. These approaches often use graphical models of the pangenome to support algorithms for sequence alignment, visualization, functional genomics, and association studies. The additional information provided to these methods by the pangenome allows them to achieve superior performance on a variety of bioinformatic tasks, including read alignment, variant calling, and genotyping. Pangenome graphs stand to become a ubiquitous tool in genomics. Although it is unclear if they will replace linear reference genomes, their ability to harmoniously relate multiple sequence and coordinate systems will make them useful irrespective of which pangenomic models become most common in the future.

1. Introduction

A pangenome models the full set of genomic elements in a given species or clade. Pangenomics thus stands in contrast to reference-based genomic approaches which relate sequences to a particular consensus model of the genome (figure 1). Genomes that are reconstructed with the aid of a reference genome can appear more similar to the reference than they actually are. Pangenomic reference systems can reduce this bias by enabling the direct relationship of new genome to all those represented in the pangenome.

Figure 1:

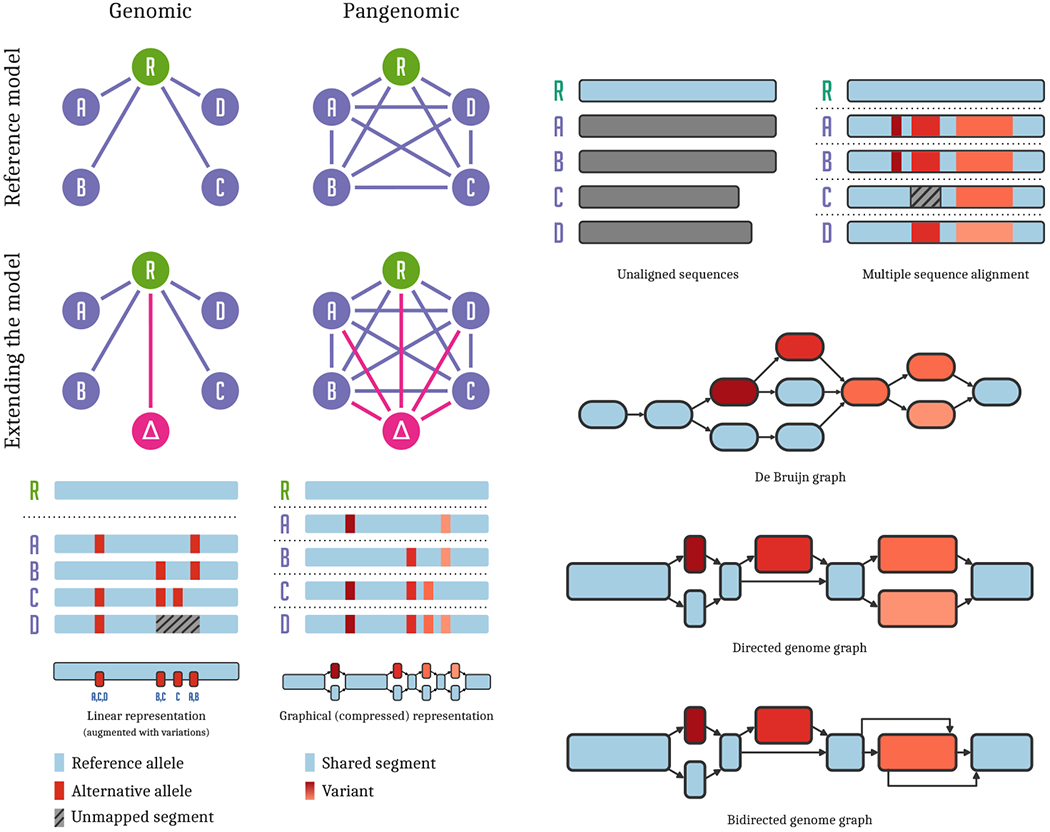
Pangenomic models. Left panel: top left: In reference based genomic analyses, all genomes (A…D) are compared to each other via their relationship to the reference genome R. top right: In a pangenomic setting, we attempt to model direct relationships between all the genomes in our analysis, of which a particular reference R is chosen arbitrarily. middle left: When extending our analysis with a new genome, Δ, we add it to the genomic model by comparing it to reference R. middle right: In contrast, adding a new genome to a pangenomic analysis compares it directly with all other genomes in the model. bottom left: Regions of some genomes are unalignable against the reference, and cannot be represented in a list of variants. bottom right: A graphical model of the genomes allows direct all-to-all comparison, capturing all of their sequence relationships. Right panel: top left: A collection of sequences representing a pangenome. top right: Multiple sequence alignment of the sequences captures their mutual relationships. middle top: In a de Bruijn graph, sequences are represented without bias, but variants may correspond to larger graph structures. middle bottom: An acyclic sequence graph is equivalent to the multiple sequence alignment. bottom: A generic sequence graph can represent a structural variant (in orange, right) compactly, using edges between the forward and reverse strands of the graph to indicate the presence of an inversion.

Pangenomics has been important to microbiology, where genomic plasticity and diversity has made it indispensable (141), and it has increasingly seen application to eukaryotic genomes (22, 46, 107). Standard pangenomic analyses focus on the presence or absence of genes from given strains and the determination of a core (commonly present) and accessory (frequently absent) pangenome (108). However, they have tended to pay less attention to variation between these sequences, and they do not typically attempt to provide a precise model relating many genomes to each other at the base level.

In contrast, most “high-throughput” analyses of large genomes depend on comparison to a single reference genome. However, in recent years, reduced sequencing and de novo assembly costs have supported the discovery of significant levels of large-scale genomic variation in many eukaryotic species, including humans (135, 58, 24, 8), arabidopsis (3), brewer’s yeast (145), and the fruit fly (25). These observations have generated wide interest in extending bioinformatic operations to use a pangenomic reference model (32). The availability of true pangenomic references for humans (28) and other model organisms will increasingly render the use of a single reference genome suboptimal. However, using pangenomes effectively requires the development of new bioinformatic methods capable of constructing, querying, and operating on them.

In this review, we consider an emerging class of bioinformatic methods that let us consider genetic diversity at every stage of analysis. We focus primarily on those methods which achieve this result by replacing linear reference genome system with a graphical, pangenomic one. To provide background, we first consider how limitations of the current dominant genome inference paradigm motivate these methods (§2). Then, we describe pangenomic models, with a particular focus on graphical ones (§3). This provides a foundation to understand how they can be constructed from sequencing data or assembled genomes (§4). We then survey index data structures that allow us to interact with them efficiently (§5). These index structures allow us to interrogate, visualize, and relate new information to pangenomes, such as in the process of read alignment (§6), yielding results in a variety of new data formats (§7). Finally, we examine a number of downstream applications of these models (§8), and reflect on the future impact of these methods on genomics (§9).

2. Resequencing reconsidered

Biological research frequently depends on our ability to infer the sequence level relationships between genomes. In an earlier era, when many sequencing studies focused on small regions or single genes, it was often feasible to relate all relevant sequences to each other. Although limited in scope, these analyses were effectively pangenomic. They were based on many-to-many relationships between sequences, typically derived by multiple sequence alignment (MSA). Precise MSA methods are expensive, with popular algorithms scaling cubically with the number of input sequences (103). It is infeasible to apply such computationally demanding methods to the data scales obtained with modern high-throughput sequencing. Instead, high-quality genome assemblies and high-throughput sequencing have encouraged resequencing methodologies, wherein reads from each sample are aligned to a single reference genome. This approach is practical and scalable. State of the art resequencing pipelines can jointly analyze tens of thousands of genomes (112) at a cost per genome that is only a small fraction of the total sequencing cost.

Although efficient and conceptually simple, resequencing has a significant limitation. Precise genomic relationships are only visible for those sequences that are similar enough to the reference genome to be alignable (figure 1). This effect is known as reference bias. It is strongest for structural variation or sequences that are absent from the reference system (135), but it can be relevant even for SNPs, which causes problems in allele specific expression (ASE) quantification (23) and in the analysis of ancient DNA (147). Given that this bias shapes the methods that we use to establish models of the truth (148), it is even difficult to evaluate without paradigmatic change in our analysis techniques.

Estimates based on short read sequencing data have placed the human pangenome at between 1% (85) and 10% (127) larger than the GRCh38 human reference assembly. Others have demonstrated up to several Mbp of sequence are present in each new individual and not in the reference (58, 8). We expect that whole genome telomere-to-telomere assemblies based on long single-molecule sequencing will provide greater insight into the extent, placement, and significance of these novel sequences (92, 77). Even if we know of their existence, the reference bias inherent in resequencing will continue to limit the ability of researchers to relate new sequences to these regions. Resequencing methods that use a pangenomic reference system should not be subject to this limitation.

3. Pangenomic models

A pangenomic model (figure 1) is a data structure that represents the genomic sequences of a population, a species, a clade, or even a metagenome (32). The model serves as a central coordinating entity to describe the collection of sequences and genomes in the pangenome. Pangenomic models may take many forms, including collections of unaligned sequences or learned sequence models, but here we will focus mostly on graphical ones.

3.1. Graphical models

The sequence graph serves to compress many redundant input sequences into a smaller data structure that is still representative of the full set (59). Sequence graphs may have their nodes or edges labeled with DNA sequences, but for simplicity we will focus on the node-labeled case. In a node-labeled sequence graph, edges indicate when concatenations of the nodes they connect occur in the sequences modeled by the graph. Walks through a sequence graph thus include the set of sequences from which it was built. We call them bidirected when they represent both strands of DNA and inversions between them. Sequence graphs were first used to represent multiple sequence alignments (59, 78). In assembly, they have been applied to represent the full information in a set of sequencing reads (as in the string graph) (98), or fixed-length k-mers (as in the de Bruijn graph (DBG)) (111).

Genome graphs are sequence graphs used to represent whole genome relationships (110). Walks through these graphs represent recombinations of the genomes included in the model. Regions of the graph where multiple paths connect a common head and tail node, often referred to as bubbles (109), represent variation. Variation graphs further structure this model by embedding the linear sequences of the pangenome as paths (51)¹. Paths provide a stable coordinate system that is unaffected by the manner in which the graph was built, thus supporting the coordination of positions, annotations, and alignments between variation graphs and linear reference genomes.

4. Building a pangenome

Methods to construct pangenomic data structures mirror the classes of pangenomic models. A pangenome may simply be a collection of sequences, in which case construction is similar to the genome or metagenome assembly problem. Or, it may include information about the alignment of sequences or genomes within it. This alignment could be compressed into a set of variants found against a set of reference sequences. If this alignment is based on k-mers, then it implies a de Bruijn graph. If it is a complete, gapped alignment, covering small and large variation, then the pangenome model can be thought of as a whole genome alignment.

4.1. Collecting sequences

A pangenome can be represented as a collection of sequences. Several approaches support the construction, annotation, and interrogation of these pangenomic sequence collections. Panseq (76) finds novel regions, determines the core and accessory genome, finds SNPs within the core pangenome, and then determines a subset of loci useful for molecular fingerprinting. PGAP (146) extends Panseq’s approach with modules for evolutionary and functional analysis, and is implemented as a single standalone executable. Recent work has focused on scaling these techniques to ever larger genomes. PanTools (126) detects and annotates homology groups in large collections of large genomes using a k-mer based approach. Its detailed graph database model connects the panproteome defined by homology groups to genomic annotations and sequences. HUPAN (38) extends the sequence collection model to human and large eukaryotic genomes, taking assembled genomes as input and finding non-reference sequences within them by comparison to a reference genome.

4.2. Adding variation

Rather than collecting unique sequences that represent a collection of genomes, we can consider small variants between the collection and a reference genome. Such a model directly implies a directed acyclic graph, ordered along the reference genome, with bubbles at the sites of variation. This pangenome construction approach is used in diverse graph genome read mappers, including GenomeMapper (125), Seven Bridges’ Graph Genome Pipeline, and (116), PanVC (140), and Gramtools (88). The variation graph toolkit, specifically VG construct (51), can be applied to transform VCF files and reference sequences into genome graphs. Some methods, like the journaled string tree (115), and methods based on elastic degenerate texts (12) such as SOPanG (29), transform the variant set and reference into a structure optimized for online sequence queries of the pangenome. Deciding which variation should be added to a graph is non-trivial, and has encouraged studies of graph utility (105) and algorithms to determine which variation is helpful (113).

4.3. Colored, linked, and compacted de Bruijn graphs

De Bruijn graph-based assemblers can be given a pangenomic quality through the addition of “colors” to their nodes (k-mers) or unitigs (unbranching components in the graph). Each color provides a mapping between a specific biosample and a subset of the graph. Cortex first demonstrated that colored DBGs could perform population scale analyses with an efficient graph implementation (66). Recent improvements to colored DBG construction, such as Bifrost (63), allow the construction of colored DBGs from very large sequence sets (the authors build a pangenome of 118,000 Salmonella genomes), and further support efficient updates of these pangenomic models. The feature which makes these methods efficient, the fixed k on which they are based, also limits their resolution of repetitive genomic features. It is not feasible to build them from noisy third-generation sequencing reads. Addressing these limitations, several methods embed linking information within the DBG that can be used to reconstruct embedded haplotypes or reads (15, 138).

A number of methods use compacted DBG² construction to elaborate pangenome graphs. SplitMEM (90) uses a suffix tree with suffix skips to derive the set of maximal exact matches ≥ k between a set of genomes. Improving on this result in both time and space efficiency, (11) demonstrated two similar pangenome graph induction algorithms based on succinct representations of the suffix tree and the Burrows–Wheeler transform (BWT) (20). TwoPaCo (95) applies a probabilistic data structure to narrow the set of candidate vertexes in the compacted de Bruijn graph of a set of genomes, supporting the efficient generation of a pangenome graph from larger genomes than previous methods.

4.4. Alignment-based sequence graphs

Sequence graphs (59) can be understood as representations of the mutual alignment of a set of sequences. Alignment-based pangenome structures form the basis of a number of pangenomic approaches. They have found use in the construction of acyclic multiple sequence alignments. The partial order aligner POA (78, 54) uses an acyclic, directed sequence graph model to build multiple sequence alignments. ProgressiveCactus (7) produces whole genome alignments that can be rendered as sequence graphs. SibeliaZ (94) finds collinear blocks within TwoPaCo’s compacted DBG and applies POA to each to yield a whole genome alignment graph. The multiple sequence/graph aligner (VG msga) (105, 51, 48) generalizes the progressive approach of POA to build generic variation graphs that include cycles and inversions.

Not all researchers have focused on generic graphs, with several arguing that completely generic models are either computationally intractable or not relevant to important practical analyses. REVEAL (86) builds a pangenome graph from a syntenic set of maximal exact unique matches of decreasing size between a pair of sequences (or graphs), and later adds inversions detected by alignment of paths through bubbles in this graph. NovoGraph (14) follows a reference-guided approach, breaking a set of genomes into syntenic alignable blocks and deriving a multiple sequence alignment for each, and yielding a VCF file as its output. Similarly, seq-seq-pan (69) employs existing whole genome alignment methods to find a set of locally collinear blocks, in which it compacts into a sequence graph that respects the synteny of the input genomes. GenGraph (4) realigns previously identified co-linear blocks yielding a genome graph from an MSA.

Recent, unpublished methods explore two new alternatives to alignment-based pangenome construction. minigraph³ extends the minimap2 (84) alignment chaining model to work on graphs. It applies this alignment model to progressively build out a pangenome graph from a series of genomes that contains large (>250bp) sequences that were not previously seen in other genomes. The resulting pangenome does not contain all input sequences and variation between them, but a representative subset and large structural variants. In contrast, seqwish⁴ (48) generates the full variation graph implied by a collection of sequences and alignments between them. The paths embedded in its output graph precisely and completely reconstruct the input sequences, while the topology of the graph describes all variants represented in the input alignments.

4.5. Positional systems in pangenomes

Reference genome sequences provide a coordinate system to catalog and exchange information about genes, protein binding sites, epigenetic profiles, variants, and homologies. In linear references, genomic coordinates are easily interpretable, and they unambiguously indicate both the layout of the sequence and the distance between bases, but this is not the case when these coordinates are embedded within a graph (117).

It is possible to use reference coordinates in a graphical pangenome by embedding reference sequences inside the graph and labeling graph nodes with their relative positions in these paths (51, 48). This has been extensively explored in variation graph based tools. However, several problems remain. The embedded coordinate systems may be incomplete, in that they may not fully cover the graph. Also, particular graph instantiations may induce ambiguity in reference positions. For instance, a copy number variant that is collapsed in the graph will contain multiple overlapping reference path coordinate ranges.

These limitations have driven the development of complete coordinate systems for genome graphs. One solution is to build a hierarchy of graph components, based on a starting reference sequence, adding a new name and coordinate range for each non-reference sequence that is included (117)⁵. Another technique is to build positional systems based solely on the topology in the graph (109). Genomic variation creates a system of nested bubble structures that can be used to spatially organize graph elements. This approach has a rigorous, if complex, mathematical basis. Similar decompositions of the graph topology have been used in assembly-based variant detection (66, 106).

5. Indexing pangenomes

Index data structures for pangenome graphs support efficient random access to elements and features of the graph. Attention must be given to ensure that these index structures do not require significant overheads relative to the information content of the graph. Naive implementations of sequence and structural indexes of the graph can incur significant runtime and memory costs, which can become problematic as graph sizes increase. Succinct data structures and careful encoding of these data are thus required to reliably fit large graphs into the main memory of commodity computing systems. Particular index models lie at the core of the highest-performing graph based visualization (§6.1), read mapping (§6.3), and variant calling systems (§8.1).

Building text indexes for sequences encoded in a graph is more involved than for linear references. In graphs with regions of dense variation, the number of k-bp paths can grow exponentially in k, often rendering their complete enumeration intractable even for low values of k. In order to limit the exponential growth, the index may only support relatively short query strings. Some indexes (132) support longer queries by doing extensive preprocessing. In others (137, 64, 88), queries mapping to complex graph regions can be slow. Instead of indexing the entire graph, the index may only contain k-mers from a simplified graph, or from specific paths of the graph.

5.1. Indexing sequences using a graph

The FM-index (42) is a text index, based on the Burrows-Wheeler transform (BWT) (20), that is frequently used with DNA sequences. One variant of the FM-index, the RLCSA (99), run-length encodes the BWT, allowing it to store and index a collection of similar sequences space-efficiently. If we know a good global alignment of the sequences, we can use that information to make the index both smaller and faster (65). This approach was developed further in the FM-index of alignment (101, 100). Both (65) and (101) use the graph induced by the alignment as a space-efficient representation of the sequences.

5.2. Indexing acyclic graphs

One class of graph indexing methods supports only acyclic graphs, often represented as directed acyclic graphs (DAGs). This constraint can exist either because the acyclicity of the graph provides guarantees that simplify the problem, or because incidental features of the method’s software implementation preclude use on cyclic graphs.

GenomeMapper (125), the first graph-based read aligner, was limited to such graphs. Its indexing was also relatively simple. GenomeMapper uses a simple hash-based k-mer index, with k ≤ 13 to limit memory usage.

GCSA (132) was the first attempt to generalize the BWT for graphs. It applies a number of graph transformations that preserve the graph’s sequence space while creating an unambiguous ordering for nodes. When the graph’s complexity is low, these transformations are reasonably fast and do not increase the size of the graph significantly. However, at a certain threshold of variant density the transformed graph quickly becomes too large to handle.

BWBBLE (64) is a BWT-based representation for VCF-based pangenome graphs. Simple substitutions are encoded in the sequence using IUPAC codes, and the sequence is indexed using a normal FM-index. Because each base can be encoded using 8 different characters, the search branches at every base to cover all possible characters which admit the base searched. In practice, most branches quickly run out of results and can be pruned from the search. BWBBLE represents insertions and deletions with extra sequences, including a given amount of context around the variant. The length of this context is an effective upper bound for query length.

The vBWT (88) took another approach to using the BWT for indexing VCF-based pangenome graphs. It encodes variants as (ref|alt1|alt2|…) in the sequence. When the search encounters a variant, it must branch to handle each allele separately. Both BWBBLE and vBWT trade faster index construction for slower queries. However, a combination of IUPAC codes for substitutions, the vBWT approach for other variants, and a k-mer index for matching the first 5–10 bases, is faster than either of the originals (21).

5.3. General graphs

Some text indexes are based on Lempel–Ziv parsing or context-free grammars. These indexes first find partial matches between the query string and the indexed phrases and then combine the partial matches into full matches using two-dimensional range queries. In the hypertext index (137), each node is a separate phrase. Queries mapping to a single node or crossing a single edge can be matched efficiently, while finding mappings to complex graph regions can be slow.

Techniques similar to the GCSA can be used to represent de Bruijn graphs (16). If the graph transformations used in GCSA construction are stopped after i steps, the resulting graph is equivalent to an order-2ⁱ de Bruijn graph. This de Bruijn graph can be used to approximate the original graph. Queries of this index yield no false negatives, but matches longer than 2ⁱ may be false positives. By using this approach, GCSA2 (130) attempts to support fast queries in arbitrary graphs.

GCSA2 faces the same issues with complex graphs as GCSA. In practice, most graphs must be simplified before they can be indexed. Typical simplifications include removing high-degree nodes and complex regions from the graph and replacing them with the reference sequence. If a collection of haplotypes is available, the removed regions can be replaced with new subgraphs that contain separate paths for each distinct local haplotype (131). This way, the index contains all k-mers from the haplotypes, while usually missing some k-mers from their recombinations.

5.4. Indexing graphs using sequences

Instead of attempting to index the entire graph, it is often sufficient to index only selected paths in it. CHOP (96) takes the paths corresponding to haplotypes and breaks them into smaller pieces. The distinct pieces form an artificial linear reference, which can be used with any read aligner. The process guarantees that any substring of the haplotypes of length k is also a substring of one of the pieces. As with BWBBLE, k represents an effective upper bound for query length.

The PSI (52) follows a similar approach with artificial paths. Instead of using haplotypes, PSI uses a greedy algorithm to find a set of paths that covers as many k bp windows in the graph as possible. When a fully sensitive index is needed, PSI can reverse the role of the query strings and the graph. While complex graph regions may contain an excessive number of k-mers, the reads mapping to them only contain a limited number of k-mers. By indexing a batch of reads and searching for the complex regions in that index, all mappings of the query strings to the graph can be found with reasonable resources.

5.5. Indexing haplotypes and genomes in variation graphs

Haplotypes in related individuals are typically highly similar, and thus compressible. A series of results lead from a compact haplotype index for biallelic SNPs to a generic haplotype index for complex variation graphs. The positional BWT (PBWT) (39) provides an efficient compressed representation of a set of haplotypes over biallelic variable sites. The PBWT, like the BWT, supports efficient haplotype matching queries such as maximal exact match finding. Later work (45) showed the PBWT to be equivalent to the wavelet matrix (30), which is to date the most efficient known encoding of strings with large alphabets supporting a variety of important random access queries. The graph positional BWT (gPBWT) (104) extends the PBWT model to haplotype walks embedded in complex sequence graphs. The graph BWT (GBWT) (131) builds on a number of assumptions that tend to hold for sequence variation graphs to improve runtime and memory costs relative to the gPBWT. Provided the variation graph on which they are built encodes the full complement of variation in the pangenome, both the gPBWT and GBWT are excellent, and in principle lossless, compressors of genomes. A GBWT for the 5008 haplotypes in the 1000 Genomes Project required 14.6 GB, or ≈1 bit per 1 kbp of encoded genomic sequence.

6. Relating new information to the pangenome

Here we focus on two major avenues to interact with pangenome graphs. By visualizing these graphs, we can gain insight into the relationship between genomes, learning about variation small and large. Pangenome models are often used as a reference system for sequence alignment, which enables the relation of a new biosample to the pangenome to support a wide variety of downstream applications.

6.1. Visualization

The visualization of pangenome graphs presents significant challenges that have proven to be difficult to resolve in a single system. We present an overview of such tools in Table 1, while Figure 2 compares different visualization methods applied to the same graph.

Table 1:

An overview of graph visualization tools. FD = Force-directed layout, Rank = GraphViz-style rank-based layout, SM = Sorted-matrix layout, A = Assembly graph, S = Scaffold graph, V = Variation graph, B = Base-level view, L = Linear view, UI = User interface, App = native application, Web = browser-based interface, CLI = command-line tool.

Tool	Layout	Graph Type	Proven Scale	Extra Views	UI	Backend
Bandage (142)	FD	A	100 Mbp		App
GfaViz (53)	FD	A, V	1 Mbp		App	OGDF (27)
SGTK (74)	FD	A, S	1 Mbp	B, L	Web	cytoscape.js (43)
AGB (93)	Rank	A	10k edgesa	L	Web	d3-graphvizb
Sequence Tube Map (13)	Tube	V	100 Mbp	B, L	Web
MoMI-G (144)	Tube, Circos	V	1 Gbp	B, L	Web	Sequence Tube Map (13), Circos (73)
vg view (51)	Rank	V	10 Kbp	B	CLI	GraphViz
vg viz (48)	SM	V	100 Kbp	B, L	CLI
odgi viz	SM	V	1 Gbp	B, L	CLI

^ahttps://github.com/almiheenko/almiheenko.github.io/blob/8f4b2f8c/AGB/Flye_Human/data/repeat_graph.jsona

^bhttps://github.com/magjac/d3-graphviz

Figure 2:

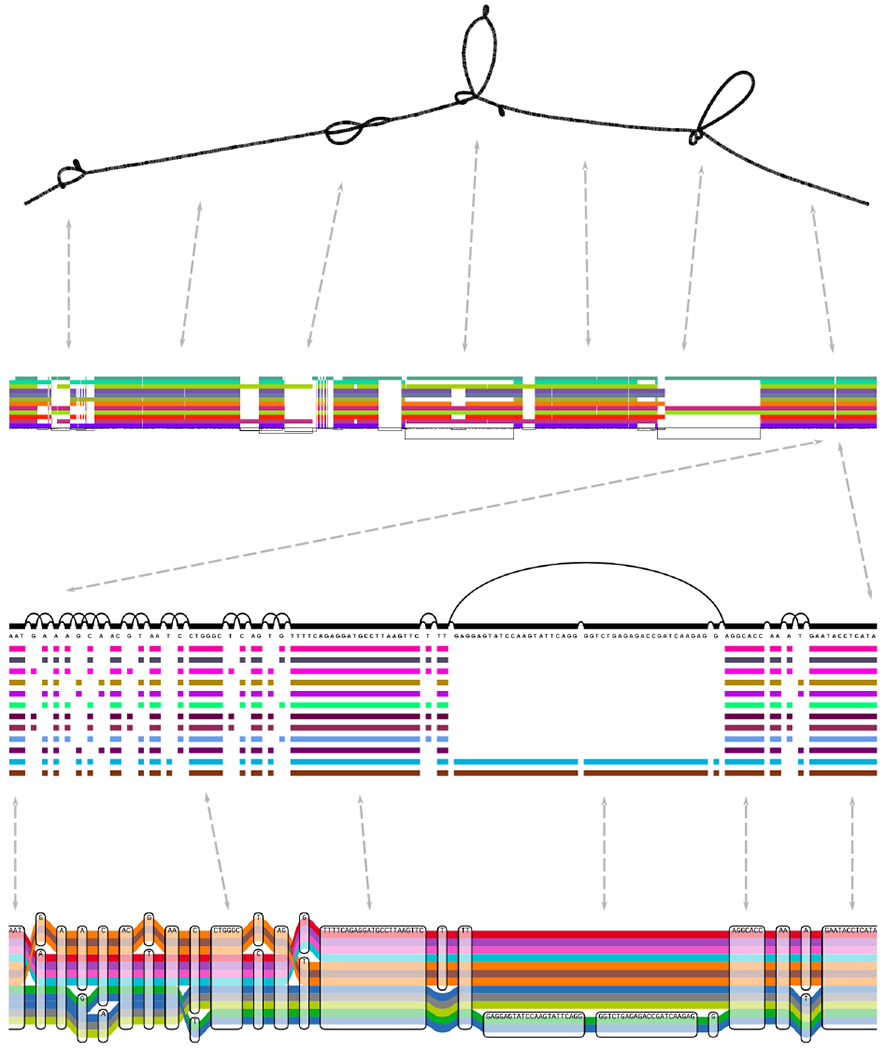
Visualizing a graph of GRCh38 and its alternate sequences in the gene HLA-DRB1 built with VG msga (48). Top: Bandage’s force directed layout reveals large scale structures (142). Top middle: ODGI viz’s binned, linearized rendering of the paths (colored bars) versus the sequence and topology of the graph (below). Bottom middle: A fragment of VG viz’s linearized rendering, showing base-level detail. Bottom: The same fragment rendered with the Sequence Tube Map (13). Dashed lines show correspondence between the visualizations. Path colors are assigned independently by each method.

Complex, nonlinear graph structures are difficult to present in a convenient number of dimensions. Traditional genome browsers organize information in a 2D rectangle, with a linear reference’s sequence space providing the horizontal dimension, and a stack of annotations plotted in the vertical dimension (57). When visualizing a graph, there are two basic approaches: attempt to mimic linear browsers and compress the graph into one dimension, or give the graph two dimensions and represent annotations using interactivity, labels, or color. Either option is challenging, as pangenome graphs are often nonplanar, requiring at least three dimensions to draw without overlapping lines. Force-directed layout, an optimization-based graph layout method, is a popular approach in the second category, but displaying annotations in this layout is challenging.

Visualization tools be categorized by the kinds of graphs they are intended to display, in addition to whether they can linearize a graph. Many tools, including Bandage (142) and GfaViz (53), are designed for interpreting assembly graphs. These tools tend to focus on displaying the overall, rather than base-level, structure of the graph, and have no visual features to reflect the pangenomic aspect of the graph.

Tools initially designed for variation graph visualization, on the other hand, tend to focus more on base-level structure and pangenomic relationships. For example, Sequence Tube Map (13) displays precise base-scale variation, haplotypes, and short read mapping locations, using a visual language inspired by transit system maps.

There is a difference in scale when moving from an assembly or scaffold graph to a comprehensive variation graph of a species pangenome, and this scale difference also separates different visualization tools. High-level assembly-graph tools like Assembly Graph Browser (AGB) (93) struggle to show fine details in the graph, while low-level variation graph tools like VG view (51) and Sequence Tube Map, cannot scale to large graphs. One tool which works well at both large scale and high detail is MoMI-G (144). Designed as a “multi-scale” graph browser, it presents both a Sequence Tube Map of base-level differences and a Circos (73) plot of chromosomal-scale connections, and can uniquely visualize long reads in the context of pangenomic haplotypes (144). ODGI viz⁶, uses binning and direct rendering to a raster image to generate visualizations representing gigabase scale pangenomes. The approach is a rasterized version of the linear layout technique of VG viz (48).

Interactively visualizing human-genome-scale, human-pangenome-detail graphs coherently across zoom levels remains an open problem.

6.2. Graph alignment algorithms

Sequence comparison is at the core of many genomic analyses, and sequence alignment is the essential method for doing so. Classic algorithms like Smith-Waterman (133) do not directly apply to genome graphs. However, the recurrence relations that drive their scoring and traceback routines can be extended to allow the alignment of sequences to acyclic sequence graphs, as popularized by the partial order aligner POA (78). Further generalizations support the alignment of sequences graphs to sequence graphs (54), sequences to cyclic graphs (102), and even cyclic sequence graphs to cyclic sequence graphs (97, 5). It is notable that many of these findings have been independently rediscovered or refined by contemporary researchers (6, 119, 68, 75). Some earlier algorithms require restricted scoring functions to achieve efficiency (119), but recent contributions have used less restricted functions that produce more biologically meaningful alignments in some contexts (68).

Graph alignment algorithms have also become faster. POA had equivalent asymptotic run time to linear alignment but required acyclic graphs (78). Later optimizations simply ran slower on general graphs (70). Algorithms are now known with equivalent run time even on general graphs (68). In addition, researchers have developed modified algorithms that run quickly in the practical context of real-world computer architectures (136, 118, 67).

6.3. Genome graph mapping

Efficient methods to map reads to large pangenome graphs have been developed in recent years. Many draw on recent research in alignment (§6.2), and advances in pangenome indexing (§5).

Although these mapping tools all target sequence graphs, there are significant differences in the types of graphs that they handle. Several tools apply only to acyclic variation graphs formed by adding variants to a linear reference. Examples include GenomeMapper (125), Seven Bridges’ Graph Genome Aligner (116), HISAT2 (72), V-MAP (139). In contrast, VG (48) and GraphAligner (120) appear to be the only tools with open ambitions of mapping to arbitrary variation graphs, including complex local and global topologies. GraphAligner can also align to generic overlap graphs and DBGs, a feature which it uses to drive the error correction of long reads using DBGs (61, 44).

The majority of these tools emphasize mapping short-read next-generation sequencing (NGS) data. To our knowledge, GraphAligner and V-MAP are the only graph mapping tools designed long read sequencing data (120, 139). While V-MAP also supports NGS reads, GraphAligner’s seeding strategy limits it to long reads. VG also supports long-read alignment (51), but this is based on a hierarchical approach that applies the alignment algorithm for short reads to chunks of long reads (48). The approach is accurate but nearly an order of magnitude slower than GraphAligner (120).

For indexing (§5), most graph mapping tools have opted for some variation of a k-mer table. GraphAligner, GenomeMapper, Seven Bridges’ mapper, and V-MAP all use this strategy (120, 125, 116, 139). The remaining mappers use succinct text indexes. VG uses the GCSA2 (130) and a longest-common-prefix array, which enable very specific queries at the expense of high memory utilization (48). HISAT2 uses a modified GCSA (132) that also encodes the graph structure itself. This helps give HISAT2 an impressively low memory footprint but a somewhat more limited set of queries (72). GraphAligner also has the option of seeding with a full text index of the node sequences of the graph, but this is not enabled by default (120).

Most graph mappers employ graph-based alignment algorithms. The exceptions are GenomeMapper, which aligns to all paths out from a seed, and HISAT2. The HISAT2 alignment algorithm relies on a complex set of heuristics that depend heavily on its exact match index. This makes it exceptionally fast, although it also can hurt alignment quality around indels. VG and V-MAP both employ some version of partial order alignment (48, 139). Seven Bridges first searches for a near-exact match using an exponential depth-first search, applying partial order alignment if this fails (116).

Due to the recent development of these methods, there have been few independent comparative studies of their performance and accuracy. In general, VG compares favorably to other tools in terms of accuracy on NGS data (117). However, it requires more memory, has slower indexing, and often maps more slowly than the alternatives (72, 139). V-MAP’s fast clustering heuristics allow it to align long reads faster than VG, but it was not compared to GraphAligner (139). GraphAligner is the only mapper to incorporate the most recent research into graph alignment algorithms. It uses a banded alignment algorithm to achieve impressive speed aligning long reads to genome graphs (120).

RNA splicing can be represented directly in a genome graph model (78). It follows that graph mappers can be applied to RNA sequencing data. HISAT2 can map RNA-seq data in addition to genomic DNA (72). It is based on the RNA mapper HISAT (71), and it retains the capacity for spliced alignment. The ability to create spliced variation graphs has also been added to VG (51). In these variation graphs, known splice junctions are added as edges, similar to the addition of a deletion event. VG supports any type of variation, but its splicing-awareness is limited to splice junctions represented in the graph. Thus, reads that span a novel splice junction will only map partially. We further discuss applications of graph mapping to functional genomics in §8.3.

7. Pangenomic data formats

A number of common data formats are used to exchange pangenomic models. Pangenomes can be stored as collections of sequences in FASTA format. Variant calls in VCF format (33) may be added to such a collection to describe small or structural variants found in the pangenome. However, to exchange graphical pangenomes, the community frequently uses a subset of version 1 of the Graphical Fragment Assembly format (GFAv1)⁷. Only a small subset of GFA is required to represent pangenome graphs, but using this format allows pangenomic analyses to use many genome assembly tools.

To represent read alignments to pangenome graphs, the VG toolkit has developed the GAM format (51), which generalizes the SAM/BAM (60) data model to pangenome graphs. GAM is produced by several other alignment tools (120, 68), and consumed by numerous downstream applications. The Graph Alignment Format (GAF)⁸ generalizes the text-based Pairwise Alignment Format (PAF)⁹ to work on graphs encoded in GFA. GAF can describe mappings to graphs encoded in rGFA¹⁰, which is a specialization of GFA for reference pangenome graphs.

8. Applications of pangenomic models

Although graphical pangenomic techniques can be applied throughout biology, most recent work has focused on a handful of applications where they can provide substantial benefits. Reduced reference bias and coherent representations of alleles yields significant improvements in structural variation detection and can decrease the runtime costs of genotyping. They have enabled haplotype reconstruction of quasispecies in metagenomic studies and transcripts in functional genomics, and supported pangenomic association studies.

8.1. Variant calling and genotyping

Typically, variant calling and genotyping indicate different aspects of a reference-guided genome inference process. Genotyping consists of determining whether a previously observed variant is present in a new sample, whereas variant calling involves detecting yet unobserved variation. When our reference system is a linear genome, these two steps are often merged. A single process will detect candidate variation and infer a sample genotype at each putatively variable locus (82, 49).

These methods are often Bayesian, and combine a model for observation and error with a simple a priori model of the pattern of variation that we expect to see, typically based on the expected rate of heterozygosity or mutation. By using multisample variant calling, genotype phasing, and genotype imputation (1, 18), we can share information between samples to improve the accuracy of our reconstruction of genomes from short reads. However, this joint calling approach is expensive, and not applicable when we only have a few new genomes to reconstruct. Furthermore, it does not help our primary interpretation of new sequencing data during read mapping.

Alignment to any allele in a pangenome reference graph is as efficient as alignment to the reference allele in a linear reference sequence. Including known genetic variation in our pangenomic reference system can thus reduce bias towards the reference allele when genotyping heterozygous variants (Figure 3). This effect is strongest for alleles that are highly divergent from the reference, suggesting that the impact of these approaches on variant calling and genotyping will be strongest for large indels and structural variants.

Figure 3:

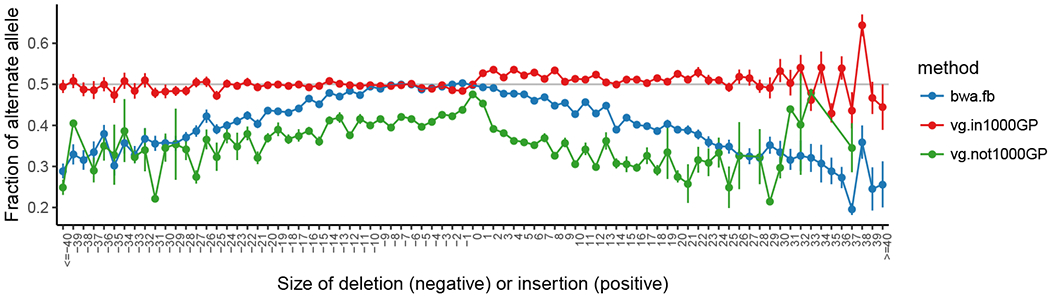
The mean alternate allele fraction at heterozygous variants in HG002/NA24385 validated in the Genome in a Bottle truth set (148) as a function of deletion or insertion size (SNPs at 0). Error bars are ± 1 s.e.m. Blue points show the allele balance metric across allele lengths for alignments with bwa mem (83) and variant calls made by freebayes (50). Variant calls were made with alignment to a variation graph built from the 1000 Genomes Project variants (1), followed by variant calling in VG. These are divided into two groups: calls at variants in the graph used for the alignment (red) and those to variants that are private to HG002 (green). Reprinted from (51).

8.1.1. Sample-specific references.

Rather than implementing genotyping or variant calling over a pangenome model, the model can be used to infer a likely haploid version of a new sample’s sequence, which is used as a reference genome for variant calling. These methods show incremental improvements in accuracy over conventional methods. Gramtools (88) and PanVC (140) both use specialized pangenome indexes to map reads for this purpose. PRG uses read k-mers from reads to choose likely haplotype paths through a graph (35).

8.1.2. Small variants.

In many ways, small variants stand to benefit the least from pangenomic variant calling and genotyping. NGS read lengths are sufficient to span their entirety, and the associated variant calling algorithms are quite mature. However, reference bias in mapping can be a source of small variant calling error, particularly for indels.

One strategy consists of realigning reads to graphs of known variation after mapping to a linear reference. This approach was pioneered in the 1000 Genomes Project, which applied Glia to establish genotype likelihoods for indels and complex alleles (1). GraphTyper refines this approach to achieve competitive accuracy in joint genotyping large cohorts with very low computational costs, providing improved genotyping performance at known variable sites described in its graph (40).

Colored de Bruijn graphs support pangenomic, reference-free variant calling. Cortex calls variants based on coverage in bubble structures in a colored de Bruijn graph, which is constructed from multiple read sets and/or reference genomes (66). Bubbleparse extends Cortex’s model to improve SNP discovery (81).

8.1.3. Genotyping structural variation.

The study of structural variants (SVs)—typically defined as variants affecting at least 50 bp—has more to gain from using genome graphs. SVs are difficult to call with NGS reads because they are large relative to the read length. Long read sequencing does not share this difficulty, but this technology remains prohibitively expensive for population-scale studies or routine use.

Bayestyper (129) compares the distribution of k-mers from sequencing reads to the distribution of k-mers along paths in the graph. It calls structural variants with high accuracy almost irrespective of the size of the variant. However, it has a high memory footprint, and later analysis has also suggested that its reliance on long exact matches makes it fragile to breakpoint uncertainty (62).

In contrast, Paragraph (26), GraphTyper2 (41), and VG call (62) use genome graphs to genotype SVs. The largest difference is that Paragraph and GraphTyper2 first map to a linear reference, then locally realign to regional graphs, whereas VG maps reads directly to a whole genome graph. These methods all use read coverage to determine the genotype, and significantly outperform competing reference-based methods.

Some pangenomic methods have sought improved accuracy and efficiency by focusing on specific regions where reference bias makes inference challenging. The highly polymorphic and medically important human leukocyte antigen (HLA) genes have received an especially large amount of attention. HLA*LA (36), Kourami (79), and HISAT-genotype (72) have all demonstrated techniques for genotyping HLA genes by aligning NGS reads to a graph encoding various HLA alleles. Their results rival gold-standard Sanger sequencing methods in accuracy. ExpansionHunter (37) and HISAT-genotype (72) used similar methodologies to achieve comparable or better accuracy than existing methods for short tandem repeats (STRs).

8.2. Inferring precise haplotypes from pangenomes and metagenomes

Current assembly approaches often produce a result that mixes both haplotypes of a diploid genome together. This inaccurate representation has led to the development of diploid assembly methods. WHdenovo (47) addresses this by using long reads to infer phase within the pangenomic space of the assembly graph. In an alternative approach to haplotype inference, pangenomic error correction methods can be used to clean small errors from long reads, rendering them precise observations of long haplotypes (122, 120). These methods build an assembly from accurate reads (NGS or PacBio circular consensus), to which reads can be aligned. The path of the alignment through the graph is taken as the corrected read.

Several methods have used pangenome graphs to support haplotype reconstruction, but in the context of a mixed population of related genomes sampled from a metagenome or quasispecies mixture. Mykrobe predictor (17) and GROOT (121) use graph-based structures of bacterial genomes and gene sets to predict antibody resistance in sequencing samples. MetaKallisto (123) performs taxonomic classification and quantification of metagenomic sequencing data using a database of known sequences represented as colored de Bruijn graphs. Virus-VG (10) builds a variation graph from assembled viral contigs in order to construct haplotypes and predict associated abundances in viral quasispecies from sequencing reads. This method was later improved in VG-Flow (9) which can scale to much larger genomes, such as bacteria.

8.3. Functional pangenomics

The effects of reference bias on analyses of allele-specific protein binding and transcription have led to ample interest in pangenomic techniques. Reference bias may also affect our ability to associate genome with phenotype in association mapping. Here, we consider ways in which pangenomic models can improve the accuracy of such assays into genome function.

8.3.1. CHiP-seq peak calling.

CHiP-seq data is mapped back to the reference genome in order to locate protein binding sites. Graph Peak Caller is based on VG and is the first tool to use a genome graph for this process (56). It was shown to find binding sites more enriched for known DNA binding motifs than linear methods on A. thaliana. It was also applied to human data to discover novel sites for enhancers (55).

8.3.2. Transcriptomics.

Some transcriptomic analyses are strongly affected by reference bias. Chief among these is allele-specific expression (ASE) (34, 134, 23). ASE analysis estimates the expression levels of genes or transcripts on each allele separately by comparing the number of RNA sequencing (RNA-seq) reads mapped to the two different alleles of heterozygous variants. A mapping bias in favor of one of the alleles can therefore create illusory differences in expression between the alleles. Using variation information during mapping can help ameliorate this and improve estimates of ASE (23, 91).

The simplest approach to using variation data in mapping involves creating a personalized diploid genome or transcriptome, which is then used as the reference for a standard linear mapping method (114). Methods using this approach have been shown to reduce reference bias, but they require diploid reconstruction of the genome in question. Variant-aware mappers like GSNAP (143), iMapSplice (87), ASElux (91), and HISAT2 (72) remove this necessity, and have been shown to reduce reference bias at known SNVs during mapping (23, 87). Variation-aware analysis of RNA-seq data is also important for accurately analyzing highly polymorphic regions, such as HLA. AltHapAlignR (80) and HLApers (2) compare reads against a collection of known HLA haplotypes yielding improved estimation of HLA expression.

8.3.3. Pangenomic association studies.

Pangenome-wide association studies (PWAS) generalize the genome-wide association (GWAS) concept to pangenomes. This new area has primarily used traditional pangenome definitions from microbiology (19). Recent work applies PWAS specifically to pangenome graphs. In the frequented region (FR) technique, a syntenic region finding algorithm similar to those used in whole genome alignment (§4.4) detects regions of a compacted DBG that are shared between many individuals (31), and these are employed as features in PWAS (89). When tested in 100 yeast strains, this approach marginally improves on standard GWAS techniques, but for some phenotypes provides a dramatic improvement in performance.

9. Discussion

In the near future, we expect complete, haplotype-resolved, “telomere-to-telomere” assemblies of large genomes to be readily obtained at low cost (92). The impeding resolution of the genome assembly problem raises new issues. To make full use of genome assemblies, we must relate them to each other. And, to maximize their value, we must make it possible to use the prior information contained in them to guide subsequent genomic analyses.

These goals drive us to work with the pangenome implied by a collection of whole genome assemblies. Pangenomes can be modeled as simple collections of DNA sequences, but this can obscure variation between genomes that is essential to unlocking insight into biology. Increasingly, researchers have explored pangenome graphs which represent both sequences and variation between them. These methods are flexible. In representing the mutual alignment of many genomes, a graphical pangenome can contain, and relate between many linear reference systems. They are also scalable. Recently-developed methods support the compact storage and query of collections of tens of thousands of genomes. And, they can improve alignment and genotyping accuracy in the context of known variation.

However, adding variation to the reference system is not without potential drawbacks. Model construction, indexing, and alignment steps typically require more time for pangenome graphs than linear reference genomes. Additional information can increase ambiguity, and care must be taken to build models that improve utility by including relevant variation. Working with a graphical reference system necessitates knowledge of graph-theoretic concepts that may be unfamiliar to many biologists. Users also must consider that, pangenome graphs are not observable in the same sense that a given genome is. Their construction is often guided more by application than a clear ground truth.

Due to these issues, some argue that it is likely that linear genomic models will remain important into the future (128). Our survey does not disagree with this possibilty. Many of the works we have considered forsee a future in which reference systems are graphical, but only a handful (primarily those based on variation graphs) produce alignments or genotype calls in the context of a pangenome graph. Linear or hierarchical coordinate systems for the pangenome may be preferred by the genomics community. If so, these reference systems are likely to proliferate as we explore the pangenome of humans and other species.

Of course, a future full of many reference genomes is essentially a pangenomic one. Whether or not the community fosters the development of standardized pangenomic reference models, the proliferation of whole genome sequences will only increase the importance of the methods that we have considered here. Pangenome graphs provide a distributed framework which we can use to bring many reference systems into the same analytical context. We can use them to build reference models optimized for particular research or clinical settings, potentially mixing public and private sources of data, without sacrificing our ability to relate our findings to standard reference models. Provided their continued improvement, graphical pangenomic methods will be well-suited to the pluralistic, decentralized attributes of a future in which genomes are easily sequenced and assembled.

Table 2:

An overview of graph mapping tools

Tool	Graph Types	Sequencing Types	Other Notes
deBGA	De Bruijn graph	NGS
BGREAT			Gapless alignment
BrownieAligner
GenomeMapper	Acyclic variation graph	NGS	No longer maintained
Graph Genome Aligner
HISAT2			Fast
V-MAP		NGS and long read
VG	Variation graph	NGS and long read	Accurate, high memory usage
GraphAligner	Variation graph or overlap graph	Long read	Fast, high memory usage