Abstract
With the rapid growth of energy demand and the depletion of existing energy resources, the new materials with superior performances, low costs and environmental friendliness for energy production and storage are explored. Di-p-tolyl disulfide (p-Tol2S2) is a typical lubricating material, which has been applied in the field of energy storage. The conformational properties and phase transformations of p-Tol2S2 have been studied by pioneers, but their polymorphs and the polymorphism induced crystal structure changes require further analysis. In this study, we perform the crystal structural screening, prediction and optimization of p-Tol2S2 crystal with quantum mechanical calculations, i.e., density functional theory (DFT) and second-order Møller–Plesset perturbation (MP2) methods. A series of crystal structures with different molecular arrangements are generated based on the crystal structure screening. As compared to long-established lattice energy calculation, we take an advantage of using more accurate technique, which is Gibbs free energy calculation. It considers the effects of entropy and temperature to predict the crystal structures and energy landscape. By comparing the Gibbs free energies between predicted and experimental structures, we found that phase α is the most stable structure for p-Tol2S2 crystal at ambient temperature and standard atmospheric pressure. Furthermore, we provide an efficient method to discriminate different polymorphs that are otherwise difficult to be identified based on the Raman/IR spectra. The proposed work enable us to evaluate the quality of various crystal polymorphs rapidly.
Subject terms: Chemical engineering, Density functional theory, Structure prediction
Introduction
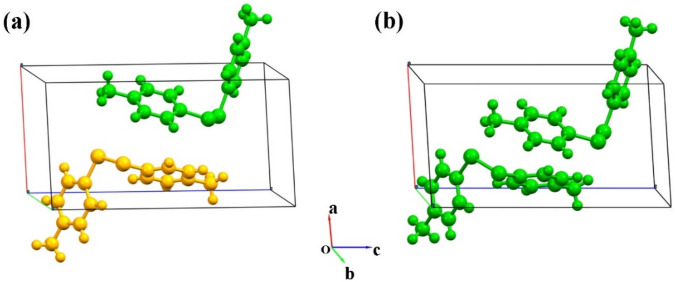
Organic disulfide has been one of the major interesting research materials due to its superior lubricating property1 and the extensive applications in storing energy2. Di-p-tolyl disulfide (p-Tol2S2, with the formula of C14H14S2), a typical representative molecule of a large group of diphenyl disulfides, has been explored in many aspects3–5. A number of analyses have examined the interplay of conformational transformation and the thermodynamic stability of the p-Tol2S2, demonstrating that the change in pressure6–9 or recrystallization10–12 would result in structural phase transition. Previous studies have primarily concentrated on the pressure effect on the conformational qualities of p-Tol2S2 and its molecular aggregation in crystalline state13–17, but the polymorphs and polymorphism induced difference either in the crystal structure or the physical and chemical properties have not been studied. The present paper focuses on the polymorphs of p-Tol2S2, studying the stability of different forms and providing an effective spectral method to distinguish them. There are several different polymorphs of p-Tol2S2 with different conformations and molecular aggregations. The two main structures are phase α and phase β. Phase α is an independent molecule (Z′ = 1), which has an asymmetric conformation, with the monoclinic unit cell of space group P21. At higher pressures (> 1.6 GPa), phase α transform into a steric hindrance and aggregated phase β with reduced lattice parameters and volume. Structure β is a triclinic phase with two independent molecules (Z′ = 2) per unit cell and has a space group of P1 (see Fig. 1). The structures of p-Tol2S2 were determined by X-ray diffraction and its cell parameters can be found in the Cambridge Structural Database (CSD).
Figure 1.
Crystal structures of p-Tol2S2. Phase α (a) has a space group of P21, while phase β (b) has a space group of P1. The molecules are colored by the symmetry operation, where the unit cells of phase α and phase β contain one and two independent molecules, respectively.
Polymorphisms, differing in their physical properties, have different solubility and dissolution rates. Therefore, discrimination of polymorphisms is important for all molecular crystal products and industrial production. Crystal structure prediction (CSP) is an emerging tool to help crystallographers determine various thermodynamically favorable crystal packings which are independent of the kinetics of crystallization. However they depend on a wide range of controllable or less easily controllable crystallization condition18–20. The advancement and development of CSP have been widely performed on different polymorphisms21–23. In this paper, to obtain more reliable structures, we use different CSP tools of MOLPAK24,25 (MOLecular PAcKing) and USPEX26–28 to perform crystal structure screening, prediction and optimization of p-Tol2S2. The MOLPAK and USPEX totally produce 9000+ possible hypothetical crystal structures which lie in the most common space groups with different molecular arrangements. The 38 candidates (20 from MOLPAK and 18 from USPEX) with the lowest lattice energies are selected to perform further optimization, where the crystal structure optimization is calculated at the DFT level using the ωB97XD/6-31G* method, and the single-point electronic energy is calculated at the MP2 level on the optimized crystal structure. The MP2 calculation is used to obtain more accurate and reliable prediction results. Besides, to treat the macromolecular system, such as the p-Tol2S2 (has 30 atoms) crystal in the present paper, the embedded-fragment method29–31 is used to obtain the total energy by taking an appropriate combination of the energies of monomers and dimers, which are embedded in the electrostatic field of the rest in the crystalline environment. Via the Gibbs free energy calculation, we determine that phase α is the most stable structure from those predicted and experimental structures.
Methods
Crystal structure predictions
The credibility of computing methods for crystal structure prediction has been improved over the past years. Here we use the MOLPAK and USPEX tools to determine the crystal forms from the molecular structure. MOLPAK can create unit cells that have the smallest volumes per molecule by allowing surrounding molecules to collapse along the three axes of a Cartesian coordinate system until a predetermined repulsion threshold with the central molecule is reached32,33. While the USPEX program, adapting the evolutionary algorithm that can find the stable structures for systems with various rigid molecular shapes26,34. The initial structures are generally generated by selected space groups with the initial known structures under atmospheric pressure. Structure relaxation is implemented from low to high precision using the VASP program. All the structures are examined and their initial sorting was performed based on lattice energy or enthalpy after full relaxation. However selected potential structures were resorted according to root-mean-square deviations (RMSDs), given in Tables S1 and S2.
Structure optimization and energy calculation
After generation of the initial crystal structures using MOLPAK and USPEX, for further calculation, 20 structures from MOLPAK and 18 structures from USPEX were selected based on lower lattice energies and enthalpies, respectively. To minimize the enthalpy, we adopt quasi-Newton algorithm35 for the crystal structure optimization. Because of the large molecular size and the quantity of molecules in the supercell, the embedded-fragment method30,31,36 with ωB97XD/6-31G* was used for the calculation of enthalpy and Gibbs free energy of the p-Tol2S2 crystal. The Hessian matrix approximation was updated using the BFGS procedure37 and the convergence criterion for the maximum gradient was set to 0.001 Hartree/Bohr. The embedded fragment method, as the name implies, is a process that breaks a large system into small fragments. The embedded fragment method divides the total energy per unit cell of the crystal into an appropriate combination of the energies of monomers and dimers, and therefore can treat the macromolecules effectively. The individual molecule is designated as a segment, and the interaction energies between two segments, in close contact with each other, are calculated by quantum mechanics (QM). The interaction energy between the two distal segments is calculated according to Coulomb interactions. The DFT calculations, accounting for the environmental influences, are embedded in an electrostatic field represented by the point charges of the remaining system.
The internal energy of a unit cell for the molecular crystal system is calculated by:
| 1 |
where the three-integer index of unit cell is represented by a variable ‘n’. The quantum mechanical (QM) energy of the ith molecules in the nth unit cell is represented by . The QM energy of dimers is represented by , where ith and jth represent number of molecules with respect to 0th central unit cell and nth unit cells29,38–41. The crystal system is represented by a supercell. The 1st part of Eq. (1) calculates all the single molecular energies in the 0th unit cell, which is in the center. The 2nd part represents the two-body QM interaction that has a shorter distance than (where is a given cutoff distance which is set to 4 Å in this work). The 3rd part of Eq. (1) provides the interactions between one molecule in the central unit cell and the other in nth unit cell whose distance is shorter than . The QM is used to calculate short range interactions (the first three parts in Eq. (1)). It is calculated in electrostatic field of the rest, where ωB97XD/6-31G* level is used to fit electrostatic potential variations. The background charges are represented by the supercell. The Coulomb’s charge-charge interaction is employed to approximately treat long-range interactions between two molecules of dimers whose distance is larger than . The long-range electrostatic interactions are represented by in a supercell.
The enthalpy for each unit cell can be calculated by considering the effect of external pressure as follow:
| 2 |
where the external pressure is represented by P and the unit cell volume is represented by V.
| 3 |
| 4 |
| 5 |
The harmonic approximation is used to calculate zero-point vibrational energy and the entropy , which are shown in Eqs. (3) and (4), respectively, where the frequency of phonon with lattice vector k is represented by . and is the Boltzmann constant. The capital K is the product of all k, which are evenly spaced grid points in the reciprocal unit cell. The k-grid of 21 21 21 has been used in this study, where K = 9261. The calculation of Gibbs free energy with effects of temperature and pressure in a unit cell is given by Eq. (5).
As MP2/6-31G* is more accurate than DFT/ωB97XD/6-31G* but its computational time and cost are very high. Therefore, to be more efficient and effective, we optimized crystal structure as well as calculated enthalpy (He) over single point energy, zero-point vibrational energy (), and entropy () at DFT/ωB97XD/6-31G* level. Moreover, to obtain better accuracy, MP2/6-31G* level was used to recalculate enthalpy (He) only, over single point energy based on crystal structure calculated by DFT/ ωB97XD/6-31G*.
Raman spectra simulation
For a periodic molecular system, the dynamical force constant matrix is calculated as follow:
| 6 |
where the masses of atoms p and q are represented by mp and mq, respectively.
The k is a Brillouin zone point which is known. The 2nd order derivative of the total energy in a unit cell which correspond to atom p and q in the 0th and the nth cell, is represented by H(rp,0, rq,n) in Eq. (6) at geometry equilibrium. The number of nearby unit cells for QM treatment was truncated at R = 1, and the number of k-points was set to 21 in each of the three dimensions. The vibrational frequencies and the corresponding normal modes of the periodic molecular system can be obtained by solving the dynamical matrix . The zone-center (k = 0) vibrations presenting nonzero intensities results in the activation of IR- and Raman spectra. The force-constant matrix D(0) was used to calculate the vibrational frequency. Therefore, we can obtain the IR intensity (In0) and Raman intensity (Rn0) for the fundamental transition of the mode in the nth phonon branch with wave vector k = 0, demonstrated by the following derivatives:
| 7 |
| 8 |
The corresponding normal mode is represented by Qn0. The dipole moment derivative and the polarizability derivative in the central unit cell can be derived with the embedded-fragment quantum mechanical method.
Results and discussion
The experimental data of the p-Tol2S2 (CH3-C6H4-S)2 in the Cambridge Structural Database42,43 is used to predict the crystal structure. Phase α has a space group of P21, with a monoclinic unit cell and a volume of 628.741 Å3. The cell lattice parameters are a = 7.5927 Å, b = 5.71318 Å, c = 14.722 Å, α = 90°, β = 94.7615°, γ = 90°. However, phase β has a space group of P1 with a unit cell volume of 545.963 Å3. The lattice parameters of unit cell are a = 7.3057 Å, b = 5.5093 Å, c = 14.038 Å, α = 95.14°, β = 97.23°, γ = 85.36°. Figure 1 represents the molecular structures of both (α and β) phases.
Crystal structure predictions
The crystal structure prediction was performed by the MOLPAK and USPEX programs. From MOLPAK, we obtained 31 standard clusters of crystal structures with common space groups of (P212121, P, P21/c, Cc, C2/c, P21, Pna21 and Pbca). Each cluster contains 300+ crystal structures. Therefore, MOLPAK generated total crystal structures more than 9000. From these 9000+ crystal structures, only 20 crystal structures were selected according to lower lattice energies, and these selected structures were further optimized. All the selected 20 structures from MOLPAK have same lattice energy of − 16.91 kcal/mol, given in Table S1. We obtained same lattice energy for 20 selected structures because of two main reasons: first, these structures are similar to each other with minor difference in their lattice parameters, and second, the MOLPAK software does not calculate lattice energy very accurately. Therefore, to obtain accurate energy landscape, we optimized selected structures and calculated their Gibbs free energy at the QM level.
On the other hand, USPEX generated 20 generations with each generation generated about 20 crystal structures. Therefore, the total crystal structures generated by USPEX were about 400. From USPEX predictions, only 18 crystal structures were selected based on enthalpy sorting. After selection of potential candidates we sorted them again, according to RMSDs, given in Table S2. The lattice parameters of phase α, phase β and the 38 predicted new crystal structures by MOLPAK and USPEX are given in Tables S1 and S2 as Supporting Information.
The Gibbs free energy
The stability of 40 crystal structures are compared in Fig. 2, including phase α, phase β and 38 predicted new structures by MOLPAK and USPEX. Figure 2 shows the difference of Gibbs free energy per unit cell among 38 predicted structures, phase α and phase β of the p-Tol2S2 as a function of unit cell RMSD. In Fig. 2, the purple and green circles represent the 38 predicted structures by MOLPAK and USPEX, whereas the green square and red diamond denote the experimental Gibbs free energies of phases α and β, respectively. The enthalpy over single point energy of 40 crystal structures was calculated at the MP2/6-31G* level based on the DFT/ωB97XD/6-31G* optimized crystal structures.
Figure 2.
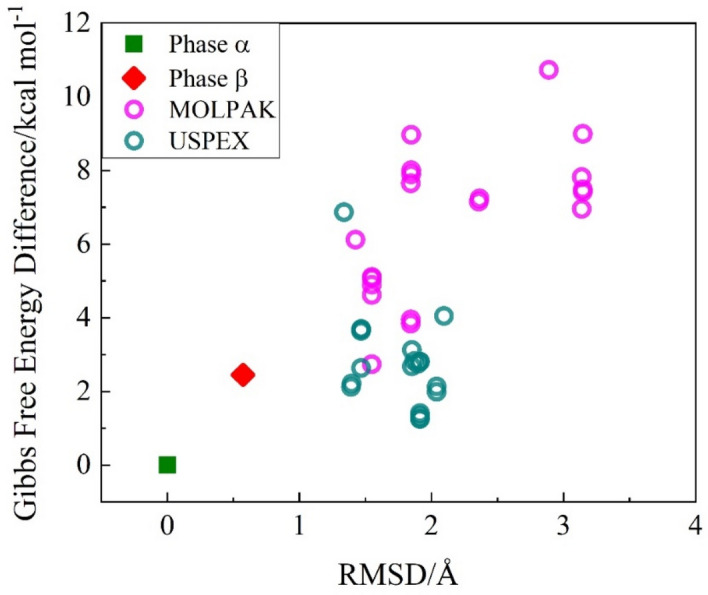
The Gibbs free energy differences per unit cell between the predicted crystal structures and experimental phase α as a function of the unit cell RMSD (with respect to phase α) under 298 K and standard atmospheric pressure, where the purple and green circles signify the 20 MOLPAK and 18 USPEX predicted structures, respectively. The green square and red diamond represent Gibbs free energies of the phases α and β, respectively, which were obtained from experiment.
The values of RMSD vary from 1 to 3.5 Å, which suggest that the crystal structure prediction method is reliable. Moreover, the lowest value of RMSD is smaller than 2 Å demonstrating the accuracy of prediction. The correlation between RMSD and Gibbs free energy (as shown in Fig. 2) reveals that the free energy of phase α, locating at the bottom of the lattice energy landscape, is the most stable structure among all predicted and experimental structures. Furthermore, the selected 20 structures from MOLPAK were possessing same lattice energies, given in Table S1. However, in Fig. 2 Gibbs free energy varies from about 1.5 to 8 kcal/mol, which is evidence of accuracy of Gibbs free energy calculation.
To verify the rationality of predicted structures, we selected eight candidates from 38 predicted structures by USPEX and MOLPAK programs to visualize overlay only. Figures S1 and S2 in the Supporting Information present the similarity of crystal structures and the molecular conformations via the calculations of the structural RMSDs, phase α and the predicted structures based on the RDKIT tool44. We selected a subset of 8 structures from 38 structures based on difference in RMSDs. The green molecules represent the structures of p-Tol2S2 phase α determined by X-ray diffraction and the red molecules denote the predicted structures based on USPEX and MOLPAK programs. The molecular overlay shows the reliability of the predicted structures.
Vibrational spectra
The crystal structure of a molecule can be identified by vibrational spectroscopy45,46. The calculated full range of Raman spectra are provided in Figs. S3 and S4 of the Supporting Information. For the purpose of highlighting the differences of phase α and phase β, we select parts of the calculated Raman and IR spectra of p-Tol2S2 crystals. The Raman and IR spectra are shown in Figs. 3 and 4. In Fig. 3, the Raman spectra are calculated from 700 to 1200 cm−1, where phase α (green curve) and phase β (red curve) are predicted to display seven and eight discernible intense Raman bands, respectively. The band 3*, locating at ~ 874 cm–1, in the red curve is the characteristic peak for phase β. Similarly, there are five and four IR bands for phase α (green curve) and phase β (red curve), respectively. The band 2*, locating at ~ 3220 cm−1, in the green curve is the characteristic peak for phase α. Therefore, the band 3* in the Raman spectra and the band 2* in the IR spectra, are the characteristic bands to distinguish phases α and β of p-Tol2S2. Figures 3 and 4 show that although the structures of phases α and β are very similar (as shown in Fig. 1), they can be identified by the characteristic bands in the vibrational spectra. The vibrational spectra of different pressure about phase α and phase β are demonstrated in Figs. S5–S8 in the Supporting Information. We can observe the vibrational spectra as a function of different pressures.
Figure 3.
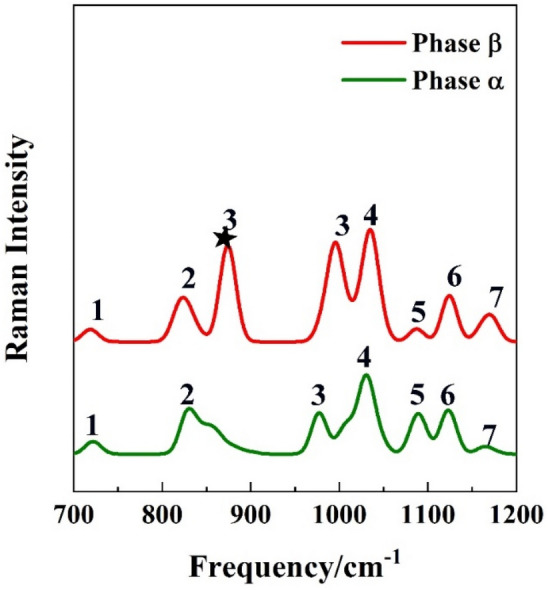
Calculated Raman spectra of p-Tol2S2 phase α (green) and phase β (red) under standard atmospheric pressure.
Figure 4.
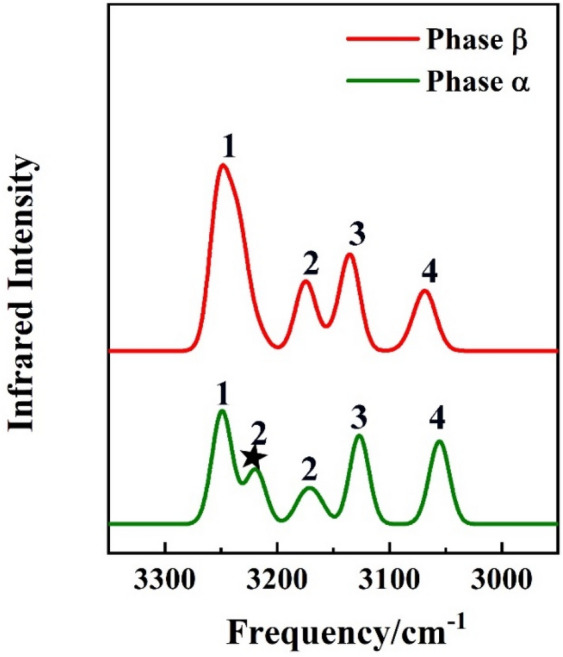
Calculated IR spectra of p-Tol2S2 phase α (green) and phase β (red) under standard atmospheric pressure.
Conclusions
It is highly desirable to control polymorph for all the manufacturing industries which manufacture and/or utilize crystalline products. This will enable us to enhance functionality of the products to next higher level. A high precision method to screen different polymorphs for designing of crystals and to find out the most stable structure that confers an optimal product would, therefore, be extremely valuable. In this paper, we carried out a theoretical approach to screen different polymorphs of p-Tol2S2, a lubricating and energy storage material, based on the DFT and MP2 methods with the embedded fragment approach. With the theoretical calculation, we pick out the most stable structure phase α from the predicted and experimental structures. Considering the small RMSDs, there will be hundreds of predicted structures between them and the conformation of existing phases α and β, the proposed method has successfully performed the predictions for sufficiently similar conformations along with the identification of the most stable structure. The predicted vibrational spectra provide an effective way to identify polymorphs with the characteristic peaks of IR and Raman spectra.
Supplementary Information
Acknowledgements
The authors are grateful for the financial support provided by the National Natural Science Foundation of China (Nos. 21901157, 21673074, 21761132022, and 21703289), the National Key R&D Program of China (No. 2016YFA0501700), the Intergovernmental International Scientific and Technological Cooperation of Shanghai (No. 17520710200), the Science and Technology Major Project of Anhui Province (No. 18030901093), the Foundation of Anhui Laboratory of Molecule-Based Materials (No. FZJ19014), the Shanghai Municipal Natural Science Foundation (No. 18ZR1412600), the Young Top-Notch Talent Support Program of Shanghai, and the NYU-ECNU Center for Computational Chemistry at NYU Shanghai. We also thank the Supercomputer Center of East China Normal University (ECNU Multifunctional Platform for Innovation 001) for providing us computational time.
Author contributions
J.L. (Jinjin Li), X.H. (Xiao He) and J.L. (Jinyun Liu) proposed the idea and supervised the project. X.H. (Xuan Hao), J.L. (Jinfeng Liu) and I.A. performed the calculation and wrote the paper. H. L., Y.H. and W.H. completed the data analysis. I.A. revised the English grammar. All authors contributed to revising of the paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Xuan Hao, Jinfeng Liu and Imran Ali.
Contributor Information
Jinyun Liu, Email: jyliu@ahnu.edu.cn.
Xiao He, Email: xiaohe@phy.ecnu.edu.cn.
Jinjin Li, Email: lijinjin@sjtu.edu.cn.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-021-86519-1.
References
- 1.Qu J, Barnhill WC, Luo HM, Meyer HM, Leonard DN, Landauer AK, Kheireddin B, Gao H, Papke BL, Dai S. Synergistic effects between phosphonium-alkylphosphate ionic liquids and zinc dialkyldithiophosphate (ZDDP) as lubricant additives. Adv. Mater. 2015;27:4767–4774. doi: 10.1002/adma.201502037. [DOI] [PubMed] [Google Scholar]
- 2.Wang BJ, Wu QQ, Sun H, Zhang J, Ren J, Luo YF, Wang M, Peng HS. An intercalated graphene/(molybdenum disulfide) hybrid fiber for capacitive energy storage. J. Mater. Chem. A. 2017;5:925–930. doi: 10.1039/C6TA09360D. [DOI] [Google Scholar]
- 3.Arisawa M, Yamaguchi M. Rhodium-catalyzed disulfide exchange reaction. J. Am. Chem. Soc. 2003;125:6624–6625. doi: 10.1021/ja035221u. [DOI] [PubMed] [Google Scholar]
- 4.Sobczak S, Katrusiak A. Colossal strain release by conformational energy up-conversion in a compressed molecular crystal. J. Phys. Chem. C. 2017;121:2539–2545. doi: 10.1021/acs.jpcc.6b11030. [DOI] [Google Scholar]
- 5.Taniguchi T, Fujii T, Idota A, Ishibashi H. Reductive addition of the benzenethiyl radical to alkynes by amine-mediated single electron transfer reaction to diphenyl disulfide. Org. Lett. 2009;11:3298–3301. doi: 10.1021/ol901084k. [DOI] [PubMed] [Google Scholar]
- 6.Wu M, Tse JS, Wang SY, Wang CZ, Jiang JZ. Origin of pressure-induced crystallization of Ce75Al25 metallic glass. Nat. Commun. 2015;6:6493. doi: 10.1038/ncomms7493. [DOI] [PubMed] [Google Scholar]
- 7.Jenei Z, Liermann HP, Cynn H, Klepeis JHP, Baer BJ, Evans WJ. Structural phase transition in vanadium at high pressure and high temperature: Influence of nonhydrostatic conditions. Phys. Rev. B. 2011;83:054101. doi: 10.1103/PhysRevB.83.054101. [DOI] [Google Scholar]
- 8.Hui X, Duclos SJ, Ruoff AL, Vohra YK. New high-pressure phase transition in zirconium metal. Phys. Rev. Lett. 1990;64:204–207. doi: 10.1103/PhysRevLett.64.204. [DOI] [PubMed] [Google Scholar]
- 9.Catalan G, Scott JF. Physics and applications of Bismuth ferrite. Adv. Mater. 2009;21:2463–2485. doi: 10.1002/adma.200802849. [DOI] [Google Scholar]
- 10.Anzellini S, Dewaele A, Mezouar M, Loubeyre P, Morard G. Melting of iron at earth's inner core boundary based on fast X-ray diffraction. Science. 2013;340:464–466. doi: 10.1126/science.1233514. [DOI] [PubMed] [Google Scholar]
- 11.Kuriakose M, Chigarev N, Raetz S, Bulou A, Tournat V, Zerr A, Gusev VE. In situ imaging of the dynamics of photo-induced structural phase transition at high pressures by picosecond acoustic interferometry. New J. Phys. 2017;19:053026. doi: 10.1088/1367-2630/aa6b3d. [DOI] [Google Scholar]
- 12.Li L, Liu T, Zhao L, Yuan WK. CO2-induced phase transition of isotactic poly-1-butene with form III upon heating. Macromolecules. 2011;44:4836–4844. doi: 10.1021/ma200988y. [DOI] [Google Scholar]
- 13.Neumann MA, de Streek JV, Fabbiani FPA, Hidber P, Grassmann O. Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat. Commun. 2015;6:7793. doi: 10.1038/ncomms8793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Boldyreva EV, Ivashevskaya SN, Sowa H, Ahsbahs H, Weber HP. Effect of high pressure on crystalline glycine: A new high-pressure polymorph. Dokl. Phys. Chem. 2004;396:111–114. doi: 10.1023/B:DOPC.0000029166.57397.2d. [DOI] [Google Scholar]
- 15.Boldyreva EV. High-pressure-induced structural changes in molecular crystals preserving the space group symmetry: Anisotropic distortion/isosymmetric polymorphism. Cryst. Eng. 2003;6:235–254. doi: 10.1016/j.cryseng.2003.11.005. [DOI] [Google Scholar]
- 16.Fabbiani FPA, Pulham CR. High-pressure studies of pharmaceutical compounds and energetic materials. Chem. Soc. Rev. 2006;35:932–942. doi: 10.1039/b517780b. [DOI] [PubMed] [Google Scholar]
- 17.Ostrowska K, Kropidlowska M, Katrusiak A. High-pressure crystallization and structural transformations in compressed R,S-ibuprofen. Cryst. Growth Des. 2015;15:1512–1517. doi: 10.1021/cg5018888. [DOI] [Google Scholar]
- 18.Terayama K, Yamashita T, Oguchi T, Tsuda K. Fine-grained optimization method for crystal structure prediction. NPJ Comput. Mater. 2018;4:32. doi: 10.1038/s41524-018-0090-y. [DOI] [Google Scholar]
- 19.Ryan K, Lengyel J, Shatruk M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 2018;140:10158–10168. doi: 10.1021/jacs.8b03913. [DOI] [PubMed] [Google Scholar]
- 20.Hoser AA, Sovago I, Lanzac A, Madsen AO. A crystal structure prediction enigma solved: the gallic acid monohydrate system—Surprises at 10 K. Chem. Commun. 2017;53:925–928. doi: 10.1039/C6CC06799A. [DOI] [PubMed] [Google Scholar]
- 21.Hulme AT, Price SL, Tocher DA. A new polymorph of 5-fluorouracil found following computational crystal structure predictions. J. Am. Chem. Soc. 2005;127:1116–1117. doi: 10.1021/ja044336a. [DOI] [PubMed] [Google Scholar]
- 22.Bhardwaj RM, Price LS, Price SL, Reutzel-Edens SM, Miller GJ, Oswald IDH, Johnston BF, Florence AJ. Exploring the experimental and computed crystal energy landscape of olanzapine. Cryst. Growth Des. 2013;13:1602–1617. doi: 10.1021/cg301826s. [DOI] [Google Scholar]
- 23.Baias M, Dumez JN, Svensson PH, Schantz S, Day GM, Emsley L. De novo determination of the crystal structure of a large drug molecule by crystal structure prediction-based powder NMR crystallography. J. Am. Chem. Soc. 2013;135:17501–17507. doi: 10.1021/ja4088874. [DOI] [PubMed] [Google Scholar]
- 24.Anghel AT, Day GM, Price SL. A study of the known and hypothetical crystal structures of pyridine: Why are there four molecules in the asymmetric unit cell? CrystEngComm. 2002;4:348–355. doi: 10.1039/B202084J. [DOI] [Google Scholar]
- 25.Holden JR, Zuyue D, Ammon HL. Prediction of possible crystal structures for C-, H-, N-, O-, and F-containing organic compounds. J. Comput. Chem. 1993;14:422–437. doi: 10.1002/jcc.540140406. [DOI] [Google Scholar]
- 26.Glass CW, Oganov AR, Hansen N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006;175:713–720. doi: 10.1016/j.cpc.2006.07.020. [DOI] [Google Scholar]
- 27.Lyakhov AO, Oganov AR, Stokes HT, Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013;184:1172–1182. doi: 10.1016/j.cpc.2012.12.009. [DOI] [Google Scholar]
- 28.Oganov AR, Glass CW. Evolutionary crystal structure prediction as a tool in materials design. J. Phys. Condens. Matter. 2008;20:064210. doi: 10.1088/0953-8984/20/6/064210. [DOI] [PubMed] [Google Scholar]
- 29.Li JJ, Sode O, Voth GA, Hirata S. A solid-solid phase transition in carbon dioxide at high pressures and intermediate temperatures. Nat. Commun. 2013;4:141–155. doi: 10.1038/ncomms3647. [DOI] [PubMed] [Google Scholar]
- 30.Liu JF, Qi LW, Zhang JZH, He X. Fragment quantum mechanical method for large-sized ion-water clusters. J. Chem. Theory Comput. 2017;13:2021–2034. doi: 10.1021/acs.jctc.7b00149. [DOI] [PubMed] [Google Scholar]
- 31.He X, Zhu T, Wang XW, Liu JF, Zhang JZH. Fragment quantum mechanical calculation of proteins and its applications. Accounts Chem. Res. 2014;47:2748–2757. doi: 10.1021/ar500077t. [DOI] [PubMed] [Google Scholar]
- 32.Ammon HL, Du ZY, Gilardi RD, Dave PR, Forohar F, Axenrod T. Structure of 1,3,5,7-tetranitro-3,7-diazabicyclo 3.3.0 octane. Structure solution from molecular packing analysis. Acta Crystallogr. Sect. B Struct. Commun. 1996;52:352–356. doi: 10.1107/S0108768195010652. [DOI] [Google Scholar]
- 33.McArdle P, Gilligan K, Cunningham D, Dark R, Mahon M. A method for the prediction of the crystal structure of ionic organic compounds—The crystal structures of o-toluidinium chloride and bromide and polymorphism of bicifadine hydrochloride. CrystEngComm. 2004;6:303–309. doi: 10.1039/B407861F. [DOI] [Google Scholar]
- 34.Kuklin MS, Karttunen AJ. Crystal structure prediction of magnetic transition-metal oxides by using evolutionary algorithm and hybrid DFT methods. J. Phys. Chem. C. 2018;122:24949–24957. doi: 10.1021/acs.jpcc.8b08238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dennis JE, Jr, More JJ. Quasi-Newton methods, motivation and theory. SIAM Rev. 1977;19:46–89. doi: 10.1137/1019005. [DOI] [Google Scholar]
- 36.Beran GJO. Modeling polymorphic molecular crystals with electronic structure theory. Chem. Rev. 2016;116:5567–5613. doi: 10.1021/acs.chemrev.5b00648. [DOI] [PubMed] [Google Scholar]
- 37.Head JD, Zerner MC. A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 1985;122:264–270. doi: 10.1016/0009-2614(85)80574-1. [DOI] [Google Scholar]
- 38.Liu JF, He X. Accurate prediction of energetic properties of ionic liquid clusters using a fragment-based quantum mechanical method. Phys. Chem. Chem. Phys. 2017;19:20657–20666. doi: 10.1039/C7CP03356G. [DOI] [PubMed] [Google Scholar]
- 39.Liu JF, He X, Zhang JZH, Qi LW. Hydrogen-bond structure dynamics in bulk water: Insights from ab initio simulations with coupled cluster theory. Chem. Sci. 2018;9:2065–2073. doi: 10.1039/C7SC04205A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liu JF, He X, Zhang JZH. Structure of liquid water—A dynamical mixture of tetrahedral and 'ring-and-chain' like structures. Phys. Chem. Chem. Phys. 2017;19:11931–11936. doi: 10.1039/C7CP00667E. [DOI] [PubMed] [Google Scholar]
- 41.He X, Sode O, Xantheas SS, Hirata S. Second-order many-body perturbation study of ice Ih. J. Chem. Phys. 2012;137:204505. doi: 10.1063/1.4767898. [DOI] [PubMed] [Google Scholar]
- 42.Bruno IJ, Cole JC, Edgington PR, Kessler M, Macrae CF, McCabe P, Pearson J, Taylor R. New software for searching the Cambridge structural database and visualizing crystal structures. Acta Crystallogr. Sect. B Struct. Commun. 2002;58:389–397. doi: 10.1107/S0108768102003324. [DOI] [PubMed] [Google Scholar]
- 43.Allen FH. The Cambridge Structural Database: a quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B-Struct. Commun. 2002;58:380–388. doi: 10.1107/S0108768102003890. [DOI] [PubMed] [Google Scholar]
- 44.Landrum, G., RDKit: Open-source cheminformatics. Release 2014.03.1. Zenodo. 10.5281/zenodo.10398.
- 45.Khalil M, Demirdoven N, Tokmakoff A. Obtaining absorptive line shapes in two-dimensional infrared vibrational correlation spectra. Phys. Rev. Lett. 2003;90:047401. doi: 10.1103/PhysRevLett.90.047401. [DOI] [PubMed] [Google Scholar]
- 46.Hirata S, Gilliard K, He X, Li JJ, Sode O. Ab initio molecular crystal structures, spectra, and phase diagrams. Accounts Chem. Res. 2014;47:2721–2730. doi: 10.1021/ar500041m. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.