Hypergravity affects cell traction forces of fibroblasts

Abstract

Cells sense and react on changes of the mechanical properties of their environment and, likewise, respond to external mechanical stress applied to them. However, whether the gravitational field as overall body force modulates cellular behavior is unclear. Different studies demonstrated that micro- and hypergravity influences the shape and elasticity of cells, initiate cytoskeleton reorganization, and influence cell motility. All these cellular properties are interconnected and contribute to forces that cells apply on their surrounding microenvironment. Yet, studies that investigated changes of cell traction forces under hypergravity conditions are scarce. Here, we performed hypergravity experiments on 3T3 fibroblast cells using the large-diameter centrifuge at the European Space Agency - European Space Research and Technology Centre. Cells were exposed to hypergravity of up to 19.5 g for 16 h in both the upright and the inverted orientation with respect to the g-force vector. We observed a decrease in cellular traction forces when the gravitational field was increased up to 5.4 g, followed by an increase of traction forces for higher gravity fields up to 19.5 g independent of the orientation of the gravity vector. We attribute the switch in cellular response to shear thinning at low g-forces, followed by significant rearrangement and enforcement of the cytoskeleton at high g-forces.

Significance

The behavior of cells critically depends on the mechanical properties of their environment. For example, external stresses and strains lead to decisions in cell differentiation as well as to collective-migration in metastasis. Gravity, as a permanently acting body force, is one of those external stresses. We demonstrate the impact of gravitational challenges on forces that cells apply to their environment. We observed a switch in cellular response with a decrease in cell traction forces for low hypergravity conditions, followed by a significant increase in cell traction forces at higher g-level. This cellular response reflects a switch in cytoskeletal organization, from a low-organization network at small hypergravity challenge to a highly organized network at high g-levels, a behavior similar to that observed for cells in fluids at varying shear levels.

Introduction

In recent years, it became accepted that cellular function is, in part, controlled by external mechanical cues. Mechanical cues were shown to be sufficient to differentiate mesenchymal stem cells (1), initiate transcriptional programs (2), drive morphogenesis (3), direct cell migration (4), and control malignancy in tumors (5). The force and stiffness-mediated responses of cells on the mechanical properties of the extracellular matrix (ECM) are attributed to, yet to be identified, mechanochemical sensor platforms that transform external mechanical cues into intracellular biochemical signals, ultimately leading to, e.g., altered gene expression (6). The multiprotein sensory units responsible for mechanosensation are summarized as cell-matrix adhesions, focal adhesions, and cell-cell adhesions (7). In focal adhesions, transmembrane receptor proteins such as integrins (8) bind to specific proteins of the ECM. On the cytosolic side, those proteins link through an extended protein-cascade to the actin cytoskeleton, the cellular machinery that can apply forces through the contraction of actin fibers through the linking myosin motor-activity (9, 10, 11).

So far, studies on the mechanochemical coupling have focused on cellular responses related to static extracellular stiffness (12) and topography (13), as well as on the direct mechanical stimulation of cells by fluid flow (14), micropipette aspiration (15,16), optical tweezers (17), optical stretchers (18), atomic-force microscopes (19), and magnetically actuated particles (20). In most of those experiments local stress was applied to the cells that resulted in a highly sensitive cellular response. Cells were shown to adapt to their local mechanical environment by among others adapting their cytoskeleton. Such restructuring of the cytoskeleton is paralleled by an increased force application of cells when placed into stiffer environments or when challenged by higher external tensions.

Surprisingly, the robust cellular response on localized mechanical cues appears more subtle for homogeneous mechanical cues such as that given by gravity. Experiments showed that hypergravity in the range of 2–20 g does influence cellular morphology and elasticity (21,22), the cytoskeletal organization (23,24) and the motility (25). The strength and impact, however, differ largely, as was reviewed for endothelial cells by Maier et al. (26). The effects observed depend on many factors that appeared difficult to disentangle. Next to different cell types, different accelerations of gravity (g-levels) applied, and different exposure times of challenge in particular, the use of small laboratory centrifuges by which hypergravity was produced are known to generate additional mechanical cues on cells (in particular inertial shear forces) that possibly overshadow the effects of gravitational cues (27).

Monici et al. exposed microvascular endothelial cells for a period of 5 $\times$ 10 min to 10 g. Cells were centrifuged under closed conditions in a thermostatic laboratory centrifuge. In the experiment, the authors showed changes in the cytoskeleton organization (23). The opposite was reported by Costa-Almeida et al. (28). In the latter experiment, human umbilical vein endothelial cells were exposed to 3 and 10 g for 4 and 16 h using the large-diameter centrifuge (LDC) at the European Space Agency - European Space Research and Technology Centre (ESA/ESTEC) in Noordwijk. No changes in cytoskeleton organization were observed.

Here, we focus on investigating the impact of hypergravity as a body force on the active cellular mechanoresponse. Given that, hypergravity has an influence on the cell morphology (21,22), cytoskeleton organization (23), membrane viscosity (29), and motility (25), we probed whether or not cells react on hypergravity by a modulation of their traction forces toward the ECM.

Materials and methods

Cell culture

3T3 fibroblasts were cultured in high-glucose Dulbecco Modified Eagle’s Medium (D6546; Sigma-Aldrich, St. Louis, MO) supplemented with 10% fetal calf serum (Thermo Fisher Scientific, Waltham, MA), 2 mM glutamine, and 100 μg/mL penicillin/streptomycin, 37°C, 5% CO₂.

Immunostaining

Five minutes after the hypergravity exposure, cells were fixed for 15 min in 4% paraformaldehyde (43368; Alfa Aesar, Haverhill, MA) in phosphate-buffered saline (PBS). After fixation, cells were permeabilized for 10 min with 0.1% Triton-X 100 and blocked for 60 min with 1% bovine serum albumin in PBS. F-actin was stained with Alexa Fluor 532-labeled phalloidin (A22282; Invitrogen, Carlsbad, CA) and the DNA with DAPI (Sigma-Aldrich).

Hypergravity exposure

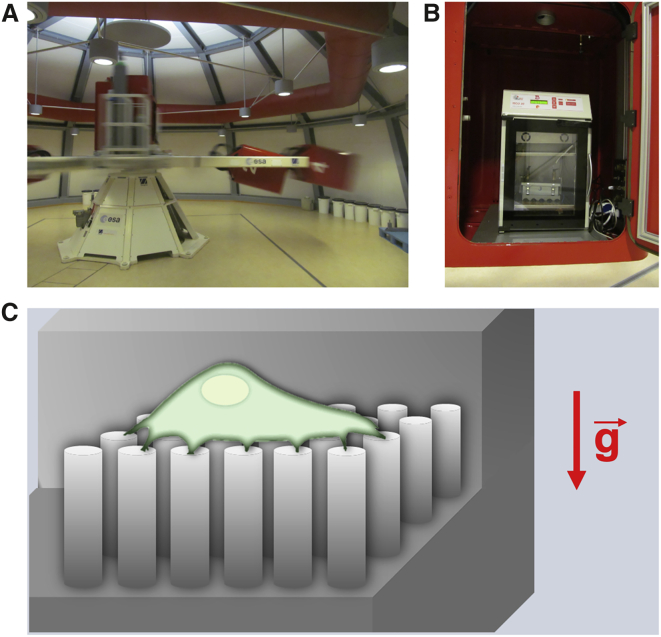
To avoid inertial shear forces (27), hypergravity experiments were performed using the LDC (Fig. 1 A) at the European Space Research and Technology Centre in Noordwijk, The Netherlands. Cells were seeded on two sets of elastic micropillar arrays, located in 12-well plates with one array per well, and incubated for 5.5 h, 37°C, 5% CO₂. After cell spreading on top of the functionalized micropillars, arrays of one set were flipped in the upside down orientation. Both sets were placed in closed metal boxes flushed with 5% CO₂ at 100% humidity and stored inside the incubators of the LDC-gondolas held at 35–37° C (Fig. 1 B). The centrifuge gondolas were placed at a distance of 2 and 4 m to the centrifuge axis, which allowed us to address two g-levels, simultaneously (30). 6.5 h after cell seeding, they were exposed for 16 h to hypergravity of 5.4 g, 10 g, and 19.5 g, respectively, as controlled by the distance of the gondolas from the axis, and the speed at which the centrifuge turned. Because of the large diameter of the centrifuge, inertial shear forces were negligible in our experiments (27). The gravitational force equivalent (g-force) acted perpendicular to the sample surface (Fig. 1 C). 1-g control experiments were prepared and conducted simultaneously under identical conditions outside the centrifuge.

Figure 1.

(A) LDC at ESA/ESTEC provided hypergravity conditions. (B) Samples were located in a metal box flushed with 5% CO₂ inside the incubator of one of the LDC-gondolas. The temperature was set to 37°C. (C) shows a schematic illustration of a cell assembled on top of a micropillar array in an upright sample orientation. The g-force was exerted perpendicular to the cell-spreading area. To see this figure in color, go online.

Elastic micropillar arrays

Polydimethylsiloxane (PDMS, Sylgard 184) micropillar arrays of 2-μm diameter, 6.9-μm length, and 4-μm spacing in a hexagonal geometry were used for cell traction force experiments. The pillar arrays were flanked by 50-μm spacers on two sides of the array. Details of this arrangement and the experimental procedures was described earlier in detail (31). In brief, pillar arrays were produced on a negative silicon-wafer master made by a two-step deep reactive-ion etching process. Wafers were passivated in trichloro-silane (448931; Sigma-Aldrich). A mixture of 1:10 PDMS (cross-linker/base ratio) was poured onto the Si-master and cured for 20 h at 110°C. After peel-off, the tops of the pillars were coated by μ-contact printing. For that, flat 1:30 PDMS stamps were incubated for 1 h with 40 μL of 50 μg/mL Alexa Fluor 647–labeled and 50 μg/mL unlabeled fibronectin (F1141; Sigma-Aldrich), then washed and dried. Subsequently, the stamps were gently loaded onto the ultraviolet-ozone-activated micropillar arrays for 10 min. After stamping, the arrays were passivated with 0.2% Pluronic (F-127, P2443; Sigma-Aldrich) for 1 h, and washed in PBS.

Microscopy

Samples were imaged at high resolution on a home-build optical microscope setup based on an inverted Axiovert200 microscope body (Carl Zeiss, Oberkochen, Germany), a spinning disk unit (CSU-X1; Yokogawa Electric, Musashino, Tokyo, Japan), and an emCCD camera (iXon 897; Andor Labs, Morrisville, NC). IQ-software (Andor Labs) was used for setup-control and data acquisition. Illumination was performed using fiber-coupling of different lasers (405 nm (CrystaLaser, Reno, NV), 514 nm (Cobolt AB, Solna, Sweden), and 642 nm (Spectra-Physics Excelsior; Spectra-Physics, Stahnsdorf, Germany)). Pillar arrays were placed upside down onto 25-mm cover glasses and inspected with an EC Plan-NEOFLUAR 40× 1.3 Oil Immersion Objective (Carl Zeiss).

Image analysis

Images of single nonoverlapping and randomly selected cells within the field of view of 176 × 176 μm were analyzed using MATLAB scripts (MATLAB R2017a; MathWorks, Natick, MA). Pillar deflections were quantified as previously described in detail (31). Deflected pillars caused by cell traction forces were distinguished from the background. The background was determined from an undeflected area of the pillar array by selecting a pillar region outside the cell area. Pillar deflections underneath the cell within the background range were discarded. The traction force per pillar was calculated by dividing the total absolute force per cell by the number of deflected pillars per cell. The cell-spreading area was calculated as the number of deflected pillars per cell multiplied by the unit-cell area of the hexagonal pillar array geometry. The unit-cell area measured 13.84 μm².

The pillar deflections of the selected background regions between all analyzed array conditions varies up to 17.2 nm, which corresponds to a force of 0.7 nN (Fig. S2, A–C). Further information are shown in the Supporting materials and methods.

Additionally, we calculated the bending modulus of pillars caused by the increase in the weight of the cell and the pillar itself at higher g-level (see Supporting materials and methods). Based on the study by Grover et al., we assumed a cell density of 1.08 g mL^–1 (32). The averaged diameter of 3T3 fibroblasts is 50 μm with a height of 15 μm measured via z-stack images. Assuming a deflection of 400 nm, the differences of the pillar deflection at 1 g to that at 20 g is 4.7 pN (Eq. S5). Hence, the additional pillar deflection is three orders of magnitude lower than that resulting from cellular traction force, and can thus be neglected.

Statistics

The following samples with cells were analyzed in the upright orientation: two control arrays with 101 cells at 1 g, one array with 72 cells at 5.4 g, two arrays with 105 cells including one repeat at 10 g, and one array with 66 cells at 19.5 g.

In the upside down orientation, we analyzed: Two control arrays with 100 cells at 1 g, one array with 65 cells at 5.4 g, one array with 54 cells at 10 g, and one array with 47 cells at 19.5 g. Hence, in total 617 cells and 20,343 deflections were analyzed.

All data sets are not normal distributed. The p-values between two groups were calculated using the two-sided Wilcoxon rank sum test in MATLAB. Comparisons between more than two groups were performed using Dunn test of multiple comparisons after a significant Kruskal–Wallis test in R. Data sets were significantly different with probabilities of p ≤ 0.05 (^∗); p < 0.01 (^∗∗); p < 0.001 (^∗∗∗); p > 0.05 (ns).

Results

Given the results of prior studies on the effect of hypergravity on cellular behavior (21,23,25), we anticipated that the effect of hypergravity on cellular force application would be small. Hence, we initially performed an extensive analysis of cell traction forces using the micropillar technique to extract a solid, experimentally confirmed baseline value for all parameters investigated.

Cells were seeded on six independently produced arrays and left for 22.5 h. After fixation and staining for actin and DNA, 321 cells leading to 9545 pillar deflections were analyzed. In a first step, the total absolute force that a cell produces was compared to the number of deflected pillars for that particular cell. The data are shown in Fig. 2 A. The total force per cell appeared highly correlated to the number of deflected pillars $\left(\left|r\right|>0.8\right)$. From this correlation, we concluded that the mean force per pillar is a robust descriptor for cellular force application. This conclusion corroborates earlier experiments in which it was shown that the force per pillar is a cellular property that depends on external chemical or mechanical cues (33). Hence, in what follows, we calculated the mean traction forces per deflected pillar.

Figure 2.

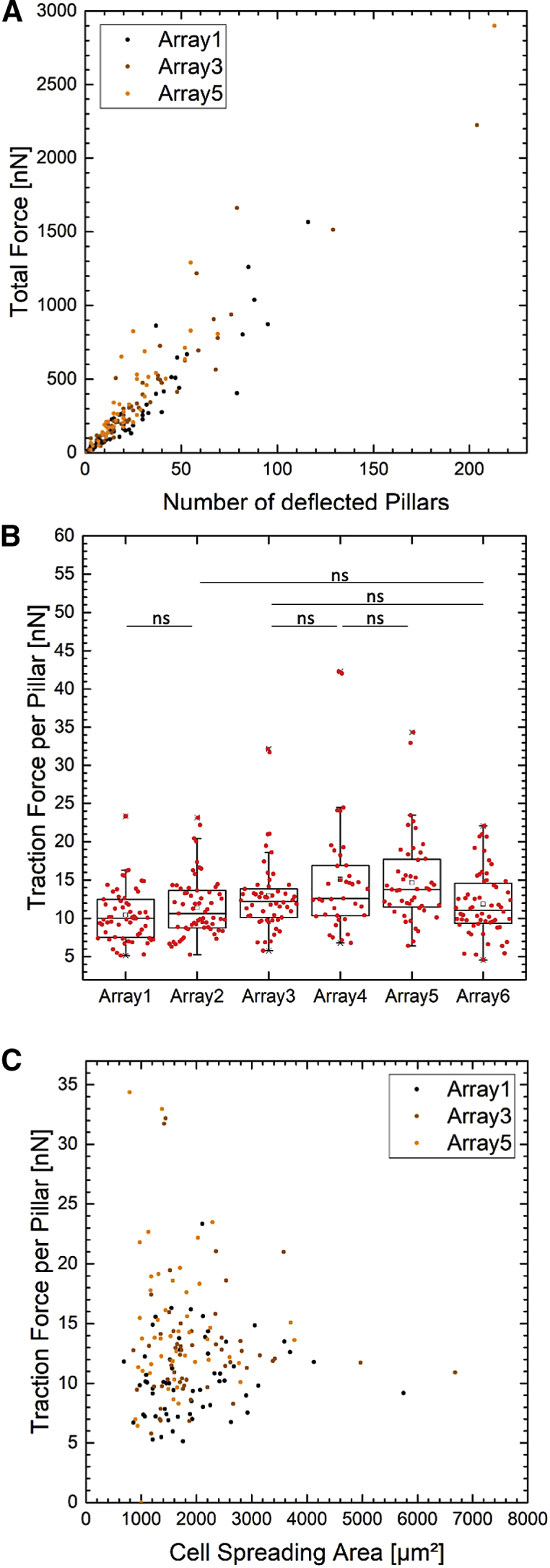
3T3 fibroblasts on six independently produced arrays under standard 1-g gravity conditions in an upright orientation were analyzed. The total force per cell increases linearly with the number of deflected pillars (A). The ratio results in the traction force per deflected pillar (B). For cells grown on identically prepared arrays the values display a significant spread between some of the arrays. A Dunn test of multiple comparisons after a Kruskal–Wallis significance test was performed to characterize the variation (only the non-significant pairs are shown in (B); ns, p > 0.05). The traction force is independent from the cell-spreading area (C). Three of six data sets randomly chosen are shown in (A) and (C). Each datapoint represent one analyzed cell. To see this figure in color, go online.

In how far the mean traction force per pillar is a robust quantity with respect to the production of micropillar arrays, we compared data from six independently produced arrays (Fig. 2 B). Mean values for the force per pillar varied for each array between 10.4 ± 3.4 nN (Array1, 59 cells) and 15.1 ± 7.8 nN (Array4, 39 cells). A nonparametric Dunn test of multiple comparisons after significant Kruskal–Wallis test confirmed that the data set of each of the array was different. Hence, this result suggests that biological and technological (e.g., pillar geometry) variability in our data could easily be underestimated. In what follows, we thus defined results of cellular forces that fall in the range of 10.4–15.1 nN as indistinguishable from the control experiment at the 1-g condition.

Furthermore, we compared the total absolute force with the ratio of the number of deflected pillars to the number of pillars underneath the cell (Fig. S3 A). This ratio gives insight in how strong the total absolute force applied by cells on substrates increases with the percentage of the corresponding adhesive and involved area. The comparison of both quantities is highly correlated $\left(0.7<\left|r\right|\le 0.9\right)$. We conclude that the total absolute force divided by the deflected pillar to total pillar ratio is another robust measure of cellular forces when technological variability is properly considered. In the following, we call this quantity force per unit area. The cellular force per unit area varied in the data set of the six independent produced arrays between 1.6 ± 0.9 mN (Array1, 59 cells) and 2.1 ± 1.2 mN (Array3, 54 cells) (Fig. S3 B).

In comparison to the previous correlation, we compared the cell size to the cellular force per pillar (Fig. 2 C). The cell size was calculated from the number of pillars underneath the cell as described in the Image analysis section. In contrast to the strong correlation between total absolute force and deflected pillar to total pillar ratio, the correlation coefficient between traction force per pillar and cell size was small $\left(0.05<\left|r\right|\le 0.27\right)$.

Subsequently, we compared the 1-g results to those obtained for hypergravity conditions. Cell-loaded micropillar arrays immersed in 12-well plates were placed into the incubators of two gondolas of the LDC at ESA/ESTEC. Together with the control at standard 1-g gravity condition, we exposed cells to three different g-levels. For statistical reasons, we performed two independent experiments for 16 h each at 1 g, 5.4 g, and 10 g and one experiment at 1 g, 10 g, and 19.5 g, respectively. The g-vector acted perpendicular to the cell-spreading area. Arrays were located in both the upright (positive g-vector) and the upside down (negative g-vector) orientation. For analysis, cells were fixed, stained, and imaged remotely.

As predicted from our 1-g experiments, the total force per cell highly correlated with the number of deflected pillars also under hypergravity conditions for both the upright and the upside down orientation. Data for the upright orientation (positive g-vector) are shown in Fig. 3 A. The correlation coefficient of $0.8\le \left|r\right|\le 1$ was equivalent to that found for 1 g. Furthermore, for both orientations and all g-levels, the correlation between the total absolute force and the ratio between the number of deflected pillars and the pillars underneath the cell was strong $\left(0.7<\left|r\right|\le 0.9\right)$ (Fig. S3, C and E). This matches our 1-g prediction as well. In addition, we verified that the force per pillar was independent on the cell-spreading area. The correlation is shown in Fig. 3 D for two sets at two different g-levels. The data were uncorrelated as inferred from the low value of the correlation coefficient, $\left|r\right|<0.11$. Hence, as for the 1-g condition, the mean force per deflected pillar and the force per unit area are robust measures to characterize cellular forces also under hypergravity conditions.

Figure 3.

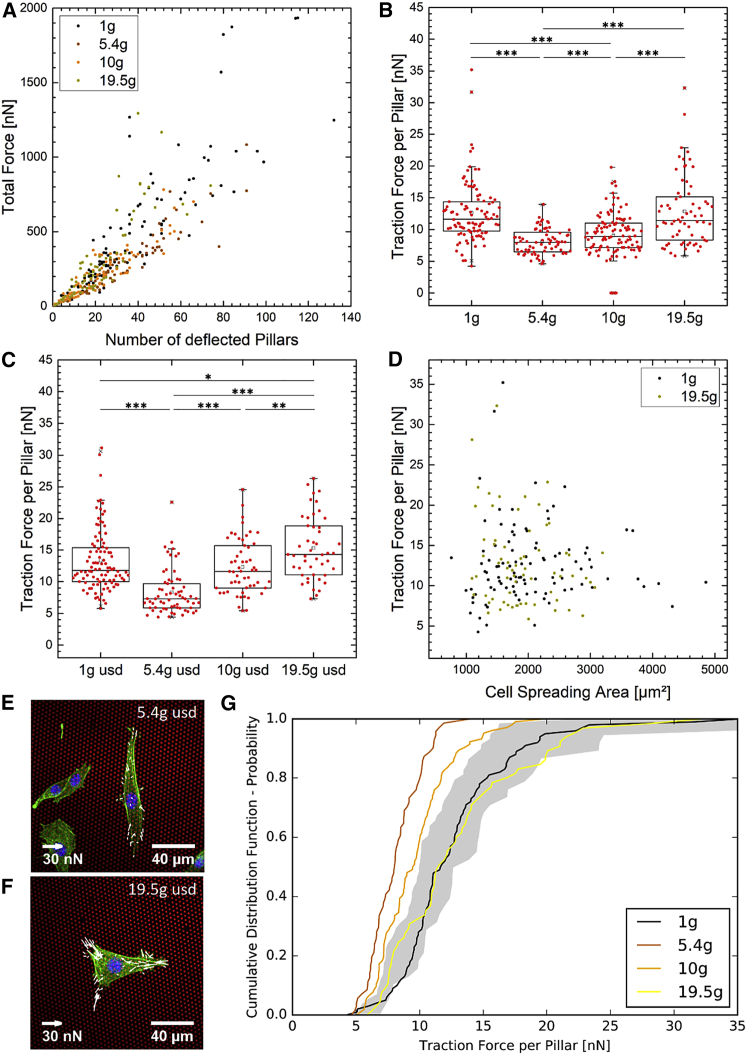
3T3 fibroblasts were exposed to hypergravity in upright and upside down (usd) orientation. The total force per cell increases linearly with the number of deflected pillars of cells exposed to 1 g, 5.4 g, 10 g, and 19.5 g in an upright orientation (A). The ratio results in the traction force per deflected pillar for cells in upright (B) and usd orientation are shown (C). Dunn test of multiple comparisons after a significant Kruskal–Wallis test was performed (*p ≤ 0.05; **p ≤ 0.01; ***p ≤ 0.001). The traction force decreases from 1 g to 5.4 g and increases from 5.4 g to 19.5 g. This effect is independent from the cell-spreading area (D, upright orientation). Two of four randomly chosen data sets are shown. Each data point represents one analyzed cell. In the usd orientation, the biggest difference is between 5.4 g (E) and 19.5 g (F). Red depicts a pillar array, green depicts an actin filament, and blue depicts a nucleus. Compared with experiments under 1-g gravity conditions, cells in upright orientation exert less force on pillars at 5.4 g and 10 g (G). The gray range is the defined force limit for cell traction forces under 1-g conditions. This limit is set by the minimal and maximal averaged cell force of the six micropillars at 1 g in Fig. 2B. To see this figure in color, go online.

In turn, we analyzed the averaged force per deflected pillar for the various hypergravity levels (Fig. 3, B and C). In both orientations, the force per pillar decreased significantly when hypergravity was changed from 1 g to 5.4 g. When hypergravity was increased further to 10 g and 19.5 g, respectively, the force per pillar increased again, finally exceeding the value at 1 g. In the upright orientation (positive g-vector, Fig. 3 B), cells applied significantly less force on pillars at 5.4 g with an average of 8.1 ± 2.0 nN and 9.1 ± 3.7 nN at 10 g, respectively. At 19.5 g, the traction force per deflected pillar with an average of 12.9 ± 5.4 nN was not significantly different from 1 g with 12.7 ± 4.8 nN. Comparisons of different g-levels with the lowest and highest distribution of 1-g arrays (Fig. 2 A), Array1 and Array4 respectively confirm the trend (Tables S1 and S2). The strongest effect and biggest difference was measured for cells in upside down orientation (negative g-vector, Fig. 3 C). In this orientation, cells applied the lowest force per pillar at 5.4 g with an average of 8.3 ± 3.5 nN and the highest force with 15.3 ± 5.0 nN at 19.5 g, which is visualized in Fig. 3, E and F. The traction force of the 1 g control with 13.3 ± 4.9 nN was significantly different to both results at 5.4 g and 19.5 g, whereas it was equivalent to the averaged force of 12.3 ± 4.4 nN at 10 g. A two-sided Wilcoxon rank sum test was used to compare the two orientations shown in Fig. 3, B and C. The force per pillar did not differ significantly for the 1 g and the 5.4 g situations. Yet, at higher g-levels, the two configurations were significantly different, with p < 0.001 at 10 g and p = 0.0044 for 19.5 g.

A clearer picture of the significance of the different results was obtained from the analysis of the cumulative distribution function of the mean force per pillar values. From the six 1-g control measurements, we constructed a significance band for the cumulative distribution (gray area in Fig. 3 G). The band was constructed such that all six 1-g control measurements fall into the given range. The forces of cells in the upright orientation exposed to 5.4 g and 10 g are fully outside of the gray range, whereas the 1-g and 19.5-g samples are equal to the standard gravity distributions. This confirms our results of the change of cell traction forces under hypergravity conditions when analyzed by Dunn test of multiple comparisons after a significant Kruskal–Wallis test (Fig. 3 B).

Additionally, we analyzed the force per unit area for all g-levels and both orientations. Equal to the results of the traction force per pillar, the force per unit area decreases significantly from 1 g to 5.4 g followed by an increase again from 5.4 g to 19.5 g (Fig. S3, D and F). The comparison between both orientations show significantly higher values for cells in upside down orientation. Differences were measured between 1 g (p < 0.009), 10 g (p < 0.001), and 20 g (p < 0.001).

Discussion

It has been shown that hypergravity influences cell morphology and behavior. Although the outcome may highly vary (26), it was well documented that hypergravity leads to a rearrangement of the cytoskeleton (23,28). Here, we investigated in how far hypergravity modulates the contractile behavior of cells in an experimental setting that minimizes any shear stress that might influence the outcome. Given that the cytoskeleton represents the main contractile machinery within cells, we anticipated that forces exerted by cells onto their environment would, likewise, change.

We cultured 3T3 fibroblasts on elastic micropillar arrays and exposed them for 16 h to hypergravity at a range of g-levels. As we predicted, cellular forces changed for hypergravity conditions: we found an initial decrease of forces from 1 g to 5.4 g, followed by a subsequent increase in forces at least up to 19.5 g. These findings cannot be explained by potential bending of pillars caused by weight gain of pillars and cells during the hypergravity impact, which we calculated to be 4.7 pN, much smaller than the experimental background in pillar detections, which is equivalent to 0.7 nN.

Our results corroborate earlier findings, elucidating the reorganization of the actin network that will have a reflection in cellular force application as investigated in our study. Versari et al. cultured human umbilical vein endothelial cells in a medium-sized centrifuge for acceleration research and found less-dense actin fibers after 96 h at 3.5 g (34). The decrease in actin stress fibers at low hypergravity levels validates our results on a decrease in traction forces at 5.4 g. Also, the more recent results by Costa-Almeida et al., who exposed human-tendon-derived cells to 5 g, 10 g, 15 g, and 20 g for 4 and 16 h (35), align well with our interpretation. After 4 h, the anisotropy of actin fibers in human-tendon-derived cells was significantly lower at 5 g as compared to 1 g and increased toward higher g-levels. It should be noted that cells initially strengthen their cytoskeleton upon gravitational challenge, yet that this fast initial response fades out after 10 min (24). Translating those studies on the organization of the cytoskeleton in terms of cellular force application appears straightforward. Cellular traction forces are the result of the actomyosin cytoskeleton contractility. Molecularly, myosin motors generate pulling forces on actin fibers, which, in turn, leads to the transfer of forces to the ECM as measured in the current study. Depolymerization of actin or inhibition of myosin activity leads to cytoskeletal rearrangements and the decrease in traction forces (36).

Other external stress measurements showed a similar effect on the actin filament formation. Kataoka et al. performed flow-imposed experiments. Using a parallel flow plate chamber, endothelial cells were exposed to different flow directions for 24 h. Under fluid-shear stress as low as 2 Pa, cells perfectly aligned with the flow direction and formed thick stress fibers (37). Kuo et al. applied an oscillatory shear stress with a frequency of 1 Hz on cells. Under lower shear stress, the phalloidin-labeled F-actin signal decreased at 0.05 Pa (38) after 0.5 h, which indicates a reorganization of actin filaments. In terms of the cell volume (density, 1.08 g mL^–1 (32); height, 15 μm), 1 g can be assigned to a shear stress of 0.16 Pa, 10 g to 1.6 Pa, and 20 g to 3.2 Pa. Likewise, Szulcek et al. performed oscillating experiments of 15 min intervals at 2 g, which showed enhanced VE-cadherin and F-actin formation in endothelial cell monolayers (39). F-actin formed a well-organized actin cortex and considerable actin stress fibers in the cytosol (40). According to our interpretation, the cortical actin might be a signature of an increase in cell-cell adhesion and will counterbalance the increase in cytosolic F-actin contractility, thereby reducing the cell-ECM adhesion and thus cell traction forces. Hence, fluid-shear stress and hypergravity seem to have a similar impact on the actin reorganization of cells and possibly on cell traction forces. Care must be taken that fluid-shear stress as a surface force acts parallel to the spread cell and only on the affected surface area. In contrast, hypergravity as a body force acts perpendicular to it and on all parts of the cell volume.

Furthermore, it was found that the internal organization of the cytoskeleton alters with mechanical challenge. Norstrom et al. studied shear thickening of cross-linked F-actin networks. Performing rheological experiments, the authors observed viscous deformation of stresses from 0.001 to 10 Pa, caused by stress stiffening and shear thickening. Surprisingly, and in contrast to earlier findings in which stress weakening of sparsely cross-linked actin network was measured, Norstrom et al. observed a stress-stiffening behavior of a densely cross-linked network (41). This finding is consistent with the report by Gardel et al. (42) who highlighted the connection between the elasticity of the actin network, the density of cross-linkers, and the actin concentration.

Combining the data of Norstrom et al. and Gardel et al. with our findings, an interaction between the external g-level acting on the cell and the elasticity of its actin network appears apparent. At low hypergravity levels, for which a loss of stress fibers have been reported (38), a less-dense, cross-linked actin network with less oriented stress fibers seems to be formed. This would result in a decrease in cell traction forces. At larger g-levels, the actin network would restructure again into an oriented, densely packed stress fiber network, which is highly cross-linked. Those fibers will result in higher traction forces because of stress stiffening. The formation of stress fibers at higher g-levels has been observed by Costa-Almeida et al. Our result of the force per unit area, the total absolute force per deflected pillars to pillars underneath the cell ratio, supports such model. First, we measured a decrease of cell contractility from 1 g to 5.4 g, as the absolute force on pillars applied by a unique cell is smaller at 5.4 g as compared to 1-g conditions. This correlates to our suggestion of a weaker actin network at 5.4 g. The increase of the total absolute force of a defined cell in size and adhesion area increases from 5.4 g to 19.5 g, which indicates to stronger actin stress fibers for higher g-levels. Additionally, we measured significantly higher forces per unit area of cells in upside down orientation. This suggests that a cell applies higher forces on pillars in this orientation (negative g-vector) compared to the upright orientation (positive g-vector), probably to prevent detachments. In future experiments, it would be interesting to look whether or not the amount of focal adhesion molecules like vinculin increases under higher hypergravity conditions, especially for negative g-vectors in the upside down orientation.

Hence, based on our results, we propose that hypergravity causes a reorganization of the actin network depending on the g-level, where gravitation acts similar to that reported for fluid-shear stress. Reorganization of the cytoskeleton subsequently causes a change in traction force that was observed in our experiments.

Conclusion

In conclusion, we demonstrated that hypergravity modulates the traction force of 3T3 fibroblasts. Dependent on the g-force level, the cell traction force first decreases for low hypergravity conditions, yet increases for higher g-levels. We found that cells in upside down orientation were more affected compared to cells in upright orientation. We propose that the change in cellular force-response reflects the reorganization of the cytoskeleton as triggered by a gravitational cue, very similar to cellular responses to fluid-shear flow. Further studies should be employed to investigate the involvement of, e.g., the myosin activity, and the actin stress fiber formation on the force transduction at altered gravity conditions. Our data should be considered to estimate potential health-risks for fighter pilots and in planned long-haul space flights.

Author contributions

Sample preparation, J.E.; conducted hypergravity experiments, J.E. and J.J.W.A.v.L.; data analysis, J.E. and T.S.; writing manuscript, J.E., J.J.W.A.v.L., L.M.E., and T.S.; initiated the study, J.J.W.A.v.L. All authors gave final approval for publication.