The influence of cell elastic modulus on inertial positions in Poiseuille microflows

Abstract

Microchannels are used as a transportation highway for suspended cells both in vivo and ex vivo. Lymphatic and cardiovascular systems transfer suspended cells through microchannels within the body, and microfluidic techniques such as lab-on-a-chip devices, flow cytometry, and CAR T-cell therapy utilize microchannels of similar sizes to analyze or separate suspended cells ex vivo. Understanding the forces that cells are subject to while traveling through these channels are important because certain applications exploit these cell properties for cell separation. This study investigated the influence that cytoskeletal impairment has on the inertial positions of circulating cells in laminar pipe flow. Two representative cancer cell lines were treated using cytochalasin D, and their inertial positions were investigated using particle streak imaging and compared between benign and metastatic cell lines. This resulted in a shift in inertial positions between benign and metastatic as well as treated and untreated cells. To determine and quantify the physical changes in the cells that resulted in this migration, staining and nanoindentation techniques were then used to determine the cells’ size, circularity, and elastic modulus. It was found that the cells’ exposure to cytochalasin D resulted in decreased elastic moduli of cells, with benign and metastatic cells showing decreases of 135 ± 91 and 130 ± 60 Pa, respectively, with no change in either size or shape. This caused benign, stiffer cancer cells to be more evenly distributed across the channel width than metastatic, deformable cancer cells; additionally, a decrease in the elastic moduli of both cell lines resulted in increased migration toward the channel center. These results indicate that the elastic modulus may play more of a part in the inertial migration of such cells than previously thought.

Significance

The effect that elasticity has on the advection of cells, particles, or vesicles and their inertial positions in channels has important applications both within and without the body. It is critical to further our understanding of such concepts because they will inform the design of in vitro diagnostic and treatment techniques such as flow cytometry and lab-on-a-chip devices, as well as facilitating a greater understanding of different illnesses in vivo, such as malaria, sepsis, or even metastatic cancer. Indeed, it may also aid the improvement of cell separation techniques, which already rely on the difference in elastic modulus between cells.

Introduction

The advection of suspended cells through microchannels is a phenomenon present in in vivo lymphatic and cardiovascular capillaries of ∼100–300 (1, 2, 3, 4, 5) and 5–10 μm (2, 3, 4, 5), respectively, as well as one that is exploited in vitro in microfluidic techniques such as lab-on-a-chip devices, flow cytometry, cell separation, and CAR T-cell therapy. Despite this, little is known about the extent of how the physical properties of these cells influence their inertial positions.

Inertial migration, first described by Segré and Silberberg in 1962 (6,7), takes place when particles flowing in a channel migrate to, and occupy, distinct locations within that channel. For example, particles flowing in a circular pipe will form an annulus at 0.6 of the channel’s radius, whereas in a rectangular channel, at low flow rates, particles migrate to the center of the two longer walls (8, 9, 10, 11). These inertial positions may change slightly because of the balance of forces acting on the particle. Wall-induced lift and shear-gradient-induced lift forces dominate; however, Saffman lift, Magnus lift, and the deformability-induced lift forces can also play key roles (12). In particular, the latter can have a strong influence when particles are replaced by suspended cells. Indeed, it has been shown computationally that the Reynolds number (Re) does not affect the inertial positions or migration time of deformable particles (13), unlike their rigid counterparts.

Deformability-induced lift affects nonrigid particles such as cells or vesicles when they experience the stresses described previously, which cause them to change their shapes. It has been argued that deformability-induced lift is due to this shape change (12,14); however, it can also be attributed to the surface tension gradients at the interface between the fluid and the particle or cell surface (15). Therefore, the capillary number (Ca), describing the surface tension gradient, and the viscosity ratio (λ_p), describing the particle shape, need to be considered. Ca can be defined as (16)

$$Ca=\frac{\mu \gamma d_p}{2G_p},$$ (1)

where μ is the fluid viscosity, γ is the velocity gradient (which can be defined as γ = $\left(32Q/\pi D^3\right)$ for pipe flow, where Q is the fluid flow rate and D is the diameter of the channel), d_p is the diameter of the particle, and G_p is the shear modulus of the cell (which can be defined as G = $\left(E/3\right)$ for human tissue (17), where E is the elastic modulus). λ_p can be defined as

$${\lambda }_p=\frac{{\mu }_p}{\mu },$$ (2)

where μ_p is the internal viscosity of the deformable particle or the cell. It has been found previously that a more deformable particle (or one with a low E) tends to migrate toward the channel center, whereas stiffer, more rigid particles remain closer to the channel walls (9,11,18). The deformability-induced lift (F_D) that deformable particles had been exposed to in a channel has been derived by several studies (9,18, 19, 20) and holds true given that the particle is not too close to the channel walls ($\left(D/2\right)$ − r > d_p, where r is the radial position of the particle in the channel) and that 1 < λ_p < 10. It has been postulated that cells experience lift forces comparable with those predicted by these equations at lower lift forces (20).

The final steady-state distribution of these particles is a balance between these lift forces and the shear-induced diffusion due to hydrodynamic interactions between vesicles (21, 22, 23, 24, 25, 26, 27). Whereas the lift forces focus particles in a laminar flow toward a point, the shear-induced diffusion causes a greater particle dispersion across the channel diameter. This shear-induced diffusion is proportional to the volume fraction times the shear rate (24,26). Previous studies examining the effect of shear-induced diffusion with respect to different volume concentrations of red blood cells (RBCs) have found that below an RBC volume fraction of 10% in a bidisperse solution, migration forces (derived from lift forces) are considerably larger than the mixing forces (or the shear-induced migration force) (24). Furthermore, at low solid volume fractions (<1%), it has been found that effects due to these shear-induced diffusions dominate solid particle trajectories at low Re (Re < 1), whereas flows transition to particles governed by inertia-induced lift forces at higher Re (Re > 10) (27). Although effects from these forces, however, can be considered negligible in dilute suspensions of solid particles, additional repulsions develop when these suspensions include deformable particles such as drops, vesicles, or cells (23).

The E of the particle also heavily influences its migration speed, with more deformable particles reaching equilibrium positions quicker (13,28). Because previous studies have shown agreement of cell behavior in comparison to that of deformable droplets (29), it is anticipated that it will similarly affect the migration speeds of cells, with more pliable cells reaching their equilibrium positions faster than their stiffer counterparts.

Different cell types within the body present different shapes, sizes, and deformabilities. RBCs need to be sufficiently compliant to squeeze through capillaries, whereas osteocytes require a much higher degree of stiffness to give structure and support to the body. Indeed, there can be differences in elastic moduli between cells of the same type, with a change in cell E having previously been shown to indicate disease progression (30). Malaria causes an increase in the shear elastic modulus of the membrane of RBCs (31,32), and leukocyte elasticity increases in patients diagnosed with sepsis (33,34). Conversely, decreased cancer cell elastic modulus is associated with increasing metastatic capabilities (35, 36, 37, 38). This is important for cells in suspension in particular (such as RBCs, leukocytes, and circulating tumor cells) because a change in E may affect the deformability-induced lift acting on the cell and therefore its inertial position. Indeed, prior studies have shown that cells experience a deformability-based shift more akin to those of deformable microparticles than rigid microparticles (29).

Previously, it has been found that microparticles of different deformabilities distribute differently across rectangular channels (29), as well as different cell types of different deformabilities in both circular and square microchannels (39, 40, 41). It was demonstrated by this group that benign, stiffer MCF-7 breast cancer cells were evenly dispersed across the square channel’s width in comparison with metastatic, deformable, MDA-MB-231 breast cancer cells, which remained at the channel center (40); further investigations found similar results in circular channels (41). It was hypothesized that this is because a lower elastic modulus results in an increased deformability-induced lift, directing the cells toward the channel center. Indeed, recent studies have shown that deformable cells travel faster in such microchannels than their more rigid counterparts of equivalent size, probably because they migrate toward the channel centerline where fluid velocities are higher (42).

It has also previously been shown, both computationally and experimentally, that the shape of rigid particles can influence their migration patterns in a microchannel (43, 44, 45, 46). It is quite likely that it will similarly affect deformable particles such as cells. Adherent MCF-7 cells appear rounded in shape, whereas MDA-MB-231 cells are more elongated in one direction and therefore spindle-shaped. It has been hypothesized that deformable particles suspended in flow experience stresses that can cause it to change its shape (14,47), and therefore, it may also affect the cells’ inertial positions; however, some of the above studies have shown that centerline-focusing particles typically have fore-aft asymmetry characteristics, similar to “fish” or “bottle”-like shapes (45), which MDA-MB-231 cells also possess when adherent. Interestingly, other studies have found that the direction of lateral migration of a deformable droplet in a ferrofluid depends on the orientation of the droplet because of uniform magnetic fields at different directions (48). This raises the question of whether a cell’s orientation will also influence its direction.

There is a lack of reported data in the literature on the quantification of cell E compared with cells’ inertial positions. Previous studies have compared the inertial positions of metastatic or infected cells with benign or healthy cells in the knowledge that there was a difference in the elastic modulus (40,41); however, this difference was never quantified, and therefore, the boundary conditions of cell E that have an influence on their inertial positions have not been investigated. In the context of cancer cells specifically, a slight contradiction exists, whereby more metastatic cancer cells are known to be more deformable. From a microfluidics perspective, this would imply that more metastatic cells are more likely to travel at the channel center, which, from a biological perspective, seems unlikely to be the case if these cells are also more likely to extravasate through the channel wall. It is hoped that this study will go toward explaining such phenomena. Furthermore, this study modifies the properties of the same two cell lines in the same system. Previous studies comparing two different cell types were limited by the assumption that differences were due to any physiological diversities between the cell types. This investigation conclusively shows that there exists an important relationship between cell deformability and inertial position.

The aim of this work is to investigate the effects that different E have on the inertial positions of cancer cells. Cytochalasin D—an alkaloid that, when used to treat cells, disrupts their actin microfilament cytoskeleton, thus altering their physical properties (49,50)—was used to decrease the elastic modulus of two representative cell lines, MCF-7 and MDA-MB-231 breast cancer cells, to different levels. These cells were chosen because they have previously been shown to occupy different inertial positions in both square and circular microchannels (40,41) as well as to possess significantly different elastic moduli (35, 36, 37, 38) and similar sizes. Additionally, both cancer cell lines are derived from the same tissue source. Particle streak imaging was used to determine their inertial positions in circular microchannels. Upon observing a shift in the locations of treated and untreated cells, as well as a difference between cell types, the sizes, shapes, and elastic moduli of the cells were investigated to determine which of these mechanical properties influenced the cells’ inertial positions. The sizes and shapes of cells in suspension were determined using cell imaging, and nanoindentation techniques were used to compare their elastic moduli. This nanoindentation technique has previously been used to determine the elastic modulus of cells (51, 52, 53, 54) and other biological materials (55). This will further knowledge of the effect that cell E has on the advection of cells and their inertial positions in channels, informing the design of in vitro diagnostic and treatment techniques. Indeed, it may also aid the improvement of cell separation techniques, which already rely on differences in E between cells (32,39,56).

Materials and methods

Cell lines and cell culture

Two representative cell lines, MCF-7 breast cancer cells and MDA-MB-231 breast cancer cells (ATCC, Middlesex, UK), were used for comparison of cells with differing elastic moduli. MCF-7 cells were maintained in cell media, consisting of Dulbecco’s modified Eagle’s medium (DMEM), (Sigma-Aldrich, Arklow, Ireland), supplemented with 10% fetal bovine serum (Sigma-Aldrich), 1% penicillin/streptomycin (Sigma-Aldrich), and 0.5% L-glutamine (Sigma-Aldrich). MDA-MB-231 cells were maintained in DMEM supplemented with 20% fetal bovine serum, 1% penicillin/streptomycin, and 1% L-glutamine. Both cell lines were cultured in an incubator at 37°C and 5% CO₂. Cell numbers and sizes were measured before experiments using a LUNA Automated Cell Counter (Logos Biosystems, Villeneuve d’Ascq, France). MCF-7 cells were found to have an average diameter of 18.2 ± 0.8 μm, and MDA-MB-231 cells were measured to be 16.0 ± 1.2 μm in diameter.

Determination of actin filament depletion in adherent cells

Cell preparation

MCF-7 and MDA-MB-231 cells were cultured as described previously in black-walled 96-well microplates (Grenier Bio-One, Kremsmünster, Austria); 12 wells contained MCF-7 cells, and three contained MDA-MB-231 cells. To alter the E of MCF-7 cells, some were treated with cytochalasin D before experimentation (49,50). Upon reaching 70–80% confluency, cells were washed with phosphate-buffered saline (PBS) and incubated with 43.75 ng/mL of N-formyl-Met-Leu-Phe (fMLP; Sigma-Aldrich) in PBS for 2 min. This was then replaced with a PBS solution containing 43.75 ng/mL of fMLP and 5.1 μg/mL of cytochalasin D (Sigma-Aldrich). Cells were incubated with this solution for different lengths of time depending on the experimental condition—condition 1, 5 min; condition 2, 15 min; or condition 3, 35 min—with three wells for each condition. After the second incubation period, the solution was removed and the cells were washed with PBS and fixed in 4% formaldehyde (Sigma-Aldrich). Actin staining was performed using phalloidin stain (Bio-Sciences, Dublin, Ireland), and nucleus staining was performed using 4’,6-diamidino-2-phenylindole (DAPI) stain (Bio-Sciences).

Experimental apparatus

Cells that had been fluorescently labeled with phalloidin and DAPI were imaged using an ImageXpress Micro Confocal High-Content Imaging System (Molecular Devices, San Jose, CA) and MetaXpress High-Content Image Acquisition and Analysis Software (Molecular Devices ). 42 sampling sites in each well were imaged. The cell sizes and phalloidin intensities in the images were analyzed using CellProfiler (Broad Institute, MA) (57), and these data are presented as ± standard errors from the mean. Statistical analysis was conducted using analysis of variance (ANOVA), and two sample unequal variances were used to calculate the p-values between groups.

Determination of cell inertial positions

Microfluidic device

To investigate the inertial positions of the cells, four differently sized circular microchannels were used. These consisted of 100 μm inner diameter (ID) perfluoroalkoxy alkane (PFA) tubing (Cluzeau Info Labo, Sainte-Foy-la-Grande, France), 150 μm ID PFA tubing (Cluzeau Info Labo), 300 μm ID tetrafluoroethylene (TFE) tubing (Sigma-Aldrich), and 800 μm ID TFE tubing (Sigma-Aldrich). In short, the tubing was housed in petri dishes (90 mm diameter; Fisher Scientific Ireland, Dublin, Ireland) that were filled with water to prevent optical distortion during image acquisition. Because water has a similar refractive index (1.33) as both PFA (1.34) and TFE (1.35), it was assumed that errors in the radial positions of the cells due to refraction during image acquisition were negligible. Similar devices have previously been used (41,58,59).

Cell preparation

MCF-7 and MDA-MB-231 cells were cultured as described previously. Upon reaching 70–80% confluency, cells were washed with PBS and incubated with an fMLP solution followed by a cytochalasin D solution, as described previously. Again, cells were incubated with this solution for 15 min. After the second incubation period, the solution was removed, and cells were washed with PBS, detached using trypsin (Sigma-Aldrich), and fluorescently labeled using CellTrace Yellow (Bio-Sciences). They were then resuspended at a concentration of ∼1000 cells/μL in serum-free DMEM and 20% Percoll (Sigma-Aldrich). Percoll was used to prevent cell settling and has no effect on the cell viability (60). To determine the optimal quantity of Percoll, cells were suspended in media with different quantities of Percoll in test tubes over 24 h, after which a visual inspection and viability assessment were carried out (for these findings, see Table 1). In the case of both cell types, a Percoll concentration of 20% was chosen as the appropriate proportion. The volume fraction of cells was calculated to be 0.32%. Previous studies have advised the use of volume fractions of <1% to minimize the effects from cell-cell interactions (9,61,62). Indeed, those examining hematocrit levels of RBCs found that activity due to this phenomenon was minimal below a volume fraction of 0.5–2% (63, 64, 65, 66, 67). The dynamic viscosity and density of DMEM with 20% Percoll were measured to be 1.17 mPa s and 1000 kg/m³, respectively.

Table 1.

Investigated Percoll concentrations, corresponding cell viability, and results of visual inspection

Percoll concentration	Cell viability (%)	Visual observations
0%	91.9 ± 1.05	sunk to the bottom
10%	92.55 ± 0.35	floating close to the bottom
15%	94.5 ± 0.3	floating close to the bottom
20%	91.9 ± 0.85	no obvious cell cluster at any point
30%	72.4 ± 0.48	floating on top
40%	62.8 ± 0.58	floating on top

Viability is presented as the mean of four samples ± SEM.

Experimental apparatus

As described previously (41), a syringe pump (Pump 11 Elite; Harvard Apparatus, Cambourne, UK) was used to infuse the solution through the in vitro model at a constant flow rate. A range of flow rates were investigated, resulting in a range of Re of 5.48–175.86, which are outlined in Table 2. Only conditions that reached a channel Re greater than 5 were used for analysis because it has been previously found that this is the point that cells typically reach their inertial positions (41), and the results garnered in this study agreed with this.

Table 2.

Channel IDs, investigated flow rates Q, and corresponding Re used in the inertial migration experiments

	Channel ID (μm)
Q (μL/min)	100	150	300	800
4.53 × 101	8.22	5.48	–	–
1.94 × 102	35.15	23.43	11.72	–
4.86 × 102	88.2	58.8	29.4	–
9.72 × 102	175.8	117.2	58.6	22.0

An inverted microscope (IX73; Olympus, Southend-on-Sea, UK), was focused on the channel center. A 40× objective lens was used for 100 μm channels, a 20× objective lens for 150 and 300 μm channels, and a 10× objective lens for 800 μm channels. These lenses possessed depths of fields of 1 μm (in the 40× objective lens), 3 μm (in the 20× objective lens), and 12 μm (in the 10× objective lens). Because the depths of fields were, at most, 2% of the channel diameter, it was determined that this was sufficient to prevent distortion from artifacts. The lens was focused ∼20 cm from the channel inlet, which has been found to be a sufficient distance for particle migration to occur, given the experimental fluidic parameters (41). A white LED light source (pE-100; CoolLED, Andover, UK) shining through a filter cube (excitation: 536/40 nm, emission: 607/36 nm) was used to illuminate the fluorescent cells (100% light intensity) as they passed through the microfluidic device. A high-speed camera (Orca Flash 2.8; Hamamatsu Photonics, Welwyn Garden City, UK), was used to capture the images, which were relayed to the computer.

Image acquisition

Images were captured using the HCImageLive software (Hamamatsu Photonics). For each inertial migration experiment, a series of 911 8-bit grayscale images with a resolution of 960 × 720 pixels were captured. The gain and exposure time were set to 200–255 and 20 ms, respectively, and each image sequence was collected over a period of 20 s.

Image processing

Image sequences were processed as previously described (41), using a MATLAB (The MathWorks, Galway, Ireland) script. The tubing wall was located, and all images were cropped to this size. An image matrix was then calculated by averaging the intensity values of the pixels. The intensity distribution function averaged these intensity values across the length of the image window. Finally, the population distribution (DP(x)) curve was calculated:

$$DP\left(x\right)=\frac{\frac{\stackrel{L}{{\sum }_{n=1}}{\left(\frac{{\sum }_{m=1}^{911}{I}_m}{911}\right)}_{x,n}}{L}}{{\int }_0^1\frac{\stackrel{L}{{\sum }_{n=1}}{\left(\frac{{\sum }_{m=1}^{911}{I}_m}{911}\right)}_{x,n}}{L}dx},$$ (3)

where DP(x) is the population distribution curve as a function of x, the position across the channel diameter. L is the length of the image in pixels, and I_m is the m^th image in the image sequence. These distribution curves were averaged for each cell type and experimental condition to obtain population density plots.

Determination of size and shape in suspended cells

Cell preparation

MCF-7 and MDA-MB-231 cells were cultured as described previously. Upon reaching 70–80% confluency, cells were washed with PBS and incubated with an fMLP solution followed by a cytochalasin D solution, as described previously. After the results of the actin staining experiments, all assays conducted hereafter were incubated with this solution for 15 min. After this second incubation period, the solution was removed, and the cells were washed with PBS and detached using trypsin. A sample of trypan blue (Sigma-Aldrich) was mixed with a sample of the cell suspension from each experimental condition.

Experimental apparatus

Cells that had been prepared with trypan blue were imaged using the LUNA Automated Cell Counter (Logos Biosystems). Three samples from three different passages for each experimental condition were obtained, with two images from each sample. The cell sizes were analyzed using the LUNA Cell Counter, and circularity was analyzed using a MATLAB script. Circularity was calculated using

$$C=\frac{4\pi A}{P^2},$$ (4)

where C is the circularity of the cell, A is the cell area, and P is the perimeter of the cell. This results in a dimensionless number between 1 and 0, where 1 is a perfect circle. The cell size and circularity data are presented as ± standard errors from the mean. Statistical analysis was conducted using ANOVA, and two sample unequal variances were used to calculate the p-values between groups.

Determination of cell elastic modulus

Cell preparation

MCF-7 and MDA-MB-231 cells were cultured as described previously in petri dishes (60 mm; Fisher Scientific Ireland). Upon reaching 70–80% confluency, cells were washed with PBS and incubated with an fMLP solution, followed by a cytochalasin D solution, for 15 min. After the second incubation period, the solution was removed, and the cells were washed in PBS, placed in fresh serum-free media, and allowed to stabilize at room temperature.

Experimental apparatus

A Chiaro nanoindenter (Optics11 Life, Amsterdam, the Netherlands) was used to measure cell elastic modulus. A cantilever with a spherical tip of 8.0 μm in radius was used with a spring constant of 0.031 N/m. Before the testing of the samples, the cantilever was submerged in serum-free media and calibrated against a thick glass slide. The sample slides were mounted onto an inverted microscope (IX73; Olympus) to allow for the focusing of the probe over the cell center. Three petri dishes of different passage numbers were used for each experimental condition, with 30 to 40 cells chosen at random and nanoindented in each petri dish (53) at room temperature. The probe was placed over the center of each cell to ensure maximal contact surface; however, it has previously been shown that there is no statistical difference between central and peripheral nanoindentation locations in both cancerous and noncancerous cells (53). Cells were indented up to 6 μm for a duration of 1 s with a loading velocity of 1 μm/s. Indentations that failed to meet a minimal load of 0.008 μN were excluded because such cells were at risk of not being properly attached to the base of the plate. Force-indentation curves were analyzed using the DataViewer Software (Optics11 Life), and the elastic modulus was calculated on the basis of the Hertizan contact model (53,68) using

$$F=\frac{4}{3}{E}_{eff}\sqrt{R_i}{h}^{\frac{3}{2}},$$ (5)

where F is the force, E_eff is the effective elastic modulus, R_i is the radius of the spherical tip, and h is the indentation depth. This model assumes that the tip is parabolic when calculating the contact radius and so is valid to the maximal indentation depth of 16% of the tip radius. Thus, force-indentation curves were analyzed from the initial 22% of the maximal load.

Statistical analysis

After data acquisition, the D’Agostino-Pearson normality test was used to check for a normal distribution in each plate, and outliers were identified using the ROUT method and excluded from the final data set. Data are presented as ± standard errors from the mean. Statistical analysis was conducted using ANOVA, and two sample unequal variances were used to calculate the p-values between groups.

Results and discussion

Effects of cytochalasin D on actin filament depletion in adherent cells

To examine the level of actin depolymerization, cells were fixed, and actin filaments and nuclei were stained with phalloidin and DAPI stains, respectively, and imaged using a confocal microscope. Example images of treated and untreated MCF-7 cells can be seen in Fig. 1. Nuclei (DAPI) are shown in blue, and the actin cytoskeleton (phalloidin) is displayed in green. Similar results were observed in MDA-MB-231 cells.

Figure 1.

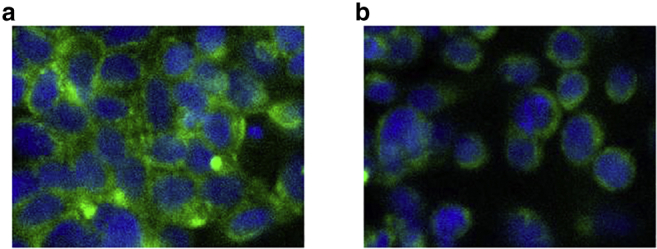
Confocal images of (a) untreated, stained MCF-7 cells and (b) stained MCF-7 cells after exposure to cytochalasin D for 15 min. Cells were stained using DAPI (blue) for nucleus staining and phalloidin (green) for actin staining. To see this figure in color, go online.

As can be seen from the initial raw images, there is a decrease in the intensity of the cells after exposure to the cytochalasin D drug, indicating that a certain degree of actin disruption has taken place. The numbers of cells was counted using nuclear staining, and there were no significant differences detected in the number of cells between treated and untreated wells. These images were then analyzed using CellProfiler (57), examining cell intensity, the results of which are displayed in Fig. 2 a.

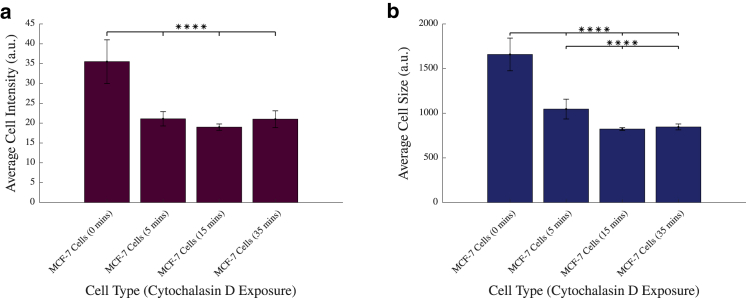
Figure 2.

(a) Average cell intensity of adherent MCF-7 and MDA-MB-231 cells with and without exposure to cytochalasin D. (b) Average cell size of adherent MCF-7 and MDA-MB-231 cells with and without exposure to cytochalasin D is shown. ^∗∗∗∗p < 0.0001; vertical bars represent the SEM. To see this figure in color, go online.

Fig. 2 a shows a significant decrease of between 40.6 and 46.5% in the fluorescent intensities of these cells between untreated MCF-7 cells and all other levels of treatment (p < 0.0001). However, this effect plateaued after longer exposure to cytochalasin D, with no significant change in cell intensities recorded between the 5, 15, and 35 min groups. For this reason, all further experiments were conducted after exposing cells to cytochalasin D for 15 min. Additionally, this exposure time has been used by previous studies examining its effects (49). Furthermore, the data illustrate, in agreement with previous literature (49), that exposure to cytochalasin D results in inhibited actin filament polymerization, leading to a reduction in phalloidin-stained actin and therefore a significant decrease in cell intensity across the plate. A significant reduction in cell size of between 36.9 and 50.4% between untreated MCF-7 cells and all treatment groups (p < 0.0001), as seen in Fig. 2 b, is consistent with decreased cell spreading and an increase in cell rounding because the reduction of supporting actin filaments causes reduced structural support in the cell, causing it to collapse in on itself, a typical effect of actin depolymerization in the cell (69).

Cell inertial positions

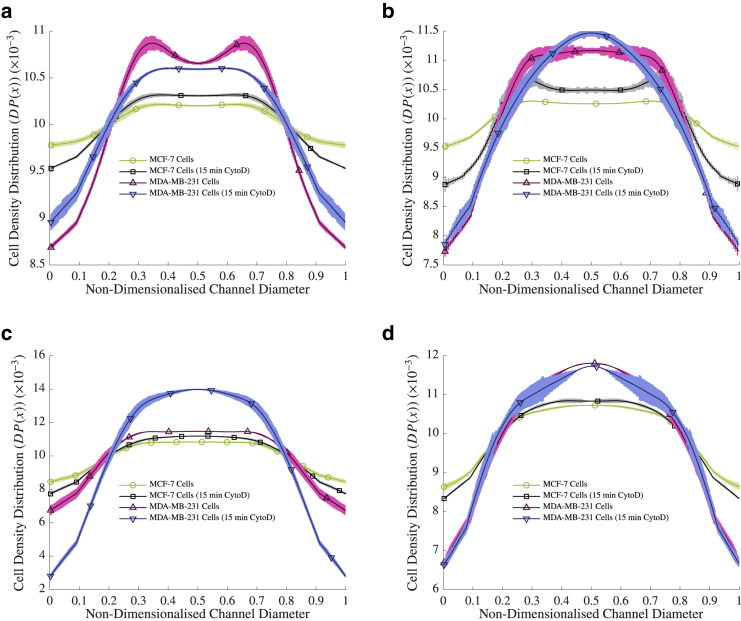
To test the inertial positions of cells in different sized channels, streak images of the cells advecting in the channels were obtained. The cells were then further perturbed with cytochalasin D to investigate whether their position would change. Population density distribution curves were calculated from 12 data sets comprising 911 images for each experimental condition, as described previously, and experiments of different η were compared to each other (where η is the particle/diameter ratio ($\left(d_p/D\right)$)). These were compared with both untreated MCF-7 cells and MDA-MB-231 cells, the results of which can be seen in Fig. 3.

Figure 3.

The population density distributions of cells at Re > 5 at (a) η ≈ 0.171, (b)$\eta \approx$ 0.114, (c)$\eta \approx$ 0.057 and (d)$\eta \approx$ 0.021. The population of the cells at each point in the diameter of the channel are plotted as a percentage of the total cell population in the channel, where 0 and 1 are the channel walls. The lighter shading represents the SEM. Note that the markers are for visualization purposes only, to differentiate between lines, and are not representative of the points measured in the experiment. To see this figure in color, go online.

The results agree with previous findings that the MDA-MB-231 cells were focused in the channel center, whereas MCF-7 cells were more evenly distributed across the channel width (9,11,18) at all η. For example, at η ≈ 0.171, 61.46% of MCF-7 cells were focused between 0.6 of the channel radius in comparison with 63.78% of MDA-MB-231 cells, whereas at η ≈ 0.021, 63.35% of MCF-7 cells were focused between 0.6 of the channel radius in comparison with 67.51% of MDA-MB-231 cells. After the addition of cytochalasin D to the rigid MCF-7 cells, inertial migration began to occur toward the center of the channel in all cases in the same direction as the MDA-MB-231 cells, with, for example, an increase of 0.23% of MCF-7 cells between 0.6 of the channel radius after cytochalasin D exposure at η ≈ 0.171 and an increase of 1.52% of MCF-7 cells between 0.6 of the channel radius after cytochalasin D exposure at η ≈ 0.114. Furthermore, the MDA-MB-231 cells, after cytochalasin D exposure, also migrated toward the channel center in all channels apart from at η ≈ 0.171. Interestingly, the extent of migration seemed to decrease in the larger η ≈ 0.021 channel after exposure to the drug. This may indicate a decreased dependency of inertial migration effects on cell E in larger channels.

Because all experimental sets were conducted over the same fluidic conditions, including flow rates and channel sizes, the discrepancies in the inertial positions of the different cells and their treated counterparts must be due to the physical properties of the cell. As previously discussed, according to the balance of particle force equations that dictate the inertial position of the cells, this could be due to either the diameter of the cell or its E.

An additional consideration to be taken into account, as mentioned previously, is the shear-induced diffusion experienced by the cells because of collisions and hydrodynamic interactions of the cells in flow. Though the volume fraction is low (∼0.32%), the shear rates encountered in this experiment are quite large (ranging approximately from 320 to 160,000 s⁻¹). Therefore, because the shear-induced diffusion is proportional to the volume fraction by the shear rate (23), it is likely that it has some effect on cell dispersion. Furthermore, the increased focusing observed with a decreasing E resulted in higher local cell volume fractions at the channel center, thereby increasing the shear diffusivity here. From these results, the local volume fraction of cells between 0.6 of the channel radius increased by up to 19.5%, which, because of the proportional relationship, would lead to a similar-sized increase in the diffusivity. Therefore, the additional spread of population distributions can be explained by collisions and interactions between the individual cells (21,25,26). This effect was then balanced out by the inertial lift forces, influenced by the deformability of the cells, to give the inertial distributions shown in Fig. 3.

A potential change in E leads to changes in Ca and λ_p, which can induce a shape change, thereby impacting the cell’s position. Indeed, it has been shown experimentally that the viscosity of a cell increases significantly with increased actin polymerization (70), implying that depolymerization results in decreased viscosity. This, in turn, reduces λ_p, which occurs with exposure to cytochalasin D. This pushes more deformable cells toward the channel center, which agrees with previous computational studies on droplets (28). For this reason, the size and shape of both treated and untreated cells in suspension were measured. The elastic modulus was chosen as a good measure of deformability because this parameter has recently been used to examine its effects on cell-like particles (29), and so, nanoindentation experiments were conducted on both treated and untreated cells from each cell type.

Effects of cytochalasin D on size and shape in suspended cells

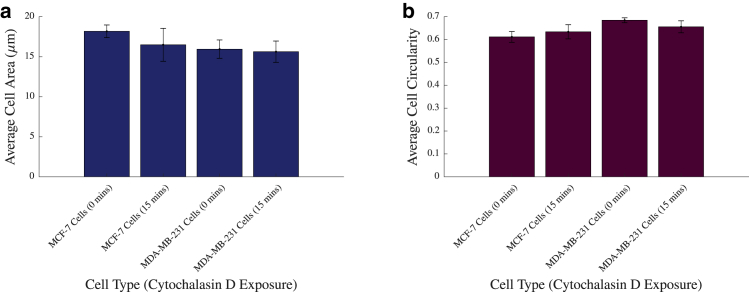
Cells in suspension were imaged to ascertain the effects of cytochalasin D on the cell size and circularity. These images were then analyzed using a MATLAB script, the results of which are displayed in Fig. 4, a and b, respectively.

Figure 4.

(a) Average cell size of suspended MCF-7 and MDA-MB-231 cells with and without exposure to cytochalasin D is shown. This is in contrast with the size of adherent cells measured in Fig. 2b. (b) Average cell circularity of suspended MCF-7 and MDA-MB-231 cells with and without exposure to cytochalasin D is shown, vertical bars represent the SEM. To see this figure in color, go online.

Fig. 4 a indicates that overall, the level of cytochalasin D exposure had no significant effect on the sizes of MCF-7 cells (p = 0.7596 and p = 0.9983). Furthermore, there was no significant size discrepancy between untreated MCF-7 cells and untreated MDA-MB-231 cells (p = 0.6702). Fig. 4 b also shows that there is no statistically significant change in circularity in these cells after treatment with cytochalasin D (p = 0.9105 and p = 0.8314 in MCF-7 and MDA-MB-231, respectively). Additionally, there were no significant differences between MCF-7 or MDA-MB-231 cells (p = 0.2186). These results indicate that, because of reduced internal support by the depletion of the actin filament, cytochalasin D does not affect the size of the cell in suspension or its shape. However, more importantly, it verifies that the changes observed in the cells’ inertial positions after treatment of cytochalasin D cannot be attributed to a change in either the size of the cell or its shape.

Cell elastic modulus

Because it was ascertained that the observed change in the inertial positioning of the cell was due to neither a change in its size nor its shape, the elastic moduli of different cell types exposed to cytochalasin D were then investigated to determine whether a change in the cells’ deformabilities had occurred. This was carried out using nanoindentation, a technique outlined previously. Because it is difficult to establish the absolute value of the elastic moduli of cells, with little agreement between previous studies (which can vary by up to five orders of magnitude (36,38,71, 72, 73)), the aim of this experiment was to establish whether there were differences between the elastic moduli of the cells, that is, to compare them relatively to each other, and not to determine their actual elastic moduli in suspension. It was therefore deemed appropriate to use the nanoindentation technique, in which cells are normally adherent during testing. These results can be seen in Fig. 5.

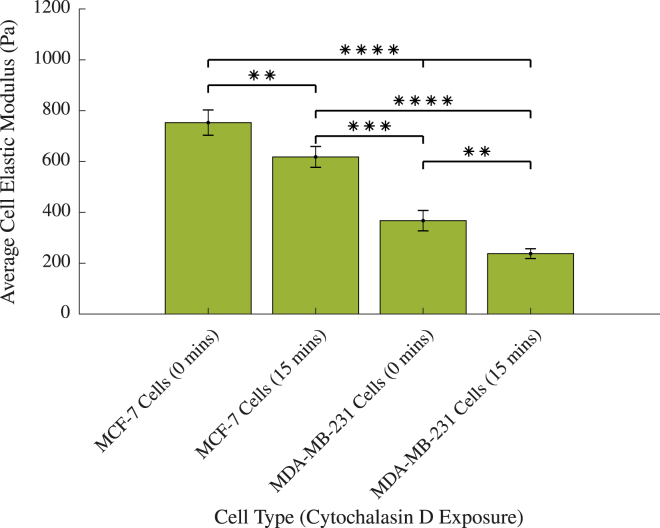
Figure 5.

The elastic moduli of MCF-7 and MDA-MB-231 cancer cells with and without exposure to cytochalasin D. ^∗∗∗∗p < 0.0001, ^∗∗∗p < 0.001, ^∗∗p < 0.01; vertical bars represent the SEM. To see this figure in color, go online.

Fig. 5 shows that as expected, there is a significant difference between the elastic moduli of untreated benign MCF-7 cancer cells and their metastatic counterparts MDA-MB-231 cancer cells (p < 0.0001), with MCF-7 cells possessing an elastic modulus of 752.3 ± 49.8 Pa and MDA-MB-231 cells an elastic modulus of 367.5 ± 40.2 Pa. This is in good agreement with previous studies, which have shown that benign cancer cells are stiffer than their metastatic counterparts (36,38,72), particularly Lee et al. (73), who reported similar values of 800 ± 20 and 500 ± 25 Pa in MCF-7 and MDA-MB-231 cells, respectively, using atomic force microscopy.

The values of the elastic modulus significantly decreased in both MCF-7 cells and MDA-MB-231 cells with the addition of cytochalasin D (p = 0.0033 and p = 0.0040, respectively). However, MCF-7 cells treated for 15 min with cytochalasin D (618.0 ± 41.1 Pa) remained significantly stiffer than untreated MDA-MB-231 cells (p = 0.0001). Furthermore, there remained a considerable difference between treated MCF-7 cells and treated MDA-MB-231 cells (p < 0.0001 between cells treated for 15 min).

The decreased E as seen in Fig. 5 implies that the shape of the cells is altered by the fluidic conditions in the channel, incited by changes in Ca and λ_p (see Eqs. 1 and 2), which lead to changes in the deformability-induced force and, consequently, the cells’ inertial position. Because there was no change in the size or shape of suspended, static cells (see Fig. 4), it can be concluded that the cytochalasin D alone did not directly affect the size and shape of the cell, but rather weakened the cell structure, allowing it to be more readily manipulated by the fluidic forces in the channel.

Because a reduction in the elastic modulus resulted in movement toward the center of the channel, it is likely that the change in the properties of the dispersed phase led to a decrease in λ_p, as seen previously in Eq. 2, and an increase in Ca, as seen previously in Eq. 1, leading to a decrease in the deformability-induced forces and a subsequent shift in the cells’ locations toward the channel center. Taking into account the experimental parameters used in this study and the investigated values of E, Ca ranged from 1.4 × 10⁻⁸–1.9 × 10⁻⁵. This is quite low in comparison with those investigated previously (16,28,33,74); however, as previously mentioned, E cannot be assumed to be the absolute value of the elastic modulus of the cells in suspension, and so this value of Ca may not be accurate. It does, however, show an increase in the Ca of 8.5% in MCF-7 cell experiments with the addition of cytochalasin D and an increase of 50.7% in the Ca of experiments conducted with MDA-MB-231 cells after the addition of cytochalasin D. It can, therefore, be concluded that there is a relationship between the deformability-induced force and the elastic modulus of the suspended particle. Similar studies examining the trajectories of vesicles computationally (28,74), vesicles experimentally (29,75), and RBCs experimentally (26,76,77) have shown that a decrease in λ_p results in increased migration toward the channel center, a finding that agrees with the results presented in this study. Furthermore, previous measures of the viscosity of MCF-7 cells (70) result in λ_p-values in this experiment of ∼2.3, which are comparable values to some of those investigated in the above studies.

While interpreting the results of this study, certain limitations must be taken into consideration. Both the actin staining of cells and nanoindentation techniques were performed on adherent cells because of the constraints of these methods. Although this allows for the relative measurement of actin depletion and E of these cells, respectively, for comparison with each other, it may not give a true indication of what these values are in suspension. Indeed, it has previously been shown that the rigidity of cancer cells in suspension may increase to improve their chances of survival in the high-shear regimes that pervade the circulatory system (78, 79, 80). For this reason, future studies might use techniques that examine cell E in circulation such as optical tweezers or T-junction deformation. Furthermore, this study examined the effects of E on the steady-state flow of cells. It may be interesting for future work to examine similar phenomena of cells in developing flow, particularly because lab-on-a-chip devices tend to be ∼44 mm in length.

From a microfluidics perspective, this study furthers the available knowledge on the migration of deformable particles. Cell-based assays, such as this, can provide similar fundamental results for particle populations that possess larger variabilities within the sample population. This is particularly useful in the area of microfluidic-based cell sorting, in which cells are divided based on their physical properties, such as E. Additionally, other separation techniques such as inertial-based techniques (81) that use spiral or curved channels may be enhanced by such findings by determining the elastic moduli of the cells under investigation to optimize their design. To this end, it may also be useful for future studies to examine whether these cell distributions segregate as a function of particle size and/or shape and to examine whether these factors have a greater or lesser influence on the inertial positions of cells than the modulus.

From a biological aspect, the results of this study have potential implications in the research of diseases that involve a change in the physical properties of suspended cells such as malaria (32), sepsis (34), or indeed cancer progression (38). It is now clear that a change in the elastic modulus of a cell will influence its inertial position in a microfluidic device, and this may well be the case in an in vivo environment as well, particularly in the lymphatics, where lower fluid velocities allow this fluid profile to be replicated as Poiseuille flow (3). Though this study was not able to clarify how more deformable cancer cells migrate to the walls for extravasation to occur, it may pave the way for future studies to examine inertial behaviors of these cells in curved or bifurcated vessels, which may give more clarity.

Conclusions

An experimental study to alter the physical properties of representative cell lines, including their elastic modulus, was carried out to investigate the impact that this change has on the inertial positions of these cells. It was found that cytochalasin D disrupts the actin filaments in a cell and therefore its physical properties, namely its elastic modulus. However, the size and circularity of suspended, static cells are not affected by cytochalasin D exposure.

The distribution of untreated MCF-7 cells and MDA-MB-231 cells and MCF-7 and MDA-MB-231 cells that had been treated with cytochalasin D was also investigated. In agreement with previous studies, benign, stiffer MCF-7 cells were found to be more evenly distributed across the channel width than metastatic, deformable MDA-MB-231 cells. A decrease in the elastic modulus of the MCF-7 cells resulted in migration toward the channel center. These results indicate that the primary factor that dictates the inertial positions of deformable particles such as cells or vesicles of similar sizes is their elastic modulus. This information may have predictive value in applications of similarly sized cell or nonrigid particle separation.

These results have implications in both microfluidics and cancer research. They develop the limited knowledge available on the effect that cell elastic modulus has on the advection of cells and their inertial positions in channels. Furthermore, these methods will inform the development of future inertial microfluidic devices, such as lab-on-a-chip and flow cytometry devices, to better and more effectively process or separate cells in suspension.

Data availability

The data sets generated during and/or analyzed during this study are available from the corresponding author on reasonable request.

Author contributions

S.C. designed and conducted experiments, results analysis, and writing. K.M. conducted research analysis for actin staining experiments. K.M. and D.N. supervised the study and revised the manuscript, and D.N. is the corresponding author. All authors read and approved the manuscript.

Editor: Cynthia Reinhart-King.