Linear Regression Metamodeling as a Tool to Summarize and Present Simulation Model Results

Abstract

Background.

Modelers lack a tool to systematically and clearly present complex model results, including sensitivity analyses.

Objective.

To propose linear regression metamodeling as a tool to increase transparency of decision-analytic models and better communicate their results.

Methods.

We used a simplified cancer-cure model to demonstrate our approach. The model computed the lifetime cost and benefit of three treatment options for cancer patients. We simulated 10,000 cohorts in a probabilistic sensitivity analysis (PSA) and regressed the model outcomes on the standardized input parameter values in a set of regression analyses. We used the resulting regression coefficients to describe various sensitivity analyses measures, including threshold and parameter sensitivity analyses. We also compared the results of the PSA to deterministic full-factorial and one-factor-at-a-time designs.

Results.

The regression intercept represented the estimated base-case outcome and the other coefficients described the relative parameter uncertainty in the model. In addition, we defined simple relationships that compute the average and incremental net benefit of each intervention. Metamodeling produced outputs similar to traditional deterministic one-way or two-way sensitivity analyses, but was more accurate since it used all parameter values.

Conclusions.

Linear regression metamodeling is a simple, yet powerful, tool that can assist modelers in communicating model characteristics and sensitivity analyses.

INTRODUCTION

Sensitivity analysis communicates decision robustness, or lack thereof, and is an important component of decision analysis. A wide array of tools are available to conduct sensitivity analyses ranging from changing one parameter at a time to value of information analyses. New methods of sensitivity analyses tend to address the short-comings of previous approaches, but they introduce new challenges. To date, modelers lack a single tool that can clearly and systematically report sensitivity analyses.

It generally is recommended to start with one-way sensitivity analysis (OWSA), where one input parameter value is varied within a meaningful range (e.g., 95% confidence interval) while holding the rest of the parameters equal to their mean values.¹ An analyst also may be interested in identifying threshold values at which the preferred intervention changes.² These approaches provide a simple overall picture of the model behavior. However, deterministic sensitivity analyses suffer from two important limitations: First, deterministic sensitivity analysis strikes a compromise between clarity and completeness. An analyst can vary only a limited number of parameters simultaneously without losing clarity. The rest of the parameters are held at their mean values. Thus, the model outcome does not adequately reflect the combined uncertainty in all parameters. Second, deterministic sensitivity analysis only partially communicate uncertainty because it ignores the parameters’ distributions.

Second order Monte Carlo simulations, or probabilistic sensitivity analysis (PSA), addresses these limitations by assigning distributions to the parameters and sampling from these distributions simultaneously.³ Thus, guidelines often recommend using PSA in decision analysis since it is a better representation of the outcomes under the overall parameter uncertainties.⁴ However, PSA introduces its own limitations, especially in communicating how uncertainties in estimating the individual parameters impact the outcome. Expected value of perfect information (EVPI) is a powerful tool that communicates the cost of perfect information regarding model parameters. However, computing EVPI can be challenging.⁵ Thus, no single measure of sensitivity analyses is perfect and decision analysts often are encouraged to perform a combination of deterministic and probabilistic sensitivity analyses.⁶

Analysts often build simulation models to represent reality. However, these models are still black-boxes and difficult to comprehend. Thus, analysts often reveal model sensitivity by varying one or more input parameters at a time and observe how the model behaves. This approach tends to be cumbersome and incomplete. Alternatively, a metamodel, or model of the model, simplifies the model’s intrinsic behavior with a simpler relationship. Metamodels have been used successfully as surrogates of simulation models for nearly half a century. Blanning⁷ and Kleijnen⁸ were among the first to operationalize the term metamodel. The original motivation of metamodeling was to reduce computing costs by defining a simpler mathematical relationship between the model outputs and inputs than the actual model. Once sufficient model results are gathered to define and validate a metamodel, the metamodel is used to replace the model upon which it is built. Although, model replacement continues to be a valid application of metamodeling, it is not the focus of our study. Instead, we focused on the advantages of using metamodeling to increase model transparency and to improve result communication.

Today, many practical metamodeling applications exist in the engineering and computer science literature.^9,10 However, only a few applications exist in medical decision making. For example, Merz and Small¹¹ used logistic regression to identify important variables that can change the decision of anticoagulation in pregnant women with deep vein thromobosis, Tappenden et al.¹² investigated several metamodeling techniques for value of information calculations in a cost-effectiveness analysis (CEA) of interferon-β and glatiramer acetate for multiple sclerosis, and Stevenson et al.¹³ used Gaussian process modeling in the CEA of treating established osteoporosis.

In this study, we combine many of the strengths of deterministic and probabilistic sensitivity analyses using linear regression metamodeling. We illustrate our approach using a simplified cancer-cure model.

METHODS

Linear Regression Metamodeling

Figure 1 illustrates a metamodel with respect to model inputs and outputs. Linear regression metamodeling involves defining a model outcome as a linear function of the model input parameters. For example, in a simple model with two input parameters, we can define the outcome as

$$y={\alpha }_0+{\alpha }_1{x}_1+{\alpha }_2{x}_2+e$$ (1)

where y is a model outcome (e.g., the simulated lifetime cost of a surgical intervention), and x₁ and x₂ are two input parameters (e.g., the probability of failing surgery and the cost of the surgical procedure, respectively). α₀ is the intercept, α₁ and α₂ are the coefficients of the model input parameters x₁ and x₂, respectively, and e is the residual term.

Figure 1: Metamodel as an add-on to simulation models.

Simulation models are approximations of real life complexity. Metamodels simplify and increase model transparency by summarizing the relationship between model inputs and outputs.

Using simple linear regression one can easily calculate the α coefficients. However, interpreting these coefficients from Equation (1) can be problematic. First, the intercept α₀ = E(y) when x₁ = 0 and x₂ = 0. Referring to our example, α₀ is equal to the lifetime intervention cost when the probability of failing surgery is zero and the procedure itself costs nothing! While mathematically sound, an analyst may be more interested in presenting the base-case outcomes when the parameters are equal to their mean values. In addition, the interpretation of α₁ and α₂ is not problem free. α₁ can be interpreted as the change in the expected cost of an intervention when the probability of failing surgery is changed by one unit (e.g., from 0 to 1), which is a large change on a probability scale. Similarly, α₂ is equal to the change of the intervention cost due to one dollar increase in the cost of the procedure, a change that can be minute relative to the actual procedure cost. Thus, one cannot directly compare the relative importance of these parameters since they are measured on different scales. Furthermore, these coefficients do not communicate any information regarding the uncertainties involved in estimating the parameter values (e.g., parameter uncertainty analysis).

Standardizing model parameters.

Model parameters are often scaled to overcome the above limitations. One scaling method is to standardize, or normalize, the parameters. The standardized value of the j^th parameter z_j is defined as

$$z_j=\frac{x_j-{\overline{x}}_j}{{\sigma }_j}$$

where ${\overline{x}}_j$ and σ_j are the mean and standard deviation (SD) values for the input parameter x_j, respectively. Using the standardized parameters, produces^*

$$y={\beta }_0+{\beta }_1{z}_1+{\beta }_2{z}_2+u$$ (2)

where β₀ is the new intercept, β₁ and β₂ are the coefficients of the standardized parameters z₁ and z₂, respectively, and u is the new residual term.

The intercept β₀ is equal to the base-case outcome when all the parameters are set equal to their mean values. In addition, β₁ and β₂ represent the change in the outcome due to one SD change in x₁ and x₂, respectively. Thus, these coefficients communicate parameter uncertainty. Furthermore, the absolute values of these coefficients can be used to rank the inputs by their relative uncertainty.

Cost-effectiveness analyses (CEA) involves more than one outcome. Specifically, CEA computes a composite measure from an intervention’s expected cost and benefit. One such quantity is the net health benefit (NHB), which is defined as

$$\text{NHB}=\text{E}-\frac{\text{C}}{\lambda }$$ (3)

where E and C are the computed actual benefit and the cost of the intervention, respectively, and λ is the willingness to pay (WTP) threshold per unit of health. NHB is measured in units of health and is calculated as the difference between the actual benefit gained investing an intervention and what could have been obtained if the resources were instead invested in a marginally cost-effective alternative.¹⁴

We can express each of the three outcomes (NHB, C and E) as a separate linear function of the standardized input parameters such that

$${\theta }_0+{\theta }_1{z}_1+{\theta }_2{z}_2={\gamma }_0+{\gamma }_1{z}_1+{\gamma }_2{z}_2-\frac{{\delta }_0+{\delta }_1{z}_1+{\delta }_2{z}_2}{\lambda }$$ (4)

where θ_j, γ_j and δ_j are the regression coefficients of standardized parameter z_j for the outcomes NHB, E, and C, respectively. Differentiating Equation (4) with respect to each standardized parameters z_j results in

$${\theta }_j={\gamma }_j-\frac{{\delta }_j}{\lambda }$$ (5)

where the variables are as previously described.

Equation (5) describes the effect of one SD change in a particular parameter j on the NHB. This equation can be interpreted similar to NHB in Equation (3) except that the expressions now refer to the outcomes conditional on one SD change in a particular parameter x_j.

We can reach a similar conclusion using the incremental NHB (ΔNHB) of an intervention T₁ relative to another intervention T₀, which is defined as:

$$\Delta \text{NHB}=\Delta \text{E}-\frac{\Delta \text{C}}{\lambda }$$ (6)

where ΔE and ΔC are the incremental benefit and incremental cost respectively of T₁ relative to T₀. We also can calculate the change in the ΔNHB due to one SD change in parameter x as

$$\Delta {\theta }_j=\Delta {\gamma }_j-\frac{\Delta {\delta }_j}{\lambda }$$ (7)

where $\Delta {\theta }_j={\theta }_j^{T_1}-{\theta }_j^{T_0}$, $\Delta {\gamma }_j={\gamma }_j^{T_1}-{\gamma }_j^{T_0}$ and $\Delta \delta ={\delta }_j^{T_1}-{\delta }_j^{T_0}$ are the changes in incremental benefit and incremental cost due to one SD change in x_j, respectively. All three expressions (Δθ_j, Δγ_j and Δδ_j/λ) are measured in units of health (e.g., quality adjusted life years, QALYs).

Threshold Analysis

Next we use Equation (7) to conduct one-way and two-way threshold analyses.

One-way threshold analysis.

This analysis shows a parameter’s value (if any) at which an T₁ becomes (or ceases to be) preferred relative to another intervention T₀ while holding the other parameters at their mean values.

A decision maker is indifferent between T₁ and T₀ when they break even (i.e., ΔNHB=0), or

$$\Delta {\theta }_0+\Delta {\theta }_1{z}_1+\Delta {\theta }_2{z}_2=0.$$ (8)

In one-way threshold analysis, except for the j^th parameter that we are interested in calculating the threshold for, the rest of the standardized parameters are equal to zero. Thus the break-even value for a parameter z_j can be calculated as

$$z_j^{*}=-\frac{\Delta {\theta }_0}{\Delta {\theta }_j},$$

where $z_j^{*}$ is the threshold value at which a decision maker becomes indifferent between T₀ and T₁, Δθ₀ is the base-case incremental $\text{NHB}(\Delta \widehat{\text{NH}}\text{B})$ where all parameters are equal to their mean values, and Δθ_j is the rate at which ΔNHB changes per unit change in z_j. Obviously, as Δθ_j approaches zero, $z_j^{*}$ approaches infinity, indicating that it takes forever for z_j to change the preferred intervention.

Figure 2 illustrates the relationship between $z_j^{*}$, Δθ₀ and Δθ_j. The region of z_j where T₁ is preferred over T₀ is conditional on the direction of Δθ_j which indicates the direction in which ΔNHB changes relative to z_j. If Δθ_j > 0, meaning that ΔNHB increases as z_j increases, then T₁ becomes preferred over T₀ where $z_j>z_j^{*}$. However, if Δθ_j is a negative value, then T₁ must be preferred over T₀ in regions where $z_j<z_j^{*}$.

Figure 2: One-way threshold analysis from regression results.

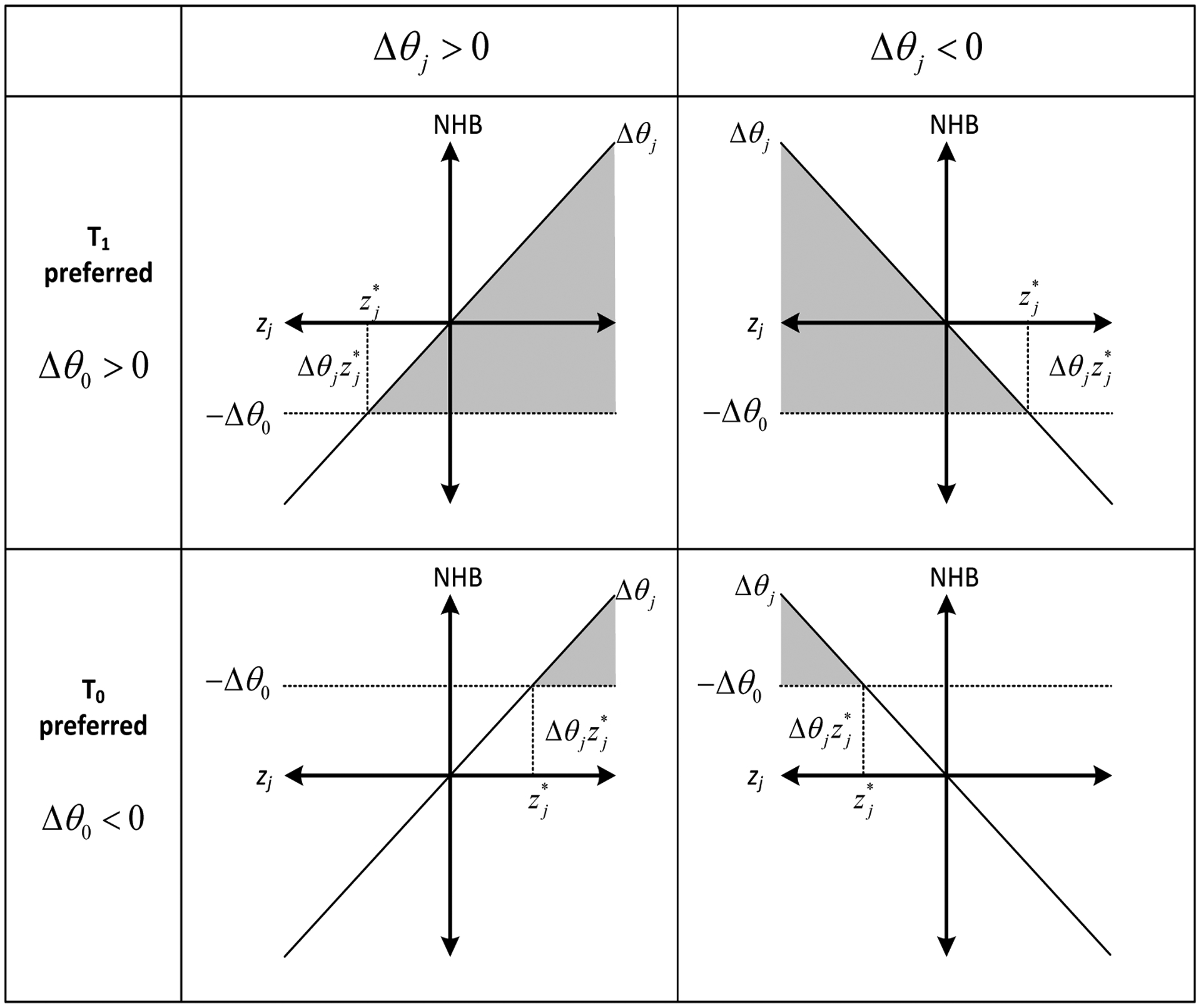
The standardized values of x_j are plotted on the X axis, and the NHB is plotted on the Y axis. The horizontal line (−Δθ₀) is equal to the negative expected value of the incremental NHB. The grayed out region represents the values of the standardized parameter z_j at which the preferred decision is reversed. $z_j^{*}$ is the value at which the decision changes and it is a function of the intercept (θ₀) and (θ_j), the coefficient of z_j, in the incremental NHB (ΔNHB) regression. The region of z_j where T₁ is preferred over T₀ is conditional on the direction of Δθ_j which indicates the direction in which ΔNHB changes relative to z_j. If Δθ_j > 0, meaning that ΔNHB increases as z_j increases, then T₁ becomes preferred over T₀ where $z_j>z_j^{*}$. However, if Δθ_j is a negative value, then T₁ must be preferred over T₀ in regions where $z_j<z_j^{*}$.

To present the threshold values on their original scales:

$$x_j>{\overline{x}}_j+z_j^{*}{\sigma }_j\text{ if Δ}{\theta }_j>0,\text{ and }$$

$$x_j<{\overline{x}}_j+z_j^{*}{\sigma }_j\text{ if Δ}{\theta }_j<0$$

where all the variables are as defined previously.

Two-way threshold analysis.

In this analysis, we examined the impact on ΔNHB of T₁ relative to T₀ while changing two standardized parameters (e.g., z₁ and z₂) simultaneously and holding the rest of the parameters equal to their mean estimates. The concept of interaction in regression analysis is closely related to two-way sensitivity analysis. Adding an interaction (cross-product) term to Equation (8), and redefining the relationship as an inequality produces:

$$\Delta {\theta }_0+\Delta {\theta }_1{z}_1+\Delta {\theta }_2{z}_2+\Delta {\theta }_3{z}_1{z}_2>0$$ (9)

where Δθ₃ is the coefficient of the interaction term z₁z₂. This coefficient captures the additional effect of z₁ on ΔNHB when z₂ is equal to +1. This coefficient can also be interpreted as the additional effect of z₂ on ΔNHB when z₁ is equal to +1. In a perfectly linear model, adding interaction terms do not change the main effects of z₁ and z₂ because all the parameters are standardized. (See appendix A for the mathematical steps).

The constraint shown in Equation (9) compares two interventions at a time. To compare K interventions, one must re-compute this constraint for all K(K − 1)/2 intervention pairs possible. Thus, for a particular intervention T to be optimal at specific values of z₁ and z₂, it must satisfy all (K − 1) constraints that involve T. The result of this analysis also can be presented graphically.

A Simplified Example

We demonstrate our approach with a simplified decision problem using TreeAge Pro (TreeAge Software, Inc., Williamstown, MA) that involves treating a 50 year old patient with a newly diagnosed curable cancer. Figure 3 illustrates the decision tree that compares three interventions: chemotherapy, radiation and surgery. These interventions may be successful and the patient may be cured (i.e., become cancer-free), or the treatment may fail, and the patient may stay in the cancer state. Chemotherapy and radiation can be tried only for a few cycles (5 and 4 years, respectively). During this period, the probability of success is assumed to be constant. If treatment fails after this period, the patient stays in the cancer state with an increased risk of death. Surgery can be tried only once and its benefit is assumed to be instantaneous; however it also carries an immediate risk of death during the procedure.

Figure 3: Decision tree outline.

This tree involves treating a hypothetical case of cancer with chemotherapy, radiation, or surgery. Each decision branch is followed by a Markov node that computes the lifetime cost and benefit of the simulated patient.

Each decision branch is followed by a Markov node. The Markov health states are cured (cancer-free), cancer, and dead. If cured, quality of life increases from 0.8 to one. The probability of cure is dependent on the type of intervention. Once cured, the patient stays cancer-free until they die of cancer or other causes. The risk of death in the cured state is obtained from standard U.S. life tables and is dependent on the patient’s age. We assumed that cancer carries an additional cancer-specific risk of death. In addition, we assumed an annual Markov cycle length and that the cost and benefit occur at the middle of each cycle. Furthermore, we used a willingness to pay threshold (λ) of $50,000 per quality adjusted life years (QALYs) and discounted the interventions’ costs and benefits by 5% annually.

Table 1 summarizes the parameter distributions used in this model. All model parameters are fictitious and are not based on evidence. The sole purpose of this exercise is to demonstrate the method outlined above using a simple transparent model.

Table 1:

Input Parameter Description. LN(μ,σ)=log normal distribution with parameters μ and σ. Beta(α,β)=beta distribution with shape parameters α and β. Mean and SD are the mean and standard deviation of the parameters mean, respectively. LB and UB=lower and upper 95% confidence bounds of the mean, respectively.

Parameter	Description	Distribution	Mean	SD	LB	UB
pFailChemo	Annual probability of failing chemotherapy	Beta(45,55)	0.45	0.050	0.353	0.547
pFailRadio	Annual probability of failing radiotherapy	Beta(50,50)	0.5	0.050	0.402	0.598
pFailSurg	Probability failing surgery	Beta(5,95)	0.05	0.022	0.007	0.093
pDieSurg	Probability of dying due to surgery	Beta(10,90)	0.1	0.030	0.041	0.159
μCancer	Cancer specific mortality rate	LN(−1.69,0.4)	0.2	0.083	0.037	0.363
cChemo	Annual chemotherapy cost ($)	LN(9.9,0.1)	20,000	2,005	16,066	23,934
cRadio	Annual radiotherapy cost ($)	LN(9.17,0.3)	10,000	3,069	3,979	16,021
cSurg	Surgery cost ($)	LN(10.05,0.4)	25,000	10,414	4,568	45,432

Parameter Sampling

We tested both probabilistic and deterministic parameter sampling. In the probabilistic parameter sampling (PSA) we simulated each intervention’s outcome for 10,000 hypothetical cohorts. Each simulation represented one cohort, the characteristics of which were sampled from eight independent random distributions described in Table 1.

In addition to PSA, we also tested two types of deterministic sensitivity analyses, in which we changed the values of each of the eight parameters deterministically among the mean, lower 95% confidence bound (LB), and upper 95% confidence bound (UB) shown in Table 1. Specifically, we tested two types of deterministic designs: one-factor-at-a-time and full-factorial designs. We performed regression metamodeling following each design.

In the one-factor-at-a-time design, we assumed that only one parameter changes at a time and the rest of the parameters were equal to their mean values. For example, in the first simulation, only the value of the first parameter is equal to its LB, but the rest of the parameters are equal to their mean values. In the second simulation the first parameter is changed to its UB. In the third simulation, the value of this parameter is returned to its mean, and the value of the second parameter is changed to its LB, and so on. This design resulted in 16 (=8 parameters × 2 simulation/parameter) simulations.

In the full-factorial design, all possible LB and UB values for each parameter were sampled. In this design no parameter was held at its mean value for any simulation. This design is particularly useful to detect interaction between parameters and exploring the entire parameter space with a limited number of simulations. This design resulted in 256 (= 2⁸) scenarios. Similar to PSA design, metamodeling following full-factorial design averages model outcome over all parameter values instead of assuming the mean values for these inputs.^15,16

Figure 4 illustrates input sampling from PSA, full-factorial and one-factor-at-a-time designs with two inputs: the cancer mortality rate (μCancer) and the probability of failing chemotherapy (pFailChemo). The full-factorial design explores the edges, or corners, of the parameter space by equating each parameter to its UB (+2 SD) or LB (−2 SD). One-factor-at-a-time design only explores the change in one parameter at a time.

Figure 4: Sensitivity analysis design.

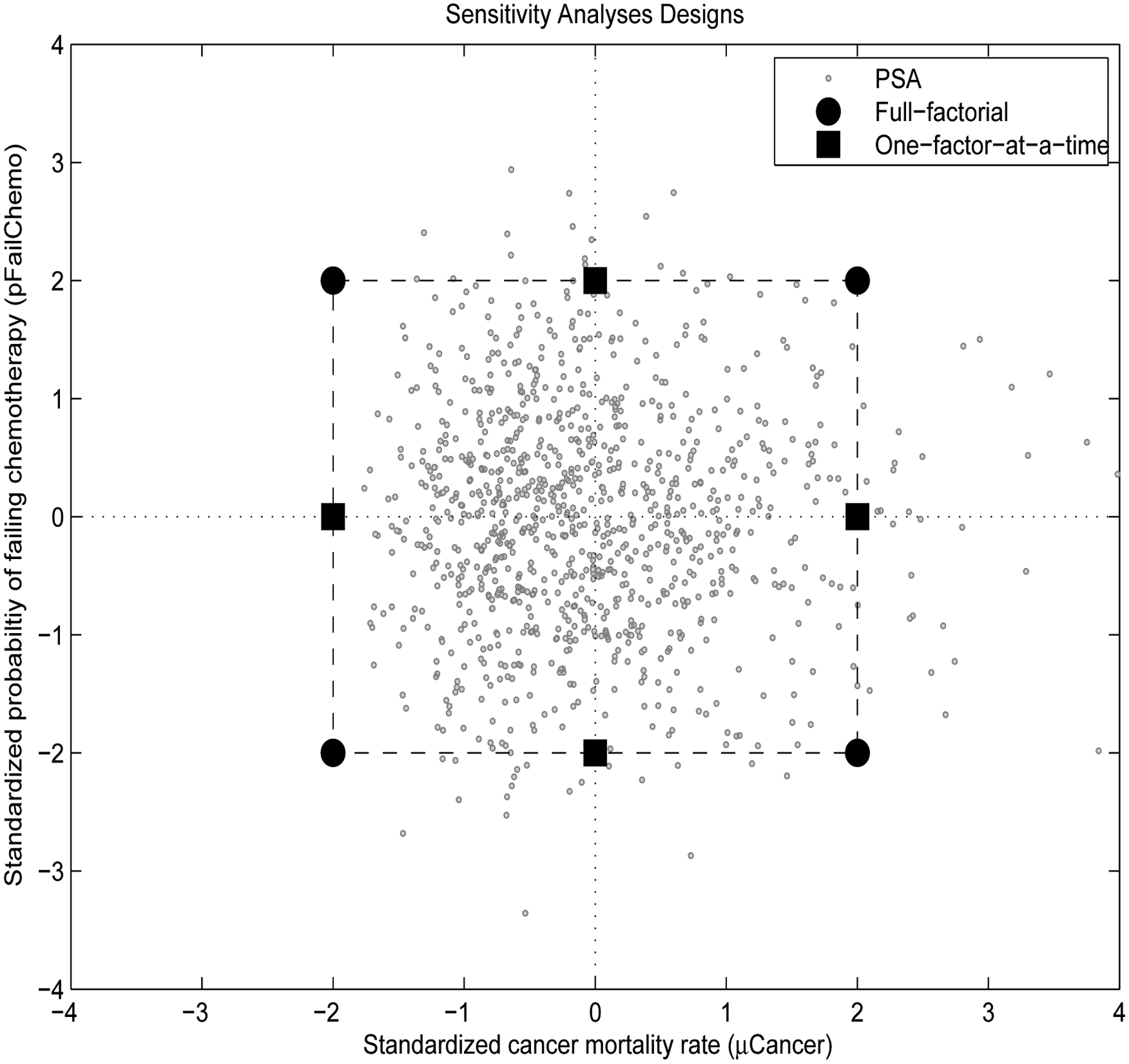
This figure shows how two parameter values are sampled in different types of simulation designs. Cancer mortality rate (μCancer) is plotted on the X axis and the probability of failing chemotherapy (pFailChemo) is plotted on the Y axis. In probabilistic sensitivity analysis (PSA), 1000 parameter pairs are sampled randomly from their distributions (Table 1). In deterministic designs, the analyst chooses the input values. In 2^K full-factorial design, the inputs are sampled from the edges, or corners, of the parameter space. In contrast, in one-factor-at-a-time design, only one parameter is varied at a time, the other parameter is held at its mean value.

In PSA, each simulation represents a hypothetical cohort. For each set of input samples, whether stochastic or deterministic, we computed the lifetime cost and benefit for that particular simulation. One-factor-at-a-time, full-factorial and PSA produced 16, 256 and 10,000 simulations, respectively.

Statistical Analysis

The three simulation datasets were exported into Stata (Stata Statistical Software, Inc., College Station, TX) for regression analyses. Each dataset consisted of 14 variables (eight input parameters and six outcomes that represent the cost and benefit of the three interventions). We primarily used the PSA dataset in our analyses. First, we regressed each intervention’s outcome on the unstandardized parameters. Then, we repeated the analyses on the standardized parameters. In addition, we performed further regressions to compare the results from the PSA with the one-factor-at-a-time and full-factorial designs.

RESULTS

Table 2 presents the results of regressing the unstandardized and standardized parameters on the cost, benefit and NHB of the chemotherapy intervention. The intercept of the unstandardized regression is the expected outcome when all parameters are set to zero. In the standardized regressions, the intercept is the expected outcome when all the parameters are equal to their mean values (i.e., their base-case estimates). In addition, the coefficients of the unstandardized regressions are interpreted relative to a one unit change in each parameter on their original scales. For example changing the cost of chemotherapy by $1 does not have a noticeable impact on the NHB of chemotherapy. This is misleading, since we expect that NHB of chemotherapy should change if this intervention costs more. Furthermore, if our uncertainty regarding the chance of failing chemotherapy changes from zero to one, then we expect an increase in the cost of chemotherapy by nearly $36,000, and a reduction in the benefit by 7 QALYs. These changes are of large magnitude and reflect an unrealistic range in the probability. Hence, standardizing parameters can produce more meaningful results.

Table 2:

Metamodel results of regressing unstandardized and standardized parameters on the outcome of the chemotherapy intervention

	Unstandardized			Standardized
Parameters	Cost	Benefit	NHB	Cost	Benefit	NHB
Intercept	−13,066	18.01	18.27	20,796	13.49	13.08
pFailChemo	35,545	−7.116	−7.827	1,742	−0.349	−0.384
pFailRadio	1	0.001	0.001	0	0.000	0.000
pFailSurg	91	0.009	0.008	2	0.000	0.000
pDieSurg	156	0.081	0.078	5	0.002	0.002
μCancer	−14,678	−6.599	−6.305	−1,226	−0.551	−0.527
cChemo	1	0.000	0.000	2,060	−0.001	−0.042
cRadio	0	0.000	0.000	0	0.001	0.001
cSurg	0	0.000	0.000	−2	0.000	0.000
Observations	10,000	10,000	10,000	10,000	10,000	10,000
R2	0.98	0.97	0.98	0.98	0.97	0.98

In the standardized regressions, the coefficients communicate parameter uncertainty and are interpreted in units of standard deviations (SD). For example, one SD change in the cost of chemotherapy (cChemo), increases the cost of this intervention by $2,060, has no noticeable impact on the benefit and reduces the NHB by 0.04 QALYs. The coefficients of the probabilities can be interpreted in a similar way. Furthermore, the absolute value of the coefficients of the standardized parameters can be used to rank these parameters by their importance. For example, the uncertainty in the mortality rate of cancer (μCancer) has the most important impact on the NHB of chemotherapy followed by the probability of failing chemotherapy (pFailChemo) and the cost of chemotherapy (cChemo). Appendix B shows the results of regressing the standardized parameters and their interactions on the cost, benefit and NHB of all three interventions. Notice that the main effects and the intercept are similar to Table 2. This is because all the parameters are centered around zero and the model is nearly linear. (See Appendix A). We also show the model’s base-case estimate when all parameters are equal to their mean values. The metamodel’s intercept reproduced the base-case results extremely well confirming that the effects were locally near-linear.

In Table 3 we summarize the regression results of the standardized parameters and their interactions on the incremental NHB of all the possible comparisons of the three interventions. For example, the second column represents ΔNHB of chemotherapy relative to radiation. The coefficients in this column summarize the effects of changing the parameters by one SD on the incremental NHB of chemotherapy relative to radiation. In addition, the coefficients from this analysis can be used in threshold analyses.

Table 3:

Results of regressing the standardized parameters and their interactions on the ΔNHB

Parameter	Chemo>Radio	Chemo>Surgery	Radio>Surgery
Intercept	0.320	0.120	−0.200
pFailChemo	−0.384	−0.384	0.000
pFailRadio	0.466	0.000	−0.466
pFailSurg	0.000	0.234	0.234
pDieSurg	−0.001	0.446	0.447
μCancer	0.054	−0.484	−0.538
cChemo	−0.041	−0.041	−0.001
cRadio	0.068	0.001	−0.067
cSurg	0.001	0.206	0.205
μCancer*pFailChemo	−0.065	−0.062	0.003
μCancer*pFailRadio	0.061	0.002	−0.059
μCancer*pFailSurg	0.000	0.017	0.017

In Table 4 we compute the one-way threshold values for each parameter at which the preferred intervention reverses in the pairwise comparisons. These threshold values are shown on the parameters original and standardized scales. For example, chemotherapy is preferred to radiation as long as the annual cost of chemotherapy (cChemo) is less than $36K (7.8 SD) while holding the other parameters at their means. In addition, if the cost of chemotherapy is less than $26K (2.9 SD) chemotherapy is also preferred over surgery. Obviously, the cost of chemotherapy should not have a direct impact on the choice between radiation and surgery. Calculating these threshold values from the model directly produced $34K and $24K, respectively, which are slightly lower than the metamodel results. The metamodel results are more accurate since it averages the outcome over all parameters instead of assuming their mean values.

Table 4:

One-way threshold analysis. Results are presented for the unstandardized and standardized parameters (in parentheses).

Parameter	Chemo>Radio	Chemo>Surgery	Radio>Surgery
pFailChemo	<0.49 (0.83)	<0.47 (0.31)	NA
pFailRadio	>0.47 (−0.69)	NA	<0.48 (−0.43)
pFailSurg	NA	>0.04 (−0.51)	>0.07 (0.85)
pDieSurg	NA	>0.09 (−0.27)	>0.11 (0.45)
μCancer	>−0.29 (−5.93)	<0.22 (0.25)	<0.17 (−0.37)
cChemo	<35,717 (7.84)	<25,803 (2.89)	NA
cRadio	>−4,382 (−4.69)	NA	<904 (−2.96)
cSurg	NA	>18,928 (−0.58)	>35,146 (0.97)

The results from Table 3 were used to construct two-way threshold analyses. Figure 5 illustrates a two-way threshold analysis of cancer mortality rate (μCancer) and the probability of failing chemotherapy (pFailChemo) over their 95% confidence intervals. Each region satisfies 2(= K − 1) constraints. For example chemotherapy is the optimal choice when chemotherapy is preferred over radiation where

$$0.320+0.054z_1-0.384z_2-0.065z_1{z}_2>0,$$

and chemotherapy is preferred over surgery where

$$0.120-0.484z_1-0.384z_2-0.062z_1{z}_2>0$$

where z₁ and z₂ represent the standardized values of μCancer and pFailChemo, respectively. The coefficients are obtained from the corresponding variables from Table 3.

Figure 5: Two-way threshold analysis from regression results.

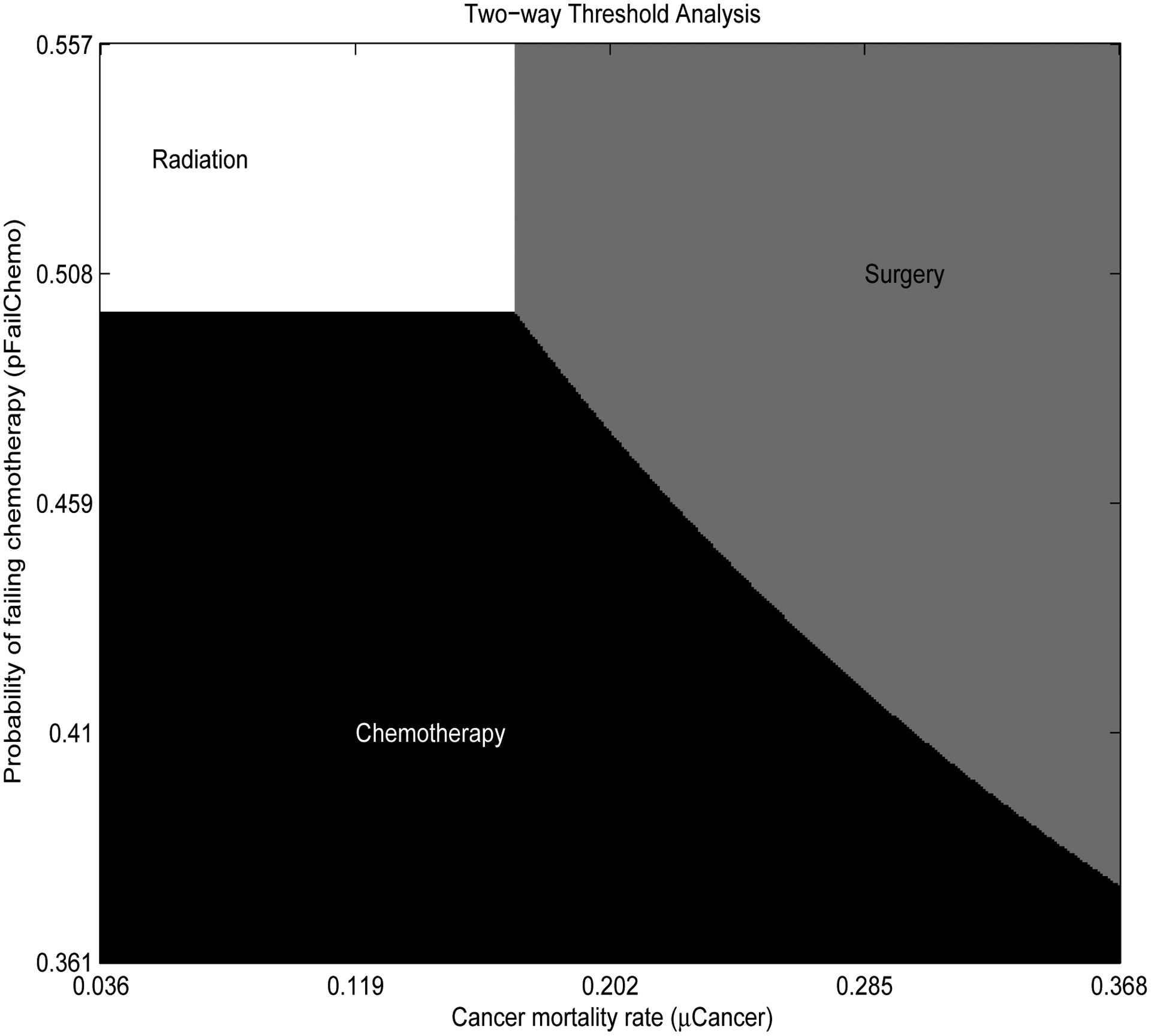
Cancer mortality rate (μCancer) is plotted on the X axis and the probability of failing chemotherapy (pFailChemo) is plotted on the Y axis. The ranges of these axes represent the parameters 95% confidence interval. The graph shows the optimal strategies for each combination of input parameters, while the rest of the parameters in the model are equal to their mean values.

Table 5 shows the results of using different parameter sampling designs on the NHB of chemotherapy. Sixteen scenarios were used in the metamodeling of the one-factor-at-a-time design, 256 were used in the metamodeling of the full-factorial design, and 10,000 scenarios were used in the metamodeling of the PSA design. The one-factor-at-a-time design was unable to detect interactions, nevertheless the beta coefficients from all the designs were very close and the input ranking did not change, indicating that the relationship between the NHB of chemotherapy and the parameters are nearly linear.

Table 5:

Results of regressing the standardized parameters on the outcome of the chemotherapy intervention. Results are shown for three designs: One-factor-at-a-time, full-factorial and PSA.

Parameter	One-factor-at-a-time(2K)	Full-factorial(2K)	PSA
Intercept	13.064	13.170	13.080
pFailChemo	−0.393	−0.345	−0.384
μCancer	−0.578	−0.584	−0.526
cChemo	−0.041	−0.042	−0.042
μCancer*pFailChemo	NA	−0.078	−0.062
cChemo*pFailChemo	NA	−0.004	−0.003
cChemo*μCancer	NA	0.003	−0.002
Observations	16	256	10,000
R2	0.98	1	0.98

In addition to regression coefficients, the importance of input parameters also can be ranked using other correlation statistics.^16,17 Linear regression metamodeling may perform better than these statistics especially when the input parameters are themselves correlated as shown by Merz, et al.¹¹

DISCUSSION

We developed a simple method to present sensitivity analysis results from CEA models using NHBs and linear regression metamodeling. We illustrated this approach with a simplified example that involves treating case patients with chemotherapy, radiation or surgery.

Our metamodeling approach summarizes the CEA results in a transparent manner and reveals important model characteristics. The intercept presents the base-case model outcome (i.e., when all the parameters are equal to their mean values). The other coefficients associated with each standardized parameter represent the change in the outcome due to one SD change of that parameter. Thus, these regression coefficients describe the relative importance of uncertainty in each parameter. We also illustrated how to conduct one-way and two-way threshold analyses using these coefficients.

An important distinction between our approach and traditional deterministic sensitivity analyses is that metamodeling summarizes the results over the entire parameter space. Traditional deterministic sensitivity analyses vary one or two parameters and hold the rest of the parameters at their mean values. Regression analyses can isolate the correlation between model parameters that vary simultaneously, thus exploring the entire parameter space.

We considered NHB more suitable for our approach than the incremental cost-effectiveness ratio (ICER). Calculating the ICER requires ranking of the interventions which may change in parameter sensitivity analysis. In NHB analyses, there is no ranking involved. Incremental NHB of two interventions is always the difference between their average NHBs. Our approach can be used to calculate the ICER in special circumstances. Specifically, our method can be applied if the ranking of the interventions do not change over the parameters ranges. This may be the case when all the interventions are compared to a common base case and ΔC and ΔE are positive.

Unlike cost-effectiveness ratio, in NHB analysis a WTP threshold must be specified. One should conduct sensitivity analyses using different WTP thresholds. Fortunately, such analysis does not involve performing extra simulations or re-estimating the regression results because a WTP threshold is only needed in the final steps in our approach.

We compared the results from the PSA design to two types of deterministic designs: a full-factorial (2^K) and a one-factor-at-a-time design. In theory, all these designs produce the same results when the model is perfectly linear. In our model, the results from all the designs were similar, but not identical. One-factor-at-a-time design only explores one parameter at a time and holds the rest of the parameters at their mean values. 2^K design is a popular approach in Design of Experiments. This design only explores the parameters at their LB and UB, and assumes the model outcome is linearly related to the parameters. Higher order designs, such as 3^K, 4^K, and 5^K designs are recommended if an analyst expects a less linear relationship.

Only full-factorial and PSA designs can detect interactions, which commonly occur among model’s input parameters as they define the outcomes. Two parameters are said to be interacting if one parameter’s effect on the outcome is conditional on the value of another parameter. Conditional probabilities are perfect examples of interactions in decision models. For example, we define pDieCancer, which is a function of muCancer, to be conditional on pFailChemo in the chemotherapy intervention. As a result, we expect an interaction between these two parameters. In metamodeling, a parameter with a small main effect is generally expected to have a small interaction with the other parameters. In addition, higher level interactions (e.g., three-way interaction) are generally considered unimportant.¹⁰

One disadvantage of PSA is the computing cost. The PSA dataset that we used consisted of 10,000 scenarios. Obtaining this simulation set using TreeAge Pro took less than one minute on a standard desktop PC and performing the regression analyses in Stata were virtually instantaneous. However, our model was relatively simple and conducting a similar analysis on a more complex model may still be computationally expensive. For a more complex model, deterministic full-factorial designs, which generally require fewer simulations, may be considered. Partial factorial designs are also available when there is a large number of parameters in the model; for a detailed description, see Kleijnen.¹⁰

Validation is an important step following metamodel specification.¹⁸ Validation is especially important when metamodels are used to replace computationally costly models (e.g., output prediction in what-if scenarios, and optimization). However, we limited our metamodel specification to enhance our understanding of model results. We considered the R² statistics and visual plotting (not shown) adequate measures of overall metamodel fit.¹⁰ Both measures indicated a nearly linear relationship between model inputs and outputs.

We only specified a first-order polynomial relationship. Extending our metamodel specification to higher order polynomials is simple using higher order inputs (e.g., x², x³ … etc). However, including these higher order terms may complicate the interpretation of the regression coefficients as they become functions of the parameter values.

Furthermore, parameters also can be scaled relative to other statistics (e.g., their mean values). Similar to the normalized parameters, the intercept represents the base-case results. However, the other coefficients denote the change in outcome due to percent change in the parameters from their mean values.

Our approach has some limitations. First, loss of detail is inevitable. State-transition models are non-linear in general. In these models, linear metamodeling is at best an approximation. Metamodeling trades detail for simplicity and ease of presentation. However, we would argue that simplicity may outweigh detail in the current presentation of CEA results.

Linear regression is the most widely used metamodeling approach by many researchers for its simplicity and ease of use.¹⁰ Our linear approximation will perform best when the relationship between model inputs and outputs are approximately linear, or locally linear. Thus, a relationship that is non-linear on the inputs entire range becomes nearly linear on a narrow range. We found linear relationships in many simulation studies, including a model by Tappenden and colleagues, who found a nearly linear relationship between model inputs and outputs of their multiple sclerosis CEA (R² = 0.93).¹² In computer science and engineering, metamodels generally, and linear regression metamodels specifically, have been tested widely and have been found to approximate the simulation models very well. In these fields, metamodeling is commonly used for prediction (i.e., to replace the simulation model). Friedman and Pressman (1988)conducted 30 simulation experiments and concluded that “simulation metamodel is a reliable and valid technique for use in post-simulation analysis, and is probably as good as the simulation model on which it is based.”⁹

Linear approximation may become problematic when a high level of accuracy is desired in a non-linear model. Specifically, if the preferred intervention is highly sensitive to a parameter’s standardized value, one may consider more advanced sensitivity analyses methods (e.g., EVPI). In most circumstances, however, the linear metamodel may be a fovorable initial analysis.

Finally, R² statistics may not be a good indicator of metamodels validity in deterministic designs. R² values were generally high in the deterministic designs because of the small sample size (number of simulations in each design), and because each input typically has two data points. When the purpose of a metamodel is model replacement (e.g., to perform quick what-if scenarios and reduce computing cost), lack-of-fit statistics (e.g., F-statistics) and cross-validation methods are more popular.^18,19

CONCLUSION

Linear regression metamodeling can reveal important characteristics of CEA models including the base-case results, relative parameter importance, interaction, and threshold and sensitivity analyses. We recommend using metamodeling as the first step of sensitivity analyses in economic evaluation. It may also prove to be the only analysis needed.

APPENDIX

Appendix A

The main effects in a regression are the same with and without including interactions when standardizing the parameters. The expected outcome of a regression with main effects only is

$$E(y)={\beta }_0+{\beta }_1{z}_1+{\beta }_2{z}_2,$$

and the expected outcome from a regression with main effects and interactions is

$$E(y)={\gamma }_0+{\gamma }_1{z}_1+{\gamma }_2{z}_2+{\gamma }_3{z}_1{z}_2,$$

therefore,

$${\beta }_0+{\beta }_1{z}_1+{\beta }_2{z}_2={\gamma }_0+{\gamma }_1{z}_1+{\gamma }_2{z}_2+{\gamma }_3{z}_1{z}_2.$$

Differentiating with respect to z₁, results in

$${\beta }_1={\gamma }_1+{\gamma }_3{z}_2,$$

but at the mean $z_2=\overline{z_2}=0$, and

$${\beta }_1={\gamma }_1$$

The same finding holds for z₂.

Appendix B

Table 6:

Standardized parameters and their interactions on all outcomes

	Chemotherapy			Radiation			Surgery
Parameter	Cost	Benefit	NHB	Cost	Benefit	NHB	Cost	Benefit	NHB
Intercept	20,796	13.49	13.08	11,058	12.98	12.76	24,912	13.46	12.96
Model base-case	20,595	13.46	13.05	10,983	12.94	12.72	25,000	13.44	12.94
pFailChemo	1,744	−0.35	−0.38	2	0	0	0	0	0
pFailRadio	0	0	0	880	−0.45	−0.47	0	0	0
pFailSurg	2	0	0	1	0	0	0	−0.23	−0.23
pDieSurg	0	0	0	1	0	0	0	−0.45	−0.45
μCancer	−1,228	−0.55	−0.53	−676	−0.59	−0.58	0	−0.04	−0.04
cChemo	2,061	0	−0.04	−2	0	0	0	0	0
cRadio	0	0	0	3,430	0	−0.07	0	0	0
cSurg	0	0	0	2	0	0	10,285	0	−0.21
μCancer*pFailChemo	−236	−0.07	−0.06	7	0	0	0	0	0
μCancer*pFailRadio	8	0	0	−117	−0.06	−0.06	0	0	0
μCancer*pFailSurg	1	0	0	1	0	0	0	−0.02	−0.02
Observations	10,000	10,000	10,000	10,000	10,000	10,000	10,000	10,000	10,000
R2	1	0.98	0.98	1	0.98	0.98	1	1	1