Mechanochemical symmetry breaking during morphogenesis of lateral-line sensory organs

Abstract

Actively regulated symmetry breaking, which is ubiquitous in biological cells, underlies phenomena such as directed cellular movement and morphological polarization. Here we investigate how an organ-level polarity pattern emerges through symmetry breaking at the cellular level during the formation of a mechanosensory organ. Combining theory, genetic perturbations, and in vivo imaging, we study the development and regeneration of the fluid-motion sensors in the zebrafish’s lateral line. We find that two interacting symmetry-breaking events — one mediated by biochemical signaling and the other by cellular mechanics — give rise to precise rotations of cell pairs, which produce a mirror-symmetric polarity pattern in the receptor organ.

Introduction

Broken symmetries in living matter often stem from regulated biological processes across different spatiotemporal scales. During development or regeneration, for example, organ-scale structures and patterns emerge as a result of broken symmetries at the level of the constitutive cells [1, 2, 3]. Such cellular polarity gives rise to systematic spatial asymmetries in morphology, protein distribution, and mechanical properties [4, 5, 6].

Because of their highly stereotyped structure, the mechanosensory epithelia of the auditory, vestibular, and lateral-line systems are especially attractive subjects for investigations of symmetry breaking in biological patterning. These organs contain precisely arranged sensory hair cells surrounded by non-sensory supporting cells. Each hair cell carries an asymmetric mechanosensory organelle, the hair bundle, that responds to mechanical deflection in a directionally sensitive manner [7, 8]. In order to respond effectively to various stimuli, these hair bundles must adopt a specific pattern of orientations across a sensory organ. Many mechanosensory epithelia, including those in the human vestibular organs, contain oppositely oriented hair cells aligned to a global polarity axis [9]. This mirror-symmetric arrangement permits a precise measurement of stimuli delivered along the organ axis. To consider the example examined in this study, the zebrafish lateral line contains compact sensory organs (neuromasts) oriented along the anteroposterior body axis. Half of the hair cells in these neuromasts are sensitive to tailward water motions, which occur for example when the animal swims forward. The complementary half of the cells respond to headward flows, which are particularly significant when a predator — usually a larger fish — strikes from behind (Fig. 1A,B; Supplementary Video 1; [10, 11, 12]).

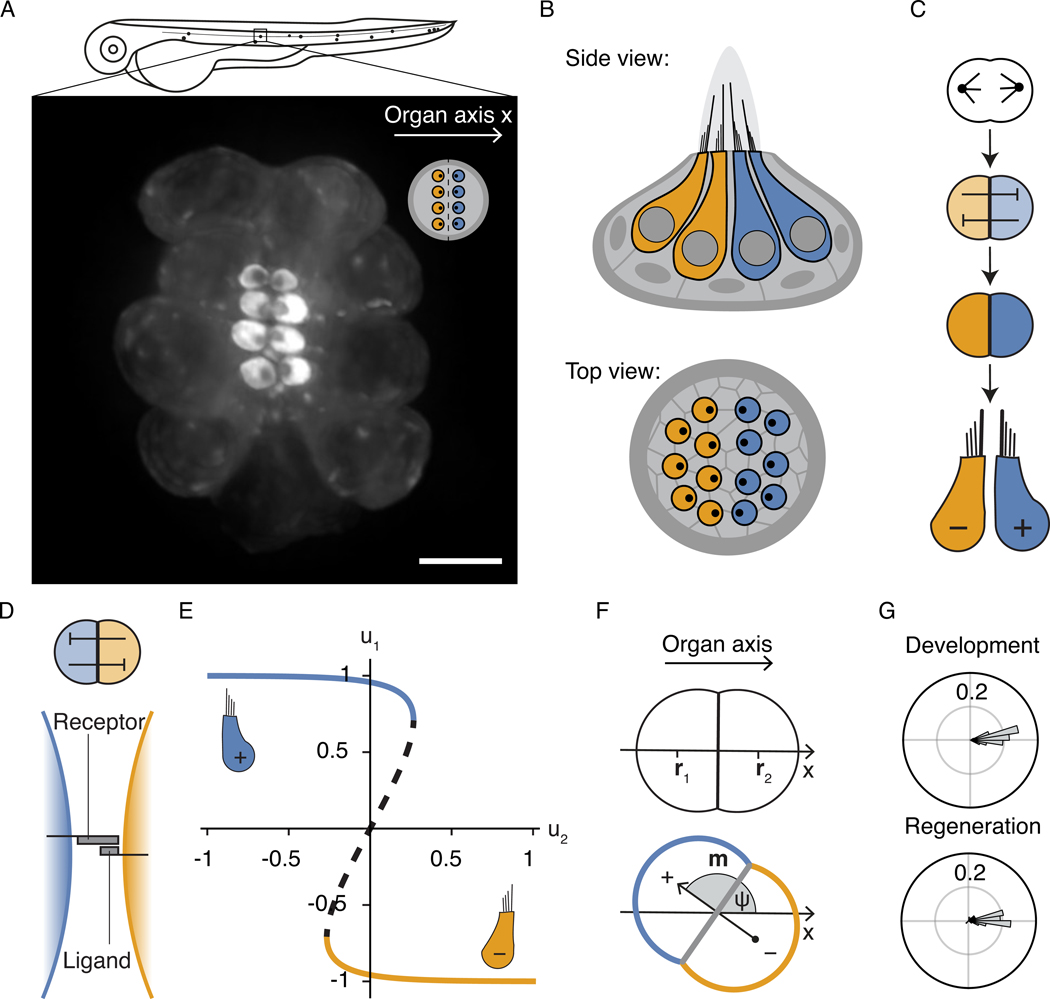
Figure 1: Mirror-symmetric polarity pattern in lateral-line neuromasts.

A, The mechanosensory organs of the zebrafish lateral line are arrayed along the anteroposterior body axis (organ axis x). The fluorescence micrograph of a neuromast from a transgenic zebrafish larva shows hair cells labeled with β-actin-GFP against the dark background of unlabeled supporting cells. The apical surfaces of the hair cells appear as bright discs with asymmetrically localized dark spots that reveal the orientations of the hair bundles. The inset shows this arrangement schematically. Scale bar: 5 μm. B, Schematic side and top views show oppositely polarized sensory hair cells (yellow and blue) arranged in a mirror-symmetric pattern across a lateral-line neuromast of the larval zebrafish. Hair cells are surrounded by supporting cells (gray). Each hair cell carries a hair bundle, a cluster of rod-like processes that increase in length in one direction on its apical surface. This structural asymmetry accords with functional anisotropy: deflecting the bundle toward its tall edge excites the associated nerve fibers, whereas movement in the opposite direction has an inhibitory effect. C, The hair cells of neuromasts are formed in pairs by the division of a precursor cell. The nascent hair cells subsequently engage in mutually suppressive Notch signaling that results in opposite cellular polarities. D, Notch signaling relies on chemical interactions between receptor and ligand molecules bound to the cell surface. A ligand-receptor binding event across a cell-cell interface activates the receptor. In many contexts, receptor activation triggers the suppression of ligand expression in the same cell, resulting in a mutual-inhibition circuit with bistable characteristics. E, A minimal model with a single dimensionless variable u for the signaling state of each cell (Eq. 1) captures the bistable behavior. The bifurcation diagram for cell state u₁ as a function of the signaling partner u₂ for symmetric coupling c₁₂ = c₂₁ = 1 shows the bistable regime, in which the two stable steady states (solid lines) are separated by an unstable state (dashed line). F, The signaling dipole of a pair of cells is given by Eq. 2. The division axis of the hair-cell precursor is typically aligned with the organ axis. For the arrangement of sibling cells shown here, the normalized axial component of the dipole is given by m = (u₂ − u₁)/2 and is governed by the double-well potential shown in Fig. 6A. In the absence of biasing factors, the positive and negative dipole configurations at +1 and −1 are degenerate. We describe the orientation of the dipole m with the angle ψ between m and the organ axis x. G, Mature hair-cell pairs reliably assume positive dipolar configurations both during development and when regenerating after chemical ablation. The angular histograms show the distribution of dipole angles ψ from 59 developing and 55 regenerating hair-cell pairs.

The alignment of neighboring hair bundles is mediated by biochemical interactions through the planar cell polarity (PCP) pathway and depends on the asymmetric distribution of PCP proteins in each cell [13]. Although the PCP pattern is uniform across all cells of the organ, the polarity of half of the hair bundles is reversed with respect to this axis [9, 14]. Hair cells of the two orientations originate in pairs from the division of a precursor cell (Fig. 1C; [10, 12]). The sibling cells subsequently acquire opposite orientations through Notch signaling, a pathway that mediates mutually inhibitory interactions across a direct cell-cell interface (Fig. 1C–E; Supplementary Fig. 1; [14], replicated in [15]). Describing the signaling state of each cell i with a unitless variable u_i, the bistability is captured by the minimal model

$$\frac{1}{k}\frac{\text{d}{u}_i}{\text{d}t}=\sigma \left(u_i-u_j\right)-u_i,$$ (1)

with σ(u) a generic sigmoidal function (Fig. 1E; Supplementary Note 1; [16]). Any small asymmetry in the initial conditions grows over a timescale set by the rate constant k and gives rise to a positive and a negative state, and the cells subsequently develop opposite polarities [17, 14].

To investigate the spatial arrangement of the cells, we introduce the signaling dipole for the pair

$$\text{m=}\frac{u_{\text{2}}\text{−}{u}_{\text{1}}}{\text{2}}\left({\text{r}}_{\text{2}}\text{−}{\text{r}}_{\text{1}}\right)\text{,}$$ (2)

in which r_i denotes the position of cell i (Fig. 1F). In reference to the PCP axis, a positive dipole corresponds to a pair whose mature hair bundles are apposed at their tall edges, whereas in a negative dipole the tall edges of the two bundles face away from one another. Although a priori the signaling-induced symmetry breaking between the daughters can give rise to both positive and negative dipoles at equal probability, mature hair-cell pairs are exclusively found in positive-dipole configurations, precisely aligned with the organ axis both during normal development and when regenerating in response to damage (Fig. 1G; Supplementary Fig. 1I; [12]).

Charge dipoles align in an external electric field; but how do pairs of hair cells organize in space to give rise to the observed organ-scale broken symmetry? We hypothesize that, rather than being driven by external input, the biological pattern emerges from cell-level interactions, as suggested by the remarkable robustness of neuromast patterning. In contrast to mammalian mechanosensory organs, in which the loss of hair cells leads to irreparable disorders of hearing and balance, neuromasts possess an inexhaustible regenerative capacity: fully functional and correctly patterned neuromasts regenerate after virtually any extent of damage [18, 19, 20].

Here we show that a combination of symmetry-breaking events mediated by biochemical signaling and active mechanical forces at the cellular level establishes an organ-scale symmetry with a pattern of oppositely oriented hair bundles. Furthermore, our results suggest a robust mechanism for the precise mosaic arrangement of hair cells and supporting cells.

Results

Dynamics of contact angles during differentiation

How does the precise spatial arrangement of cells in the neuromast arise? To approach this issue, we studied the shape changes, movements, and mechanical properties of maturing hair cells over time, focusing first on the cell-cell contacts. Hair cells exchange neighbors during maturation: sibling hair cells initially share a direct cellular interface, but once mature, they are fully surrounded by glia-like supporting cells (Fig. 1B; [21]).

By expressing fluorescent proteins under the control of a hair cell-specific promoter, we visualized the hair cells against the dark background of unlabeled supporting cells (Figs. 1A and 2A; Supplementary Video 1). After precursor division, we observed a flat interface between the sibling cells with a contact angle α ≈ 90°, which subsequently decreased until the cells detached from one another, allowing the intercalation of supporting cells. Using deep learning-assisted live imaging, we quantified the contact angle between hair-cell pairs from precursor division until cell-cell detachment and documented highly stereotyped dynamics across 24 hair-cell pairs from different neuromasts (Fig. 2C; Supplementary Video 2).

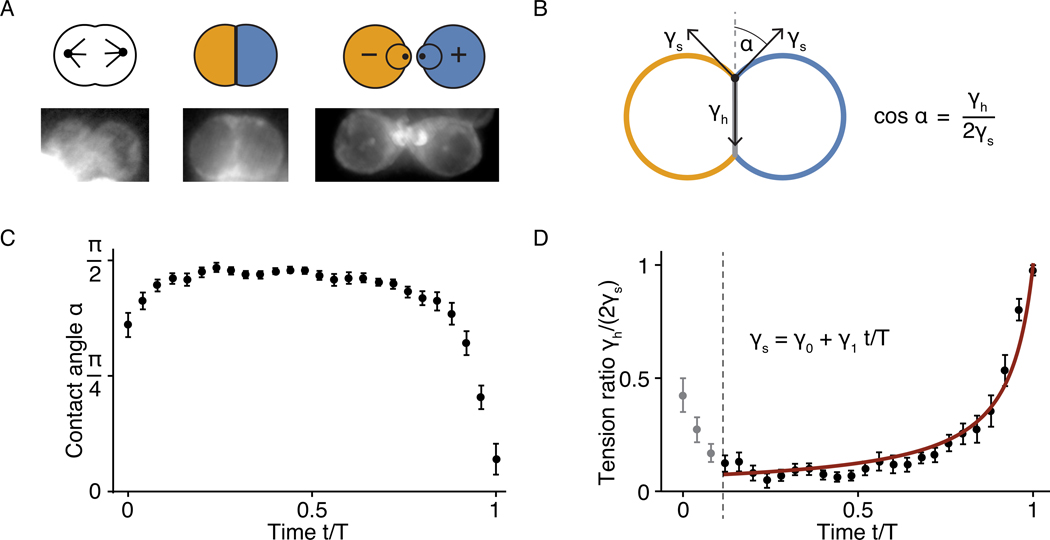
Figure 2: Contact-angle dynamics of maturing hair-cell pairs.

A, Neuromast hair cells undergo a stereotypical series of shape changes during maturation. Following division, they form a round doublet with a flattened contact surface before developing apical surfaces with hair bundles. Mature hair cells are always completely surrounded by supporting cells. The lower panels show fluorescence images of the corresponding stages from larvae expressing β-actin-GFP in hair cells. Note that the expression level of β-actin-GFP increases substantially over the course of maturation. Because the display range is optimized to contrast the developing hair-cell pair, images may include saturated parts of neighboring mature hair cells, in which the intensity of β-actin-GFP fluorescence is much higher. B, The contact angle α between the cells is controlled by the cellular surface tensions γ_h and γ_s, in which γ_h is associated with the interface between the two hair cells and γ_s with that between hair cells and supporting cells (see Supplementary Note 2.2). C, As shown on a timescale normalized to the doublet’s lifetime T, the contact angles in 24 pairs of developing hair cells underwent stereotyped dynamics between cell division and cell-cell detachment. After mitosis, each doublet assumed a round shape that persisted for several hours. The contact angle then decreased sharply until the cells detached from each other. The average time T was 314 ± 26 min. D, The timecourse of the ratio of surface tensions for the data in panel C accords with a first-order linear decrease in γ_s with a single fitting parameter γ₁/γ₀ = 0.93±0.01 (see Supplementary Note 2.2). The initial decrease in the surface tension ratio likely reflects an overall loss of cell contractility following mitotic rounding. The error bars denote standard errors of the mean (SE), computed as the standard deviation divided by the square root of the number of datapoints.

To better understand the underlying mechanics, we considered the effective surface tensions associated with the different cellular interfaces. The cellular surface tension is a mesoscopic variable arising from a variety of active and passive molecular processes, including intercellular adhesion at the membranes and active contractility of the underlying actomyosin cytoskeleton [22, 23, 24, 25]. As such, cellular surface tension is subject to active spatiotemporal regulation by various biochemical and genetic processes. Indeed, hair cells and supporting cells in the mammalian cochlea differentially express heterophilic adhesion molecules whose interactions underlie the mosaic arrangement of the cells required for sensory function [26, 27]. We inquired whether differential adhesion might explain the characteristic contact dynamics of nascent hair cells in a neuromast. If adhesion molecules that mediate heterophilic interactions between hair cells and supporting cells were expressed under a hair cell-specific genetic program, the expected mesoscale effect would be a gradual decrease of the associated surface tension during differentiation. We define the surface tension γ as an effective energetic cost per unit area for the associated interface, conjugate to the interfacial area A in the expression for the surface potential of the system [28]. A hair-cell doublet has two types of interfaces: the contact area between the two hair cells A_h and the contacts of each hair cell with the surrounding supporting cells A_s,1 and A_s,2. The effective surface energy is accordingly given by

$$E=\int \text{d}{\mathcal{A}}_{\text{h}}{\gamma }_{\text{h}}+\int \text{d}{\mathcal{A}}_{\text{s},1}{\gamma }_{\text{s},1}+\int \text{d}{\mathcal{A}}_{\text{s},2}{\gamma }_{\text{s},2}.$$ (3)

We assume here that the surface tensions differ predominantly based on the types of cells forming an interface, and neglect variations among the supporting cells surrounding the hair-cell pair. When the cell doublet is in a configuration that minimizes Eq. 3, the contact angle α between the two cells is controlled by the surface tensions (Fig. 2B; Supplementary Fig. 2; Supplementary Note 2.1). If the supporting-cell tensions in the contact point are equal, γ_s,i = γ_s, the contact angle is cos α = γ_h/(2γ_s). Using this relation, we inferred the ratio of the interfacial tensions from our measurements of the contact angles and found that the dynamics is reproduced surprisingly well by a single-parameter fit of a first-order decline in γ_s over time (Fig. 2D). This finding suggests that the morphological rearrangements are driven primarily by hair cell-intrinsic changes in the strength of the adhesive interactions between hair cells and supporting cells.

Polarity of active protrusions and directed cellular movements

During the later stages of their maturation, hair cells extend cytoskeletal protrusions that resemble the actin-filled lamellipodia of migrating cells [29, 30]. Within the context of surface tension, such protrusions can be interpreted as the signature of a phenomenon analogous to a wetting transition: the interfacial tension γ_s,i crosses a threshold beyond which the corresponding interfacial area is maximized rather than minimized under the constraints of the system [31, 32]. We observed that protrusions formed predominantly at the opposite poles of hair-cell pairs, suggesting that the interfacial tension γ_s,i developed a broken symmetry in space (Supplementary Fig. 3A; Supplementary Video 2). Oriented gradients of surface tension might produce directed protrusive activity along a particular cellular axis [33, 34, 35].

To investigate whether the orientation of protrusions was related to hair-bundle polarity, we measured both angles relative to the axis of PCP. In addition to the oppositely polarized hair-cell pairs of wild-type larvae, we imaged mutant animals in which the loss of functional Notch receptors had disrupted the chemical circuit that regulates polarity reversal, leading to uniformly oriented hair cells [14]. We also examined the misaligned hair cells in mutants with disrupted PCP signaling [12]. In Notch mutant and wild-type cells, we found that the orientations of protrusions closely aligned with the polarities of the hair bundles (Supplementary Fig. 3; Supplementary Video 3).

We further ascertained that hair cells moved actively in the direction of their protrusions. In oppositely polarized pairs of hair cells, these movements increased the separation between sibling cells whereas the centroid of the pair remained stationary. By contrast, in uniformly polarized mutant pairs the intercellular separation remained small as the cells translocated together in the direction of their protrusions (Fig. 3).

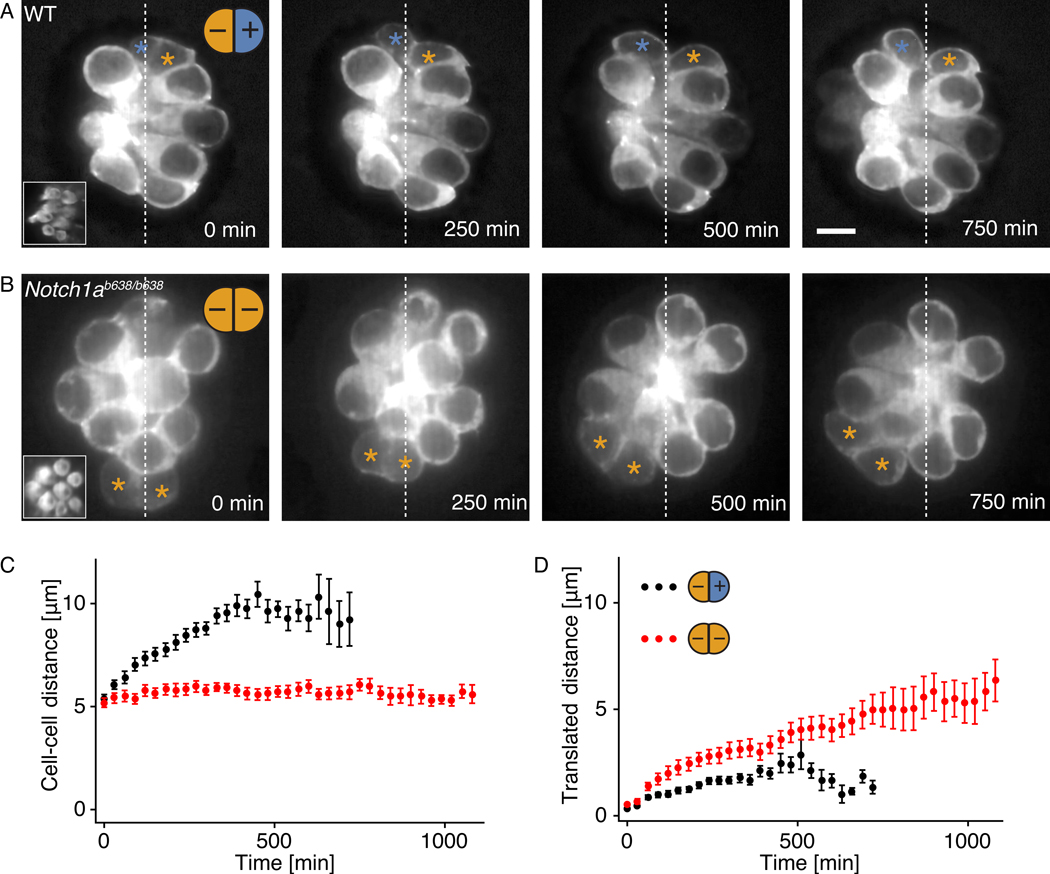
Figure 3: Relationship of polarity to cellular movements.

A, Fluorescence micrographs show β-actin-GFP in the hair cells of a wild-type larva. In the oppositely polarized pairs of newly formed hair cells (asterisks), the center-to-center distance between cells increases during the protrusive stage of maturation, but net translation within the neuromast is minimal. Insets show the apical surface of the neuromast. Scale bar: 5 μm. B, Instead of moving apart, the uniformly polarized hair cells in Notch1a mutants translate as pairs in the direction of protrusive activity. C, The average timecourse for the intercellular separation of 28 hair-cell pairs from wild-type larvae (black) differs from that of 31 pairs from Notch1a mutants (red). D, The average timecourse for the translated distance shows that wild-type cells (black) separate almost symmetrically from their starting positions, whereas mutant cells (red) undergo a net migration. The error bars denote SEs, computed as the standard deviation divided by the square root of the number of datapoints.

Taken together, our results suggest that hair-cell polarity not only defines the axis of hair-bundle orientation and the corresponding direction of maximal mechanical sensitivity, but also controls the directed protrusive and motile activities in maturing hair cells.

Coordination of hair-cell maturation by surface mechanics

We next explored the theoretical implications of a broken symmetry in the hair cell’s mechanical properties. In particular, our observations of oriented cellular protrusions motivated a surface-mechanical description, in which the surface tension at the supporting-cell interface γ_s has a gradient along the axis of polarity.

We considered small perturbations from the uniform case which depend weakly on a cell-intrinsic coordinate (x − x_i), in which x is the global organ axis and x_i is a reference point within cell i. With Δγ_s denoting the magnitude of the tension drop along the cell, we considered the surface tension profile for cell i

$${\gamma }_{\text{s},i}={\gamma }_{\text{s}}-u_i\Delta {\gamma }_{\text{s}}\frac{x-x_i}{\lambda },$$ (4)

in which λ is a gradient length scale of the order of a cell’s size. The sign of the gradient along x is given by the signaling states u_i, such that oppositely polarized cells have oppositely oriented surface-tension gradients.

The state space of the cell pair for different values of γ_s and Δγ_s shows a critical line for the transition at which the protrusions appear first at the cellular poles (Fig. 4A). To infer the approximate course of the cell pair through the state space during maturation, we estimated the overall decline in γ_s/γ_h from our measurements of the contact-angle dynamics (Figs. 2C and 4A). Although we have no direct readout for the dynamics of the tension drop Δγ_s, we established the initial point by assuming that no gradient was present during the signaling phase, when the cells had not yet committed to their polarity fates. By measuring the time when the first protrusion appeared on the surface of each cell, and relating the corresponding contact angle to the surface-tension ratio, we additionally established when the cell doublet crossed the effective “wetting” threshold.

Figure 4: Surface mechanics of hair-cell maturation and active dipole transitions.

A, A state diagram depicts the possible behaviors and morphologies of developing hair-cell pairs in the presence of a polarity-induced broken symmetry in the surface tensions γ_s,i (Eq. 4). The distinct regimes of the baseline tension γ_s and the tension drop Δγ_s are bounded by the two critical lines ${\gamma }_{\text{D}}^{*}=\gamma h$ and ${\gamma }_{\text{P}}^{*}=\Delta \gamma h$. The detachment threshold ${\gamma }_{\text{D}}^{*}$ indicates where the interface between the hair cells disappears, and Min[γ_s,i(x-x₀)] = 0 at ${\gamma }_s={\gamma }_{\text{P}}^{*}$, for which the protrusive threshold is crossed at the cellular poles. The two cells form actin protrusions within the green region and are wholly separated by supporting cells within the hatched region. For Δγ_s > 0, cell pairs can undergo dipole transitions from negative to positive configurations (yellow region). The approximate state-space trajectory of the cell doublet over the course of maturation (red arrows) is mapped by measuring the timing of hair-cell maturation events relative to our estimate of the dynamics of the surface-tension ratio (inset; Fig. 2). In particular, determining the onset of actin protrusions allows us to pinpoint the combination of parameters at the wetting transition (black circle). The successive stages of hair-cell matur;ation in the schematic diagrams include Notch signaling (I), dipole transitions (II), protrusion formation (III), and cell-cell detachment (IV). B, In about half of the cell pairs, dipole transitions occurred in which the sibling cells switched position along the axis of PCP during the early stages of maturation. Our observations did not indicate a preferred handedness of the rotations. Fluorescent images from a cell pair expressing β-actin-GFP demonstrate the nearly round shape of the cell pair during these rearrangements. C, Twenty-two of 43 developing hair-cell pairs and 19 of 38 regenerating hair-cell pairs underwent a dipole transition in wild-type neuromasts with oppositely polarized cells, but none of the 18 uniformly polarized pairs in Notch mutants did so. D, The angular trajectories of the wild-type hair cells displayed sharply binary outcomes: the cells either completely switched position or remained stationary. E The angular velocity profile of the 22 rearranging pairs agrees quantitatively with the theoretical prediction ω = −ω₀ sin ψ with a single fitting parameter ω₀ = (0.25 ± 0.01)10⁻³ · π/s. The error bars denote SEs, computed as the standard deviation divided by the square root of the number of datapoints.

The interpolated trajectory passes through three distinct regimes in the state space, recapitulating the successive stages of hair-cell maturation: the initial round morphology, the formation of protrusions, and the separation of sibling cells (Supplementary Video 2). Only two surface-mechanical changes are therefore required to explain the precise sequence of hair-cell maturation events: first, a differentiation-induced increase in heterophilic adhesion leading to a decline in γ_s; and second, a polarity signaling-induced increase in Δγ_s. Note that these two processes are themselves coupled: the large cell-cell interface in the initial configuration enables the signaling interaction, which in turn induces the spatial broken symmetry that appears in the formation of polarized protrusions and concludes in the detachment of the two cells. In summary, a highly parsimonious theoretical framework self-consistently explains the key phenomena of hair-cell maturation.

Polarity-driven transitions from negative to positive cell-pair dipoles

A polarity-directed broken symmetry in the surface tension also allows cell pairs to actively transition from negative- to positive-dipole configurations during maturation. In fact, such rearrangements of nascent pairs of hair cells have been observed in lateral-line neuromasts (Fig. 4B; Supplementary Video 4; Supplementary Figs. 5, 6; [36, 37]). We quantified the trajectories of 43 developing hair-cell pairs over time and observed that 22 underwent a dipole transition, whereas the remainder retained their initial configuration. For regenerating hair-cell pairs, we observed 19 rotations out of 38 pairs. In contrast, none of the 18 uniformly polarized hair-cell pairs that we observed in Notch mutants underwent a rearrangement (Fig. 4C–D). We did, however, observe a rotation in one of the oppositely polarized pairs that rarely occurred in the mutant background, further supporting that the rotations are driven by the opposing polarities in a pair (Supplementary Fig. 7).

Dipole transitions consistently occurred during the initial stages of maturation and lasted up to 100 min, during which the contact angle between the cells was nearly constant and close to a value of 90° (Fig. 4B). This simple geometry permitted an analytical treatment of the surface mechanics and a prediction for the angular velocity ω of the dipole to linear order in perturbations around an initial reference state for which γ_s,i = γ_s. Denoting the position of a point on the contact line by r_C, the net torque acting on the contact line is given by

$$\tau =\int {\text{r}}_{\text{C}}\times \text{f}\text{d}{s}_{\text{C}},$$ (5)

in which s_C parameterizes the arc length of the contact line and f is the force density. Given a polarity-dependent surface tension Eq. 4, the force component acting perpendicular to the contact line at each point is f_⊥ = 4uΔγ_s x_C/λ, in which x_C is the axial coordinate of r_C, and u = |u_i| (Supplementary Fig. 8; Supplementary Note 2.4). Using that the contact line is circular in the reference state, we obtain the linearized torque τ = τ₀ sin ψ e_z’, with z’ the axis of rotation perpendicular to the polarity axis. The balance of moments then induces the angular velocity

$$\omega =-\frac{4u\Delta {\gamma }_{\text{s}}}{\lambda \xi }\sin \psi ,$$ (6)

in which we have introduced a dissipative coefficient ξ (Supplementary Note 2.4). Fitting a single constant of proportionality ω₀ to the measured average velocity profile yielded a good agreement between theory and data (Fig. 4E).

In analogy to the classical expression for an electric dipole in an external field, the torque on the hair-cell pair can also be written as τ = m x F using definition Eq. 2 and with F a force directed along the PCP axis and proportional to Δγ_s. We note, however, that the tension gradient results from active processes intrinsic to the hair cells themselves.

Hair-cell doublet shapes and oppositely oriented surface tension gradients

In addition to the distinct switches in the cellular morphology during hair-cell maturation, the surface-mechanical description predicts more subtle changes in the shape of the hair-cell pair. To formulate these, we parameterize the cell-doublet surface with spherical coordinates θ and ϕ, such that the radial coordinate takes the values R(θ, ϕ) on the surface (Fig. 5A). The shape R is determined by the balance of forces on the surface, and deviations from the spherical reference case R = R₀, which is the solution for positive and uniform surface tension [28], are correspondingly of the order of the tension gradient. Using Eq. 4, we calculated the shapes of the cellular doublets for the positive and negative dipolar configurations as a function of the relative gradient Δγ_s/γ_s and the contact angle α. We obtained the first-order solution

$$\frac{R}{R_0}=1+\frac{4\log (\sin \theta +1)\sin \theta -1}{6}\frac{\Delta {\gamma }_{\text{s},i}}{{\gamma }_{\text{s}}}+\left(\frac{1}{2}-\sin \theta \right)\left(\alpha -\frac{\pi }{2}\right),$$ (7)

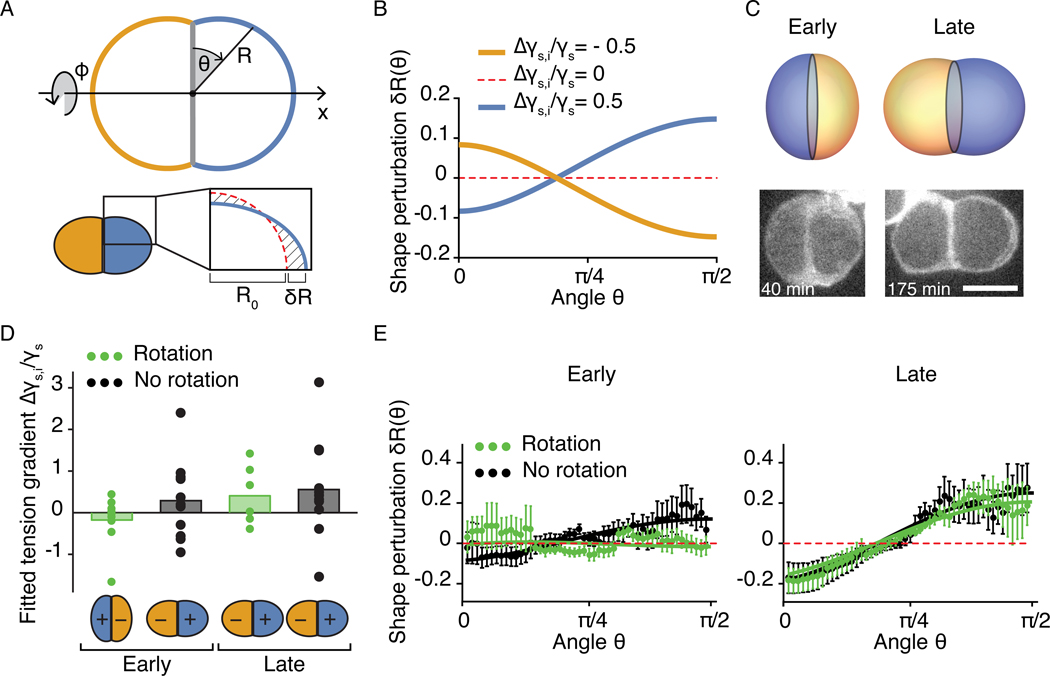
Figure 5: Relation of hair-cell doublet shapes to surface-tension gradients.

A, The interface between hair cells and supporting cells is parameterized in spherical coordinates (θ, ϕ). For a nonzero surface-tension gradient, the cell shape R deviates from the spherical solution R₀ (red dotted line) by a perturbation δR which is of the order of the tension gradient. We calculate the perturbations for the configurations in which the pair is aligned with the PCP axis and the shape of the cell doublet is axisymmetric. B, The perturbations from the spherical solution for different surface-tension gradients show the dependence on the sign of the gradient for boundary angle α = π/2. C, Negative (left) and positive (right) dipolar configurations lead to different doublet shapes. Fluorescent micrographs show a distinctively shaped hair-cell pair before and after it underwent an exchange of positions along the polarity axis. Scale bar: 5 μm. D, The means and individual values of the relative surface-tension gradients Δγ_s,i/γ_s estimated by fitting shape measurements are shown for nine hair-cell pairs that underwent an exchange of positions (green) and 12 hair-cell pairs that did not (black). Early and late stages were defined as the first ~100 min after division and the last ~100 min before the onset of protrusions, respectively. The theory predicts the sign change for pairs undergoing a dipole transition. Moreover, the magnitude of the estimated gradient increases with maturation stage, in agreement with the state-space trajectory shown in Fig. 4A. E, Average profiles of shape perturbation in hair-cell doublets at early and late maturation stages are shown together with the theoretical curves Eq. 7 for the mean fitted estimates of the surface-tension gradient and the measured boundary angles. The error bars denote standard errors of the mean (SE), computed as the standard deviation divided by the square root of the number of datapoints.

in which Δγ_s,i = u_iΔγ_sR₀/λ (Fig 5A–C; Supplementary Note 2.4.2). Comparing this solution to shape measurements obtained from live imaging, we recovered the predicted increase in the gradient from early to late maturation stages and found a close agreement between the theoretical curves and the experimental data. Our measurements additionally confirmed the switch in dipolar state from early to late stages of maturation in cells undergoing a rotation (Fig. 5D,E).

Interacting symmetry-breaking events

The biochemical and mechanical mechanisms underlying dipole formation can be described by a unified theory that elucidates the principle of polarity patterning in this system. The initial symmetry breaking between the two cells is triggered by bistable chemical signaling and gives rise to positive and negative signaling states u₁ = −u₂ (Eq. 1). This process can be represented as the relaxation of the dipole m (Eq. 2) within an energy landscape that resembles a rotationally symmetric Goldstone potential (Fig. 6A; Supplementary Note 1). Immediately after division of a precursor, the pair of nascent hair cells occupies the unstable state atop the central peak. The system then relaxes to one of the degenerate minima around the base and the polarities of the two cells are established. A priori, the potential is invariant with respect to the dipole angle ψ, but the subsequent manifestation of cellular polarity in the form of oppositely oriented forces gives rise to a second, explicit symmetry breaking: the appearance of polarity-induced gradients in surface tension tilts the potential landscape along the global axis of the organ. This process eliminates the degeneracy of the minima at the bottom of the well and yields a unique stable state for the cell pair. The set of states at the bottom of the tilted potential corresponds to the effective surface potential of the cell doublet (Eq. 3), in which the dependence on the organ axis x appears explicitly through Eq. 4. The surface-tension gradients are initially small, so the tilt can be considered linear and the surface potential simplifies to

$$E_{\text{norm}}=1-\frac{u\Delta {\gamma }_{\text{s}}}{2{\gamma }_{\text{s}}}\cos \psi ,$$ (8)

with $E_{\text{norm}}=\left(E-{\gamma }_{\text{h}}{\mathcal{A}}_{\text{h}}\right)/\left({\gamma }_{\text{s}}{\mathcal{A}}_{\text{s},1}+{\gamma }_{\text{s}}{\mathcal{A}}_{\text{s},2}\right)$ (Supplementary Note 2.4.1). The unstable equilibrium positions at ψ = ±π correspond to the negative dipolar configuration of the pair, whereas the dipole points along the organ axis in the minimum ψ = 0 (Fig. 6B). The magnitude of the torque driving the interfacial rotations (Eq. 5) can be recovered from τ = −∂E/∂ψ.

Figure 6: Symmetry-breaking events underlying polarity patterning.

A, Biochemical signaling breaks the symmetry between the two sibling cells, creating a non-zero pair dipole m. The mutually suppressive Notch interactions give rise to a Goldstone-type signaling potential, as shown in a cross-sectional view (left) and portrayed in three dimensions (right). As they undergo signaling, initially similar cells poised near m = 0 move to one of the degenerate states at the bottom of the well (dashed line). Because divisions of hair-cell precursors are often oriented along the organ axis x, most pairs have initial angles near ψ = π (I) or ψ = 0 (II). B, Active mechanical forces subsequently give rise to an explicit symmetry-breaking event. Once the two hair cells have converged to positive and negative signaling states, they manifest opposite cellular polarities that induce active cell movements in opposite directions along the organ axis, by which the symmetry with respect to ψ is broken. The mechanical forces governed by cellular polarization tilt the Goldstone potential (right), such that the circular set of states at the bottom of the well assumes a cosine shape as a function of ψ (left), with a maximum at the negative and a minimum at the positive dipolar configuration (Eq. 8). C, The theory predicts that precursor cells dividing out of alignment with the axis of PCP should nonetheless produce hair-cell pairs that rearrange into the correct dipolar configuration. The products of occasional off-angle divisions indeed always attain the correct final state (arrowheads).

The divisions of precursor cells in a neuromast are typically aligned with the organ axis as a consequence of PCP signaling, such that the initial distribution of cellular orientations is not uniform [12]. Rather than occupying all states at the bottom of the potential well with equal probability, the pairs cluster in two populations corresponding to positive and negative-dipole configurations. When the explicit symmetry-breaking event renders the negative-dipole state unstable, the pairs at the top of the tilt transition to the stable positive-dipole configuration, whereas the remaining pairs maintain their original arrangement. An important prediction from our theory therefore concerns oblique cell divisions. For the proposed mechanism to produce the correct dipoles, PCP signaling is relevant for selecting the axis of the tilt (Fig. 6B), but not for biasing the pair’s initial orientation. As predicted, the occasional oblique divisions that we observed were always followed by partial rearrangements, precisely aligning the cell pair in the correct final configuration (Figs. 4D and 6C).

To confirm this role for PCP, we additionally investigated a second type of neuromast present in the lateral-line system, in which the PCP field is oriented perpendicular to the antero-posterior body axis of the animal (Supplementary Fig. 5A, [38]). Both during development and regeneration, we observed near-180° rotations of hair-cell pairs in 50 % of instances, giving rise to dipole patterns precisely aligned with the dorso-ventral axis (Supplementary Fig. 5B–D). Furthermore, when we investigated PCP mutants in which bundle polarity remained intact while alignment across the cells was lost, we observed that pairs of sibling cells tended to acquire opposite orientations relative to each other. This finding indicates that cell-intrinsic polarity and polarity-driven movements operated even in the absence of PCP-mediated alignment to the organ axis (Supplementary Fig. 9). Taken together, these results support a role for PCP as a guiding cue that selects an axis along which hair cells orient a cell-intrinsic polarity system in opposite directions.

Discussion

Combining experimental and theoretical approaches, we found that two interacting symmetry-breaking events mediate mirror-symmetric polarity patterning in a vertebrate sensory organ. In the first event, Notch signaling between the daughters of a cell division yields a pair of cells with positive and negative signaling states (Fig. 1; Supplementary Fig. 1; Supplementary Note 1; [14]). This signaling interaction acts as an unbiased bistable switch that produces both positive- and negative-dipole configurations (Supplementary Fig. 1I). However, a cell’s adoption of positive or negative Notch status influences not only the orientation of its hair bundle, but also the direction in which the cell moves actively during maturation (Fig. 3). Oppositely oriented mechanical polarization thus constitutes a subsequent explicit symmetry breaking, which aligns the cell-pair dipoles and segregates the positive and negative cells to opposite halves of the organ (Figs. 4, 6; Supplementary Figs. 4, 5, 6). Although these pairs behave like electric dipoles in an external electric field, the underlying physics is different owing to the active properties of the living system. Rather than performing work on the dipole, the PCP field merely provides signaling cues to select an axis along which cell-intrinsic forces drive movements (Supplementary Fig. 9). These forces result from metabolically driven processes within each cell’s cytoskeletal and adhesive machinery. Thus, cellular polarity drives active dipole transitions in this system.

Although surface tension-driven movements on substrates have been well explored both for passive droplets and for active cells [39, 40, 33], to our knowledge this study represents the first theoretical treatment of a system with two coupled, active “droplets” with oppositely oriented gradients in surface tension. The resulting phenomenon represents a form of collective motility, in which rather than moving uniformly—as in convergent extension [5]—the polarized cells undergo pairwise rotations that result in a mirror-symmetric polarity pattern at the organ scale. Relying on only two control parameters, our description of hair-cell surface mechanics not only quantitatively recapitulates the rotational trajectories, contact-angle dynamics, and cellular shapes measured in vivo, but also self-consistently explains the full sequence of distinct morphologies observed over the course of hair-cell maturation (Figs. 2, 4, 5; Supplementary Note 2). In fact, the precise temporal regulation of the successive maturation events is parsimoniously interpreted as a natural consequence of two simple surface-mechanical changes in the hair cells. These mechanical processes are in turn triggered by two underlying differentiation events: first the commitment to become a hair cell, which introduces heterophilic interactions at the interface with the supporting cells; and subsequently the polarity-fate decision, which generates a spatial gradient in the surface tension.

In conclusion, biochemical and mechanical interactions at the cellular level lead to the emergence of organ-scale patterns in neuromast morphogenesis. We propose that feedback effects coordinate the different cellular processes in time and promote robustness; moreover, we suggest that the regenerative capacity of this organ relies on these self-organizing principles. The coupling of directed mechanical forces during development to functional and morphological cellular polarity in the mature stage provides a powerful mechanism for long-range patterning that bridges the levels of cells and organs.

Materials and Methods

1. Animal handling and genetics

Experiments were performed in accordance with the standards of Rockefeller University’s Institutional Animal Care and Use Committee. Zebrafish were raised in E3 medium (5mM NaCl, 0.17mM KCl, 0.33mM CaCl₂, 0.33mM MgSO₄, 1 μg mL⁻¹ methylene blue) in an incubator maintained at 28 °C. Wild-type TL zebrafish were obtained from the Zebrafish International Resource Center. The following transgenic zebrafish lines were used: Tg(myo6b:actb1-EGFP) [41], Tg(5xUAS-E1b:6xMYC-notch1a-intra) [42], Tg(myo6b:GAL4FF) allele ru1012Tg [30], and Tg(−8.0cldnb:lynEGFP) [43]. In addition, we used the mutant line Notch1a−/− allele b638 [44] and the Vangl2 mutant trilobite, allele m209 [45]. Embryos and larvae were staged as described in [46].

1.1. Treatment of larvae

To ablate mature hair cells in regeneration experiments, we treated 3 dpf larvae for 2 hr at 28 ◦C with 1 μM CuSO₄ in E3 medium. The animals were thoroughly washed and maintained overnight in E3 medium, then used for live imaging or fixed for immunofluorescence imaging on the following day.

2. Immunofluorescence labeling

Immunofluorescence labeling for Delta D was conducted on regenerating neuromasts of 4 dpf larvae. Larvae were fixed overnight at 4 °C in 4 % formaldehyde in phosphate-buffered saline solution (PBS). On the following day, the larvae were washed for 5 min in PBS with 1 % Tween-20 (PBST) and placed for 2 hr in blocking solution containing PBS, 10 % NDS, 0.5 % Triton X-100, 2 % bovine serum albumin, and 1 % dimethylsulfoxide. The primary antibody, murine anti-Delta D (1:100; zdd2, Abcam) [47], was diluted in fresh blocking solution and incubated with the larvae overnight at 4 °C. Larvae were washed for 2 hr with PBS containing 0.1 % Triton X-100. Pre-adsorbed AlexaFluor 555-conjugated anti-mouse secondary antibody (Invitrogen, Molecular Probes) was applied overnight at 4 °C at a dilution of 1:200 in blocking solution. The pre-adsorption step was introduced to increase the specificity of the antibody in order to minimize background signal. Larvae were then washed for 2 hr in PBS containing 0.1 % Triton X-100 and stored at 4 °C in VectaShield.

3. Image acquisition and analysis

We performed time-lapse confocal fluorescence microscopy for up to 40 hrs on live animals. Embryos of 2–5 dpf were anesthetized in 600 μM 3-aminobenzoic acid ethyl ester methanesulfonate in E3 medium and mounted in a 35 mm glass-bottomed dish in 1 % low-melting-point agarose.

Transgenic larvae expressing actb1-EGFP were imaged under a 100X/NA 1.35 silicone-oil objective lens on an Olympus IX81 microscope equipped with a microlens-based, super-resolution confocal system (VT iSIM, VisiTech International). Neuromasts were imaged at intervals of 5 min as Z-stacks acquired with 0.5 μm steps under laser excitation at 488 nm. To keep the regions of interest within view over the imaging period, we developed a customized tracking algorithm that automatically updated the stage position, correcting for sample drift. The code is available at https://github.com/a-jacobo/AutoTracker.

Transgenic larvae expressing lynEGFP were imaged under a 60X/NA 1.3 silicone-oil objective lens with an Olympus IX81 microscope equipped with a spinning-disk confocal system (Ultraview, Perkin-Elmer, Waltham, MA). Neuromasts were imaged at intervals of 5 min as Z-stacks acquired with 0.5 μm steps under laser excitation at 488 nm.

3.1. Deep learning-assisted long-term imaging

Because protrusions and movement at nascent stages as well as hair-bundle orientation at mature stages had to be measured in the same cells, the data presented in Figs. 2 and 3 required long-term imaging at high temporal and spatial resolution. To prevent sample deterioration due to photodamage, we acquired images at low laser power and 300 ms exposures, then used a neural network to perform content-aware image restoration [48]. To train the network, we acquired both ground-truth images with high signal-to-noise ratios at high laser power, and images of the identical samples and imaging regions at low signal-to-noise ratios. The total size of the training dataset was 30 Z-slices each from 20 neuromasts.

3.2. Image analysis

Prior to analysis, images were subjected to automatic drift (translation) correction with the MultiStackReg Fiji plugin [49] and cropping. For illustrative purposes, the images displayed in Figs. 3–4 were additionally processed by applying a 1000-point rolling-ball background subtraction algorithm and a three-point Gaussian blur filter.

In transgenic larvae expressing β-actin-GFP under the hair-cell specific promotor myo6b, the fluorescence intensity of β-actin in hair cells increased over the course of hair-cell differentiation, such that nascent and immature hair-cell pairs often appeared very faint compared to mature hair cells with actin-rich hair bundles and cuticular plates. The display range in the images shown in Figs. 2–6 was therefore adjusted to better contrast the features of young hair-cell pairs, leaving some actin-rich parts of neighboring mature hair cells saturated.

Semi-automatic extraction of the quantities measured from time-lapse recordings of Tg(myo6b:actb1-EGFP) larvae — hair-bundle polarities, contact angles, protrusion orientations, and cell trajectories — was performed with custom ImageJ (National Institutes of Health, Bethesda, MD) extensions written in Python.

The angular trajectories of hair-cell pairs in Fig. 4D and Supplementary Fig. 9C were obtained as follows. In time-lapse recordings of neuromasts from Tg(−8.0cldnb:lynEGFP) larvae, the nascent hair-cell pair of interest was identified and a Z-slice near the centroid of the pair was manually selected for each frame. In this set of slices, the outlines of the two cells were segmented using a “morphological snakes” method [50]. After the algorithm had been initialized at the correct position by manual selection of points near the center of each cell in the first frame, the algorithm automatically obtained the outlines of the two cells and calculated their centroids, which were used to run the morphological segmentation algorithm on the subsequent frame. Occasional incorrect segmentations were resolved by manual re-selection of the cell centers. This algorithm produced a list of relative distances and angles as a function of time for each selected pair of hair cells. To compensate for variations in the imaging axis, we aligned the measured angles to the organ axis for each pair.

To obtain the regions of interest (ROIs) for quantifications of the Delta D immunolabeling in Supplementary Fig. 1, we manually traced the cell outlines and constructed eight-pixel-wide line ROIs for the intensity measurements at the cellular boundaries, and an area ROI for the mean intensity measurement for each cell. To reduce observer’s bias, we performed these manual steps on the β-actin-GFP image only, then automatically obtained the average Delta D fluorescence intensities in the respective ROIs. The surface accumulation at a respective cellular boundary B is defined as (I_B − $\overline{I}$)/$\overline{I}$, with $\overline{I}$ the mean intensity (Supplementary Fig. 1G). The age classification for Supplementary Fig. 1I (nascent versus protrusive) was performed on the basis of the morphological characteristics of the cells. Cell pairs with a shared interface and without protrusions or emerging apical surfaces were classified as “nascent”, and cell pairs with protrusions or small apical surfaces but without fully formed bundles were classified as “protrusive”.

The measurements of doublet shape in Fig. 5 were performed on the first or second hair-cell pairs in neuromasts of 2 dpf Tg(myo6b:actb1-EGFP) larvae to reduce segmentation errors due to crowding. Shape quantifications were obtained from maximum-intensity projections of Z-stacks, in which at least one cellular region extending from the contact point between the two cells to the pole of one cell was not obstructed by neighboring cells. Fluorescence-intensity profiles were then obtained within this region along radial lines in angular increments of 0.01π, and the position of the cellular surface was subsequently determined by Otsu thresholding. Each shape profile was normalized to the median radius. The selection of the time periods for “early” versus “late” stages of maturation was based on our independent measurements of the average timing of maturation events (see inset in Fig. 4A). The “early” period refers to the time interval between the division of the precursor and the average onset of rotational rearrangements, and “late” refers to the period between the end of rearrangements and the onset of protrusions. Fitting was then performed on the average profiles for each cell pair and maturation stage.

4. Calculations, data fitting, and visualization

Calculations shown in Supplementary Note 1–2, data visualization, data fitting (Figs. 2, 4, 5), parameter error computation and statistical testing were performed with Mathematica (Wolfram Mathematica 11.3.0.0). The average evolution of the contact angle shown in Fig. 2 was obtained as follows. We first measured the lifetime T of each cell-pair doublet by determining the timepoints of the cell division t_Div and cell-cell detachment t_Det events. We then measured the evolution of the contact angle over this period and collapsed the individual pair traces by normalizing the timepoints to the respective doublet lifetimes, t/T = (t_Abs -t_Div)/(t_Det -t_Div), in which we have denoted the timestamps of the image recordings as t_Abs. To average over all doublets, we computed linear interpolations between the data points for each doublet and averaged over evaluations taken at a resolution Δt/T = 0.04.

For the average cell-cell trajectory data plotted in Fig. 3E, individual trajectories were aligned without normalizing to the timepoint at which the first protrusion appeared and averaged across pairs in 30 min bins. To obtain the angular velocity profile shown in Fig. 4D, the individual trajectories were first smoothed by applying an unweighted moving-average filter with a 15 min window. The velocity was subsequently determined from each trajectory prior to averaging over the cell pairs.