Deep neural networks identify sequence context features predictive of transcription factor binding

Abstract

Transcription factors (TFs) bind DNA by recognizing specific sequence motifs, typically of length 6–12bp. A motif can occur many thousands of times in the human genome, but only a subset of those sites are actually bound. Here we present a machine learning framework leveraging existing convolutional neural network architectures and model interpretation techniques to identify and interpret sequence context features most important for predicting whether a particular motif instance will be bound. We apply our framework to predict binding at motifs for 38 TFs in a lymphoblastoid cell line, score the importance of context sequences at base-pair resolution, and characterize context features most predictive of binding. We find that the choice of training data heavily influences classification accuracy and the relative importance of features such as open chromatin. Overall, our framework enables novel insights into features predictive of TF binding and is likely to inform future deep learning applications to interpret non-coding genetic variants.

Introduction

Binding of transcription factors (TFs) to DNA is one of the major transcriptional regulation mechanisms. TFs typically recognize short motifs of 6–12bp¹. However, there is often only partial overlap between sequences matching the motif for a particular TF in the genome and experimentally determined binding sites¹. For example, we found that <1% of approximately 3.6 million SP1 motifs across the human genome are actually bound in a human lymphoblastoid cell line (GM12878). Whether a particular motif instance is bound depends on multiple factors, including chromatin accessibility², nucleosome positioning³, cooperative and competitive binding with other factors⁴, local GC content⁵, local DNA tertiary structures^6,7, and inter-position dependencies within motifs⁷. Many of these features are related to sequence context in the immediate vicinity of the TF motif itself⁸, implying that TF binding may be predicted directly from sequence information.

Several machine learning methods^9–16 have proven successful in predicting TF binding from sequence. Many of these methods, such as DeepSEA¹⁶ and DanQ¹³, rely on convolutional neural networks (CNNs), which infer important sequence context features and learn combinations and orientations of these features that are predictive of binding. However, these frameworks face several limitations. First, they focus on open chromatin regions that are active in at least one cell type of interest, but do not consider regions inactive in all cell types as controls. Thus, they do not learn general features that distinguish bound vs. unbound genomic regions. Second, while these models have shown excellent prediction accuracy for a variety of marks and cell types, interpreting CNNs to derive meaningful biological insights remains challenging.

Here, we expand on existing CNN models to develop a framework for predicting whether a particular instance of a TF motif will be bound and interpreting the specific nucleotides with the strongest influence on binding status. By conditioning on sequences that contain the core TF motif in both the positive and negative samples, our framework specifically learns context features in the vicinity of the core motif. Next, we apply Grad-CAM¹⁷, a post-analytical method for neural networks, to compute importance scores for each nucleotide in the context regions and characterize sequence features predictive of TF binding. We find that TF binding is largely predicted by open chromatin, and to a lesser extent by TF-specific sequence features. The relative importance of these features depends heavily on how positive and negative training sets are chosen. Overall, our framework enables novel insights into sequence features predictive of TF binding.

Results

Predicting binding status of TF motif occurrences

We focused on 38 TFs active in GM12878 with ChIP-sequencing datasets available from ENCODE¹⁸ and motifs available from JASPAR¹⁹ (Supplementary Tables 1–2). For each TF, we scanned the human reference genome (hg19) to identify all instances of its motif, which we refer to as the core motif. We extracted 1kb genomic sequences centered on each core motif instance and labeled each sequence as bound (positive) vs. unbound (negative) based on overlap with binding sites identified by ChIP-sequencing (Online Methods, Fig. 1a). On average for each TF, we obtained 18,892 sequences as input for our baseline model.

Figure 1: AgentBind Overview.

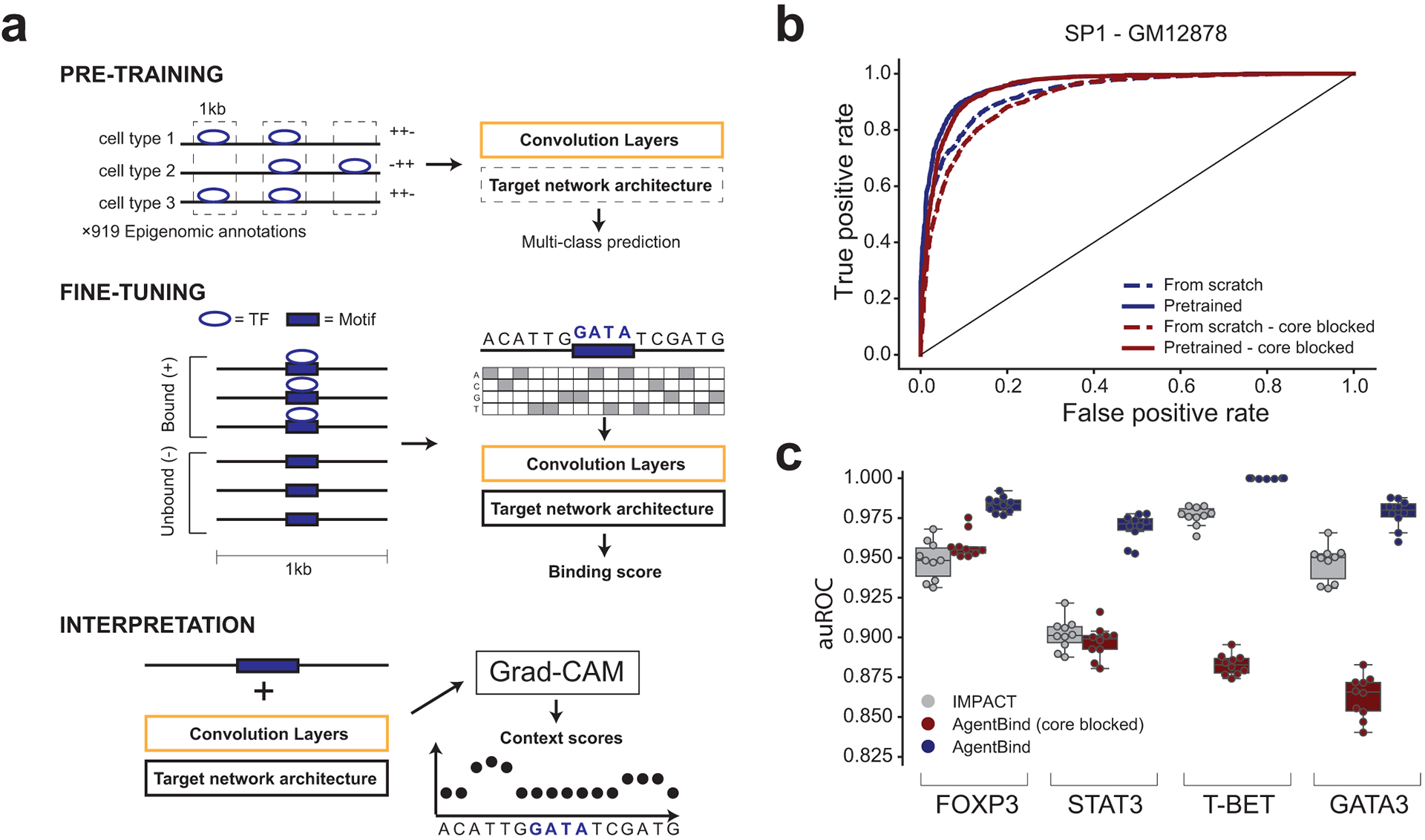
(a) Method schematic. AgentBind pre-trains a convolutional neural network on epigenomic annotations from multiple cell types (top). It then fine-tunes on sequences containing a core motif (purple box) for a target TF that are either bound (+) or unbound (−) to learn important context features (middle). Grad-CAM is then used to score the contribution of each nucleotide to binding predictions (bottom). (b) Pre-training improves TF binding predictions. Receiver operator curves (ROC) are shown for the TF SP1 in GM12878 using baseline models with a DanQ architecture. Dashed and solid lines show performance with and without pre-training, respectively. (c) Comparison to IMPACT. We compared the ability of AgentBind and IMPACT to distinguish bound vs. unbound motifs for four TFs in CD4+ Th17 cells. Boxplots show distributions of auROC values for 10 rounds of randomly selecting training (80%) vs. testing (20%) motif instances. Middle lines give medians and boxes span from the 25th percentile (Q1) to the 75th percentile (Q3). Whiskers extend to Q1–1.5*IQR (minima) and Q3+1.5*IQR (maxima), where IQR=Q3-Q1. Dots show the auROC values for individual rounds. Gray=IMPACT. For (b) and (c), dark blue=AgentBind without the core motif blocked, dark red=AgentBind with the core motif blocked.

Our model framework, AgentBind, consists of (1) pre-training CNNs using ChIP-sequencing and DNaseI-sequencing profiles collected from ENCODE¹⁸ and the Epigenomics Roadmap Project²⁰ across dozens of cell types and (2) fine-tuning an individual model for each TF to identify bound vs. unbound sequences as described above. This framework is compatible with theoretically any CNN-based architecture. As examples, we evaluated its performance using two popular architectures, DeepSEA¹⁶ and DanQ¹³ (Online Methods). We evaluated performance using area under the receiver operating characteristic curve (auROC) and the precision recall curve (auPRC), and partial auROC (pAUC) with false positive rate less than 0.1²¹. Full results are reported in Supplementary Tables 3–4. Average performance across all TFs is high (auROC=0.941 for DanQ and 0.928 for DeepSEA), suggesting that binding is largely predictable by local sequence features within a few hundred base pairs of the core motif. In both evaluation experiments, pre-training noticeably improves the performance compared with models trained from scratch (Fig. 1b), especially for TFs with low sample sizes such as FOS. This improvement is expected, since pre-trained DanQ and DeepSEA are models optimized for large datasets. Fine-tuned TF-specific models consistently outperform multi-class models for this classification task, with an average auROC increase of 0.033 (range from 0.002 [NFYA] to 0.123 [NRSF]) for DanQ. Because of its consistently higher performance, subsequent results are reported for DanQ unless otherwise specified.

We tested whether our classification performance could be driven by differences either in core motif sequences or nucleotide content not directly relevant to the context features we aimed to identify. We first repeated our analyses with the central core motifs masked. In most cases performance is only slightly reduced after masking (average auROC decrease 0.015; Supplementary Table 5). CTCF is a notable exception (auROC=0.945 and 0.798 before and after blocking, respectively), suggesting its bound vs. unbound regions have key differences within core motifs despite being similarly scored by position weight matrices (PWMs). We further observed that model performance is correlated with the difference in GC content between bound vs. unbound regions (Pearson r=0.58; two-sided P=0.00012; n=38, Extended Data Fig. 1a–b). To ensure that our models focus on more specific sequence features, we retrained models using negative and positive datasets with matched GC percentages (Online Methods, Supplementary Tables 6–7). These models, which we refer to as GC-controlled, have only slightly lower performance (mean decrease in auROC=0.013).

We hypothesized that our models are learning a combination of general sequence features characteristic of active regulatory regions in open chromatin and more specific sequence features required for each TF. To determine the extent to which our predictions are driven by features of open chromatin, we re-trained GC-controlled models restricting all sequences to be within DNaseI hypersensitive sites in GM12878 (Online Methods). As expected, overall performance for these models, which we refer to as DNaseI-controlled, decreases (mean decrease in auROC=0.133 compared to the GC-controlled model, Supplementary Table 7), suggesting open chromatin features make a major contribution to classification accuracy for most TFs. Notably, controlling for DNaseI results in greatly reduced sample sizes (mean decrease 50%) which may in part drive this trend (Supplementary Table 6; Extended Data Fig. 1c–d). Even after controlling for DNaseI, auROC values are above 0.7 for 32/38 TFs, indicating that while open chromatin is a major predictor, it does not completely determine binding.

To additionally investigate the predictive power of chromatin accessibility alone, we predicted binding of each TF using GM12878 DNaseI-seq output of pre-trained DanQ models (Supplementary Table 8). For baseline and GC-controlled datasets, DNaseI alone is highly predictive of binding (mean auROC=0.882 and 0.841), although fine-tuned TF-specific models outperform DNaseI alone (mean auROC=0.941 and 0.928 for baseline and GC-controlled datasets). On the other hand, for DNaseI-controlled data, DNaseI alone is a relatively poor predictor as expected (mean auROC=0.634, compared to 0.795 for TF-specific models).

To further determine whether our models identify context features specific to each TF, we performed a pairwise comparison in which we used models for each TF to predict binding at motifs for all other TFs. For GC-controlled models, binding for most TFs could be predicted well using models for most other TFs (Extended Data Fig. 1e–f). Still, most (33/38) are predicted best by their own model (median gain in auROC=0.017 compared to the next best model). For the 5 TFs predicted better by other models, the performance difference is negligible (median difference in auROC=0.0060). For DNaseI-controlled models, TF-specific models tend to show higher performance compared to the next best model (Extended Data Fig. 1g–h). Taken together, these results suggest as expected that GC-controlled models largely learn features indicative of open chromatin but capture some TF-specific features, whereas DNaseI-controlled models better capture features specific to each TF.

We compared our results with two alternative methods, KSM⁷ and IMPACT²², which are not based on deep learning. KSM represents TF motifs as a set of aligned k-mers that are overrepresented at TF binding sites and more accurately predicts in vivo binding sites than PWM models. We identified KSM motifs for each TF using the same set of training and test data as used for AgentBind (Online Methods). For GC-controlled models, AgentBind outperforms KSM in predicting binding status for all TFs (Supplementary 9; median gain in auROC=0.261). For DNaseI-controlled models, AgentBind outperforms KSM for 33/38 TFs (median gain in auROC=0.182). IMPACT tackles a similar classification task to Agentbind but uses a broad range of experimentally determined epigenomic features including ChIP-sequencing, ATAC-sequencing, and DNaseI-sequencing profiles. While IMPACT has a variety of applications such as prioritizing causal variants for gene expression and complex traits, we only evaluate the application of binding site prediction here. We benchmarked each method on four TFs active in CD4+ T cells and applied the same training scheme as the IMPACT study (Online Methods). AgentBind demonstrated higher auROC than IMPACT in all four cases (Fig. 1c, Supplementary Table 10). This suggests that the majority of determinants of binding for these TFs can be learned directly from local sequence features. For FOXP3 and STAT3, performance was comparable to IMPACT even with core motifs blocked, meaning classification decisions were largely based on context sequence rather than differences in the core motifs themselves.

Identifying the context-specific determinants of TF binding

Although deep neural networks achieve high classification accuracy, compared to simpler linear models they are not trivially interpretable. Several techniques, including in silico mutagenesis^11,16, DeepLIFT²³, and saliency maps²⁴, have previously been applied to interpret CNN results on DNA sequences. Grad-CAM¹⁷, an advanced version of saliency maps, has been shown to outperform vanilla saliency maps in many computer vison applications. We adapted a previously published evaluation scheme²³ and designed a simulation experiment to benchmark the ability of these model interpretation methods to score important context nucleotides. We applied five metrics to evaluate the performance of each interpretation method (Online Methods, Supplementary Table 11).

Our results demonstrate that each interpretation method has unique strengths and weaknesses. For example, in silico mutagenesis generally shows superior classification of individual bases but its run time is two orders of magnitude higher than the other methods. DeepLIFT identifies more embedded motif instances whereas Grad-CAM better pinpoints specific important bases (Fig. 2a). Due to its fast run time, high classification accuracy at base pair resolution, and applicability to the better performing DanQ architecture, we chose Grad-CAM for downstream analyses.

Figure 2: Interpreting context-specific determinants of TF binding.

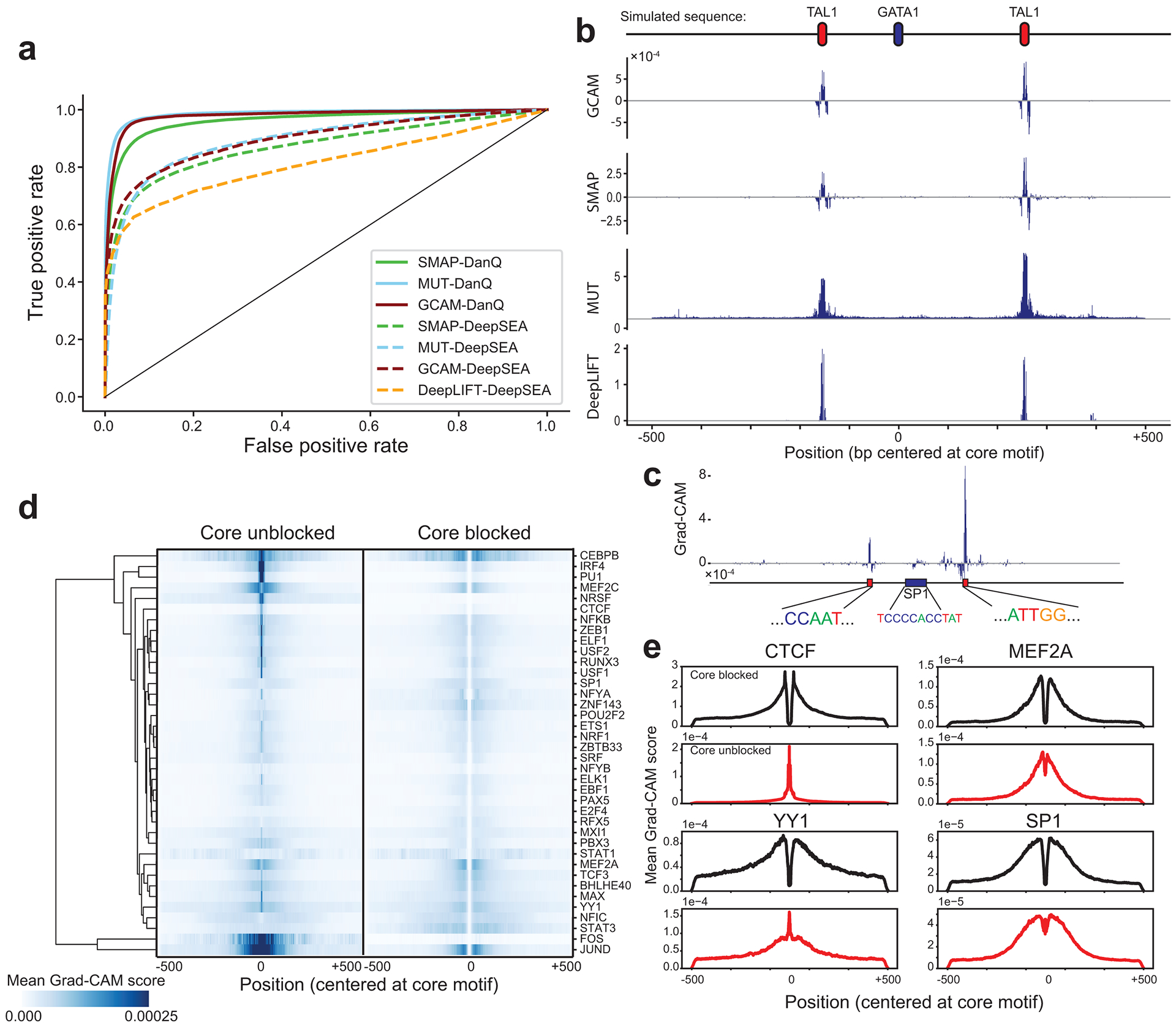
(a) Comparison of model interpretation methods. ROC curves are shown comparing performance of each method to distinguish simulated important vs. neutral context bases. Dashed and solid lines denote DeepSEA and DanQ architectures respectively. Green=saliency map (SMAP), cyan=saturated mutagenesis (MUT), red=Grad-CAM (GCAM), orange=DeepLIFT. (b) Example importance scores for a simulated region. The top shows an example simulated sequence, with a central GATA motif and two context TAL1 motifs. Importance scores are shown for each method based on a DeepSEA architecture. (c) Example Grad-CAM scores for a region (chr1:12289432–12290431 in hg19) containing an SP1 motif. The y-axis shows the Grad-CAM score of each nucleotide based on the GC-controlled model. Sequences are shown for the central SP1 motif and two regions with high scores corresponding to NFY motifs. (d) Aggregate Grad-CAM score profiles. For each TF, we computed the average absolute value of the Grad-CAM score per position in positive sequences using GC-controlled models with the core motif unblocked (left) or blocked (right). Values were Z-normalized across rows. The dendrogram is based on hierarchical clustering of the rows. (e) Example aggregate Grad-CAM profiles. For four representative TFs, average Grad-CAM scores are shown for models with the core motif blocked (dark blue) or unblocked (dark red).

We applied Grad-CAM to interpret the GC-controlled models for the 38 TFs and computed importance scores for each base in input sequences. As expected, aggregating scores across all input sequences for each TF shows that sequences closest to the core motif tend to have the highest impact (Fig. 2d). However, aggregate score profiles differ noticeably for different TFs. For example, whereas the important bases for predicting CTCF binding are highly concentrated directly adjacent to the motif, important bases for YY1 are spread across the entire 1 kb region (Fig. 2e). In concordance with our results above, differences in core motifs themselves receive high importance scores for some TFs (e.g., PU1, CTCF) but not others (e.g., MEF2A, SP1, Fig. 2e). Context scores for bound (positive) sequences show far more distinct patterns than for unbound (negative) sequences (Extended Data Fig. 2). Therefore, we focus on scores for bound sequences for downstream analyses.

Grad-CAM scores give insight into features of TF binding

We next sought to use Grad-CAM score profiles to identify context sequence features with strongest impact on binding status for each motif. We extracted 5-mers from positive sequences accounting for the strand of the core motif, and tested whether each unique 5-mer is enriched among 5-mers with highest average Grad-CAM scores for each TF (Online Methods). Our results using the baseline models recapitulate multiple known trends (Fig. 3a). First, the top scoring sequences for a TF often closely match the core motif of the TF itself, consistent with previous literature showing homotypic clusters of TF motifs can promote binding²⁵. For example, 5-mers from the NRF1 (5’-TGCGCATGCGCA-3’) and ZEB1 (5’-CAGGTG-3’) motifs score highly for NRF1 (Fisher’s exact test one-sided P<10⁻²⁰⁰; OR=14.1 for ATGCG) and ZEB1 (P<10⁻²⁰⁰; OR=18.2 for CAGGT), respectively. In some cases, these enrichments are strand-specific. For instance, the ZEB1 motif is consistently enriched in important context bases for ZEB1, whereas its reverse complement is not. Similar trends are observed for other factors such as YY1 and ZNF143. Second, top 5-mers capture known co-binding relationships. For example, the NFY motif scores highly among known co-binders SP1²⁶ and RFX5²⁷. Additionally, the motif for AP-1 (5’-TGA G/C TCA-3’), bound by of a dimerization of JUN and FOS²⁸, scores highly for known co-binders CEBPB²⁹ and IRF4³⁰. These trends are also observed using GC-controlled and DNaseI-controlled models (Fig. 3b–c).

Figure 3: Identifying key context sequence features for TF binding in GM12878.

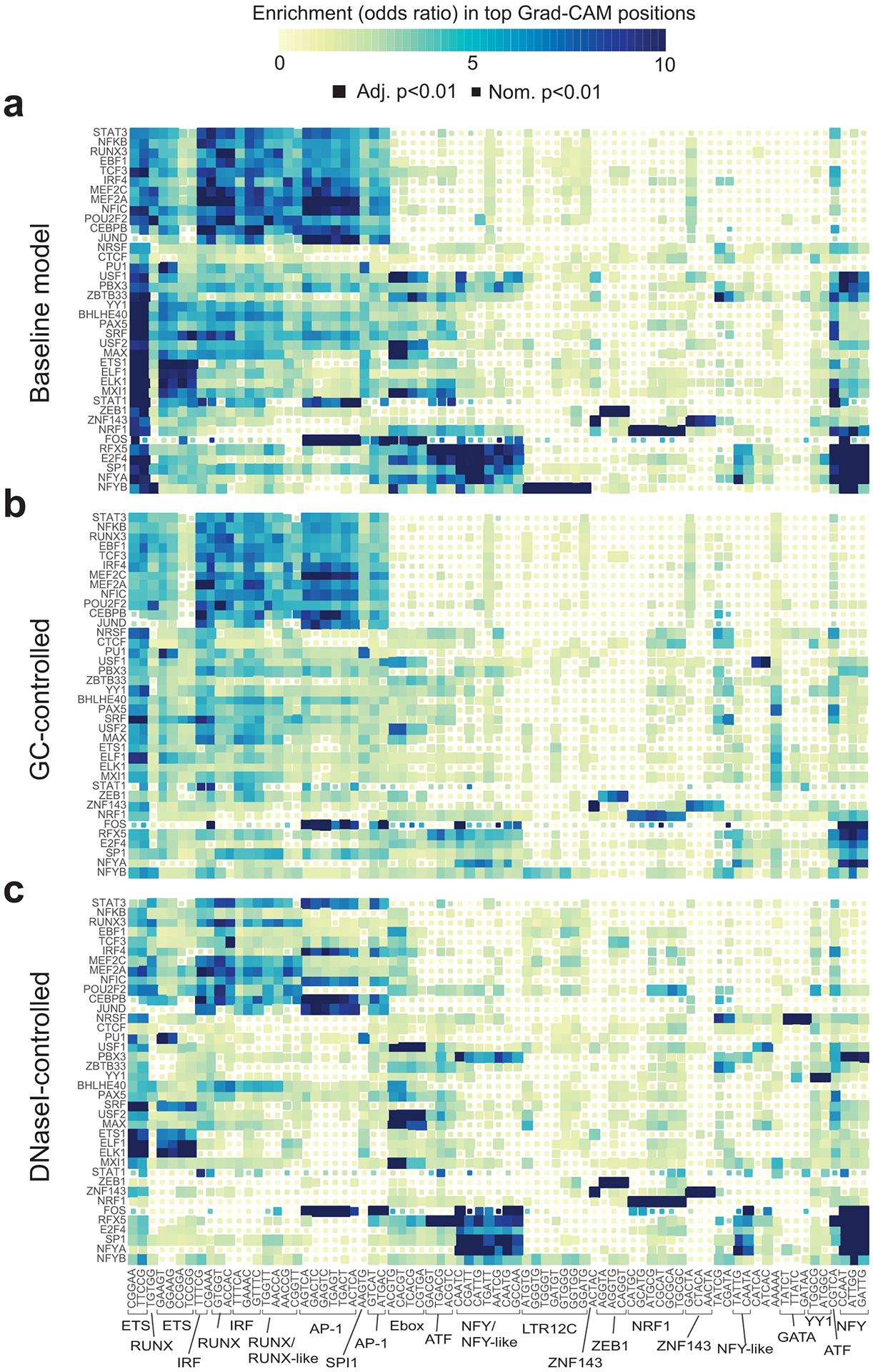
(a) Enrichment of 5-mers in the most influential context regions. The heatmap shows the enrichment of each sequence in regions with the highest Grad-CAM scores for each TF using baseline models (Online Methods). Heatmaps in (b-c) are the same as in (a) but show data for GC-controlled (b) and DNaseI-controlled (c) models. Only 5-mers corresponding to top 50 5-mers in at least one of the three models are shown. Colors denote odds ratios and the sizes of the boxes denote statistical significance based on one-sided P-values computed using Fisher’s exact tests. Adjusted P-values are based on a Bonferroni correction for the number of 5-mers tested. The color scale is capped at 10. Odds ratios higher than 10 are all colored the same. Boxed and annotated 5-mers correspond to known motifs. The order of TFs (y-axis) and 5-mers (x-axis) is the same for all plots and is based on hierarchical clustering of the odds ratio matrix for the baseline model.

While our three different models (baseline, GC-controlled, and DNaseI-controlled) capture many similar trends, they also each highlight orthogonal context features relevant to TF binding. Baseline models identify many key elements of promoter regions (Fig. 3a), which comprise approximately 56% of ChIP-seq peaks analyzed. For example, top-scoring 5-mers include the NFY and ETS motifs, both of which have previously been shown to act as cardinal elements of certain promoter regions³¹. Both baseline and GC-controlled models identify clusters of TFs with highest scoring context 5-mers corresponding to known pioneer factors (e.g., NFY²⁷, RUNX³²/AP-1²⁸, and interferon regulatory factors [IRFs]³³) which open chromatin and enable additional TFs to bind. These pioneer factors motifs are far more strongly enriched in our fine-tuned models compared to pre-trained DanQ models not trained on negative sequences (Extended Data Fig. 3).

In DNaseI-controlled models, which only consider sequences already in open chromatin, motifs for pioneer factors such as AP-1, RUNX, and IRF are less prevalent in top-scoring 5-mers for many TFs (Fig. 3c), suggesting the pioneer factors do not directly co-bind with those TFs. On the other hand, pioneer motifs remain enriched for TFs known to physically co-bind (e.g. AP-1 motif for IRF4 and CEBPB). We hypothesize these DNaseI-controlled models instead identify 5-mers that represent cooperative relationships between TFs or sequence elements near the core motif required for binding. For some TFs, top 5-mers in DNaseI-controlled models are distinct from those in the other models. For example, in the baseline model for NRSF, 5-mers corresponding to the pioneer IRF and promoter ETS motifs are most significant, whereas the GATA motif (5’-GATAA-3’) is only moderately enriched (one-sided P=0.000045, OR=1.7). However, in the DNaseI-controlled model, the GATA motif is highly significant (one-sided P=1.2×10⁻²⁴⁵, OR=11.5) for NRSF, suggesting a potential role for this sequence in promoting nearby NRSF binding after the surrounding region is made accessible by pioneer factors.

We hypothesized that the sequence context features which promote binding of a particular TF to its core motif might differ between motifs in promoter (+/− 3kb from transcription start sites [TSS], denoted as “proximal” vs. enhancer regions (>3kb from the nearest TSS, denoted as “distal”). We repeated our analysis of top 5-mers separately for proximal and distal binding sites (Extended Data Fig. 4). In some cases, such as for SP1, the highest scoring 5-mers differ dramatically between proximal and distal sites. Overall, NFY and NFY-like motifs score highly for proximal binding sites, but have less influence on distal sites. On the other hand, RUNX, AP-1, and IRF motifs show stronger scores for distal sites. These results suggest that many features influencing binding are orthogonal at promoter vs. enhancer regions and these sites are likely governed by separate sets of pioneer and other factors.

To investigate the ability of our framework to capture cell-type specific regulatory features, we trained separate GC-controlled models to predict STAT3 binding using ChIP-sequencing data from GM12878, CD4+ Th17, and HeLa cells and used each model to predict binding in all three cell types. As expected, STAT3 binding in each cell type was best predicted by a model trained on that cell type. We computed Grad-CAM scores for each bound sequence and repeated the analysis of top scoring 5-mers as described above. Our analysis reveals that some enriched 5-mers are shared across multiple cell types whereas others are highly cell-type specific (Fig. 4). For example, RUNX and IRF motifs are enriched only in GM12878 whereas FOX and T-box motifs are enriched only in Th17. AP-1 and BATF motifs are enriched in both HeLa and GM12878, and ETS motifs are enriched in both Th17 and GM12878. Overall these results are consistent with a model whereby STAT3 binds to regions made accessible by different combinations of pioneer factors in each cell type.

Figure 4: Cell-type specific enrichment of 5-mers influential for STAT3 binding.

Enrichments were computed using Fisher’s exact tests as in Fig. 3 using GC-controlled models trained separately in either GM12878, HeLa, or CD4+ Th17 cells. (a) Comparison of top-scoring 5-mers for GM12878 vs. CD4+ Th17 cells. (b) Comparison of top-scoring 5-mers for GM12878 vs. HeLa cells. (c) Comparison of top-scoring 5-kmers for HeLa vs. CD4+ Th17 cells. The inset table shows the auROC obtained from training each model on one cell type and using it to predict STAT3 binding status in another cell type. Dashed horizontal and vertical lines denote an adjusted P-value threshold of 0.05, based on a Bonferroni correction for the number of 5-mers tested.

Finally, we investigated whether top-scoring SNPs are enriched for properties characteristic of causal variants. We find that SNPs with top-scoring Grad-CAM scores (top 0.5%) show significantly higher signals of negative selection based on observed allele frequencies compared to other SNPs in context regions (Online Methods; two proportion z-test one-sided P=3.3×10⁻⁸; Extended Data Fig. 5). Further, we compared Grad-CAM scores to effects of SNPs on expression measured through massively parallel reporter assays (MPRA)³⁴ in LCLs and find that Grad-CAM scores are significantly higher for SNPs that induce expression changes in MPRA (Mann-Whitney two-sided P=0.013; Online Methods), although still are only moderately predictive of causal variants for gene expression (Supplementary Discussion). Overall, these results suggest that context bases most influential for TF binding identified by our framework may be helpful in prioritizing variants relevant to human traits.

Discussion

Here we present AgentBind, a machine learning framework to predict whether particular instances of TF motifs in the genome are bound vs. unbound in a given cell type and to identify the most influential context bases. While we focused on TFs in GM12878 using the DanQ architecture, this framework can similarly be applied to a flexible range of CNN model architectures for any TF and cell type of interest for which ChIP-sequencing data is available.

Our results support the hypothesis that a variety of context features work together to determine whether a motif instance will be bound. The large decrease in auROC values after controlling for DNaseI (mean=0.133) suggests the most important binding determinant for most TFs is whether its motif falls in a region of active chromatin previously opened by a pioneer factor. However, in all of our model settings a TF is usually predicted best by its own model. This suggests that even after a region is open, for some TFs additional context sequence features, such as additional copies of its own motif or those of co-binding TFs, are important for determining whether the core motif is bound.

We generated three different models for each TF, each of which identifies distinct sequence features most predictive of TF binding. These different settings highlight how the choice of negative vs. positive sequences for training models has a major impact on the features learned. In the baseline and GC-controlled models, we fine-tune existing DanQ models with negative training samples from regions of the genome that are inactive in most cell types. Accordingly, the most prominent features learned correspond to known motifs for pioneer factors, which predict whether a region is open or closed. DNaseI-controlled models, which only consider both positive and negative sequences in open chromatin, give decreased importance to pioneer factors and likely highlight sequence features most directly related to TF binding. Importantly, the appropriate model may depend on the application of interest. For example, baseline models may be most appropriate for predicting the impact of a medically relevant variant, where it is simply desirable to have the highest prediction accuracy. On the other hand, for the application of learning sequence features that directly interact with the TF of interest, DNaseI-controlled models are best.

Our study faced several limitations: (i) modifications to the training process, such as varying the lengths of context sequences or training separate models for distal vs. proximal regions, are likely to improve performance. (ii) Further, we rely on PWMs to identify motif instances. PWMs suffer from known limitations, including an inability to capture dependencies between positions, which may trivially distinguish bound vs. unbound sequences in some cases. (iii) Model interpretation techniques can be further improved to extract more complex rules for TF binding such as motif spacing, orientation, and combinations. Visualization techniques such as DeepResolve³⁵ may reveal additional patterns such as interactions between important sequence features learned by CNNs. (iv) TF binding does not necessarily imply regulatory function and thus a high-scoring Grad-CAM site may ultimately not affect gene regulation of downstream phenotypes (Supplementary Discussion). Other methods based on a combination of deep-learning and k-mer based approaches have been developed to specifically predict expression from sequence content^10,36. In future work, our scores could be integrated into similar frameworks to improve prioritization of disease-associated variants. (v) Finally, we mainly focused on the GM12878 cell type. While our results for STAT3 on multiple cell types indicate that important context bases are highly cell-type specific, future work is needed to further investigate other cell types.

Altogether, our study provides a valuable machine-learning framework for helping decode the rules by which TFs bind their target sites and identifying specific non-coding nucleotides with the strongest effects on binding. To facilitate future applications, Grad-CAM scores for all TF models studied here and code for running AgentBind on additional datasets are available at https://github.com/Pandaman-Ryan/AgentBind.

Online Methods

ChIP-sequencing datasets and preprocessing

We used FIMO³⁷ v4.12.0 to identify all instances of the motif for each TF across the human reference genome (hg19). FIMO takes the reference genome and target motifs for each TF as input and returns all occurrences of the target motif (using the default p-value threshold p<10⁻⁴). Motifs for each TF were obtained from JASPAR (Supplementary Table 1). We intersected motif instances with binding sites as identified by ChIP-sequencing available for each TF in GM12878 from the ENCODE Project¹⁸ (peak file accessions given in Supplementary Table 1) using a custom script. ENCODE ChIP-sequencing experiments for each TF were performed in duplicate and peaks were scored against an appropriate control designated by the ENCODE Analysis Working Group. Motif instances (core motifs) were labeled as positive if they were fully within ChIP-sequencing peaks for the TF. All other instances were labeled as negative. We extended each core motif region to include 1 kb centered at the motif. For each sequence, we included it and its reverse complement sequence for the training procedure described below. In the experiments that required core motifs to be blocked, we substituted the motif region with a string of “N”‘s of the same length as the JASPAR motif.

The binary datasets we acquired above were highly imbalanced: on average we identified 433 times more negative than positive sequences (Supplementary Table 2). In order to balance the dataset ratio while alleviating effects of differences within the core motif, we chose an identical number of negative and positive sequences for each TF while requiring the distribution of motif match p-values to be similar. To obtain p-value matched sets, we binned -log₁₀ P-values of motif matches into bins of size 0.1. For baseline models, we randomly selected the same number of positive and negative sequences from each P-value bin. For GC-controlled models, within each P-value bin, we further binned sequences based on their GC contents to ensure the selected sequences shared the same distribution of GC contents in positive and negative datasets. For the DNaseI-controlled models, we only considered both positive and negative sequences whose core motifs fall within DNaseI hotspots in GM12878 (ENCODE accession ENCFF491BOT). We then followed the same procedures as in the GC-controlled models to match motif P-values and GC content between positive and negative sequences.

CNN model architecture and training

We implemented DeepSEA and DanQ architectures using TensorFlow³⁸ v1.9.0. The well-trained models and their associated code are available in our Github repository (https://github.com/Pandaman-Ryan/AgentBind). DeepSEA consists of three convolutional layers and two fully connected layers, and DanQ consists of one convolutional layer, one bi-directional recursive neural network layer and two fully connected layers. We applied sigmoid cross entropy as the loss function for both models.

The sizes of input datasets vary widely, from 182 to 107,539 total sequences per TF (Supplementary Table 2). To enable our framework to accommodate smaller datasets, we applied a two-step transfer learning scheme, including a pre-training step and a fine-tuning step. Transfer learning has been shown to dramatically reduce the amount of training needed for related classification tasks and improves the overall predictive performance compared to training from scratch³⁹. For pre-training, we downloaded a dataset consisting of 4,863,024 1kb sequences annotated with a total of 919 ChIP-seq and DNase-seq profiles available on the DeepSEA website. We left out sequences on chromosome 8 for cross validation and sequences on chromosome 9 for testing. We applied one-hot encoding to convert nucleotide sequences into 4-element vectors as has been done in previous studies^11,16. “N”s were converted into vectors with entries of 0.25 for each of the four nucleotides. During training, we initialized all model parameters with random Gaussian noise with mean 0 and standard deviation 1e-2, and trained this model on the DeepSEA compendium dataset until the loss function converged. In the fine-tuning step, we used the same architectures as in the pre-training step, and we built an independent model for each TF of interest using the labeled dataset described in the previous section. Same as the pre-training step, we left out sequences on chromosome 8 and 9 for cross validation and testing respectively. From the pre-trained model, we transferred its convolutional layers and RNN layer into the new models, but initialized the fully connected layers again with random Gaussian noise. These new models were further fine-tuned on our TF binary datasets until convergence.

Benchmarking experiment against KSM

In the KSM experiment, to identify KSMs for each TF, we used the same set of training and test data as we used in the GC-controlled and DNaseI-controlled models and kept the central 61bp in each sequence. KMAC is a de novo motif discovery method for KSM⁷. We applied KMAC to identify KSM motifs with k_win set as 61, k_min as 5, k_max as 13, and k_top as 10. Finally, we applied KSM to predict the TF binding status of our test data with motifs identified by KMAC as input. We quantified the performance evaluation using auROC, partial auROC, and auPRC (Supplementary Table 9).

Benchmarking experiment against IMPACT

The IMPACT study focused on TFs active in T cells and created their own binary (bound vs. unbound) datasets for TFs including FOXP3 (Treg), GATA3 (Th2), STAT3 (Th17) and T-BET (Th1). The coordinates of motif instances for these four TFs were published on the IMPACT Github repository (https://github.com/immunogenomics/IMPACT). In our benchmarking experiment, we used an identical set of motif instances, extending them into 1 kb sequences to train our model.

We applied an identical training scheme as was used by IMPACT: we randomly selected 80% of the sequences in the input dataset for training and tested on the remaining samples. We evaluated our method in four situations using different architectures and core motif treatments (DeepSEA or DanQ architecture, with core motif blocked or unblocked), and for each situation we conducted 10 parallel trials with different selections of the test set (Supplementary Table 10).

Model interpretation simulation experiments

We simulated a binary dataset consisting of 50,000 sequences for training, 1,000 for cross validation and 1,000 for testing for evaluating interpretation methods. Labels were assigned evenly with same number of positives and negatives. All sequences were length 1kb and contained the GATA1 motif (http://compbio.mit.edu/encode-motifs/) in the center. Context bases were generated by sampling the nucleotides A, C, G, and T at each position with probabilities 0.3, 0.2, 0.2 and 0.3 respectively. The number of TAL1 motifs (http://compbio.mit.edu/encode-motifs/) embedded in positive sequences followed a Poisson distribution but truncated after 3. No TAL1 motifs were embedded in negative sequences. These simulated sequences were fed into our AgentBind framework and annotated at nucleotide resolution using the model interpretation methods described below.

Model interpretation methods

We implemented four separate model interpretation techniques using the simulated data described above. Each of these methods computes individual scores for each nucleotide of the input sequence indicating its importance in determining the model’s prediction.

For in silico mutagenesis, we performed computational mutations to assess the importance of every base of the input sequences. More specifically, we substituted each base with its three possible nucleotide substitutions and recorded the changes made by them in terms of the output prediction scores. The greatest score change was used to represent the importance of this base.

For vanilla saliency maps, the importance of each base was quantified using the gradient of the output prediction score with respect to this base. This step was accomplished using a TensorFlow built-in function “gradients”.

In our implementation of Grad-CAM, we chose the first convolutional layer as the layer of interest. This layer contains distribution maps for various sequence features. Following the weighting method proposed by the Grad-CAM authors¹⁷, we quantified the importance of these sequence features and computed a weighted summation of all the distribution maps. In comparison with vanilla saliency map which evaluates the importance of each base individually, this aggregated map highlights the regions that are important to the binding activities. To combine the best aspects of these two maps, we then merged the aggregated distribution map with the vanilla saliency map through element-wise multiplication.

For DeepLIFT, we used version v0.6.10.0-alpha together with Keras v2.3.1 and applied its “revealcancel_fc, rescale_conv” mode for model interpretation. Since DeepLIFT is only compatible with Keras, we first constructed a DeepSEA architecture in Keras matching our TensorFlow implementation and then imported our pre-trained DeepSEA model parameters into this Keras model. The training procedures of fine-tuning were the same as our TensorFlow implementation.

Interpretation methods were evaluated using five metrics: (1) run time. All timing experiments were tested in a Linux environment running Centos 7.4.1708 on a server with 28 cores (Intel^® Xeon^® CPU E5–2660 v4 @ 2.00 GHz), NVIDIA^® Tesla^® K40c GPU, and 125GB RAM. Only a single core was used for timing. (2) the percentage of the top 5% scoring bases that overlap embedded motifs (accuracy). (3) the percentage of embedded motifs for which at least half of the motif bases are in the top 5% scoring bases (recall). (4) auROC when we move the threshold of top scoring bases from 100% to 0% in (3). (5) signal-to-noise ratios computed as the ratio of scores in embedded motifs to scores in background regions. We evaluated all interpretation methods with a DeepSEA architecture, and all except DeepLIFT with a DanQ architecture (Fig. 2a, Supplementary Table 11) since DeepLIFT doesn’t currently support hybridized architectures containing RNNs.

K-mer enrichment analysis

In this analysis, we first segmented all the input sequences into 5-bp subsequences using a sliding window and removed subsequences overlapping core motifs in the center. Next, for each subsequence, we quantified its importance by averaging the Grad-CAM scores of each base. For each factor, we ranked all the subsequences based on their Grad-CAM scores and marked the top 1% as top 5-mers. We used a Fisher’s Exact test to determine whether each 5-mer was enriched among top 5-mers for each TF. Fisher’s Exact tests were performed using the fisher_exact function in the stats module of the Python scipy⁴⁰ library v1.3.1. 5-mers were matched to published motifs in the Hocomoco⁴¹ database based on manual inspection. For Fig. 3 and Extended Data Figs. 3–4 we obtained the top 50-mers ranked by the maximum odds ratio across all TFs separately in each of the three models (baseline, GC-controlled, and DNaseI-controlled). We merged this set for a total of 77 unique 5-mers and clustered matrices of odds ratios for each 5-mer in each TF. For clustering, all insignificant odds ratios (nominal P≥0.01) were set to 0. To make heatmaps visually comparable, we used the ordering of 5-mers and TFs based on clustering results from the baseline models in each 5-mer heatmap. For the comparison of proximal and distal sites, proximal sites were defined as sequences for which the core motif is within +/− 3kb from the nearest transcription start site (TSS) and distal sites were defined as sequences for which the core motif is >3kb from the nearest TSS. Transcription start sites were annotated based on GENCODE v19.

Cross cell-type comparison of STAT3 models

GC-controlled models for STAT3 in three cell types were trained using the procedure described above. Samples were labeled as positive vs. negative based on overlap with STAT3 peaks in GM12878 (Supplementary Table 1), HeLa (ENCODE data obtained from http://hgdownload.cse.ucsc.edu/goldenpath/hg19/encodeDCC/wgEncodeAwgTfbsUniform/wgEncodeAwgTfbsSydhHelas3Stat3IggrabUniPk.narrowPeak.gz) and CD4+ Th17 cells (GEO accession GSM2545819). Input datasets consisted of 2,648, 792, and 7,652 sequences for GM12878, CD4+ Th17, and HeLa, respectively, with equal numbers of positive and negative sequences.

Allele frequency analysis

To quantify selection for a set of genomic positions, we assessed whether those positions are depleted of common genetic variation compared to nearby positions. We focused on single nucleotide polymorphisms (SNPs) present in gnomAD⁴² overlapping sites that were scored by Grad-CAM using GC-controlled models for each TF, and computed the percentage of SNPs for which the alternate allele is observed only once (termed singletons). This “percent singleton” metric has previously been used as a proxy for deleteriousness of a set of SNPs⁴³.

For each TF, we overlapped bound sequences scored by Grad-CAM with SNPs in the control samples reported in the gnomAD v2 dataset⁴². For positions overlapping gnomAD SNPs, we recorded observed counts of minor alleles. We then labeled sites where the minor allele counts were 1 as singletons. We only included samples annotated in gnomAD as healthy controls (n=5,442 individuals) in our analysis and required a minimum total allele count of 1000. Sites not overlapping a gnomAD SNP (i.e. minor allele count of 0) were excluded from singleton analysis. The singleton ratio of a group of sites is then simply defined as the percentage of SNPs in that category that are singletons.

Comparison to MPRA

We obtained MPRA results for expression quantitative trait loci (eQTLs) tested in two lymphoblastoid cell lines from Table S1 of Tewhey, et al.³⁴. We converted SNP rsids to hg19 coordinates based on dbSNP⁴⁴ build 147 and retained only SNP variants which overlapped positions scored by Grad-CAM in at least one TF of interest in DNaseI-controlled models. We further filtered SNPs for which the regulatory effect was not scored in the Tewhey et al. dataset (C.Skew.fdr column set to NA) indicating one or both alleles of the SNP did not drive expression of the reporter in the MPRA experiment. We treated variants with FDR<5% in the MPRA data (based on the column C.Skew.fdr) as true positives and FDR>=5% as true negatives. A total of 116 true positive and 226 true negative SNPs were included in the analysis. We then set the Grad-CAM score for each variant as the maximum value recorded across all TFs considered at the locus.

Data availability

Variant annotation scores for each TF analyzed can be found at https://github.com/Pandaman-Ryan/AgentBind.

Peak files for ENCODE ChIP-sequencing datasets can be found at http://hgdownload.cse.ucsc.edu/goldenpath/hg19/encodeDCC/wgEncodeAwgTfbsUniform.

Peak files for STAT3 in CD4+ T cells were obtained from the Gene Expression Omnibus (GEO accession GSM2545819).

Code availability

Code used for training models and performing analyses are available in our Github repository https://github.com/Pandaman-Ryan/AgentBind (doi:10.5281/zenodo.4281456).

Extended Data

Extended Data Fig. 1. Model performance related to GC content and open chromatin.

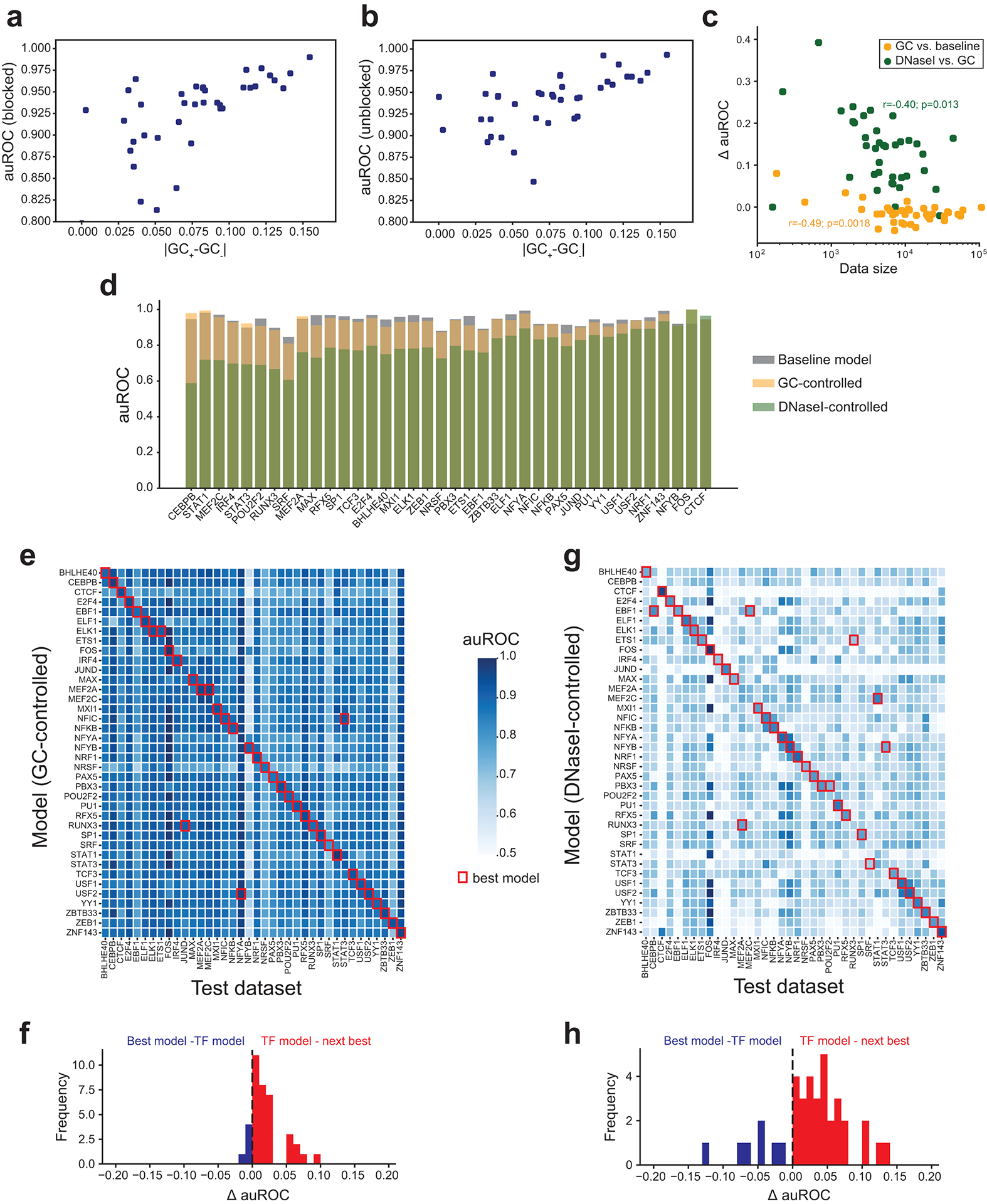
(a-b) GC content differences correlated with model performance. The x-axis shows the absolute value of the difference in mean GC content for positive vs. negative sequences with the motif for each TF. The y-axis shows auROCs. Each dot represents one TF. Results in a-b are for baseline models with motifs blocked (a) or unblocked (b). (c) Comparison of training data size and change in model performance. The x-axis (log₁₀ scale) shows the number of training samples. Orange points show the difference in auROC (y-axis) for baseline vs. GC-controlled models. Green points show GC-controlled vs. DNaseI-controlled models. Each dot represents one TF. (d) Model performance for each TF. The y-axis gives the auROC obtained for different models for each TF. Gray=baseline; orange=GC-controlled; green=DNaseI-controlled. TFs are ranked by the change in auROC between the DNaseI and GC-controlled models. (e) Comparison of cross-TF model performance. Heatmaps show the auROC using a GC-controlled model trained on one TF (rows) and tested on another TF (columns). Red squares denote the model with highest auROC for each TF. (f) Distribution of the difference in auROC between top models and TF-specific models. For TFs where the TF-specific model was best, we computed the difference between the TF-specific model and the next best model (red). For all other TFs, we compared performance of the best model to the TF-specific model (blue). (g-h) are the same as in e-f but based on DNaseI-controlled models.

Extended Data Fig. 2. Aggregate Grad-CAM score profiles for each TF.

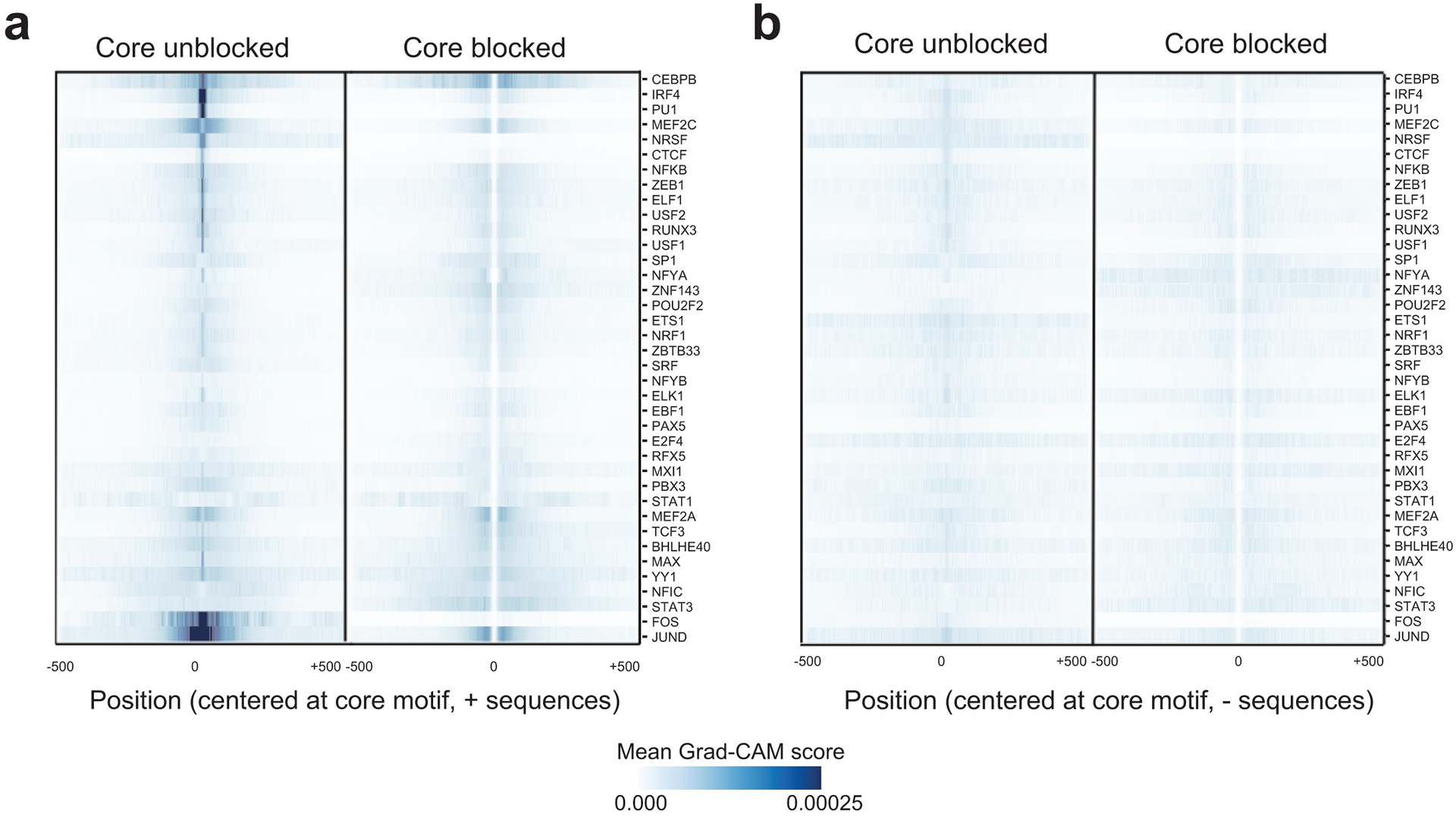
For each TF, we computed the average absolute value of the Grad-CAM score per position in positive sequences using either models with the core motif unblocked (left) or blocked (right). Values shown are Z-normalized across rows. (a) shows aggregate scores for sequences labeled as positive (bound) and is reproduced from Fig. 2d. (b) shows aggregate scores for sequences labeled as negative (unbound).

Extended Data Fig. 3. Comparing key context sequence features identified in pre-trained vs. fine-tuned models.

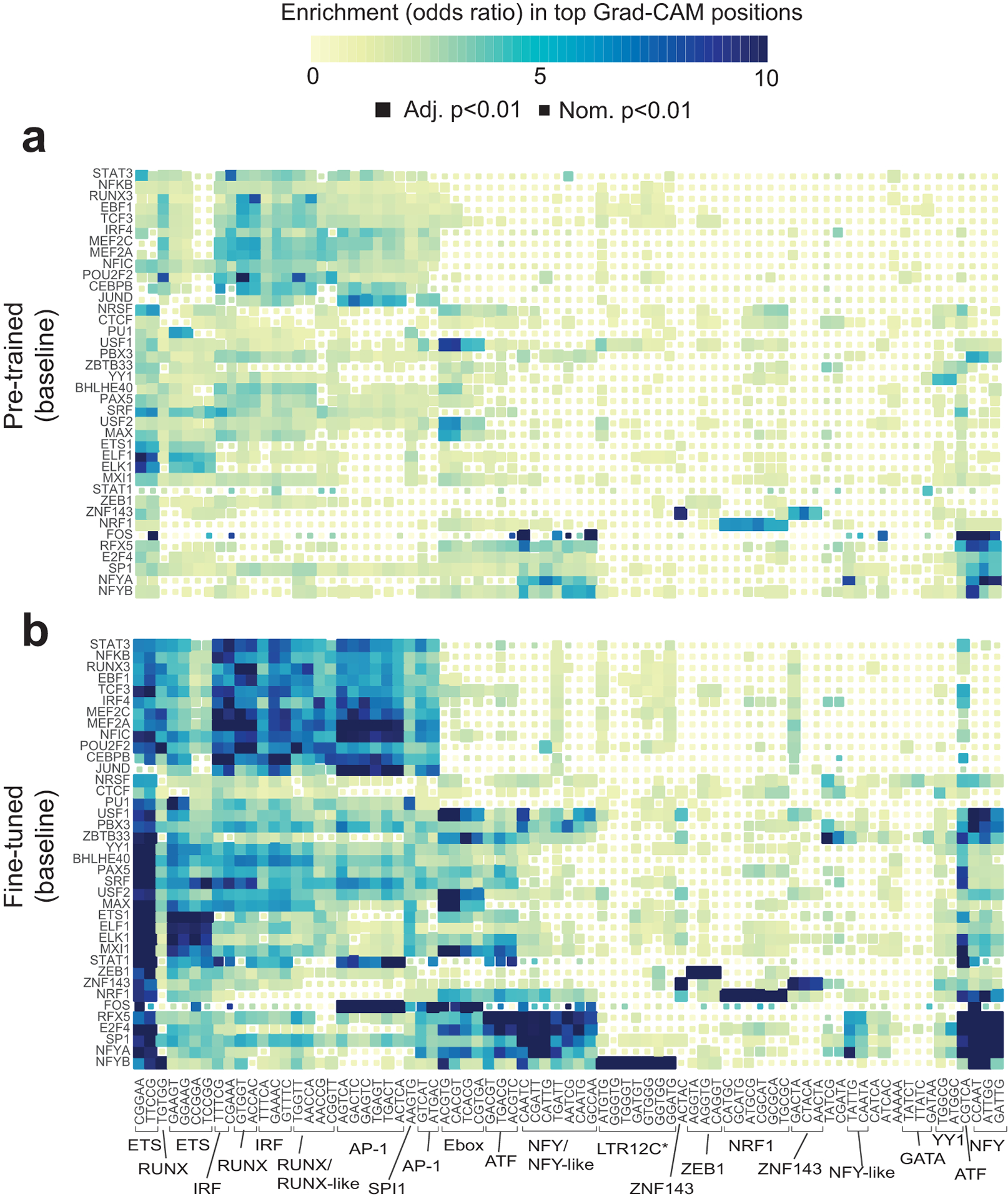
The heatmap shows the enrichment of each 5-mer in regions with the highest Grad-CAM scores for each TF using baseline models before (a) and after (b) fine-tuning. Rows and columns are ordered the same as in Fig. 3. Colors denote odds ratios and the sizes of the boxes denote statistical significance as in Fig. 3. Panel (b) is reproduced from Fig. 3a for comparison

Extended Data Fig. 4. Context sequence features specific to proximal vs. distal sites.

(a) Enrichment of 5-mers in high-scoring Grad-CAM regions for proximal (left) and distal (right) binding sites. Proximal and distal TF binding sites are defined as described in Online Methods. Rows and columns are ordered the same as in Fig. 3. (b-c) are the same as in (a) but show data for GC-controlled (b) and DNaseI-controlled (c) models. For (a-c), colors denote odds ratios and the sizes of the boxes denote statistical significance as in Fig. 3. (d) Comparison of top scoring 5-mers in proximal vs. distal SP1 sites. Bars show the odds ratio of enrichment of each sequence in top 5-mers for all (gray), proximal (red) and distal (blue) SP1 sites. The top 20 5-mers ranked by the best odds ratio across all three SP1 models (all, proximal, and distal sites) are shown. Error bars show 95% confidence intervals on odds ratios. (e-f) are the same as in (d) but show data for GC-controlled (e) and DNaseI-controlled (f) models.

Extended Data Fig. 5. Singleton rate of context SNPs vs. core motif regions. (a) Singleton rate of context SNPs.

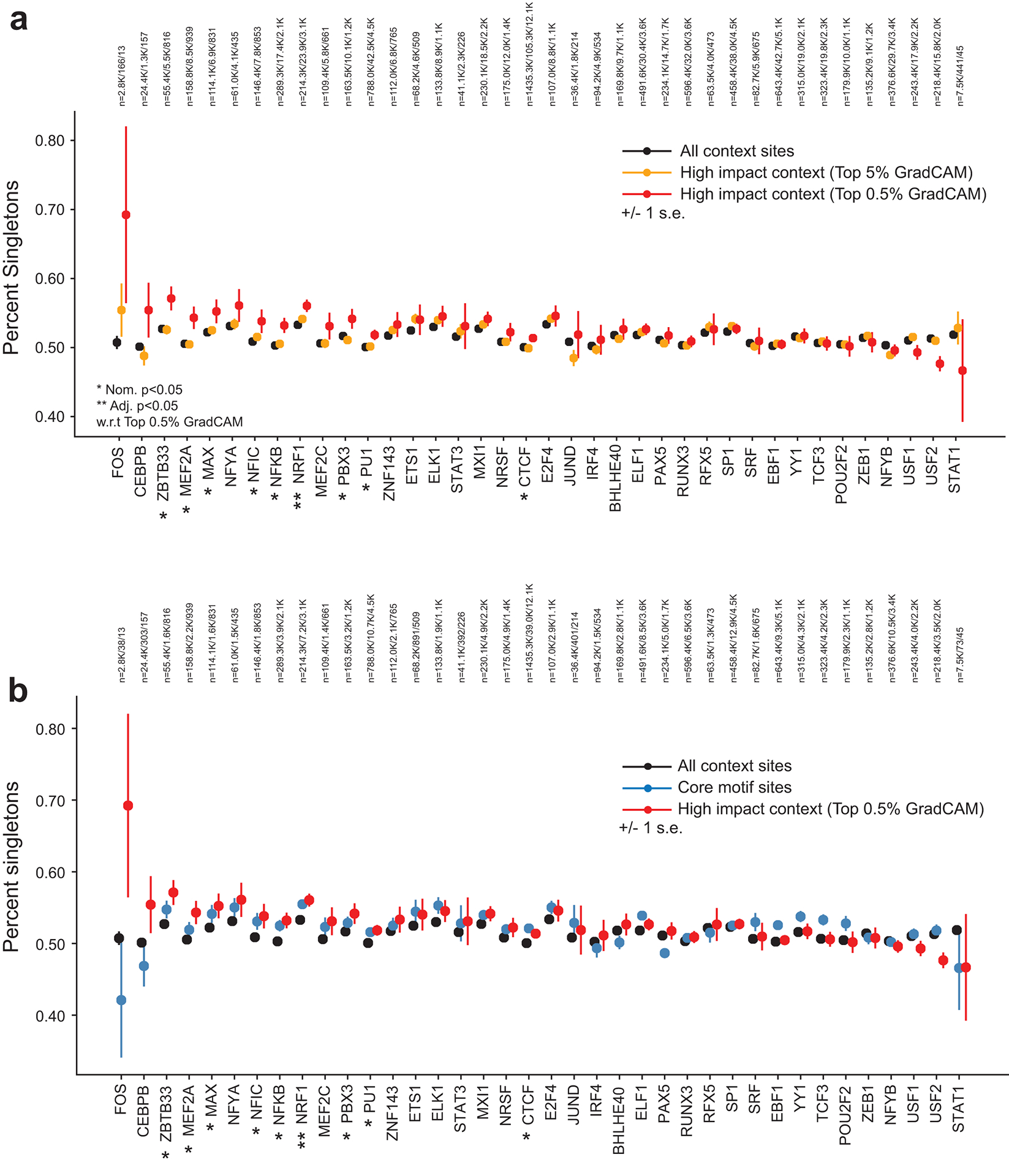
The plot shows the percent of SNPs in each category that are singletons. Black=all context sites, orange=context sites with top 5% Grad-CAM scores, red=context sites with top 0.5% Grad-CAM scores. Error bars show +/− 1 s.e. (b) is the same as (a), but additionally shows singleton rates for SNPs in core motif regions (blue). The number of SNPs in each category for each TF is annotated above each plot.