Development of a Mixture Model (SMM) Allowing for Smoothing Functions of Longitudinal Trajectories

Abstract

In the health and social sciences, two types of mixture models have been widely used by researchers to identify participants within a population with heterogeneous longitudinal trajectories: latent class growth analysis (LCGA) and the growth mixture model (GMM). Both methods parametrically model trajectories of individuals, and capture latent trajectory classes, using an expectation-maximization (EM) algorithm. However, parametric modeling of trajectories using polynomial functions or monotonic spline functions results in limited flexibility for modelling trajectories; as a result, group membership may not be classified accurately due to model misspecification. In this paper, we propose a mixture model (SMM) allowing for smoothing functions of trajectories using a modified algorithm in the M step. Specifically, participants are reassigned to only one group for which the estimated trajectory is the most similar to the observed one; trajectories are fitted using generalized additive mixed models (GAMM) with smoothing functions of time within each of the resulting sub-samples. The SMM is straightforward to implement using the recently released ‘gamm4’ package (version 0.2–6) in R 3.5.0. It can incorporate time-varying covariates and be applied to longitudinal data with any exponential family distribution, e.g., normal, Bernoulli, and Poisson. Simulation results show favorable performance of the SMM, when compared to LCGA and GMM, in recovering highly flexible trajectories. The proposed method is illustrated by its application to body mass index data on individuals followed from adolescence to young adulthood and its relationship with incidence of cardiometabolic disease.

1. INTRODUCTION

In the health and social sciences, mixture models have been used to identify participants within a population with heterogeneous longitudinal trajectories.^{1, 2} Two types of parametric mixture models have been developed and widely used by researchers: the growth mixture model (GMM) proposed by Muthen et al and latent class growth analysis (LCGA) proposed by Nagin et al.^{3, 4} Both models allow different sets of parameter values for mixture components corresponding to different unobserved subgroups of individuals, and capture latent trajectory classes with different growth curves by using an expectation-maximization (EM) algorithm. The main difference between the two models is that GMM allows for variation across individuals within the same group while LCGA assumes individuals within groups are homogenous.⁵ Although mixture models with nonparametric, semiparametric, or smoothed trajectories have been developed for normally distributed outcomes, for discrete or categorical outcomes GMM and LCGA require specification of parametric functions (e.g., polynomial functions) for the trajectories.^6–9 As a result, both GMM and LCGA have somewhat limited flexibility for modelling trajectories of non-normally distributed outcomes. Because of this lack of flexibility for modelling trajectories, group membership may not be classified accurately to represent the true unobserved subgroups due to model misspecification.

Semiparametric mixture models with smoothing functions of covariates have been developed.^9–11 However, some limitations of these models are that they can only be applied to normally distributed data, they do not handle binary or count outcomes, and there is little existing software to implement them.¹² We note that smoothing splines have been widely applied to model covariates nonlinearly in longitudinal data, e.g., in generalized linear models ^{13, 14} and generalized estimating equations.^15–18 To allow for mixed effects in models for longitudinal data, they were further implemented within generalized linear mixed models (GLMM),^19–22 creating a new class of models referred to as generalized additive mixed models (GAMM).²³ GAMM provides nonparametric functions of covariates and uses random effects to account for correlation in longitudinal data.²³ Although GAMM is computationally intensive, it is straightforward to apply using the package ‘gamm4’ (version 0.2–6) in R 3.5.0, which performs well not only for continuous data, but also for binary and count data.²⁴ As GAMM can model covariates with a high degree of flexibility and accounts for within-individual correlation, a natural extension is to consider a GAMM applied to trajectory analysis within latent classes. Similar to GMM and LCGA, which are essentially a combination of GLMM with latent class analysis, in this paper we develop a smoothing mixture model (SMM) allowing for smoothing functions of trajectories by combining GAMM with latent class analysis.

As parameter estimation of our model based on maximum likelihood estimation (MLE) would be very computationally demanding, we use a more convenient approach to mixture modelling known as “classification maximum likelihood (CML)”.²⁵ The key difference between classification and conventional mixture modelling approaches is that in the former each observation is assigned to a single, unique class whereas in the latter each observation is assigned a probability of originating from each class. Results from a simulation study that compared CML to the conventional maximum likelihood (ML) approach for mixture models do not suggest a general superiority of mixture ML over the CML approach in finite samples.²⁶ Adopting this CML approach, we use a modified algorithm in the M step that simplifies parameter estimation: rather than assigning to all classes with different membership probabilities, each individual is assigned to only one class with the highest membership probability; the existing package ‘gamm4’ is applied directly to estimate model parameters within each group.²⁴ This algorithm avoids having to maximize intractable likelihoods, greatly simplifying model development and application.

2. METHOD

In this section, we introduce some notation and describe the main features of the proposed mixture model (SMM) allowing for smoothing functions of trajectories.

2.1. Notation.

Let the sample consists of $n$ individuals. Consider the data on individual $i$ to consist of a vector ${\mathit{Y}}_{\mathit{i}}$ of p repeated measurements over time ${\mathit{T}}_{\mathit{i}}$, and a (p x q) matrix ${\mathit{X}}_{\mathit{i}}$ of q covariates. The components of ${\mathit{Y}}_{\mathit{i}}$ can be continuous, count, or binary data. For example, ${\mathit{Y}}_{\mathit{i}}$ could be repeated measures of lifestyle factors across adulthood. Let k denote the number of latent classes or groups.

2.2. Log-likelihood (LL) of SMM.

The density of observing ${\mathit{Y}}_{\mathit{i}}$ in latent group m can be expressed as $d_m\left({\mathit{Y}}_{\mathit{i}}\right)={\prod }_{j=1}^{p}d\left(Y_{ij}|g^{-1}\left({\mathit{X}}_{\mathit{i}}^T{\mathit{\beta }}_{\mathit{m}}+f_m\left(t_j\right)+{\mathit{Z}}_{\mathit{i}}^T{\mathit{b}}_{mi}\right)\right)$, where $Y_{ij}$ is the outcome for individual $i$ at the j^th time-point $t_j$, $g(.)$ is the link function, $f_m(.)$ is a non-parametric penalized smoothing function of time, ${\mathit{\beta }}_{\mathit{m}}$ is a q × 1 vector of regression coefficients associated with covariates ${\mathit{X}}_i$, b_mi are independent b × 1 vectors of random effects associated with covariates ${\mathit{Z}}_i$ (the latter usually a subset of ${\mathit{X}}_i$ and/or ${\mathit{T}}_i$). The marginal density of ${\mathit{Y}}_i$ is the weighted sum of the density of observing ${\mathit{Y}}_i$ in each latent group, where the weight ${\pi }_{im}$ is the probability individual i belongs to group $m$, and can be expressed as $d\left({\mathit{Y}}_i\right)={\sum }_{m=1}^k{\pi }_{im}{d}_m\left({\mathit{Y}}_i\right)$. Thus, the log-likelihood $\left(ll\right)$ for the observed data is given by $ll={\sum }_{i=1}^n\text{log}\left(d\left({\mathit{Y}}_i\right)\right)$.

In principle, the model parameters can be estimated using the EM algorithm. Theoretically, in step 1, we would randomly assign individuals into k groups to obtain an initial estimate of ${\pi }_{im}$ and posterior estimates ${\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{b}}}_{\mathit{m}\mathit{i}},\hspace{0.17em}{\widehat{\mathit{f}}}_{\mathit{m}}$. In step 2, we would calculate d_m(Y_i) and obtain the posterior probabilities of individual $i$ belonging to group m as $\frac{{\pi }_m\hspace{0.17em}{d}_m\left(Y_i\right)\hspace{0.17em}}{{\sum }_{m=1}^k{\pi }_m{d}_m\left(Y_i\right),\hspace{0.17em}}$. In step 3, we would use the estimates of ${\pi }_{im}$ to obtain estimates of ${\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{b}}}_{\mathit{m}\mathit{i}},\hspace{0.17em}{\widehat{\mathit{f}}}_{\mathit{m}}$ by maximizing the $ll$. The EM algorithm iterates steps 2 and 3 until the $ll$ remains unchanged. However, a practical difficulty with implementing the EM algorithm is that maximizing $ll$ in step 3 is difficult and time consuming, due to the smoothing function of time $({\widehat{\mathit{f}}}_{\mathit{m}})$, correlation between repeated measures of ${\mathit{Y}}_{\mathit{i}}$, and the inclusion of random-effects $({\widehat{\mathit{b}}}_{\mathit{m}\mathit{i}})$.

Therefore, in this paper, we propose estimation of the model parameters using a modified algorithm in the M step. Instead of calculating the probabilities of individual i belonging to each group and maximizing the $ll$, we use the CML approach of assigning individuals to the group with the highest probability. In this case, the $ll$ is replaced by $cll={\sum }_{m=1}^k({\sum }_{i=1}^{n_m}\text{log}(d_m({\mathit{Y}}_{\mathit{i}}))={\sum }_{m=1}^{k}l{l}_m\hspace{0.17em}$, where $n_m$ is number of individuals in group m. Maximizing this $cll$ is equivalent to fitting models $g\left(E\left({\mathit{Y}}_{\mathit{i}}\right)\right)={\mathit{X}}_{\mathit{i}}^T{\widehat{\mathit{\beta }}}_{\mathit{m}}+{\widehat{f}}_m\left(t_j\right)+{\mathit{Z}}_{\mathit{i}}^T{\widehat{\mathit{b}}}_{\mathit{m}\mathit{i}}$ within each group and maximizing the $ll$ within each group,$l{l}_m$. That is, in the proposed algorithm we directly fit GAMM models within each group, modeling time with flexible smoothing functions and incorporating random effects to account for correlation between repeated measures. The estimates of ${\widehat{\mathit{\beta }}}_{\mathit{m}},{\widehat{\mathit{b}}}_{\mathit{m}\mathit{i}},\hspace{0.17em}{\widehat{\mathit{f}}}_{\mathit{m}}$, and $l{l}_{\mathit{m}}$ can be directly obtained from ‘gamm4’ package (version 0.2–6) in R3.2.5.

2.3. Model estimation of SMM

Initially, we divide participants into k groups according to the mean value (or any other suitable summary) of a participant’s observed trajectory. Let individual $i$ be assigned to the mth group. The group assignment, and estimation of the smooth trajectories for each group, is achieved by iterating the following E and M steps.

Step 1. Maximization step (M step)

• Using individuals in the mth group, fit a nonparametric GAMM model with smoothing spline for time, e.g., using ‘gamm4’ package (version 0.2–6) in R 3.5.0;

  $$g\left(E\left({\mathit{Y}}_i\right)\right)={\mathit{X}}_{\mathit{i}}^T{\mathit{\beta }}_{\mathit{m}}+f_m\left({\mathit{t}}_{\mathit{i}}\right)+{\mathit{Z}}_{\mathit{i}}^T{\mathit{b}}_{mi}.$$

  The smoothing function is fit using s(.) function, and we use default parameters controlling the smoothness (bs=“tp” for thin plate regression splines and m=2 for second derivative penalty).

• Although the vector ${\mathit{Y}}_{\mathit{i}}$ for individual $i$ only contributes to parameter estimation in the mth group, we obtain $k$ vectors of mean predicted value ${\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{1}\right)},{\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{2}\right)},\dots ,{\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{k}\right)}$ estimated from GAMMs fitted in the 1st, 2nd, …, kth groups, respectively. Given estimates from the k fitted GAMMs, the mean predicted value ${\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{m}\right)}$ can be expressed as $g^{-1}({\mathit{X}}_{\mathit{i}}^T{\widehat{\mathit{\beta }}}_{\mathit{m}}+{\widehat{f}}_m\left({\mathit{t}}_{\mathit{i}}\right))$.

Step 2. Expectation step (E step)

• For individual $i$, we obtain the log likelihood contributions ${\mathcal{l}}_{i\left(1\right)},{\ell }_{i\left(2\right)},\dots ,{\ell }_{i\left(k\right)}$ of individual $i\text{'}\text{s}$ mean trajectory of responses belonging to the $1st,2nd,\dots ,kth$ groups. For the mth group, the ${\ell }_{i\left(m\right)}$ conditional on $b_{mi}$ can be expressed as ${\ell }_{i\left(m\right)}\left({\mathit{Y}}_{\mathit{i}}|{\mathit{\beta }}_{\mathit{m}},{\mathit{t}}_{\mathit{i}}\right)=-\frac{1}{2\varnothing }{D}_i({\mathit{Y}}_{\mathit{i}};{\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{m}\right)})$, where $D_i({\mathit{Y}}_{\mathit{i}};{\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{m}\right)})$ is the deviance. The deviance statistic can be approximated by the Pearson chi-square statistic, where

  $$-\frac{1}{2\varnothing }{D}_i({\mathit{Y}}_{\mathit{i}};{\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{m}\right)})\approx -{\sum }_{j=1}^p\frac{{(Y_{ij}-{\widehat{Y}}_{ij\left(m\right)})}^2}{a(\varnothing )v({\widehat{Y}}_{ij\left(m\right)})}$$

  ${\widehat{\mathit{Y}}}_{\mathit{i}\left(\mathit{m}\right)}$ can be estimated directly from the fitted GAMM in the mth group. For exponential family distributions, $\varnothing$ is the dispersion parameter, $a(\varnothing )$ is a function of the dispersion parameter, and $v(.)$ is the variance function. Specifically, if $Y_{ij}$ has a normal distribution $\text{N}\left(\mu ,{\delta }^2\right)$, $\varnothing$ is ${\delta }^2$, $a(\varnothing )$ is ${\delta }^2$, and $v(.)$ is 1. If $Y_{ij}$ has a Bernoulli distribution $\text{B}\left(1,\text{p}\right)$, $\varnothing$ is 1, $a(\varnothing )$ is 1, and $v(.)$ is $\text{p}\left(1-\text{p}\right)$. If $Y_{ij}$ has a Poisson distribution $\text{P}\left(\mu \right)$, $\varnothing$ is 1, $a(\varnothing )$ is 1, and the $v(.)$ is $\mu$.

• We compare ${\ell }_{i\left(1\right)},{\ell }_{i\left(2\right)},\dots ,{\ell }_{i\left(k\right)}$. In a departure from the traditional EM algorithm for a conventional mixture model where in the E step individual $i$ is reassigned to all of the $k$ groups with different probabilities, in our proposal, individual $i$ is reassigned to the group with the largest log likelihood (or modal probability),${\ell }_i=\text{max}\left({\ell }_{i\left(1\right)},{\ell }_{i\left(2\right)},\dots ,{\ell }_{i\left(k\right)}\right)$).

The above two steps of the EM algorithm are iterated until the model converges. Model convergence is determined when the group membership for all individuals no longer change, and the sum of the largest log likelihood for all individuals ${\sum }_{i=1}^n{\ell }_i$ remains the same.

2.4. Number of groups.

The Bayesian information criterion (BIC) is used to compare model fit assuming different numbers of groups, k.^27–29 Consider that we divide all individuals’ trajectories into $k$ groups. Upon model convergence, the $\log L_1,\log L_2,\dots ,\log L_k$ are the log likelihoods estimated using GAMM in the 1st, 2nd, …, kth groups, and $p_1,p_2,\dots ,p_k$ are the respective degrees of freedom. The BIC for our mixture model is defined as $BIC=-2*{\sum }_{m=1}^k\log L_m+\left(\log \left(\#of\hspace{0.17em}observations\right)\right)*({\sum }_{m=1}^k{p}_m+k-1)$. $\log L_m$ and $p_m$ can be readily obtained using the mer and edf components from the ‘gamm4’ output in R 3.5.0, which can be applied to data with any exponential family (e.g., normal, Bernoulli, and Poisson) distribution.

3. SIMULATION

We conducted a simulation study to assess the performance of the proposed SMM, comparing it to LCGA and GMM in terms of LL, BIC, identification of number of groups, classification of group membership, and delineation of identified trajectories.

3.1. Simulation strategy.

We simulated datasets with 2, 3, and 4 groups of trajectories, with 100 individuals in each group and 20 repeated measures of the outcome for each individual at time points evenly spaced between 0 to 1. We simulated each individual’s trajectory using the function shown below, which could produce a variety of trajectory shapes with high degree of flexibility; this function was used to generate data with normal, Bernoulli, and Poisson distributions. Specifically, for individual $i$ at time $j$ in the mth group, $g\left(E\left(Y_{mij}\right)\right)$ was generated from:

${\beta }_{1m}*{\left(t_j\right)}^{r_{1m}}*{\left(10*\left(1-t_j\right)\right)}^{r_{2m}}+{\beta }_{2m}*{(10*t_j)}^{r_{3m}}*{\left(1-t_j\right)}^{r_{4m}}+{\beta }_{3m}+{\beta }_{mi}$, where $r_{1m}$, $r_{2m}$, $r_{3m}$, $r_{4m}$, ${\beta }_{1m}$, ${\beta }_{2m}$, and β_3m were group-specific parameters, and ${\beta }_{mi}$ was an individual-specific parameter with a standard normal distribution. For generating data from a normal distribution, $g(.)$ was an identity function, and we included a random error ${\epsilon }_{mij}~\text{N}\left(0,\hspace{0.17em}1\right)$ to the $E\left(Y_{mij}\right)$ when simulating Y_mij. For generating data from a Bernoulli distribution, $g(.)$ was a logit function. We obtained $E\left(Y_{mij}\right)=\frac{\text{exp}\left(g\left(E\left(Y_{mij}\right)\right)\right)}{1+\text{exp}\left(g\left(E\left(Y_{mij}\right)\right)\right)}$, and sampled each binary observation $Y_{mij}$ from a Bernoulli distribution with probability of success,$E\left(Y_{mij}\right)$. For generating data from a Poisson distribution, $g(.)$ was a log function. We obtained $E\left(Y_{mij}\right)=\text{exp}\left(g\left(E\left(Y_{mij}\right)\right)\right)$, and sampled each observation Y_mij from a Poisson distribution with mean,$E\left(Y_{mij}\right)$. For normal, Bernoulli, and Poisson distributions, we generated trajectories with high, medium, and low separation between groups by assigning different values to the variance of β_mi. Compared to trajectories with high separation, trajectories with low separation had larger individual-specific random-effects. The parameter settings with high, medium, and low separation are shown in Table S1 for data with normal, Bernoulli, and Poisson distributions. The mean trajectories simulated are shown in Figure 1 for data with normal, Bernoulli, and Poisson distributions.

Figure 1.

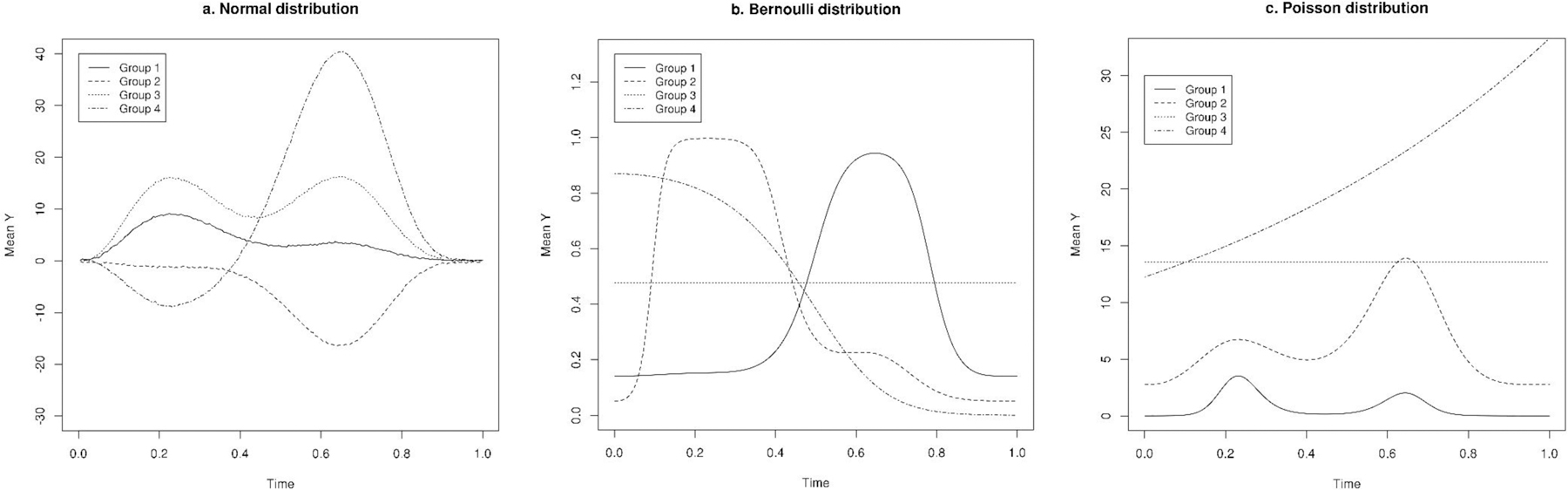
True underlying mean curves used to generate longitudinal data with normal, Bernoulli, and Poisson distributions (we present all four groups for medium separation setting).

3.2. Model fit.

We have developed R scripts for the proposed smoothing mixture model with normal, Bernoulli, and Poisson distributions, and the scripts can be accessed in Github (https://github.com/mingding-hsph/Smoothing-mixture-model). We initially assigned individuals to different groups based on the rank of the average value of Y across time points. To obtain model estimates, the EM algorithm was iterated 20 times, which suggested model convergence as indicated by BIC from each iteration. The LCGA was fitted using the “proc traj” command in SAS version 9.2 for UNIX (SAS Institute Inc).³⁰ We modeled trajectories with cubic polynomials for time using LCGA; this was reduced to quadratic or linear functions if the model did not converge. The GMM with random subject effects was fitted using the ‘lcmm’ package (Version 1.9.2) in R 3.5.0,³¹ and we modeled the trajectories with cubic polynomial functions. We randomly simulated 1000 datasets with normal, Bernoulli, and Poisson distributions and fit the three models to each of the simulated datasets.

For each simulated dataset, we fitted LCGA, GMM, and SMM separately assuming different number of groups. Specifically, for simulated data with two trajectory groups, we fitted models assuming one, two and three groups; for simulated data with three trajectory groups, we fitted models assuming two, three, and four groups; for data with four trajectory groups, we fitted models assuming three, four, and five groups. First, by assuming different number of groups, we obtained LL, BIC, the correlation coefficient between predicted and observed values, and the adjusted Rand index (ARI) between true underlying group membership and assigned groups. Of note, ARI assesses similarity between 2 group assignments and counts the number of pairwise agreements and disagreements between group assignments.³² The closer the value of ARI is to 1, the better the agreement between group assignments. Next, we compared BIC assuming different number of groups, chose the model with the lowest BIC, and presented the corresponding LL, BIC, number of groups, correlation coefficient, and ARI.

3.3. Results.

Compared to LCGA and GMM, SMM showed the best fit to the data as indicated by lowest LL and highest BIC for most of the scenarios of high, medium, and low separation (Tables 1–3). We obtained the highest correlation between predicted and observed values using SMM when compared to LCGA and GMM, particularly for data with normal and Poisson distributions. Consistently, the trajectories predicted using SMM were most similar to the true underlying trajectories (Figure 2–4). The SMM assigned group membership with high accuracy and successfully classified most of the individuals as indicated by ARI when there was high and median separation between groups, particularly for data with normal and Poisson distributions; for binary data, the ARI was discernibly weaker. However, the SMM model tended to identify more groups than necessary in scenario where there was low separation and also in the binary data setting.

Table 1.

Summary of simulation study results from fitting latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) to longitudinal data with normal distribution (1000 simulated datasets).

	Model	Number of groups identified*	LL	BIC	Adjusted Rand Index (ARI)#	Correlation between predicted and observed values &
High separation
Two groups	LCGA	2 (100%)	−4831	9709	1.00	0.70
	GMM	2 (67%), 3 (33%)	−9511	19096	1.00	0.91
	SMM	2 (100%)	−5922	12018	1.00	0.95
Three groups	LCGA	3 (100%)	−10550	21180	1.00	0.83
	GMM	2 (9%), 3 (32%), 4 (59%)	−15245	30613	1.00	0.92
	SMM	3 (100%)	−8902	18082	1.00	0.99
Four groups	LCGA	4 (100%)	−17541	35196	0.71	0.87
	GMM	3 (50%), 4 (21%), 5 (29%)	−24598	49338	0.71	0.88
	SMM	4 (100%)	−11889	24163	1.00	0.98
Medium separation
Two groups	LCGA	2 (30%), 3 (70%)	−5737	11526	0.71	0.70
	GMM	2 (90%), 3 (10%)	−9760	19586	1.00	0.84
	SMM	2 (82%), 3(18%)	−6189	12558	1.00	0.87
Three groups	LCGA	3 (100%)	−11400	22880	0.87	0.82
	GMM	3 (82%), 4 (18%)	−15538	31185	1.00	0.90
	SMM	3 (35%), 4 (65%)	−9692	19718	0.85	0.96
Four groups	LCGA	3 (22%), 4 (78%)	−17619	35340	0.89	0.88
	GMM	3 (29%), 4 (61%), 5 (10%)	−24650	49450	0.99	0.88
	SMM	3 (3%), 4 (52%), 5 (45%)	−12887	26212	0.94	0.95
Low separation
Two groups	LCGA	3 (100%)	−6186	12429	0.17	0.72
	GMM	2 (94%), 3 (6%)	−9943	19950	1.00	0.66
	SMM	2 (5%), 3 (95%)	−9052	18358	0.31	0.87
Three groups	LCGA	3 (100%)	−11951	23982	0.31	0.80
	GMM	3 (63%), 4 (37%)	−15802	31718	1.00	0.77
	SMM	3 (15%), 4 (85%)	−13958	28265	0.34	0.92
Four groups	LCGA	4 (100%)	−18056	36225	0.52	0.85
	GMM	3 (26%), 4 (57%), 5 (17%)	−25009	50172	1.00	0.77
	SMM	4 (38%), 5 (62%)	−17336	35099	0.57	0.91

LL: log likelihood; BIC: Bayesian information criterion. Presented are median values over 1000 simulated datasets.

^*Number of groups were identified by lowest Bayesian information criterion (BIC). We compared BIC assuming 1, 2, and 3 groups for simulated data with two groups, BIC assuming 2, 3, and 4 groups for simulated data with three groups, and BIC assuming 3, 4, and 5 groups for simulated data with four groups. Data presented is frequency of identified groups over 1000 simulated datasets.

^#Adjusted Rand index assesses similarity between 2 group assignments by counting the number of pairwise agreements and disagreements between group assignments. The closer the value is to 1, the better the agreement between group assignments. Presented are median values over 1000 simulated datasets.

^&Pearson correlation coefficient between predicted and observed values assuming simulated number of groups; data presented is median value over 1000 simulated datasets.

Table 3.

Summary of simulation study results from fitting latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) to longitudinal data with Poisson distribution (1000 simulated datasets).

	Model	Number of groups identified*	LL	BIC	Adjusted Rand Index (ARI)#	Correlation between predicted and observed values &
High separation
Two groups	LCGA	2 (100%)	−7607	15262	1.00	0.81
	GMM	2 (82%), 3 (18%)	−9418	18907	1.00	0.81
	SMM	2 (82%), 3 (18%)	−6247	12662	0.92	0.88
Three groups	LCGA	3 (100%)	−13259	26598	1.00	0.88
	GMM	2 (15%), 3 (52%), 4 (33%)	−15310	30734	1.00	0.88
	SMM	3 (81%), 4 (19%)	−11667	23540	0.96	0.90
Four groups	LCGA	4 (97%), 5 (3%)	−19538	39191	1.00	0.92
	GMM	3 (3%), 4 (37%), 5 (60%)	21819	43809	1.00	0.91
	SMM	4 (75%), 5 (25%)	−17515	35275	0.97	0.92
Medium separation
Two groups	LCGA	2 (98%), 3 (2%)	−7667	15382	1.00	0.81
	GMM	2 (86%), 3 (14%)	−9491	19054	1.00	0.81
	SMM	2 (87%), 3 (13%)	−6268	12701	0.92	0.88
Three groups	LCGA	3 (100%)	−13467	27014	1.00	0.88
	GMM	2 (18%), 3 (44%), 4 (38%)	−15435	30988	1.00	0.87
	SMM	3 (86%), 4 (14%)	−11756	23715	0.96	0.90
Four groups	LCGA	5 (100%)	−19860	39864	0.91	0.92
	GMM	4 (46%), 5 (54%)	−21989	44134	1.00	0.91
	SMM	4 (82%), 5 (18%)	−17696	35635	0.97	0.92
Low separation
Two groups	LCGA	3 (100%)	−7919	15912	0.79	0.81
	GMM	2 (66%), 3 (34%)	−9828	19728	0.98	0.80
	SMM	2 (89%), 3 (11%)	−6355	12879	0.90	0.86
Three groups	LCGA	3 (44%), 4 (56%)	−14471	29009	0.74	0.85
	GMM	3 (37%), 4 (63%)	−15837	31797	0.92	0.86
	SMM	3 (76%), 4 (24%)	−12310	24851	0.79	0.87
Four groups	LCGA	5 (100%)	−21124	42391	0.67	0.91
	GMM	4 (14%), 5 (86%)	−22611	45397	0.88	0.89
	SMM	3 (41%), 4 (35%), 5 (24%)	−18898	38036	0.62	0.86

LL: log likelihood; BIC: Bayesian information criterion. Presented are median values over 1000 simulated datasets.

^*Number of groups were identified by lowest Bayesian information criterion (BIC). We compared BIC assuming 1, 2, and 3 groups for simulated data with two groups, BIC assuming 2, 3, and 4 groups for simulated data with three groups, and BIC assuming 3, 4, and 5 groups for simulated data with four groups. Data presented is frequency of identified groups over 1000 simulated datasets.

^#Adjusted Rand index assesses similarity between 2 group assignments by counting the number of pairwise agreements and disagreements between group assignments. The closer the value is to 1, the better the agreement between group assignments. Presented are median values over 1000 simulated datasets.

^&Pearson correlation coefficient between predicted and observed values assuming simulated number of groups; data presented is median value over 1000 simulated datasets.

Figure 2.

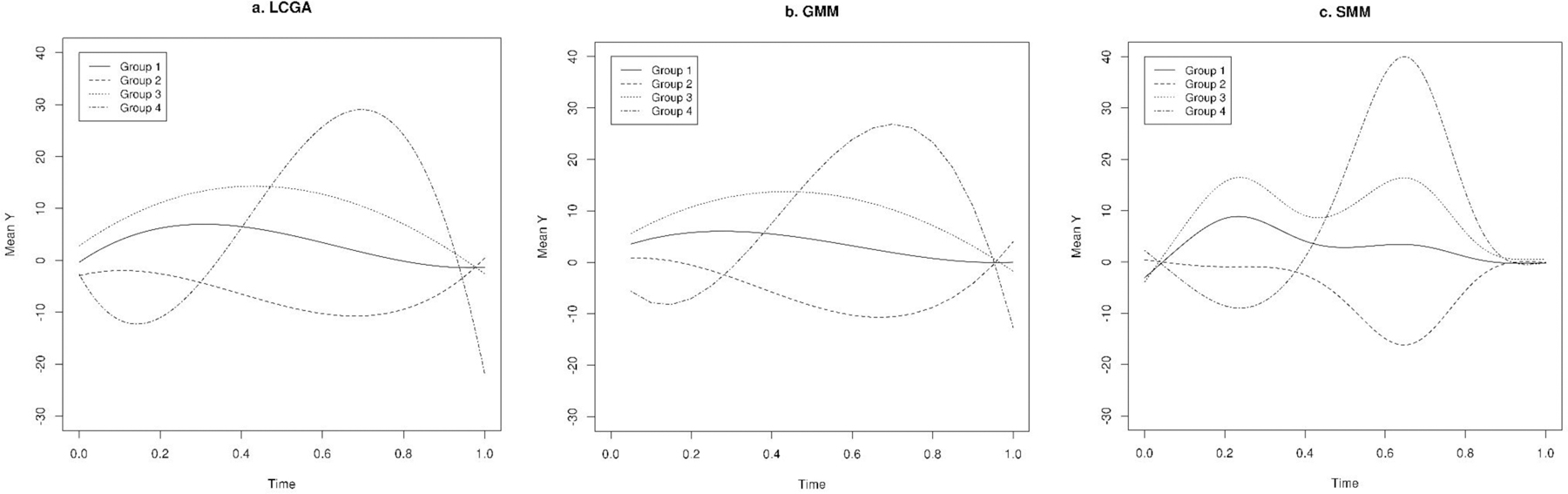
Predicted trajectories in a single randomly simulated dataset with normal distribution using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) (we used simulated data for all four groups for medium separation setting).

Figure 4.

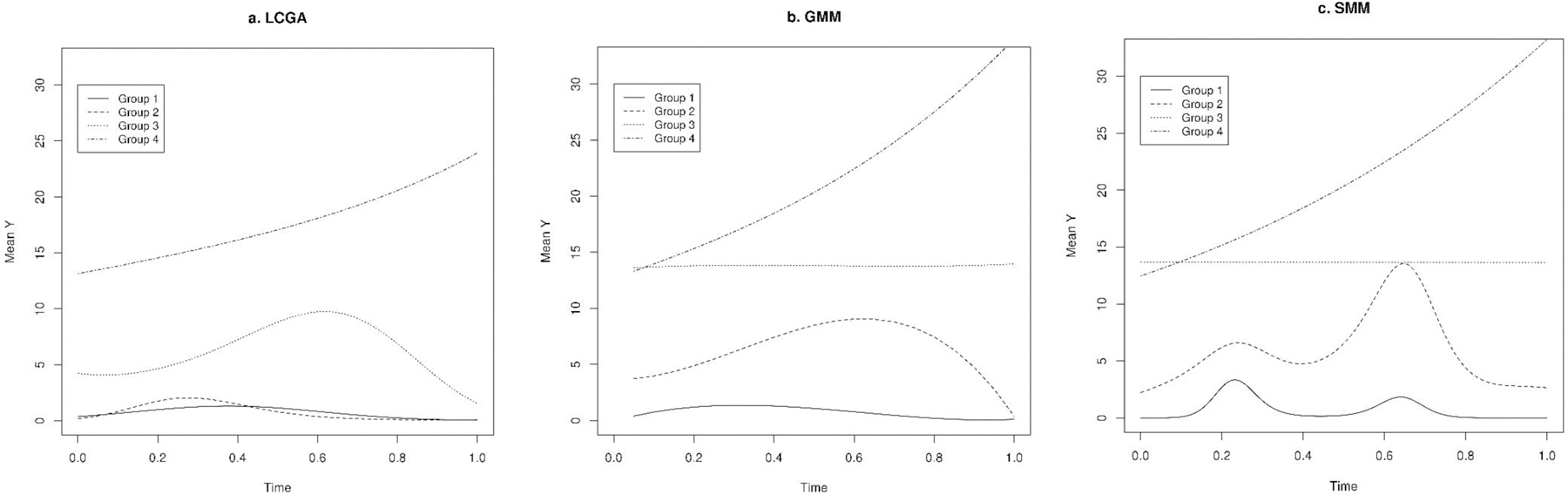
Predicted trajectories in a single randomly simulated dataset with Poisson distribution using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) (we used simulated data for all four groups for medium separation setting).

4. APPLICATIONS

The Growing-up Today Study (GUTS) was established in 1996 when women participating in the Nurses’ Health Study II (NHSII) were invited to enroll their children aged 9 to 14 years into this new cohort. A total of 16,882 children responded to the baseline questionnaires. Participants have been followed up with yearly self-administered follow-up questionnaires between 1997 and 2001 and with biennial questionnaires thereafter through 2013. GUTS participants reported their height and weight at baseline, and updated these data on follow-up questionnaires. Adolescents have been found to be able to provide valid reports of height and weight ^33–35. Body mass index (BMI) was calculated as the ratio of weight (kg) to height (m) squared. In adolescents (<18 y), obesity was defined as a BMI at or above the age- and sex-specific cutoffs proposed by the International Obesity Task Force (IOTF) ³⁶. In adults (≥18 y), obesity was defined as BMI ≥30 kg/m². In 2010 and 2013, participants were asked to report in questionnaires whether they developed diabetes, hypertension, and hypercholesterolemia, and the year of diagnosis (<1996, 1996–1999, 2000–2005, and 2006–2013). We created a composite outcome for cardiometabolic incidence, defined as incidence of diabetes, hypertension, or hypercholesterolemia. To minimize reverse causation, we excluded participants who were diagnosed before 1999 and censored BMI reported after diagnosis of cardiometabolic disease. We further excluded individuals with less than two BMI measurements. For participants who were siblings, we randomly chose one participant to avoid between-person correlation of BMI. In total, we included 10,743 participants among whom 1043 were cases of cardiometabolic disease. We collected information on total energy intake and physical activity in 1996, 1997, 1998, and 2001 using self-reported questionnaire.

We identified BMI trajectories of GUTS participants using LCGA, GMM, and SMM. We assumed random subject effects for SMM, and iterated the EM algorithm 50 times, which seemed sufficient for model convergence as indicated by the values of BIC from each iteration. The LCGA was fitted using the “proc traj” command in SAS version 9.2 for UNIX (SAS Institute Inc),³⁰ and the GMM with random subject effects was fitted using the ‘lcmm’ package (Version 1.9.2) in R 3.5.0.³¹ We modeled the age trajectories with cubic polynomial functions using LCGA and GMM. We compared the SMM to the LCGA and GMM in terms of log likelihood (LL), BIC, ARI between identified groups, percentage of individuals that were correctly classified (individuals that remained in the same group), and trajectories delineated by the fitted models. To validate the groups identified, we examined associations of identified trajectories with risk of cardiometabolic disease using logistic regression.

We delineated trajectories of BMI from 9 to 30 years adjusting for time-stable (sex) and time-varying covariates (total energy intake and physical activity). SMM yielded the highest LL and lowest BIC in comparison to LCGA and GMM (Table 4). We observed moderate agreement between classified membership using GMM and SMM as indicated by ARI. Consistently, the majority of participants were classified in the same groups using GMM and SMM. Although BIC decreased with increase in the number of groups using all three models, we chose three groups as a parsimonious model that captures a large amount of the variation in trajectories. Of the three trajectory groups identified using SMM, one had consistently high BMI throughout the follow-up period (on average, participants in this group were obese at 47% of the repeated assessments); one had consistently medium BMI (participants in this group were obese 3% of the time); and the other trajectory had consistently low BMI (participants in this group were not obese at any assessment) (Figure 4). In general, the trajectories estimated using LCGA and GMM were similar to those estimated using SMM. For all three trajectories, BMI increased with age; and the growth rate of BMI was high in adolescence and slowed after adulthood (age ≥18 years). We examined associations of trajectories identified using the three methods with risk of cardiometabolic diseases, and found that the odds ratio of cardiometabolic disease was significantly higher in medium and high BMI groups in a dose-response manner when compared to the consistently low BMI group (Table 5).

Table 4.

Comparison of model fit and classification for trajectories of body mass index (BMI) using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) in the Growing-up Today Study (GUTS).

Number of groups classified	Model	LL	BIC	Adjusted Rand Index (ARI)#	Percentage (%) of individuals classified in same groups*
2	LCGA	−153622	307364	0	66
2	GMM	−135185	270529	0.36	84
2	SMM	−129152	258565	1.00	100
3	LCGA	−145499	291183	0	42
3	GMM	−133606	267445	0.11	56
3	SMM	−124450	249284	1.00	100
4	LCGA	−141649	283548	0	32
4	GMM	−132712	265730	0.17	46
4	SMM	−121378	243262	1.00	100
5	LCGA	−139645	279605	0	26
5	GMM	−132171	264722	0.13	40
5	SMM	−119257	239145	1.00	100

LL: log likelihood; BIC: Bayesian information criterion.

^#Adjusted Rand index assesses similarity between 2 group assignments by counting the number of pairwise agreements and disagreements between group assignments. The closer the value is to 1, the better the agreement between group assignments.

^*Percentage (%) of individuals classified in same groups was obtained by permutating groups classified using two models, and the permutation with the largest percentage was used. For example, for 2 groups identified using SMM and GMM, we obtained percentage of individuals who were in groups 1 and 2 using SMM and GMM and percentage of individuals who were in group 2 using SMM and group 1 using GMM and who were in group 1 using SMM and 2 using GMM, and take the percentage with larger value.

Trajectories adjusted for sex and time-varying variables including total energy intake and physical activity.

Table 5.

Associations of trajectories of body mass index with risk of cardiometabolic disease using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) in the Growing-up Today Study (GUTS).

	Low BMI	Medium BMI	High BMI
LCGA
Number of cases/participants	463/5803	404/3787	176/1153
Odds ratio (95% CI) of cardiometabolic disease	1.00	1.38 (1.20, 1.58)	2.08 (1.72, 2.50)
GMM
Number of cases/participants	602/7117	306/2862	135/764
Odds ratio (95% CI) of cardiometabolic disease	1.00	1.30 (1.12, 1.50)	2.32 (1.89, 2.85)
SMM
Number of cases/participants	416/5390	434/4095	193/1258
Odds ratio (95% CI) of cardiometabolic disease	1.00	1.42 (1.23, 1.63)	2.17 (1.80, 2.60)

CI: confidence interval.

5. DISCUSSION

In this study, we developed a mixture model allowing for smoothing functions of trajectories using a modified algorithm in the maximization or M step. We reassigned participants to only one group for which the estimated trajectory was the most similar to the observed one, and utilized the recently released ‘gamm4’ package to fit GAMM models with smoothing functions of time within each group. When compared to existing mixture models, including LCGA and GMM, the key advantages of SMM lie in modeling trajectories with high flexibility, especially for non-normally distributed data (e.g., data with Bernoulli, Poisson, and gamma distributions). In addition, the proposed SMM can be readily implemented using existing software for fitting GAMM models.

In a simulation study, we simulated highly flexible longitudinal trajectories with low, medium, and high group separations to evaluate performance of our model when compared to LCGA and GMM. For settings with medium to high separation for a quantitative outcome (e.g., normal and Poisson), the proposed SMM model performed well in fitting the data and delineating trajectories. In LCGA and GMM, cubic polynomial functions of time were used to model trajectories, where the number of knots and the knot positions need to be chosen. A larger number of knots allows greater flexibility but may cause problems due to overfitting. Smoothing functions in GAMM use non-parametric penalized splines, and thus can produce highly flexible trajectories without causing overfitting problem to arise. This is potentially the main reason why our proposed model generated trajectories most similar to the true underlying curves and yields the highest correlations between the observed and predicted values in the simulation study. The highly flexible trajectories produced by the SMM model suggests that it may potentially have wide application to settings with highly non-linear longitudinal trends.

While recognizing the model has some potential advantages for highly flexible modelling of trajectories and convenient application to data from a wide collection of non-normal distributions, we acknowledge several limitations of the SMM. First, using BIC as criterion, the model tended to identify too many groups in the scenario of low separation among groups, although it performed well in the scenario of medium to high separation with relatively low heterogeneity in trajectories. In our simulation study, for binary data, the SMM model tended to identify more groups than necessary in scenario where there was low separation, resulting in that the SMM assigned group membership with the lowest accuracy as indicated by ARI comparing to LCGA and GMM. However, this is also a common issue for all types of mixture models; for example, it occurred for LCGA and GMM in the GUTS application considered in the previous section and also in some of the scenarios in the simulation study. A topic for future research is to consider alternatives to BIC for selecting the number of groups. For example, it may be useful to use a “scree plot”, of the type frequently used in factor analysis, to choose the number of groups. A measure of prediction accuracy, e.g., based on the sum of squared error, could be plotted against the number of groups and examined for evidence of an “elbow” where it does not yield discernibly better performance with increasing groups. We note that a measure based on the sum of squared error is particularly straightforward to obtain with our model given that there is only a single prediction for the class to which an observation belongs (unlike with conventional mixture models where the model provides many different prediction, one for each group to which an individual might belong to). Another option would be to examine a scree plot of the log-likelihood. Regarding the choice of the number of groups, Nagin et al holds the viewpoint that the most basic test of adequacy is whether the final model adequately addresses the research question,¹ and Bauer et al suggests that the number of groups and the shapes of trajectories should be guided by a priori expectation.³⁷ Second, our study used a modified algorithm in the M step by assigning an individual to only one group with the highest membership probability and ignored that there is group membership uncertainty. This uncertainty would need to be properly accounted for in the construction of confidence intervals and/or tests of hypotheses concerning group trajectories. Although bootstrap methods would be computationally quite costly because of the requirement for running an EM algorithm within each of many bootstrap replications, they might provide more accurate standard errors; this is a topic that warrants further research. Third, the CML approach can result in asymptotic biases, particularly when one of the groups is rare.²⁵ However, results from our simulation study suggest that the CML approach performs well in finite samples unless there is low separation among groups. Fourth, although we used a CML approach, the application of our method can still be computationally demanding. The reason for this is that in the M step the ‘gamm4’ package needs to estimate between-person random effects and the EM algorithm can require a large number of iterations to converge. Thus, for our proposed method, computation time may be a concern for datasets with both large sample sizes and many repeated measurements. Fifth, by using an iterative, hill-climbing procedure, the EM algorithm may converge to a local maximum, and initial assignments of group membership may affect the local maximum identified and the speed of convergence. In our study, we used the rank of the mean value of an individual’s vector of outcomes to assign initial group membership. Compared to other initialization procedures, such as random starting values and a k-means algorithm, this method is simple to apply and reduces computation time by avoiding multiple initial assignments.³⁸

In the GUTS application, we identified trajectories of BMI across adolescence and young adulthood using the three methods. The identified BMI trajectories increased with age, and the growth rate of BMI slowed down after individuals entered adulthood. This is consistent with the depictions of growth charts of U.S. adolescence, which show that growth spurts begin at 10–12 years, last throughout adolescence, and end at 18–20 years with the cessation of rapid growth ³⁹. Results from our study suggest that individuals with high, medium, and low BMI at baseline share similar growth patterns, and individuals with high BMI in adolescence are highly likely to remain obese in young adulthood. Moreover, we found that individuals with high BMI in adolescence are associated with higher risk of cardiometabolic diseases in early adulthood. A potential mechanism may be that childhood obesity is associated with chronic inflammation and elevation of inflammation biomarkers ⁴⁰. This can lead to insulin resistance, dyslipidemia, and high blood pressure, which enhance the development and progression of cardiometabolic diseases. Overall, the application to the GUTS study showed the importance of adopting a healthy BMI in adolescence and maintaining a low-BMI growth trajectory for the prevention of obesity and cardiometabolic diseases in young adulthood. By applying the SMM model to applications in life-course epidemiology, it may potentially have significant public health implication in enhancing our understanding of how early exposure over time affects health outcomes. Given the high flexibility for trajectory modeling, in addition to convenient application to outcome data from many different types of distributions, we expect the model may have broad application in the health and social sciences.

In the application of our model to trajectories of BMI across adolescence and young adulthood, we would like to clarify two potential concerns. First, in the M step of the EM algorithm, instead of estimating parameters using an overall likelihood fitted to the entire dataset, we split the dataset into several groups and fitted a GAMM within each group. Thus, for covariates included in the SMM, the underlying assumption is that associations of the covariates with BMI may differ across trajectory groups. Second, we censored BMI after the development of cardiometabolic disease. This might lead to different patterns of exposure distribution associated with the outcome, as individuals who did not develop disease would have exposures repeatedly measured at more time points. Thus, how to extend the SMM model to handle time-to-event outcomes would be an interesting direction for future research.

In summary, we have developed a mixture model that allows for smoothing functions of trajectories in a computationally cost-effective manner. The model can be applied to normal, Bernoulli, and Poisson distributed data, and has favorable performance in generating highly flexible trajectories when compared to existing methods such as LCGA and GMM. The model may be particularly useful in studies of life course epidemiology in the health and social sciences.

Figure 3.

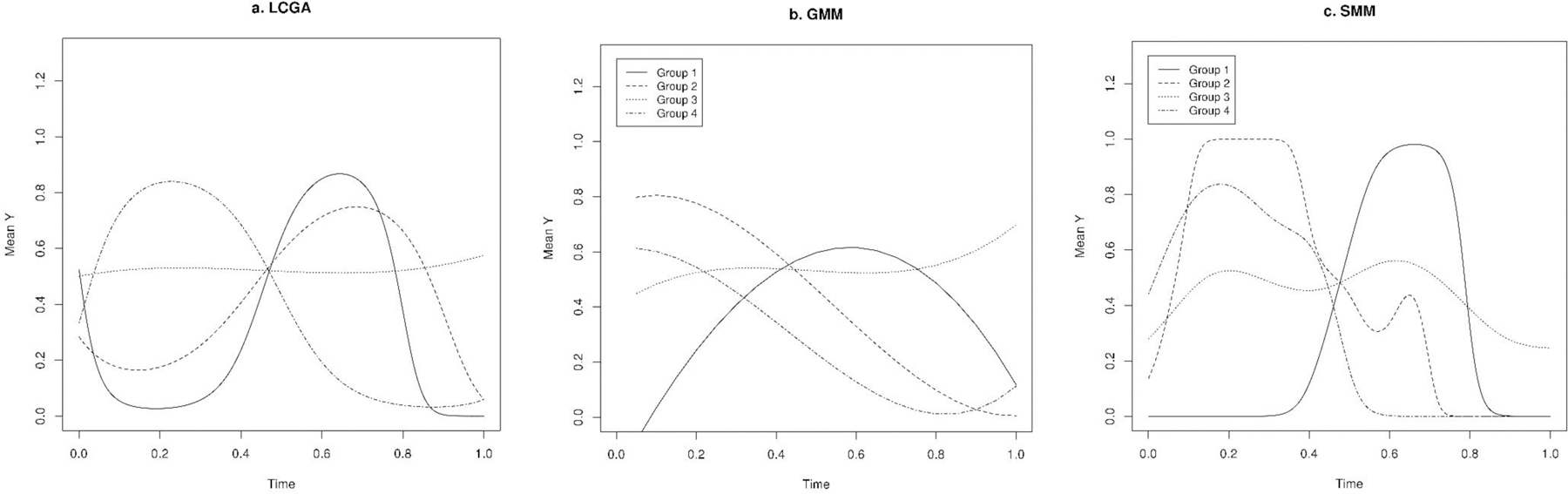
Predicted trajectories in a single randomly simulated dataset with Bernoulli distribution using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) (we used simulated data for all four groups for medium separation setting).

Figure 5.

Trajectories of body mass index (BMI) delineated using latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) in the Growing-up Today Study (GUTS). Models adjusted for sex and time-varying variables including total energy intake and physical activity.

Table 2.

Summary of simulation study results from fitting latent class growth analysis (LCGA), growth mixture model (GMM), and smoothing mixture model (SMM) to longitudinal data with Bernoulli distribution (1000 simulated datasets).

	Model	Number of groups identified*	LL	BIC	Adjusted Rand Index (ARI)#	Correlation between predicted and observed values &
High separation
Two groups	LCGA	2 (100%)	−1913	3874	1.00	0.62
	GMM	2 (91%), 3 (9%)	−1967	4000	1.00	0.62
	SMM	2 (68%), 3 (32%)	−1641	3443	0.92	0.64
Three groups	LCGA	2 (100%)	−3567	7185	0.52	0.46
	GMM	2 (7%), 3 (86%), 4 (7%)	−3629	7362	0.75	0.53
	SMM	3 (30%), 4 (70%)	−3360	6947	0.16	0.41
Four groups	LCGA	3 (98%), 4 (2%)	−4459	9002	0.46	0.53
	GMM	3 (87%), 4 (8%), 5 (5%)	−4539	9191	0.55	0.57
	SMM	3 (2%), 4 (52%), 5 (46%)	−3925	8149	0.14	0.46
Medium separation
Two groups	LCGA	2 (100%)	−1930	3908	1.00	0.62
	GMM	2 (95%), 3 (5%)	−1981	4026	1.00	0.62
	SMM	2 (58%), 3 (42%)	−1681	3527	0.86	0.63
Three groups	LCGA	2 (100%)	−3576	7203	0.52	0.46
	GMM	2 (3%), 3 (93%), 4 (4%)	−3621	7346	0.76	0.53
	SMM	3 (25%), 4 (75%)	−3158	6572	0.16	0.41
Four groups	LCGA	3 (93%), 4 (7%)	−4471	9025	0.45	0.52
	GMM	3 (84%), 4 (11%), 5 (5%)	−4538	9191	0.55	0.56
	SMM	3 (3%), 4 (44%), 5 (53%)	−3942	8181	0.17	0.47
Low separation
Two groups	LCGA	2 (100%)	−1974	3996	1.00	0.61
	GMM	2 (92%), 3 (8%)	−2011	4088	1.00	0.61
	SMM	2 (24%), 3 (76%)	−1933	4048	0.25	0.55
Three groups	LCGA	2 (100%)	−3604	7260	0.51	0.45
	GMM	3 (98%), 4 (2%)	−3601	7304	0.75	0.52
	SMM	3 (36%), 4 (64%)	−3235	6696	0.11	0.39
Four groups	LCGA	3 (83%), 4 (17%)	−4464	9015	0.45	0.54
	GMM	3 (51%), 4 (34%), 5 (15%)	−4519	9169	0.54	0.56
	SMM	3 (8%), 4 (22%), 5 (70%)	−3962	8235	0.18	0.47

LL: log likelihood; BIC: Bayesian information criterion. Presented are median values over 1000 simulated datasets.

^*Number of groups were identified by lowest Bayesian information criterion (BIC). We compared BIC assuming 1, 2, and 3 groups for simulated data with two groups, BIC assuming 2, 3, and 4 groups for simulated data with three groups, and BIC assuming 3, 4, and 5 groups for simulated data with four groups. Data presented is frequency of identified groups over 1000 simulated datasets.

^#Adjusted Rand index assesses similarity between 2 group assignments by counting the number of pairwise agreements and disagreements between group assignments. The closer the value is to 1, the better the agreement between group assignments. Presented are median values over 1000 simulated datasets.

^&Pearson correlation coefficient between predicted and observed values assuming simulated number of groups; data presented is median value over 1000 simulated datasets.