Validation of a deep-learning semantic segmentation approach to fully automate MRI-based left-ventricular deformation analysis in cardiotoxicity

Abstract

Objective:

Left-ventricular (LV) strain measurements with the Displacement Encoding with Stimulated Echoes (DENSE) MRI sequence provide accurate estimates of cardiotoxicity damage related to chemotherapy for breast cancer. This study investigated an automated and supervised deep convolutional neural network (DCNN) model for LV chamber quantification before strain analysis in DENSE images.

Methods:

The DeepLabV3 +DCNN with three versions of ResNet-50 backbone was designed to conduct chamber quantification on 42 female breast cancer data sets. The convolutional layers in the three ResNet-50 backbones were varied as non-atrous, atrous and modified, atrous with accuracy improvements like using Laplacian of Gaussian filters. Parameters such as LV end-diastolic diameter (LVEDD) and ejection fraction (LVEF) were quantified, and myocardial strains analyzed with the Radial Point Interpolation Method (RPIM). Myocardial classification was validated with the performance metrics of accuracy, Dice, average perpendicular distance (APD) and others. Repeated measures ANOVA and intraclass correlation (ICC) with Cronbach’s α (C-Alpha) tests were conducted between the three DCNNs and a vendor tool on chamber quantification and myocardial strain analysis.

Results:

Validation results in the same test-set for myocardial classification were accuracy = 97%, Dice = 0.92, APD = 1.2 mm with the modified ResNet-50, and accuracy = 95%, Dice = 0.90, APD = 1.7 mm with the atrous ResNet-50. The ICC results between the modified ResNet-50, atrous ResNet-50 and vendor-tool were C-Alpha = 0.97 for LVEF (55±7%, 54±7%, 54±7%, p = 0.6), and C-Alpha = 0.87 for LVEDD (4.6 ± 0.3 cm, 4.6 ± 0.3 cm, 4.6 ± 0.4 cm, p = 0.7).

Conclusion:

Similar performance metrics and equivalent parameters obtained from comparisons between the atrous networks and vendor tool show that segmentation with the modified, atrous DCNN is applicable for automated LV chamber quantification and subsequent strain analysis in cardiotoxicity.

Advances in knowledge:

A novel deep-learning technique for segmenting DENSE images was developed and validated for LV chamber quantification and strain analysis in cardiotoxicity detection.

Introduction

A deep convolutional neural network (DCNN) is a convolutional neural network (CNN) that is characterized by feature classification and multiscale predictions conducted by a deep network that has intermediate hidden layers.^1–13 It is a subset of artificial intelligence (AI) and machine-learning used extensively in object recognition and motion and deformation analysis.^2,4,13–17 In cardiac image analysis, CNN technology provides vital information on ventricular detection, function and pathologies related to dysfunction of the myocardium.^5,9,18–25 Using ventricular imaging networks, key parameters based on population samples are built during learning to provide detailed spatiotemporal information on the myocardium at any point in space or time during the cardiac cycle.^{11,20,22,26,27} The underlying evolutionary architecture generally consists of an input layer, an output layer and in-between functional layers of the transformational kind.^{10,11,13,19,28–31} These transformations are performed by different combinations of convolutional, rectified linear unit (ReLU), batch-normalization (BN), addition, pooling, fully connected, and softmax layers to extract localized feature maps from the input. One of the greatest challenges in ventricular segmentation is efficient, end-to-end pixel-wise segmentation, for which a CNN variant called a fully convolutional neural network (FCN) is commonly employed and was used in this study.^{11,13,20,24,27} FCNs have an encoder–decoder structure with the encoder transforming the input into high-level feature representations, whereas the decoder interprets the feature maps and recovers spatial details back to the image space through upsampling operations.^{11,13,20,21,24,27,28} Indeed, to obtain image segmentation results that match input dimensions, a large variety of deep-learning with FCN and similar CNN methods have been architected to segment the ventricles in cine MRI images acquired with the steady-state free precession (SSFP) protocol.^{11,20,22,27,32,33} Such approaches include biventricular segmentation by Isensee et al²², who used a 2D + 3D U-Net ensemble to improve accuracy, Khened et al²⁷, who developed a dense U-Net with inception modules to combine multiscale features, and Jang et al³², who designed a 2D M-Net model with weighted cross-entropy loss. To meet the challenges of spatiotemporal context in ventricular segmentation, Poudel et al³⁴ architected a 2D FCN with a recurrent neural network (RNN) to model interslice coherency, and Wolterink et al³³ architected a dilated U-Net to segment end-diastolic and end-systolic data simultaneously. For meeting the challenges of multidomain application of their model, Tao et al³⁵ trained a 2D U-Net CNN by acquiring a heterogeneous multivendor, multiscanner, labeled training-set from patients diagnosed with cardiovascular diseases. Multidomain cardiac segmentation was also addressed by Chen et al³⁶, who proposed a 2D U-Net data normalization and augmentation pipeline that enabled training from a single-scanner to generalize across multiscanner, multisite data sets. Thus, deep-learning approaches can provide valuable clinical information regarding ventricular extent and function, such as estimates of left-ventricular (LV) ejection fraction (LVEF), in the context of both healthy and pathological studies.^{11,21,22,33,37–39}

This is a novel, translational study on segmenting cine displacement encoding with stimulated echoes (DENSE) images with automated DCNN technology, and motivated by an ultimate goal to provide a single-scan, diagnostic tool for comprehensive LV function analysis.^{2–4,40–46} The diagnostic tool is primarily intended for the routine surveillance of LV contractility necessary to prevent cardiotoxicity, which may arise from the administrations of anti neoplastic chemotherapy agents (CTA) such as anthracyclines and trastuzumab in breast cancer.^47–50 In relation to detecting cardiotoxicity, previous and our studies show that an echocardiographic quantification of LVEF may not always provide timely information regarding its subclinical occurrence.^48,51–53 Hence, an effective way of monitoring subclinical LV contractile abnormalities in cardiotoxicity is by combining computations of both LV chamber quantification and 3D myocardial strains, which we aim to provide with an accessible, single-scan, DENSE MRI-based analysis.^{51,52,54–59} An additional novel part of this study and its unique challenge was segmenting cine DENSE images with a DCNN methodology that is unprecedented and has not been conducted previously.

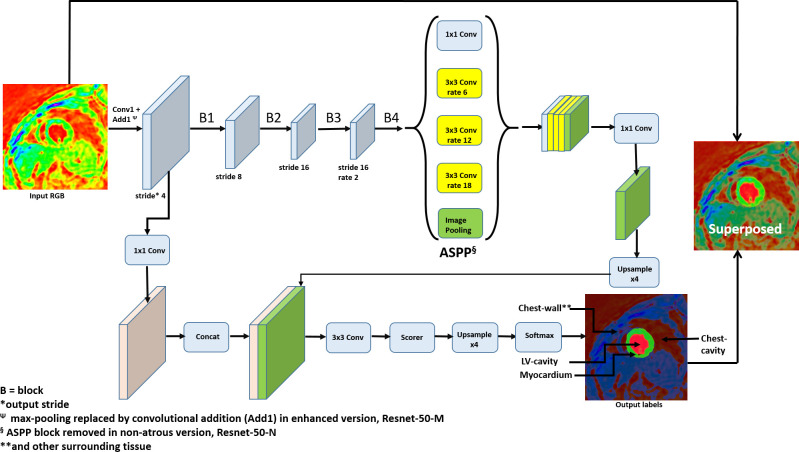
Therefore, this study’s primary goal was to develop an automated, supervised DCNN-based segmentation and chamber quantification module for our existing 3D strain analysis tool with DENSE MRI that monitors the possibility of cardiotoxicity in CTA-treated breast cancer patients.^{2–4,40–44} The classification-based segmentation of the LV and surrounding anatomy was conducted on 42 patient data sets with the tool’s DeepLabV3 +FCN architecture and its underlying ResNet-50 backbone.^{2–4,7,10,12,17,60} Our second goal was to investigate three different versions of the ResNet-50 backbone in the DCNN and determine which achieved the highest accuracy for segmenting the LV in DENSE images.^45,61–64 The backbone versions consisted of the: (1) ResNet-50-N, which is the original model without atrous convolution or atrous spatial pyramid pooling (ASPP), (2) ResNet-50-A, which is the default DeepLabV3 +backbone with atrous convolution and ASPP, and (3) ResNet-50-M, with atrous convolution, ASPP and modifications to enhance network performance such as using Laplacian of Gaussian (LoG) convolutional filters. An important part of our second goal was to investigate if the modified, atrous ResNet-50-M would yield higher segmentation accuracy and also network speed. A schematic of the DCNN with the ResNet-50-A backbone, input, output, transformational layers and modifications related to the non-atrous and atrous versions is shown in Figure 1. Automated semantic segmentation was performed with the three networks following training to learn the weights and biases for various layers and accuracy improved via backpropagation operations.^3,4,12 Following segmentation, the outputs were processed for chamber quantification parameters, such as LV end-diastolic diameter (LVEDD) and LVEF, and subsequent 3D strain analysis. A third goal was to statistically validate our technique by conducting repeated measures and reliability tests on the chamber quantification and strains computed via the three networks and also computed with a pre-existing vendor tool, Circle CVI42 (v. 42, Circle Cardiovascular Imaging Inc., Calgary, Alberta).

Figure 1.

The DeepLabV3 +DCNN with modified Renet-50 backbone for feature recognition of the LV myocardium in DENSE images, shown with convolution, rates, output strides, ASPP, upsampling, scorer and softmax. The modifications include Laplacian of Gaussian filters at the first convolutional layer (Conv1) and fourth block (B4) and replacing the max-pooling with convolutional addition (Add1). The non-atrous version is without atrous convolution and ASPP. ASPP, atrous spatialpyramid pooling; DCNN, deep convolutional neural network; DENSE, displacement encoding with stimulated echoes.

Methods and materials

Human subjects database

We tested the DCNN for LV segmentation and the possibility of LV dysfunction in 42 DENSE data sets acquired on adult female breast cancer survivors. All patients had undergone CTA treatment consisting of one of two regimens, with either anthracyclines or trastuzumab, with details on drug-specific regimens given in our previous studies.^45,46 Recruitment consisted of careful screening of patients to reduce the effect of various other cardiac comorbidities on cardiotoxicity analysis. Patients were recruited only if they had non-acute cardiac complications that existed before chemotherapy or developed afterward, as done previously.⁴⁶ They sighed informed consents based on Institutional Review Board (IRB) guidelines and volunteered access to their MRI data and medical histories.

Background theory

In this work, we performed the task of semantic segmentation of the DENSE cardiac images using the latest development in DCNNs with atrous (dilated) convolution, which has been shown to provide sharper feature detection.^3,4,8,60 The atrous characteristics were retained in two of the network backbones in this study, ResNet-50-A and ResNet-50-M. Without atrous convolution, the commonly deployed downsampling in DCNNs achieve invariance but has a toll on localization accuracy. The atrous convolution is applied in two different ways, of which the first is by applying a rate, r, corresponding to the stride with which we sample the input signal, as shown in Figure 1. This rate allows explicit control of the resolution at which the model computes feature responses without increasing the number of parameters or amount of computation.⁴ Secondly, by use of ASPP which is an atrous version of the spatial pyramid pooling used in SPP-Net^4,8,12 (Figure 1). ASPP probes convolutional features with filters (or pooling) at multiple sampling rates and effective fields-of-view to segment objects at multiple scales. The ASPP is followed by the decoder’s upsampling layers, a scorer function for computing the pixel-wise probabilities for classification, and a softmax layer for cross-entropy loss computation. Detailed theory on the layers implemented (or modified) in the network, are outlined next. Explanations are provided on the functioning of convolutional (including atrous), batch normalization (BN), rectified linear unit (ReLU) and softmax layers, as well as computation of the gradients of their functions.

To explain atrous convolution, consider a layer with predicted output, y_i, given by,⁴

$$y_i={\sum }_j{\gamma }_{ij}{z}_j+{\beta }_i{\gamma }_i{z}_j+{\beta }_i\left(1a\right)$$

where $z_j$ is the input signal, γ_i is the filter and the bias is β_i. The general loss function, $L$, of convolution based on the predicted and true output label, ${\widehat{y}}_i$, of length N is given by,

$$L=\frac{1}{N}{\sum }_{i=1}^N{\left(\widehat{y}|i-y_i\right)}^2=\frac{1}{N}{\sum }_{i=1}^N{\left(\widehat{y}|i-\left({\gamma }_i{z}_j+{\beta }_i\right)\right)}^2\left(1b\right)$$

If a rate parameter, r, is defined that corresponds to the stride of sampling the input signal, then $y_i={\sum }_j{\gamma }_{ij}{z}_{rj+j_0}+{\beta }_i$, and we define $z_{j`}=z_{rj+j_0}$. It is equivalent to convolving the input with upsampled filters via inserting r-1 zeros between two consecutive filter values along each dimension in space. Once we modify the loss function according to r, the change in the gradients for updating the output, input, weights and biases are given by,

$$\frac{dL}{d{y}_i}=\frac{-2}{N}\left(\widehat{y}|i-\left({\gamma }_i{z}_{j`}+{\beta }_i\right)\right)\left(1c\right)$$

$$\frac{dL}{d{z}_{j`}}=\frac{-2}{N}{\sum }_{z_{rj+j_0}}{\gamma }_{ij}\left(\widehat{y}|i-\left({\gamma }_i{z}_{j`}+{\beta }_i\right)\right)\left(1d\right)$$

which is summed over only those derivatives of $L$ with respect to$z_{rj+j_0}.$

$$\frac{dL}{d{\gamma }_{ij}}=\frac{-2}{N}{\sum }_{i=1}^N\left(\widehat{y}|i-\left({\gamma }_i{z}_{j`}+{\beta }_i\right)\right)z_{j`}\left(1e\right)$$

$$\frac{dL}{d{\beta }_i}=\frac{-2}{N}{\sum }_{i=1}^N\left(\widehat{y}|i-\left({\gamma }_i{z}_{j`}+{\beta }_i\right)\right)\left(1f\right)$$

Segmentation by edge detection is an essential tool in digital image analysis that requires identification and subsequent classification of certain objects and their edges. To find edges the algorithm looks for contours in the image where abrupt changes in intensity, discontinuities or illumination in a scene are present. One such method for edge detection is by using the LoG filter where the Laplacian is a 2D isotropic measure of the second derivative of an image.⁶⁵ We applied the LoG at the first convolution kernel following input with a goal to sharpen edge detection and enhance the DCNN’s capacity to learn the variances and invariances of the image set. We also preserved the full learning capacity of the network weights by maintaining backpropagation parameter optimization. The LoG is a multidimensional generalization of the Ricker wavelet and derived from the function, f(i,j)=I(i,j)*G(x,y), which is the convolution of an image, I(i,j), with the Gaussian filter, G(x,y). Here, (i,j) are the pixel coordinates and (x,y) are local scale-space coordinates. The Laplacian kernel function, L(i,j), which is the second derivative of f(i,j) is given by,

$$L\left(i,j\right)={\nabla }^{2}f\left(i,j\right)=\frac{{\partial }^{2}f\left(i,j\right)}{{\partial x}^2}+\frac{{\partial }^{2}f\left(i,j\right)}{{\partial y}^2}\left(2a\right)$$

The LoG filter is then given by,

$$log\left(x,y\right)=\frac{-1}{{\pi \sigma }^4}$$

where $\sigma$ is the filter radius. Therefore, the layer weights are initialized as, ${\gamma }_{ij}=log\left(x,y\right)$, and the gradients, ${∆\gamma }_{ij}$, are learned using backpropagation in its kernel.

BN is the step following convolution that reduces the internal covariate shift via regularizing the change in the distribution of network activations. The shifts occur due to the change in network parameters during training.^1,10,29 As BN generally has a slowing effect, the internal covariate shift problem is addressed by normalizing each mini-batch for layer inputs.^1,10 Consider a $D$-dimensional input to a layer, $x=\left[x^{\left(1\right)}\dots x^{\left(D\right)}\right]$, where $x^{\left(k\right)}$ is each input to the layer. Then, the BN scaled and shifted output is given by, $y^{\left(k\right)}={BN}_{\gamma ,\beta }{\widehat{x}}^{\left(k\right)}={{\gamma }^{\left(k\right)}\widehat{x}}^{\left(k\right)}+{\beta }^{\left(k\right)}$, where ${BN}_{\gamma ,\beta }{\widehat{x}}^{\left(k\right)}$ denotes the BN function$,$ and the learnable parameters are ${\gamma }^{\left(k\right)}$ and ${\beta }^{\left(k\right)}$. The input normalization, ${\widehat{x}}^{\left(k\right)}$, corresponding to input $x^{\left(k\right)}$, is given by,

$${\widehat{x}}^{\left(k\right)}=x^{\left(k\right)}-\frac{E\left[x|\left(k\right)\right]}{\sqrt{Var\left[x^{\left(k\right)}\right]}}\left(3a\right)$$

where $E\left[x|\left(k\right)\right]$ is the expectation (mean) and $Var\left[x^{\left(k\right)}\right]$ is the variance. These parameters are learned along with the original model parameters, boost the representation power of the network and speed it up. Thus, in the batch setting of the stochastic gradient descent (SGD) training that follows, we have $B=1\dots m$values of activations in a mini-batch with the output defined as, $y_i={BN}_{\gamma ,\beta }{\widehat{x}}_i$, in which $\widehat{x_i}$ is the normalization of input $x_i$. To calculate the Loss, $L$, and its gradients, and to learn the weight and bias parameters, $\gamma$ and $\beta$, the functions implemented for the layer are given by,

$$\widehat{x_i}=\frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}\left(3b\right)$$

$${\mu }_B=\frac{1}{m}{\sum }_{i=1}^m{x}_i\left(3c\right)$$

$${\sigma }_B^2=\frac{1}{m}{\sum }_{i=1}^m{\left(x_i-{\mu }_{\beta }\right)}^2\left(3d\right)$$

where ${\mu }_B$ is the mean and ${\sigma }_B$ the standard deviation for the mini-batch. The loss,$L$, and its gradients with respect to the normalization, input, weight and bias, where ${\widehat{y}}_i$ is the true output, are given by,

$$L=\frac{1}{m}{\sum }_{i=1}^m{\left({\widehat{y}}_i-\gamma \widehat{x_i}-\beta \right)}^2=\frac{1}{m}{\sum }_{i=1}^m{\left({\widehat{y}}_i-\gamma \frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}-\beta \right)}^2\left(3e\right)$$

$$\frac{\partial L}{\partial \widehat{x_i}}=\frac{\partial L}{\partial y_i}\bullet \gamma =\frac{-2}{m}\left({\widehat{y}}_i-\gamma \frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}-\beta \right)\left(3f\right)$$

$$\frac{\partial L}{\partial x_i}=\frac{\partial L}{\partial \widehat{x_i}}\frac{1}{\sqrt{{\sigma }_B^2+ϵ}}+2\frac{\partial L}{\partial {\sigma }_B^2}\frac{x_i-{\mu }_{\beta }}{m}+\frac{\partial L}{\partial {\mu }_B}\frac{1}{m}\left(3g\right)$$

$$\frac{\partial L}{\partial \gamma }={\sum }_{i=1}^m\frac{\partial L}{\partial y_i}\bullet {\widehat{x}}_i\left(3h\right)$$

$$\frac{\partial L}{\partial \beta }={\sum }_{i=1}^m\frac{\partial L}{\partial y_i}\left(3i\right)$$

The BN transform can be added to a network to manipulate any activation, which depends on the training and other examples in the mini-batch.^1,10,29

The scaled and shifted output y^(k) is then passed to the ReLU layer. The ReLU is the default activation function in ResNet-50 that transforms the summed weighted input via a piecewise linear function.^16,30 The output, $y_i$, will be the input, $z_i$, if is positive, otherwise zero. ReLU’s rectified output is given by,

$$y_i=ReLU\left(z_i\right)=\left\{\begin{array}{c}{z}_i{z}_i\S amp;gt;0\\ 0z_i\S amp;lt;0\end{array}\right.\left(4a\right)$$

The gradient of ReLU is given by,

$$\frac{d\left(y_i\right)}{d{z}_i}=\frac{dReLU\left(z_i\right)}{d{z}_i}=\left\{\begin{array}{c}1z_i\S amp;gt;0\\ 0z_i\S amp;lt;0\end{array}\right.\left(4b\right)$$

ResNet-50’s blocks of convolution are followed by a series of deconvolution layers, scoring, softmax and labeling via the DCNN’s DeepLabV3 +architecture. These later layers produced score maps and semantic label predictions, which follow a streamlined decoder conducting an initial bilinear upsampling, concatenation with low-level features of the same dimension, convolutional smoothing and a final bilinear upsampling.^3,7,31 In this encoder–decoder model, the softmax function, ${\theta }_i$, of an input pixel, $z_i$, for an arbitrary N number of inputs is given by,

$${\theta }_i=\frac{e^{z_i}}{{\sum }_j{e}^{z_j}}\left(5a\right)$$

where $i\in \left[1\dots N\right]$. The corresponding softmax cross-entropy function, E, for loss computation before output is given by,

$$E\left(t_i,{\theta }_i\right)=-{\sum }_{i=1}^N{t}_{i}log\left({\theta }_i\right)\left(5b\right)$$

where $t_i$ is one hot label for pixels of a class. Here the derivative of the softmax, ${\theta }_k=\frac{e^{z_k}}{{\sum }_{j=1}^C{e}^{z_j}}$, for classes $k\in \left[1\dots C\right]$, and cross-entropy, $E$, in relation to any input, $z_i$, are given by,

$$\frac{d{\theta }_k}{d{z}_i}={\theta }_k\left({\delta }_{k,i}-{\theta }_i\right)\left(5c\right)$$

$$\frac{dE}{d{z}_i}=\frac{d}{d{z}_i}\left[-{\sum }_{k=1}^C{t}_{k}log\left({\theta }_k\right)\right]={\theta }_i-t_i\left(5d\right)$$

Note that our network does not have learnable parameters for the softmax layer.

Tailoring the DCNN for DENSE segmentation

Inherent challenges always exist in relation to segmenting the LV myocardium with a FCN-DCNN, a majority of which occur due to classification inaccuracies, poorly defined contours and low network speed.^11,24,66,67 Additionally, inaccuracies due to imaging limitations can occur at the very apical and basal slices where LV boundaries merge with surrounding anatomy, or when there are T1-relaxation artifacts, or due to low SNR toward the very early or later phases of the systolic period.^{43,61,63,64,68} To aggressively combat the above challenges and maximize accuracy of a novel segmentation technique, this study’s supervised learning consisted of training three different versions of the ResNet-50 backbone to perform classification tasks. Modifications were made to some layers of the original ResNet-50 architecture to devise the three networks, consisting of the non-atrous ResNet-50-N, the default, atrous ResNet-50-A in DeepLabV3+, and the modified, atrous ResNet-50-M for improved classification. These modifications were conducted while keeping receptive field sizes of different layers the same. Our goal was investigating any improvements in accuracy achieved with atrous backbones in the DCNN in comparison to a non-atrous architecture, and additionally, any improvements in accuracy or network speed achieved with modifying the atrous version. Given below are further details on the modifications and the network they were applied to, which along with hierarchical information in the original network performed the classifications.

• The weights in the first convolutional layer (Conv1 in Figure 1) following the input of RGB images are initialized using a LoG function for a filter of size 5 × 5. The Laplacian is used for zero-crossing edge detection that highlight the regions of rapid intensity change in the image. This modification was applied to ResNet-50-M such that any improvement due to better edge detections could be observed.

• Network speed was improved by cutting out the max-pooling layer for convolutional addition (or strided convolution), shown as Add1 in Figure 1.^3,4 With this replacement, downsampling is done with the same output size of the old pooling layer and the model size reduced. Additionally, the learning optimization improves via the modifications of weights and biases during backpropagation, which a parameterless pooling layer cannot achieve. This modification was applied to ResNet-50-M to observe any improvement in speed or accuracy from removing max-pooling.

• The weights in the final convolution block (B4 in Figure 1) are initialized using a LoG function for a filter of size 3 × 3. This LoG initialized convolutional layer remains connected to two convolutional layers with kernel size 1 × 1, and channel depths remain the same as the original one from ResNet-50. This modification was also applied to ResNet-50-M to observe the effect of LoG filtering on performance.

• Following the fusion of feature maps from each convolution stage, we modified the classification weights of the cross-entropy layer (Softmax in Figure 1) for loss computation. The classification weights were assigned according to the median frequency of pixels belonging to the: (1) chest-cavity (CC), (2) chest wall (CW) and surrounding-anatomy (including liver and others), (3) myocardium, and (4) LV-cavity (LVC) as shown in Figure 1. This modification was applied to all three backbones to specifically address class imbalance affecting final scores of small objects like the myocardium.^26,32

Note that being a FCN for dense prediction tasks, DeepLabV3 +does not have a final fully connected layer. The last block using atrous convolution via ASPP and different dilation rates to capture multi scale context was retained for the networks with ResNet-50-A and ResNet-50-M (ASPP in Figure 1) but not ResNet-50-N. After the ASPP and decoder layers, a convolution-based scorer function computes the pixel-wise probabilities and the loss is computed by the softmax cross-entropy function (with weights for the myocardium, LVC, CW and CC) before the final output layer. For segmentation, the systolic period, apex-to-base, DENSE LV data (42 data sets, n = 8568 images) were divided in a similar way for all three DCNNs, consisting of a training cohort (21 data sets, n = 4284 images), a validation cohort (9 data sets, N = 1836 images) and a testing cohort (12 data sets, n = 2448 images). The DICOM data were converted into three-channel RGB images in Portable Network Graphics (PNG) format which is the default input format for ResNet-50. The transformation is based on the RGB gamut of colors in computer/television monitors that are obtained from the perception of hue (H), saturation (S), and value (V) in a grayscale image according to the Hexcone Model as outlined by Smith⁶⁹. Thus, using the MATLAB (v. 2020a, MathWorks, Natick, MA) function ind2rgb, the 16-bit DICOM intensities are mapped to indexed HSV of the same range (n = 2¹⁶) and corresponding color range per RGB channel. During training with a mini-batch size of 50 for every epoch, the weights are updated via the SGD optimization algorithm. From the fine-tuning of parameters, via the gradient noise-scale plotting method outlined by Smith,⁷⁰ the learning rate and the number of max epochs were determined as 0.001 and 60, respectively, to ensure efficient training.⁷⁰ All three networks were implemented with the Deep-learning Toolbox^™ Model for DeepLabV3 +with underlying ResNet-50 backbone in MATLAB.⁷¹ Our training experiments were performed on a machine with specifications: Intel Xeon E5-2690 Processor at 2.60 GHz CPU, NVIDIA Pascal Titan X GPU, and 128 GB RAM. The systolic period end-diastolic to end-systolic 2D images in every slice-position in the training cohort were applied to train all three DeepLabv3 +networks, with data augmentation occurring randomly during selection of the mini-batch at each iteration. The extent of mini-batch augmentations included x- or y-direction translations (0–5%), rotations (±45^○) and zooming (75–125%).

DENSE protocol for acquisition

Navigator-gated, spiral 3D DENSE data were acquired on a 1.5T MAGNETOM Espree (Siemens Healthcare, Erlangen, Germany) scanner with displacement encoding applied in two orthogonal in-plane directions and one through-plane direction.^43,44,61,63 Typical imaging parameters included a field of view of 360 × 360 mm, matrix size of 128 × 128, echo time of 1.04 ms, repetition time of 15 ms, flip angle of 20°, voxel size of 2.81 × 2.81 × 5 mm, 21 cardiac phases, an encoding frequency of 0.06 cycles/mm and simple 4-point encoding and 3-point phase cycling for artifact suppression.^61,68 For receiving patient signals from the Espree, an anterior 18-channel array coil in combination with elements of the table-mounted spine array coil was used. Heart rates (HR) and diastolic and systolic blood pressures (DBP and SBP) were continuously monitored during the scans.

Chamber quantification

Following training and segmentation, the classified myocardium from the three DCNNs were chosen for full-LV reconstruction, chamber quantification and validation in comparison to the existing Circle CVI42 tool. Chamber quantification included measuring the LVEF, LVEDD, LV end-systolic diameter (LVESD), end-diastolic volume (LVEDV), end-systolic volume (LVESV), stroke volume (LVSV) and mass (LVM). The results of chamber quantification via all three backbones and Circle CVI42 were compared with intraclass correlation coefficients (ICCs) and repeated measures analysis as outlined in the next section. Global strains (radial, circumferential and longitudinal) and torsion (apical) were analyzed in the myocardium with the existing meshfree Radial Point Interpolation Method (RPIM) approach, details of which are given in our previous work.^45,63,64,72 The strains computed in the three DCNNs and vendor tool generated LV chambers were compared.

Performance metrics and statistical analysis

The performance metrics of segmentation evaluated on the validation and test sets after training each DCNN were,

• Average Perpendicular Distance (APD): The distance from the automatically segmented contour to the corresponding ground-truth contour, averaged over all contour points.⁷³

• Percentage of good contours (GC): It implies a good segmentation if the APD is less than 5 mm.

• Dice: A measure of contour overlap defined by two times the intersections between contour areas generated by the DCNN and ground-truth and divided by the sum of the two.⁷³

• Hausdorff-distance: It measures the maximum perpendicular distance between the contours generated with the DCNN and ground-truth.^74,75

• Accuracy: Ratio of correctly classified pixels in each class to the total number of pixels belonging to that class according to the ground-truth, which semantic segmentation metric was evaluated with the Computer Vision Toolbox^™ in MATLAB following training.⁷⁶

• Sensitivity/Specificity Analysis: For each class, these were the ratio of true positives to the sum of the true positives and false negatives and the ratio of true negatives to the sum of the true negatives and false positives, respectively.

• Receiver operating characteristic curve (ROC) and area under the curve (AUC): This metric illustrates the diagnostic ability of the network for classification and was evaluated from the scores of semantic segmentation and corresponding class labels per image with the Computer Vision Toolbox^™ in MATLAB.⁷⁶

• The pixel-based confusion matrix presented in tabular layout was generated cumulatively from all images for both validation and test sets to provide one-to-one comparison between actual and predicted classes, and was evaluated with the Computer Vision Toolbox^™ in MATLAB.⁷⁶

Means and standard deviations were computed on the patients’ demographic data, chamber quantification parameters, global strains (radial, circumferential and longitudinal) and apical torsion. The results of chamber quantification via the three networks and Circle CVI42 were statistically compared using,

• Repeated measures ANOVA conducted with SPSS (v. 26, IBM Corp., Armonk, NY), which we justify as the method for comparing multiple segmentation techniques on the same data. Mauchly’s test of sphericity was used to test the assumption that the relationship between the different pairs of measurements was similar. The confidence interval adjustment to keep the Type 1 error minimized for multiple measurement comparisons was with the Bonferroni correction. In the case of sphericity assumption violated the Greenhouse-Geisser corrected p value was reported for any significant differences found between the measurements.

• Reliability tests by estimating the Cronbach’s α (C-Alpha) ICC index with SPSS. We chose this test to show that the chamber quantification results via segmentation with the three DCNNs and Circle CVI42 were interrelated.

• Bland–Altman plots. This visual test was chosen to assess agreements between estimates of LVEF.⁷⁷

Results

Table 1 shows the demographic information on patients who volunteered their cardiac MRI data for the chamber quantification and strain analysis via the DCNNs and Circle CVI42. Table 1 also details their existing comorbidities and the number of clinically detected cardiotoxicity cases following chemotherapy. The time to recruiting patients from the end of chemotherapy was 2.7 ± 0.8 months.

Table 1.

Patient demographics

Parameter	Value
Demographics
Age (years)	55.3 (8.3)
DBP (mmHg)	73.5 (11.2)
SBP (mmHg)	123.5 (14.5)
HR (bpm)	73.0 (10.7)
Body mass (kg)	71.8 (13.9)
BMI (kg/m2)	26.9 (4.2)
BSA (m2)	1.8 (0.2)
Comorbidities
Hypertension	9
Hypercholesterolemia	7
Diabetes mellitus	9
Radiotherapy	14
Detected casesa	8

BMI, Body mass index; BSA, Body surface area; DBP, Diastolic blood pressure; HR, Heart rate; SBP, Systolic blood pressure.

^aClinician detected cardiotoxicity. (): Standard deviations.

Deep-learning output with multiclass classification

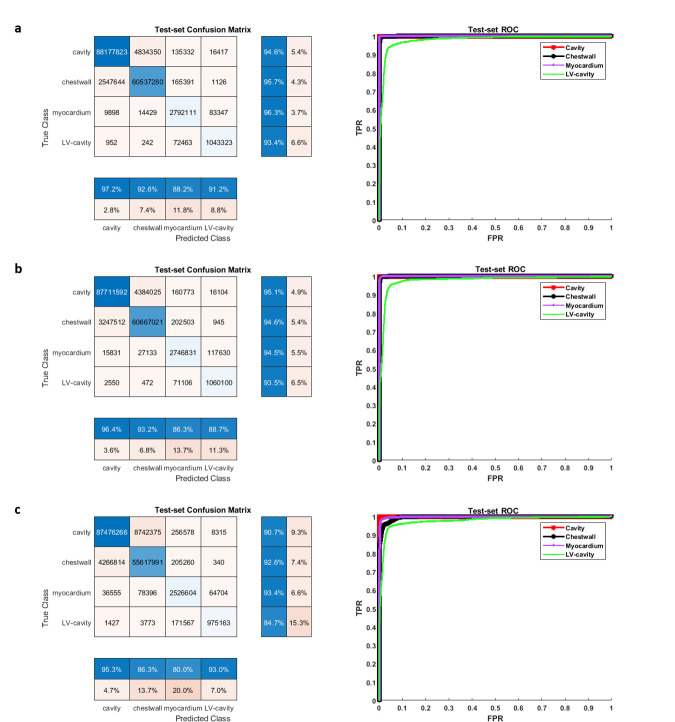
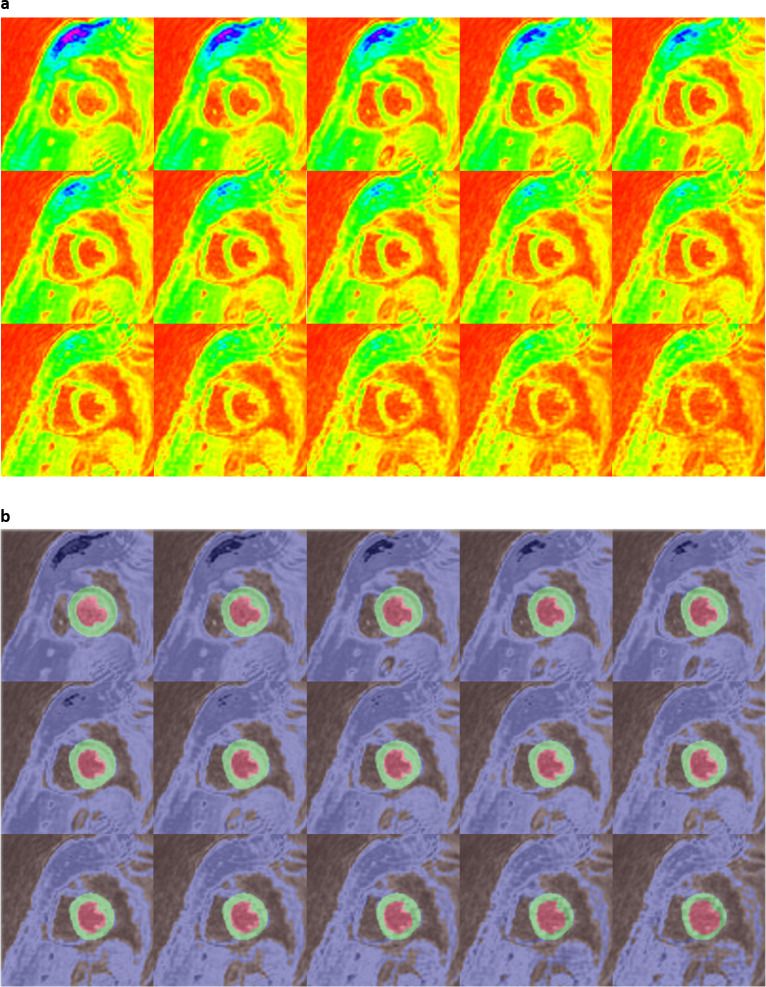
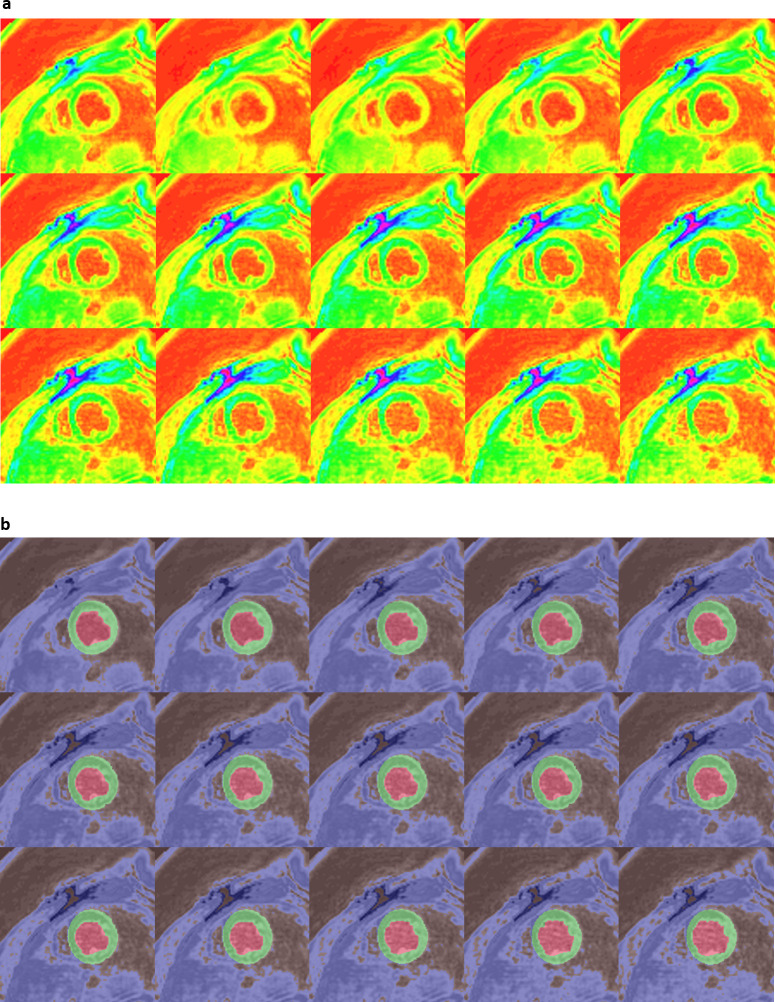
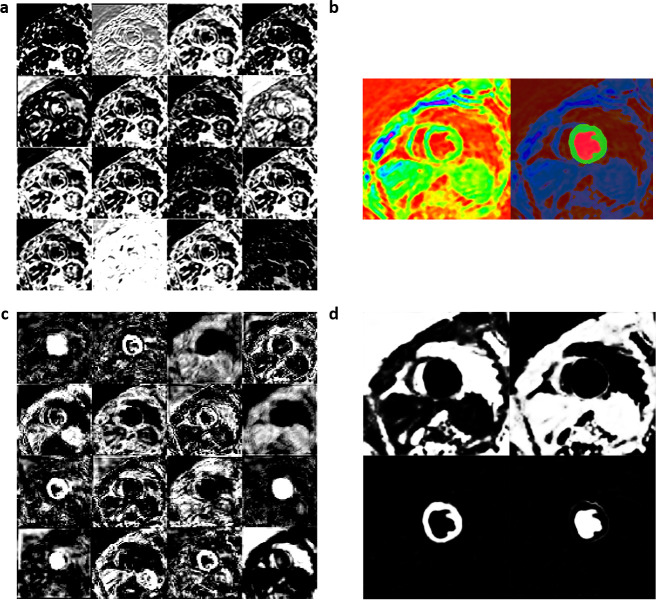
We achieved final training accuracies above 90% and cross-entropy losses less than 0.1 after 60 epochs and 5140 training iterations for each of the 3 DCNNs. The approximate training durations for the DCNNs with ResNet-50-M, ResNet-50-A and ResNet-50-N were 10.32 h, 10.44 h and 10.26 h, respectively, as performed in a Windows environment with training specifications outlined earlier in the Methods. Additional time spent on semantic segmentation of the independent test-set was 0.3–0.4 s per image. Table 2 shows the results of validation against ground-truth, where it is seen that a mean pixel classification accuracy of 95% (based on the four classes) was achieved from segmenting the test-set with ResNet-50-M as backbone in the DCNN. It was followed by mean pixel accuracies of 94% with ResNet-50-A and 90% with ResNet-50-N for backbones. Table 2 also shows that the sensitivity and specificity results (96 and 100%) of myocardium segmentation in the test-set was the highest with ResNet-50-M. Figure 2a, b shows the ROC acquired for each class from segmenting all test-set images with ResNet-50-M and ResNet-50-A, with AUC results for both networks approximately equal to 1.0 for CC, CW, and myocardium and equal to 0.98 for LVC. The AUCs from segmentation with ResNet-50-N were approximately equal to 1.0 for CC and myocardium, 0.99 for CW and 0.98 for LVC (Figure 2c). Additionally, we determined the predictive statistics of each DCNN for labeling pixels in all test-set and validation-set images by confusion matrix as shown in Figure 2 and Supplementary Material 1. It is seen from the confusion matrices that for predicting the myocardium, the test-set exhibited a recall of 96.3% and precision of 88.2% when segmented with ResNet-50-M, a recall of 94.5% and precision of 86.3% with ResNet-50-A, and a recall of 93.4% and precision of 80.0% with ResNet-50-N. For predicting LVC, both precision and recall (91.2 and 93.4%) were >90% with ResNet-50-M compared to either lower precision with ResNet-50-A or lower recall with ResNet-50-N (Figure 2). Figure 3a shows a series of mid-ventricular RGB images in a validation-set patient from the systolic period and Figure 3b shows the corresponding labels predicted by the DCNN with ResNet-50-M on that slice. Figure 4a, b show similar RGB images from the systolic period and predicted labels in a test-set patient. Shown in Figure 5a are some of the activations of the convolutional layer, Conv1 (in Figure 1), during a forward pass, which followed the RGB image inputs to the DCNN with ResNet-50-M. Conv1 is the first convolutional layer of the DCNN whose filter weights (γ in Eqn. 1) are initialized by the LoG function given in Eqn. 2 and the activations are computed by the convolution (dilation factor = 1) given in Eqn. 1a. During backpropagation, the differences between the forward and backward activations are computed to estimate the loss function and its derivatives given by Eqn. 1, according to which the layer’s weights and biases are then updated. Figure 5b shows the corresponding RGB image of the LV and its output label. Figure 5c shows the scorer layer input activations, which are scored and upsampled for input to the final softmax layer, and Figure 5d shows the output activations of the softmax layer for the four classes. The activations are computed according to the softmax function, θ in Eqn. 5a, and each pixel’s final label is based on the maximum of θ evaluated for it according to the four classes. During training the softmax cross-entropy loss is computed and backpropagation starts from estimating the derivatives of softmax and loss with respect to the input, which is given in Eqn. 5.

Table 2.

(a) Validation metrics of segmenting dense LV images with modified resnet-50-m backbone in DCNN

Segment	Accuracya (%)	Good Contourb (%)	Dice Score	APD (mm)	Hausdorff Dist. (mm)	Sensitivity (%)	Specificity (%)
(a)
Validation Set
Chest cavity	94	100	0.96 (0.02)	1.6 (0.6)	15.3 (3.8)	94 (3)	96 (4)
Surrounding frame	95	99	0.93 (0.04)	2.7 (1.1)	15.7 (3.4)	95 (4)	95 (3)
LV myocardium	98	100	0.93 (0.02)	1.2 (0.4)	5.5 (1.9)	98 (2)	100 (<1)
LV cavity	93	100	0.93 (0.06)	1.0 (0.4)	4.4 (1.2)	92 (5)	100 (<1)
All	95	100	0.93 (0.04)	1.6 (0.8)	10.2 (7.0)	95 (4)	98 (3)
Test Set
Chest cavity	95	100	0.96 (0.02)	1.7 (0.7)	15.2 (3.9)	94 (3)	96 (4)
Surrounding frame	96	98	0.93 (0.04)	2.8 (1.2)	15.8 (3.3)	95 (4)	96 (3)
LV myocardium	97	100	0.92 (0.03)	1.2 (0.4)	5.5 (2.0)	96 (4)	100 (<1)
LV cavity	93	100	0.91 (0.09)	1.1 (0.6)	4.7 (1.9)	92 (6)	100 (<1)
All	95	100	0.93 (0.06)	1.7 (0.9)	10.3 (6.9)	94 (5)	98 (3)
(b)
Validation Set
Chest cavity	95	99	0.96 (0.01)	2.2 (0.9)	14.7 (3.9)	95 (3)	95 (4)
Surrounding frame	95	99	0.93 (0.04)	2.3 (0.8)	15.8 (3.2)	95 (4)	95 (3)
LV myocardium	96	100	0.91 (0.02)	1.7 (0.6)	6.0 (1.7)	96 (3)	99 (<1)
LV cavity	93	100	0.91 (0.07)	1.3 (0.6)	5.5 (1.7)	91 (6)	100 (<1)
All	95	100	0.93 (0.05)	1.9 (0.8)	10.5 (6.5)	94 (5)	97 (3)
Test Set
Chest cavity	95	99	0.96 (0.02)	2.3 (1.0)	14.7 (3.9)	95 (3)	95 (4)
Surrounding frame	94	98	0.93 (0.04)	2.4 (1.0)	15.9 (3.4)	93 (5)	95 (3)
LV myocardium	95	100	0.90 (0.03)	1.7 (0.6)	5.8 (2.2)	94 (6)	99 (<1)
LV cavity	93	100	0.90 (0.10)	1.3 (0.7)	5.8 (1.8)	91 (6)	100 (<1)
All	94	99	0.92 (0.06)	1.9 (0.9)	10.6 (6.5)	93 (6)	97 (4)
(c)
Validation Set
Chest cavity	91	95	0.93 (0.06)	2.5 (1.5)	15.7 (3.2)	90 (7)	94 (4)
Surrounding frame	93	84	0.90 (0.06)	3.9 (2.2)	15.9 (3.4)	94 (6)	91 (5)
LV myocardium	96	100	0.87 (0.05)	1.6 (0.7)	6.7 (2.3)	96 (6)	100 (<1)
LV cavity	87	100	0.87 (0.14)	1.6 (0.9)	5.8 (1.8)	85 (11)	100 (<1)
All	92	95	0.89 (0.09)	2.4 (1.7)	11.0 (6.5)	91 (9)	96 (4)
Test Set
Chest cavity	91	90	0.92 (0.07)	2.8 (2.0)	15.9 (3.2)	90 (8)	93 (5)
Surrounding frame	92	82	0.89 (0.08)	4.1 (2.5)	15.9 (3.3)	92 (8)	91 (6)
LV myocardium	94	99	0.86 (0.08)	1.7 (1.0)	6.9 (2.7)	94 (6)	100 (<1)
LV cavity	85	97	0.85 (0.15)	1.7 (1.2)	5.7 (1.9)	83 (13)	100 (<1)
All	90	92	0.88 (0.11)	2.6 (2.0)	11.1 (6.6)	90 (11)	95 (5)

APD, Average perpendicular distance; DCNN, Deep convolutional neural network.

(b) Validation metrics of segmenting dense LV images with atrous resnet-50-a backbone in DCNN. (c) Validation metrics of segmenting dense LV images with non-atrous resnet-50-n backbone In DCNN.

^aCalculated as the % of correctly identified pixels for a class.

^bCalculated as % of contours with APD < 5mm. (): Standard deviations.

Figure 2.

Pixel-based confusion matrices and ROCs from segmenting the DENSE LV test-set images (N = 2448, 12 sets) with the DCNN and its three backbones consisting of the (a) modified and atrous ResNet-50-M, (b) default atrous ResNet-50-A in DeepLabV3+, and (c) non-atrous ResNet-50-N. Similar results on the validation-set with the three networks are given in Supplementary Material 1. DCNN, deep convolutionalneural network; DENSE, displacement encoding with stimulated echoes; LV, left-ventricular;ROC, receiver operating characteristic.

Figure 3.

(a) Systolic-period 16-bit DICOM-converted RGB input files of a mid-ventricular LV slice from a validation-set patient and (b) corresponding output labels from the modified, atrous ResNet-50-M DCNN. DCNN, deep convolutionalneural network; LV, left-ventricular.

Figure 4.

(a) Systolic-period 16-bit DICOM-converted RGB input files of a mid-ventricular LV slice from a test-set patient and (b) corresponding output labels from the modified, atrous ResNet-50-M DCNN. DCNN, deep convolutionalneural network; LV, left-ventricular.

Figure 5.

Shown from segmentation with the DCNN and its modified ResNet-50-M backbone are: (a) 16 of 64 activations at the output of the first convolutional layer with LoG filters (Conv1 in Figure 1), (b) the corresponding RGB image and its output label, (c) 16 of 256 inputs to the scorer layer for weighted scoring activations (Scorer in Figure 1), (d) the four class-based output activations of the softmax layer (Softmax in Figure 1). DCNN, deep convolutionalneural network; LoG, Laplacian of Gaussian.

Comparison of chamber quantification between DCNN and vendor tool

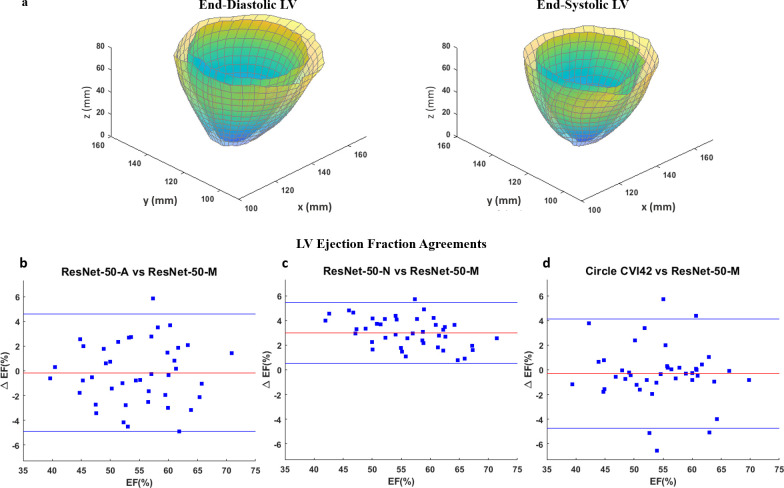
Table 3 shows the results of repeated measures analysis on chamber quantification following segmentation with the DCNN models and Circle CVI42. Significant differences were not found between measurements with ResNet-50-M, ResNet-50-A and Circle CVI42 as seen from the repeated measures p-values in Table 3, which was an important finding related to validating LV segmentation with the atrous DCNNs. Table 3 also shows the results of ICC analysis between the above two backbones and Circle CVI42 for chamber quantification, 3D strains and torsion. An ICC C-Alpha of 0.97 is seen between LVEF estimated with the three techniques, again indicating the soundness of using an atrous network for LV segmentation. In contrast, significant differences were found from the repeated measures analysis on several chamber quantification parameters with the inclusion of the non-atrous ResNet-50-N backbone as shown in Table 3. These differences occurred following EDD and EDV overestimations with ResNet-50-N compared to the other backbones and Circle CVI42. Figure 6a shows the full-LV end-diastolic and end-systolic chamber and cavity dimensions estimated in a patient following segmentation with ResNet-50-M. Figure 6b–d shows the Bland–Altman agreements between LVEF estimated from segmentation with ResNet-50-M and the other two backbones, ResNet-50-A and ResNet-50-N, and Circle CVI42.

Table 3.

LV chamber quantification and strain analysis with three DCNN versions and vendor tool

Parameter	Deep learning Resnet-50-Ma	Deep learning Resnet-50-Aa	Vendor toolb	Deep learning Resnet-50-Na	P valuec	P valued	ICCe
LV EDD (cm)	4.6 (0.3)	4.6 (0.3)	4.6 (0.4)	4.8 (0.3)	<0.01	0.7	0.87
LV ESD (cm)	3.2 (0.3)	3.2 (0.3)	3.2 (0.3)	3.2 (0.3)	0.2 GG	0.5	0.91
LV EDV (ml)	112 (14)	112 (12)	112 (11)	118 (12)	<0.01	0.8	0.85
LV ESV (ml)	50 (10)	51 (9)	51 (9)	50 (9)	0.4 GG	0.7 GG	0.91
LV SV (ml)	62 (12)	61 (11)	61 (10)	68 (11)	<0.001 GG	0.7 GG	0.93
LV EF (%)	55 (7)	54 (7)	54 (7)	58 (6)	<0.001 GG	0.6 GG	0.97
LVM (gm)	120 (8)	120 (6)	119 (6)	123 (7)	<0.05 GG	0.4	0.84
Global Err (%)	33 (3)	33 (2)	33 (3)	33 (4)	0.4	0.4	0.78
Global Ecc (%)	−21 (2)	−21 (2)	−21 (2)	−21 (3)	0.4	0.6	0.89
Global Ell (%)	−15 (2)	−15 (1)	−15 (2)	−16 (2)	<0.05 GG	0.5	0.59
Apical Torsion (o)	6.9 (2.0)	7.2 (1.6)	7.1 (1.8)	8.0 (2.1)	<0.05 GG	0.4	0.84

DCNN, Deep convolutional neural network; EDD, End-diastolic diameter; EDV, End-diastolic volume; EF, Ejection fraction; ESD, End-systolic diameter; ESV, End-systolic volume; Ecc, Global circumferential strain; Ell, Global longitudinal strain; Err, Global radial strain; LVM, LV mass; SV, Stroke volume.

^aEstimated with the modified, atrous Resnet-50-M, the atrous Resnet-50-A, and the non-atrous Resnet-50-N.

^bEstimated with Circle CVI42.

^cFrom repeated measures analysis with Resnet-50-M, Resnet-50-A, Resnet-50-N and CircleCVI42.

^dFrom repeated measures analysis with Resnet-50-M, Resnet-50-A and Circle CVI42. GG Reported with the Greenhouse-Geisser test ofwithin-subjects effects.

^eICC: Intraclass correlation coefficient computed with the Cronbach’s Alpha index between Resnet-50-M, Resnet-50-Aand Circle CVI42, range: 0-1. (): Standard deviations.

Figure 6.

(a) Reconstructed end-diastolic and end-systolic LV geometries generated for chamber quantification from segmentation of DENSE short-axis slices with the DCNN and its modified ResNet-50-M backbone. Agreements between LVEF estimated with the modified, atrous ResNet-50-M backbone in the DCNN and (b) default, atrous ResNet-50-A and (c) non-atrous ResNet-50-N backbones in the DCNN and (d) Circle CVI42. DCNN, deep convolutionalneural network; DENSE, displacement encoding with stimulated echoes; LV, left-ventricular;LVEF, left-ventricular ejection fraction.

Discussion

In this study, we designed and validated a new, automated DCNN-based segmentation methodology for the chamber quantification required in strain analysis during LV contraction. The training and testing were conducted in a subpopulation of breast cancer patients whose LV strains are tracked to observe the possibility of cardiotoxicity occurrence. As our study was conceptualized due to the necessity for automated chamber quantification before strain analysis, the DCNN model created for segmenting the DENSE images is novel. To determine an optimal design, three different DCNNs were modeled and trained, without atrous convolution (ResNet-50-N), with atrous convolution (ResNet-50-A), and atrous with modifications (ResNet-50-M) consisting of LoG filtering for edge detection and elimination of max-pooling for strided convolution. The results show that the DeepLabV3 +DCNN with ResNet-50-M backbone performed better than the others toward meeting the segmentation challenges. In the context of performance, we first consider how previous studies have used different machine-learning and CNN approaches on SSFP MRI to meet the challenges of segmenting the myocardium, examples of which are DCNN approaches in combination with auto-encoders for multiclass classifications, RNN and other techniques.^{10,18,19,26,38,39} It is noted that due to the unprecedented nature of segmenting DENSE images, we can only compare our encoder–decoder and atrous convolutional model to similar SSFP-based machine-learning approaches. Among the earlier neural network approaches for segmenting the myocardium in cine SSFP MRI, some earned top results at the Automatic Cardiac Diagnosis Challenge (ACDC) contest.^22,23,26,78 State-of-the-art segmentation results verified on the ACDC cardiac data set include accuracies of 0.96 achieved by Khened et al⁷⁸ (Random Forest algorithm), and 0.92 by both Cetin et al²³ (Support Vector Machine (SVM)) and Isensee et al²² (Random Forest).²⁶ Another earlier study, by Emad et al³⁹, targeted improving the automatic localization of differently sized LVs in short-axis MRI images by using a six-layer DCNN and a fully connected softmax layer, and tested it on a publically available database of 33 patients. They used pyramids of scales to augment the differently sized LVs (similar to the ASPP approach in our study) and obtained 98.7%, 83.9% and 99.1% for accuracy, sensitivity and specificity, respectively. Comparable to the above high values is the accuracy of 97% obtained from segmenting the myocardium with ResNet-50-M, which substantiates the use of atrous convolution and the modifications applied. Machine-learning has also been applied toward accurate cardiac segmentation that guides diagnosis and therapy management, with previous studies aimed at detecting myocardial infarction (MI).²⁵ In a MRI study by Zhang et al²⁵ to develop a fully automatic framework for chronic MI delineation via deep-learning on non-contrast cardiac cine data, differences were not found between the non-enhanced and late gadolinium-enhanced (LGE) analyses in per-patient MI area (6.2 vs 5.5 cm², p = 0.3). With similar statistical analysis, we have shown that LVEF obtained with the atrous networks (ResNet-50-M and ResNet-50-A backbones) were not different from measurements with a non-DCNN tool, Circle CVI42 (55% vs 54% vs 54%, p = 0.6). Recently, Bai et al²⁰ conducted a study on automated segmentation with a fully convolutional network on a large-scale cardiac data set from the UK Biobank. In a 600-subjects test-set, the authors showed that the difference in performance metrics of LV segmentation was insignificant between a subgroup with cardiovascular diseases (Dice = 0.87) vs the entire set of healthy subjects and patients (Dice = 0.88). In this study, the Dice score similarities between the networks with ResNet-50-M (Dice = 0.92) and ResNet-50-A (Dice = 0.9) backbones show the consistency of segmenting with atrous convolution on the same data.

Next, we discuss the unique outcome of our novel, fully automated deep-learning framework for detecting the myocardium in an original DENSE data set. From the training completion times given in the Results, a modest gain in network speed (~0.12 h or 1%) is observed from replacing the max-pooling layer in ResNet-50-M. This small difference is attributed to replacing just one max-pooling layer with strided convolution in a network of 200 plus layers.⁴ However, this replacement did contribute partly to improving accuracy as outlined in the Results, seen from Table 2, and discussed next. Using an independent test-set, it was shown that the ResNet-50-M (Table 2a) performed better than the others with accuracy = 97%, Dice = 0.92, APD = 1.2 mm, and GC = 100% for segmenting the myocardium. These results show that our deep-learning approach can detect the presence, position, and size of the myocardium in a cohort of breast cancer patients, a fraction of whom have confirmed cardiotoxicity. Similarly, it is seen from the test-set means of the four classes in Table 2a (accuracy = 95%, Dice = 0.93, APD = 1.7 mm, and GC = 100%) that ResNet-50-M performed better than the other two networks in overall segmentation. The benefit of using the ResNet-50-M with enhanced features is also observed from its confusion matrix in Figure 2 where both recall and precision for predicting LVC is >90%. In comparison, the lower precision with ResNet-50-A indicates that a higher portion of pixels retrieved as LVC was actually of a different class, and the lower recall with ResNet-50-N indicates a low extent of LVC pixels retrieved as itself with the rest assigned a different class (Figure 2). Furthermore, the achieved high sensitivity, specificity, and AUC for detecting the myocardium are due to the DCNN framework’s output of a dense vector with classification probabilities for each input pixel. Hence, we were able to obtain the desired output resolution (same as that of the input layer) by applying the decoder’s upsampling to features extracted from the ResNet-50-M backbone and ASPP block.^3,4 Via the use of atrous sampling, the enhancements and the decoder, our study has benefited from the vast development in deep-learning, which is acknowledged for its superior performance in a broad range of medical image analysis.^5,6,9,79 Then, in the tradition of previous studies that harnessed cardiac deep-learning and reported their results, we reported ours with the performance metrics on systolic period, frame-wise LV segmentation in a heterogeneous (with and without cardiotoxicity) patient group. In this context, our MATLAB-based DCNN code is open-source and accompanied by sample data sets, with which (or other similarly acquired DENSE data) one can assess the performance of our network tool.

The LV chamber quantification and strains from segmentation with all three network were analyzed and validation tests were conducted following similar parameter estimations with Circle CVI42.^62–64 Therefore, in addition to the ground-truth validations shown in Table 2, we also undertook validations via repeated measures and ICC analyses as shown in Table 3 to establish the soundness of our automated DCNN-based approach. The chamber quantification and strain computation results in Table 3 demonstrate the saving of valuable operator time and manual effort when computation is automated with DCNN-based segmentation. It is deduced from the similarities in chamber quantification and ICC results between the atrous models and Circle CVI42 (p = 0.6, C-Alpha = 0.97 for LVEF and p = 0.7, C-Alpha = 0.87 for EDD) that the high segmentation accuracies seen in Table 2 contributed to the repeatability and reliability of our methodology. The small percentage of inaccuracies occurred in the very early or later systolic period phases when the DCNN failed segmentation due to a lack of contrast between the myocardium and surrounding tissue or cavity.^80,81 These inaccuracies were quickly and automatically tracked from the accuracy reports of semantic segmentation on individual slices and manually adjusted before chamber quantification. The chamber quantification results (LVEF = 58%) from the network with ResNet-50-N were significantly different in comparison to the similarities between the atrous approaches and Circle CVI42 (LVEF = 55%, 54%, 54%, p = 0.6), which followed the lower accuracy and precision of the non-atrous segmentation. The low Bland–Altman agreement limits (<5%) for LVEF in Figure 6 between the ResNet-50-M and both ResNet-50-A and Circle CVI42, and the ICCs achieved for global strains (Table 3) show there is consistency in our methodology. Thus, the above findings show the benefits of using a network with atrous convolution, LoG filters and elimination of max-pooling. From background research on LV strain ranges in cardiotoxicity, we found previous studies that reported similar low (dysfunctional) strains when CTA doses of anthracyclines and trastuzumab were administered in breast cancer patients.^42,54,82,83 These previous studies also reported reductions in peak systolic longitudinal strains down to ~16% without seeing substantial LVEF reductions.^52,82 The reduced strains and torsions found are also similar to results in recent studies we conducted on cardiotoxicity (with a quantization-based approach for detecting the LV myocardium), which support the viability of strain analysis via the DCNN-based segmentation method.^45,46

The first limitation of this study is that backbone networks such as Xception, Inception, ResNet-101, U-Net and others were not tested for LV segmentation.^3,4,17,28 The authors of DeepLabv3 +have shown that some of these other networks (as standalone or in combination) can improve the accuracy of feature recognition with sharper edge detections. A second limitation is that with cine DENSE only a portion of the cardiac cycle is imaged, which is during the systolic period.^43,45,46,61 Hence, we could not determine the performance accuracies of our network for detecting the diastolic contours, which would be possible if the acquisitions were SSFP-based.^20,22,23,84 We may see a better performance if more cardiac phases from the full cardiac cycle are obtainable in the future with DENSE. A third limitation is that ground-truth contours of the endocardium and epicardium were initially delineated with a semi-automated quantization technique, which could have biased expert decision when they used the preliminary quantized contours for labeling.^45,46,64 A final limitation is that DENSE image segmentation with Circle CVI42 is not fully automated and required considerable manual interventions. The likely reason for this is the presence of black blood in DENSE images compared to the white blood found in SSFP, which is the default sequence for feature-tracking in Circle CVI42. However, finding the exact cause behind this limitation requires investigating vendor-specific information, which lies outside the scope of our current study.

Conclusion

This study introduced a novel DCNN architecture with a modified, atrous ResNet-50 backbone to automate LV myocardium segmentation in DENSE acquisitions for chamber quantification. The primary goal was accurate and automated chamber quantification for LV strain analysis in a subpopulation of breast cancer patients susceptible to chemotherapy-related cardiotoxicity. The goal was met following validation that compared chamber quantification between three different architectures of ResNet-50 in the DCNN and an existing vendor tool, and the study findings show cardiac dysfunction in the patient subpopulation that may occur following chemotherapy. In conclusion, the findings emphasize that automated segmentation with the modified, atrous DCNN provides accurate estimates of the LV chamber quantification required for strain analysis.