The influence of small field output factors simulated uncertainties on the calculated dose in VMAT plans for brain metastases: a multicentre study

Abstract

Objectives:

This multicentric study was carried out to investigate the impact of small field output factors (OFs) inaccuracies on the calculated dose in volumetric arctherapy (VMAT) radiosurgery brain plans.

Methods:

Nine centres, realised the same five VMAT plans with common planning rules and their specific clinical equipment Linac/treatment planning system commissioned with their OFs measured values (OFbaseline). In order to simulate OFs errors, two new OFs sets were generated for each centre by changing only the OFs values of the smallest field sizes (from 3.2 × 3.2 cm² to 1 × 1 cm²) with well-defined amounts (positive and negative). Consequently, two virtual machines for each centre were recommissioned using the new OFs and the percentage dose differences ΔD (%) between the baseline plans and the same plans recalculated using the incremented (OFup) and decremented (OFdown) values were evaluated. The ΔD (%) were analysed in terms of planning target volume (PTV) coverage and organs at risk (OARs) sparing at selected dose/volume points.

Results:

The plans recalculated with OFdown sets resulted in higher variation of doses than baseline within 1.6 and 3.4% to PTVs and OARs respectively; while the plans with OFup sets resulted in lower variation within 1.3% to both PTVs and OARs. Our analysis highlights that OFs variations affect calculated dose depending on the algorithm and on the delivery mode (field jaw/MLC‐defined). The Monte Carlo (MC) algorithm resulted significantly more sensitive to OFs variations than all of the other algorithms.

Conclusion:

The aim of our study was to evaluate how small fields OFs inaccuracies can affect the dose calculation in VMAT brain radiosurgery treatments plans. It was observed that simulated OFs errors, return dosimetric calculation accuracies within the 3% between concurrent plans analysed in terms of percentage dose differences at selected dose/volume points of the PTV coverage and OARs sparing.

Advances in knowledge:

First multicentre study involving different Planning/Linacs about undetectable errors in commissioning output factor for small fields.

Introduction

In the last ten years volumetric modulated arc therapy (VMAT) has gained popularity and intra cranial stereotactic radiosurgery VMAT treatments are routinely performed in both leading academic medical centres and in smaller, non-academic centres.¹ Stereotactic Radiosurgery (SRS) procedures use small radiation fields leading to a possible increase of dosimetric uncertainties.²

Accurate characterization of small fields is challenging due to the lack of lateral electronic equilibrium, the partial occlusion of the finite radiation source, the perturbation of the charged particle fluence caused by the detector, the high dose gradients and peaked dose distributions. Therefore, a good practice for small field dosimetry is to select suitable detectors and to take into account their perturbation correction factors.³ As regards the latter, Alfonso et al introduced a specific formalism.⁴ Interestingly, a new code of practice was published⁵ which offered comprehensive data on all of the detectors available on the market at that time and their correction factors. According to this code of practice, after applying the appropriate correction factor, more than one detector must be used in order to verify the consistency of the measurements. Moreover, for an accurate experimental determination of small field output factors (OFs),^6,7 it is essential to verify the calculated small field OFs in order to identify potential dose discrepancies.⁸

Although the topic of small field OF measurements has been widely investigated in the literature,^9–16 few studies have assessed how inaccuracies in the measurement of small field OFs affect treatment planning system (TPS) dose calculation accuracy in clinical cases.^7,8,17,18

The purpose of this work is to evaluate, in the context of large multi centre study, how undetectable errors in the measurement of small fields OFs values can affect the accuracy of dose calculations in VMAT brain radiosurgery treatments. To this aim, two new OFs sets were generated for each TPS/centre by varying the small field OFs values into known amounts (positive and negative). Consequently, differences between the original plans (that used the OF_baseline set) and the same plans recalculated using two new virtual machines and configured with the incremented (OF_up) and decremented (OF_down) OFs values, were analysed.

Methods and materials

Nine centres, with teams of expert medical physicists capable of performing SRS plans using VMAT techniques, participated in the study. For this study, we decided to use VMAT technique only because is potentially more sensitive to the variation of small fields output factors respect to easier techniques, in terms of fields complexity, such as IMAT (conformal arc therapy) or the use of stereotaxic cones.¹⁹ Details of the TPSs, linacs, MLCs, detectors and OFs set-up measurements are reported in Table 1.

Table 1.

Patients, lesions number and size, prescription dose, VMAT techniques, PTV and OARs dose–volume constraints for plans optimization

# Patient	# Lesions	Size of lesions	Prescription dose	VMAT techniques	Planning rules
					PTV coverage	OARs		Constraints
1	1	d = 8 mm, V = 0.3 cm3	36 Gy in three fractions	Five non-coplanar arcs	V100% = 95%	Brainstem	V18Gy<0.5cc		V23.1Gy ≤0.035cc
2	1	d = 1 cm, V = 0.4 cm3	27 Gy in three fractions	Five non-coplanar arcs		Brain	-		V28.8Gy <3–7cc
3	1	d = 2 cm, V = 1.5 cm3	27 Gy in three fractions	Five non-coplanar arcs		Cord	V18Gy<0.35cc		V21.9Gy ≤0.035cc
4	1	d = 3 cm, V = 9 cm3	35 Gy in five fractions	Five non-coplanar arcs		Opt. Pathway	V15.3Gy <0.2cc		V17.4Gy ≤0.035cc
5	3	d1 = 2.2 cm, V1 = 3.3 cm3 d2 = 2.5 cm, V2 = 7.7 cm3 d3 = 1.7 cm, V3 = 2.8 cm3	27 Gy in three fractions	Six non-coplanar arcs (single isocentre)

#: number d: diameter; V: volume

All of the centres, measured OFs according to the IAEA TRS-398 code of practice and to type-specific TPS/linac reference conditions. Using the different next-generation detectors, small fields measurements were taken and analysed in terms of ratio of detector readings according to the formalism proposed by Alfonso.⁴ Correction factors were not considered, since each TPS was commissioned before the factors were available in the literature. A good agreement between calculated and measured OFs was reported during the beams modelling by each centre, in accordance with international methodological recommendations.^20–22

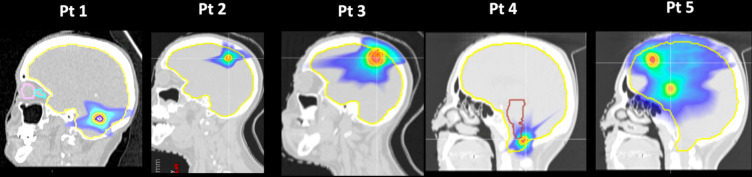
Five patients were enrolled in the study, four with single brain metastases and one with multiple metastases, in order to diversify the cases in size and position. The relative CT images and structures were converted into Dicom-RT format and shared between all of the participating centres. Of note, data uncertainties in RT structures should be taken into account as different software were used in the study. A strongly dependence was reported from the initial phantom’s voxel resolution (0.1 × 0.1 × 1 mm) and the boundary locations algorithm as well.²³ Here, the maximum variation in the volumes of lesions among centres was within 5% showing that the used computational phantom’s resolution was suitable to be shared for a correct reconstruction by all TPSs. Every centre developed a plan for each patient (defined here ‘baseline’ plan) using their clinical equipment Linac/TPS (therefore their OF_baseline values) and common planning rules: dose prescription to the tumour and organs at risks (OARs) constraints all satisfied (Table 2), VMAT planning beam geometry (five and six non-coplanar arcs), dose calculation grid (1 mm), isocentre position and beam energy (6 MV). Patients and planning characteristics are reported in Figure 1 and Table 1. The immobilization equipment was carefully contoured and each Houfield unit (HU) value was converted to mass density via linear interpolation of the mass density-to-HU calibration curve clinically commissioned in each centre.

Table 2.

TPSs, Linacs, MLCs and OFs measurements details of the enrolled centres

TPSs

LINACs/MLCs

OFs MEASUREMENTS DETAILS

Centres

Type

Version

Algorithm

Type

MLC

MLC leaves number/width (mm)

Maximum collimator field size (cm2)

JTT

Set- up

Fields size definition

Detector used for small fields

Minimum field size measured & commissioned (cm2)

1

Monaco  (ElektaAB, Stockholm, Sweden)

5.11.02

MC

Synergy  (Elekta)

Agility  (Elekta)

160/5

40 × 40

YES

SSD = 90 cm  Depth = 10 cm

MLC (transversal)  Jaws (longitudinal)

CC01 (IBA)

1 × 1

2

Pinnacle (Philips Radiation Oncology Systems, Fitchburg, WI)

9.10

CCC

Synergy (Elekta)

Beam Modulator (Elekta)

80/4

16 × 21

NO

SSD = 90 cm Depth = 10 cm

MLC (jaw fixed to 16 × 21 cm)

Gaf Chromic EBT3 film

0.8 × 0.8

3

Pinnacle (Philips Radiation Oncology Systems, Fitchburg, WI)

9.10

CCC

Trilogy (Varian)

HD 120 (Varian)

120/5–2.5

40 × 22

NO

SSD = 90 cm Depth = 10 cm

MLC +Jaws

CC01 (IBA)

1 × 1

4

Eclipse (Varian Medical Systems, Palo Alto, CA)

13.7

AAA & Acuros

True Beam (Varian)

HD 120 (Varian)

120/5–2.5

40 × 22

YES

SSD = 100 cm Depth = 5 cm

MLC

Diode E (PTW)

1 × 1

5

Pinnacle (Philips Radiation Oncology Systems, Fitchburg, WI)

16

CCC

Synergy (Elekta)

Agility (Elekta)

160/5

40 × 40

YES

SSD = 90 cm Depth = 10 cm

MLC +Jaws

Microdiamond (PTW)

1 × 1

6

Ray Station (RaySearch Laboratories, Stockholm)

7.0

CCC

True Beam (Varian)

HD 120 (Varian)

120/5–2.5

40 × 22

YES

SSD = 90 cm Depth = 10 cm

Jaw

Microdiamond (PTW)

1 × 1

7

Ray Station (RaySearch Laboratories, Stockholm)

7.0

CCC

Axesse (Elekta)

Beam Modulator (Elekta)

80/4

16 × 21

NO

SSD = 90 cm Depth = 10 cm

MLC (jaw fixed to 16 × 21 cm)

TLD100, Gaf Chromic EBT3 film, micro Lion (PTW)

1 × 1

8

Ray Station (RaySearch Laboratories, Stockholm)

7.0

CCC

Synergy (Elekta)

Agility (Elekta)

80/5

40 × 40

YES

SSD = 90 cm Depth = 10 cm

MLC (transversal) Jaws (longitudinal)

EDGE Detector (Sun Nuclear)

1 × 1

9

Pinnacle (Philips Radiation Oncology Systems, Fitchburg, WI)

9.10

CCC

True Beam (Varian)

HD 120 (Varian)

120/5–2.5

40 × 22

YES

SSD = 100 cm Depth = 10 cm

MLC

Razor (IBA)

1 × 1

MLC, multileaf collimator; OF, output factor; TPS, treatment planning system.

Figure 1.

Patients enrolled in the study.

For each centre, two new sets of OFs values were generated by changing only the values of the smallest OFs field sizes with well-defined amounts (up to ±3% of the OFs _baseline). The amounts of variation were established fitting the Sauer model²⁴ to the incremented and decrements new OFs data.

First, the OF_baseline set for field sizes ranging from 1 × 1 cm² to 40 × 40 cm², normalised to 10 × 10 cm², was fitted using the Sauer equation reported also by Cagni et al.⁹ :

$$OF\left(FS\right)=P_{\infty }\frac{{FS}^n}{l^n+{FS}^n}+S_{\infty }\left[1-\exp \left(-bFS\right)\right]$$ (1)

where FS is the field size and P_∞, S_∞, l, b and n are fit coefficients. More specifically, P_∞ represents the maximum primary dose component and S_∞ represents the maximum scatter component. The function was forced to be equal to one at the reference field (OF = 1; FS_Ref = 10 cm) as a boundary condition in the fit. Sets of FIT parameters were calculated using data obtained from all of the centres.

Then, for each centre, the OF_baseline values for field sizes ranging from 3.2 × 3.2 cm² to 1 × 1 cm² were modified up to a maximum of ±3% (the new OF_up and OF_down sets), that is until data were still well fitted by the Sauer model (both visually and numerically (root-mean-square deviation (R²)), in order to simulate hardly detectable errors (Table 3).

Table 3.

Variations of OFs _baseline values, from the field 3.2 × 3.2 cm² to 1 × 1 cm² up to a maximum of + 3% (OF_up set) and a minimum of −3% (OF_down set) for the field size 1 × 1 cm²

Field size (cm2)	Increment of the OFs baseline value (%)	Decrement of the OFs baseline value (%)
3.2 × 3.2	+0.8	−0.8
3.0 × 3.0	+1.0	−1.0
2.4 × 2.4	+1.6	−1.6
2.0 × 2.0	+2.0	−2.0
1.6 × 1.6	+2.4	−2.4
1.0 × 1.0	+3.0	−3.0

A total of 9 With Flattening Filter (WFF) 6 MV beams plus 3 Flattening Filter (FF) Free beams (available only in three centres) were collected and lastly, two new virtual treatment machines were recommissioned for each TPS/centre using the new incremented (OF_up) and decremented (OF_down) values. Maintaining the fixed number of monitor units (μ), each baseline plan, for each centre, was recalculated using the new virtual machines. The percentage dose differences, ΔD (%) defined as $\left(\frac{DuporDdown-Dbaseline}{Dbaseline}\right)\times 100$ between recalculated plans and the relative baseline plans were analysed to assess planning target volume (PTV) coverage and OARs sparing at selected dose/volume points: D_95%, D_80%, D_50%, D_2%and D_{7cc Brain}, D_{mean Brain}, D_{0,1cc Brainstem}, respectively. The Student’s t-test was used to compare the results with a statistical significance level of p ≤ 0.05 value after testing for normality with the Shapiro-Francia test using MedCalc v. 15.8. The same analysis was carried out for plans optimised also with 6 MV FFF energy.

The data were then analysed according to the following factors: patients (size and number of targets), TPSs (algorithms), type of MLCs, and delivery mode (Static Jaw (SJ) vs Jaw Tracking (JT)). A three-way analysis of variance (3w-ANOVA) was performed to determine the F-test statistics; p values of each variance component were computed and a post-hoc Scheffé test (PHSt) was carried out in order to identify intragroup differences or each factor identified as a significant predictor of OFs differences.

Results

On applying Equation 1, the OF_baseline fits showed a coefficient of determination R² = 0.987. The deviation of the OF_up/down from the OF_baseline fitted curves proved to be ≤10% with R² = 0.982 for both the OF_up and OF_down fits.

The absolute percentage dose differences between the recalculated plans and the relative baseline plans at selected dose/volume targets and OAR points, as the mean of the data for all centres and patients, are shown in Figure 2a and b. No statistically significant differences were found for all of the dose–volume points analysed. However, compared to baseline plans, and using 6 MV energy, the treatment plans with OF_down values resulted in higher differences ranging between −1.6% and −3.4% to PTVs and OARs respectively, while plans with OF_up values resulted in lower differences within +1.3% to both PTVs and OARs. When comparing 6 MV FFF and 6 MV beams, slightly higher percentage dose differences were observed for both OF_up and OF_down plans of approximately +0.1% and −1% respectively, with no statistically significant differences between them.

Figure 2.

Average absolute percentage differences between recalculated plans (using the OF_up set and the OF_down set) and the relative baseline plans (with the OF_baseline set) at: 2a) selected dose/volume points: D_95%, D_80%, D_50%, D_2% for the PTV and 2b) D_{7cc Brain}, D_{mean Brain}, D_{0,1cc Brainstem} for the OARs. OAR, organ at risk; OF,output factor; PTV, planning target volume

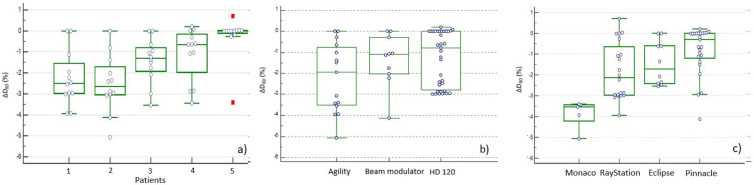
Focusing on the outcome variable ΔD₈₀(%) to PTV, the analysis performed according to the size and number of targets showed statistically significant differences between patient number five and patients’ number 1 and 2 (p < 0.001) (Figure 3a). Moreover, while no statistically significant differences were observed for the three different MLC models (Figure 3b), they were found for the Monaco TPS (Elekta AB, Stockholm, Sweden) (Figure 3c and Table 4) compared to the other TPSs (p < 0.001). The Scheffé test also showed statistically significant differences between RayStation (RaySearch Laboratories, Stockholm) and Pinnacle (Philips Radiation Oncology Systems, Fitchburg, WI) which are both based on the Collapsed Cone Convolution (CCC) algorithm (p < 0.001). No differences were found between the Acuros (AXB) and the Analytical Anisotropic Algorithm (AAA) in the Eclipse TPS (Varian Medical Systems, Palo Alto, CA) therefore the AAA was selected to represent the data. Finally, the analysis on all the plans, showed median ΔD₈₀ (%) values of −0.80% [range (−4.12; 0.71)] and −1.38% [range (−5.06; 0.20)] for the SJ vs the JT delivery mode respectively, with a trend towards a greater variation observed for the JT delivery mode, although not statistically significant (p = 0.14).

Figure 3.

Average percentage dose differences ΔD₈₀ (%) between recalculated plans (using the OF_down sets) and the relative baseline plans (with the OF_baseline set) at dose/volume points D₈₀ for the PTV according to: 3a) size and number of targets volume (patients); 3b) MLC models and 3c) algorithms/TPS. OF, outputfactor; PTV, planning target volume; TPS, treatment planning system

Table 4.

Average percentage dose differences ΔD (%) between recalculated plans (using OF_down sets) and the relative baseline plans at selected dose/volume points: D_95%, D_80% (showed also in Figure 3c), D_50%, D_2% for the PTV and D_{7cc Brain}, D_{mean Brain}, D_{0,1cc Brainstem} for the OARs referred to the four algorithms/TPS

Algorithms	PTV				Brain		Brainstem
	ΔD95%	ΔD80%	ΔD50%	ΔD2%	ΔD7cc (%)	ΔDmean (%)	ΔD0.1cc (%)
MC	−4,4 ± 0,5a,c,d	−3,8 ± 0,7a,c,d	−3,4 ± 0,8a,c,d	−2,6 ± 0,9a,c,d	−0,5 ± 2,5	2,0 ± 2,9a,c,d	−2.4 ± 1.9
								CCC	−1,7 ± 1,4b,c	−1,7 ± 1,4b,c	−1,6 ± 1,4b,c	−1,5 ± 1,5b,c	−2,4 ± 1,2c	−1,6 ± 1,5b	−1.8 ±1.4c
AAA	−1,4 ± 1,1b	−1,4 ± 1,1 b	−1,4 ± 1,1 b	−1,3 ± 1,2 b	−1,8 ± 0,8	−1,5 ± 1,0b	−1.4 ± 1.1
								CCC*	−0,8 ± 1,3b,d	−0,7 ± 1,1b,d	−0,7 ± 1.0b,d	−0,6 ± 1,0b,d	−0,9 ± 1,4d	−0,6±1,2b	−0.6 ±1.2d

TPS Pinnacle TPS RayStation; AAA = Analytical Anisotropic Algorithm, TPS Eclipse; CCC*=Collapsed Cone Convolution, TPS Monaco; CCC = Collapsed Cone Convolution,MC = Monte Carlo;OAR, organ at risk; PTV, planning target volume.

Statistical significance: ^a Test vs AAA; ^b Test vs MC; ^c Test vs CCC* (Pinnacle); ^d Test vs CCC (Ray Station).

Statistically significant differences (p < 0.05) for each algorithm towards the alternative ones are also reported.

Discussion

In volumetric modulated arc therapy (VMAT) the accuracy of dose calculation for treating intra cranial tumours depends on various dosimetric parameters, such as MLC modelling, the calculation algorithm and the field size dependence of small field output factors.^9,16 This is the first large multicentre study to evaluate the impact of each parameter on calculated doses, through purposely generated inaccuracies of OFs values.

Azimi et al evaluated the effect of modifying small field OF values (for the fields 2 × 2 cm² and 3 × 3 cm²) commissioned in a single TPS (Pinnacle) by a considerably amounts,±5%, ±10% and ±20%, from the measured values.⁶ It was observed that the extent of the discrepancy between measured and calculated intensity modulated radiotherapy (IMRT) plans depends on the jaw tracking ability of the accelerator. Kairn et al also investigated the effects of a set of OFs, acquired using an inaccurate detector, on planned doses.⁷ They concluded that errors in excess of 10% may occur in radiotherapy treatments using fields smaller than 15 mm, if accurate data measurements are not acquired. Interestingly, they suggested that the overall clinical effects of inaccurate small field OFs may depend on the shape and volume of the targets (inaccurate OF measurement effects may be overcome when beam segments of various sizes are combined together, but not when treatment plans involve the use of small beam segments).

This study focused on spherical single or multiple targets with volumes ranging from the smallest measuring 0.3 cm³ (Patient 1) to the largest of 9 cm³ (Patient 4). The OF_baseline values for each centre were modified up to a maximum of ±3% for the 1 × 1 cm² field so that the two new OFs sets were still well described by the equation proposed by Sauer with the aim of simulating errors that cannot be easily identified even by a skilled medical physicist. Plans with OF_down sets resulted in higher variation of doses within 1.6 and 3.4% to PTVs and OARs respectively, while plans with OFs_up sets resulted in lower variation of doses within 1.3% to both PTVs and OARs. Our study suggests that slight errors in small field OFs achieve dose calculation accuracies within 3% with discrepancy inversely proportional (but not significant) to the size of the lesions considered (Figure 3a). Our results are in line with Azimi et al,⁶ who found that decreasing/increasing the OFs by 5% resulted in approximately 0.8% higher and 2.9% lower calculated doses respectively.

In order to achieve high accuracy, other authors suggested fixing the jaws above the minimum size and generating shielding and modulation by the MLC, thus disabling the JT technique.^25–27 According to Azimi et al and Sendani et al,^6,17 also our analysis showed a trend towards less dependence from OFs values without Jaw tracking (p = 0.14). We can find a further indication of this by looking at the data represented in Figure 3a: in Patient 5, where all the TPS/MLC had to work with the more open jaws, given the presence of a number of metastases equal to three (single isocenter), the percentage variations of ΔD_80(%) are certainly less than in all other patients with a single lesion.

It is interesting to note that in this scenario Monte Carlo dose calculation algorithm is essential, in fact the Figure 3c shows that Monaco is the most sensitive TPS to OF variations (p < 0.05)²⁸ ;

This was an important confirmation but it doesn't surprise so much because the MC approach is generally considered the gold-standard for determining dose distributions in any medium and it has been used to determine the accuracy of different dose calculation techniques by many authors.^29–32 Also, in the specific context of small fields using an anthropomorphic head phantom, Behinaein et al³³ found the average dose differences between measurements and MC, AAA and AXB equal to 0.2%, 3.2 and 2.7% respectively for small field sizes up to 0.5 × 0.5 cm².

Unlike Mzenda et al,³⁴ who used both RayStation and Pinnacle TPS to develop comparable high-quality treatment plans, in our study small but statistically significant differences were found between the two algorithms in terms of target coverage and OARs sparing (Figure 3c and Table 4) with a trend of RayStation data towards the MC. Although the dose calculation algorithm is the same for both TPSs a different customization of the clinical machine in the physics module could be of importance.

Moreover, by adding a flattening filter weight to the RayStation TPS, Chen et al,³⁵ improved dose calculation accuracy for MLC defined fields to within 2%. In our study, no significant differences were observed in dose accuracy, irrespective of whether the FF component was used or not, however only three of the centres use FF Free beams which may be considered as one of the limitations of the analysis.

A great deal of time and effort was spent collecting the data from nine centers which enabled us to carry out an analysis that allow to highlight various individual factors and this is the true strength of this study. The authors are aware that the final results include various inseparable aspects (individual equipment, single or multiple targets, MLC type, algorithm, FF vs FFF) that may be subject for further investigation in the future.

However, framing the results of this work in the context of their clinical significance, we could say that errors up to ±3% in the measurement of OFs small fields have a small impact on the final dose calculation of VMAT radiosurgery treatment plans; in addition, our data emphasised that a fine algorithm is needed to highlight small uncertainties.

Therefore, our work could define a ‘comfort zone’ within a measurement errors on small fields does not translate into a relevant clinical error. Anyway, the goal of pursuing accuracy in measurements thought the use of suitable detectors and the search for their correction factors, should be the standard for a good clinical practice.

Conclusions

The commissioning process and beam modelling for dosimetric accuracy continues to be a major challenge for medical physicists.³⁰ The aim of our study was to evaluate how OFs undetectable inaccuracies in small fields can affect dose calculation in VMAT brain radiosurgery treatment plans. It was observed that simulated measurement OFs errors (up to ±3%) on small fields does not translate into a relevant clinical error. These errors are purely calculation based and do not take into account any machine related daily fluctuations or deviations from the commissioning data that might have occurred over time.