Disentangle, align and fuse for multimodal and semi-supervised image segmentation

Abstract

Magnetic resonance (MR) protocols rely on several sequences to assess pathology and organ status properly. Despite advances in image analysis, we tend to treat each sequence, here termed modality, in isolation. Taking advantage of the common information shared between modalities (an organ’s anatomy) is beneficial for multi-modality processing and learning. However, we must overcome inherent anatomical misregistrations and disparities in signal intensity across the modalities to obtain this benefit. We present a method that offers improved segmentation accuracy of the modality of interest (over a single input model), by learning to leverage information present in other modalities, even if few (semi-supervised) or no (unsupervised) annotations are available for this specific modality. Core to our method is learning a disentangled decomposition into anatomical and imaging factors. Shared anatomical factors from the different inputs are jointly processed and fused to extract more accurate segmentation masks. Image misregistrations are corrected with a Spatial Transformer Network, which non-linearly aligns the anatomical factors. The imaging factor captures signal intensity characteristics across different modality data and is used for image reconstruction, enabling semi-supervised learning. Temporal and slice pairing between inputs are learned dynamically. We demonstrate applications in Late Gadolinium Enhanced (LGE) and Blood Oxygenation Level Dependent (BOLD) cardiac segmentation, as well as in T2 abdominal segmentation. Code is available at https://github.com/vios-s/multimodal_segmentation.

I. Introduction

IN medical imaging multiple acquisitions of the same subject capture complementary information. Within Magnetic Resonance (MR), different pulse sequences (modalities) attenuate different tissue characteristics to identify anatomical and functional information and produce images of different contrasts. Automatic segmentation of such data remains important and relies on accurate annotations, which however can be expensive to acquire, thus resulting in scarce or imperfectly annotated datasets. To overcome this, many solutions have been proposed for example with the use of unlabelled data [1].

We approach this problem with a method that leverages data from a secondary modality and is based on disentangled representations. Our method is designed to address challenges of multimodal data that include differences in signal intensities, lack of annotated data, and anatomical and temporal misalignments due to varying spatial resolutions or due to moving organs, as in the case of dynamic heart imaging.

Multimodal learning allows capturing of information present in one modality (e.g. the anatomy) for use in another modality that has greater contrast. As a motivating example, myocardial segmentation in LGE is challenging, since LGE nulls myocardial signal to accentuate signal originating from myocardial infarction. In fact, in clinical practice, analysis of LGE is typically combined with cine-MR [3].

A naive way to propagate knowledge between modalities would be co-registration. This has been successful in the brain (see Section II-B) but precise multimodal registration needs modality independent metrics [4] and the brain remains static within an imaging session, whereas the heart is constantly moving. Furthermore, multimodal cardiac data are often inconsistent both in the number of images (different slices, cardiac phases, and perhaps more penalising resolution differences, e.g. slice thickness) and in the number of annotations. In addition, some sequences are static (LGE) and others dynamic (cine-MR). These challenges necessitate solutions that alleviate misregistrations and can pair input images.

A. Overview of the proposed approach

We propose a mechanism that can propagate knowledge for segmentation and can learn with and without annotations using a reconstruction objective as self-supervision. Moreover, our approach co-registers data within an anatomical representation space, becoming thus robust to variations in imaging contrast. Our 2D approach, Disentangle Align and Fuse Network (DAFNet), achieves the above by mapping multimodal images of the same subject into disentangled anatomy and modality factors.¹ At inference time, as Figure 1 shows, DAFNet fuses the disentangled anatomy factors to combine multimodal information and extract segmentation masks.

Fig. 1:

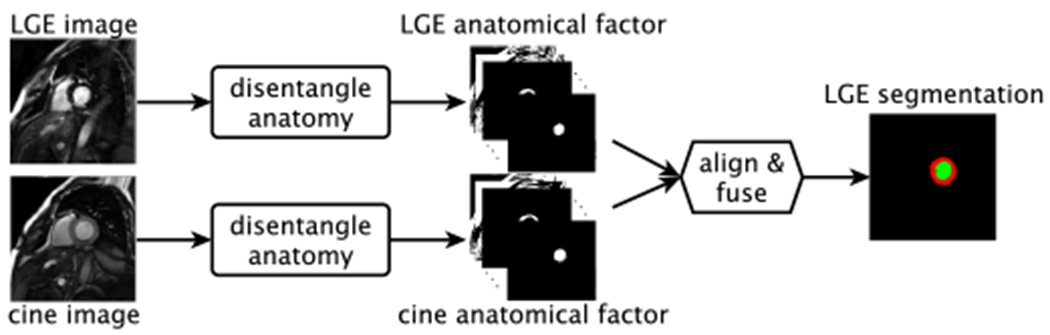
DAFNet schematic in an LGE segmentation exemplar task using LGE and cine-MR inputs. Firstly, disentangled anatomical factors are extracted from the inputs. Then, they are aligned (with a Spatial Transformer [2]) and combined to a fused anatomy that infers the final LGE segmentation. Our approach can use multi-input (multimodal) data at training and inference. The latter is extremely useful when training with zero annotations for an input and also in removing outliers.

Anatomy factors are represented as categorical feature maps with each category corresponding to input pixels that are ideally spatially similar and hence belong to the same anatomical part. This promotes semantic consistency and helps learn spatial correspondences between anatomical parts from different modalities. Modality factors encode pixel intensities in a smooth multivariate Gaussian manifold as per the Variational Autoencoder (VAE) [6]. Anatomy factors are used by a segmentation network to obtain masks, whereas a decoder re-entangles both factors to achieve image reconstruction.

Learning a disentangled representation is encouraged by minimising the information capacity of each factor respectively: thresholding the anatomy factors, which results in binarised discrete feature channels, prevents the storage of image intensity information as continuous values, which impairs disentanglement [7], whereas the variational objective minimises information in the modality factors [8]. Disentanglement is also influenced by the decoder design, either through inductive biases (see discussion in Section III-D and evaluation in Section V-H), or through learning constraints (see cross-modal decoding of one anatomy in the modality of another in Section III-D, similar to [5]).

However, a disentangled representation with modality invariant anatomy factors is not enough for multimodal learning. A multimodal representation also requires similar anatomy factors across modalities, such that each feature channel corresponds to the same anatomical region for any modality. This is achieved by weight sharing in the anatomy encoders, as well as by shared segmentation and decoder networks. These constraints implicitly create common anatomy semantics, which are essential when no labels, but only images, are available for one of the modalities. In this case we project all images to the common anatomical space, where a single segmentation network is trained with supervision only on the annotated modalities. Finally, when input data are not paired a new loss term in the cost function selects the most “informative” multimodal pairs by comparing anatomy factors.²

Our contributions are summarised as follows:

1. We propose a 2D method for learning disentangled representations of anatomy and modality factors in multimodal medical images for segmentation.

2. We demonstrate the importance of semantic anatomy factors, achieved through the model design, since they allow learning registration and fusion operators.

3. We propose a loss term in the cost function that enables the selection of the most “informative” multimodal pairs.

4. We demonstrate our method’s robustness over other approaches with extensive experiments on several datasets, in cardiac MRI and abdominal segmentation.

5. We show that our model works both on single-modal and multimodal inference, and that it outperforms other variants when trained with different amount (semi-supervised) or zero annotations for one of the modalities.

6. We discuss decoder designs using FiLM [10] and SPADE [11] respectively and evaluate disentanglement by estimating the dependence between anatomy and modality factors with distance correlation [12].

II. Related work

Multimodal machine learning is a research area that involves diverse modalities. While in computer vision modalities might refer to heterogeneous sources of information, such as text and images, here, as common in the medical domain, we restrict to different image acquisitions. We consider multimodal learning as combining information from different images, present at training or more critically at inference time. Using image translation or domain adaptation as augmentation strategy to reconcile lack of annotated data also enables training, although not inference, with multimodal images (we term this multimodal inference).³

We review work on disentangled representations, the main focus of our method, and also on multimodal medical imaging, split in spatially registered or unregistered inputs. We further discuss differences between other methods and ours regarding the representation semantics and the approach to fusion, in particular when having misaligned inputs and limited annotations. We highlight that currently no work exists that is able to simultaneously achieve multimodal fusion from unregistered data for segmentation, be robust to the number of training annotations, and be applied to single or multimodal inference.

A. Disentangled representation learning

Disentangling content from style for style transfer is gaining popularity in computer vision with many examples, such as [5]. In medical imaging, disentangled representations have been used for semi-supervised cardiac segmentation [7], [21], multi-task learning [7], [22], lung nodule synthesis [23], and multimodal registration [24]. Disentangling multimodal images has also been used for liver segmentation with domain adaptation [25] albeit without information fusion, and for brain tumour segmentation [26] although using registered images.

For anatomical features to be useful in clinical tasks, they need to be semantic and quantifiable. This is not guaranteed in disentanglement techniques used in style transfer [5] and in medical segmentation [25], [26] that do not impose restrictions on the content features. Semantic representations have recently been pursued in computer vision in the form of feature masks [27] or by learning geometry with landmarks [28]. Instead, we disentangle quantifiable anatomical features so that they are useful in segmentation, whereas interpretability is promoted with explicit design constraints (Section III-A).

B. Multimodal learning with registered images

Early work on multimodal deep learning concatenated co-registered images in different input channels to improve MR brain segmentation [29]. Robustness to missing modalities [30] was achieved with encoders per modality that mapped images to modality invariant features. Common features with multiple encoders was also proposed for cross-modal classification [31].

Another aspect of multimodal learning is information fusion. Most commonly, fusion is performed on latent features [29], [30], although fusion at multiple levels can be achieved with densely connected layers [32] to exploit multiscale correlations. Furthermore, cross-modal convolutions are used to weigh each modality’s contribution [33]. Finally, attention modules and residual learning focus on specific regions for brain MRI segmentation [34]. In contrast to the above, we take advantage of the strictly defined anatomy factors and use a max fusion operator to combine all distinct features.

C. Multimodal learning with unregistered images

Unfortunately, misalignment between multimodal images remains common. Correcting small misalignments is possible with a Spatial Transformer Network (STN) [2] applied on features [30]. Alternatively, encoder-decoder setups can be trained with multimodal data to learn common features. An exploration of different setups [35] showed that separate encoders and decoders sharing their last and first layer respectively, achieve the highest performance.

In cardiac image analysis approaches are limited. Multiple inputs can be combined by adapting segmentation masks with contour models [36], [37]. Alternatively, reducing the field of view (to patch level) and ensembling (fusing results from several atlases) can alleviate the effect of errors [38]. Recently, simultaneous segmentation and registration of multimodal cardiac MR, models the joint distribution as Multivariate Mixtures [39]. Multimodal images can also be used as samples of the same data distribution to form an expanded dataset [40]. Finally, multimodal registration, although susceptible to errors, can create “noisy” labels [41]. Our method is the first to learn a suitable representation for segmentation, co-registration, and information fusion, but in a semi-supervised setting.

III. Methodology

Here we describe DAFNet, a multi-component 2D model for multimodal and semi-supervised segmentation that is illustrated (at training time) in Figure 2. Initially, input images are encoded into anatomy and modality factors (Section III-A). Anatomy factors are aligned (with a STN) and fused (Section III-B), and participate in segmentation losses (Section III-C). Training also employs image reconstruction (Section III-D) and modality reconstruction losses (Section III-E). Finally, a multimodal pairing loss allows to dynamically learn how to pair image sources (Section III-F). Below we detail the individual components, as well as the employed cost functions.

Fig. 2:

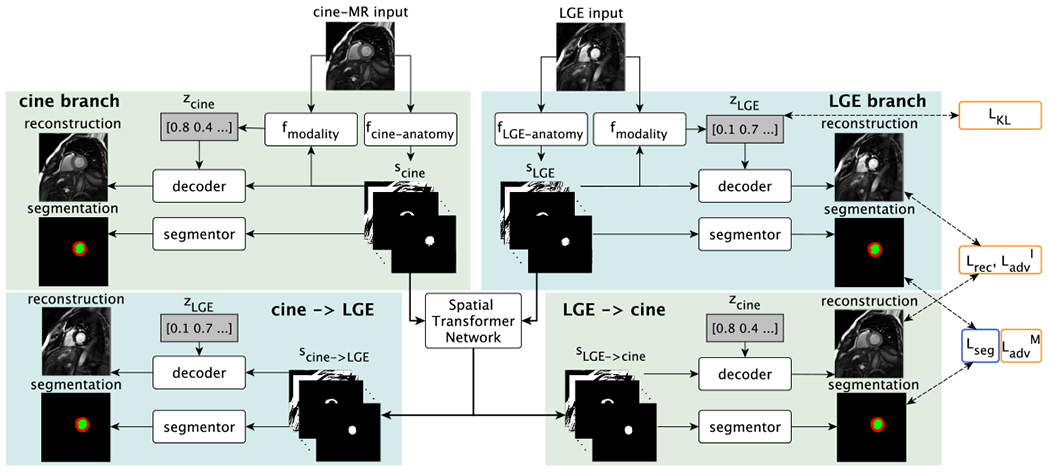
Training schematic with cine-MR and LGE input images. Each input image is disentangled into anatomical and modality factors. With a Spatial Transformer Network the deformation branches (lower parts) enable cross-modal synthesis and segmentation by deforming the anatomy factors s_cine and s_LGE. Losses are indicated on the right and are also symmetrically applied to the cine-MR branch outputs. Yellow or blue outlines indicate if a loss is used when training with zero or full supervision, respectively. $L_{rec}^z$ is not shown. See text for definitions.

A. Encoding into anatomy and modality factors

Given modality i ∈ {M₁,…, M_n} with samples x_i ∈ X_i, where $X_i\subset {\mathbb{R}}^{H\times W}$ is the set of images, and H and W are the height and width respectively, the encoding process achieves a disentanglement of anatomy and modality factors. Anatomy factors s_i are tensors produced by encoders dedicated to each modality i: s_i = f_anatomy (x_i|θ_i), where θ_i are the encoder parameters. The encoder architecture is modelled after the U-Net [42] and is shown in Figure 3a. To reduce model parameters and encourage a common anatomical representation among the multimodal data, we employ weight sharing in the decoder of each U-Net. Thus, parameters θ_i are split into individual parameters ϕ_i of the encoding path, and shared parameters ρ of the decoding path: s_i = f_anatomy(x_i|ϕ_i, ρ).

Fig. 3:

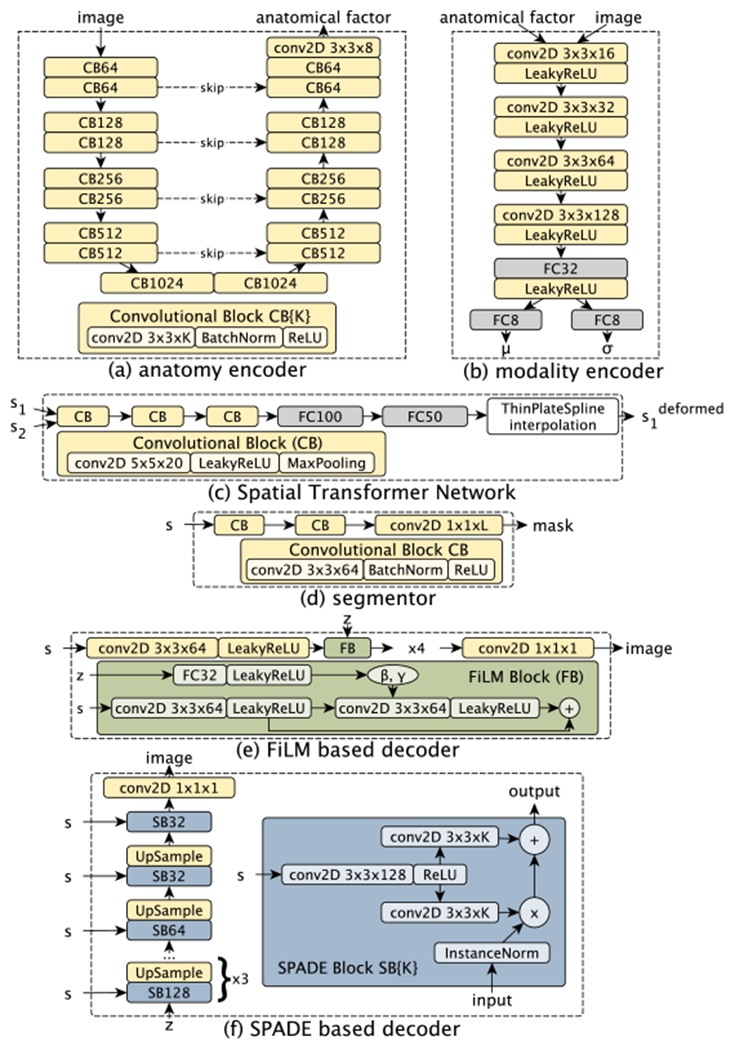
Architecture diagrams of the individual components. (a) Encoder extracts anatomy factors; (b) Modality encoder extracts parameters μ, σ of a Gaussian distribution. The modality factor is a sample from this distribution; (c) The segmentation network produces a mask given an anatomy factor; (d) The Spatial Transformer Network receives two anatomy factors and produces the 2D co-ordinates of 25 control points used for interpolation; (e) Decoder architecture based on FiLM [10]; (f) Decoder architecture based on SPADE [11].

An anatomy factor is represented as a binary tensor that is also a one-hot encoding in the channel dimension. A binary anatomy factor cannot store different pixel intensities of an image as continuous values and this promotes the factorisation process [7]. Furthermore, this one-hot encoding encourages a particular image region to appear in a single channel. More formally, s_i ∈ {0, 1}^H×W×C, s.t. ${\sum }_{c=1}^C{s}_i^{h,w,c}=1\forall h\in \{1,\dots ,H\},\omega \in \{1,\dots ,W\}.$. Two example anatomy factors produced by a cine and a LGE image can be seen in Figure 4.

Fig. 4:

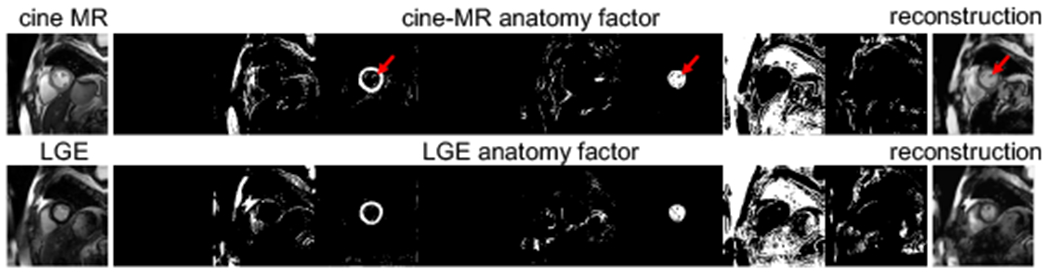
Cine and LGE anatomy factors. Observe that the same anatomical regions appear in the same channels. Also, encoding papillary muscles (marked in red arrows) in myocardium and left ventricle channels allows their reconstruction (which would be impossible if these channels were segmentations).

Although binary, the anatomy factors are not segmentations. Instead they must be useful in segmentation and image decoding tasks described in the following sections.⁴

Divergence loss L_KL:

Our model also decomposes images into a modality factor z_i, which aims to capture intensity and texture characteristics of the input data. The modality factors $z_i\in Z:={\mathbb{R}}^{n_z}$ are vectors produced by a single stochastic encoder, which, given an image sample x_i and its anatomy factor s_i, learns aprobability distribution q(z_i|x_i, s_i). In order to encourage a smooth space and also minimise the encoded information [8], the posterior distribution is optimised to follow a multivariate Gaussian prior, $p\left(z_i\right)=\mathcal{N}(0,\mathbf{I})$, using the K L–divergence and the re-parameterisation trick [6]:

$$L_{KL}=\int p(z_i)\log \frac{p(z_i)}{q(z_i|x_i,s_i)}d{x}_{i}d{s}_i.$$

The modality encoder is shown in Figure 3b and predicts the mean and standard deviation of a Gaussian, which are used to draw a random sample vector z_i = f_modality (x_i, s_i).

B. Alignment and fusion of the anatomy factors

Following factor encoding, two anatomy factors s_i and s_j of modalities i and j respectively, are aligned using non-linear registration. Given a grid of 5 × 5 control points, a STN (architecture in Figure 3c) first predicts the grid’s offsets. Then, thin plate spline interpolates the surface passing through the control points to register s_j with s_i. The result of alignment $s_i^{deformed}$, is a deformed anatomy factor corresponding to s_j and vice versa ($s_j^{deformed}$ corresponds to s_i). We optimise STN with gradients in image space (self-supervised cost of Section III-D) and with the segmentation cost of Section III-C, since we aim to align segmentation masks.⁵

During inference the deformed anatomies are combined to produce a fused representation, containing all unique and shared features that are present in the constituent anatomy factors. Since they are spatially aligned, a pixel wise operation such as the pixel-wise max is able to preserve all encoded features. More formally, $s_i^{fused}=\max (s_i,s_j^{deformed})$ and $s_j^{fused}=\max (s_j,s_i^{deformed})$. One benefit of max-fusion is that it is invariant to the number of inputs and is therefore directly applicable in cases with more than two modalities.

C. Segmentation

Given an anatomy factor s_i, a simple neural network (architecture in Figure 3d) infers a corresponding segmentation mask m_i = h(s_i), s.t. m_i ∈ M_i := {0, 1}^H×W×L, where M_i is the set of masks of modality i and L is the number of segmentation classes. The segmentation network is common for all modalities, is applied to the deformed and fused anatomies of Section III-B and is optimised as follows.

Supervised loss L_sup:

Given a set of images paired with masks (x_i, m_i), a supervised cost is defined as a weighted sum of the differentiable Dice loss and Cross Entropy (CE):

$$L_{sup}=\alpha (1-Dice(h(s_i),m_i))+\beta CE(h(s_i),m_i),$$

where α and β control the contribution of each loss. The cross entropy and differentiable Dice are respectively defined as:

$$CE(h(s_i),m_i)=-\sum _l(m_{h,w,l}\log (p_{h,w,c})),$$

$$Dice(h(s_i),m_i)=2\times \left[\frac{{\sum }_{h,w,c}(h(s_{i_{h,w,c}})\times m_{i_{h,w,c}})}{{\sum }_{h,w,c}(h(s_{i_{h,w,c}})+m_{i_{h,w,c}})}\right],$$

where h, w, and c refer to the height, width and channel, and p_h,w,l is the probability for a pixel belonging to class l.

Adversarial loss $L_{adv}^M$:

An unsupervised segmentation cost is also defined with a mask discriminator D_M, modelled after LS-GAN [43]. The adversarial objective given real masks sampled from all modalities m ~ M_i, i ∈ {1, 2,… n} is:

$$L_{adv}^M=D_M{\left(h\right(s_i\left)\right)}^2+{\left(D_M\right(m)-1)}^2,$$

where the discriminator is adversarially trained against the segmentation network. The discriminator’s architecture consists of 4 convolutional layers followed by LeakyReLU and a final single neuron layer and uses Spectral Normalisation [44] to stabilise training. In both segmentation costs, the anatomy factors s_i come either from the input images directly or are the result of the alignment step of a secondary j modality: $s_i\in \{f_{\mathit{anatomy}}(x_i|{\theta }_i),s_j^{deformed}\}$. In the latter case, the gradients produced by the segmentation cost are back-propagated to the STN module to learn its parameters.⁶

Segmentation losses help learn better anatomy factors that separate the anatomies of interest in respective channels (see myocardium and left ventricle in Figure 4). If supervision is not available for modality i, training is performed with the adversarial loss $L_{adv}^M$. In addition, the deformed anatomy factor $s_i^{deformed}$ participates in the supervised segmentation of another modality j. The latter encourages anatomy factors to be similarly represented across modalities and thus enables unsupervised segmentation of modality i.

D. Decoding

The anatomy factors are further decoded into an output image of a style dictated by a modality factor z_i: y_i = g(s_i, z_i). This factor entanglement can be performed with different decoders, which also indirectly influence the type of disentanglement, or in other words the type of information captured by the anatomy and modality factors. We investigate two decoder architectures based on FiLM [10] and SPADE [11].

The input of the FiLM-based decoder (Figure 3e) is the anatomy factors, which, after a series of convolutions, are conditioned by z samples. These are used to predict a scale and an offset parameter $\gamma \in {\mathbb{R}}^C$ and $\beta \in {\mathbb{R}}^C$, which modulate each intermediate feature map $F\in {\mathbb{R}}^{H\times W\times C}$, where H, W and C are the height, width and number of channels respectively: FiLM(F|γ, β) = F ʘ γ + β.

We also consider a SPADE-based decoder (Figure 3f), which has been demonstrated to generate texture details on synthetic images given segmentation masks. The input to this decoder is a z sample, which is processed by a series of convolutional layers and conditioned by the anatomy factor defining the output “shape”. An Instance Normalisation layer with parameters μ and σ is firstly applied to a feature map $F\in {\mathbb{R}}^{H\times W\times C}$, which is then modulated by tensors Γ and B (same size as F) $\mathit{SPADE}(F|\mathbf{\Gamma },\mathbf{B})=\mathbf{\Gamma }ʘ\frac{F-\mu }{\sigma }+\mathbf{B}$.

Self-supervised costs L_rec and $L_{adv}^{I,i}$:

The decoders are trained to reconstruct the input with the ℓ₁ loss:

$$L_{rec}={\Vert x_i=g(s_i,z_i)\Vert }_1.$$

In addition, synthesis of realistic images is encouraged with an image discriminator D_{I, i} for a modality i, modelled after LS-GAN. This defines an adversarial loss:

$$L_{adv}^I=D_{I,i}{(g(s_i,z_i))}^2+{(D_{I,i}(x_i)-1)}^2.$$

As in the segmentation case, s_i is an encoding of image x_i or a deformed encoding of another image $x_j:s_i\in \left\{f_{anatomy}(x_i|{\theta }_i),s_j^{deformed}\right\}$. When s_i = f_anatomy (x_i|θ_i), the model acts as an auto-encoder. This is critical to allow the use of non-annotated images and thus enable semi-supervised learning. In the case where $s_i=s_j^{deformed}$, the backpropagated gradients train the STN module and also aid the factorisation process (since the “style” of the output image $g(s_j^{deformed},z_i)$ as specified by z_i, corresponds to modality i and not j).

The decoder also participates in the following loss that promotes disentanglement.

E. Reconstruction of the modality factor loss $L_{rec}^z$

In order to encourage disentanglement, and also avoid posterior collapse of the modality factor, we reconstruct the modality factor of a synthetic image. This prevents the decoder from ignoring the z-factors and only use the anatomy factors for image synthesis. We minimise the following loss:

$$L_{rec}^z={\Vert z-f_{modality}(y,f_{anatomy}(y))\Vert }_1,$$

where z is a sample from a unit Gaussian and y is the synthetic image produced by this z sample. Encouraging the use of modality factors by the decoder is further achieved by cross-reconstructing a deformed anatomy in a modality dictated by the corresponding z-factor, as described in Section III-D.

F. Non-expert pairing

Better multimodal fusion and STN registration will be achieved by multimodal image pairs {x_i, x_j} that are more similar in terms of their spatial and temporal positions. In cases where the multimodal images are not expertly paired, we can automatically measure anatomical similarities with an optional cost, which directly compares the anatomy factors, and “selects” only the most informative image pairs.

During training, and given an image x_i and a set of k candidate images from modality $j:\left\{x_j^1,x_j^2,\dots ,x_j^k\right\}$, the multimodal segmentation and reconstruction losses for a sample x_i are weighted accordingly by k weights, s.t. ${\sum }_{l=1}^k{w}_l=1$:

$$L_{\mathit{sup}}=\sum _{l=1}^k{w}_l{L}_{\mathit{sup}}(m_i,m_l),L_{rec}=\sum _{l=1}^k{w}_l{L}_{rec}(x_i,y_l),$$

where $m_l=h(f_{anatomy}(x_j^l)),$, and $y_l=g(s_j^{deformed,l},z_i)$. By weighting the loss functions, the STN module does not need to learn deformations for all pairs, as well as prevents it from trying to match slices with different anatomical content.

Due to the semantics of the anatomy factors, and the fact that they are categorical, we can directly evaluate their overlap in terms of the Dice score. The Dice for each pair, becomes the input to a small neural network of two fully connected layers that outputs the weights, and is similar to the temperature scaling technique proposed for calibrating classification outputs [45]. At inference time, the most accurate m_i segmentation is produced from the weighted sum of the fusion with different slices $s_j^{fused,1},s_j^{fused,2},\dots s_j^{fused,k}$:

$$m_i=w_{1}h(s_j^{fused,1})+w_{2}h(s_j^{fused,2})+\dots +w_{k}h(s_j^{fused,k}).$$

This optional weighting of the cost function is only used in unpaired data, and as shown in experiment V-C converges to the same result as manual pairing.

IV. Experimental setup

A. Training details

The model is trained with a multi-component loss function $L=0.1·L_{KL}+10·L_{\mathit{sup}}+L_{adv}^M+L_{rec}+L_{adv}^I+L_{rec}^z.$ A higher L_sup weight encourages separation of segmentation classes. A reduced L_{K L} weight prevents posterior collapse, in which the decoder ignores the z factor; however, an even lower L_{K L} would not well approximate the Gaussian prior leading to a non-smooth intensity manifold. Number of s channels and z dimensions are set to C=8 and n_z=8 respectively, as in [7].

Code is written in Keras (https://keras.io) and is available at https://github.com/vios-s/multimodal_segmentation along with pseudocode of the training process. We train with Adam (learning rate 10⁻⁴) and use Stochastic Weight Averaging [46] to reliably compare methods. Training takes approximately 12 hours on a Titan-X GPU and inference of one image takes 50 ms. Quantitative evaluation is performed on 3-fold cross-validation, where the training, validation and test sets correspond to 70%, 15% and 15% of the data volumes.

B. Data

Experiments use three multimodal datasets of a source and a target modality that have been rescaled to [−1, 1].

1. For LGE segmentation, we use cine-MR and LGE data of 28 patients [47], acquired at Edinburgh Royal Infirmary (ERI), with spatial resolution 1.562mm²/pixel, and slice thickness 9mm. End diastolic myocardial contours are provided. The image size is 192 × 192 pixels. The number of segmented images is 358 (for each of cine-MR, LGE).

2. To evaluate robustness on different medical data, we use abdominal T1-dual inphase and T2-SPIR images from CHAOS [48] dataset, for T2 segmentation. Images of 20 subjects with liver, kidneys and spleen segmentations are acquired by a 1.5T Philips MRI scanner, which produces 12-bit DICOM images of 256 × 256 resolution. We resample to an x-y spacing of 1.89mm, and crop to 192 × 192 pixels. In total, there are 1594 images.

3. Finally, we evaluate BOLD segmentation with a dataset (shorthand BOLD) of cine-MR and CP-BOLD images [49] of 10 (mechanically ventilated) subjects, with an in-plane resolution of 1.25mm × 1.25mm, acquired at baseline and severe ischemia (inflicted as controllable stenosis of the left-anterior descending coronary artery (LAD) on a 1.5T Espree (Siemens Healthineers). The image acquisition is at short axis view, covering the midventricle, and is performed using cine-MR and a flow and motion compensated CP-BOLD sequence, where each sequence is applied one after the other in the protocol in separate breath-holds. The pixel resolution is 192 × 114. In total there are 129 cine-MR and 264 CP-BOLD images with expert segmentations from all cardiac phases.

C. Baseline and benchmark methods

We consider the following baselines, which assume source masks being available at inference time. If predicted masks were used e.g. the result of a U-Net, an additional confounder would be introduced. Thus, we report numbers with ground truth masks for a bias-free estimate, which albeit is elevated.

1. A lower bound computes the Dice score between real masks of two modalities, which is also a measure of misalignment of the multimodal data. This is referred to as “copy” and can be used for segmenting a target modality without annotations from the target modality.

2. This lower bound can be improved after registering the multimodal images and applying the registration field to the source masks. The deformation field is calculated by affine registration using mutual information, followed by symmetric diffeomorphic using cross-correlation [50]. This is referred to as “register” baseline and can also be used without annotations of the target modality. “Copy” and “register” are common in clinical evaluation.

3. Finally, we implement a version of a non-coupled active contour model akin to the one in [37]. We initialised the contour using the “copy” above. Then via grid search, we found optimal contour length, smoothness, and stepping hyperparameters as: for ERI [0.5, 0.15, 0.7], BOLD [0.01, 0.15, 0.7] and CHAOS [0.5, 0.15, 0.7], respectively.

We also consider the following deep learning benchmarks.

1. As a supervised benchmark we train a UNet on annotated data of the target modality and refer to it as UNet-single. We further re-train a UNet on mixed training data of all modalities to evaluate its capability of concurrently handling multimodal data and refer to it as UNet-multi.

2. We train SDNet [7] with full or semi supervision on data of the target modality and refer to it as SDNet-single. We also train SDNet by mixing multimodal data, as demonstrated in [7], and refer to it as SDNet-multi.

3. We get two final benchmarks by training MUNIT [5] for image translation. The first uses MUNIT to translate images from source to target modality [17], and the second translates multimodal images to a domain invariant space [25]. In both cases, segmentation is performed post-hoc with a UNet on the combined data. We refer to these approaches as Translation and DADR respectively.

4. Finally, we implement DualStream [35], the most recent Deep Learning based method for handling multimodal data which does not require registered data.

For all benchmarks we use the architectures of the original papers, resulting in a comparable number of parameters. For UNet, SDNet, MUNIT, DualStream and DAFNet these are approximately in millions 35, 35, 26, 56 and 52, respectively.

V. Experiments and discussion

Sections V-A and V-B present segmentation results, assuming a source modality that always contains annotations during training. The source modality is cine-MR for ERI and BOLD datasets, and T1 for CHAOS. The target modality is LGE, BOLD and T2 for ERI, BOLD and CHAOS, respectively. Unless explicitly specified, DAFNet uses a FiLM-based decoder, and we report test Dice of the fused anatomies. We evaluate the effects of input pairing (Section V-C), registration (Section V-D), and a SPADE-based decoder (Section V-G). Then, Section V-H evaluates disentanglement of each decoder design. Where appropriate, bold font denotes the best (on average) method and an asterisk (*) denotes statistical significance of paired t-tests (p < 0.05 assessed via permutations) comparing with the second best (to avoid multiple comparisons).

A. Multimodal segmentation: full and zero supervision setting

The prime contribution of our work is the ability to learn and infer in a multimodal setting. Thus, we first demonstrate that multiple inputs at training and inference time benefit segmentation. Table I presents test Dice scores on three datasets for DAFNet and the benchmarks of Section IV-C. Two setups are evaluated, assuming either that annotations are available for the target modality or not.

TABLE I:

Segmentation results on three datasets when full (100%) or zero (0%) target modality annotations are available. For each dataset we show results on the target modality assuming the other is the source (and vice versa). Single input-output models cannot be trained with no annotations and are marked with n/a. We omit results marked with –, since training of these methods did not converge.

				100% target annotations
Methods	Train	Test	Masks in test	ERI		BOLD		CHAOS
				LGE	cine	BOLD	cine	T2	T1
copy	–	multi	Yes	6706	6706	8001	8001	7110	7110
register	–	multi	Yes	6807	6705	8104	8405	7007	7305
AC	–	multi	Yes	6615	6613	6802	7205	6522	6522
UNet	single	single	No	7804	8508	9101	8901	8517	8605
SDNet	single	single	No	8003	8409	8903	8804	8316	8508
UNet	multi	single	No	8103	8308	8903	8802	8515	8803
SDNet	multi	single	No	8005	8605	8902	8703	8511	8801
DualStream	multi	single	No	8006	8609	8909	8802	8516	8509
Translation	multi	single	No	7906	8405	8306	8802	8309	8706
DADR	multi	single	No	7905	8306	8804	8602	8416	7222
DAFNet	multi	single	No	8203	8602	8801	9102	8317	8801
DAFNet	multi	multi	No	8203	8402	9101	9101	${\mathbf{85}}_{05}^{\ast }$	8701
				0% target annotations
Methods	Train	Test	Masks in test	ERI		BOLD		CHAOS
				LGE	cine	BOLD	cine	T2	T1
copy	–	multi	Yes	6706	6706	8001	8001	7110	7110
register	–	multi	Yes	6807	6705	8104	8405	7007	7305
AC	n/a	multi	Yes	6615	6613	6802	7205	6522	6522
UNet	single	single	No	n/a	n/a	n/a	n/a	n/a	n/a
SDNet	single	single	No	n/a	n/a	n/a	n/a	n/a	n/a
UNet	multi	single	No	3823	6812	6823	8505	–	–
SDNet	multi	single	No	6118	7307	8003	8503	5109	6313
DualStream	multi	single	No	3823	6812	6823	8505	–	–
Translation	multi	single	No	3723	6113	6110	7407	–	4511
DADR	multi	single	No	4619	6313	6811	8501	–	4917
DAFNet	multi	single	No	7206	7805	7802	8203	7212	7406
DAFNet	multi	multi	No	${\mathbf{74}}_{04}^{\ast }$	7604	${\mathbf{85}}_{03}^{\ast }$	8602	${\mathbf{74}}_{03}^{\ast }$	7106

In the 100% case, training with multiple inputs improves accuracy, even when multimodal data simply constitute an augmented dataset. When segmenting the target modality, the usage of multiple inputs at inference time by DAFNet, obtains similar Dice as other benchmarks, but considerably reduces the standard deviation, such as in CHAOS from 11% to 5%.

In the 0% case the (learned) benchmark methods do not produce accurate target segmentations for all datasets. As expected, models trained only on the source modality learn modality-specific features, and as such cannot generalise to the unseen target modality. DAFNet on the other hand, consistently maintains a better average and smaller variance by leveraging information from the source modality. This is due to the aligning (in an embedding sense) of the multimodal representations in the anatomy space, which allows the shared segmentor trained with supervision on the source, to also segment the target modality with “zero” supervised examples.

We then exchange source and target and report the cine-MR and T1 Dice by training new models where appropriate. The CP-BOLD sequence is very similar to cine, showing anatomy, but has elevated T2 contrast (the BOLD effect) [49]. In addition, these data are acquired in controlled experiments, with the cine-MR and BOLD images acquired one after the other in the protocol. Thus, for the BOLD dataset all methods perform well in the 0% case of cine-MR segmentation, with multiple inputs further improving DAFNet performance. On the contrary, segmenting LGE (and T2) is more difficult. The Dice is overall lower than the cine-MR in the single-output DAFNet with the difference being bigger in the 0% case. As a result, this hurts the multi-output cine-MR Dice. This is expected since the benefit of multimodal segmentation comes when one modality is easier to segment.⁷ Therefore LGE benefits when considering cine-MR images, but the contrary would only be beneficial in cine-MR reconstruction problems, e.g. in the presence of motion artefacts [51].

B. Semi-supervised segmentation

Here we evaluate the sensitivity of all methods on different amounts of ground truth annotations available during training. Table II presents the average (across all labels) cross-validation test set Dice score. Exemplar test results are shown in Figure 5. The number of images for both source and target modalities are fixed, but the amount of target annotations varies. Sampling the amount of annotations is performed on a subject-level, to avoid having a mixture of annotated and non-annotated images of the same subject in the training set. The DAFNet results correspond to using multiple inputs at inference time.

TABLE II:

Segmentation results of LGE, BOLD and T2, when training with a varying amount of annotations for ERI, BOLD, and CHAOS datasets respectively.

ERI: Target LGE Dice (Source cine)
Method	50%	25%	12.5%
copy	6706	6706	6706
register	6807	6807	6807
AC	6615	6615	6615
UNet-single	7612	6614	5121
SDNet-single	7604	6909	5418
UNet-multi	7608	6711	5019
SDNet-multi	7604	7307	6419
DualStream	7603	6113	4423
Translation	7507	6714	6214
DADR	7705	6611	5719
DAFNet	${\mathbf{78}}_{04}^{\ast }$	${\mathbf{76}}_{05}^{\ast }$	${\mathbf{74}}_{05}^{\ast }$
BOLD: Target BOLD Dice (Source cine)
Method	50%	25%	12.5%
copy	8001	8001	8001
register	8104	8104	8104
AC	6802	6802	6802
UNet-single	7917	5927	4929
SDNet-single	8403	6817	6414
UNet-multi	8703	7517	7213
SDNet-multi	8607	8503	8003
DualStream	8601	5826	4928
Translation	8402	7906	4726
DADR	8702	7901	7115
DAFNet	8701	8603	${\mathbf{85}}_{03}^{\ast }$
CHAOS: Target T2 Dice (Source T1)
Method	50%	25%	12.5%
copy	7110	7110	7110
register	7007	7007	7007
AC	6522	6522	6522
UNet-single	8017	7615	7217
SDNet-single	8214	7716	7514
UNet-multi	8415	7916	7516
SDNet-multi	8411	8013	7809
DualStream	8119	7816	7516
Translation	8107	7511	7010
DADR	8411	7714	7411
DAFNet	8405	8203	${\mathbf{79}}_{05}^{\ast }$

Fig. 5:

Panel of LGE segmentation examples from ERI dataset, obtained with different amount of LGE annotations.

Average Dice for all methods is comparable when the number of annotations is high, although DAFNet achieves the lowest variance. With a reducing number of annotations, the performance of the competing methods is also reduced with a simultaneous increase in the variance. DAFNet maintains good results and robustness to edge cases, as evidenced by the small variance achieved throughout all setups.

C. Effect of pair matching

The results of Sections V-A and V-B correspond to expertly paired multimodal inputs. Here, we evaluate the sensitivity of DAFNet on unpaired multimodal images, as well as the effect of the automated pairing cost proposed in Section III-F.

We randomly shuffle the multimodal pairs by two positions, with the shuffled pairs differing up to two spatial slices within a 3D volume.⁸ We measure the LGE segmentation Dice score on ERI data when using 100% and 0% LGE annotations. We thus compare our automated method with expert pairing (upper bound) and a random shuffle (lower bound). Table III presents the results of copy method, as well as of DAFNet evaluated with both cine-MR and LGE inputs.

TABLE III:

LGE segmentation results when multimodal images are not expertly paired.

Pair matching	copy	DAFNet 0%	DAFNet 100%
expert	6706	7404	8203
automated	n/a	7106	8003
random	4416	6508	7706

Shuffling the multimodal pairs decreases the copy performance considerably. In both cases, automated matching of candidate pairs based on the semantics of the anatomy factors proves effective in ignoring distant slices (in the volume), with results very closely approaching the ones achieved by expert pairing. To show how our model learns appropriate weights, the evolution of weights across training epochs is shown in Figure 6, in which w₁ corresponds to the closest pair converged to a probability of one early on in training.

Fig. 6:

Evolution of weights w_j across epochs. Weights are used as a measure of similarity between each candidate multimodal pair. For more details see text.

During inference, a “soft” segmentation mask is produced as a weighted sum between each weight with its corresponding mask. However, this converges to using the prediction of the “closest” pair, as evidenced by Figure 6.

D. Effect of STN

We assess the need for a registration module with an ablated model. We compare the accuracy of a fused segmentation that is obtained with and without the STN module. Two DAFNet models are compared, trained on ERI data with 100% and 0% LGE annotations. The mean Dice without the STN is measured to be 75 ± 6% and 71 ± 6% respectively. This is lower than the Dice of DAFNet with STN that is 82 ± 3% and 74 ± 4%. Furthermore, in the 100% case the difference is statistically significant at the 1% level. Thus, clearly registration helps.

An example anatomy alignment is shown in Figure 7. Although not a perfect alignment of the images is required, the left ventricle and myocardium of the cine-MR have deformed to match the corresponding LGE (marked in red boxes).

Fig. 7:

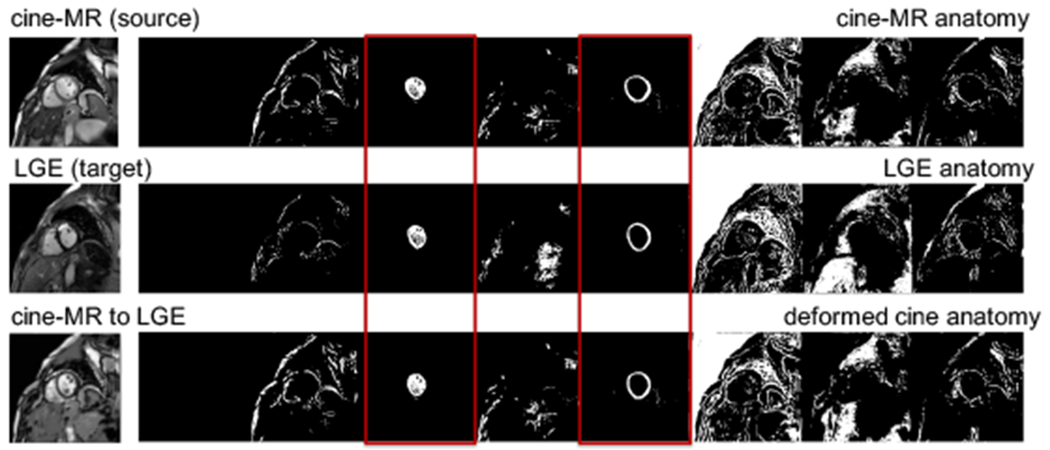
Example anatomy alignment. The cine-MR anatomy (row 1) is deformed by the STN to match the LGE one (row 2), resulting in the anatomy of the last row. Red boxes mark channels of areas of interest (left ventricle and myocardium).

E. Ablation study on cost components

We assess the contribution of cost components in the fused segmentation on ERI with 100% and 0% LGE annotations. We evaluate the effect of losses involved in reconstruction, the adversarial training losses on masks ($L_{adv}^M$) and images ($L_{adv}^I$), and the modality factor reconstruction loss ($L_{rec}^z$).⁹ Table IV shows that best results are achieved with all cost components. Removing the disentanglement and reconstruction losses significantly reduces performance at 0% supervision, which conclusively shows their role in learning without annotations.¹⁰ In addition, the data-driven reconstruction cost (via the image discriminator) contributes by encouraging more accurate synthesis, which helps learn better anatomical representations.

TABLE IV:

Ablation study on the effect of individual cost components on LGE segmentation accuracy.

LKL	Lrec	$L_{adv}^M$	$L_{adv}^X$	$L_{rec}^z$	DAFNet 0%	DAFNet 100%
—	—	✓	—	—	6607	8103
✓	✓	—	✓	✓	7202	8003
✓	✓	✓	—	✓	6505	7117
✓	✓	✓	✓	—	7104	8103
✓	✓	✓	✓	✓	7404	8203

F. Ablation on factor sizes C and n_z

In all experiments, factor sizes are set to C=8, and n_z=8. C is determined experimentally, so that there is enough capacity for all segmentation classes and background anatomy. A large C does not affect segmentation, and the redundant capacity is ignored, see “empty” channels of Figure 4. This is confirmed with ablated models with C=4 or C=16 trained with 100% annotations on ERI and CHAOS. The ERI model achieves 82± 2% for both setups, the same as when C=8. The CHAOS model achieves 74 ± 12% and 85 ± 5% for C=4 and C=16, respectively. The performance significantly drops when C=4, since there is not enough capacity.

Size n_z is determined according to our previous [7], and related work [5]. We experimented with n_z=4 and n_z=16 and 100% annotations on ERI and CHAOS. We find no effect on segmentation accuracy. However, n_z affects the information capacity, approximated by the average variance [52], of each z-dimension, where smaller variance implies higher informativeness. With n_z = 16, the lowest variance is 0.63, the first 8 dimensions have an average of 0.86 and the remaining 8 an average of 0.95. For n_z=8, the variance ranges between 0.47 and 0.80, and for n_z=4, between 0.43 and 0.60. Admittedly, lower n_z results in higher information content in each dimension, thus large n_z seems redundant in this setup.

G. Effect of decoder design on segmentation accuracy

The modular design of DAFNet permits incorporation of components with different designs. We evaluate segmentation accuracy achieved by two decoder architectures: FiLM and SPADE. Specifically, we train a SPADE-based DAFNet on ERI and CHAOS and compare with the FiLM-based DAFNet for 100% and 0% annotations.

With 100% annotations, the SPADE-based DAFNet achieves 82 ± 3% and 85 ± 5% on ERI and CHAOS respectively, identical to the Dice achieved by FiLM. With 0% annotations, the SPADE-based DAFNet achieves 73 ± 4% and 75±7%, whereas FiLM-based results are 74±4% and 74±3% respectively on ERI and CHAOS.

We can conclude that the regularising effect of the reconstruction process on extracting segmentations, is similar with both decoder variants. However, different decoder designs influence the way the anatomy and modality factors interact to produce a synthetic image. We explore this next.

H. Evaluating disentanglement

Even though FiLM and SPADE decoders do not result in evident differences in segmentation accuracy, they produce synthetic images of different quality (Figure 8). Since the anatomy factors contain flat regions, FiLM-based conditioning with scalar parameters tends to produce images with less texture details than SPADE-based conditioning.

Fig. 8:

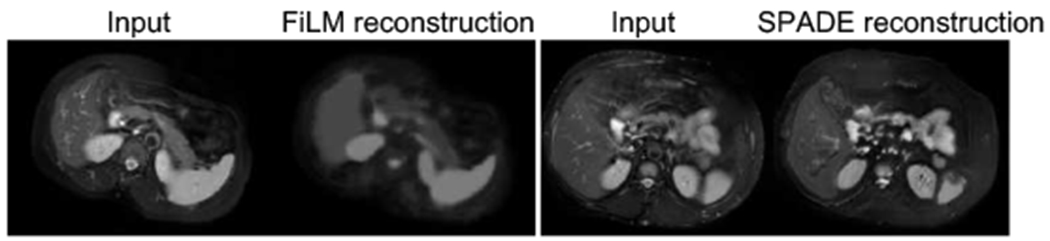
Reconstructions with two decoders. The FiLM synthetic image is more flat and lacks texture in contrast to the SPADE synthetic image. Images taken from CHAOS dataset.

Here, we assess the information retained in the modality factors and characterise the achieved disentanglement. This is a challenging problem not addressed in existing literature: all assume vector latent variables (e.g. BetaVAE score [6]). In DAFNet, and typically in content/style disentanglement, the factors of variation are not of the same dimensionality, with the anatomy being spatial. For the experiments below, we use models trained on CHAOS with 100% T2 annotations to assess (dis)entanglement using classification tests, factor arithmetics, and a proposed metric of independence of random variables.

1). Modality classification:

On the premise that the common modality encoder correctly extracts modality features, a classifier should detect the modality type, given just the z-factor. We assess this hypothesis, by training a logistic regression classifier to predict whether different z-factors correspond to T1 or T2 images. The classifier’s accuracy is 99% and 97% for FiLM and SPADE, respectively, on a test set of three subjects.

We further evaluate whether specific dimensions in z capture the modality type by repeating the experiment for each dimension. In the FiLM model, the 2nd dimension achieves 100% accuracy, whereas the rest vary between 54% and 64%. Similarly, in the SPADE model the 7th dimension achieves 97% accuracy vs. 42% and 63% of the others.

2). Modality factor arithmetics:

We qualitatively examine the information retained in each dimension of vector z with latent space arithmetics. The likelihood of the modality factor approximates a Gaussian prior, and therefore interpolating in the range [−3, 3] covers the probability space. Figure 9 shows synthetic images arranged in a grid; images of each row are produced by interpolating the values of a single dimension of z, with the remaining ones fixed. The final two columns highlight affected regions by calculating the per-pixel Pearson correlation, as well as the difference, Δ_image, between the synthetic images at extreme z values −3 and 3, respectively.

Fig. 9:

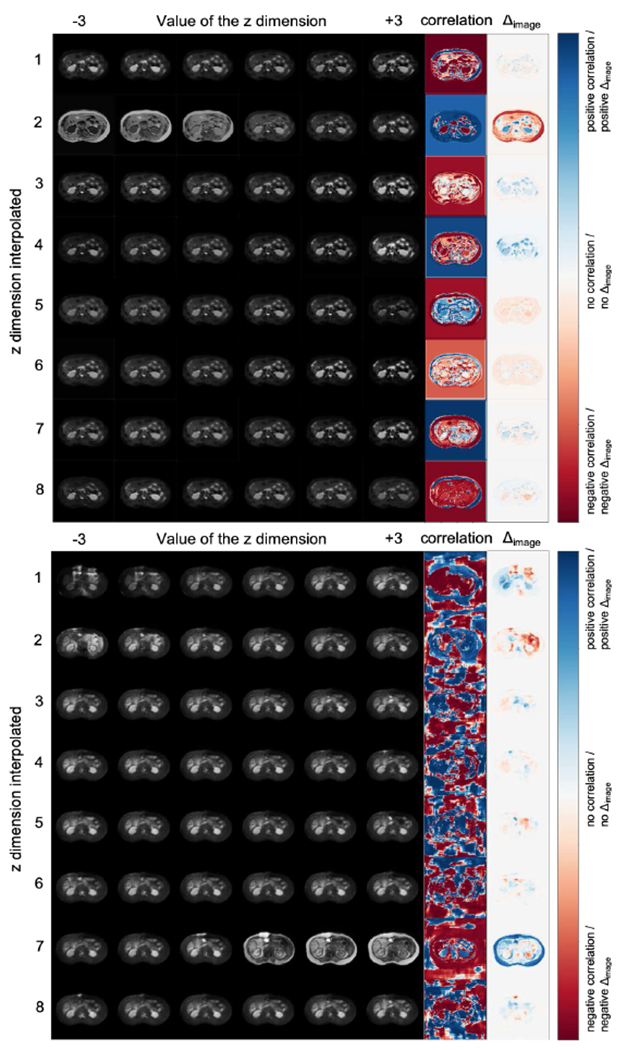
(a) FiLM and (b) SPADE based reconstructions. Images per row correspond to interpolating a single z dimension. Last two columns (correlation, and difference image Δ_image), indicate regions mostly affected by each z dimension.

Both decoders have one z-dimension with a global effect (2 and 7 respectively) controlling the “modality” type. This finding is inline with the classification results above. Furthermore, some dimensions of the FiLM decoder, e.g. the 8th, appear focused on specific regions, whereas the dimensions of the SPADE decoder produce more diffused correlation images. The latter likely relates to SPADE generating texture better.

3). Disentanglement metric:

We propose distance correlation [12] as a metric of factor independence, which is invariant to the input variable dimensionality, and can also detect linear and non-linear associations. While it has been used before for reducing data leakage [53], we use distance correlation for measuring (dis)entanglement. Distance correlation is equal to

$$dCor(s,z)=\frac{dCov(s,z)}{\sqrt{dVar(s)dVar(z)}},$$

where dCov(s, z) is the distance covariance of s and z, and dVar(.) is the distance variance respectively. Given n random samples s_k and z_k with k ∈ [1, n], the distance covariance is the product of two distance matrices (one for each variable) averaged by n², where each distance matrix d(.) is double centred by subtracting the mean row, the mean column and the overall mean from each element $dCo{v}^2(s,z)=\frac{1}{n^2}{\sum }_{i=1}^n{\sum }_{j=1}^{n}d(s_i,s_j)d(z_i,z_j).$. The distance variance is then dVar²(s) = dCov²(s, s), and dVar²(z) = dCov²(z, z).

The distance correlation between s and z values from a FiLM-based model is dCor = 0.55, whereas the equivalent for a SPADE-based model is dCor = 0.78. This suggests that factors obtained by the FiLM decoder are more independent and therefore the FiLM-based model is more disentangled. Although distance correlation cannot explicitly evaluate the type of information in each variable, this result can be explained intuitively by the decoder design. The SPADE decoder allows more flexibility to the z factors as evidenced in the synthetic images, which contain more texture, but also in the diffused correlation images of Figure 9b, implying a higher anatomical correlation (and higher entanglement) between factors.

VI. Conclusion

We have presented a method for multimodal learning and specifically multimodal segmentation, that is robust to the requirement for registered and paired input images. This has been made possible by disentangling images into semantic anatomy factors that are consistently represented across modalities and modality factors that model the intensity variability of the multimodal inputs into a smooth latent space.

We have proposed DAFNet, which, to the best of our knowledge, is the first work that enables multimodal segmentation by aligning disentangled anatomical representations and can be trained with zero annotations for one of the modalities. We presented the benefit of multimodal (over single-modal) learning in cardiac and abdominal segmentation, where we achieve high accuracy and low variance by fusing anatomical information of different modalities. We further demonstrated robustness to misalignments between multimodal images (achieved by a spatial transformer network) and robustness to the quality of the multimodal pair matching (with an optional pair weighting), both made possible by comparing the anatomy factors. Finally, we made a first step in evaluating the quality of the content/style disentanglement using the distance correlation.

The significance of our work lies in the potential for the use of disentangled representations in other challenging problems of medical research. Future directions include the learning of further factorisations suitable for medical data, capturing pathological information and specific artefacts for instance, as well as a theoretical characterisation of the disentangling process and precise quantification of the type of information that is captured by each factor. Admittedly this is more complex in content/style disentanglement than in vectorised latent spaces for which metrics have been recently suggested [54].