Abstract
We describe an efficient method for the simultaneous solution of all free energies within a relative binding free energy (RBFE) network with cycle closure and experimental/reference constraint conditions using Bennett Acceptance Ratio (BAR) and Multistate BAR (MBAR) analysis. Rather than solving the BAR or MBAR equations for each transformation independently, the simultaneous solution of all transformations are obtained by performing a constrained minimization of a global objective function. The nonlinear optimization of the objective function is subjected to affine linear constraints that couple the free energies between the network edges. The constraints are used to enforce the closure of thermodynamic cycles within the RBFE network, and to enforce an additional set of linear constraint conditions demonstrated here to be subsets of (1 or 2) experimental values. We describe details of the practical implementation of the network BAR/MBAR procedure, including use of generalized coordinates in the minimization of the free energy objective function, propagation of bootstrap errors from those coordinates, and performance and memory optimization. In some cases it is found that use of restraints in the optimization is more practical than use of generalized coordinates for enforcing constraint conditions. The fast BARnet and MBARnet methods are used to analyze the RBFEs of 6 prototypical protein-ligand systems, and it is shown that enforcement of cycle closure conditions reduces the error in the predictions only modestly, and further reduction in errors can be achieved when one or two experimental RBFEs are included in the optimization procedure. These methods have been implemented into FE-ToolKit, a new free energy analysis toolkit. The BARnet/MBARnet framework presented here opens the door to new, more efficient and robust free energy analysis with enhanced predictive capability for drug discovery applications.
Graphical Abstract
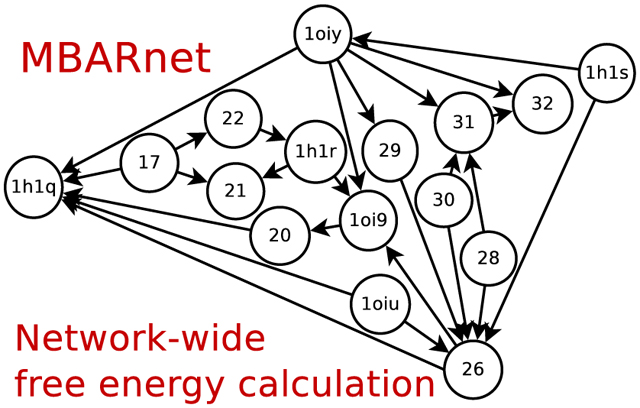
1. Introduction
Alchemical free energy methods play a key role in lead optimization by enabling the prediction and ranking of the relative binding affinities of ligands to their protein targets in order to prioritize them for further synthesis and testing.1,1–11 Often these calculations take the form of computing the relative binding free energy (RBFE) between ligands by alchemically mutating one ligand into another, both in solution and bound to the protein.12–17 The ease at which such transformations can be computed robustly to high precision depends in part on the similarity of the ligands.18–20 To take advantage of this in practice, a topological thermodynamic network can be constructed to connect ligands in such a way that their RBFEs can be optimally computed.21–25 This network can be thought of as a “directed graph” where each edge corresponds to an alchemical transformation between ligands. When solving for the RBFE values between ligands, one can independently analyze the corresponding edge using an established free energy method such as Bennett’s Acceptance Ratio (BAR) method,26 the multistate-BAR (MBAR) method,27 unbinned weighted histogram analysis method (UWHAM),28 or thermodynamic integration (TI) method29 However, these original approaches will not guarantee that certain theoretical cycle closure constraints are obeyed, nor do they allow integration of experimental values as constraints into the analysis.
Herein we present a robust, efficient method for the network-wide BAR and MBAR analysis of RBFEs of entire sets of ligands with arbitrary linear constraints, including both theoretical cycle closure conditions and experimental (or generally derived) reference value constraints or restraints. The former leads to more precise computed values that obey the cycle closure conditions in the limit of infinite precision (complete sampling), whereas the latter leads to improved prediction for unknown ligands by constraining RBFE values of ligands with known binding affinities. These methods have been implemented into the graphmbar program distributed within FE-ToolKit, a new free energy analysis toolkit that is available from the authors.30
A few methods have been introduced that enable the enforcement of theoretical cycle closure constraints.31,32 Here, we build upon the MBAR/UWHAM equations27,28,33–35 which can be solved efficiently by non-linear optimization of a convex function.28 Rather than solving these equations for each transformation independently, the simultaneous solution of all edges of the thermodynamic network are obtained by performing a constrained minimization of a global objective function. The nonlinear optimization of the global objective function is subjected to affine linear constraints that couple the free energies between the network edges. This is a general approach that is not restricted to simple cycle closure constraints, but could include select experimental or high-precision reference values, or any linear combination thereof. We formulate global objective functions that correspond to both BAR and MBAR solutions for the thermodynamic network, referred to as BARnet and MBARnet, respectively. Practical considerations in terms of computational efficiency and memory requirements for the network data are discussed. The methods are demonstrated in the calculation of RBFEs of 6 prototypical protein-ligand systems, and it is shown that enforcement of cycle closure conditions can lead to a modest reduction of the error in the predictions, and further error reduction can be achieved when one or two experimental RBFEs are included in the network analysis.
In order to establish context and motivation for the present methods, we outline a typical use case for alchemical free energy calculations in the lead optimization stage of drug discovery.5,11 At the lead optimization phase, initial lead compounds have been identified through high throughput screening and lead generation. The goal of lead optimization is to develop and synthesize new compounds with improved potency, selectivity and pharmacokinetics. This optimization is achieved by creating trial modifications of initial lead compounds that are informed by structure-activity relationships, and in many cases structural data of the target-lead (protein-ligand) complex. Computational free energy simulations are used at this point to make predictions about the relative binding affinities (and in some cases selectivity) in order to prioritize the most promising compounds for synthesis and further characterization. The goal is often to rank a series of trial compounds that involve chemical modifications of a common molecular scaffold in terms of their binding affinity to the target protein. To achieve this, a thermodynamic network21–24 is constructed such that the RBFEs of the series can be optimally computed, as discussed above. This network will contain the unknown compounds for which predictions are desired, but also contains some known reference compounds for which crystallographic and binding affinity data has been measured. As the free energy is a state function, the number of linearly independent RBFEs is Nlig−1, where Nlig is the number of ligands. However, the number of alchemical transformation edges in the thermodynamic network, Nedges, is typically considerably larger than the theoretical degrees of freedom (Nedges > Nlig − 1). This overdetermined set of computational variables (the free energy values for each edge transformation) give rise to a number of theoretical “cycle closure” conditions that need to be satisfied (this set of conditions is not unique, but has fixed rank). Further, as some of the compounds have been measured, the RBFEs between these compounds are also known. Nonetheless, by including these known compounds in the calculations along with the unknown compounds, the data can, in principle, be leveraged to improve the predictions for the RBFEs of the unknown compounds. More generally, if for some reason, it is known that values for certain sets of edges (or linear combinations thereof) are more reliable, then it might be advantageous to either constrain or restrain these values in the global optimization. It should be acknowledged that in some cases where data may be systematically biased, imposition of constraints or restraints could lead to worse predictions. In the present work, we create a tool to explore the use of experimental or other reference constraints (or restraints), in addition to the theoretical cycle closure constraints, in the global optimization of the network-wide free energy function with the goal to improve predictive capability.
2. Methods
Fast Solution for Large Scale MBAR/UWHAM Equations.
We begin by reviewing the MBAR/UWHAM equations,27,28,33–35 first derived in Ref. 28, using a notation based on the description found within Ref. 34. In the context of their work, they considered an alchemical transformation, e, that mutates state A to state B using Me intermediate alchemical states (λ-states). In the present work, we use the subscript “e” to identify this transformation as particular edge within the RBFE graph. The goal is to calculate Me free energy values, , where i indexes the value of λ-state within transformation e. Simulations are performed for the Me states, each generating Nie frames of coordinates , where k indexes the frame within the trajectory. Furthermore, the reduced potential energy uie (scaled by (kBT)−1, where kB and T are the Boltmann constant and absolute temperature, respectively) of each state must be evaluated for each of the frames. The MBAR/UWHAM objective function is shown in Eq. 1.
| (1) |
The bie values (Eq. 2) are used for notational compactness.
| (2) |
The expression does not contain β = (kBT)−1 terms within it because it is presumed throughout this manuscript that the potential and free energies are in reduced energy units; that is, they have been pre-multiplied by β. The gradient of the objective function (Eq. 1), which may or may not be necessary depending on the chosen nonlinear optimization algorithm, is given in Eq. 3.
| (3) |
Network Optimization using the Multistate Bennet’s Acceptance Ratio Method.
We extend the MBAR/UWHAM equations, first derived in Ref. 28, by minimizing a global objective function that weights and sums Eq. 1 for each edge, and subjects the minimization to linear constraints that couple their simultaneous solution.
| (4) |
| (5) |
The we values weight each edge in the sum. In the current work, we set all weights to unity. Ncon. is the number of constraints and is the target value of constraint c. The constraint is a linear combination of free energy values, where Ccon.,(c,ie) is the contribution from λ-state i within edge e to contraint c. The grouping of the subscripts in Ccon.,(c,ie) is meant to view this quantity as a matrix with Ncon. rows and columns.
The constraint coefficients are typically nonzero only for the λ = 0 and λ = 1 states of an alchemical transformation because the free energy of the process is the difference between those two states, ΔG = G (λ = 1) − G (λ = 0). As an example, if a ΔG value is constrained, then the elements of Ccon.,(c,ie) corresponding to the G (λ = 1) and G (λ = 0) states would be 1 and −1, respectively. As a more complicated example, consider a case where Ntrial independent simulations of an alchemical transformation are included in the analysis. Each trial will produce a slightly different ΔG value. A constraint on ΔG could be applied to each of the Ntrial trials (one constraint for each independent trial); however, we prefer to apply a single constraint to the average 〈ΔG〉 value. In this case, the nonzero Ccon.,(c,ie) values are and for each trial’s λ = 1 and λ = 0 states, respectively. The application of constraints to trial averages easily extends to more elaborate constraints. For example, an “edge free energy” – the free energy difference between two physical states – could be divided into a series of stages, such as “decharge”, “softcore Lennard-Jones”, and “recharge” stages. A constraint on the edge free energy average involves all λ = 0 and λ = 1 states from each trial of each stage. Furthermore, a constraint on a cycle closure average involves all λ = 0 and λ = 1 states from each trial of each stage for each edge tracing the closed path.
There are many numerical methods for performing the constrained optimization in Eq. 4. The constrained problem has only equality constraints, and the method of Lagrange multipliers could be used to convert it into an unconstrained problem involving Ncon. + M parameters by constructing a Lagrange function (Eq. 6) and searching for its saddle point(s): .
| (6) |
This approach is not ideal only because many of the widely available numerical optimization software libraries are designed to find local minima (or maxima) rather than saddle points. Fortunately, many unconstrained optimization algorithms can be adapted to constrained problems via “the penalty method” or the closely related “augmented Lagrangian method”.36,37 In the special case that the equality constraints are linear, one can use a “substitution method”,38 whereby the explicit presence of constraint conditions are removed by replacing the full set of parameters by a smaller set of generalized parameters that only (but fully) span the space of feasible solutions.
The penalty method is a well-known approach for finding approximate solutions to constrained problems.36,37 The method augments the primary objective function with penalty functions that deter the optimization algorithm from exploring the unfeasible solutions. The objective function using a quadratic penalty function to enforce equality constraints is: O(G*) = F(G*)+Σckchc(G*)2. The procedure is to set kc = 0 and optimize O to obtain a guess at the parameters. To enforce the constraints, kc is increased by 10 (or some chosen amount) and O is reoptimized starting from the previous solution. The process of increasing kc and reoptimizing the objective is repeated until the constraints are satisfied to within a desired tolerance. The constraints are strictly enforced as the kc values approach infinity; however, if strict enforcement of the constraints are required, use of the augmented Lagrangian method should be prefered. If it is satisfactory to enforce the constraints to only several digits of accuracy, then the penalty method is quite efficient and widely applicable. One might consider the kc values to be additional parameters introduced by the penalty method; however, it is better to view the penalty method as introducing a tolerance on the acceptable enforcement of the constraints – in much the same way that one places tolerances on the numerical algorithm to terminate the search for an optimal set of parameters.
The substition method can enforce linear equality constraints by performing the optimization in a reduced set of generalized parameters whose freedom is limited to the feasible regions of the constrained optimization.38 The goal is to find a set of Mfree = M − Ncon. generalized parameters q that will always satisfy the constraints. A relationship must be found to express the full set of parameters as a function of the generalized parameters to rewrite the constrained optimization problem as an unconstrained optimization of the generalized parameters.
| (7) |
To begin, consider a solution for the parameters from the linear equality constraints (Eq. 8).
| (8) |
If there are fewer linearly independent constraints than parameters, then a strictly-enforced, nonunique solution can be found from a generalized inverse; this solution will be denoted by .
| (9) |
As we shall see below, Eq. 9 is only one of many possible solutions that satisfy the constraints, and we seek to find a formula that generalizes Eq. 9 to include all feasible solutions satisfying the constraints. The generalized inverse of Ccon. (denoted ) can be computed from a singular value decomposition (SVD, see Eq. 10), where U is a Ncon. × Ncon. matrix of left-singular vectors, V is a M × M matrix of right-singular vectors, and Σ is a Ncon. × M matrix of singular values along its diagonal.
| (10) |
Given Ncon. linearly independent constraints, the diagonal of Σ will contain Ncon. nonzero elements. The remaining Mfree columns of Σ are the null space of Ccon., and the corresponding Mfree rows of VT span the space of feasible solutions satisfying the constraints. Let us define a Mfree × M transformation matrix, T, whose Mfree rows are the row vectors of VT spanning the null space Ccon.. Perturbing Eq. 9 by qT · T for any vector q will continue to satisfy the constraints; therefore, the general expression for the parameters that satisfy the constraints is given by Eq. 11.
| (11) |
By rearranging Eq. 11, one can derive the reverse transformation for the generalized parameters.
| (12) |
There are three types of constraints that we will consider: (1) We constrain the free energy of each λ = 0 alchemical state to be zero. This constraint does not have a practical effect on the results other than improving the readability of the output. (2) If a partial list of reference RBFEs are known, then we constrain the calculated RBFEs to match the reference values. The motivation behind this is for situations when a few reference RBFEs (either experimental RBFE values or highly-converged simulation results) are known and one attempts to use that partial knowledge to aid the prediction of RBFEs that remain experimentally unknown. (3) We enforce thermodynamic cycle closure conditions. The free energy is a thermodynamic state function; therefore, the sum of free energies along a closed path should be zero. The reader is free to implement the constraints using whatever method is readily available to them. In the present work, we choose to use the substitution method described above for linear equality conditions for enforcing the first two types of constraints described above. One advantage of our use of singular value decompositions to come up with generalized coordinates that obey the constraint conditions is that the constraint coefficient matrix itself can be overdetermined. From a user perspective, this is convenient in that one can impose multiple redundant cycle closure and other constraint conditions without concern of linear dependencies, and the SVD provides a robust method for determining the generalized coordinates that spanned by the free parameters under the constraint conditions.
We also use the penalty method for enforcing the cycle closure constraints, because of the potential of encountering linear dependencies between the cycle closure conditions. In principle, the presence of linear dependencies is not an insurmountable obstacle; however, in practice the singular vectors defining the free parameters can become highly oscillatory as a linear dependency is approached, thereby limiting the effective precision due to round off error. Our experience is that cycle closure constraints are often satisfied to within 0.001 kcal/mol using restraint force constants of 10(kBT)2, which is much smaller than the uncertainty in the free energy values. This degree of constraint enforcement is sufficient for our purposes, so the penalty method can be terminated after the first use of nonzero kc values. The penalty method, in our application, can thus be viewed as a “restraint” applied to the primary objective function. In this view, the cycle closure constraint penalties can be explicitly written into the objective function and refered to as restraints, denoted by the subscript “res.”.
| (13) |
The algorithm for finding and choosing the closed paths, given a list of edges (a list of molecule pairs), follows:
Assign each molecule a unique (but otherwise arbitrary) index.
For each molecule, generate a list of directly connected neighbors from the set of edges.
For each connected neighbor, use a Depth First Traversal algorithm to find the shortest path(s) that connects the molecule to the neighbor, excluding the direct connection. The resulting path is a list of molecules starting with the entry molecule and ending with the connected neighbor.
To avoid redundant duplication of the same path with others that may differ only from the starting molecule or traversal direction, shift the entries in the path list such that the first element has the lowest molecule index and the second element has a lower molecule index than the last element. This second condition controls the “clockwise-ness” of the cycle.
Append the end of the path list with the first element to close the cycle.
If the path has not yet been restrained, then include it as an additional restraint.
The algorithm does not include all possible closures; instead, it includes all smallest closed paths such that the selected paths do not encircle two or more smaller closed paths. Although this was our chosen algorithm, other choices for selecting the cycle closure conditions are certainly possible.
As a technical note, the constrained objective function F is convex if we ≥ 0 for all edges, because each f is convex and the sum of convex functions is also convex. Furthermore, one can show that the Hessian in generalized parameters, ∂2F/∂qi∂qj, is positive semidefinite because the Hessian in the full set of paramters, , is positive semidefinite28 and there is a linear relationship between the generalized set and full set of parameters (Eq. 11).
In summary, the MBARnet procedure consists of the following steps:
Read the potential energies from file and convert to reduced energy units.
Make an initial guess for the reduced free energies .
Generate the generalized coordinate transformation matrix Ti,(je) and vector from singular value decomposition of the constraint matrix (Eqs. 9–10 and).
Use Eq. 12 to obtain an intial guess for the free parameters.
Initiate the nonlinear optimizer, providing it the objective function and Mfree generalized coordinates.
For each objective function evaluation, convert the generalized coordinates to values and evaluate Eq. 11.
If the optimization method requires parameter gradients, then evaluate Eqs. 14 and 15.
When a minimum is found, convert the generalized coordinates to reduced free energies and divide them by the appropriate value β to express them with the desired energy units.
| (14) |
| (15) |
Network Optimization using the Bennett Acceptance Ratio Method.
We extend the MBARnet method by defining an objective function for BAR analysis such that the free energy network can be similarly constrained and restrained during the optimization. The BARnet optimization is similar to Eq. 13.
| (16) |
The fBAR objective function is a sum of BAR objective functions corresponding to each adjacent pair of alchemical states:
| (17) |
For example, the expression for is shown in Eq. 18.
| (18) |
Bootstrap Error Analysis.
To estimate the BARnet and MBARnet errors in the calculated values of , we perform many optimizations of F to obtain many optimal sets of generalized coordinate parameters. The optimizations differ by having constructed new ensembles for each state by random sampling with replacement. To account for correlation within the data, we calculate the statistical inefficiency of each trajectory’s reduced potential energy timeseries and group the trajectory into blocks, whose size is chosen to be twice the statistical inefficiency. The bootstrap is performed blockwise by sampling from the available blocks. The resulting distributions for each generalized coordinate has a mean value and unbiased sample variance . Given sufficient resampling effort, the transformation of the average values will match the optimized parameters from the initial ensembles; that is,
| (19) |
The standard errors of are propagated from the generalized coordinate variances:
| (20) |
In the present work, we estimate the errors from 300 bootstrap calculations.
Network Anaylsis using Multiple, Independent Simulations.
The bootstrap BARnet and MBARnet error analysis provides a measure of the uncertainty caused by fluctuations within the observed ensembles. Because the simulations are performed for a finite length of time, the observed ensembles are only an approximation of the theoretically converged ensembles generated from infinite sampling. One can estimate the error caused by finite time length simulations by performing multiple, independent trial simulations that differ only by their initial conditions. This is sometimes called the “Ensemble Average Approach”.39,40 Each simulation’s trial is included in the global optimization and they are each optimized with their own free energy parameters. The constraints and restraints involving the multiple trials are chosen such that the average value across all trials satisfy the condition, rather than having each trial satisfy the condition.41 When performing the error analysis, we combine the standard deviation among the trials with the bootstrap errors from each trial.42 For notational purposes, let be the free energy of trial t of state i within edge e, and is the corresponding standard error from bootstrap analysis. We compute the average-across-trials for state i in edge e, , and combined standard error, , from Eqs. 21 and 22, respectively.
| (21) |
| (22) |
Adjustment of edge weights.
The we weights appearing in Eqs. 4 and 16 are unity in the present work. If constraints are not applied to the objective functions, then the unequal weighting would not effect the result because each edge is decoupled from all other edges. When a constrained optimization is performed, the parameters (free energies) within each edge become coupled throughout the thermodynamic network and the optimization solution then depends on the relative weight applied to each edge. Undoubtedly, approaches can be adopted such that these weights can be adjusted to improve robustness and predictive capability. This is an area of ongoing active research, but not one that we are able to address in the present work. We note that one of the major challenges to developing any such approach is the lack of very high-precision benchmark quality simulation results for non-trivial protein-ligand systems that can serve as target reference data. Nonetheless, an important direction for future research is to test different approaches for adjustment of the weights in order to reduce statistical errors and improve predictions.
Computational details.
The tables and figures summarize the RBFE analysis of CDK2 (PDBID: 1H1Q),43 MCL1 (PDBID: 4HW3),44 p38 (PDBID: 3FLY), Tyk2 (PDBID: 4GIH),45 PTP1B (PDBID: 2QBS),46 and Thrombin (PDBID: 2ZFF) protein targets previously studied in Ref. 8 The CDK2 system has 16 ligands whose RBFEs are connected by 25 edges. The MCL1, p38, Tyk2, PTP1B, and Thrombin systems have 42, 33, 16, 23, 10 ligands, respectively, connected by 71, 54, 24, 48, 10 edges, respectively. Each ligand transformation is performed in three stages (decharge, softcore, and recharge) and two environments (protein-bound and in solution), and the RBFE is the free energy difference between the protein-bound and aqueous-phase transformation free energies. The decharge stage removes the charges of the atoms that are being deleted; the recharge stage adds the charges of the atoms that being inserted. The softcore stage linearly mutates the remaining potential energy terms between the initial and final states except for the Lennard-Jones (LJ) interactions, which are modeled using the (nonlinear) softcore LJ potential described in Ref. 47. For completeness, the general form of the alchemical potential energy function is given by Eqs. 23–27.
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
The decharge and recharge stages linearly scale the electrostatic interactions Uelec. The superscript (0) within Eq. 25, for example, indicate that the parameter values describe the λ = 0 state. Similar equations can be written for the λ = 1 state. The bonded energy (Eq. 24) contains terms that model bond, angle, and dihedral components. The kb and kθ values are spring force constants. The r0 and θ0 values are spring equilibrium positions. The Vin values control the mangitude of the periodic torsion potential, and γi is a phase offset. The qi values are electric charges, and ϵij and σij are the LJ well-depth and the point where the LJ crosses zero, respectively. The α = 0.5 is a control parameter of the softcore LJ potential. The softcore stage linearly transforms the bonded energy and nonlinearly modifies the nonbonded Lennard-Jones interactions using Eqs. 26–27. The decharge and recharge stages were performed using 5 evenly-spaced λ states. The softcore stages were performed using 12 states: λ = 0.0, 0.0479, 0.1151, 0.2063, 0.3161, 0.4374, 0.5626, 0.6839, 0.7937, 0.885, 0.9521, and 1.0. Each simulation was performed with Amber’s graphics processing unit (GPU) accelerated version of PMEMD for 2 ns using a 4 fs timestep and hydrogen mass repartitioning.42,48,49 The ligand was modeled using the GAFF2 force field,50 and the condensed phase environment was explicitly modeled with TIP3P51 waters. MBAR potential energies were output every 100 steps (0.4 ps). Each simulation was performed 10 times with differing initial random number seeds.
The simulations were run in the isothermal-isobaric ensemble (NPT). Pressure was regulated with Berendsen barostat to maintain a pressure of 1 atm using a 5 ps collision frequency.52 The Langevin thermostat was used to maintain a temperature of 298.15 K.53 The Lennard-Jones potential was truncated at 8 Å, and a a long-range tail correction is used to model the interactions beyond the cutoff. The long-range electrostatics were evaluated with the particle mesh Ewald method using a 1 Å3 grid spacing.54,55 The simulation data was taken from Ref. 56 and further details can be found therein.
To perform the nonlinear optimizations of the BARnet and MBARnet global objective functions, we used the Low-storage Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm57 implemented in the NLopt software library.58 When constraints and restraints are unused, the initial guess for each free energy is zero. When constraints and/or restraints are used, we first perform an optimization without constraints nor restraints and then reoptimize the free energies with the constraints and/or restraints activated.
The simulations were performed on NVidia GeForce GTX 1080 Ti GPUs. The protein-bound and solution-phase simulations require approximately 0.3 and 0.06 GPU hours to complete, respectively. Each edge requires approximately 80 GPU hours to complete 10 trials of each simulation in both environments. The 6 protein systems consist of a total of 232 edges, corresponding to an aggregate of 2 GPU years of simulation.
After the simulations are performed, the MBAR energies are extracted from the output files. We store the energies in energy timeseries files. A timeseries file is a text file containing two columns of numbers. The first column is the simulation time and the second column is a potential energy. MBAR requires each λ state trajectory be evaluated with all λ state potentials within the stage. For example, a single trial of a decharge stage produces 25 timeseries files because the stage is performed with 5 λ states. All 3 stages of a single trial produce 194 files. Considering that the transformations need to be performed in 2 environments and repeated 10 times, each edge produces 3880 files. Each timeseries file contains 5000 rows and uses 140 KB of disk storage. The storage of each edge’s timeseries files thus requires 530.5 MB of disk space.
The calculated RBFEs will be compared to experimental values. The experimental ligand binding free energies for the protein systems examined in this work were compiled in Ref. 8. The CDK259 and P3860 binding free energies were computed from the reported IC50 values using Eq. 28.
| (28) |
The Tyk2,61,62 MCL1,63 and PTP1B64 binding free energies were computed from the reported Ki dissociation constants using Eq. 29
| (29) |
The Thrombin8,65 binding free energies were obtained from isothermal titration calorimetry.
3. Results and Discussion
Figure 1 illustrates the correspondence of the BARnet/MBARnet results with and without cycle closure constraints for the set of 71 MCL1 RBFEs. The RBFEs computed with BARnet and MBARnet are in good agreement and yield similar error estimates. When the MBARnet analysis is treated as the target values, the MCL1 MUE of BARnet is only 0.024 to 0.040 kcal/mol, depending on the use of cycle closure restraints, which is an order of magnitude smaller than the uncertainties in both the BARnet and MBARnet values. Analogous comparisons for the other protein RBFEs yield similar results. The BARnet method requires far fewer reduced potential energies to be stored, which is its primary advantage when performing network-wide analysis. For the specific case of the MCL1 RBFEs, MBARnet analysis requires 37 gigabytes (GB) of potential energy timeseries files, whereas BARnet analysis requires storage of only 12 GB of raw data. Only MBARnet results will be presented and discussed henceforth because of the similarity between the BARnet and MBARnet results.
Figure 1:
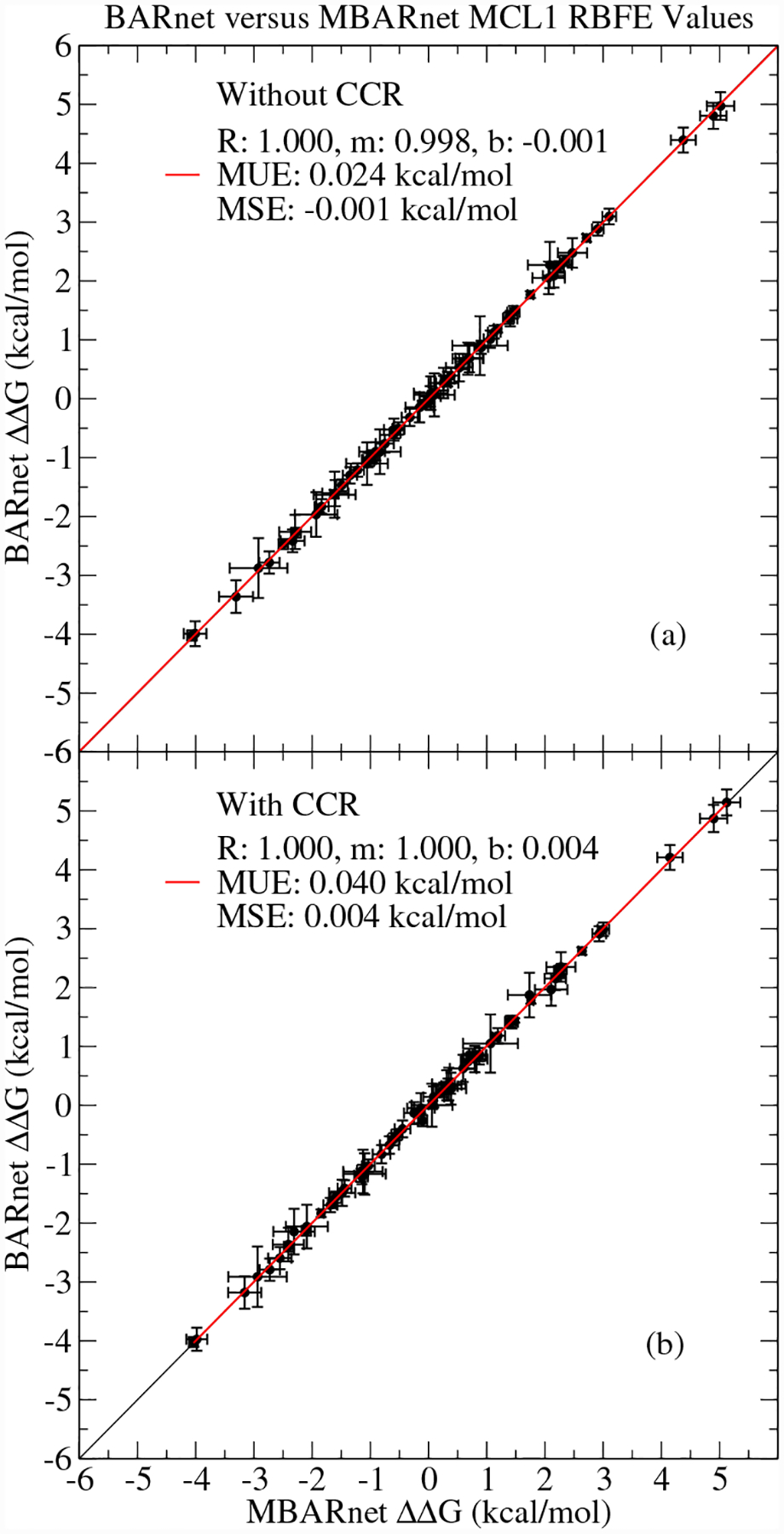
Comparison between BARnet and MBARnet RBFEs for MCL1 both (a) without and (b) with cycle closure restraints. The red line is a linear fit to the data. The error bars are the standard error of the calculated values.
Table 1 summarizes the number of restrained thermodynamic cycles in the RBFE network and the associated error in the free energy closure conditions. The cycles included in the summary only include those thermodynamic paths that cannot be decomposed into two or more smaller cycles. The number of closed paths included in the summary is shown in the column labeled Nres.. The free energy is a state function, so the sum of free energies along a closed path should theoretically be zero. In practice, limited sampling often causes the free energy sum to erroneously be nonzero. We compute the free energy sum for each of the Nres. cycles and report the average and standard deviation of the Nres. error values in the ΣΔG* and σ columns, respectively. The cycle closure errors are less than 1 kcal/mol on average when restraints are not applied. Application of restraints within the optimization procedure lower the cycle closure errors to 0.001 kcal/mol.
Table 1:
Cycle closure information for each system. The Nlig. and Nedge columns list the number of ligands and connected edges in the transformation graph, respectively. The Nres. values are the number of thermodynamic cycles included in the summary. The columns labeled “CCR” and “no CCR” indicate whether cycle closure restraints are applied to the optimization. The ΣΔG* and σ columns report the average and standard deviation of the cycle closure errors, respectively.
| System | Nlig. | Nedge | Nres. | no CCR | CCR | ||
|---|---|---|---|---|---|---|---|
| Σ ΔG* | σ | Σ ΔG* | σ | ||||
| CDK2 | 16 | 25 | 22 | 0.88 | 1.65 | 0.00 | 0.00 |
| P38 | 33 | 54 | 42 | 0.83 | 1.42 | 0.00 | 0.00 |
| MCL1 | 42 | 71 | 70 | 0.91 | 1.20 | 0.00 | 0.00 |
| Tyk2 | 16 | 24 | 18 | 0.24 | 0.35 | 0.00 | 0.00 |
| PTP1B | 23 | 48 | 50 | 0.47 | 0.68 | 0.00 | 0.00 |
| Thrombin | 10 | 10 | 2 | 0.13 | 0.17 | 0.00 | 0.00 |
Table 2 summarizes the edge RBFE mean unsigned errors (MUEs) with and without cycle closure restraints for each protein target, and it further examines how the edge RBFE MUEs are affected when 0, 1, or 2 edges in the graph are constrained to match the experimental RBFE. The MUEs measure the agreement between the calculated RBFEs and corresponding differences between experimental binding free energy values. For a protein target graph consisting of Nedge edges, there are Nedge possible ways of constraining 1 edge. The RBFEs are reoptimized using each of the possible constraint conditions, and the values reported in the table are the mean and standard deviation from the distribution of MUEs. There is only one MUE to consider when there are no experimental constraints, so no standard deviation is reported in this case. When two edges are constrained, there are formally Nedge(Nedge − 1)/2 possible constraint conditions; however, to generate the statistics, we randomly selected 100 constraint conditions to generate the MUE distribution. The use of cycle restraints appears to lower the MUEs in most cases, but the average change (less than 0.1 kcal/mol) is less than the uncertainty of the calculations. The Tyk2 RBFE MUE relative to experiment increased by 0.01 kcal/mol upon enforcement of the cycle closure conditions. This observation emphasizes that there is no guarantee that closure conditions enforcement alone will cause better agreement with experiment. The magnitude of this change is much smaller than the calculation’s uncertainty and a rigorous exploration of systematic bias in the comparison requires a set of highly converged simulation results, which may necessitate further development of enhanced sampling techniques to sufficiently explore the ensemble of bound ligand conformations. As expected, including experimental RBFE constraints decreases the MUEs. When cycle closure restraints are also included, the reduction is amplified because the constraint(s) then effect the solution for the other RBFEs via their coupling through the restraints. The improvements continue to be modest, however, with MUE reductions on the order of 0.1 kcal/mol when two experimental constraints are applied.
Table 2:
MBARnet-calculated RBFE average mean unsigned errors relative to experiment when 0, 1, or 2 graph edges are constrained to match experiment.
| System | Number of Reference (Expt.) Constraints | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | ||||
| no CCR | CCR | no CCR | CCR | no CCR | CCR | |
| CDK2 | 0.95 | 0.93 | 0.91 ± 0.03 | 0.88 ± 0.05 | 0.87 ± 0.04 | 0.82 ± 0.07 |
| P38 | 0.70 | 0.66 | 0.69 ± 0.01 | 0.64 ± 0.02 | 0.68 ± 0.01 | 0.63 ± 0.02 |
| MCL1 | 1.31 | 1.28 | 1.29 ± 0.02 | 1.25 ± 0.04 | 1.27 ± 0.02 | 1.21 ± 0.08 |
| Tyk2 | 0.96 | 0.97 | 0.92 ± 0.03 | 0.91 ± 0.05 | 0.89 ± 0.04 | 0.86 ± 0.06 |
| PTP1B | 0.90 | 0.89 | 0.88 ± 0.02 | 0.85 ± 0.06 | 0.86 ± 0.02 | 0.81 ± 0.07 |
| Thrombin | 0.41 | 0.41 | 0.37 ± 0.04 | 0.37 ± 0.03 | 0.33 ± 0.05 | 0.32 ± 0.05 |
Figure 2 compares the convergence of the MBARnet-analyzed RBFEs with and without cycle restraints. In the context of this figure, our interest is comparing how much data each method requires to approach the force field’s expected result; therefore, the reference RBFEs are computed from MBARnet using all available production data and optimized with cycle restraints. The abscissa of the plots shown in Figure 2 are percentages of the production data used in the analysis. For example, the values shown at 10% are the RBFE MUEs when only the first 1/10th of the production data is analyzed. In addition to illustrating the convergence of the RBFEs with and without cycle restraints, we also make comparison to the maximum likelihood estimator (MLE) method described in Ref. 32 for enforcing cycle closure conditions. Unlike the optimization method described in this work, the MLE method does not enforce cycle closures from the analysis of the raw data. Instead, the MLE method maximizes the following objective function to obtain cycle-corrected estimates of the RBFEs, , provided one’s best estimate of the RBFEs ΔGa→b and their standard errors .
| (30) |
The product operator appearing in Eq. 30 multiplies the normal distributions of each edge, e, in the cycle c.
Figure 2:
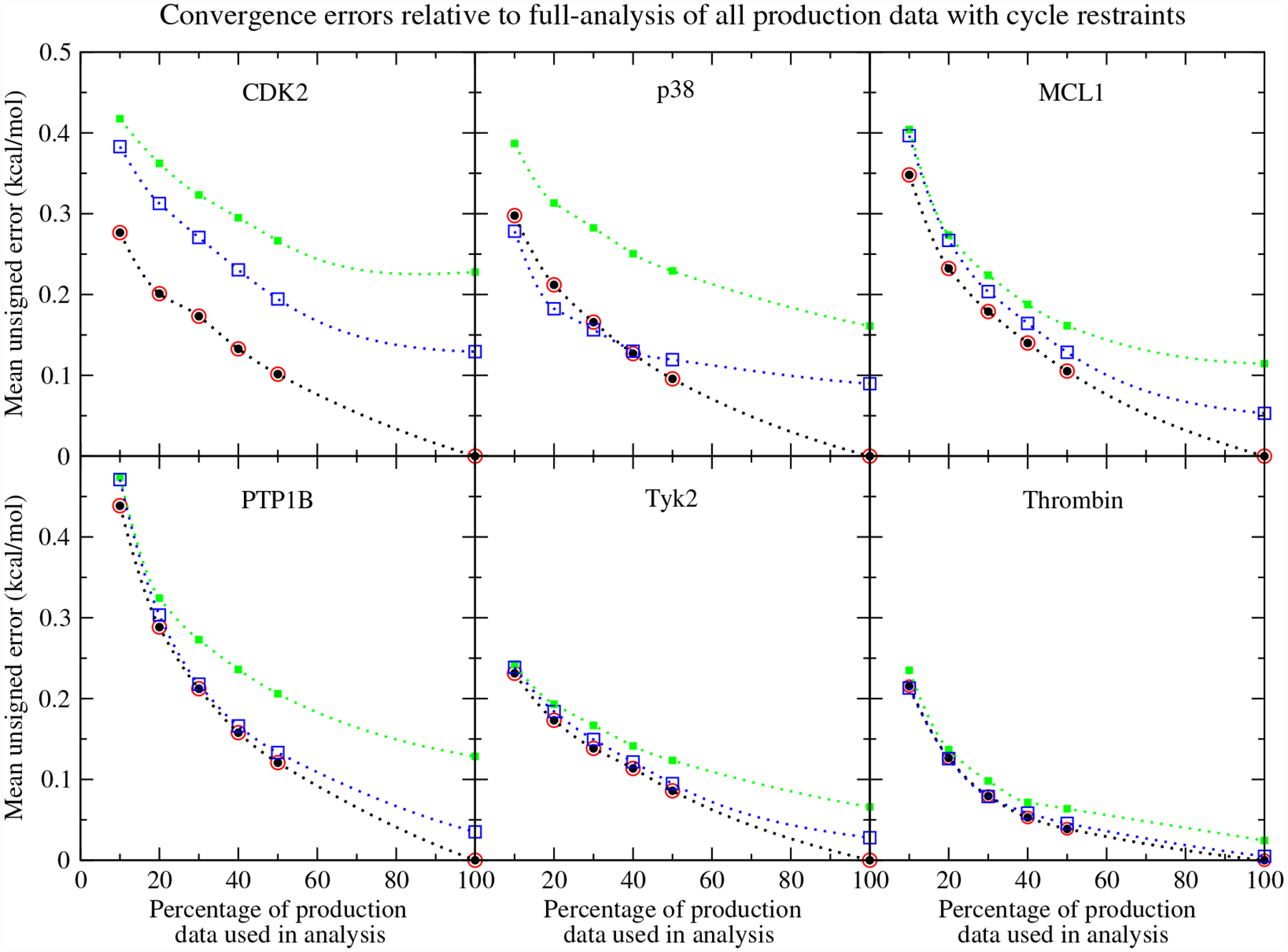
Convergence of the MBARnet mean unsigned errors relative to the MBARnet analysis of all production data with cycle restraints. Filled black circles: MBARnet optimization with cycle restraints. Open red circles: MBARnet optimization with cycle restraints and post-optimization MLE correction. Filled green squares: MBARnet optimization without cycle restraints. Open blue squares: MBARnet optimization without cycle restraints and post-optimization MLE correction.
Figure 2 shows that inclusion of cycle closure restraints in the optimization of partial sets of data produces results that match the analysis of the complete set of data more closely than other approaches. The MBARnet optimizations without cycle closure restraints yield the largest MUEs. Application of the MLE method to our cycle-restrained optimized RBFEs has no effect because, in this case, our RBFEs already enforce the cycle closure conditions. For this reason, the red and black circles appearing in Figure 2 always coincide. When the MLE method is applied to the unrestrained MBARnet results, the RBFE MUEs are reduced, and they appear to approach our cycle-restrained MBARnet results. The extent to which the MLE method succeeds in approaching our cycle-restrained results varies. The MLE method does well for Tyk2 and Thrombin likely because the unrestrained MBAR results on which they are based are already similar to the cycle-restrained values.
4. Conclusions
We develop BARnet and MBARnet methods for use in network-wide free energy analysis with restraints and affine linear constraints. The BARnet and MBARnet results are nearly identical (within 0.04 kcal/mol), however the BARnet objective function requires only a fraction of the amount of disk storage relative to the MBARnet approach. Restraints were used in the non-linear optimization to enforce the closure of thermodynamic cycles within the free energy network, and the constraints were chosen to enforce the reproduction of known RBFEs. The utility of the constraints is demonstrated in situations where a partial list of experimental free energies are known, in which case the solution for the other RBFEs are affected by coupling their solutions through the cycle closure restraints. We analyzed the RBFEs of 6 protein targets and showed that the use of cycle closure restraints yields a modest improvement relative to the experimental RBFEs, and the estimates were improved more substantially when one or two constraints to experimental values were included. The BARnet/MBARnet framework enables efficient and robust free energy analysis with enhanced predictive capability for drug discovery applications.
Acknowledgments
The authors thank Woody Sherman and co-workers for providing us with the energies from their protein-ligand RBFE simulations used to perform the analysis shown in this work. The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485). Computational resources were provided by the National Institutes of Health under grant no. S10OD012346, the Office of Advanced Research Computing (OARC) at Rutgers, the State University of New Jersey, Rutgers Discovery Information Institute (RDI2), the State University of New Jersey, and by the Extreme Science and Engineering Discovery Environment (XSEDE),66 specifically resources COMET and COMET GPU, which is supported by National Science Foundation grant no. ACI-1548562 (allocation number TG-CHE190067). The authors also acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources, specifically the Frontera Supercomputer, that have contributed to the research results reported within this paper. URL: http://www.tacc.utexas.edu
References
- (1).Gallicchio E; Levy RM Recent theoretical and computational advances for modeling protein-ligand binding affinities. Adv. Protein Chem. Struct. Biol 2011, 85, 27–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Gallicchio E Role of Ligand Reorganization and Conformational Restraints on the Binding Free Energies of DAPY Non-Nucleoside Inhibitors to HIV Reverse Transcriptase. Comput. Mol. Bio 2012, 2, 7–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Gallicchio E; Levy RM Advances in all atom sampling methods for modeling protein-ligand binding affinities. Curr. Opin. Struct. Biol 2011, 21, 161–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Boresch S; Tettinger F; Leitgeb M Absolute binding free energies: a quantitative approach for their calculation. J. Phys. Chem. B 2003, 107, 9535–9551. [Google Scholar]
- (5).Lee T-S; Allen BK; Giese TJ; Guo Z; Li P; Lin C; T. DM Jr.; Pearlman DA; Radak BK; Tao Y; Tsai H-C; Xu H; Sherman W; York DM Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. Journal of Chemical Information and Modeling 2020, 60, 5595–5623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Cournia Z; Allen B; Sherman W Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model 2017, 57, 2911–2937. [DOI] [PubMed] [Google Scholar]
- (7).Steinbrecher TB; Dahlgren M; Cappel D; Lin T; Wang L; Krilov G; Abel R; Friesner R; Sherman W Accurate Binding Free Energy Predictions in Fragment Optimization. J. Chem. Inf. Model 2015, 55, 2411–2420. [DOI] [PubMed] [Google Scholar]
- (8).Wang L; Wu Y; Deng Y; Kim B; Pierce L; Krilov G; Lupyan D; Robinson S; Dahlgren MK; Greenwood J; Romero DL; Masse C; Knight JL; Steinbrecher T; Beuming T; Damm W; Harder E; Sherman W; Brewer M; Wester R; Murcko M; Frye L; Farid R; Lin T; Mobley DL; Jorgensen WL; Berne BJ; Friesner RA; Abel R Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (9).Rizzi A; Jensen T; Slochower DR; Aldeghi M; Gapsys V; Ntekoumes D; Bosisio S; Papadourakis M; Henriksen NM; de Groot BL; Cournia Z; Dickson A; Michel J; Gilson MK; Shirts MR; Mobley DL; Chodera JD The SAMPL6 SAMPLing challenge: assessing the reliability and efficiency of binding free energy calculations. J. Comput.-Aided Mol. Des 2020, 34, 601–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Gapsys V; Pérez-Benito L; Aldeghi M; Seeliger D; van Vlijmen H; Tresadern G; de Groot BL Large scale relative protein ligand binding affinities using non-equilibrium alchemy. Chem. Sci 2020, 11, 1140–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Mortier J; Rakers C; Bermudez M; Murgueitio MS; Riniker S; Wolber G The impact of molecular dynamics on drug design: applications for the characterization of ligand-macromolecule complexes. Drug Discovery Today 2015, 20, 686–702. [DOI] [PubMed] [Google Scholar]
- (12).Shivakumar D; Williams J; Wu Y; Damm W; Shelley J; Sherman W Prediction of Absolute Solvation Free Energies using Molecular Dynamics Free Energy Perturbation and the OPLS Force Field. J. Chem. Theory Comput 2010, 6, 1509–1519. [DOI] [PubMed] [Google Scholar]
- (13).Jiang W; Chipot C; Roux B Computing Relative Binding Affinity of Ligands to Receptor: An Effective Hybrid Single-Dual-Topology Free-Energy Perturbation Approach in NAMD. J. Chem. Inf. Model 2019, 59, 3794–3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Wang M; Mei Y; Ryde U Host-Guest Relative Binding Affinities at Density-Functional Theory Level from Semiempirical Molecular Dynamics Simulations. J. Chem. Theory Comput 2019, 15, 2659–2671. [DOI] [PubMed] [Google Scholar]
- (15).Abel R; Wang L; Mobley DL; Friesner RA A Critical Review of Validation, Blind Testing, and Real- World Use of Alchemical Protein-Ligand Binding Free Energy Calculations. Curr. Top. Med. Chem 2017, 17, 2577–2585. [DOI] [PubMed] [Google Scholar]
- (16).de Ruiter A; Boresch S; Oostenbrink C Comparison of thermodynamic integration and Bennett acceptance ratio for calculating relative protein-ligand binding free energies. J. Comput. Chem 2013, 34, 1024–1034. [DOI] [PubMed] [Google Scholar]
- (17).Pickard FC; König G; Simmonett AC; Shao Y; Brooks BR An efficient protocol for obtaining accurate hydration free energies using quantum chemistry and reweighting from molecular dynamics simulations. Bioorg. Med. Chem 2016, 24, 4988–4997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Yang Q; Burchett W; Steeno GS; Liu S; Yang M; Mobley DL; Hou X Optimal designs for pairwise calculation: An application to free energy perturbation in minimizing prediction variability. J. Comput. Chem 2020, 41, 247–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).König G; Brooks BR; Thiel W; York DM On the convergence of multi-scale free energy simulations. Mol. Simul 2018, 44, 1062–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Li Y; Nam K Repulsive Soft-Core Potentials for Efficient Alchemical Free Energy Calculations. J. Chem. Theory Comput 2020, 16, 4776–4789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Liu S; Wu Y; Lin T; Abel R; Redmann JP; Summa CM; Jaber VR; Lim NM; Mobley DL Lead optimization mapper: automating free energy calculations for lead optimization. J. Comput.-Aided Mol. Des 2013, 27, 755–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Loeffler HH; Michel J; Woods C FESetup: Automating Setup for Alchemical Free Energy Simulations. J. Chem. Inf. Model 2015, 55, 2485–2490. [DOI] [PubMed] [Google Scholar]
- (23).Klimovich PV; Mobley DL A Python tool to set up relative free energy calculations in GROMACS. J. Comput.-Aided Mol. Des 2015, 29, 1007–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Bruckner S; Boresch S Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett’s acceptance ratio method. J. Comput. Chem 2011, 32, 1303–1319. [DOI] [PubMed] [Google Scholar]
- (25).Gapsys V; Michielssens S; Seeliger D; de Groot BL pmx: Automated protein structure and topology generation for alchemical perturbations. J. Comput. Chem 2015, 36, 348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Bennett CH Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- (27).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Tan Z; Gallicchio E; Lapelosa M; Levy RM Theory of binless multi-state free energy estimation with applications to protein-ligand binding. J. Chem. Phys 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Kirkwood JG Statistical mechanics of fluid mixtures. J. Chem. Phys 1935, 3, 300–313. [Google Scholar]
- (30).Giese TJ; York DM FE-ToolKit: The free energy analysis toolkit. https://gitlab.com/RutgersLBSR/fe-toolkit.
- (31).Cui D; Zhang BW; Tan Z; Levy RM Ligand Binding Thermodynamic Cycles: Hysteresis, the Locally Weighted Histogram Analysis Method, and the Overlapping States Matrix. J. Chem. Theory Comput 2020, 16, 67–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Wang L; Deng Y; Knight JL; Wu Y; Kim B; Sherman W; Shelley JC; Lin T; Abel R Modeling Local Structural Rearrangements Using FEP/REST: Application to Relative Binding Affinity Predictions of CDK2 Inhibitors. J. Chem. Theory Comput 2013, 9, 1282–1293. [DOI] [PubMed] [Google Scholar]
- (33).Ding X; Vilseck JZ; Hayes RL; Brooks CL Gibbs Sampler-Based λ-Dynamics and Rao-Blackwell Estimator for Alchemical Free Energy Calculation. J. Chem. Theory Comput 2017, 13, 2501–2510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Ding X; Vilseck JZ;; Brooks CL III Fast Solver for Large Scale Multistate Bennett Acceptance Ratio Equations. J. Chem. Theory Comput 2019, 15, 799–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Zhang BW; Xia J; Tan Z; Levy RM A Stochastic Solution to the Unbinned WHAM Equations. J. Phys. Chem. Lett 2015, 6, 3834–3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Powell MJD Algorithms for nonlinear constraints that use Lagrangian functions. Math. Program 1978, 14, 224–248. [Google Scholar]
- (37).Hestenes MR Multiplier and Gradient Methods. J. Optimiz. Theory App 1969, 4, 303–320. [Google Scholar]
- (38).Raju NVS Optimization Method for Engineers; PHI Learning Private Limited: Delhi, 2014. [Google Scholar]
- (39).Bhati AP; Wan S; Hu Y; Sherborne B; Coveney PV Uncertainty Quantification in Alchemical Free Energy Methods. J. Chem. Theory Comput 2018, 14, 2867–2880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Bhati AP; Wan S; Wright DW; Coveney PV Rapid, accurate, precise and reliable relative free energy prediction using ensemble based thermodynamic integration. J. Chem. Theory Comput 2016, 13, 210–222. [DOI] [PubMed] [Google Scholar]
- (41).White AD; Dama JF; Voth GA Designing Free Energy Surfaces That Match Experimental Data with Metadynamics. J. Chem. Theory Comput 2015, 11, 2451–2460. [DOI] [PubMed] [Google Scholar]
- (42).Giese TJ; York DM A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14, 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Davies TG; Bentley J; Arris CE; Boyle FT; Curtin NJ; Endicott JA; Gibson AE; Golding BT; Griffin RJ; Hardcastle IR; Jewsbury P; Johnson LN; Mesguiche V; Newell DR; Noble MEM; Tucker JA; Wang L; Whitfield HJ Structure of human Thr160-phospho CDK2/cyclin A complexed with the inhibitor. Nat. Struct. Biol 2002, 9, 745–749. [DOI] [PubMed] [Google Scholar]
- (44).Friberg A; Vigil D; Zhao B; Daniels RN; Burke JP; Garcia-Barrantes PM; Camper D; Chauder BA; Lee T; Olejniczak ET; Fesik SW Discovery of Potent Myeloid Cell Leukemia 1 (Mcl-1) Inhibitors Using Fragment-Based Methods and Structure-Based Design. J. Med. Chem 2013, 56, 15–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Liang J; Tsui V; Van Abbema A; Bao L; Barrett K; Beresini M; Berezhkovskiy L; Blair WS; Chang C; Driscoll J; Eigenbrot C; Ghilardi N; Gibbons P; Halladay J; Johnson A; Kohli PB; Lai Y; Liimatta M; Mantik P; Menghrajani K; Murray J; Sambrone A; Xiao Y; Shia S; Shin Y; Smith J; Sohn S; Stanley M; Ultsch M; Zhang B; Wu LC; Magnuson S Lead identification of novel and selective TYK2 inhibitors. Euro. J. Med. Chem 2013, 67, 175–187. [DOI] [PubMed] [Google Scholar]
- (46).Wilson DP; Wan Z-K; Xu W-X; Kirincich SJ; Follows BC; Joseph-McCarthy D; Foreman K; Moretto A; Wu J; Zhu M; Binnun E; Zhang Y-L; Tam M; Erbe DV; Tobin J; Xu X; Leung L; Shilling A; Tam SY; Mansour TS; Lee J Structure-Based Optimization of Protein Tyrosine Phosphatase 1B Inhibitors: From the Active Site to the Second Phophotyrosine Binding Site. J. Med. Chem 2007, 50, 4681–4698. [DOI] [PubMed] [Google Scholar]
- (47).Steinbrecher T; Joung I; Case DA Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem 2011, 32, 3253–3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Lee T-S; Hu Y; Sherborne B; Guo Z; York DM Toward Fast and Accurate Binding Affinity Prediction with pmemdGTI: An Efficient Implementation of GPU-Accelerated Thermodynamic Integration. J. Chem. Theory Comput 2017, 13, 3077–3084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Lee T-S; Cerutti DS; Mermelstein D; Lin C; LeGrand S; Giese TJ; Roitberg A; Case DA; Walker RC; York DM GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model 2018, 58, 2043–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).He X; Man VH; Yang W; Lee T-S; Wang J A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys 2020, 153, 114502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (52).Berendsen HJC; Postma JPM; van Gunsteren WF; Dinola A; Haak JR Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- (53).Loncharich RJ; Brooks BR; Pastor RW Langevin dynamics of peptides: the frictional dependence of isomerization rates of N-acetylalanyl-N’-methylamide. Biopolymers 1992, 32, 523–535. [DOI] [PubMed] [Google Scholar]
- (54).Darden T; York D; Pedersen L Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (55).Essmann U; Perera L; Berkowitz ML; Darden T; Hsing L; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (56).Lee T-S; Lin Z; Allen BK; Lin C; Radak BK; Tao Y; Tsai H-C; Sherman W; York DM Improved Alchemical Free Energy Calculations with Optimized Smoothstep Softcore Potentials. J. Chem. Theory Comput 2020, 16, 5512–5525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Nocedal J Updating quasi-Newton matrices with limited storage. Math. Comput 1980, 35, 773–782. [Google Scholar]
- (58).Johnson SG The NLopt nonlinear-optimization package. http://github.com/stevengj/nlopt.
- (59).Hardcastle IR; Arris CE; Bentley J; Boyle FT; Chen Y; Curtin NJ; Endicott JA; Gibson AE; Golding BT; Griffin RJ; Jewsbury P; Menyerol J; Mesguiche V; Newell DR; Noble MEM; Pratt DJ; Wang L-Z; Whitfield HJ N2-Substituted O6-Cyclohexylmethylguanine Derivatives: Potent Inhibitors of Cyclin-Dependent Kinases 1 and 2. J. Med. Chem 2004, 47, 3710–3722. [DOI] [PubMed] [Google Scholar]
- (60).Goldstein DM; Soth M; Gabriel T; Dewdney N; Kuglstatter A; Arzeno H; Chen J; Bingenheimer W; Dalrymple SA; Dunn J; Farrell R; Frauchiger S; La Fargue J; Ghate M; Graves B; Hill RJ; Li F; Litman R; Loe B; McIntosh J; McWeeney D; Papp E; Park J; Reese HF; Roberts RT; Rotstein D; San Pablo B; Sarma K; Stahl M; Sung M-L; Suttman RT; Sjogren EB; Tan Y; Trejo A; Welch M; Weller P; Wong BR; Zecic H Discovery of 6-(2,4-Difluorophenoxy)-2-[3-hydroxy-1-(2-hydroxyethyl)propylamino]-8-methyl-8H-pyrido[2,3-d]pyrimidin-7-one (Pamapimod) and 6-(2,4-Difluorophenoxy)-8-methyl-2-(tetrahydro-2H-pyran-4-ylamino)pyrido[2,3-d]pyrimidin-7(8H)-one (R1487) as Orally Bioavailable and Highly Selective Inhibitors of p38α Mitogen-Activated Protein Kinase. J. Med. Chem 2011, 54, 2255–2265. [DOI] [PubMed] [Google Scholar]
- (61).Liang J; Tsui V; Van Abbema A; Bao L; Barrett K; Beresini M; Berezhkovskiy L; Blair WS; Chang C; Driscoll J; Eigenbrot C; Ghilardi N; Gibbons P; Halladay J; Johnson A; Kohli PB; Lai Y; Liimatta M; Mantik P; Menghrajani K; Murray J; Sambrone A; Xiao Y; Shia S; Shin Y; Smith J; Sohn S; Stanley M; Ultsch M; Zhang B; Wu LC; Magnuson S Lead identification of novel and selective TYK2 inhibitors. Euro. J. Med. Chem 2013, 67, 175–187. [DOI] [PubMed] [Google Scholar]
- (62).Liang J; van Abbema A; Balazs M; Barrett K; Berezhkovsky L; Blair W; Chang C; Delarosa D; DeVoss J; Driscoll J; Eigenbrot C; Ghilardi N; Gibbons P; Halladay J; Johnson A; Kohli PB; Lai Y; Liu Y; Lyssikatos J; Mantik P; Menghrajani K; Murray J; Peng I; Sambrone A; Shia S; Shin Y; Smith J; Sohn S; Tsui V; Ultsch M; Wu LC; Xiao Y; Yang W; Young J; Zhang B; Zhu B.-y.; Magnuson S Lead Optimization of a 4-Aminopyridine Benzamide Scaffold To Identify Potent, Selective, and Orally Bioavailable TYK2 Inhibitors. J. Med. Chem 2013, 56, 4521–4536. [DOI] [PubMed] [Google Scholar]
- (63).Friberg A; Vigil D; Zhao B; Daniels RN; Burke JP; Garcia-Barrantes PM; Camper D; Chauder BA; Lee T; Olejniczak ET; Fesik SW Discovery of Potent Myeloid Cell Leukemia 1 (Mcl-1) Inhibitors Using Fragment-Based Methods and Structure-Based Design. J. Med. Chem 2013, 56, 15–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Wilson DP; Wan Z-K; Xu W-X; Kirincich SJ; Follows BC; Joseph-McCarthy D; Foreman K; Moretto A; Wu J; Zhu M; Binnun E; Zhang Y-L; Tam M; Erbe DV; Tobin J; Xu X; Leung L; Shilling A; Tam SY; Mansour TS; Lee J Structure-Based Optimization of Protein Tyrosine Phosphatase 1B Inhibitors: From the Active Site to the Second Phophotyrosine Binding Site. J. Med. Chem 2007, 50, 4681–4698. [DOI] [PubMed] [Google Scholar]
- (65).Baum B; Mohamed M; Zayed M; Gerlach C; Heine A; Hangauer D; Klebe G More than a Simple Lipophilic Contact: A Detailed Thermodynamic Analysis of Nonbasic Residues in the S1 Pocket of Thrombin. J. Mol. Biol 2009, 390, 56–69. [DOI] [PubMed] [Google Scholar]
- (66).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD; Roskies R; Scott JR; Wilkins-Diehr N XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]


