In-vivo evaluation of needle force and friction stress during insertion at varying insertion speed into the brain

Abstract

Background

Convection-enhanced delivery (CED) infuses drugs directly into brain tissue. Needle insertion is required and results in tissue damage which can promote flowback along the needle track and improper targeting. The goal of this study was to evaluate friction stress (calculated from needle insertion force) as a measure of tissue contact and damage during needle insertion for varying insertion speeds.

New method

Forces and surface dimpling during needle insertion were measured in rat brain in vivo. Needle retraction forces were used to calculate friction stresses. These measures were compared to track damage from a previous study. Differences between brain tissues and soft hydrogels were evaluated for varying insertion speeds: 0.2, 2, and 10 mm/s.

Results

In brain tissue, average insertion force and surface dimpling increased with increasing insertion speed. Average friction stress along the needle-tissue interface decreased with insertion speed (0.58 ± 0.27 to 0.16 ± 0.08 kPa). Friction stress varied between brain regions: cortex (0.227 ± 0.27 kPa), external capsule (0.222 ± 0.19 kPa), and CPu (0.383 ± 0.30 kPa). Hydrogels exhibited opposite trends for dimpling and friction stress with insertion speed.

Comparison with existing methods

Previously, increasing needle damage with insertion speed has been measured with histological methods. Friction stress appears to decrease with increasing tissue damage and decreasing tissue contact, providing the potential for in vivo and real time evaluation along the needle track.

Conclusion

Force-derived friction stress decreased with increasing insertion speed and was smaller within white matter regions. Hydrogels exhibited opposite trends to brain tissue.

1. Introduction

Modern clinical techniques developed to diagnose or treat neurological diseases have come to include the insertion and implantation of devices like needles, probes, and electrodes in affected central nervous system (CNS) tissues. With implantation, surrounding soft brain tissue is mechanically damaged, e.g. torn, stretched, or compressed. Thus, the mechanics of insertion can have a direct effect on the resulting tissue-implant interface. In addition, localized injury such as edema, hemorrhage, and glial reaction is introduced (Edell et al., 1992; Manaencko, et al. 2011; White et al., 2011; Xue and Del Bigio, 2003). In this study, we are focusing on convection-enhanced delivery (CED) which is one of few local drug delivery methods that bypass the blood brain barrier (BBB) and provides large distribution volumes for macromolecular agents. It is an infusion-based method in which a cannula or needle is surgically implanted and infusate is pumped directly into CNS tissues to enhance extracellular transport (Bobo et al., 1994). For controlled flow rates, this procedure has been conducted without side effects or histological evidence of major tissue damage (Degen et al., 2003). However, localized tissue damage changes tissue-infusate interactions around the needle and this can influence drug targeting, e.g. the extent of infusate that flows back along the needle track (backflow) (Chen et al.,1999; Raghavan et al., 2006). Therefore, insertion tissue damage may limit the potential of CED treatment and new methods to evaluate insertion events in real-time are needed.

The extent of brain tissue damage is dependent on the mechanics of the needle insertion. Needle force measurement is a useful tool to evaluate tissue response to deformation and damage as a function of insertion depth and speed (Andrei et al., 2012; Peidong et al., 2012; van Gerwen et al., 2012; Welkenhuysen, et al., 2011). High insertion forces are generally associated with a larger extent of tissue damage across tissue types (Mahvash and Dupont, 2010; Peidong et al., 2012; van Gerwen et al., 2012). Therefore, monitoring of insertion force may be a simple way to evaluate the influence of insertion parameters on damage in vivo and in real time. In brain tissue, increased insertion force has been previously observed with high speed insertion of neural probes (Andrei et al., 2012). Also with needle insertion, the surface of the brain is primarily displaced downward in the axial direction before surface puncture. This surface dimpling (surface deformation before puncture) introduces large deformations of tissue under the needle tip (DiMaio and Salcudean, 2003) and corresponding stored energy is released with puncture. Therefore, tissue dimpling may also predict the extent of tissue damage introduced with implantation. Previous electrode insertion studies have found surface dimpling to increase with increasing insertion speeds (Andrei et al., 2012).

Insertion factors like needle diameter, needle tip geometry and insertion speed affect tissue damage and insertion force (Alterovitz et al. 2003; Peidong et al., 2012). Relatively few studies have looked at how insertion speed affects local tissue damage in CNS (Polikov et al., 2005). Previous ex vivo electrode insertion studies by Bjornsson et al. show less vasculature rupture at higher insertion speeds which suggests less tissue damage with increasing insertion speed (Bjornsson, et al., 2006). Other electrode insertion studies find greater insertion force and increasing tissue deformations for a higher speed (0.1 mm/s) in comparison with lower insertion speed (0.05 and 0.01 mm/s) suggesting greater tissue damage for fast insertion (Andrei et al., 2012). In contrast, electrodes inserted at slower speeds have shown better performance, which is thought to be due in part to less initial tissue damage (Nicolelis et al., 2003).

In previous studies by our group, the influence of needle insertion speed on tissue damage and local tissue stresses was evaluated in a tissue phantom material and in rat brain (Casanova et al., 2012; Casanova et al., 2014). Holes left in tissue slices were used to evaluate damage and corresponding changes in the compressive radial stress at the needle-tissue interface (pre-stress) for varying insertion speeds. Pre-stress provided a spatially-varying measure of tissue compression at the needle interface. Tissue damage increased while pre-stress decreased for increasing insertion speed. Under the same conditions, the effect of needle insertion speed on damage and CED backflow in hydrogels (Casanova et al., 2012) was found to be opposite that in brain tissue (Casanova et al., 2014). Local tissue swelling also increased pre-stress with time. Therefore, to better characterize the influence of needle insertion speed on acute tissue damage, pre-stress or an equivalent measure should be evaluated during in vivo insertion.

Brain tissue is heterogeneous. Therefore, mechanical response and acute tissue damage are influenced by differences in tissue composition in different regions along the needle pathway, e.g. gray matter vs. white matter regions (Elkin et al., 2011; Lee et al., 2014). In our previous study (Casanova et al., 2014), we found that the heterogeneity of brain tissue affected tissue damage and interfacial pre-stresses. Greater damage (larger holes) and smaller pre-stresses were found in white matter regions compared to gray matter regions, possibly due to pre-existing tensile residual stresses in white matter regions (Xu et al., 2009). During insertion, needle forces, deformation, pre-stresses, and damage are also expected to vary regionally due to differences in stiffness (Elkin et al., 2011; Lee et al., 2014) and failure strength (Franceschini et al., 2006).

In this study, needle insertion force was used to provide improved understanding of the influence of speed and brain region on the mechanics of brain tissue penetration. Measurements were performed in vivo in rat brain. Force measurements were used to calculate friction stress (product of pre-stress and friction coefficient) at the needle-tissue interface (Sharp et al., 2009). Similar to our previous measures of pre-stress, friction stress values were used to evaluate variation in tissue contact at different insertion speeds and in different brain regions along the needle track. Friction stress was then evaluated as a quantitative indicator of local tissue damage by comparing results with measures of tissue damage from histology and a previous study with the same insertion conditions (Casanova et al., 2014). In addition, the magnitude of surface deformation before needle penetration (surface dimpling) was measured. Agarose hydrogel has been used as a tissue phantom for needle insertion and brain infusion studies (Chen et al., 2004; Raghavan et al., 2010). In our previous studies (Casanova et al., 2011; Casanova et al., 2014), we have also evaluated insertion damage in tissue surrogate hydrogels. Insertion force, friction stress and dimpling were further tested as indicators of the extent of tissue contact and damage in this material with different failure behavior. Overall, this study provides a new methodology to evaluate the mechanics of insertion in real time and as a function of insertion speed and depth. In CED, acute tissue damage at the needle-tissue interface can result in flow of the infusate back along the needle track. This backflow phenomenon is directly dependent on the extent of tissue contact and damage at the needle-tissue interface, with lower friction stress resulting in the likelihood of more backflow. In future studies, established metrics may be used to predict extent of interfacial tissue stress. These data may also be used to improve insertion processes for needles or electrodes in the brain.

2. Methodology

2.1. Animal preparation and surgical procedures

Experiments were performed on 15 young male Sprague-Dawley rats (300 – 350 g) using protocols and procedures approved by the University of Florida Institutional Animal Care and Use Committee. Anesthesia was initiated with xylazine (10 mg/kg, SQ) and isoflurane (4%) in oxygen delivered at 1 L/min. The head was shaved and disinfected with iodine/alcohol cotton swabs. Then animals were placed on a stereotaxic frame (model 900, David Kopf Instruments, Tujunga, CA), and inhalation anesthesia (1.5% in 0.5 L/min of oxygen) was delivered via a nose mask. Body temperature was maintained (~37°C) by means of a heating pad during the entire procedure. The skull was exposed by a mid-sagittal incision that began between the eyes and extended caudally to the level of the ears to expose bregma and lambda. Two holes with 2 mm diameter were drilled into the skull above the right and the left caudate putamen (CPu) (AP = 0.5, ML = ± 3, DV = −5). In this way, bilateral needle insertions were conducted on each rat. The CPu region was chosen because it is a relatively homogeneous region composed mainly of gray matter and has been used previously in CED backflow studies (Chen et al., 1999; Neeves et al., 2006). To reach the CPu, the needle passed through the cortex (mostly gray matter) and the external capsule (mostly white matter). Fig. 1 shows a coronal section of the rat brain (Paxinos and Watson, 1989) where the position of the needle is schematically represented. The dura mater was considered to be a tough membrane covering which would add excessive surface deformation during needle insertion. Therefore, the dura mater was carefully removed. Blood was removed from the exposed surface of the brain and tissue was kept hydrated during the entire experiment with 1X phosphate-buffered saline (1XPBS). At the end of experiments, three of the rats were euthanized by perfusion fixation (1XPBS and 10% formalin) as explained in section 2.3. The rest of the rats were euthanized by overdose of isoflurane (5%) in oxygen delivered at 1 L/min followed by decapitation.

Fig. 1.

Coronal section of the rat brain showing a schematic of the needle track (in red) targeting the caudate putamen (CPu). Slice image from (Paxinos and Watson, 1989).

2.2. Force measurements in brain tissue

A 32 g stainless steel needle (outer diameter = 0.235 mm, Hamilton Company, Reno, NV) with a blunt tip was used for insertion tests. Blunt tips have been used in clinical trials (Sampson et al., 2010), as well as in our previous studies (Casanova et al., 2012; Casanova et al., 2014). Moreover, even though new cannulas to minimize backflow have being designed (Rosenbluth et al., 2011; Yin et al., 2010), the geometry at the tip of these cannulas are usually similar to a basic blunt tip needle. To minimize tissue coring (tissue entering into the needle tip), the inner lumen of the needle was filled with cyanoacrylate glue. Based on our previous needle studies (Casanova et al., 2012; Casanova et al., 2014), three insertion speeds were used: 0.2, 2, and 10 mm/s. Experiments were repeated 10 times for each insertion speed.

Needle insertion was controlled using a linear stage system (LP28T, Applied Motion Products, Watsonville, CA) mounted on a metal frame as described in (Casanova et al., 2013). The stereotaxic frame and rat were placed on an x-y table to position the rat under the needle such that drilled holes in the rat skull (target coordinates AP = 0.5 and ML = ±3) were aligned with the needle tip. Needle insertion and retraction forces were measured with an axial tension/compression miniature load cell (model 31, Honeywell-Sensotec, Columbus, OH). The needle was attached to the load cell with a custom polyether ether ketone (PEEK) holder which also provided axial alignment. Load cell signal was recorded at varying rate depending on the insertion speed: 1 kHz (0.2 mm/s), 5.8 kHz (2.0 mm/s), and 17.5 kHz (10 mm/s).

Before needle insertion, a baseline signal was recorded from the load cell over ~5 s to provide a zero-force level. The zero position was set by positioning the needle tip on the brain tissue surface. To insert at constant velocity inside tissue, the needle was moved upward 5 mm before start of testing to allow initial acceleration of the needle (300 mm/s²) outside of the tissue. The needle was considered to be in contact with the tissue surface once the measured force increased above noise level (0.06 mN). Needles were inserted to a depth of 5 mm into the CPu, then stopped and left in place for 2 min before being retracted at 0.2 mm/s. The needle was cleaned with hydrogen peroxide (3%) followed by 1XPBS after each retraction.

The recorded force profile was used to determine the peak force at the point of surface puncture (F_in), the force measured at needle stop (F_stop), 2 min after the needle was at rest (F_rest), the average force from the tissue puncture until the needle was stopped (F_avg), the maximum force during needle retraction (F_drag), the depth or location of the peak dragging force (D_drag) and the average force during the needle retraction (R_avg). Surface dimpling (D_in) defined as the difference between the spatial coordinate where the needle made contact with the tissue surface and the point of tissue puncture was also determined. Force during retraction was used to calculate friction stress as explained in section 2.5. To reduce high frequency force variation, e.g. systole-associated brain pulsatility, force was filtered using a low pass filter with a cutoff frequency of 2.5 Hz.

2.3. Tissue histology

After needle retraction, three of the rats from force measurement experiments were immediately euthanized by perfusion fixation (200–300 ml of 1X PBS followed by 300 ml of 10% formalin). After perfusion, brains were extracted from the skull and stored in formalin (10%) overnight. Then brains were moved to sucrose (30%) for 2 days. Rat brains were sliced into 50 μm thick slices in the transverse plane (perpendicular to the needle) using a cryostat (~−20°C). Tissue slices were mounted on microscope slides and standard methods for Hematoxylin and Eosin (H&E) staining were followed (White et al., 2011). Stained slices were imaged using an optical microscope (model IX-71, Olympus America Inc., Center Valley, PA) and a digital camera (model SPOT RT3, Diagnostic Instruments, Inc., Sterling Heights, MI) with bright light.

2.4. Force measurement in agarose hydrogel

The methodology for force measurements on hydrogels was the same as described for brain tissue. 0.6% (w/v) agarose-based hydrogel (TreviGel 5000, Trevigen Inc., Gaithersburg, MD) was prepared by mixing and heating agarose powder in deionized water. Mixtures were then poured into Petri dishes (10 mm thickness) and allowed to solidify at room temperature. After solidification, a thin layer (~1 mm) of deionized water was maintained on top of samples to prevent dehydration.

2.5. Friction stress model

An approach similar to that used in a previous study (Sharp et al., 2009) was used to calculate friction stress at each point along the needle track during retraction. Friction stress is defined as the product of the pre-stress and the friction coefficient. This value is used since the friction coefficient for in vivo needle insertion in brain tissue has not been previously reported. This model assumes that there is contact between the needle tip and tissue as the needle is being retracted and that this generates contact stresses in normal (σ_r) and axial directions (τ_f), see Fig. 2. The radial contact stress is defined as the pre-stress, and the axial shear stress is the friction stress which contributes to the axial force measured by the load cell.

Fig. 2.

Schematic representation of stresses and forces acting on the needle during needle retraction in tissue (l = length of the needle in contact with tissue at time t, F = measured retraction force, σ_r = pre-stress, and τ_f = friction stress)

Friction stress and pre-stress are related by

$${\tau }_r=\mu {\sigma }_r$$ (1)

where μ is the friction coefficient which is produced by either contact between the needle and the solid components of tissue, or viscous fluid forces created by a layer of fluid between the needle and the tissue, or a combination of these effects. To avoid velocity-dependent variation in this coefficient, retractions were all performed at the same speed.

It was assumed that contact tissue stresses were not necessarily constant along the length of the track. Applying balance of forces to the needle provided a relation between retraction force and pre-stress at each point in time,

$$\underset{A}{\int }{\tau }_{f}dA=\underset{0}{\overset{l}{\int }}\mu {\sigma }_r\pi \mathit{Ddz}=F$$ (2)

where dA is the differential surface area of tissue contact, l is the length of the needle in contact with tissue, d is the differential spatial coordinate, and D is the needle diameter. The fundamental theorem of calculus was then used to calculate the spatial derivative and determine the relation between radial stress at the tip of the needle σ_r(z) and the measured axial force.

$${\sigma }_r(z)=\frac{1}{\pi \mu D}\frac{dF}{dz}$$ (3)

The force derivative was calculated using the forward difference method in intervals of ~0.1 mm.

2.6. Statistical analysis

Average dimpling slope (S_dim), surface dimpling (D_in), penetration force (F_in), force at the end of insertion (F_stop), average rest force (F_rest), dragging force (F_drag), depth of maximum dragging force (D_drag), were compared for the three insertion speeds by using one-way analysis of variance (ANOVA). Because the insertion force along the needle track presented a non-Gaussian distribution, ANOVA was not used for the comparison between average insertion force within tissue (F_avg), average retraction force (R_avg), and friction stresses for the three insertion speeds and considering all the points along the needle track. Instead the Kruskal-Wallis test was used. This test was also used to compare friction stresses at the different regions in the brain along the needle track. Data are presented as mean ± 1standard deviation. All p-values <0.05 were considered significant.

3. Results

3.1. Needle insertion in brain tissue

A typical force vs. time curve for in vivo needle insertion into the CPu is shown in Fig. 3. After the needle made contact with tissue, the force increased approximately linearly until the tissue was punctured or penetrated. After surface penetration, the force sometimes decreased slightly and then increased again. After puncture, the force increased with insertion depth until approximately ~3 mm depth. With greater insertion depths, the force did not show a clear increasing or decreasing trend and varied with spatial location. Once the needle stopped, the force decreased before reaching an approximately constant value.

Fig. 3.

Typical axial force measured during needle insertion into the caudate putamen (CPu) (F_in : surface puncture force, F_stop : force at the stop of insertion). This experiment was conducted in vivo at a 0.2 mm/s insertion speed.

Surface penetration was characterized by surface dimpling, the slope (S_dim) of the force vs. distance curve between the surface contact point and puncture, and the force at puncture (F_in), see Table 1. Of these values, dimpling was found to be sensitive to increasing insertion speed, with a significant difference between the lowest (0.2 mm/s) and highest (10 mm/s) speeds. Also, F_in at 0.2 mm/s was significantly smaller than at the higher speeds tested. There was no significant difference in F_in between 2 mm/s and 10 mm/s (p-value = 0.6). S_dim did not significantly vary with insertion speed (p-value = 0.2).

Table 1.

Needle insertion and retraction measurements for brain tissue and 0.6% hydrogel: dimpling slope (S_dim), surface dimpling (D_in), penetration force (F_in), average insertion force within tissue (F_avg), force at the end of insertion (F_stop), average rest force (F_rest), dragging force (F_drag), depth of maximum dragging force (D_drag), and average retraction force (R_avg). Data are presented as the average of n = 10 measures ± 1 standard deviation.

		Brain tissue		Hydrogel
Speed	0.2 mm/s	2 mm/s	10 mm/s	0.2 mm/s	2 mm/s	10 mm/s
Sdim (mN/mm)	1.45 ± 1.22	2.32 ± 1.68	1.95 ± 0.85	1.92 ± 0.21a	2.51 ± 0.17	2.52 ± 0.09
Din(mm)	0.65 ± 0.17a	0.74 ± 0.23	0.90 ± 0.22a	1.15 ± 0.02a	1.06 ± 0.02a	0.94 ± 0.02a
Fin(mN)	0.92 ± 0.60a	1.60 ± 0.92	1.77 ± 1.01	22.11 ± 2.5	26.77 ± 1.8a	23.82 ± 1.2
*Favg(mN)	1.51 ± 0.50a	2.2 ± 0.75a	3.51 ± 0.92a	11.8 ± 8.7a	3.83 ± 2.4a	4.29 ± 2.3a
Fstop(mN)	2.29 ± 0.80a	3.02 ± 0.43a	4.42 ± 0.51a	4.51 ± 2.0	3.96 ± 0.85	4.32 ± 1.20
Frest(mN)	1.05 ± 0.22a	0.62 ± 0.02a	0.26 ± 0.15a	1.75 ± 0.15	0.79 ± 0.12	0.53 ± 0.19
Fdrag(mN)	2.49 ± 0.52a	2.00 ± 0.33a	1.17 ± 0.46a	1.01 ± 0.19	0.64 ± 0.13a	1.11 ± 0.30
Ddrag(mm)	4.39 ± 0.01a	4.58 ± 0.11a	4.75 ± 0.06a	4.79 ± 0.05a	4.91 ± 0.01	4.91 ± 0.01
*Ravg(mN)	0.83 ± 0.51a	0.61 ± 0.32a	0.25 ± 0.15a	0.06 ± 0.05a	0.26 ±0.13a	0.28 ± 0.15a

^adenotes significant difference from other values with respect to insertion speed (p-values < 0.05).

^*indicates the Kruskal-Wallis test was used. Other parameters were compared using one way ANOVA

Insertion forces (average value at each depth point) from the point when the needle made contact with tissue until the needle was stopped are shown in Fig. 4a through 4c. Within brain tissues, insertion force was found to increase with increasing insertion speed. These data were also averaged along the tissue track (F_avg) after surface puncture until the needle was stopped, see Table 1. Higher insertion speeds resulted in higher F_avg, where each value was significantly different from the others (p-value <0.05 in all cases). Also, force at the end of insertion (F_stop) was found to significantly increase with insertion speed.

Fig. 4.

Insertion force in brain (left column) and 0.6% hydrogel (right column) for three different needle insertion speeds: 0.2 mm/s (1^st row), 2 mm/s (2^nd row), and 10 mm/s (3^rd row). Graphs show average +/− 1SD at each depth, n=10, from the point of surface contact to when the needle was stopped (F_stop).

3.2. Needle insertion in hydrogel

In hydrogel, surface dimpling was significantly different for each insertion speed and decreased with increasing insertion speed, which was opposite to the trend observed in brain tissues. Fig. 4d through 4f show insertion force vs. displacement in hydrogel. Compared to brain tissue, a higher peak force was measured at surface puncture (>13-fold), see Table 1. F_in at 2 mm/s was significantly higher than F_in for 0.2 and 10 mm/s, and there was no difference between F_in at 0.2 and 10 mm/s (p-value = 0.058). For the insertion speeds of 0.2 and 2 mm/s, a second peak force (38.15 ± 2.2 mN and 7.1 ± 0.7 mN) was also observed (in 9 out of 10 trials). No clear second peak was observed at 10 mm/s. There was no difference in S_dim between insertion speeds of 2 and 10 mm/s (p-value = 0.8).

F_avg was found to be different for each of the insertion speeds tested, see Table 1, and higher than measured in brain tissues (>1.19-fold). F_avg increased with increasing insertion speed, which is also opposite to the trend found in brain tissue. Although F_stop presented maximum values at 0.2 mm/s and minimum values at 2 mm/s insertion speed, the difference among the three averages values was not significant. Thus for hydrogels, force measures did not show clear sensitivity over the range of insertion speed tested. Surface dimpling was more sensitive to the rate of needle insertion.

3.3. Needle retraction in brain tissue

With needle retraction, needle force changed from a compressive resting force value (+ sign), to a tensile value (− sign), see Fig. 5. This tensile, pulling force reached a maximum magnitude value (F_drag) before decreasing to approximately zero as the needle reached the surface of the brain. Initially, measured axial needle forces were the combination of friction force and the elastic response of compressed tissues at the needle tip. With sufficient distance, there was loss of normal contact with tissue at the needle tip (peak value) and needle force was due to friction only. This frictional needle force decreased in magnitude with decreasing contact surface area as the needle was retracted from tissue.

Fig. 5.

Typical needle retraction force vs. time for brain tissue. Retraction speed was 0.2 mm/s; insertion speed was 0.2 mm/s. Retraction was started 2 min after the end of the insertion. Positive force values correspond to compression and negative values correspond to tension. Dotted red line denotes the start time for retraction.

Variation in retraction force with depth and insertion speed is shown in Fig. 6a. Resting forces (F_rest) were found to be smaller with increasing insertion speeds (Table 1) with statistically significant difference. Retraction forces were found to decrease with decreasing needle insertion speed. Peak dragging force (F_drag) decreased with decreasing insertion speed, see Table 1. The location of the maximum dragging force (D_drag) was significantly different for the three insertion speeds. It was shallower for slow insertion (Fig. 6a) which means that for this speed, tissue is in normal contact with tissue at the tip over a longer distance. The average retraction forces over the entire needle track length (R_avg) also decreased with decreasing insertion speed and were all significantly different from each other (Table 1).

Fig. 6.

Needle retraction force vs. depth for varying insertion speeds in: a) brain tissue (average for n=10) and b) 0.6% agarose hydrogel (average for n = 10). Retraction speed was 0.2 mm/s in all the experiments. Resting and dragging forces are indicated on the force profile for a needle inserted at 2 mm/s.

3.4. Needle retraction in hydrogel

Compared with brain tissue, opposite rate-dependent behavior was found for retraction force (Table 1). Hydrogel retraction force, Fig. 6b, decreased with increasing insertion speed. Average dragging force (F_drag) was smallest for the 2 mm/s insertion speed. Average retraction force (R_avg) increased for increasing insertion speed.

3.5. Friction stress in brain tissue

The needle retraction force (between the peak dragging force and the brain surface) was used to determine the friction stress between the needle and tissue. The location of the peak dragging force varied with needle insertion speed. Slower insertion speed resulted in decreasing D_drag depths. Thus, friction stresses were not calculated for depths between 4.5 and 5 mm. Fig. 7a, 7b, and 7c show the calculated friction stresses along the needle track for varying insertion speeds. Spatial variation in friction stress was found with a minimum value between 2 and 3 mm depths, which corresponded to the white matter region of the external capsule. The friction stress was higher for slower insertion speeds, and it was close to zero for the entire needle track for the highest insertion speed (10 mm/s). The difference in friction stress between insertion speeds was significant except at ~2.8 mm depth and close to the surface of the brain (Fig. 7d).

Fig. 7.

Friction stress vs. needle depth for varying insertion speeds in brain tissue (a, b, and c), and 0.6% agarose hydrogel (e, f, and g). Each data point corresponds to the average of n = 10 measures. To evaluate significant differences in friction stress with insertion speed at each depth, p-values in (d) brain tissue and (h) hydrogel are also shown. A line is drawn at p = 0.05.

Friction stress for the three main regions along the needle track, cortex, external capsule and CPu, are listed in Table 2. Average friction stress in the CPu was calculated to be significantly greater than in other regions. There was no significant difference between average friction stress in the cortex and external capsule (p-value = 0.15). In all three regions, the friction stress decreased with increasing insertion speed. The track average friction stress (average for all three regions, see Table 2) for each insertion speed was closer to the average value found in the CPu. Track average friction stresses at different insertion speeds were significantly different from each other.

Table 2.

Average friction stress (kPa) values for varying needle insertion speeds along the entire needle track and within each brain region: caudate putamen (CPu), external capsule (ec), and cortex. Friction stresses for hydrogel are also included.

Speed	0.2 mm/s	2 mm/s	10 mm/s
Track-averaged	0.585 ± 0.47a	0.390 ± 0.34a	0.167 ± 0.18a
CPu	0.792 ± 0.47ab	0.552 ± 0.30ab	0.215 ± 0.19ab
ec	0.394 ± 0.30a	0.352 ± 0.22b	0.156 ± 0.17a
Cortex	0.483 ± 0.45ab	0.299 ± 0.33ab	0.140 ± 0.17ab
Hydrogel	0.070 ± 0.06a	0.142 ± 0.06a	0.171 ± 0.04a

^adenotes significant difference among average values inside the same region with respect to insertion speed (p-values < 0.05, Kruskal-Wallis test).

^bdenotes significant difference with respect to brain region for the same insertion speed (p-values < 0.05)

3.6. Friction stress in hydrogel

When the needle was inserted at 0.2 mm/s, the friction stress was close to zero for the middle part of the needle track and was higher near the end and at the surface of the hydrogel sample (Fig. 7e). For higher insertion speeds, the friction stress was more uniform along the needle track and, in general, higher than that obtained at 0.2 mm/s (Fig. 7f, and 7g). The difference in friction stress between insertion speeds was significant along the majority of the track, although not significant at the needle tip and close to the surface (Fig. 7h). The average friction stresses for hydrogel are also included in Table 2. All the three averages were significantly different.

3.7. Histology

H&E images in cortical tissue show a layer with slightly different intensity attributed to bleeding around the hole created by the needle (Fig. 8). This intensity difference was not observed in other regions of the external capsule or caudate putamen.

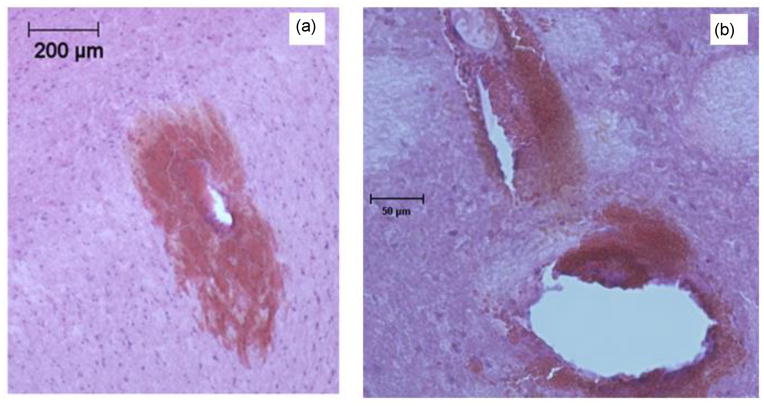
Fig. 8.

H&E stained cortical brain tissue slices showing tissue damage for needles inserted at: a) 0.2 mm/s, b) 2 mm/s, and c) 10 mm/s. H&E staining was in 50 μm fixed tissue slices following needle retraction. All images are at the same magnification.

The main characteristic observation was increasing hole size with increasing insertion speed. Another main difference between insertion speeds was greater hemorrhage and tissue fracturing observed for higher insertion speeds, mainly in the white matter region of the external capsule (Fig. 9a). Although in some cases, similar damage was also found in the caudate putamen (Fig. 9b). Tissue fracturing was defined as a crack or narrow opening in interior regions of the tissue slice with bleeding. Blood that was present in the extracellular space before the rat death is not cleared with perfusion fixation. Therefore, the presence of blood indicated that fracturing occurred in vivo and not during the tissue processing, e.g. slicing and mounting. Cracks ranging between 20 and 150 μm were observed in the external capsule and caudate putamen.

Fig. 9.

H&E stains showing needle tissue damage: a) hemorrhage in white matter region of external capsule; b) tissue fracture and hemorrhage in the caudate putamen. Needle insertion speed was 10 mm/s. Images are of 50 μm fixed brain tissue slices.

4. Discussion

Needle insertion force, deformation, and calculated friction stress were evaluated as in vivo and real-time measures of insertion events. The goal of this study was to characterize and determine the sensitivity of these measures in brain tissues. Tests varied insertion speeds to compare with our previous tests measuring tissue damage (Casanova et al., 2014). These mechanical parameters have the potential to evaluate the extent of tissue contact and damage introduced along the needle track with insertion. Such real-time measures may be eventually used to determine likelihood of CED backflow.

4.1. Brain tissue insertions

Increased insertion speed produce greater force which is in agreement with previous studies of electrode insertion performed on rat brain tissue in vivo (Andrei et al., 2012; Welkenhuysen et al., 2011). This rate-dependency is the opposite of cardiac tissues in which insertion forces and tissue damage have been shown to decrease with high insertion speeds (Mahvash and Dupont, 2010; van Gerwen, et al., 2012). This mechanical behavior is likely due to rate-dependent properties such as failure strength and stiffness which are ultimately dependent on the composition and structure of the tissues, as well as, needle tip geometry. Stress distribution at the needle tip is dependent on the tissue interface geometry and includes shear, tensile, and compressive stress regions. Cutting is often associated with shear failure, however other modes of failure may also occur in tissues. Viscoelastic ECM fibers may be stretched and fail in tension in a rate-dependent manner. Also discrete cells may shift or simply move out of the needle pathway. In this case, slower insertion velocities may allow more cell accommodation. Additional studies at the microscopic level are needed to better characterize these rate-dependent tissue failure modes.

At the macroscopic scale, rate dependent failure appears to be best characterized by surface dimpling. Greater surface dimpling before failure results in larger regions of deformed tissue and more energy storage in tissue before needle penetration. Resulting tissue penetration generates a larger release of energy and provides a greater potential for tissue damage since more tissue is being moved in the axial direction following puncture. This energy transfer may be one reason why damage in tissue was observed relatively far away from the needle surface. In this study, surface dimpling increased with increasing insertion speeds, indicating that more energy was transferred over a larger region and increasing the potential for injury. This rate-dependent damage was seen in histological sections where, for high insertion speed, hemorrhage and tissue fracturing was observed in a wide region around the needle; whereas for low insertion speed, no significant damage was observed in proximity to the needle hole.

Following surface penetration of the needle, increasing force with increasing insertion speed was found in brain tissues. This may also be due to contributions from friction stresses at the needle-tissue interface. However, friction stresses likely decrease with insertion speed since larger tissue holes were measured with increasing insertion speeds indicating lower frictional stresses. The increasing insertion force may also be due to contributions from pressurized fluid in tissue. Brain tissue has often been characterized as a biphasic or poroelastic materials in which fluid-solid behavior is coupled (Chen and Sarntinoranont, 2007; Smith and Garcia, 2009; Smith and Garcia, 2011). Rapid deformation results in greater pressurization of fluid filled spaces if fluid does not have time to redistribute, making the tissue effectively stiffer. This may occur in compacted tissues below or surrounding the needle and result in increasing needle forces with increasing needle speed. Other possible reasons for the rate-dependent behavior may be viscoelastic cellular and extracellular matrix components, or stresses that are transferred differently through larger cell components (cell membrane and neurofilaments) that can move relative to each other.

In brain tissue, F_avg and F_stop force measurements were most sensitive to changes in insertion speed over the range tested. These values increased with insertion speed. Measures of F_rest were also sensitive to insertion speeds. F_rest is the combination of friction stress along the needle and compressive stress at the tip. This value, like friction stress and pre-stress, decreased with increasing insertion speed and lower values may be associated with loss of tissue contact or greater tissue damage. However it should be noted that for all tissue measurements, the needle force generally increased with insertion depth due to increasing contact area with tissue. Insertion force was also dependent on tissue region. Insertion forces reached a maximum at approximately the boundary between the external capsule and CPu. This transition region was also approximately where greatest tissue hemorrhage was observed. Beyond this boundary (depths > 3 mm), the insertion force did not show a clear increasing or decreasing trend, and varied in value. In this region, the extent of needle-induced injury may change resulting in differences in tissue contact and friction compared with other tissue regions. There may be a different mode of tissue response within CPu due to differences in tissue structure; a lower rupture strength or a different failure mechanism may produce different hole geometry as evidenced by the smaller aspect ratio of the holes found in our previous study of tissue injury in the CPu (Casanova et al., 2014).

In a previous study by our group we have used the same insertion protocol and speeds, and measured tissue damage by measuring changes in tissue hole size. We found statistically significant increases in tissue hole sizes for increasing insertion speed (Casanova et al., 2014). Given that the same experimental procedures were followed, this allows us to compare current force, deformation and friction-stress trends with previous histological damage assessment. These previous findings are in agreement with the tissue injury observed in our current study. At high insertion speeds, damage was found in proximity to the needle hole (bigger hole) but also relatively far away as hemorrhage and tissue fracturing. Extensive hemorrhage is a undesired condition because it may result in vasogenic brain edema, cell inflammation, cell death and microglial reaction (Xue and Del Bigio, 2003). On the other hand, tissue fracturing and hemorrhage were not observed at the lower insertion speed. Therefore, CED with low insertion speed should be a safer procedure. Similar observations on localized tissue fracturing and bleeding have been previously reported by (White et al., 2011). However, this damage was noted mainly as a consequence of high infusion pressures and was not associated with injury in the white matter region as seen in this study.

Friction stress was introduced to quantify spatially-varying tissue compression along the tissue track. It is easily measurable and may be used to assess the combination of tissue contact and track damage in real-time. As expected, friction stress was found to decrease with increasing insertion speed as this has been found to increase tissue hole size. The sensitivity of calculated friction stress to variation in needle insertion speed indicates that it is a potential real-time indicator of tissue damage. Friction stress was not constant along the needle track. It was smallest in white matter regions where the inner cortex and the external capsule were located (between 2 and 3 mm depth). This parameter depended on tissue contact stresses (pre-stress), contact area, and the interfacial friction coefficient. The friction coefficient may vary (e.g. with changes in cellular density) but be approximately constant within different tissue regions of the cortex, external capsule and CPu. If the friction coefficient and contact area within each tissue region is assumed to be approximately constant, the smaller friction stress calculated for high insertion speed is due to lower pre-stress which is consistent with greater tissue hole size. The low friction stress within white matter regions may be due to residual tensile stresses (Xu et al., 2009) and the lower stiffness of white matter (Lee et al., 2011) that result in lower pre-stresses. Interestingly, spatial variation of friction stress was similar to the pattern estimated for pre-stress obtained in our previous study (Casanova et al., 2014), where minimum pre-stress was also within white matter regions. In our previous study, pre-stress was estimated from holes measured in excised tissue slices. Pre-stress was found to be smallest for the slow 0.2 mm/s insertion rates which is consistent with the current study. However these calculated pre-stresses were less sensitive to changes at 2 and 10 mm/s insertion rates.

4.2. Hydrogel insertions

In hydrogels, the needle insertion and retraction forces were generally higher than in brain tissues. More importantly, insertion speed trends were very different from those of brain tissues with lower insertion forces and less damage found for higher insertion speeds. This different behavior is attributed to different failure behavior that included accumulation of material around the needle tip as seen in our previous study (Casanova et al., 2012). This behavior was not noted in brain tissues. In hydrogel, accumulation was more likely at slower needle insertion rates. Two force peaks were observed for insertion speeds 0.2 and 2 mm/s. The second peak which occurred within the sample is thought to be due to accumulation of material at the needle tip. With material build up in front of the needle tip, insertion force increased to a peak value, at which point there was likely a sudden release or penetration of the accumulation that resulted in a sudden decrease in the force. Greater material build-up introduced a greater zone of damage, greater insertion force, and lower friction stress. In 0.2 mm/s tests, regions where accumulation was minimal (close to the surface of the sample and after release of the build-up) were found to have higher friction stress values that were equivalent to 10 mm/s tests where accumulation was assumed to be minimal. The difference in insertion mechanics between hydrogel and brain tissue is likely because of microstructural and compositional differences. Hydrogel is formed by cross-linked polymer chains (Barrangou et al., 2006) which may become fully extended and more readily ‘cut’ at higher strain (insertion) rates.

Dimpling and friction stress were also found to be indicators of the extent of tissue contact and damage in this material with different failure behavior. As in brain tissue, hydrogel dimpling was closely related to the extent of eventual material damage. In this case, dimpling decreased and damage decreased with increasing insertion speed. Decreasing material damage with insertion speed was also reflected in higher friction stresses. In hydrogel, friction stress was also greater for high insertion speed which explains the low backflow with high insertion speed obtained previously in this material (Casanova et al., 2012). Overall, the opposite behavior found for this agarose-based hydrogel suggest that, while it is a useful test medium for infusions (Chen et al., 2004), it does not replicate the mechanics of needle insertion for brain tissues.

4.3. Clinical CED implications

In brain tissue, loss of tissue contact and greater track damage with high insertion speed resulted in increased backflow in our previous study (Casanova et al., 2014). With greater damage, low pre-stresses at the tissue-needle interface are easily overcome and fluid can easily flow back along the needle track. Thus, insertion procedures that minimize damage and pre-stress are desirable for reducing backflow. This study highlighted the importance of using lower insertion speeds when introducing infusion needles in order to minimize tissue damage, decrease CED backflow and improve targeting. In the current study, we evaluated the use of real-time measures of brain surface dimpling and needle force, both of which may be measured during surgery. F_avg, F_stop, F_rest, F_drag, D_drag, and R_avg were all found to be clearly sensitive to insertion rate and are potential predictors of the extent of tissue damage and backflow. Less sensitive to insertion rate were surface dimpling and F_in. Thus, certain force measurements have the potential to be used to predict the extent of tissue damage during insertion into different brain regions.

We also present a method for extracting a spatially varying parameter, friction stress, along the length of the track and within different tissue regions. This parameter accounts for the extent of tissue contact and damage at the needle-tissue interface. Significant damage (greater hole size and reductions in friction stress) within white matter regions have important implications for understanding why these regions are susceptible to CED backflow. With further investigation, these force and friction stress measures may eventually used to predict the likelihood of CED backflow before the start of infusions based on extent of damage and distance to white matter regions. Such information is needed to further optimize and improve CED targeting.

Highlights.

• Friction stress can be evaluated in vivo, in real time, by measuring forces during needle insertion and retraction.

• Faster needle insertion produced less friction stress which matches greater track damage from our previous study.

• Smaller friction stress was measured within white matter regions compared to gray matter regions.