Assessing via Simulation the Operating Characteristics of the WHO Scale for COVID-19 Endpoints

ABSTRACT

Many clinical trials of treatments for patients hospitalised for COVID-19 use an ordinal scale recommended by the World Heath Organisation. The scale represents intensity of medical intervention, with higher scores for interventions more burdensome for the patient, and highest score for death. There is uncertainty about use of this ordinal scale in testing hypotheses. With the objective of assessing the power and Type I error of potential endpoints and analyses based on the ordinal scale, trajectories of the score over 28 days were simulated for scenarios based closely on results of two trials recently published. The simulation used transition probabilities for the ordinal scale over time. No one endpoint was optimal across scenarios, but a ranked measure of trajectory fared moderately well in all scenarios. Type I error was controlled at close to the nominal level for all endpoints. Because not tied to a particular population with regard to baseline severity, the use of transition probabilities allows plausible assessment of endpoints in populations with configurations of baseline score for which data is not yet published, provided some data on the relevant transition probabilities are available. The results could support experts in the choice of endpoint based on the ordinal scale.

1. INTRODUCTION

In many ongoing and planned clinical trials, the efficacy of treatments of patients with the COVID-19 disease caused by SARS-CoV-2 is being measured by an ordinal scale whose categories represent severity of illness over time via the degree of medical intervention applied, with higher scores for interventions that are more burdensome for the patient, and highest score for death; alternatively, an endpoint based on a selected score of the scale is being used (von Cube, 2020). The ordinal scale was suggested by the World Health Organization (WHO) in their R&D Blueprint Master Protocol (WHO 2020a, p.6). The WHO scale consists of the categories as set out in Table 1.

The scale is very close to one proposed and assessed in detail by Peterson et al. (2017) for influenza. While the above scale has been recommended by the WHO R&D Blueprint group, it has a number of weaknesses: it has not been formally validated; it is a surrogate measure rather than a direct measure of patient health; and transition from category to category in the scale may be largely determined by clinical judgement (Powers 2017) which may itself be limited by availability of staff or resources. In addition, because COVID-19 is new, and because candidate treatments of its symptoms are only now being explored, knowledge of typical or likely changes or trajectories over time in medical intervention under candidate treatments is sparse. Therefore, there is a sparsity of evidence on which to base decisions about to how to use the ordinal scale or level of medical intervention so as to distinguish promising from ineffective treatments efficiently, and to facilitate inference that could lead to approval of new treatments.

Rather than validating the scale, the objective of this paper is to assess how well the assumptions of proposed analyses fit selected candidate endpoints derived from the scale; and to estimate the sensitivity of these endpoints in detecting differences between treatments – that is, to estimate the relative power of the endpoints - under scenarios based as closely possible on what is known about the distribution and trajectories over time that have been observed for the scale, but also under theoretical scenarios that could pertain to planned treatments of COVID-19. It will be seen that the scenarios simulated cover a wide range of potential efficacy.

1.1 Literature search

A search was conducted for sources of data about the distribution and trajectory of outcomes over time. The search was limited to published papers and submitted manuscripts that included sufficient data on categories of the WHO scale, or a scale mappable to the WHO scale, for at least three post-baseline time points. Both randomized control trials and observational studies were included in the search. WHO (2020b; 2020c) maintains a list of randomized clinical trials of treatments for COVID-19, and a list of observation trials of treatments for COVID-19, updated daily. The lists include references to the relevant papers and, where available, to submitted manuscripts not yet published. Of the 17 references to randomized trials listed at the time of submission of this paper, only one (Cao et al. 2020) included data at time points up to 28 days for the WHO scale or a scale that could be mapped to the WHO scale. Of the references to observational trials available at the time of submission, five featured counts of a scale that could be mapped to the WHO scale, but only one (Grein et al. 2020) presented counts of post-baseline categories at more than two time points. To assess the endpoints derived from the ordinal scale, the patient trajectories over the typical follow-up duration of current COVID-19 clinical trials (von Cube 2020) were simulated, based on data presented in the papers by Grein (2020) and Cao (2020).

1.2 An ordinal scale to measure intensity of medical intervention

Cao et al. (2020) and Grein et al. (2020) have published detailed 28-day outcome data from clinical trials of hospitalised patients with the associated COVID-19 infection. The trials described by Cao et al. (2020) and Grein et al. (2020) used variants of the WHO scale. The seven-category ordinal scale of Cao et al. (2020) uses scores 1 to 8 of the WHO-recommended scale, collapsing scores 6 and 7 into a single category and renumbering the WHO category 8 to 7. Grein et al. (2020) provide a status for all patients on each day of follow-up in Figure 2 of the paper. This status can be mapped to the categories of the ordinal scale as defined in Cao et al. (2020). Table 2 gives the definitions of the categories given by Cao et al. (2020) and indicates how the status given in Grein et al. (2020) is mapped to the scale in Cao et al. (2020).

The score values used in Cao et al. (2020) and Grein et al. (2020), as defined in the respective papers, map quite closely to one another; the two studies differ in the definition of Categories 1 and 2 in Table 2 above of the ordinal score recorded but, because both of these “best” values indicate that the subject could be discharged from hospital, it was felt clinically justifiable to treat Categories 1 and 2 as representing discharge. The code provided as supplementary material is designed to be easily adapted to allow the assessment of variants of the ordinal score with more or fewer categories and/or with different probabilities of transition.

As noted, not all planned and ongoing trials use the entire range of this measure, but many use some elements of the ordinal scale to define a primary endpoint – see the survey of current trials in von Cube (2020). Von Cube et al. report that, as of 27 March 2020, six of 23 registered clinical trials use an ordinal scale similar to the WHO scale as the primary endpoint, with the number of categories varying between six and eight. Von Cube et al. found that other trials used endpoints based on the ordinal scale; for example, the ACTT trial (National Institute of Health 2020) used time to recovery as the primary endpoint, with recovery defined via the ordinal scale. The primary analysis for the Cao et al. (2020) trial was based on the ordinal scale, and was defined as time to clinical improvement, i.e., time from randomization to an improvement of two points or more (from the status at randomization) on the ordinal scale, or live discharge from the hospital, whichever came first.

With results from just two studies, the generalisability of our findings is limited, and our findings are of course limited to endpoints based on the WHO scale. Nevertheless, applicability of the assessments from the simulations presented here is supported by their use of information from a wide variety of trajectories, because the simulations are based on individual patient outcomes over time. In addition, as discussed later and as is evident from Figure 2a)-c), the three treatment groups for which the outcomes are available varied considerably in levels of worsening and in levels of improvement achieved in the 28 days of follow up. Thus, we argue that the results are more generalisable than if based only on summary level data, and cover candidate treatments whose strength of efficacy, as seen at least in the widely-used WHO scale, varies considerably. The results may therefore be useful in planning future studies for a treatments with a fairly wide range of expected efficacy. Furthermore, the code that accompanies this paper as supplementary material is designed to be amended easily to accommodate other expected trajectories, and can be thus adapted to explore the characteristics of other potential treatments of COVID-19 whose effect on trajectory is expected to differ from those found in our sources.

Planned follow-up in clinical trials of patients with COVID-19 tends to be relatively short, matching the typical trajectory of the disease, and the main follow-up is usually of 28 days’ duration or less (Von Cube 2020).

1.3 The problem

It is far from clear how to make best use of the ordinal WHO scale in clinical trials to assess treatments of patients with COVID-19. Table 3 presents a selection of options, some of which have already been noted in von Cube (2020) and in regulatory guidance (FDA 2020). We note that each endpoint and analysis measures a different aspect of the experience of the patient hospitalized for COVID-19. The choice of endpoint and analysis will depend not only on the operating characteristics and statistical properties that are assessed in this paper, but also on the questions regarding patient health trajectory whose answers are sought by the stakeholders in the clinical trial that is planned. These stakeholders will include patients and clinicians, and will probably also include regulators and the general public. The estimand required by each stakeholder may differ, and will depend upon the precise question required to be answered, as well as on the statistical properties and sensitivity and specificity of a particular endpoint and analysis.

We note that the follow up time for each endpoint in Table 3 is chosen so as to maximise the sensitivity of the endpoint and its analysis, while giving a result relevant to stakeholders. For the time-to-event outcomes, the full 28 days’ follow up was required to be taken into account, in order for the results to be clinically meaningful. For the binary endpoints, results from simulations (not shown) showed that Day 15 was the most sensitive scheduled time point to detect differences in the treatment groups (see also point 1 below).

Apart from the sparsity of data on outcomes over time observed so far for COVID-19 as noted in the outcome of the literature search above, the problem of measuring a treatment effect is made more difficult by a number of factors including the following:

1. At least for the populations in Cao et al. (2020) and Grein et al. (2020) it seems that, by Day 28, the majority of patients will have improved; the result is that irrespective of treatment, proportions improving by Day 28 tend to be similar across randomized treatment groups, so that an analysis of the ordinal scale at the end of the study (i.e. at Day 28) is unlikely to be optimally sensitive, at least in detecting differences between treatment groups in proportions of subjects who improved.

2. Allied to 1), more generally, if using a binary outcome of improvement at a time point, from the available data on outcomes it is not clear at which time point the endpoint of improvement would be most sensitive in distinguishing promising from ineffective treatments. Our ability to predict the most sensitive time point for a binary outcome will no doubt grow with our knowledge of the pathophysiology of COVID-19.

3. One may try to bypass the problem of timing of improvement by using time to improvement as the endpoint; however, from Figure 2 in Cao et al. (2020) it seems that hazards associated with time to improvement as measured by the WHO scale may well not be proportional, making a summary of hazard ratio potentially difficult to interpret.

4. A second issue with the endpoints of time to improvement/discharge/recovery and time to worsening as defined in Table 3 is that the former may have a semi-competing risk of death and the latter a semi-competing risk of discharge; that is, the event of death may result in the censoring of time to improvement/discharge/recovery, but not vice versa; and the event of discharge may result in the censoring of time to worsening, but not vice versa (Varadhan 2010). However it is not clear in practice how to take these semi-competing risks into account in a way that will provide evidence that can straightforwardly support regulatory decision making. The standard approach for semi-competing risks in clinical trials (Austin and Fine 2017) is either to include the competing risk as a component of a composite time-to-event endpoint; to estimate the cumulative risk of the particular event of interest in a specified time interval (Gray 1988); or to model cause-specific hazard. However neither of these approaches attempt to take into account the censoring event in the resulting estimate of treatment effect as is required by the regulator (FDA 2020). In the case of the ordinal score and in the case of COVID-19 health trajectories generally, the competing-risk approach gives results that are difficult to use and to interpret. In the case of time to improvement, for example, the competing risks approach considers the time to improvement in the risk set of subjects who can in fact improve, because not dead. Thus, under the competing risks approach, a treatment that is associated with a risk of death higher than that of the control group may be estimated to be superior to control, in time to improvement. Such a result could of course be assessed alongside a competing-risks estimate of hazard of mortality, and this would help to ensure that a treatment associated with higher rates of death than control is not judged superior to control. But we suggest that, for the assessment of hospitalized COVID-19 patients, death contains important information with regard to improvement, and we question the value of the competing risk approach here in either the clinical or regulatory context.

5. From the results in Tables 2 and 3 in Cao et al. (2020) and from Figure 2 in Grein et al. (2020), it seems likely that a patient’s trajectory for the ordinal scale over time may vary considerably in character, depending on the baseline value of the scale, with relatively few deaths in patients with moderate scores at baseline, and a higher proportion of deaths in those with severe scores. Thus it may be difficult to be sure whether a worsening or an improvement-based endpoint will be more sensitive in distinguishing whether any given treatment is ineffective or promising.

6. For ordinal scales such as the WHO scale, an attractive option statistically could be a proportional odds analysis; this analysis makes good use of the full range of the ordinal scale, estimating the odds of improvement from current score to the next best score, conditional on the current score; however, this analysis at least in theory assumes that these odds of improvement are the same for progress from any score to the next best score; this assumption may be not always be plausible; for example this approach might not detect the effectiveness of a treatment that inhibits worsening but is not expected to dramatically improve symptoms.

7. Similarly, a measure of improvement such as the WHO scale may miss the efficacy of a treatment in improving the overall experience of the patient; for example, a treatment may be only as good as the standard of care (SOC) in time to improvement, but could shorten time in the Intensive Care Unit (ICU), but this would probably not be reflected in a standard comparison using the ordinal scale.

8. Mortality, while unfortunately a feature of the trials of patients with COVID-19 for which outcomes are available is, for all but the most seriously ill populations, relatively infrequent, compared to other endpoints; therefore this “hard” endpoint would often not be optimal to distinguish promising from ineffective treatments.

In ongoing discussions, researches have suggested options that might address some of the above difficulties.

With regard to 6), the Cochrane-Mantel-Haenszel (CMH) test makes a use of the whole of the ordinal scale similar to that the proportional odds approach, but does not rely on the assumption of proportional odds – thus the CMH test might be a viable alternative for testing the null hypothesis. Attempting to address 7), but also 2) - 5), Carl-Fredrik Burman (personal communication, April 14, 2020) has suggested ranking subjects by their intensity of treatment undergone, by items such as a patient’s most severe post-baseline score; by a patient’s final score; by a patient’s the duration of the most severe score; by a patient’s (descending) best score that occurs after the worst score, and by a patient’s time on that best score; Burman suggested treatment groups could be tested for difference in ranks via the stratified Wilcoxon (or van Elteren) test. In addressing 7) it would be important to provide a precise definition of the estimand so that it is clear which aspects of the patient experience are being assessed.We note that a further problem in planning a clinical trial for a treatment of COVID-19 is that the SoC differs by region, site and availability of staff and equipment; furthermore, SoC is expected to change over time (FDA 2020). While we have not directly attempted to address how changes in SoC could affect the performance of endpoints, simulations are included of a Scenario that compares two candidate treatments for COVID against one another; the relatively small estimated treatment effects in this Scenario may help inform decisions when the SoC for a planned clinical trial includes a potentially efficacious new treatment.

1.4 Objective of this research

The choice of endpoint for a clinical trial is logically driven by the questions that stakeholders desire to be addressed by the trial and from those questions a definition of the estimand will emerge. The endpoint and its population-level summary are two of the five attributes of the estimand (ICH 2019, Section A.3.3). In the case of trials whose objective is to assess treatments of COVID-19, the choice of endpoint and the choice of the summary analysis provide particular challenges, because so little is yet known, given that the disease has been known for a very short time.

The objective of the paper is to simulate, based as closely as possible on available data, the entire trajectory of the ordinal scale over 28 days in COVID-19 patients to explore the options for endpoint and analysis, and to assess which of the above posited issues are serious ones. A second objective is to to support the choice of endpoint for some new treatment or treatments, for which evidence of likely or plausible trajectory is available, by simulating a variety of trajectories over time in the ordinal scale. Specifically, simulations could help assess

• the relative power of a selection of time-to-event approaches;

• the degree to which any breach of the proportional hazard assumption noted in 3) could affect the power and Type I error in COVID-19 treatments;

• the relative merits of the CMH test versus a proportional odds approach;

• the power of the ranking approach suggested by Burman.

This paper describes an attempt at such a simulation.

With the objective of supporting further uses of the simulations under a variety of configurations of baseline score, and to allow the assumptions of the simulations to be changed as new data regarding patient outcome trajectories on COVID-19 ordinal-scale become available, programming code and a formal specification for the simulation are available for download.

2. METHODS

To provide supportive evidence to assess the above questions, and to provide a tool that could be used more generally to cast light on the relative usefulness of new or posited endpoints for clinical trials of patients with COVID-19, this paper uses the outcomes presented in Cao et al. (2020) and Grein et al. (2020) as a basis for a simulation of individual subject trajectories over 28 days in the WHO-recommended ordinal scale, reflecting the observed differences in trajectories that pertain to each observed baseline score at each visit for which data is available. Table 2 above describes the mapping of statuses in Grein et al. (2020) to those defined in Cao et al. (2020). The simulation reflects the ideas of von Cube et al., who note that the patient experience of COVID-19 can be viewed via a multistate model, with estimable probabilities of transition from one category of the WHO ordinal scale to another. Given a multinomial distribution for baseline scores, the probabilities of transition for each baseline (Day 1) category to every other category at Day 7 can be estimated from published data in Cao et al. (2020) and Grein et al. (2020), and patient trajectory to Day 7 thus simulated via a new set of multinomial probabilities. This process is then repeated for transitions from Day 7 to Day 14 and from Day 14 to Day 28. Note that a Markov process is assumed; that is, it is assumed that the probability of transition from Visit k to Visit k + 1 is dependent only on the state at Visit k, and independent of values at Visit k-1 or other earlier visits. The assumption of a Markov process is a limitation of the simulations. It is likely, for example that, conditional on score at previous visit, a subject’s baseline score on the WHO scale is associated with differences in transition probabilities. However, there is not enough data yet available with which to estimate the more comprehensive model; with the accumulation of data about patterns of transition in the WHO scale it will be possible to take account of this and other factors, in addition to the score at previous visit. Further research on this will be possible as data on COVID-19 outcomes accumulates.

More formally, if an outcome X has categories i = 1, 2…I, then for subject j randomized to treatment m at visit k, let p_ijkm be the probability that X_jkm = category i. The simulation is implemented as follows. First, counts of the occurrence of X_j1m are simulated as multinomial with p_ij1m calculated based on the observed counts at baseline Visit 1 (=Day 1). The probabilities p_ij2mare then calculated based on p_ij2m|(X_j1m=1, 2,…I). These conditional probabilities are calculated from the observed counts, for each baseline category of X_j1m, of transitions to each observed value of the X at the next visit. For example, if for treatment =1 we observe 11 patients with score =3 at baseline (Visit 1) and, of these, nine transition to score =3 at Visit 2 (no change) and two transition to score =2, then for the simulation, p_3j21|(X_j1m=3) = 9/11 and p_2j21|(X_j1m=3) = 2/11. Note that while transition probabilities of zero are for the most part not plausible, for simplicity and to keep consistency with the results of the source trials, where at Visit = k + 1 a category has no transitions observed from subjects with given category at Visit k, the simulation assumes the transition probability of zero for that particular transition. Further details of the simulation are available in the formal specification for the simulation, which is as noted available online as supplementary material.

To approximate outcomes at each day, given the sparse evidence about daily transitions, a day of change of score from previous visit was drawn at random from a uniform distribution of length equal to the duration of follow-up between previous and current visit.

The above simulation set-up could be used to simulate longitudinal outcomes for populations with a range of baseline severities, Thus, for example, instead of the baseline proportions observed in Cao et al. (2020), the probabilities p_ij1m for the more severe baseline scores could be increased and the less severe decreased. The same transition probabilities as observed in, say, Cao et al. (2020) could be used with a range of hypothetical scenarios for baseline, since the transition probabilities condition on the p_ij1m, and should remain clinically plausible, other baseline attributes being equal. The code accompanying this paper allows for such hypothetical baseline scenarios. However, for this paper we simulate all outcomes assuming the baseline probabilities pertaining to Cao et al. (2020). We use the baseline probabilities from Cao et al. (2020) also when simulating based on Grein et al. (2020), but of course for the simulation based on Grein et al. (2020) the transition probabilities for the study treatment presented in Grein et al. (2020) are calculated from Grein et al. (2020), and reflect the (presumably different) trajectories over time in the ordinal scale that are observed with the study treatment group in Grein et al. (2020). Use of the same baseline distribution for all scenarios allows for some comparison across the scenarios. Finally, in addition addition we modified the Experimental arm in Scenario D to form Scenarios E1-E9, and Scenarios F1-F9, in order to simulate two theoretical varieties of efficacy, to reflect efficacy gain in the form of ore improvement or of less worsening. For the first variety of efficacy we assume the transition probabilities of the SoC arm from Cao et al. (2020) as in Scenario D, but simulate in the Experimental arm a series of scenarios E1-E9 where at all visits there are successive increases of 10%, 20%, …90%, respectively, in all probabilities of transitions to improved categories. For the second variety of efficacy we again assume the transition probabilities of the SoC arm from Cao et al. (2020) as in Scenario D, but simulate in the Experimental arm a series of scenarios F1-F9 where successive decreases of 10%, 20%, …90%, respectively, pertain in all probabilities of transitions to worse categories. For convenience we also include Scenarios E0 and F0 based simply on the SoC arm of Cao et al. with out modification – the efficacy of Scenarios E0 and F0 follows the null hypothesis of no treatment difference, as does that of Scenario D.

The scenarios simulated are listed in Table 2.

Scenarios A-C and E0-E9, F0-F9 were used to assess robustness of approaches to a variety of longitudinal trajectories of the ordinal scale. Scenario D was used to assess Type I error for the approaches.

It is noted also that power will of course vary by sample size and true treatment effect. We have plotted results for sample sizes in the range seen for example in the ongoing ACCORD-2 trial (EU Clinical Trials Register 2020). With regard to treatment effect, in Scenarios A-C the simulated trajectories were closely based on observed trajectories in clinical trials for which outcomes were available: in these scenarios, rather than estimating sample sizes required to achieve a particular power, our aim was to assess the relative power of endpoints and analyses for a given scenario, as well as the control of Type I error, across a range of sample sizes. In Scenarios E0-E9 and F0-F9, the increased treatment effect for a single sample size (90 patients per arm) is imposed via imposed changes to the transition probabilities. This latter set of scenarios could inform planning conditioned on an estimated treatment effect.

Selected analysis-plus-endpoint approaches were implemented and power and Type I error calculated from the simulated data. Statistical significance was assessed at the one-sided 2.5% level. It was assumed that there would be no missing data. (The trials whose data is used here are in the hospital setting; no missing data were reported in Cao et al. (2020); Figure 2 in Grein et al. (2020) indicates that some patients were censored).

For the analyses of improvement/recovery/discharge presented below, death is treated as censoring the event of interest at the time point of maximum scheduled follow-up, on Day 28, rather than censoring at the time of death. For analyses of time to death and time to worsening, we did not censor at time of discharge, instead making the simplying assumptions with regard to discharge that a) death would be expected to be reported even if occurring after discharge since this is standard practice (e.g., as implied by ICH (2019), pp. 6, 8); and b) the probability of worsening after discharge but within the 28-day follow-up period was very small. The approach of censoring improvement at the latest possible follow-up time for absorbing events is not completely satisfactory, and any use of the results from such an analysis should be accompanied by the provision of precise definition of the estimand, including the details of the censoring.

For the endpoint of ranked trajectory in Table 3, the following ranking was used: patients were sorted in order of

• death (0/1 = No/Yes)

• score on WHO scale at Day 28

• best score on WHO scale occurring after the worst

• (descending order) duration of the best score as defined in the previous bullet

• worst score on WHO scale

• days on worst score

Patients were then ranked in sort order. Ranks closer to unity were reflected better patient experience, with first rank being best.

The statistical model for all approaches included just two factors, treatment group and the baseline categories of the ordinal scale. For Scenarios A-D, power or Type I error was calculated for sample sizes of 60, 90, 120, and 150 per treatment arm. For Scenarios E0-E9 and F0-F9, power/Type I error was calculated for a sample size of 90 per treatment arm, for the range of theoretical efficacy in E0-E9 and F0-F9.

For certain analyses, some sparse baseline and endpoint categories of the ordinal scale were pooled – see the formal specification in the supplementary material for details.

3. Results

All analyses and endpoints controlled Type I error at approximately the nominal rate of 2.5%, for all sample sizes assessed – see Figure 1.

The proportional odds analysis controlled Type I error, despite its perhaps questionable assumption of consistent treatment effect across categories of the WHO scale. It should be noted that since both arms for Scenario D were simulated from the control arm of Cao et al. (2020), the issue of Type I error under non-proportional hazards is not fully addressed by the present paper because the assumption of proportional hazards is not breached by Scenario D; if this assumption were breached in a COVID-19 setting, as seems likely, it is possible that this could affect the control of Type I error for the time to event analyses.

Average Kaplan-Meier probabilities for the events of improvement, worsening and death are presented for the three arms, i.e., SOC, Cao Experiemental, and Grein arms in Scenarios A, B and C, for the 10,000 replicates, in Figure 2a-c.

The variety of patterns of time-to-event outcome in the three arms simulated can be seen in Figure 1a)-c). In all plots, simulations based on Grein et al. (2020) have the most favourable outcomes, and those based on SOC the least favourable. The endpoints of worsening and death may particularly favour the simulations that were based on Grein et al. (2020). The superiority of both simulated experimental treatment groups to simulated SOC in time to improvement looks fairly pronounced.

The simulations gave rise to a technical issue that may be relevant in the planning of future trials: the inclusion of the baseline categories as categorical covariate in the proportional odds and binary improvement analyses was associated with the “quasi-separation of data points” error in a proportion the simulated datasets for each of the Scenarios. This occurred despite the fact that, as noted, small adjacent categories had been pooled in the baseline variable. This issue was most pronounced for Scenario A: for this Scenario, in simulations with the highest sample size – 150 per treatment arm - the proportion of simulated datasets with this error was 5.1% and 5.3% for the proportional odds and binary (logistic) analyses, respectively. For the simulations with the lowest sample size – 60 per treatment arm, the proportion with the error was 30% and 36%, respectively. For Scenarios B and C, the error occurred for at most 7.7% of the simulations for the lowest sample size simulated, and at most for 2.3% for higher sample sizes (90, 120 and 150/arm). This issue did not occur for the implementation of the closely-allied CMH test. Estimates of power for the CMH and the proportional odds approaches tended to be similar.

A shortcoming of the simulation approach presented here of using transition probabilities tied to scheduled visits, with a day of change of score selected randomly between the visits, is the loss of information that would be contained about the treatment effect, were enough data available to model realistic patterns of day-to-day change in the WHO scale, differences in which could be associated with certain treatment groups. This handicaps certain endpoint-plus-analysis approaches, but not others. Thus, for example, the time-to-event analyses in a real study could be expected to benefit from informative day-by-day event data in a real clinical trial, in a way that is not fully possible with the outcomes simulated here. Hence, while the simulations presented here can provide useful comparisons of power among the time-to-event approaches, the results should not be used directly to assess power of time-to-event approaches versus the power of the other approaches that are visit-oriented by nature.

The trajectory ranking approach suggested by Burman similarly suffers from the lack of granularity in the visit-based outcomes in the simulated trial. This difficulty could be avoided in practice in a clinical trial in the hospital setting, where the ordinal scale could be collected daily.

Another issue with the lack of day-by-day information about trajectory between visits in the simulated outcomes is noticeable in the results from the simulation of Scenario A. Cao et al. (2020, p.4) estimate a hazard ratio for time to improvement of 1.31. Figure 2 in Cao et al. (2020) suggests a possible crossing of the hazards for the two treatment groups at approximately Day 16. For the simulations, as noted above, time of change of score is randomly selected, so the possible crossing seen in the plotted hazards for improvement for the treatment groups at Day 16 may have been missed in many of the simulated instances of Scenario A. For this or for some other reason, the mean hazard ratio estimate for improvement in the simulated trials based on Scenario A is higher than that presented by Cao et al. (2020), at 1.67.

With these caveats, the results for Scenario A are presented in Figure 3.

With relatively low proportions of mortality and of worsening, and relatively poor differentiation between the simulated treatment groups in their hazard rates, these two endpoints lacked power for Scenario A (Experimental arm and SOC based on Cao et al. (2020)).

The proportional odds analysis and the closely allied CMH analysis also had relatively poor estimated power for this Scenario. The proportional odds approach, as noted, gave rise to sparsity-related errors in a significant proportion of simulations of Scenario A. However, the closely-related CMH analysis, which did not give rise to these errors, had almost exactly the same estimated power on average (lines almost overlap in the Figure). This suggests that the CMH analysis may be preferred to the proportional odds approach, despite the fact that the CMH approach does not give an estimate of the size of the treatment effect; if the CMH is used for hypothesis testing purposes, an estimate of treatment effect could perhaps be provided from one of the other analyses.

The ranked trajectory endpoint and the binary improvement endpoint (at Day 14) had relatively good estimated power of about 70%for 60 patients per arm to over 95% for 150 patients per arm. It is notable that a particularly large difference between treatment groups in proportions of patients with improvement was observed for the Cao et al. (2020) trial at Day 14 (45.5% vs. 30% in experimental arm and SOC, respectively). The two analyses of time to improvement (time to 2-point improvement and time to discharge – overlapping each other in the plot), had good estimated power similar to that of the binary improvement endpoint.

The results for Scenario B are presented in Figure 4.

Results from Scenario B (Experimental arm from Grein et al. (2020) vs. SOC from Cao et al. (2020)), differed from those of Scenarios A and C in that the range of estimated power for the endpoints was narrower and power was generally high – lowest power for any endpoint at the sample size of 60 per arm was 86.4%. For this Scenario, the proportional odds, CMH, binary improvement and ranked trajectory approaches were all estimated to be almost equally powerful (the lines almost overlap in the plot), and to have relatively high power. The four time-to-event approaches (time to improvement, to death, to worsening and to discharge) all had slightly smaller power than these, with endpoint of time to death estimated to have the highest power among the time-to-event endpoints

The results for Scenario C are presented in Figure 5.

For Scenario C (experimental arm from Grein et al. (2020) versus experimental arm from Cao et al. (2020)), the spread of estimated power for the sample size of 60 per treatment group is wide, as in Scenario A, but the pattern of relative power differs from that Scenario. For Scenario C, the time to improvement and time to discharge endpoints have mean hazard ratios of just 1.31 and 1.21, respectively, and are now relatively less powerful than the time to worsening and time to death endpoints; while for Scenario A the time to improvement and time to worsening endpoints were estimated as the more powerful. The four approaches of time to death, proportional odds, CMH and time to death are estimated to perform relatively well in Scenario C. Next in terms of power for Scenario C are the ranked trajectory and binary improvement approaches. While, of the directional endpoints, those measuring worsening have relatively good power for this scenario, it must be noted that the binary improvement at Day 14 endpoint has moderately good power here also, although not comparable with its estimated power for both the other scenarios.

Power for a sample size of 90 per treatment arm for Scenarios E1-E9 (SOC based on Cao et al. (2020) but with transition probabilities for improvement increased by 10%, 20%, …90%) and F1-F9 (SOC again based on Cao et al. (2020) but with transition probabilities for worsening/death decreased by 10%, 20%, …90%) is presented in Figure 6.

The results for the Scenerios with efficacy systematically imposed clarify that, as seen in Figures 2 and 4, one endpoint may not suit all COVID treatments. Events based on improvement in the WHO scale may not suit treatments whose effect is to decrease the probability of worsening; and events based on worsening/death may not suit treatments whose effect is to increase the probability of improvement. Figure 6 also suggests that the proportional odds approach may not perform well for COVID when a treatment decreases the probability of worsening but does not directly increase the probability of improvement. The ranked trajectory endpoint is estimated to be relatively powerful to detect differences under both the scenario of increased improvement and the scenario of decreased worsening is the ranked trajectory.

4. DISCUSSION

Using publicly available data for ordinal outcomes based on the WHO scale, a variety of 28-day trajectories were simulated. Results of analyses of endpoints based on the simulated outcomes suggested that the rate of “false positive” findings – the Type I error rate - was controlled at very close to the nominal rate for all endpoints and analyses, despite apparent lack of proportional odds in some time to event endpoints. In simulations based closely on outcomes from recent trials, no one endpoint had the best power for all scenarios. The power of time to event endpoints and the proportional odds approach was seen to differ markedly depending upon the pattern of trajectories in the treatment groups compared. Figure 1 a)-c), which uses outcomes based on Cao et al. (2020) and Grein et al. (2020), suggests that potential treatments of patients hospitalised for COVID-19 could in some cases differentiate themselves from a control group by superiority in reducing the hazard of worsening, and in some cases differentiate themselves by superiority in time to improvement. Two endpoints had relatively good power in two out of three scenarios based on recent trials, and relatively moderate power in the third scenario: these were 1) a binary endpoint of a 2-point improvement in the WHO scale at Day 15; and 2) a ranked trajectory based on the patient’s score on the WHO scale over the entire course of the trial. In a second series of scenarios that imposed efficacy via increased improvement and a third series that imposed efficacy via decreased worsening, the ranked trajectory endpoint had moderate power for both varieties of efficacy, while all other endpoints had poor power for one or other of the series of scenarios.

The results suggest, what might be expected, that one primary endpoint will not fit all candidate treatments and SOCs for COVID-19 trials. If candidate treatments and controls vary similarly to those simulated in Scenarios A-C presented here, the primary endpoint for a COVID-19 trial may need to vary depending on the expected trajectory of a candidate treatment, and on how it is expected to show superiority to SOC, insofar as this can be guessed – one size will not fit all for this indication. A two-stage approach, such as is envisaged for the ACCORD-2 platform trial, may be advisable. Stage 1 of ACCORD-2 is planned to have 60 subjects per arm. Stage 2 is planned to have approximately twice this number per arm. The Steering Committee of ACCORD-2 are empowered to change the endpoint and sample size of Stage 2, based on results from Stage 1. Stage 2 does not share subjects with Stage 1, and thus inference from Stage 2 is not compromised by such changes to endpoint and/or sample size.

It is a limitation of the present paper that data day-to-day transitions are approximated from outcomes at three scheduled time points as published for recent clinical trials. The time to event data thus lack potential extra information about treatment effects that could have been estimated from true day-to-day information about the events of interest. This coarsening also handicaps the estimate of power of the endpoint that ranks subjects by their outcome trajectory. Despite this, the power of the ranked trajectory endpoint was estimated to be among the best for two of the three scenarios, and moderately good in a third scenario. The ranked patient health trajectory endpoint could also address the clinical concern that simpler directional endpoints (e.g., change from baseline in the ordinal WHO scale) may not adequately reflect the mixture of worsenings and improvements in the patient experience associated with a treatment. As more data on COVID-19 outcomes become available, further research into the ranked trajectory endpoint is warranted in this respect. Furthermore, the ranked trajectory has the potential to address relapses of patient outcome and durability of response as suggested by recent FDA guidance (2020). We note that only one variation of the ranked trajectory was explored; further explorations of variations of this endpoint could be fruitful, and would be possible using the code provided in the supplementary material for this paper. Other limitiations of the simulation are discussed in the Results section.

SAS macros to implement the simulations presented are available as supplementary material for this paper. The macros are parameterized so as to allow user input of baseline distributions of the ordinal scale, and user input transition probabilities for each value of the ordinal scale, at each time point of interest, for each treatment group. A formal specification for the simulations and the analysis is also available as supplementary material for this paper.

In conclusion, simulation of the scale recommended by WHO for COVID-19 suggests that, while Type I error is controlled for a wide selection of endpoints based on the scale, no endpoint is likely to be optimal for all treatments; consideration should be given to a ranked trajectory endpoint because it takes worsening as well as improvement into account, and is estimated to have moderate to good power for a wide range of trajectories of the WHO scale.

Table 1.

Categories in the WHO-recommended ordinal scale

Patient state	Descriptor	Score
Uninfected	No clinical or virological evidence of infection	0
Ambulatory	No limitation of activities	1
	Limitation of activities	2
Hospitalized - mild disease	Hospitalized - no oxygen therapy	3
	Oxygen by mask or nasal prongs	4
Hospitalized - severe disease	Non-invasive ventilation or high-flow oxygen	5
	Intubation and mechanical ventilation	6
	Ventilation and additional organ support - pressors, RRT, ECMO	7
Dead	Death	8

Table 2.

Categories in Grein et al. (2020) as mapped to those in Cao et al. (2020)

Status in Figure 2 of Grein et al. (2020)	Definition of category in Cao et al. (2020)	Score in Cao et al. (2020)
Discharge	Not hospitalized with resumption of normal activities	1
	Not hospitalized, but unable to resume normal activities	2
Ambient air	Hospitalized, not requiring supplemental oxygen	3
Low-flow oxygen	Hospitalized, requiring supplemental oxygen	4
High-flow oxygen; NIPPV	Hospitalized, requiring nasal high-flow oxygen therapy, noninvasive mechanical ventilation, or both	5
ECMO; Mechanical ventilation	Hospitalized, requiring ECMO, invasive mechanical ventilation, or both	6
Death	Death	7

NIPPV: Noninvasive positive pressure ventilation; ECMO: extracorporeal membrane oxygenation

Table 3.

A selection of posited endpoints based on the WHO ordinal scale.

Endpoint	Use of ordinal scale	Follow-up time
Improvement in the scale at a time point	Improvement from any point on the scale, conditional on being at that point or worse (proportional odds approach)	Day 14
Improvement in the scale at a time point	Mean ranks based on the scale, stratified by baseline score (Cochrane-Mantel-Haenszel test)	Day 14
Improvement at a time point (Y/N)	2 scale points reduction from baseline, or achieving score < = 2	Day 14
Patient trajectory in scale over time	Ranking based on best and worst score achieved, and time on these	28 days
Time to improvement	Two scale points reduction at any time or achieving score < = 2	28 days
Time to discharge	Achieving score < =2 at any time	28 days
Time to recovery	Achieving score < =3 at any time	28 days
Time to worsening	Worsening by 2 scale points or death at any time	28 days
Time to death	Score indicates death	28 days

Table 4.

Scenarios simulated

Scenario	Experimental arm	Control
A	Experimental arm from Cao et al.	Standard of Care (SOC) arm from Cao et al.
B	Experimental arm from Grein et al.	SOC arm from Cao et al.
C	Experimental arm from Grein et al.	Experimental arm from Cao et al.
D	SOC arm from Cao et al.	SOC arm from Cao et al.
E0-E9	SOC arm from Cao et al., with increased probabilities of improvement on the WHO scale	SOC arm from Cao et al.
F0-F9	SOC arm from Cao et al., with decreased probabilities of worsening on the WHO scale	SOC arm from Cao et al.

Note: for all scenarios, the distribution of the baseline scale reflects the balance found in Cao et al. (2020), with the arm listed under “Experimental” based on that of the experimental arm in Cao et al. (2020); and the baseline scale simulated for the arm listed under the heading “Control” based on that of the control arm in Cao et al. (2020).

Figure 1.

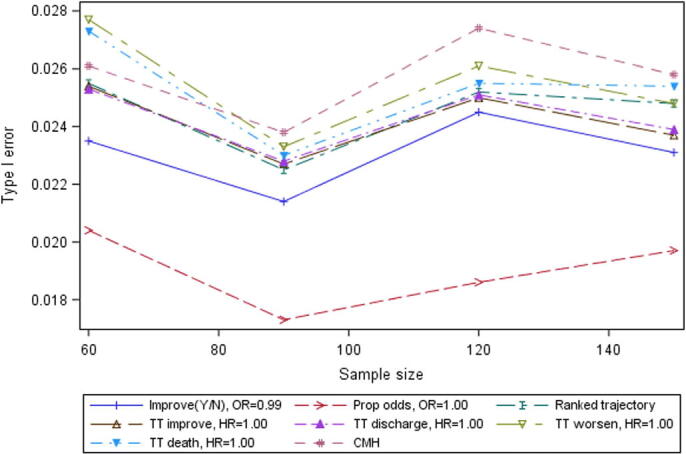
Type I error by sample size for selected endpoints, Scenario D (both arms based on SOC from Cao et al. (2020)).

Improve(Y/N)=Day 14 improvement by >2 in WHO scale or discharge; OR = odds ratio; Prop odds = Proportional odds; Ranked trajectory = Ranked trajectory in WHO score99999; TT = Time to; HR = hazard ratio; CMH = Cochran-Mantel-Haenszel test.

Figure 2.

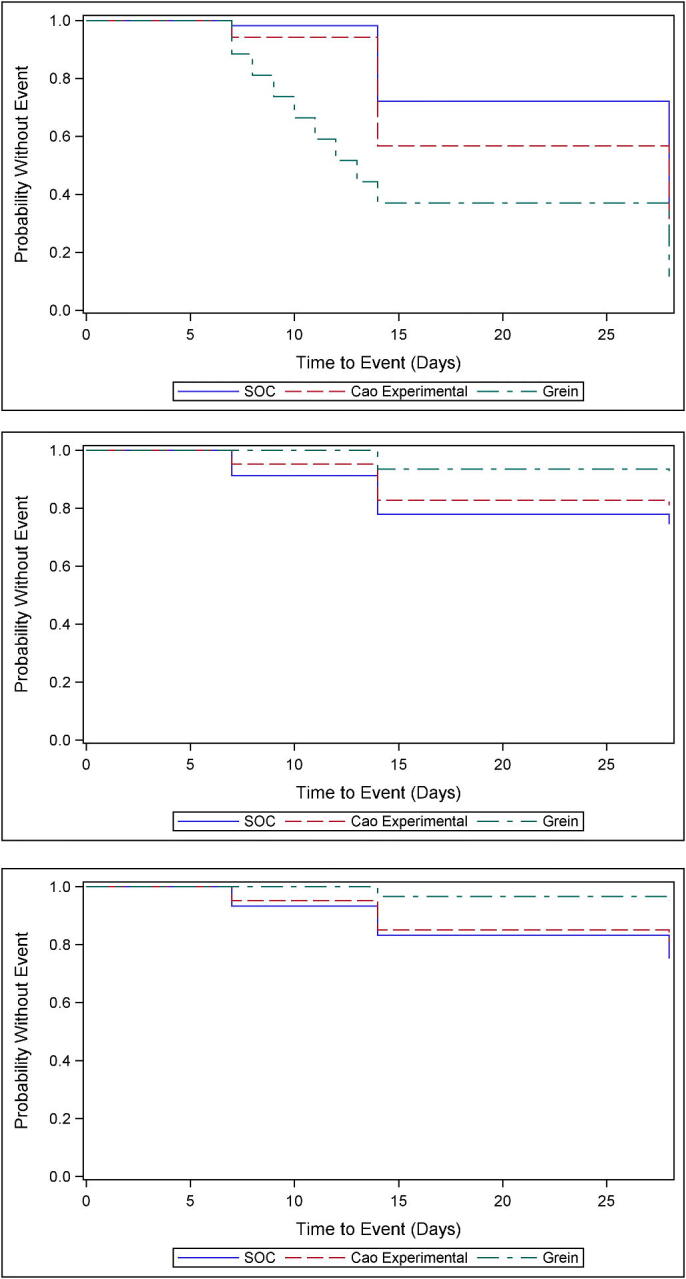
Kaplan-Meier estimates of survival probability, showing a) time to improvement (top); b) time to worsening (middle); c) time to death (bottom).

Figure 3.

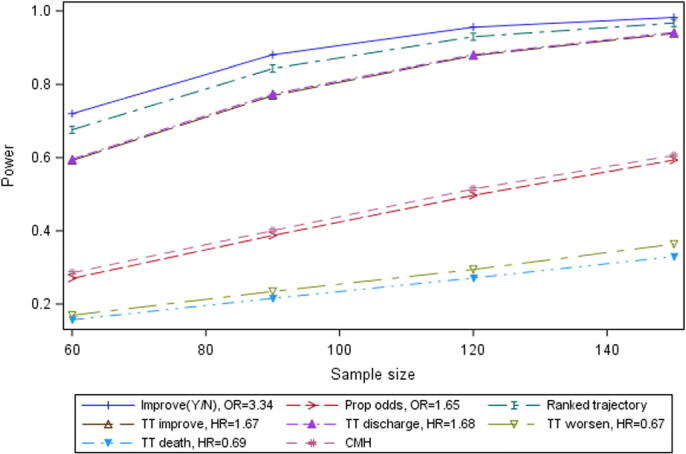
Power by sample size for selected endpoints, Scenario A.

Figure 4.

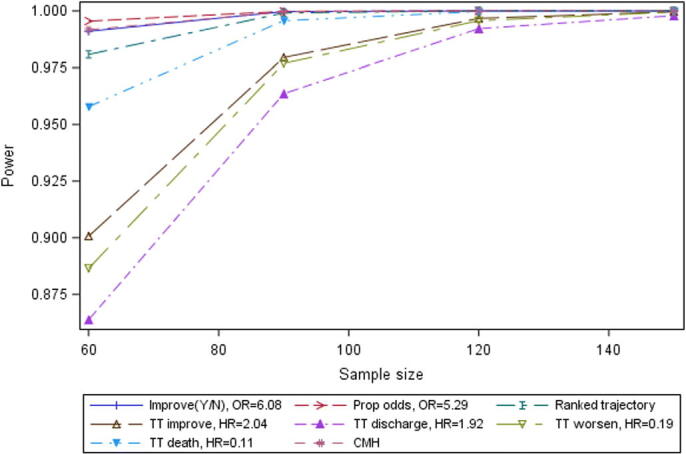
Power by sample size for selected endpoints, Scenario B.

Figure 5.

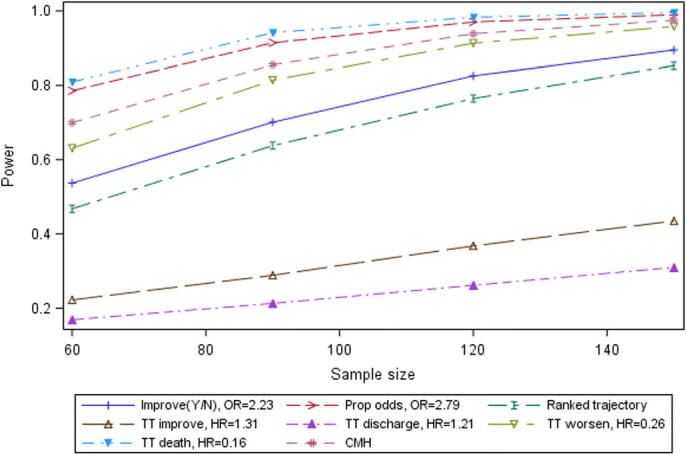
Power by sample size for selected endpoints, Scenario C.

Figure 6.

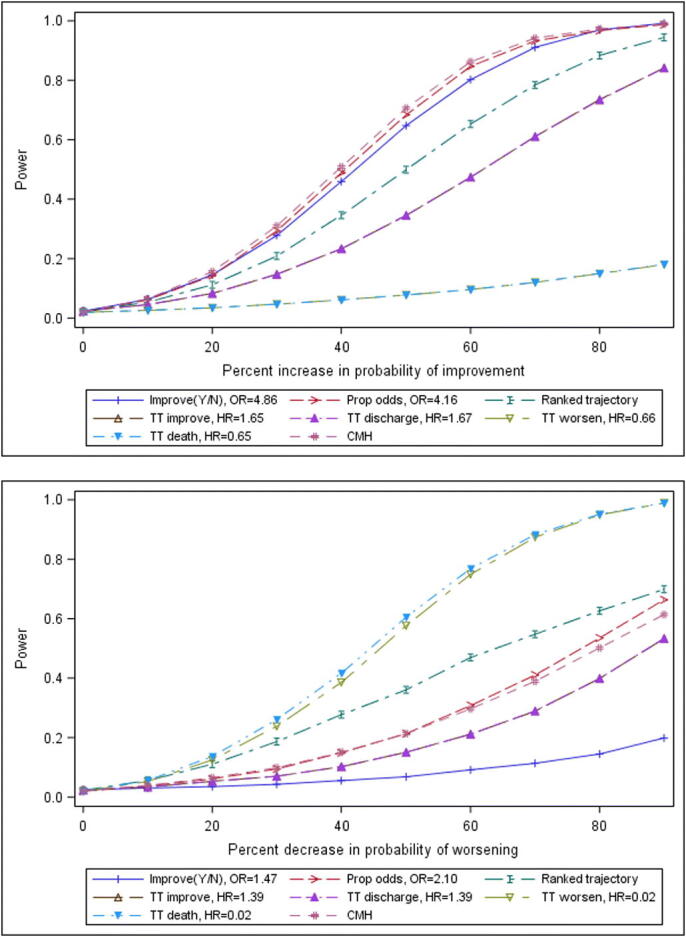
Power for a sample size of 90 per arm by level of efficacy for selected endpoints, a) Top: Scenarios E0-E9: transition probabilities for improvement increased by 0%, 10%,…90%; b) Bottom: Scenarios F0-F9: transition probabilities for worsening decreased by 0%, 10%,…90%. For both plots, results for time to improvement and time to discharge overlap; and results for time to worsening and time to death also overlap.

5. Acknowledgements

The authors gratefully acknowledge that this paper benefitted from discussions with many other statisticians involved in developing clinical trials in subjects with COVID-19. We acknowledge in particular the contribution of Carl-Fredrik Burman, who suggested the ranking of the trajectory of the ordinal scale over time. Finally, we acknowledge comments from the reviewers of the paper, which greatly improved the paper.

The authors work for IQVIA, who paid for their time while preparing the manuscript. MOK is a member of the team designing the ACCORD-2 trial in patients hospitalised for COVID-19.

6. Supplementary materials

Specification for the simulation (.pdf)

SAS code to create simulated longitudinal outcomes and analyse endpoints based on the simulated outcomes (.zip)