Development of Empirical Bioavailability Models for Metals

Abstract

Recently, there has been renewed interest in the development and use of empirical models to predict metal bioavailability and derive protective values for aquatic life. However, there is considerable variability in the conceptual and statistical approaches with which these models have been developed. In this paper, we review case studies of empirical bioavailability model development, evaluating and making recommendations on key issues, including: species selection, identifying toxicity modifying factors (TMFs) and the appropriate environmental range of these factors, use of existing toxicity datasets and experimental design for developing new datasets, statistical considerations in deriving species-specific and pooled bioavailability models, and normalization of species sensitivity distributions using these models. We recommend that TMFs be identified from a combination of available chemical speciation and toxicity data, and statistical evaluations of their relationships to toxicity. Experimental designs for new toxicity data must be sufficiently robust to detect non-linear responses to TMFs and should encompass a large fraction (e.g., 90%) of the TMF range. Model development should involve a rigorous use of both visual plotting and statistical techniques to evaluate data fit. When data allow, we recommend using a simple linear model structure and developing pooled models rather than retaining multiple taxa-specific models. We conclude that empirical bioavailability models often have similar predictive capabilities compared to mechanistic models and can provide a relatively simple, transparent tool for predicting the effects of TMFs on metal bioavailability to achieve desired environmental management goals.

INTRODUCTION

Considerable progress has been made in the last 30 years in the development of metal bioavailability models for use in setting protective values for aquatic life (PVALs) and conducting aquatic risk assessments (Di Toro et al. 2001, Paquin et al. 2002, Niyogi and Wood 2004, Van Sprang et al. 2009, De Schamphelaere and Janssen 2010, Farley et al. 2015, Brix et al. 2017). Recently, a “Technical Workshop on Bioavailability-based Aquatic Toxicity Models for Metals” was organized to evaluate the state-of-the-science regarding metal bioavailability models and their regulatory applications, particularly in setting PVALs (for simplicity, we define PVALs as synonymous with other terminologies such as water quality criteria, water quality guidelines and environmental quality standards that are used in various regulatory jurisdictions).

The workshop was organized into five working groups, each with specific objectives related to the incorporation of bioavailability in derivation of PVALs. The objective of our working group and the subject of this paper was to explore the data needs and technical approaches for developing empirical bioavailability models such as multi-linear regression (MLR) models (Brix et al. 2017, DeForest et al. 2018). The other four working groups considered the history and scientific basis for incorporation of bioavailability in the assessment of freshwater metal toxicity (Adams et al. In Review); the development and use of mechanistic bioavailability models such as the biotic ligand model (BLM) (Mebane et al. In Review); validation methods for metal bioavailability models (Garman et al. In Review); and the application of metal bioavailability models in PVAL derivation (Van Genderen et al. In Review).

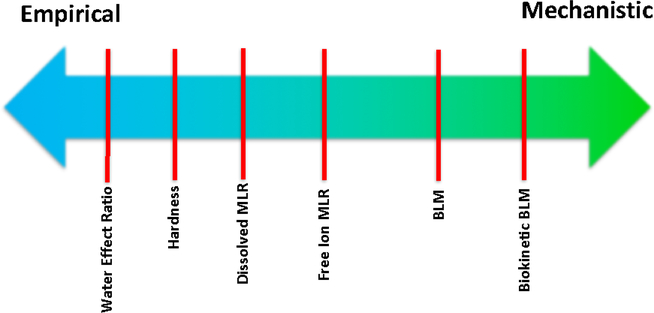
Empirical bioavailability models are statistical models developed from experimental data collected to examine relationships between toxicity and one or more toxicity modifying factors (TMFs; e.g., pH, calcium, dissolved organic carbon (DOC)). From a mechanistic perspective, TMFs can influence not only the uptake of metals (i.e., what some might consider true bioavailability) but also the physiological response of the organism in a way that makes it more or less sensitive to a metal (e.g., temperature) (see Adams et al. (In Review) for a more detailed discussion). Clear distinctions do not exist between empirical and mechanistic bioavailability models. Indeed, the range of metal bioavailability models that have been developed can be viewed as an empirical-mechanistic continuum (Fig. 1). Models range from simple empirical ratios such as the Water Effect Ratio (USEPA 2001), to more simple linear and multi-linear empirical models (Brix et al. 2017), to quasi-mechanistic models such as the BLM (Di Toro et al. 2001) and fully mechanistic models such as the biokinetic BLM (Veltman et al. 20014). Many models are actually hybrids having both empirical and mechanistic components or being informed by mechanistic or empirical data in developing model structure (Deleebeeck et al. 2008, Van Regenmortel et al. 2015, Brix et al. 2017, DeForest et al. 2018).

Figure 1.

Empirical-Mechanistic Model Continuum.

The earliest empirical bioavailability models were hardness-based PVALs developed by USEPA (1985). Similar approaches have been applied in other countries (HMSO 1989) and have continued to be used by the USEPA (2016). With the development of models such as the BLM (Di Toro et al. 2001) that are more mechanistically based and consider the effects of multiple TMFs on metal bioavailability (Di Toro et al. 2001), use of empirical models for setting PVALs has generally been considered less scientifically robust. However, interest in developing empirical bioavailability models that consider multiple TMFs for deriving PVALs has recently increased (CCME 2016, USEPA 2018), as they can be more transparent and easier to use than BLM-based approaches. Further, multiple-TMF empirical models are mathematically similar to, and simple extensions of, the widely accepted hardness-based PVALs for metals.

The advantages and disadvantages of empirical and mechanistic models may vary depending on the complexity and interactions of TMFs that modify bioavailability for a given metal, the specific model structure, the model’s combination of empirical and mechanistic elements, data requirements and availability, intended model use, and other scientific, practical, and policy considerations. Given all the factors that can influence model selection, our goal is not to recommend one approach over the other, but rather to provide best practice guidance on how to develop empirical bioavailability models for metals once the decision is made to pursue this general modeling framework.

Development of empirical bioavailability models for use in PVAL derivation is an iterative process involving multiple steps: (1) Identifying the biological species for model development; (2) Identifying TMFs to be considered in model development; (3) Determining TMF ranges to be covered by the models; (4) Identifying and/or generating appropriate and sufficient data for model development; (5) Deriving models for individual species; (6) Developing pooled multi-species models for extrapolation to other species; and (7) Incorporating models into species sensitivity distributions (SSDs). The current paper considers each of these steps, describing how they have been addressed in past efforts and how they should be addressed in future efforts.

SPECIES SELECTION

Except when only a particular species is of concern, PVALs are based on data for a broad array of species representative of an aquatic community. Because models can be developed for only a small subset of these species, the selection of these species needs to consider which are necessary and sufficient for establishing the relationship of PVALs to TMFs.

PVALs focus on sensitive organisms and the effects of TMFs can vary as a function of metal concentration such that the influence of TMFs can differ for sensitive and insensitive taxa (Santore et al. 2002). Consequently, while it is desirable to have data for species across the full range of metal sensitivity (particularly when the full SSD will be used to develop the PVAL), it is important that species sensitive at concentrations near the PVAL be evaluated to ensure the model is properly parameterized at the PVAL.

We recommend that models be developed for a minimum of one fish, one invertebrate and one alga/plant. Currently available data suggests fish species generally respond to TMFs in a similar manner and the physiological processes in fish with respect to metal uptake are generally similar across species (Niyogi and Wood 2004, Brix et al. 2016, Brix et al. 2017). However, invertebrates have greater diversity in ion transport physiology and differential responses to TMFs have been observed across invertebrate taxa (Schlekat et al. 2010, Esbaugh et al. 2012). As such, information for multiple invertebrate taxa (e.g., crustacean, insect, mollusk) would be desirable. Data on the response of algae and aquatic plants to TMFs are limited to a few species, but available information indicates their responses to TMFs can differ substantially compared to fish and invertebrates (De Schamphelaere et al. 2005).

IDENTIFICATION OF TOXICITY MODIFYING FACTORS

Selection of TMFs for empirical bioavailability models should include both existing empirical evidence as well as mechanistic considerations regarding regulation of metal bioavailability and toxicity. The chemical speciation of metals in water is of central importance to bioavailability because different metal species will be more or less readily taken up by an organism; thus, those TMFs important to speciation need consideration. This includes information on mechanisms of metal uptake and toxicity, both in determining how metal speciation might affect uptake and how physicochemical variables of exposure water might otherwise affect uptake and toxicity. Attention should be given to correlations among TMFs that can make it difficult to separate effects of individual TMFs and lead to erroneous model formulations if not considered.

Dissolved organic carbon, pH, and hardness are often identified as TMFs for divalent metals (Niyogi and Wood 2004). Water hardness is generally a function of Ca and Mg concentrations, although other elements can contribute. Calcium is often the primary component of hardness influencing metal toxicity (Heijerick et al. 2002), although Mg can also influence toxicity for some metals (Peters et al. 2011, Brix et al. 2017b). Use of water hardness as a TMF incorporates effects from both ions, but does not consider variation in Ca:Mg ratios, which can substantially influence hardness-dependent metal toxicity (Welsh et al. 2000). Similarly, the chemical composition of DOC can vary, affecting its metal-binding capabilities and thus its effect on toxicity (Al-Reasi et al. 2011).

It is important to recognize, however, that DOC, pH, and hardness may not be important TMFs for some metals and/or taxonomic groups. Various forms of nitrogen and phosphorus are important TMFs for algae and plants (Lee and Wang 2001). For metals and metalloids that occur predominantly as oxyanions, chemically similar anions can affect bioavailability. Sulfate (SO₄²⁻), for example, has been reported to be an important TMF for selenate (SeO₄²⁻) for fish, invertebrates, and algae (Brix et al. 2001, DeForest et al. 2017).

Interestingly, perhaps the most ubiquitous TMF is temperature (Sokolova and Lannig 2008), but this is rarely considered in empirical or mechanistic bioavailability models (Erickson et al. 1987, Santore et al. 2018). Most model development (empirical and mechanistic) involves evaluating how well a model predicts laboratory toxicity test data where test temperatures are largely standardized in order to generate toxicity data that can be compared across chemicals. Consequently, temperature has not typically been identified as an important explanatory variable in normalizing metal toxicity data. However, application of these models to the field where temperature is much more variable could potentially lead to significant under- or over-estimation of toxicity. This is a consideration that we recommend needs to be addressed in future bioavailability studies and models.

In addition to the TMFs described above, which may vary by taxon and metal, there are likely other TMFs associated with each species-metal combination that have relatively minor influences on metal toxicity. The relative importance and need to assess these “minor” TMFs will vary and can be assessed statistically and using best professional judgement. Importantly, we do not recommend blindly using the results of statistical tests to make decisions regarding inclusion/exclusion of TMFs and caution against over-parameterizing models which can lead to a model that is not sufficiently generalized to other datasets to which it may be applied. For example, Erickson et al. (1987) demonstrated Na is a TMF for Cu toxicity to Pimephales promelas. However, Na reduces Cu toxicity only at concentrations >1 mM Na, and toxicity is reduced by slightly less than a factor of 2 in the presence of 4 mM Na. Given that ~65% of surface waters in the United States have <1 mM Na and ~90% of surface waters have <4 mM Na, inclusion of Na in an empirical model for P. promelas will have a relatively minor effect on toxicity predictions except in unusually saline freshwaters. Further discussion of how best to assess the inclusion or exclusion of TMFs can be found in later sections on development of species-specific and pooled models.

TMF RANGES

For development and application of empirical bioavailability models, various linked issues regarding TMF ranges need to be considered. First, it is important to consider how the minimum TMF range necessary for a statistically reliable model relates to the range of water quality conditions to which the model will be applied. Because empirical models should generally be used only within the range of water quality for which they have been evaluated, one should assess the collective scope of applicability for available models and how this range differs from the desired scope of applicability for a PVAL. After model development, recommendations should be made to indicate if PVALs need to be restricted in any way until more data are generated. It is important to specify the range of parameters to which a model applies to avoid misuse and misinterpretation of data outside the intended TMF range, especially if this leads to the PVAL not being protective.

Issues regarding TMF ranges are evident in the development and application of the early USEPA hardness-dependent water quality criteria (WQC) for metals. To support adequate estimation of hardness slopes, USEPA (1985) recommended that hardness concentrations for tests for a given species span at least 100 mg l⁻¹ with the highest concentration at least 3-fold greater than the lowest concentration, but these minimum requirements might cover less than half of the range of hardness to which WQC might be applied. However, because multiple species satisfying these range requirements were combined into pooled models, the resultant models generally had broader ranges than these minimum data requirements. This broader range was still less than the hardness range to which WQC might apply though, so restrictions were necessary regarding WQC outside this range (e.g., USEPA (2016)).

More recently, with regard to minimum ranges needed for reliable model development, in developing MLR models for Cu and Zn, Brix et al. (2017) and CCME (2016) required minimum ranges for hardness (100 mg l⁻¹), pH (1.5 units), and DOC (5 mg l⁻¹) for a given species. In developing an empirical bioavailability model for PVALs, consideration should be given to ranges of TMFs that reflect wide environmental relevance. USEPA does not provide specific guidance regarding this, but in the EU the 5–95^th percentile of TMFs are recommended (European Commission 2011). For a model with three TMFs that are not significantly correlated, testing within the 5^th to 95^th percentiles for all the TMFs will include only about 75% of the total range of water compositions, while testing within the 10^th to 90^th percentiles will only include about 50% of the total range of water compositions. Alternatively, if TMFs are correlated, testing at the 5^th and 95^th percentiles for multiple TMFs might involve water compositions that do not naturally occur in the environment. For example, a water with low pH (e.g., 6.5) and high hardness (e.g., 420 mg l⁻¹), is unlikely to occur naturally. However, it is important to recognize that regulatory applications will need to address unusual conditions, and in some cases, formulation of model equations might benefit from testing certain extreme compositions. For example, the low pH/high hardness scenario just described is unlikely to occur naturally but can occur in effluent dominated streams receiving wastewater from metal and other resource extraction activities. Consequently, development of a model that includes these conditions is desirable for regulatory application.

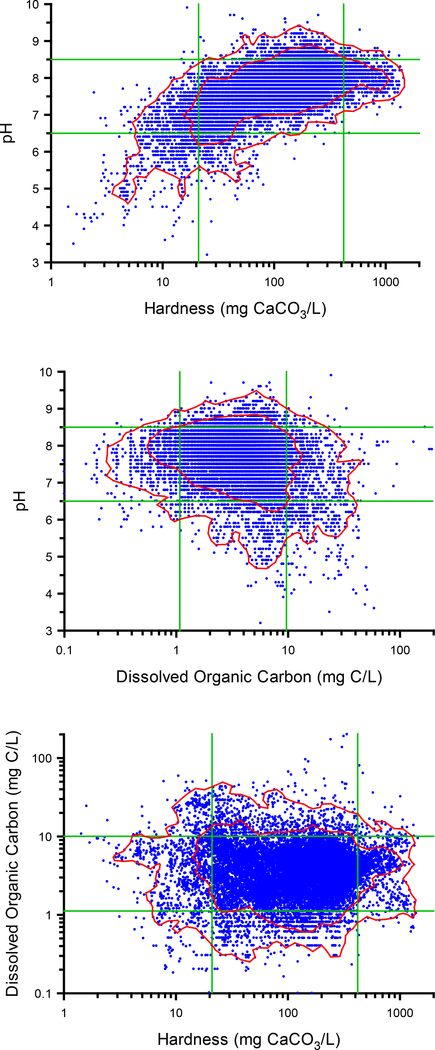
Resolving issues of TMF ranges would benefit from more rigorous analysis of the water compositions to which PVALs should apply. As an example of a more comprehensive analysis for characterizing ranges of multiple TMFs, we evaluated a compilation of over 20,000 water chemistry data from the Water Quality Portal (http://www.waterqualitydata.us) for several potential metal TMFs spanning 65 of the 84 ecoregions in the U.S. (Ryan, Unpublished, Table 1). Figure 2 provides scatter plots of these data for pH vs. hardness, DOC vs. hardness, and pH vs. DOC, and shows the 5^th and 95^th percentiles of each TMF to illustrate the coverage provided by such limits. This figure also illustrates how the correlation between hardness and pH should be considered in selecting realistic combinations of these variables, but even when variables are not substantially correlated (DOC vs. either pH or hardness), the utility of testing combinations at extreme percentiles of both variables that are unlikely to occur may be questionable. Because the >20,000 points in these plots are densely overlaid in the middle of the distributions, it is difficult to assess how well existing data for a given metal may cover the distribution of these variables and how to design experiments to generate new data to improve coverage (see Dataset Development section). To better illustrate suitable ranges for variables, the joint probability distributions for pairs of these variables were characterized by kernel density estimation (KDE)(Silverman 1986). Results from the KDE analysis were used to define constant-density contours enclosing 90% and 99% of the data (red lines in Figure 2; see Supplemental Information 3 for method details). These contours allow visualization of more appropriate parameter values for testing, in particular, the contours for the pH/hard relationship illustrate how the rectangle defined by the 5^th and 95^th percentiles of the individual parameters includes some improbably parameter combinations, while excluding some important ones.

Table 1.

Summary Distribution of Select Toxicity Modifying Factors in the United States. All units in mg l⁻¹ except pH (Ryan, Unpublished).

	DOC	pH	Hardness	Ca	Mg	Na	Alkalinity
5th Percentile	1.1	6.5	21	5.4	1.3	1.6	17
10th Percentile	1.5	7.0	31	8.6	1.8	2.5	27
50th Percentile	3.5	7.8	136	37	9.7	14	103
90th Percentile	7.7	8.3	324	84	28	97	210
95th Percentile	9.9	8.5	420	105	38	160	240

Figure 2.

Pairwise relationships between hardness, pH, and DOC in natural waters occurring across the US (n = 22,076). Green lines represent 5^th and 95^th percentiles of each parameter. Red lines denote constant-density contours enclosing 905 and 99% of the data based on kernel density estimation (see Supplemental Information for analysis methods). Data from Ryan (Unpublished).

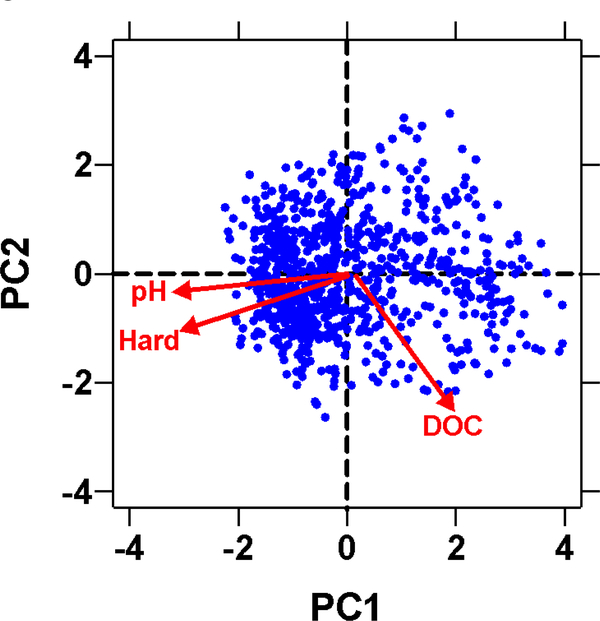
Another option for processing these data into useful descriptions of environmentally realistic combinations of TMFs is the use of principal component analysis (PCA) (Jolliffe 2002). Scatterplots of the principal component scores from a PCA based on monitoring data for all TMFs considered can be used to characterize the space occupied by naturally occurring combinations of TMFs (Fig. 3). The test set (i.e., the optimal set of TMF combinations) may be further refined by focusing on specific areas within the PCA plot to ensure that waters likely to have high bioavailability are tested. Similar to the KDE analysis described above, ranges developed from a PCA-based approach may be quite different for some parameters than pre-defined ranges (percentiles) for the univariate TMF. As for any method of selecting TMF ranges, combinations of TMFs selected for toxicity testing should not induce physiological stress to the test organisms.

Figure 3.

Example of a PCA-based analysis of TMFs within a specific geographical region.

DATASET DEVELOPMENT

Dataset development for empirical bioavailability models will vary depending on existing data and on assessment goals. The models in Table 2 were developed using data from individual laboratory studies in which one or more TMFs were systematically varied while others were held constant, from multiple studies that collectively cover a range of TMFs, and from combinations of both approaches. Model development has sometimes relied solely on existing data, but at other times has included generation of new supplementary data to comprehensively address model needs. The amount of data used in model development has varied depending on their source and quality. This section will describe some of these datasets to identify noteworthy issues in their development, and then discuss aspects of experimental design for generating new data to augment available datasets.

Table 2.

Summary of Empirical Metal Bioavailability Models

Metal/Species	Endpoint	Modela	N	Adj. R2	Reference
Aluminum
Ceriodaphnia dubia	Chronic	ln(EC20) = −41.026 + (0.525 × ln[DOC]) + (2.201 × ln[Hard]) + (11.282 × pH) – (0.663 × pH2) – (0.262[ln(Hard) × pH])	23	0.73	DeForest et al. 2018, USEPA 2017
Pimephales promelas	Chronic	ln(EC20) = −14.029 + (0.503 × ln[DOC]) + (3.443 × ln[Hard]) + (3.131 × pH) – (0.494[ln(Hard) × pH])	22	0.87	DeForest et al. 2018, USEPA 2017
Pseudokirchneriella subcapitata	Chronic	ln(EC20) = −61.952 + (1.678 × ln[DOC]) + (4.007 × ln[Hard]) + (17.019 × pH) – (1.020 × pH2) – (2.04[ln(DOC) × pH]) – (0.556[ln(Hard) × pH])	27	0.96	DeForest et al. 2018, USEPA 2017
Copper
Pimephales promelas	Acute	log(LC50) = −0.308 + (0.192 × pH) + (0.136[pH × log DOC])	21	0.92 b	Welsh et al. 1993, 1996
Pimephales promelas	Acute	log(LC50) = −0.856 + (0.166 × pH) + (0.095[pH × log DOC]) + (0.237 × Ca)	18	0.82 b	Welsh et al. 1993, 1996
Pimephales promelas	Acute	log(LC50) = −1.003 + (0.195 × pH) + (0.104[pH × log(DOC)]) + (0.211 × Ca)	17	0.82 b	Welsh et al. 1993, 1996
Pimephales promelas	Acute	log(LC50) = −1.003 + (0.195 × pH) + (0.104[pH × log(DOC)]) + (0.211 × Ca)	18	0.79 b	Welsh et al. 1993, 1996
Pimephales promelas	Acute	log(LC50) = −0.426 +( 0.061 × pH) + (0.005[pH × log(colour)]) + (0.116 × Hard)	17	0.89 b	Welsh et al. 1993, 1996
Daphnia magna	Acute	EC50[Cu2+] (nM) = 308 + (42.6 × Ca [mM]) – (41.3 × pH)	25	0.53 b	De Schamphelaere et al. 2002
Daphnia magna	Chronic	NOEC = −160.5 + (7.652 × DOC [mg/L]) + (25.50 × pH)	35	0.75 b	De Schamphelaere and Janssen 2004
Daphnia magna	Chronic	EC50 (μg/L) = −212.4 + (10.41 × DOC [mg/L]) + (34.36 × pH)	35	0.76 b	De Schamphelaere and Janssen 2004
Pomacea paludosa	Acute	log(LC50) = 0.540 + (0.008 × Age [d]) + (0.024 × DOC) + (0.120 × pH)	14	0.92 b	Rogevich et al. 2008
Ceriodaphnia dubia	Acute	ln(LC50) = −9.535 + (6.703 × ln[DOC]) + (0.144 × ln[Hard]) + (1.511 × pH) – (0.776[ln(DOC) × pH])	87	0.78	Brix et al. 2017
Daphnia magna	Acute	ln(LC50) = −4.005 + (0.947 × ln[DOC]) – (0.254 × ln[Hard]) + (0.628 × pH) + (0.101[ln(Hard) × pH])	307	0.87	Brix et al. 2017
Daphnia obtusa	Acute	ln(LC50) = −6.245 + (4.224 × ln[DOC]) + (0.139 × ln[Hard]) + (1.131 × pH) – (0.353[ln(DOC) × pH]) – (0.171[ln(DOC) × ln(Hard)])	53	0.89	Brix et al. 2017
Daphnia pulex	Acute	ln(LC50) = −9.932 + (0.6931 × ln[DOC]) + (0.172 × ln[Hard]) + (1.502 × pH) – (0.782[ln(DOC) × pH])	35	0.92	Brix et al. 2017
Pimephales promelas	Acute	ln(LC50) = −6.744 + (1.620 × ln[DOC]) + (1.065 × ln[Hard]) + (0.925 × pH) – (0.241[ln(DOC) × ln(Hard)])	206	0.80	Brix et al. 2017
Daphnia magna	Chronic	ln(EC20) = 0.200 + (0.848 × ln[DOC]) + (0.235 × ln[Hard]) + (0.172 × pH)	77	0.87	Brix et al. 2017
Pooled Model	Acute	ln(LC50) = InterceptSpeciesi + (0.786 × ln[DOC]) + (0.582 × ln[Hard]) + (0.966 × pH)	688	0.81	Brix et al. 2017
Lead
Ceriodaphnia dubia	Acute	ln(LC50) = −6.994 + (0.589 × ln[Ca]) + (0.992 × ln[DOC]) + (0.745 × pH)	23	0.82	Esbaugh et al. 2011
Pimephales promelas	Acute	ln(LC50) = 0.932 + (0.784 × ln[DOC]) + (0.443 × ln[ionic strength (mM)])	25	0.63	Esbaugh et al. 2011
Ceriodaphnia dubia	Chronic	ln(EC50) = −5.168 + (1.001 × ln[DOC] (μM)) + (0.322 × ln[TCO2] (μM) ) + (0.371 × ln[Na] (μM) )	22	0.55	Esbaugh et al. 2012
Lymnaea stagnalis	Chronic	ln(EC50) = −2.919 + (1.089 × ln[DOC] (μM))	7	0.82	Esbaugh et al. 2012
Philodina rapida	Chronic	ln(EC50) = 19.376 - (3.018 × pH) + (1.503 × ln[Ca] (μM))	6	0.92	Esbaugh et al. 2012
Zinc
Daphnia pulex	Acute	ln(LC50) = 3.196 + (0.284 × ln[DOC]) + (0.845 × ln[Hard])	25	0.58	CCME 2016
Daphnia magna	Acute	ln(LC50) = 3.083 + (0.191 × ln[DOC]) + (0.865 × ln[Hard])	7	0.97	CCME 2016
Daphnia spp. Pooled	Acute	ln(EC50) = 3.224 + (0.240 × ln[DOC]) + (0.833 × ln[Hard])	32	0.81	CCME 2016
Oncorhynchus mykiss	Chronic	ln(LC10) = 7.041 + (0.999 × ln[DOC]) + (0.886 × ln[Hard]) – (0.937 × pH)	14	0.79	CCME 2016

Models based only on hardness or with adjusted R² <0.50 are excluded.

^aUnless otherwise noted, units for metals are μg l⁻¹ and units for DOC, hardness, and calcium are mg l⁻¹.

^bAdjusted R² was calculated from the R² based on sample size (n) and the number of parameters (k) included in the model:

$\text{Adj. }{\mathrm{R}}^2\text{= 1-}\left(\frac{\left(\text{1-}{\text{R}}^{\text{2}}\right)\left(\text{n-1}\right)}{\text{n-k-1}}\right)$

For a single TMF, the number and range of data points should be sufficient to define the shape of the relationship and to encompass the range of applicability desired for the PVAL. OECD QSAR guidance (2007) recommends a minimum of 5 data points per independent variable for univariate regression analyses. If suitably spaced and satisfying considerations regarding the TMF range (see previous section), 5 data points would support developing an empirical bioavailability model for a single TMF, including assessing the need for a nonlinear model, and even fewer points might suffice depending on prior knowledge regarding the form of the model equation, the quality of the data, and the assessment needs.

However, attention must also be given to how the data were obtained. If the data come from multiple studies, with no single study covering a substantial range of the TMF, differences in sensitivity across the studies could affect results, and more data would be necessary to test for study effects and provide confidence in a final model. Even if the data come from a single study in which a single TMF was systematically varied, care must be taken that the TMF was not confounded by other factors that might modify toxicity. For example, several studies on the effect of hardness on Ag toxicity, in which hardness was varied using chloride salts, were confounded by chloride complexation of silver until this effect was identified (Bury et al. 1999). A model resulting from such data would only be applicable to waters in which hardness was similarly correlated with chloride.

For multiple TMFs, the dataset must consider not only the separate data issues for each TMF, but also the possibility of interactions among the TMFs. Brix et al. (2017), for example, used all available data for a given species to define relationships between Cu toxicity and multiple TMFs (hardness, DOC, and pH). This involved large datasets with broad coverage for each TMF. While this dataset was able to support estimation of TMF interactions, correlations and unevenness in the data coverage can distort model parameters, so methods described in this study for assessing model fit should be used to assure that model assumptions are met, and fit is adequate for any study related TMF or test species subsets within the larger dataset. Tools for addressing such dataset limitations are discussed in the Model Development section, some of which were employed by Brix et al. (2017).

In contrast, DeForest et al. (2018) based the development of a model for Al toxicity to the alga Pseudokirchneriella subcapitata on a single study by Gensemer et al. (2018), which tested toxicity in a complete factorial design with 3 levels for each TMF (hardness, pH, DOC). Although the TMF ranges were more restricted than would be desirable for WQC, this dataset still provided broad coverage of the TMFs and established clear relationships for model development, with model predictions nearly always being within the error bounds of observed values. Even with just 3 levels for each TMF, the total of 27 TMF combinations and the consistency of effects observed across the entire matrix argues for the sufficiency of this particular dataset and the potential strengths of the factorial study design for testing across multiple TMFs (including reduction of cross-study variance).

Empirical bioavailability models should be based on existing data but generate, as needed, new data that will improve model performance and applicability while minimizing testing efforts to reduce use of resources and test animals. When existing data are found to be inadequate, new systematic experiments should be conducted. New data can come from a single factorial design in which all combinations of low and high values for each TMF are tested (e.g., 5^th and 95^th percentiles in Fig. 2) or include TMF combinations that have not been adequately tested in previous studies. For 3 TMFs, this constitutes 8 treatment combinations at the corners of a cube in the 3-dimensional TMF space. Although a minimal study with just these 8 treatments could be conducted (perhaps including a treatment with intermediate values for all TMFs; i.e., the center of the cube), this would not support evaluating non-linearities and interactions, or meet reasonable standards for the number of data points per variable (OECD 2007). Including an intermediate value for each TMF in a full factorial design would entail 27 tests (as in the Gensemer et al. (2018) algal tests). A less data demanding option would be to include the TMF combinations at the center of each face of the cube, thereby testing three levels of each TMF at the intermediate values for the other two. This would involve 15 total tests rather than the 27 tests for the full factorial design and satisfy the OECD recommendation that a minimum of 3 data points over an adequate range is needed to discriminate between linear and non-linear responses. Ultimately, model performance will dictate whether the number of TMF combinations tested is sufficient and initial model development will provide feedback regarding additional data generation.

Simple factorial designs like those just described have the drawback that the corners of the factorial cube could represent unlikely combinations of TMFs (see TMF Range section). To avoid this problem and to incorporate environmental realism, we recommend investigating the distribution of actual field data (Figure 2) to select more realistic combinations. The joint distributions of variables, as in Figure 2, can be assessed (e.g., by KDE) to describe surfaces in the TMF space that enclose a certain percentage (e.g., 95%) of the data. The experimental design could then test effects at systematic points within the joint space of all TMFs and allow both main effects and interactions to be estimated. The same approach could be conducted via PCA analysis, as discussed in the TMF Range section, to select TMF combinations that reflect the interactions of the TMFs embodied in the PCs (Figure 3).

DEVELOPMENT OF SPECIES-SPECIFIC MODELS

Developing empirical bioavailability models is usually an iterative process involving both statistical and qualitative evaluation of issues such as model performance, validity of model assumptions, and perceived costs and benefits involved in development and application of a model. For example, what kind of evidence should be required to justify the use of linear vs. nonlinear models, the inclusion of interaction terms in a model, or use of data from a study that did not vary all water quality parameters? How should models be compared to assess the benefits of one over the other? Can mechanistic knowledge of metal bioavailability (speciation, uptake pathways, and toxicity mechanisms) inform empirical model development?

Given differences among metals and species in the mechanisms of toxicity and availability of data to develop empirical models, a lack of formal, prescriptive criteria for model development, and the varieties of models to consider, it is not feasible to describe a fixed process for developing empirical bioavailability models. However, based on previous experience, it is possible to suggest some particularly useful tools for testing assumptions and evaluating model performance. These should be incorporated into the iterative model development process and used to develop an awareness of the strengths and limitations of a model that will affect how it is applied.

What form of model should be used and how to decide?

The first steps of model development should involve exploratory analyses. Graphical analyses should be used liberally to develop an understanding of distributions and relationships among variables and help identify unusual cases that may affect model results. Graphical analyses are a critical component in every stage of model development as they reveal: adequacies and inadequacies of the data and the model; whether statistical performance criteria are capturing important aspects of model fit; whether assumptions of the model and the mechanistic conceptual framework are consistent; and numerous other issues that can be overlooked without visualizing the data and model. All the tools of exploratory data analysis (e.g., boxplots, cumulative frequency distributions, color coding data by subsets such as species, region, study) should be considered for helping understand the adequacy of the model structure and the data (see Garman et al. (In Review) for examples of these approaches).

Based on current experience with metal bioavailability models, standard linear models should generally be considered first. USEPA guidelines for deriving aquatic life WQC (USEPA 1985) consider the linear relationships of log metal effect concentration (EC) vs. log hardness that were recognized at the time, and provided a methodology for regression of the data to develop metal WQC as a function of hardness. Subsequent efforts have addressed additional TMFs, such as pH and DOC (Welsh et al. 1996, Rogevich et al. 2008, Esbaugh et al. 2011, Esbaugh et al. 2012, Fulton and Meyer 2014, Brix et al. 2017, DeForest et al. 2018). In Canada, a MLR-based draft water quality guideline for Zn has been issued (CCME 2016), and USEPA recently released a final aquatic life WQC for Al (USEPA 2018) primarily based on the MLR model of DeForest et al. (2018).

Methods for assessing performance of linear models are highly developed (Harrell 2015). Within the linear framework, it is important to determine the need for transformation of any of the dependent or independent variables to create linearity in the response and homogenize variance. It is also important to assess collinearity among independent variables via correlation tables, Variance Inflation Factors (Zuur et al. 2010), unexpected signs of coefficients, significance of individual parameters and the model as a whole (p values), and model performance (e.g., adjusted R², Akaike and Bayesian Information Criteria (AIC/BIC)) (Burnham and Anderson 2004). Within each of these arenas, comparison of model performance criteria across models and distribution of residuals are the main tools for evaluating different model formulations.

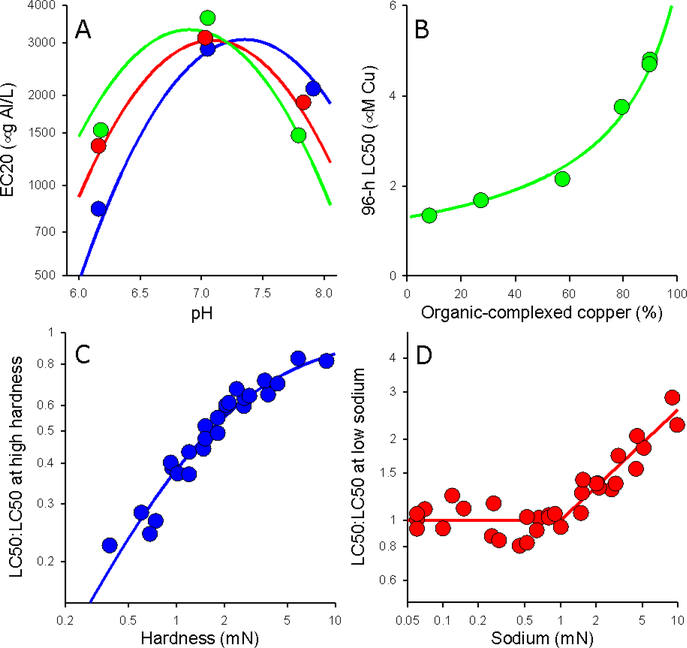
Exploratory data analysis or evaluation of deviations from linear models can indicate nonlinear relationships between ECs and TMFs. For example, DeForest et al. (2018) reported that aluminum EC20s for the algae Raphidocelis subcapitata were higher at pH 7 than at both pH 6 and pH 8 (Figure 4A). The authors attributed this nonlinearity to pH-dependent changes in Al speciation and addressed it by including a pH × pH (i.e., pH²) interaction term in the model, providing a parabolic shape to the relationship with a maximum within the pH 7.0–7.5 range. This model is mathematically linear relative to the set of independent variables (individual TMFs and their interactions) and can therefore still be addressed by linear statistical tools. However, inclusion of a squared term should only be undertaken when data convincingly demonstrate a maximum or minimum within an environmentally relevant range for the TMF, because if there is only a reduction in slope as a TMF increases, a parabolic shape might be erroneously inferred when asymptotic behavior would be more appropriate. Furthermore, such a parabolic shape makes extrapolation beyond the range of the data from which it was derived particularly uncertain. For similar reasons, higher order polynomials should be avoided in favor of models that functionally address observed nonlinearities.

Figure 4.

Examples of non-linear relationships between TMFs and metal toxicity. A) Relationship between pH and Al toxicity to Raphidocelis subcapitata (DOC = 4 mg l⁻¹, hardness = 22 (blue), 60 (red), and 120 (green) mg l⁻¹ (DeForest et al. 2018), B) Relationship between organic-complexed Cu and Cu toxicity to Pimephales promelas (Erickson et al. 1987), C) Relationship between hardness and Cu toxicity to P. promelas (Erickson et al. 1987), D) Relationship between Na concentrations and Cu toxicity to P. promelas (Erickson et al. 1987).

Sometimes relationships between ECs and TMFs are inherently nonlinear and unsuited to linear statistical analysis tools. Erickson et al. (1987) modeled the relationships between Cu toxicity to fathead minnows (P. promelas) and several TMFs. Log ECs varied linearly with some TMFs over the range tested (e.g., pH, temperature), but the relationships for other TMFs were inherently nonlinear. Nonlinear models that were applied included a joint toxicity relationship for Cu complexed and not complexed by DOC (Figure 4B), an asymptotic relationship with declining slope for the effect of hardness (Figure 4C), and a linear relationship of log EC to log [Na] but with a threshold below which Na had no effect (Figure 4D). When one or more of the relationships of the EC to TMFs is inherently nonlinear, the selected equations should, as simply as possible, incorporate important attributes of the data, for which Erickson et al. (1987) provide some examples (e.g., linearity of log EC vs. log hardness at low hardness but declining slopes at high hardness, Figure 4C). Analyses like those described above for linear models should be conducted to establish that deviations from linearity are significant and to test the relative merits of different possible nonlinear models. Formulating nonlinear models often requires ECs at several TMF values well distributed over a broad range, so when data are limited, a linear model will often have to serve as the best possible approximation.

How are model residuals distributed and how do these distributions compare across models?

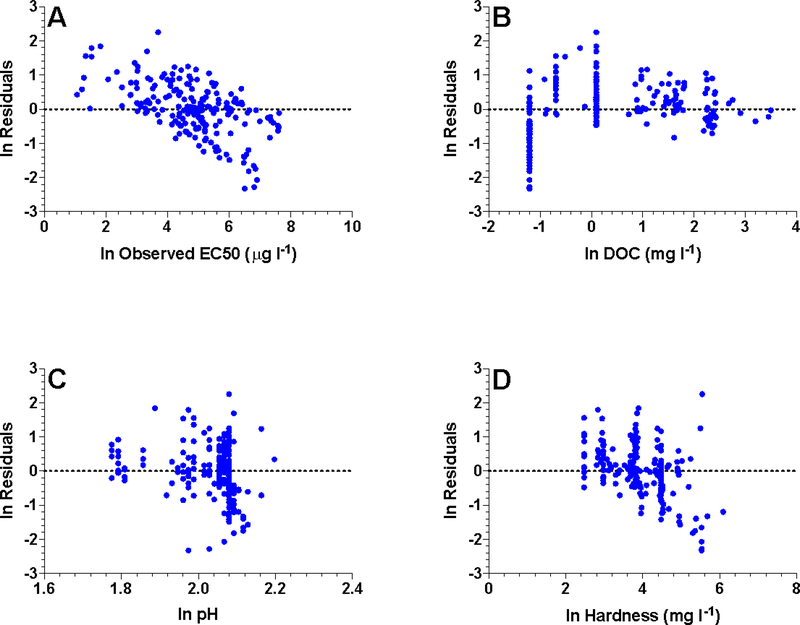
Residual analysis is a primary tool for revealing interactions among parameters and should be conducted for all independent variables in the model (e.g., species, DOC, hardness, pH, interactions) as well as the dependent variable using a variety of approaches to ensure that important patterns are detected. In addition to scatterplots of predicted vs. observed values, quantile-quantile (QQ) plots of the residuals, scatterplots of residuals vs. predicted values and each independent variable, and plots of residuals of one model vs. residuals of another (when comparing models) can all provide slightly different perspectives on residual distributions and lead to insights about how a model might be refined (e.g., Figure 5).

Figure 5.

Residuals for Pimephales promelas based on the pooled Cu MLR in Brix et al. (2017) plotted as a function of A) observed LC50s, B) DOC, C) pH, and D) hardness. Note the similar structure in model residuals as a function of LC50 and hardness. This suggests that the pooled model is over-predicting the effect of hardness on Cu toxicity to P. promelas.

When investigating residuals, homogeneity of variance and normality should be evaluated to verify that model assumptions have been met. It is especially important to investigate patterns that indicate environmental conditions where the model does not fit well. This will identify areas where data for water quality conditions or species are not adequate to develop strong model relationships and assess the need for additional model terms (interactions, other variables, etc.). Patterns of residuals should be investigated to help identify inadequately parameterized effects of variables already in the model (e.g., need for interactions) as well as effects of variables that were not considered for which data are available. Residual plots should also be used to evaluate whether individual or a few data points may be creating a statistically significant effect that is inconsistent with our understanding of chemical and physiological mechanisms.

The distribution of residuals for important subsets of the data should be explored to understand how differences among these subsets affect overall model performance and how well the subsets are predicted by the model. For example, the effects of individual species on a pooled model or the effects of individual studies on a species-specific model should be investigated. Boxplots and QQ plots of residuals for different subsets of the data and color-coding points in residual plots by data subset are all useful tools for understanding how the model may be influenced by specific data and how well it describes the overall dataset.

Statistical versus Practical Considerations

We have focused on describing potential mathematical structures and the array of statistical techniques and tools for developing empirical bioavailability models for metals. A robust use of statistical tools and methods is certainly important in model development. However, we also advocate consideration of practical issues rather than dogmatic acceptance of results from statistical tests in model development. For example, both Brix et al. (2017) and DeForest et al. (2018) tested for effects of interaction terms (e.g., pH × DOC) in their empirical models for Cu and Al given the strong mechanistic underpinnings for these interactions, and used AIC and BIC to statistically assess inclusion of interactions. For Cu, Brix et al. (2017) observed that species-specific models with interaction terms provided modest improvement of some toxicity predictions (adjusted R² values increased by 0.00 to 0.15) and balanced these modest improvements in species-specific model performance against the advantages of a pooled model without interactions for PVAL derivation. In contrast, DeForest et al. (2018) observed large improvements in Al MLR performance when interaction terms were included in a species-specific model for R. subcapitata (adjusted R² increased by ~0.60) but only modest improvement for C. dubia (adjusted R² increased ~0.08) and P. promelas (adjusted R² increased ~0.03). Despite only modest improvements for C. dubia and P. promelas, DeForest et al. (2018) concluded that evidence regarding the underlying mechanisms for these interactions for Al and the strength of their significance for a species with adequate data to test for their effects justified their retention in the species-specific models.

Empirical models based on free cationic metal (hybrid models)

Although empirical models can be informed by a mechanistic understanding of bioavailability, the model structure is not dictated by this understanding but rather by statistical tests of the observed relationship of effects concentrations to the TMFs. In contrast, current mechanistic models such as the BLM structure are based on the mechanistic assumption that toxicity is elicited by the binding of the free metal cation (or possibly a hydroxyl complex of the metal) to a biological receptor (biotic ligand), with competitive binding of other nontoxic cations (e.g., Ca²⁺, H⁺) reducing the binding and consequent effects of the toxic metal (Di Toro et al. 2001). The structure of the BLM thus must involve (a) a speciation model that determines the free toxic metal cation activity, and thereby dictates the impact of ligands (e.g., DOC) in the exposure water on bioavailability and hence toxicity, and (b) equations for the competitive interactions of various cations at the biotic ligand. Toxicity data are used to calibrate certain parameters in this model structure, but do not determine the model structure.

However, in some cases, deviations from the assumptions of the BLM have been observed. Notably, Deleebeeck et al. (2008) reported that the effect of pH on chronic Ni toxicity to Daphnia magna did not adhere to the mechanism of competitive H⁺ binding. Instead, an empirical equation was used to describe the pH effect. This resulted in a model that combined certain mechanistic aspects of the BLM with empirical equations, thereby raising the possibility of hybrid models that have a mechanistic foundation, but are more explicitly informed by empirical data.

Another possibility for combining empirical and mechanistic tools is to base empirical models on the free ion activity of the metal instead of dissolved metal as is the case with the empirical models thus far developed. Such an approach would use a speciation model to address the effect of complexation by DOC and inorganic ligands, thereby incorporating a major element of the BLM mechanistic framework but allow for the treatment of other TMFs as empirical. De Schamphelaere et al. (2002) provide an example of this approach for acute Cu toxicity to D. magna and Erickson et al. (1987) used free copper measurements to address the effect of DOC in a similar manner for P. promelas.

Such free metal activity-based empirical models would lose the advantage of being expressed as a simple function of measured dissolved metal, requiring instead first applying a speciation model. However, this complication might be alleviated by developing an empirical relationship between free metal activity, DOC, and pH (S. Lofts Pers. Comm.). This would be analogous to the bio-met and M-BAT tools (Peters et al. 2016) used to estimate the output of BLM programs as a function of a limited number of TMFs.

To further assess the utility of such free ion activity-based empirical models, we re-analyzed the dataset used by Brix et al. (2017) to develop dissolved acute Cu MLR models for six species (C. dubia, D. magna, Daphnia obtusa, Daphnia pulex, Oncorhynchus mykiss, P. promelas) (Supplemental Information 1). Free ion Cu (Cu²⁺) concentrations were estimated using WHAM 7 (Tipping et al. 2011). We compared adjusted R² for the final stepwise linear regression models selected from 3 full models: 1.) Toxicity [Cu dissolved] = DOC + Ca + pH, 2.) Toxicity [Cu²⁺] = Ca + pH, and 3.) Toxicity [Cu²⁺] = Ca. All combinations of arithmetic and log transformed concentrations of dependent and independent variables were attempted. In addition, the log-log versions of models 1 and 2 were rerun substituting hydrogen ion concentration (as 10^-pH) for pH and again substituting hardness for Ca.

In all cases, the log-log models had the highest adjusted R² and Model 1 (dissolved Cu) had the highest adjusted R² of the 3 models (Table 3), with adjusted R² being 5–60% lower for the two models based on Cu²⁺ activity compared to the dissolved Cu models. This analysis indicates that empirical models based on dissolved metal (at least for Cu) perform substantially better than free ion-based models. This may be the result of some Cu complexes (e.g., CuOH⁺) being bioavailable to varying degrees as has been postulated in previous studies (De Schamphelaere et al. 2002). Whether these findings for Cu can be generalized to other metals may warrant further investigation.

Table 3.

Adjusted R² of Dissolved and Free-Ion Activity MLR Models for Cu

	C. dubia	D. magna	D. obtusa	D. pulex	O. mykiss	P. promelas
Model 1	0.635	0.814	0.816	0.789	0.625	0.749
Model 2	0.043	0.470	0.239	0.738	0.498	0.515
Model 3	0.012	0.468	0.239	0.738	0.301	0.494

Model 1: ln[dissolved Cu] = ln(DOC) + ln(Ca) + pH, Model 2: ln[Cu²⁺] = ln(Ca) + pH, Model 3: ln[Cu²⁺] = ln(Ca). Toxicity data sets from Brix et al. (2017).

DEVELOPMENT OF POOLED SPECIES MODELS

Typically, species-specific empirical bioavailability models for a given metal will be developed for multiple species but will not be available for all of the species needing consideration in PVAL development. Rather than having to choose from among individual species-specific models to apply to species without models (Schlekat et al. 2010), it may possible to use data/models from multiple species to develop a pooled model useful for a broader set of species. The term “pooled model” has been used to describe approaches where data from multiple species have been pooled and approaches where coefficients from species-specific models have been pooled (e.g., averaged) to develop an all species model. These approaches are not equivalent, and we discuss them further later in this section.

A pooled model developed from a diverse representation of aquatic taxa is generally desirable for PVAL development. Being based on more data, such a model can increase confidence in applying the model to other species in the SSD, including the hypothetical “5^th percentile” organism that is typically the basis for PVALs. Further, pooled models will often encompass a broader range of TMFs than individual species-specific models, thereby allowing bioavailability normalizations to be performed for a greater range of conditions.

Pooled models may be developed from a phylogenetically diverse set of species (e.g., across phyla), by categories of taxonomic groups (e.g., algae, invertebrates, and fish), or more refined classifications of organisms (e.g., crustaceans, molluscs). How species-specific models or the data on which they are based are, or are not, pooled will depend on the data available for a metal, metal-specific characteristics, and consideration of PVAL protectiveness over a broad range of water chemistry conditions. Some important considerations are whether and how relationships between TMFs and toxicity are influenced by the magnitude of metal concentrations (i.e., sensitive versus insensitive species) and whether TMFs act similarly across taxonomically diverse species. We provide several conceptual examples of these issues and then discuss specific methodologies for developing pooled models.

Conceptual Considerations in Developing Pooled Models

Historically, the USEPA and other regulatory bodies have used pooled hardness models in deriving hardness-based PVALs for metals (USEPA 1985, CCREM 1987, HMSO 1989). In such models, a common (pooled) slope is assumed for all species, but each species has its own intercept; this entails including species identity as a factor in the analysis to estimate separate intercepts while imposing a single shared slope. Similar approaches have now been used to consider multiple TMFs. For example, Brix et al. (2017) first developed acute Cu MLR models for the cladocerans C. dubia, D. magna, D. obtusa, and D. pulex and the fathead minnow (P. promelas). These individual species models included DOC, hardness, and pH as TMFs and performed well, with adjusted R² values ranging from 0.63 to 0.86. Although four of the models were for closely related daphnid species, the influence of DOC, hardness, and pH on Cu toxicity to the fathead minnow was generally consistent with the daphnids. Thus, a pooled MLR model was developed based on data for all five species and the adjusted R² values remained relatively consistent when the pooled model was applied to each of the five species, with a range of 0.56 to 0.86. In this case, the authors recommended a pooled MLR for PVAL development.

For some metals, TMFs do not influence metal toxicity consistently across taxa and in these cases, more than one model is needed. In the EU, the decision was made to develop separate algae, invertebrate, and fish BLMs for application to SSDs (European Commission 2010). For some metals, such as Cu and Zn, this decision appears to be reasonable as algae respond to TMFs differently than fish and invertebrates (which respond similarly). A similar example is the previously described empirical bioavailability models developed for Al (DeForest et al. 2018), in which effects of DOC, hardness, and pH on the chronic toxicity of Al to an alga (P. subcapitata), a cladoceran (C. dubia), and a fish (P. promelas) differed substantially in terms of the parameters included in the models. As such, it was not reasonable to develop a pooled model. Furthermore, the relative sensitivities of algae, invertebrates, and fish in the chronic Al SSD varied substantially depending on water chemistry conditions. Fish, for example, were most sensitive in conditions of low pH and hardness, but invertebrates became more sensitive with increasing pH and hardness. In this case, it was recommended that multiple MLR models be applied to species in the SSD, to account for changes in the relative sensitivity of species with changing water chemistry conditions. Similarly, bioavailability normalizations for Zn in Europe find invertebrates to be the most sensitive species under relatively acidic conditions, but plants and algae are more sensitive under neutral to alkaline pH conditions where invertebrates are less sensitive (Van Sprang et al. 2009).

We generally recommend the conceptual considerations described above for determining whether to pool or not pool empirical models. However, other considerations and rationales have been used to address this issue. For example, CCME (2016) evaluated species-specific models for Zn based on precision and level of protection. Model precision was evaluated as the percentage of data for that species predicted by the model to be within a factor of 2 of observed toxicity values. Level of protection was evaluated as the percentage of all data (i.e., across species) that was protected by a given species-specific model. Hence, CCME did not require species-specific models to have similar slopes. Instead, emphasis was placed on selecting a species-specific model that was protective of nearly all data in the toxicity dataset on the premise that differing responses between species are not important as long as the model is protective. CCME found that 98% of data for all species under all conditions tested were above the value predicted by the model for D. magna and this model was selected for PVAL derivation (CCME 2016). While this approach eliminated the need for SSD normalization (see SSD Normalization), it also reduced the environmental range over which the influence of TMFs on PVALs could be predicted.

Statistical Approaches to Pooled Model Development

Different methods have been proposed and implemented for pooling empirical bioavailability models. As mentioned above, the vocabulary and terminology involved with specifying species-specific and pooled models can become confusing. Linear models, specifically, Analysis of Covariance (ANCOVA), provide a complete framework within which species-specific and pooled models can be specified using the same dataset.

As a simple example, assume a toxicity dataset containing 3 species and concentration data for 3 TMFs (DOC, hardness, and pH). The variable names in the dataset are: sp (species), ltox (ln toxicity), ldoc (ln DOC), lhard (ln hardness), ph (pH). A “pooled” model that does not consider any species-specific effects would be specified as:

$$ltox=a+b*ldoc+c*lhard+d*ph$$ (Eq. 1)

This model fits one intercept and one slope for each TMF across all the species. That is, it assumes that the same intercept and slopes apply equally to all species (see Supplemental Information 2 for example R code).

A pooled model that normalizes to species but pools across slopes would be specified as:

$$ltox=a*sp+b*ldoc+c*lhard+d*ph$$ (Eq. 2)

This model fits a separate intercept for each species to account for different species sensitivities and assumes that the same slopes apply across all species (parallel slopes). An early univariate example is that described in the USEPA guidelines (USEPA 1985), in which ANCOVA is used to test for differences in the slope of the relationship between hardness and toxicity for multiple species.

For a model with species-specific intercepts, the model output will be affected by the kind of “contrasts” that are specified (see Supplemental Information 2 for example R code). Contrasts are similar to a priori multiple comparisons; the contrast specific for the model determines what hypotheses are tested. While the contrast and resulting output affect how species-specific coefficients are calculated from the output, the final coefficients are not affected by the contrast.

It is possible to specify and test a wide variety of linear contrasts and the topic of linear contrasts is beyond the scope of this paper. Commonly used contrasts include “deviance” contrasts, which compare each group to the mean of all groups and “treatment” contrasts, which compare each group (https://stats.idre.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/).

For the example above, specifying deviance contrasts would test the null hypothesis that each species’ intercept is equal to the mean of all the species intercepts (this average will not always equal the intercept in the pooled model, in which no species effects were specified). The ANOVA output from the model will report whether any of these species-specific intercepts differ from the mean. The regression output (usually just the model summary) will report the mean intercept as the intercept along with a line for each species (each contrast) that includes the difference between the species’ intercept and the mean intercept, as well as the standard error and p-value of the difference. Note, the intercept for the third species must be calculated as the difference between the mean intercept and the total of all the species-specific differences (See Table 1 in Supplemental Information 2 for example output and Table S11 in Brix et al. 2017 for examples of calculating species-specific intercepts from the regression output of pooled models with species-specific intercepts using deviance contrasts).

Specifying treatment contrasts tests the null hypothesis that each species’ intercept is equal to a reference species’ intercept. The regression output from the model will report the reference species’ intercept as the intercept along with a line for each species that includes the difference between the species’ intercept and the reference intercept. The standard error and p-value for this difference will also be reported.

Finally, a fully “species-specific” model, with intercepts and slopes calculated separately for each species, would be specified by adding an interaction between species and each TMF in the model, in addition to the interaction specified in the previous model with the intercept:

$$ltox=a*sp+b*ldoc+c*lhard+d*ph+e*ldoc*sp+f*lhard*sp+g*ph*sp$$ (Eq. 3)

As for the models above with a species-specific intercept term, the output of this “species-specific model” could be used to calculate the coefficients for each species for each TMF, and the significance of the difference between species’ coefficient and the coefficient for the TMF specified by the contrast (e.g., mean or reference group). Likewise, the calculation of each species’ coefficient will depend on the kind of contrast that was specified for the model. For each TMF, the output table would include a slope term for each TMF that would equal either the mean slope (using deviance contrasts) or the slope of a reference group (using treatment contrasts) along with rows for differences between species-specific slopes and the slope to which they are being compared (see Table S10 in Brix et al. 2017 for an example of calculating species-specific slopes and intercepts from a model with deviance contrasts). The coefficients calculated from the output table will be identical to the coefficients calculated by running a separate MLR for each species. Using the ANCOVA framework simply allows testing of null hypotheses of interest.

An example of using ANCOVA in a multivariate model (DOC, hardness, and pH) to test for differences among species in slopes and intercepts was recently described for Cu in Brix et al. (2017). Deviance contrasts were used to test for differences between species slopes and intercepts and the mean slope and intercept. In the multivariate case, the effect of pooling species data with statistically different slopes on the final predicted toxicity value is not as straightforward as in a simple linear regression and will depend on the relative importance of each water quality variable on model predictions and the number of variables within a model that are different than those in the pooled model. In the Cu example, the authors decided to ignore differences in slopes for individual TMFs in several cases and pooled data from multiple species-specific models. They justified this approach by demonstrating that despite statistically significant differences in slope for single TMFs in the species-specific model, the pooled model was comparable to the species-specific model in predicting the toxicity dataset for that species.

An alternative approach for developing a pooled model is to simply average TMF model coefficients (e.g., slopes) for individual species. These mean coefficients may then be used to assemble an MLR model. The acceptability of this pooled MLR model can then be evaluated relative to its performance in predicting toxicity to the individual species that were used to develop the model. The averaging of model coefficients provides an equal weighting to each individual species tested, regardless of the number of tests performed on each species and avoids weighting the final model towards those species which have been most extensively tested. A comparison of the coefficient averaging approach from individual species models to the pooled approach described in Brix et al. (2017) demonstrates that, at least for that particular dataset, the two approaches are comparable in terms of response to TMFs and overall performance (Table 4).

Table 4.

Comparison of DOC, hardness, and pH slopes based on averaging of individual species models versus pooled data model. Individual species models and pooled model from Brix et al. (2017).

	Slopes
Species	ln(DOC)	ln(Hardness)	pH	n	Adj. R2
C. dubia	0.625		0.877	87	0.63
D. magna	0.941	0.503	1.042	307	0.86
D. obtusa	0.843	0.233	0.670	53	0.82
D. pulex	0.875	0.406	0.838	35	0.81
P. promelas	0.670	1.030	0.855	206	0.76
Mean slopes	0.791	0.543	0.856	688	0.80
Pooled model slopes	0.786	0.582	0.966	688	0.81

While simply averaging slopes for a TMF across species is an attractive option, care must be taken in this type of analysis. First, all of the species-specific models should have the same model structure in terms of TMFs and interaction terms considered. It is possible that a species-specific model will not have all of the TMFs included in the models for other species. If this is because data are unavailable for that species, then the model should be excluded from the averaging analysis. In contrast, if the TMF term is missing because the slope was insignificant, then it should be included in the analysis and a slope of zero should be used for averaging purposes. However, both considerations are automatically taken care of in a formal pooled analysis, which should generally be the preferred method for developing a pooled model.

SSD NORMALIZATION

The derivation of a bioavailability-normalized PVAL usually requires that the intrinsic sensitivity of each individual species included in the toxicity database can be corrected to the specific water chemistry conditions to which it is applied. When a single pooled bioavailability model is derived, SSD normalization is straightforward as the same model is applied to all species. However, when this is not the case, how bioavailability models available for selected species should be applied to other species must be addressed.

One approach has been to select the most appropriate model for normalization of species data to specific water chemistry conditions. In this approach, model application to a species is based on the species-specific model that best predicts the response to TMFs using information such as adjusted R² and other goodness of fit indicators previously described (e.g., Q-Q plots, residual plots). Schlekat et al. (2010) used this type of approach in applying Ni BLMs to species for which BLM parameters were not available. For empirical models, this approach might be appropriate if the species dataset is too small to develop a species-specific model, but large enough to evaluate the performance of existing species-specific models in normalizing toxicity data for this new species. When adequate data are not available, it is not possible to assess the performance of an empirical model derived for another species and alternative approaches may be required to pragmatically identify an appropriate model for data normalization.

When model selection cannot be definitively based on model performance, most regulatory jurisdictions have taken an approach of basing model selection on phylogenetic relatedness. This approach is sometimes used as a scientific rationale for model selection in the absence of data on which to make a more informed decision, while in other cases it is used somewhat more arbitrarily. For example, European bioavailability-based approaches which have been applied to date have generally required different models to normalize data for algae/plants, invertebrates, and vertebrates, regardless of any differences or similarities which may exist between these groups (European Commission 2010). As discussed above, we recommend that when scientifically supportable, application of a pooled model is preferable to this approach.

In the US, where algae/plants have not historically been included in SSDs, it has generally been possible to use a single bioavailability model for SSD normalization, although occasional differences between animal models have been observed. In Europe, where it is required that algae/plants be included in SSDs, multiple models have been required. Relatively consistent and significant differences in the response to TMFs have been observed between algae/plants and animals, particularly with respect to the effect of pH on toxicity (De Schamphelaere et al. 2003, De Schamphelaere et al. 2005). As a result, it is generally not appropriate to apply the same normalization model to plants as would be used for animals.

Finally, not all regulatory approaches for deriving PVALs require that the entire SSD be normalized for each water chemistry condition of interest and this may also influence decisions regarding use of species-specific models or strategies for pooling models. For example, in deriving its hardness-based metals criteria, the USEPA first normalizes the SSD to a common hardness condition and then defines the sensitivity of the 5^th percentile organism as the intercept. The hardness slope and that intercept can then be used to calculate the criterion for any hardness without needing to normalize the SSD for every hardness condition. This same type of approach was used to derive an MLR-based PVAL for Cu following USEPA guidelines (Brix et al. 2017), which results in a considerably simpler calculation of the PVAL than approaches which require that all of the data in the SSD be normalized to calculate the PVAL. In this case a simplified approach was possible because a single pooled bioavailability model was applied to all species in the SSD, so the relative sensitivity of each species is always the same regardless of water chemistry conditions. This allowed the sensitivity parameter in the bioavailability model to be set based on the HC5 derived from the SSD rather than on the sensitivity of any individual species. This simplified approach would not work if more than one bioavailability model is applied to the SSD; in those cases, the SSD would need to be normalized for each water chemistry condition of interest, as was the case with Al (DeForest et al. 2018, USEPA 2018).

CONCLUSION AND PERSPECTIVE

Empirical bioavailability models are a useful tool in risk assessment and for deriving PVALs for metals (and potentially other classes of toxicants). More mechanistic models such as the BLM may provide a more scientifically rigorous approach to accounting for the effects of TMFs on metal bioavailability and may require less initial testing to formulate a new model but may not be more accurate in their predictions. Moreover, these models may be more complex than is needed to achieve the desired environmental management goals in some regulatory settings. In these cases, empirical bioavailability models can provide a simpler, more transparent tool for predicting the effects of TMFs on metal bioavailability and often have similar predictive capabilities.

As with all models, empirical bioavailability models must be developed by rigorous assessment of model performance using both visual plotting and statistical assessment tools to check for model bias and accuracy. We recommend taking advantage of available toxicity data and the same theoretical understanding used to develop mechanistic models such as the BLM to make informed decisions about which TMFs to include in empirical bioavailability models. Model validation using independent datasets and/or comparison to other models such as the BLM is also critical.

While we have found that empirical bioavailability model performance is generally comparable to more mechanistic models, the temptation often arises to include more complexity in the model to improve performance. For example, in this paper we investigated the potential of using free ion rather than dissolved metal concentrations to develop a hybrid model for predicting metal bioavailability. While this example did not improve model performance, inclusion of other variables may. In such cases, comparison of final models using different fit statistics such as R², AIC and BIC, can be helpful for assessing whether improved model performance justifies increased model complexity. On the other hand, as we discussed for temperature, there may be TMFs that are important in applying models to field conditions but are not typically included in models because these TMFs are not addressed in typical laboratory testing.