Inferring Nighttime Ionospheric Parameters With the Far Ultraviolet Imager Onboard the Ionospheric Connection Explorer

Abstract

The Ionospheric Connection Explorer (ICON) Far Ultraviolet (FUV) imager, ICON FUV, will measure altitude profiles of OI 135.6 nm emissions to infer nighttime ionospheric parameters. Accurate estimation of the ionospheric state requires the development of a comprehensive radiative transfer model from first principles to quantify the effects of physical processes on the production and transport of the 135.6 nm photons in the ionosphere including the mutual neutralization contribution as well as the effect of resonant scattering by atomic oxygen and pure absorption by oxygen molecules. This forward model is then used in conjunction with a constrained optimization algorithm to invert the anticipated ICON FUV line-of-sight integrated measurements. In this paper, we describe the connection between ICON FUV measurements and the nighttime ionosphere, along with the approach to inverting the measured emission profiles to derive the associated O⁺ profiles from 150–450 km in the nighttime ionosphere that directly reflect the electron density in the F-region of the ionosphere.

1. Introduction

Ultraviolet (UV) remote sensing of the terrestrial ionosphere from space-borne platforms provides the most comprehensive means of quantifying the ionospheric state on a global scale. Remote sensing of the Earth’s ultraviolet emissions has been used as a primary means for quantifying the ionospheric state for decades [3, 12, 17]. Particularly, the ultraviolet imagers launched in recent space missions [1, 16, 22] have yielded a large amount of scientific data and the related analysis has significantly advanced our understanding of the ionosphere and thermosphere. NASA’s upcoming missions, the Ionospheric Connection Explorer (ICON) and the Global-scale Observations of the Limb and Disk (GOLD), will also use ultraviolet remote sensing as a means to investigate the global-scale response of the ionosphere to solar activity and to the forcing from the neutral atmosphere.

ICON’s planned orbit is a circular 575 km altitude, 27 degree inclination orbit. The ICON Far Ultra-Violet (FUV) instrument, ICON FUV, is a spectrographic imager producing spectrally filtered two dimensional images. ICON FUV, will measure limb viewing integrated emissions (tangent altitude profiles) of OI 135.6 nm to infer nighttime ionospheric parameters. The observations will be processed as limb altitude profiles. The ICON FUV optic axis is pointed 20 degrees below local horizontal and has a steering mirror that allows the field of view to be steered up to 30 degrees forward and aft, to keep the local magnetic meridian in the field of view.

Accurate estimation of the ionospheric state requires the development of a comprehensive radiative transfer model from first principles to quantify the effects of physical processes on the production and transport of the 135.6 nm photons in the ionosphere including the mutual neutralization contribution as well as the effect of resonant scattering by atomic oxygen and pure absorption by oxygen molecules. This forward modeling is then used in conjunction with a constrained optimization algorithm to invert the ICON FUV measurements.

Quantification of the ionospheric state based on ultraviolet remote sensing requires the solution of an inverse problem to reconstruct plasma densities from integrated line-of-sight measurements. Over the last two decades, various approaches to the development of inversion algorithms for this task have been pursued. These techniques are typically based on either a maximum likelihood approach [20] to seek the least-squares minimum-norm estimate of the ionospheric parameters through iteratively minimizing the residual error between consecutive projections of a forward model and measured data [e.g., 3, 18], or regularized inversion methods by direct incorporation of prior knowledge in the objective function resulting in a constrained optimization problem that achieves stabilized solutions in the presence of noise [e.g., 2, 12, 13]. Accuracy of the reconstruction depends on the completeness of the underlying physics assumed in the forward model linking the parameters of interest to measurements, and the effectiveness of the regularization method used for minimizing the estimation errors introduced by measurement noise and amplified by the ill-conditioned nature of the problem.

In this paper, we first describe the development of a comprehensive radiative transfer model of the OI 135.6-nm emission [23] which provides a rigorous forward model as the foundation for subsequent development of an optimal inverse model. We then describe the algorithm developed for inferring the nighttime ionosphere from the inversion of ICON FUV data. Through numerical experiments based on typical anticipated ICON FUV observations, we validate the reconstruction performance and illustrate that it meets the mission requirements for achieving ICON’s science goals. Finally, we provide a description of our approach to propagating estimation uncertainties through the inversion.

2. UV emissions production and transport mechanisms

The forward model for the nighttime ICON FUV instrument incorporates a comprehensive radiative transfer model of OI 135.6-nm emission to achieve optimal accuracy. Details of the radiative transfer model have been presented by Qin et al [23], and the implications for the omission of various governing physical processes have been discussed in [24]. Provided below is a brief review of the important physical processes. The model includes the two primary production mechanisms of OI 135.6-nm emission in the nighttime ionosphere, namely radiative recombination (RR) of electrons with O⁺ and mutual neutralization (MN) of O⁺ with O⁻ [e.g., 9, 30]:

$${\text{O}}^{+}+\text{e}\to {\text{O}}^{\ast }+h\nu$$ (1)

$${\text{O}}^{-}+{\text{O}}^{+}\to {\text{O}}^{\ast }+\text{O}$$ (2)

where O^∗ and hν represent the excited oxygen atoms and the direct recombination photons, respectively. Following the above two processes, the excited atoms O^∗ emit line radiations at 135.6, 130.4, 102.7, 98.9, and the 91.1-nm continuum from recombination into the ground state of O, as well as a variety of visible and infrared wavelengths [17], [25]. The 135.6-nm photons result from the following electric dipole intercombination transition

$$\text{O}{(}^5{\text{S}}_2)\to \text{O}{(}^3\text{P})+h{\nu }_{135.6}$$ (3)

that consists of a doublet, (⁵S₂→³P₂) and (⁵S₂→³P₁). The source volume emission rate, 4πε₀, can be calculated as:

$$4\pi {\epsilon }_0={\alpha }_{135.6}\left(T_{\text{e}}\right)N_{\text{e}}\left[{\text{O}}^{+}\right]+{\beta }_{135.6}{k}_1{k}_2\frac{N_{\text{e}}[\text{O}]\left[{\text{O}}^{+}\right]}{k_2\left[{\text{O}}^{+}\right]+k_3[\text{O}]}$$ (4)

where ε₀, α_135.6, N_e, and [O⁺] are the isotropic source volume emissivity, the partial rate coefficient of RR yielding 135.6-nm photons, the electron density, and the O⁺ density, respectively, β_135.6 is the proportion of the excited atoms O* resulting from MN that emit 135.6-nm radiation, and k₁, k₂, and k₃ are the related rate coefficients [19].

In its baseline operation mode, the ICON FUV nighttime inversion algorithm includes only the above processes for computational efficiency, since these are the dominant processes contributing to the accuracy of the inferred parameters. In its more comprehensive mode, the forward model incorporates the effects of multiple scattering and absorption, as described below.

The effects of resonant scattering by O and pure absorption by O₂ on the transport of the nighttime OI 135.6-nm emission are taken into account by solving the following time-independent radiative transfer equation, assuming a plane parallel atmosphere [21, 27]:

$$\mu \frac{\text{d}I}{\text{d}z}=-\chi (x,z)I(x,\mu ,z)+\epsilon (x,\mu ,z)$$ (5)

where I(x, μ, z) is the specific intensity in units of photons cm⁻² s⁻¹ hz⁻¹ ster⁻¹, ε(x, μ, z) is the total volume emissivity defined as the total number of photons emitted cm⁻³ s⁻¹ hz⁻¹ ster⁻¹ at altitude z in the direction μ, and x = (ν − ν₀)/Δν_D is the frequency measured from the line center ν₀ in units of the Doppler width Δν_D. The extinction coefficient χ(x, z) is given by

$$\chi (x,z)=k_0(z)\varphi (x,z)+k_{\text{O}2}(z)$$ (6)

where k₀ is the line center scattering coefficient, and k_O2 is the pure absorption coefficient. Without external radiation sources, the formal solution to the above radiative transfer equation is

$$I(x,\mu ,z)=\int \epsilon \left(x,\mu ,z^{\prime }\right)e^{-\left|{\tau }_x-{\tau }_x^{\prime }\right|/\mu }\text{d}{z}^{\prime }/\mu$$ (7)

where τ_x represents the optical depth τ(x, z). For the condition of radiative equilibrium, the total volume emissivity is the sum of the source volume emissivity ε₀ and the contributions from multiple resonant scattering

$$\epsilon (x,\mu ,z)={\epsilon }_0(x,\mu ,z)+2\pi \int I\left(x^{\prime },{\mu }^{\prime },z\right)R\left(x,x^{\prime },\mu ,{\mu }^{\prime },z\right)\text{d}{x}^{\prime }\text{d}{\mu }^{\prime }$$ (8)

where R(x, x′, μ, μ′, z) is the redistribution function defined as the probability per unit volume that a photon of frequency x′ coming from the direction μ′ will be absorbed and then reemitted at frequency x in the direction μ [10]. Under the assumptions of zero natural width, isotropic scattering, Maxwell-Boltzmann velocity distribution, and complete frequency redistribution, R(x, x′, μ, μ′, z) is given by

$$R=\frac{1}{4\pi }{k}_0\varphi \left(x^{\prime },z\right)\frac{\varphi (x,z)}{\sqrt{\pi }}$$ (9)

where 1/4π is the angular probability for isotropic scattering, k₀ϕ(x′, z) is the absorption probability of a photon with frequency x′ by atomic oxygen at altitude z, and ϕ(x, z)/$\sqrt{\pi }$ is the probability of the photon being reemitted with a frequency x. The total volume emissivity ε can be expressed as

$$\epsilon (x,\mu ,z)=\epsilon (z)\frac{\varphi (x,z)}{\sqrt{\pi }}$$ (10)

where ε(z) is the total volume emissivity in photons cm⁻³ s⁻¹ ster⁻¹, which is given by the integration of ε(x, μ, z) over all frequencies, and ϕ(x, z) is the frequency profile given by

$$\varphi (x,z)=r(z)e^{-r{(z)}^2{x}^2}$$ (11)

where $r(z)=\sqrt{T_0/T(z)}$, and T₀ is the exospheric temperature. After some manipulations, the total volume emissivity can be expressed as

$$\epsilon (z)={\epsilon }_0(z)+\int \epsilon \left(z^{\prime }\right)H\left(\left|{\tau }_x-{\tau }_x^{\prime }\right|\right)\text{d}{z}^{\prime }$$ (12)

where the Holstein probability is given by

$$H\left(\left|{\tau }_x-{\tau }_x^{\prime }\right|\right)=\frac{1}{2\sqrt{\pi }}\frac{k_0(z)}{r(z)}\int r{e}^{-r^2{x}^2}{r}^{\prime }{e}^{-r^{\prime 2}{x}^2}{e}^{-\left|{\tau }_x-{\tau }_x^{\prime }\right|/\mu }\text{d}x\frac{\text{d}\mu }{\mu }$$ (13)

which is the probability that a photon emitted in dz′ at z′ will be resonantly absorbed in dz at z.

Once the total volume emissivity ε is obtained by solving equation (12), the column emission rate of OI 135.6-nm emissions observed at a given location can be calculated by integrating the effective volume emissivity along the line of sight. Expressed in Rayleighs, the brightness I_135.6 is given by

$$4\pi I_{135.6}={10}^{-6}\int J(s)\left[B_{5}T\left({\tau }_x^{\prime }\right)+B_{3}T\left({\tau }_x^{\prime \prime }\right)\right]\text{d}s$$ (14)

where J(s) = 4πε(s) is the total volume excitation rate at location s along the line of sight, ${\tau }_x^{\prime }$ and ${\tau }_x^{\prime \prime }$ represent the optical depths of the two lines from the emission location s to the observer. Here the function T(τ_x) represents the Holstein transmission probability given by

$$T\left({\tau }_x\right)=\frac{1}{\sqrt{\pi }}\int r{e}^{-r^2{x}^2}{e}^{-{\tau }_x}\text{d}x$$ (15)

which is the probability that a photon will traverse a path with optical depth τ_x without being scattered or absorbed [17, 26]. The radiative transfer problem of the OI 135.6-nm emission in the nighttime ionosphere can be solved numerically by properly discretizing equations (12) and (14).

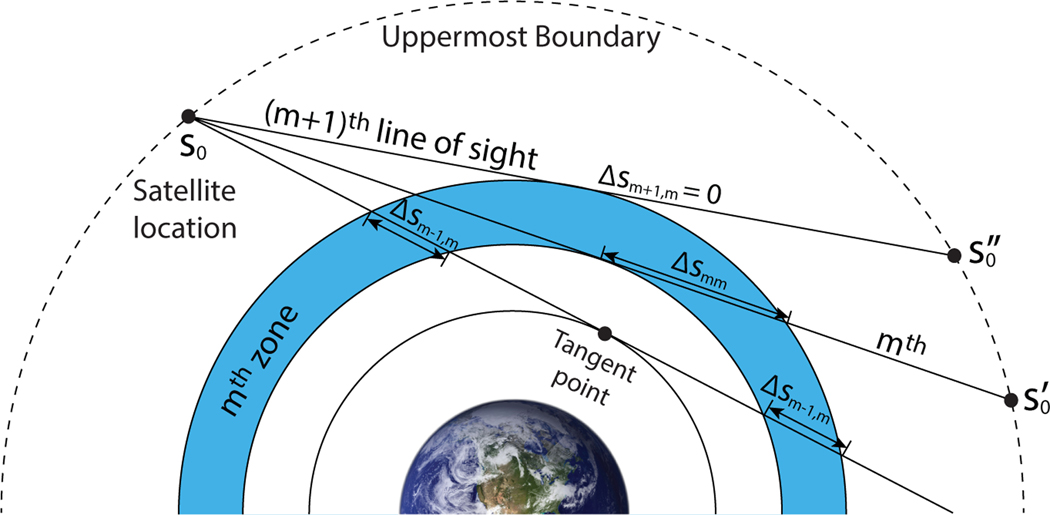
To construct a matrix form of the radiative transfer equations, the upper atmosphere is divided into N zones with variable width, in which the lower and upper boundaries of the nth zone are represented by z_n and z_n+1, respectively, as shown in Figure 1. The integral in equations (12) and (14) can then be evaluated zone by zone. Assuming that ε(z) is constant in each zone, the emissivity equation (12) can be approximated as

$${\epsilon }_n={\epsilon }_{0n}+\sum _{m=1}^n{G}_{nm}{\epsilon }_m$$ (16)

and the matrix elements G_nm are given by

$$G_{nm}={\int }_{z_m}^{z_{m+1}}H\left(\left|{\tau }_n-{\tau }_x^{\prime }\right|\right)\text{d}{z}^{\prime }$$ (17)

where τ_n is the optical depth at the center of the nth zone, and ${\tau }_x^{\prime }$ represents τ_x(z′). The total volume emissivity ε can be computed numerically by inverting the matrix (I − G), namely

$$\epsilon ={(\mathbf{I}-\mathbf{G})}^{-1}{\epsilon }_0$$ (18)

where I is the identity matrix. In general, equation (14) can be expressed in the following matrix form

$$I_n=\sum _{m=1}^N{T}_{nm}{\epsilon }_m$$ (19)

where ε_m is the total volume emissivity in the mth zone that is assumed to be constant inside each zone, and T is a N × N square matrix with each element T_nm given by

$$T_{nm}=T\left({\tau }_{nm}\right)\Delta s_{nm}$$ (20)

where Δs_nm represents the distance intersected by the nth line of sight in the mth zone. Combining equation (18) with I_135.6 = Tε leads to

$$\mathbf{b}=\mathbf{A}\mathbf{x}$$ (21)

where b = 4πI_135.6 and x = 4πε₀ represent the noise-free brightness data and the source volume emission rates, respectively, and the matrix A = T(I − G)⁻¹ is constructed based on the important physical processes discussed above, namely the production and transport of the 135.6-nm emission, to relate x and b.

Fig. 1:

Schematics of zone divisions and the lines of sight in the case of limb observations from a ICON FUV.

The inversion process essentially amounts to the reconstruction of x, from which the ionospheric plasma densities can be obtained by solving the following equation that is reconstituted from equation (1) by assuming N_e = [O⁺] in the F-region ionosphere:

$${\mathbf{N}}^3+\left(\frac{k_3}{k_2}+\frac{{\beta }_{135.6}}{{\alpha }_{135.6}}\right)[\text{O}]{\mathbf{N}}^2-\frac{4\pi \mathbf{x}}{{\alpha }_{135.6}}\mathbf{N}=\frac{4\pi \mathbf{x}{k}_3[\text{O}]}{{\alpha }_{135.6}{k}_2}$$ (22)

where N represents the electron or O⁺ density profile. Note that in real measurements, noise is inevitably present in the brightness data: errors in the inversion results can be introduced by the measurement noise, or by the simplifications in the forward model A.

While the exact form of the noise depends on the ICON FUV performance characteristics and the approximations in the forward model, the dominant component is that of most optical observations where a detecter such as an intensified CCD is used: the main source of measurement noise has components from the incident photon counting process which is characterized by a Poisson distribution, as well as the multiplication noise in the intensifier. Other components due to the dark current fluctuations and the readout noise in the CCD can be negligible because of the high gain (on the order of 650) of the intensifier [Mende et al., Space Science Reviews, this issue]. Furthermore, it can also be assumed that the time-invariant or fixed pattern noise sources can be minimized by normalizing the images with a calibration image. Hence the overall noise model may collectively be well approximated by additive Gaussian noise. Therefore, the linear model above may be expressed more completely by the addition of the noise or measurement uncertainty component denoted by w, resulting in the overall observation model: y = b + w = Ax + w.

The implication is that although the matrix A is square and triangular, it is ill-conditioned and hence prone to noise amplification; consequently, simple inversion through Gaussian elimination for instance fails to provide a physically meaningful solution. Therefore, the approach to the inversion of ICON FUV must be formulated such that it can circumvent the ill-conditioning of the forward model A.

3. Inversion of ICON FUV measurements

The inversion task amounts to estimating the vector x given the vector of measurements y, the forward model matrix A, and all known information, statistical or otherwise, regarding the measurement noise vector w.

The ill-conditioned nature of A implies that a systematic approach to the incorporation of additional constraints in the solution space is required. In other words, it becomes necessary to replace the original ill-conditioned problem with another inverse problem with better conditioning that is close to the original one.

A formal mechanism for addressing this requirement is through regularization which leads to the minimization of an appropriately formulated cost function [7]. This approach incorporates prior knowledge concerning the unknown solution in a least squares setting. The prior information can be introduced in a deterministic way [5, 15, 28], or in a statistical setting [11], which is related to the Bayes paradigm of [4].

A general formulation for the cost function (the objective function) can be expressed as:

$$\mathit{\text{Φ}}(\mathbf{x})=\parallel \mathbf{y}-\mathbf{A}\mathbf{x}{\parallel }_{\mathcal{W}}^2+\sum _i{\gamma }_i{C}_i(\mathbf{x})$$ (23)

where $\parallel \mathbf{y}-\mathbf{A}\mathbf{x}{\parallel }_{\mathcal{W}}^2$ denotes the weighted residual norm, i.e., (y − Ax)^T$\mathcal{W}$(y − Ax), C_i and γ_i are the i-th regularization functional and regularization parameters respectively, and W is an appropriate weight, all to be chosen according to the specifics of the problem. The first term controls data fidelity (i.e., how faithful the reconstruction is to the data), whereas the second term (the regularization term) controls how well the reconstruction matches our prior knowledge of the solution.

Tikhonov (quadratic) regularization [29] is perhaps the most common technique used for regularization and is equivalent to maximum a posteriori (MAP) estimation, assuming Gaussian statistics for both the unknown image and noise [14]. Assuming w ∼ $\mathcal{N}$(0, Σ_w) and x ∼ $\mathcal{N}$(x₀, Σ_x), where $\mathcal{N}$(μ, Σ) represents the normal distribution with mean μ and covariance Σ, the MAP estimate is:

$$\begin{gathered} {\widehat{\mathbf{x}}}_{\text{MAP}}=\arg \underset{\mathbf{x}\in {ℝ}^N}{\min }[-\log p(\mathbf{y}\mid \mathbf{x})-\log p(\mathbf{x})] \\ =\arg \underset{\mathbf{x}\in {ℝ}^N}{\min }\left[\parallel \mathbf{y}-\mathbf{A}\mathbf{x}{\parallel }_{{\mathit{\text{Σ}}}_{\mathbf{w}}^{-1}}^2+\parallel \mathbf{x}-{\mathbf{x}}_0{\parallel }_{{\mathit{\text{Σ}}}_{\mathbf{x}}^{-1}}^2\right] \\ ={\mathbf{x}}_0+{\left({\mathbf{A}}^T{\mathbf{\Sigma }}_{\mathbf{w}}^{-1}\mathbf{A}+{\mathbf{\Sigma }}_{\mathbf{x}}^{-1}\right)}^{-1}{\mathbf{A}}^T{\mathbf{\Sigma }}_{\mathbf{w}}^{-1}\left(\mathbf{y}-\mathbf{A}{\mathbf{x}}_0\right) \end{gathered}$$ (24)

The connection between this MAP formulation of Tikhonov regularization and the variational form just discussed becomes apparent by assuming independent identically distributed (IID) Gaussian noise and taking ${\mathit{\Sigma }}_{\mathbf{x}}=\frac{1}{{\gamma }^2}{\left({\mathbf{L}}^T\mathbf{L}\right)}^{-1}$ and x₀ = 0, hence arriving at the well known Tikhonov regularization functional:

$$\begin{gathered} {\widehat{\mathbf{x}}}_{\text{Tik}}=\arg \underset{\mathbf{x}\in {ℝ}^N}{\min }\left[\frac{1}{{\sigma }_{\mathbf{w}}^2}\parallel \mathbf{y}-\mathbf{A}\mathbf{x}{\parallel }_2^2+{\gamma }^2\parallel \mathbf{L}\left(\mathbf{x}-{\mathbf{x}}_0\right){\parallel }_2^2\right] \\ =\arg \underset{\mathbf{x}\in {ℝ}^N}{\min }\left[\parallel \mathbf{y}-\mathbf{A}\mathbf{x}{\parallel }_2^2+\lambda \parallel \mathbf{L}\mathbf{x}{\parallel }_2^2\right] \\ ={\left(\frac{1}{{\sigma }_{\mathbf{w}}^2}{\mathbf{A}}^T\mathbf{A}+{\gamma }^2{\mathbf{L}}^T\mathbf{L}\right)}^{-1}\frac{1}{{\sigma }_{\mathbf{w}}^2}{\mathbf{A}}^T\mathbf{y} \end{gathered}$$ (25)

where L is a positive definite regularization matrix (often a derivative operator) and λ = (γσ_w)² where ${\sigma }_w^2$ is the variance of the noise samples. A special case is when L = I, which results in λ being inverse of the signal-to-noise ratio. Although we assumed IID noise, more general forms of noise covariance have also been applied in different imaging applications.

The choice of a quadratic regularization functional leads to an optimization problem with a stable solution. Furthermore, the choice of the quadratic regularization in conjunction with the choice of L as a derivative operator generally results in a reconstruction that is globally smooth, hence appropriate for the task of extracting ionospheric peak hight and density from a smooth profile.

Selection of an optimal regularization parameter can be achieved using the L-curve criterion proposed by Hansen [6]. The L-curve criterion states that when plotted in a log-log scale, the curve of the seminorm $\parallel \mathbf{L}{\mathbf{x}}_{\lambda }{\parallel }_2^2$ versus the residual norm $\parallel \mathbf{A}{\mathbf{x}}_{\lambda }-\mathbf{y}{\parallel }_2^2$ has a characteristic L-shaped appearance, and that the corner of the L-curve corresponds to a good choice of the regularization parameter. It has been demonstrated that if the corner is well-defined (sharp) the optimal regularization parameter can be selected by locating the point on the L-curve that has maximum curvature [8]. The curvature, κ, is defined as

$$\kappa (\lambda )=\frac{{\rho }^{\prime }{\eta }^{″}-{\rho }^{″}{\eta }^{\prime }}{{\left[{\left({\rho }^{\prime }\right)}^2+{\left({\eta }^{\prime }\right)}^2\right]}^{3/2}}$$ (26)

where $(\rho (\lambda ),\eta (\lambda ))=\left(\parallel \mathbf{A}{\mathbf{x}}_{\lambda }-\mathbf{y}{\parallel }_2^2,\parallel \mathbf{L}{\mathbf{x}}_{\lambda }{\parallel }_2^2\right)$, and the superscripts (′) and (″) denote the first and the second derivative, respectively, with respect to λ.

For ICON FUV inversion, we select the regularization parameter based on the maximum second derivative of the L-curve, that is

$${\lambda }_{\text{opt}}=\max \frac{{\eta }^{″}(\lambda )}{{\rho }^{″}(\lambda )}$$ (27)

Note that κ(λ) = η″(λ)/ρ″(λ) in the case when η′(λ)/ρ′(λ) ≪ 1.

The proposed rule selects the regularization parameter that corresponds to the point on the L curve where the decrease of the seminorm with respect to an increasing residual norm passes its most rapid phase, thus preventing a rapid increase of the residual norm which would lead to an over-smoothed solution.

4. Simulation results and numerical validation

A representative ICON partial orbit and the corresponding set of FUV viewing geometry data were generated and used in combination with the forward model described in the previous sections to create a set of airglow volume emission rates and limb-viewing intensity profiles for the 135.6 nm emission. The simulation spans one nightside orbital pass, from 00:19 to 01:10 UT on 20 Mar 2009 (i.e., solar minimum, F10.7 = 68.2 sfu). For each ICON FUV exposure, the simulations correspond to a single-column ionospheric electron density along the line of sights representing a spherically symmetric, vertically stratified ionosphere described in the forward model of the previous sections. The limb-viewing measurements through these layers are therefore inverted as a single profile for each exposure. Note that while horizontal gradients or structured features caused by ionospheric instabilities may exist in the nighttime ionosphere, ICON FUV is built and operated specifically to reduce the effects of ionospheric instabilities in the estimation of ionospheric state by steering its field of view to always contain the local magnetic meridian. The steered turret mechanism is designed to minimize the effect of horizontal gradients produced by spread-F or other field-aligned irregularities.

The simulated (true) electron density profiles and volume emission rates were generated using IRI and MSIS models, together with the baseline forward model of 135.6 nm emission containing radiative recombination and mutual neutralization. These were then run through an FUV instrument simulator using the pre-flight instrument characterization, e.g., FUV sensitivity of 0.0873 counts/res-cell/sec/R, and 12 second integration (Mende et al., Space Science Reviews, this issue) to generate a full set of FUV viewing images and to create realistic ICON FUV level 1 data profile sets with realistic representation of the anticipated (noisy) input data for level 2 processing.

Figure 2 shows an example of a single simulated FUV brightness profile (generated for 10 PM local time at 0 latitude, 0 longitude) and the corresponding reconstructed volume emission rate and electron density profiles based on the inversion of the simulated FUV brightness profile. As can be seen from this figure the entire ionospheric profile, and in particular peak density and height, are reconstructed with high fidelity.

Fig. 2:

Example of an end-to-end ICON FUV inversion corresponding to 10 PM local time at 0 latitude, 0 longitude. Left panel: simulated FUV brightness as a function of zenith angle based on an IRI electron density profile and corresponding volume emission rate using MSIS and 135.6 nm emission containing radiative recombination and mutual neutralization. The simulated brightness was obtained based on ICON FUV viewing geometry and instrument characteristics. Middle panel: solid black curve shows the reconstructed volume emission rate from the simulated brightness of the left panel. Dotted black curve shows the original (simulated) true volume emission rate. The dotted red and blue curves show the contributions from radiative recombination and mutual neutralization processes respectively which in combination result in the total simulated volume emission rate in dotted black curve. Right panel: Solid curve shows the reconstructed electron density profile in comparison with the dotted line which shows the simulated (true) profile.

Figure 3 shows the result of the simulation described above for an ICON partial orbit containing 255 orbit measurement points obtained from limb images, spanning from −100 to 100 degrees longitude and −20 to 22 degrees latitude. The bottom panel shows the partial orbit path. The green line in the top panel shows the simulated peak brightness level (R) using ICON FUV instrument characteristics (e.g., sensitivity). The volume emission rate is reconstructed from the simulated brightness for each point in the orbit and the electron density is calculated, followed by the extraction of the F2 peak parameters and comparison with the “true” (original) F2 peak parameters of the electron density simulated from the IRI model. The top panels show the resulting errors in NmF2 and hmF2 for each measurement. As can be seen from the figure, the reconstruction errors are within the requirements (20 Km for hmF2, 10% for NmF2, Immel et al., Space Science Reviews, this issue) for time intervals when there is sufficient source signal.

Fig. 3:

An ICON partial orbit containing 255 orbit measurement points, spanning from −100 to 100 degrees longitude and −20 to 22 degrees latitude is shown in the bottom panels. The green line shows the simulated peak brightness (R) using ICON FUV instrument characteristics (sensitivity). The volume emission rate is reconstructed from the simulated brightness for each point in the orbit and the electron density is calculated followed by extraction of the F2 peak parameters and comparison with the “true” (original) F2 peak parameters of the electron density simulated from the IRI model. The top panels show the resulting errors in NmF2 and hmF2 errors for each measurements (in blue) and the ICON requirements (in red). As can be seen from the figure, the reconstruction errors are within the requirements (20 Km for hmF2, 10% for NmF2, Immel et al., Space Science Reviews, this issue) for time intervals when there is sufficient signal.

Between 01:00 and 05:00 SLT, the brightness is low due to the low electron density. This causes a significant degradation in the precision of the measurements, but the accuracy is also affected, at least for hmF2, which has a positive bias during this period. This bias arises from the fact that the regularization term penalizes the profile’s derivative equally at all altitudes, while real electron density profiles are steeper on the bottomside than the topside. This bias is also apparent in the example in Figure 2. In the future, we plan to investigate alternative regularization schemes that do not produce this bias, perhaps using altitude-dependent penalties.

Figure 4 shows the errors in NmF2 and hmF2 calculated for each of the 255 points in the orbit, plotted as a function of peak source brightness. Note that for brightness values above 10 R, the reconstruction errors are within the specified specifications of the ICON mission for both NmF2 and hmF2.

Fig. 4:

NmF2 and hmF2 errors for the 255 orbit points as a function of the simulated brightness. This figure exhibits the correlation between source brightness and reconstruction error. For brightness values above 10 R, the reconstruction errors are within the specified specifications of the ICON mission for both NmF2 and hmF2.

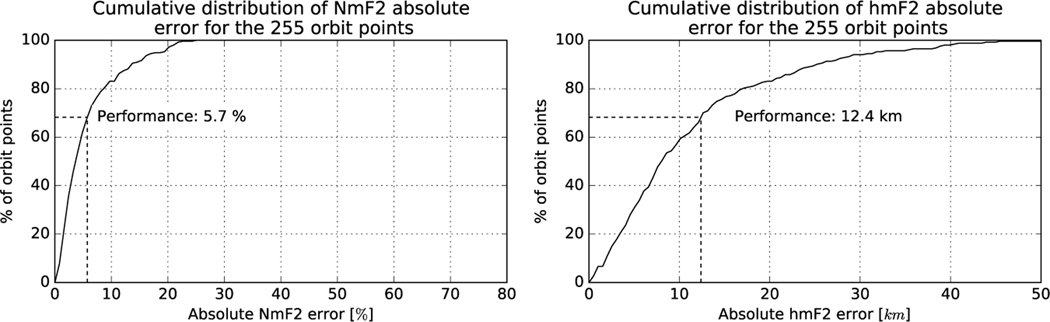
Figure 5 shows the cumulative distribution function of errors in NmF2 and hmF2 calculated for each of the 255 points in the orbit, whereby the fraction (%) of orbit points within an error range is depicted. Note that 1 standard deviation (1-sigma) value corresponding to a normal distribution is shown with the dashed lines for both NmF2 and hmF2, and both fall well within the requirements.

Fig. 5:

Cumulative distribution function of errors in NmF2 and hmF2 calculated for each of the 255 points in the orbit, whereby the fraction (%) of orbit points within an error range is depicted. Note that 1 standard deviation (1-sigma) value corresponding to a normal distribution is shown with the dashed lines for both NmF2 and hmF2, and both fall well within the requirements.

5. Uncertainties in the estimated ionospheric parameters

In addition to providing estimates of the electron density profile, NmF2, and hmF2, the FUV nighttime data product includes estimated errors in these quantities. The only errors included in this estimate are statistical errors propagated from the brightness data. Systematic errors can be introduced via regularization and inaccurate knowledge of [O] in the MSIS model, but these are not included in the reported error.

The errors in the measured brightness profile are provided in the Level 1 data product and are dominated by Poisson counting statistics. Errors are propagated through the algorithm described in the previous sections, which comprises three steps: (1) a Tikhonov-regularized inversion to convert a brightness profile, y, to a volume emission rate (VER) profile, x, (2) a solution of Equation 22 to obtain an electron density profile, N, and (3) a peak-finding step to extract hmF2 and NmF2. In order to propagate errors through these steps, various assumptions are used, which are described below. These assumptions are then validated by a Monte Carlo simulation.

Step 1 is a regularized inversion with a non-negativity constraint. For the purposes of propagating error, we ignore the non-negativity constraint, which only affects the lowest altitudes, not hmF2 and NmF2. Without this constraint, the inversion is linear, so the covariance matrix of x, denoted Σ_x, is simply

$${\mathbf{\Sigma }}_{\mathbf{x}}=\mathbf{M}{\mathbf{\Sigma }}_{\mathbf{y}}{\mathbf{M}}^T$$ (28)

where Σ_y is the covariance matrix of the measured brightness, assumed to be diagonal (i.e., measurement errors at different angles are uncorrelated), and M is the inversion matrix from (25):

$$\mathbf{M}={\left(\frac{1}{{\sigma }_{\mathbf{w}}^2}{\mathbf{A}}^T\mathbf{A}+{\gamma }^2{\mathbf{L}}^T\mathbf{L}\right)}^{-1}\frac{1}{{\sigma }_{\mathbf{w}}^2}{\mathbf{A}}^T$$ (29)

Step 2 is nonlinear, involving the solution of a third order polynomial. To propagate error through this step, we assume MN is negligible compared to RR (i.e., [O]= 0), which simplifies the solution of (22) to

$$\mathbf{N}=\sqrt{\frac{4\pi \mathbf{\text{x}}}{{\alpha }_{135.6}}}$$ (30)

The nonlinearity of (30), which is especially significant for low VER, is too large for linearized error propagation, so actual confidence intervals are calculated, approximating the distribution of N as a multivariate Gaussian. Thus, the propagated covariance matrix of N is

$${\mathbf{\Sigma }}_{\mathbf{N}}^{ij}=\{\begin{array}{ll}\frac{4\pi }{{\alpha }_{135.6}}\left(\sqrt{x_i+{\sigma }_x^i}-\sqrt{x_i}\right)& \text{if}i=j\\ \frac{{\sigma }_N^i{\sigma }_N^j}{{\sigma }_x^i{\sigma }_x^j}{\mathbf{\Sigma }}_{\mathbf{x}}^{ij}& \text{if}i\ne j\end{array}$$ (31)

where ${\sigma }_x^i$ and ${\sigma }_N^i$ are the uncertainty of VER and electron density at altitude i:

$${\sigma }_x^i=\sqrt{{\mathbf{\text{Σ}}}_{\text{x}}^{ii}}$$ (32)

$${\sigma }_N^i=\sqrt{{\mathbf{\text{Σ}}}_{\text{N}}^{ii}}$$ (33)

Step 3 uses a peak-finder, which is not an analytic function, so errors are propagated using a Monte Carlo method. Many realizations of electron density profiles are calculated by sampling from a multivariate Gaussian distribution with mean N and covariance matrix Σ_N. The parameters hmF2 and NmF2 are estimated from each trial. The standard deviation of the trials provides the final estimated error, σ_hmF2 and σ_NmF2. In practice 100 trials are used.

We validate this error propagation algorithm with an end-to-end Monte Carlo simulation. Using a “true” electron density profile from IRI and neutral oxygen profile from NRL-MSISE00, along with an assumption of spherical symmetry, 1000 brightness profiles are simulated with different shot noise realizations. Each profile is fed through the inversion, resulting in 1000 estimates of hmF2 and NmF2, and 1000 propagated values of σ_hmF2 and σ_NmF2. The mean 68.3% confidence ellipse determined from σ_hmF2 and σ_NmF2 agrees well with the sample error ellipse determined from the 1000 values of hmF2 and NmF2, as shown in Figure 6. Indeed, 69.6% of the 1000 trials lie within the propagated ellipse, closely matching the expectation of 68.3% for Gaussian statistics. This validates the assumptions used above. A small correlation (ρ = −0.2) is seen between the samples of hmF2 and NmF2. A small but significant bias exists between the true hmF2 and NmF2 and the mean estimated hmF2 and NmF2, which is also seen in the simulation results in Figure 3. This validation was performed for a low SNR (corresponding to a measured brightness of 10 R on the limb). As SNR increases, the correlation and bias both tend towards zero.

Fig. 6:

The error propagation algorithm is validated with a Monte Carlo simulation. A model electron density profile is used to simulate 1000 noisy measurements, from which 1000 samples of hmF2 and NmF2 are generated. The covariance ellipse of these samples is compared to the mean propagated error.