A general framework for estimating volume-outcome associations from longitudinal data

Abstract

Recently, there has been much interest in using volume-outcome data to establish causal associations between measures of surgical experience or quality and patient outcomes following a surgical procedure, such as coronary artery bypass graft, total hip replacement, and radical prostatectomy. However, there does not appear to be a standard approach to a volume-outcome analysis with respect to specifying a volume measure and selecting an estimation method. We establish the recurrent marked point process as a general framework from which to approach a longitudinal volume-outcome analysis and examine the statistical issues associated with using longitudinal data analysis methods to model aggregate volume-outcome data. We review assumptions to ensure that linear or generalized linear mixed models and generalized estimating equations provide valid estimates of the volume-outcome association. In addition, we provide theoretical and empirical evidence that bias may be introduced when an aggregate volume measure is used to address a scientific question regarding the effect of cumulative experience. We conclude with the recommendation that analysts carefully specify a volume measure that most accurately reflects their scientific question of interest and select an estimation method that is appropriate for their scientific context.

1. Introduction

Volume-outcome studies are typically used to evaluate whether patients treated by high-volume healthcare providers (e.g., surgeons or hospitals) experience better post-treatment outcomes than those treated by low-volume providers. Examples include evaluating the association between surgeon volume and patient mortality following coronary artery bypass graft [1] and estimating the effect of hospital volume on patient mortality following treatment with mechanical ventilation [2]. Volume-outcome studies are important among health services researchers because the results may have direct policy implications [3], such as regionalization of health care into large healthcare centers [4] or selective referral of patients to high-volume providers [5]. In our motivating example, interest lies in estimating the effect of surgeon volume, as a measure of surgeon experience, on patient mortality following lung resection, in which cancerous regions are removed.

1.1. Estimation methods for longitudinal outcomes

Even though volume-outcome analyses have become common in the applied literature, there does not appear to be definitive guidance on appropriate estimation methods in the methodological literature. Volume-outcome studies typically involve repeatedly collecting patient information on the same surgeons or hospitals over time, often from an administrative database. Collecting information in this fashion motivates the application of longitudinal data analysis methods, which account for temporal dependence. These include a semi-parametric generalized estimating equation (GEE) approach [6] and a likelihood-based generalized linear mixed model (GLMM) approach [7]. Results of case studies have been used to determine appropriate methods for a volume-outcome analysis [8]. Illustrative examples [9] and simulation studies [10, 11] have explored the statistical properties of an estimating equation estimator and a mixed-model estimator in the context of volume-outcome data.

A volume-outcome analysis raises unique methodological issues because volume represents not only the time-dependent exposure of interest but also the cluster size [10–13]. If the outcome is dependent on cluster size, then cluster size is termed ‘informative’ or ‘non-ignorable.’ Several specialized estimation methods have been proposed to generate inference when cluster size is ‘informative’. One approach is based on within-cluster resampling (WCR) [12, 14] and is similar in spirit to multiple imputation [15]. Another approach is to weight each cluster by the inverse cluster size [13, 16] and analyze the data by using a weighted estimating equation [17]. Researchers recently developed specialized methods to provide efficiency gains over WCR and cluster-weighted GEE [18].

To provide guidance on appropriate estimation methods, we adopt the recurrent marked point process [19] as a general framework from which to approach a longitudinal volume-outcome analysis. The defining characteristic of recurrent marked point process data is that an outcome (e.g., post-surgery patient mortality) exists if and only if an event (e.g., a surgery) occurs. The recurrent marked point process setting motivates specific assumptions regarding any time-dependent exposure process and the event-time process that determine which repeated measures regression methods are appropriate. The latter assumption regarding the timing of events—specifically, the endogeneity between past outcomes and occurrence of a subsequent event—is a natural assumption to explore in the context of volume-outcome data and facilitates consideration of the ‘informative’ cluster size issue. For example, if a patient experiences an adverse outcome, then the surgeon may obtain fewer patient referrals due to his or her past surgical performance. Therefore, the surgeon will have a smaller cluster size, which will appear to be ‘informative’ of an adverse outcome for his or her patients.

1.2. Volume as a longitudinal covariate

Whereas a growing body of statistical literature has focused on the comparison of multilevel marginal methods and mixed-model methods, and on issues related to potentially informative cluster sizes, little attention has been given to two key longitudinal aspects that are central in volume-outcome studies. First, the ‘volume’ for a given provider is not a fixed quantity but rather a time-dependent quantity that changes over the course of study. In most volume-outcome studies, the ‘cluster’ of outcome data from a given provider is linked to a volume measure that is determined on a coarse time scale, such as the annual total procedures performed in the current calendar year. Using an annual volume measure risks using a mismeasured covariate that is also subject to endogeneity because the volume used as a predictor for patient i at time t is actually an aggregate of past (earlier in the year) and future (later in the year) procedure occurrences. Second, many volume-outcome studies do not discuss the selection of the appropriate volume measure for the scientific question of interest, and there are two key options to consider: recent volume and cumulative volume. In this setting, recent volume may be the number of procedures performed in the last year; an analysis that uses recent volume assumes that ‘acute’ experience is of primary interest. Alternatively, cumulative volume is analogous to cumulative exposure used in epidemiological studies and would be calculated by considering volume accumulated over all years.

A critical consideration in a volume-outcome analysis is selecting a volume measure that is appropriate for the type of healthcare provider under study. Volume-outcome data are often composed of a patient outcome and information regarding patient case mix. In this situation, the data are non-aggregate in the sense that the outcome and exposures are measured on a fine time scale, that is, at each surgery time. Conversely, in much of the applied literature, surgeon volume and hospital volume are modeled in an aggregate fashion on a coarse time scale, usually as a yearly total, that is, the total number of surgeries performed in a calendar year, or a yearly average, that is, the cumulative volume at the end of follow-up divided by the length of follow-up. However, hospital volume and surgeon volume are typically used to quantify different provider characteristics. Hospital volume is typically used as a measure of hospital size [2] or quality. In this case, an aggregate volume measure may be appropriate because hospital size is roughly constant over shorter durations of time [20]. Surgeon volume is typically used as a measure of surgeon experience [21]. In this case, an aggregate volume measure may not be appropriate because surgeon experience is an evolving process on a fine time scale. An aggregate measure of surgeon volume on a coarse time scale may ignore this serial structure [22,23].

A related issue in a volume-outcome analysis is selecting a volume measure that most accurately addresses the scientific question of interest. Suppose that primary interest lies in surgeon volume as a measure of surgeon experience. In this situation, there is more than one volume measure that may be used to quantify surgeon experience. For example, consider two surgeons who both accumulated 100 patients during their career. The first surgeon attained this experience in 5 years, with 20 patients per year, whereas the second surgeon attained this experience in 20 years, with five patients per year. These surgeons have identical cumulative volume but different contemporaneous volume. A non-aggregate measure of surgeon volume may more accurately quantify cumulative surgeon experience. An aggregate measure of surgeon volume, such as a yearly total, may more accurately quantify contemporaneous experience. However, the applied literature does not typically distinguish between cumulative volume and contemporaneous volume as measures of surgeon experience [21,22].

In this paper, we consider situations in which the primary target of inference is a regression model that quantifies the association between provider volume and a post-surgery patient outcome among those who receive surgery. Our goals are to provide a general framework from which to approach a longitudinal volume-outcome analysis, and to articulate the statistical issues associated with an aggregate analysis. We establish the recurrent marked point process as a general framework in Section 2.2 and review assumptions for generating valid inference regarding the volume-outcome association from non-aggregate data in Section 2.4. We examine the statistical issues associated with selecting an aggregate volume measure in Sections 2.5 and 2.6. In Section 3, we explore via simulation the potential for bias when estimating a volume-outcome association if the recurrent marked point process assumptions are violated and/or surgeon volume is specified using an aggregate measure. In Section 4, we describe a motivating example by using Surveillance, Epidemiology, and End Results (SEER)-Medicare data and illustrate non-aggregate and aggregate analyses of volume-outcome data. We provide concluding discussion in Section 5.

2. Statistical methods

2.1. Notation

We assume that an outcome exists if and only if a surgery occurs and therefore limit our focus to observations collected in discrete time. Let X_i(t) and Y_i(t) denote a patient-level exposure and post-surgery patient outcome (or mark), respectively, observed for surgeons i = 1, …, n at discrete calendar times t = 1, …, T. Similarly, let N_i(t) denote cumulative surgeon volume, that is, the total number of surgeries performed by surgeon i through time t. We denote the complete history of each variable ascertained retrospectively at time t by ${\mathcal{X}}_i(t)=\left\{X_i(s)\mid s⩽t\right\}$; ${\mathcal{N}}_i(t)=\left\{N_i(s)\mid s⩽t\right\}$ and ${\mathcal{Y}}_i(t)=\left\{Y_i(s)\mid s⩽t\right\}$. In addition, we use the notation dN_i(t) = N_i(t) − N_i (t − 1) that such that dN_i(t) = 1 indicates a surgery at time t.

For simplicity of presentation, surgeons are assumed to be independent. However, in practice, surgeons are typically nested (either fully or partially) within hospitals, and patient outcomes collected within the same hospital may be correlated. In our application, we accommodate the clustering of surgeons within hospitals by using hierarchical generalized linear models [24]. There are also options for specifying a hierarchical structure within a marginal model [25,26].

2.2. Recurrent marked point process framework

Table I provides an illustration of recurrent marked point process data for a hypothetical surgeon at 12 calendar times during three calendar years and alternative specifications for time-dependent surgeon volume during year 3. The symbol ‘×’ indicates the occurrence of a surgery; the symbol ‘−’ indicates that a surgery did not occur. Non-aggregate volume is computed at each calendar time: total volume is calculated by summing the number of surgeries through each calendar time, and recent volume is calculated by summing the number of surgeries in, for example, the year previous to each calendar time. Aggregate volume is computed at each calendar year, with the option of either including the year-3 surgeries in the calculation or lagging by, for example, a calendar year and excluding the year-3 surgeries from the calculation. Given the apparent differences between these specifications, selecting a volume specification therefore represents the primary challenge of a volume-outcome analysis. A secondary issue is considering the factors that influence the occurrence of a surgery.

Table I.

Illustration of recurrent marked point process data and alternative specifications for time-dependent volume at t = 10, 11, 12; the symbol ‘×’ indicates the occurrence of a surgery, and the symbol ‘−’ indicates that a surgery did not occur.

Time t	1	2	3	4		5	6	7	8		9	10	11	12
Surgery	×	×	-	×		×	×	-	-		-	×	×	×
Year j					1					2					3
Volume	Non-aggregate					Total						6	7	8
						Recent						2	2	3
	Aggregate					Total (not lagged)						8	8	8
						Total (lagged)						5	5	5
						Recent (not lagged)						3	3	3
						Recent (lagged)						2	2	2

2.3. Target of inference

Suppose that primary scientific interest lies in quantifying the volume-outcome association between surgeon volume N_i(t) and a post-surgery patient outcome Y_i(t) among individuals who receive surgery, that is, dN_i(t) = 1. As the target of inference, we identify a marginal (or ‘partly conditional’ [27]) regression model:

$${\mu }_i(t)=\text{E}\left[Y_i(t)\mid d{N}_i(t)=1,{\mathcal{N}}_i(t),{\mathcal{X}}_i(t)\right]={\mathit{x}}_{it}\mathit{\beta }\text{.}$$ (1)

The vector of covariates x_it is composed of the relevant components of the exposure and event-time processes. Parameters β quantify the association between these components and the average outcome. Note that dN_i(t) = 1 is required in μ_i(t) because, otherwise, Y_i(t) would not exist.

The marginal model in Equation (1) is a useful target of inference for a volume-outcome analysis in which primary interest lies in describing the marginal association between a full or partial history of the event-time process and the mark process after adjusting for a full or partial history of the exposure process. In particular, the marginal model may be used to quantify the volume-outcome association among a population of patients who receive surgery. It may also be used to predict a future patient outcome as a function of the observed exposure and event-time processes.

2.4. Assumptions for time-dependent covariates

To ensure consistency of a covariance-weighted GEE estimator or a likelihood-based mixed-model estimator for β, it is sufficient to assume that for all t′ > t:

• Assumption 1

  $$Y_i(t)\perp N_i\left(t^{\prime }\right)\mid {\mathcal{X}}_i(t),{\mathcal{N}}_i(t),d{N}_i(t)=1,$$ (2)
• Assumption 2

  $$Y_i(t)\perp X_i\left(t^{\prime }\right)\mid {\mathcal{X}}_i(t),{\mathcal{N}}_i\left(t^{\prime }\right),d{N}_i(t)=1,$$ (3)

where ⊥ denotes independence. If either of these conditions is not satisfied, then an independence estimating equation (IEE) is the only estimating equation option that can generally be used for consistent estimation of β [19,28].

Assumption (1) states that the current patient outcome is conditionally independent of the future number of events for a particular surgeon given the history of the exposure and event-time processes. Assumption (1) implies that there is no causal association between a patient outcome and the occurrence of a subsequent surgery for the surgeon. This is an important association to explore in the context of volume-outcome data because if a patient experiences an adverse outcome, then the surgeon may subsequently obtain fewer patient referrals due to his or her past surgical performance. Therefore, the surgeon will have a smaller cluster size, which will appear to be ‘informative’ of an adverse outcome for his or her patients. Assumption (1) therefore facilitates direct consideration of a mechanism for ‘informative’ cluster size, secondary to the volume-outcome association of interest.

Assumption (2) states that the current patient outcome is conditionally independent of a future patient-level exposure, given the history of the exposure process and the future history of the event-time process. Assumption (2) implies that there is no causal association between a patient outcome and a subsequent patient-level exposure for a particular surgeon. This is also an important association to explore in the context of volume-outcome data because if a patient experiences an adverse outcome, then the surgeon may subsequently be assigned patients with a lower risk of an adverse outcome. In this case, biased estimates of the exposure-outcome association may result due to endogeneity between outcome and exposure, so that the volume-outcome association may not be properly adjusted for patient-level exposures. It is generally possible to evaluate Assumptions (1) and (2) by using the observed data [19].

In summary, the recurrent marked point process setting provides a general framework from which to approach a longitudinal volume-outcome analysis. It is a realistic framework to consider because a patient outcome exists if and only if a surgery occurs. It motivates specific assumptions regarding the exposure and event-time processes that determine which longitudinal data analysis methods generate valid inference regarding the volume-outcome association. In Section 3, we evaluate the potential for bias when estimating a volume-outcome association if the recurrent marked point process assumptions are violated.

2.5. Aggregate specifications for cumulative volume

Recall that $N_i(t)={\Sigma }_{s=1}^{t}d{N}_i(s)$ denotes a non-aggregate specification for cumulative volume, that is, the total number of surgeries performed by a surgeon i through time t. Suppose that N_i(t) is aggregated using $f\left[{\mathcal{N}}_i\left(T_j\right)\right]$, a function of ${\mathcal{N}}_i\left(T_j\right)$ for time j = 1, …, J . Consider the following specifications for $f\left[{\mathcal{N}}_i\left(T_j\right)\right]$. First, a running average—an average that includes cumulative volume through the previous year:

$$f_1\left[{\mathcal{N}}_i\left(T_j\right)\right]=N_i\left(T_{j-1}\right)+\frac{{\delta }_j}{2}=N_i\left(T_{j-1}\right)+\frac{N_i\left(T_j\right)-N_i\left(T_{j-1}\right)}{2}=\frac{N_i\left(T_j\right)+N_i\left(T_{j-1}\right)}{2}.$$ (4)

Second, a total average—an average of cumulative volume at the start and end of follow-up:

$$f_2\left[{\mathcal{N}}_i\left(T_j\right)\right]=\frac{N_i\left(T_J\right)+N_i\left(T_0\right)}{2}\equiv {\overline{N}}_i=\frac{1}{2}\sum _{s=1}^{T_J}d{N}_i(s)\text{ if }{N}_i\left(T_0\right)=0.$$ (5)

Figure 1(a) presents aggregate specifications for cumulative volume, along with non-aggregate volume, for a hypothetical surgeon. Non-aggregate surgeon volume () represents the total number of surgeries performed by the surgeon through each calendar time. Running average () and total average () represent aggregate measures that quantify cumulative surgeon experience at each calendar year. Both specifications appear to provide a satisfactory approximation to non-aggregate volume. Non-aggregate volume is an increasing step function; running average and running total simply have larger steps.

Figure 1.

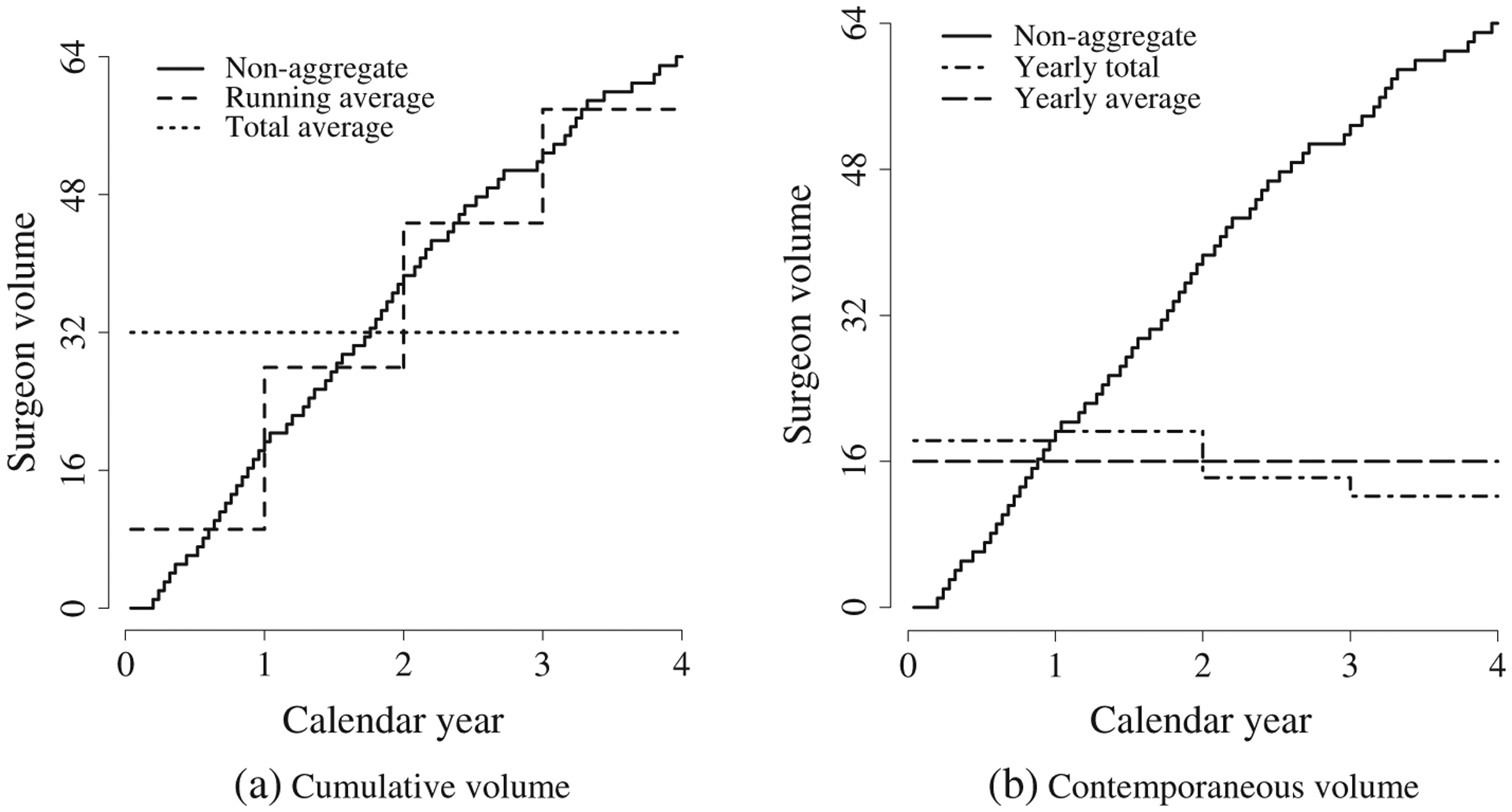
Aggregate specifications for surgeon volume.

The impact of specifying surgeon volume by using a running average can be explored by examining the estimating function for estimation of β. Assume a cross-sectional model for the expectation of Y_i(t): μ_i(t) = β₀ + β₁X_i(t) + β₂N_i(t). However, suppose that the fitted mean model for Y_i(t), denoted by ${\mu }_i^{\star }(t)$, includes $f\left[{\mathcal{N}}_i\left(T_j\right)\right]$:

$${\mu }_i^{\star }(t)={\beta }_0+{\beta }_1{X}_i(t)+{\beta }_{2}f\left[{\mathcal{N}}_i\left(T_j\right)\right]={\mathit{x}}_{it}^{\star }\mathit{\beta }\text{.}$$ (6)

The vector of covariates ${\mathit{x}}_{it}^{\star }$ includes the running average specification for cumulative volume. Let w_itt′ denote the (t, t′) element of the inverse of a working covariance matrix V_i. Then the estimating equation for estimation of β is:

$$\begin{gathered} {\mathcal{U}}_{\beta }(\mathit{\beta })=\sum _{i=1}^n{\mathit{X}}_i^{\star \text{T}}{\mathit{V}}_i^{-1}\left({\mathit{Y}}_i-{\mathit{\mu }}_i^{\star }\right)\mathit{d}{\mathit{N}}_i \\ =\sum _{i=1}^n\sum _{j=1}^J\sum _{t^{\prime }=T_{j-1}}^{T_j}\sum _{t=T_{j-1}}^{T_j}{\mathit{x}}_{i{t}^{\prime }}^{\star }{w}_{it{t}^{\prime }}\left\{Y_i(t)-{\mu }_i^{\star }(t)\right\}d{N}_i(t)d{N}_i\left(t^{\prime }\right). \end{gathered}$$ (7)

Recall that consistency of $\widehat{\mathit{\beta }}$ relies on the assumption that the estimating function is unbiased. Examine each summand of ${\mathcal{U}}_{\beta }(\mathit{\beta })$:

$$\begin{gathered} {\mathit{x}}_{i{t}^{\prime }}^{\star }{w}_{it{t}^{\prime }}\left\{Y_i(t)-{\mu }_i^{\star }(t)\right\}d{N}_i(t)d{N}_i\left(t^{\prime }\right) \\ ={\mathit{x}}_{i{t}^{\prime }}^{\star }{w}_{it{t}^{\prime }}\left\{Y_i(t)-{\beta }_0-{\beta }_1{X}_i(t)-{\beta }_{2}f\left[{\mathcal{N}}_i\left(T_j\right)\right]\right\}d{N}_i(t)d{N}_i\left(t^{\prime }\right) \\ ={\mathit{x}}_{i{t}^{\prime }}^{\star }{w}_{it{t}^{\prime }}\left\{Y_i(t)-{\beta }_0-{\beta }_1{X}_i(t)-{\beta }_2{N}_i(t)+{\beta }_2{N}_i(t)-{\beta }_{2}f\left[{\mathcal{N}}_i\left(T_j\right)\right]\right\}d{N}_i(t)d{N}_i\left(t^{\prime }\right) \\ ={\mathit{x}}_{i{t}^{\prime }}^{\star }{w}_{it{t}^{\prime }}\left\{Y_i(t)-{\mu }_i(t)+{\beta }_2{N}_i(t)-{\beta }_{2}f\left[{\mathcal{N}}_i\left(T_j\right)\right]\right\}d{N}_i(t)d{N}_i\left(t^{\prime }\right). \end{gathered}$$ (8)

In this case, consistency of $\widehat{\mathit{\beta }}$ requires that either $\text{E}\left\{N_i(t)-f\left[{\mathcal{N}}_i\left(T_j\right)\right]\right\}=0$ or β₂ = 0. For the running average specification defined in Equation (4), recall that δ_j = N_i(T_j) − N_i(T_{j – 1}) and examine $N_i(t)-f_1\left[{\mathcal{N}}_i\left(T_j\right)\right]$ for T_{j – 1} ⩽ t ⩽ T_j:

$$\begin{gathered} \sum _{t=T_{j-1}}^{T_j}\left\{N_i(t)-f_1\left[{\mathcal{N}}_i\left(T_j\right)\right]\right\}=\sum _{t=T_{j-1}}^{T_j}\left\{N_i(t)-\left[N_i\left(T_{j-1}\right)+\frac{{\delta }_j}{2}\right]\right\} \\ =\sum _{t=T_{j-1}}^{T_j}\left\{\left[N_i(t)-N_i\left(T_{j-1}\right)\right]-\frac{{\delta }_j}{2}\right\} \\ =\left[\sum _{s=1}^{{\delta }_j}s\right]-\left({\delta }_j+1\right)\times \frac{{\delta }_j}{2} \\ =\frac{{\delta }_j\left({\delta }_j+1\right)}{2}-\frac{{\delta }_j\left({\delta }_j+1\right)}{2} \\ =0. \end{gathered}$$ (9)

Therefore, in a linear model, a running average specification for surgeon volume provides a consistent estimate of the effect of cumulative surgeon experience.

The total average specification defined in Equation (5) can be viewed as a reparameterization of β₂N_i(t) that partitions the variability in N_i(t) into within-surgeon and between-surgeon variability:

$${\beta }_2{N}_i(t)={\beta }_2\left[N_i(t)-{\overline{N}}_i+{\overline{N}}_i\right]={\beta }_2\left[N_i(t)-{\overline{N}}_i\right]+{\beta }_2{\overline{N}}_i.$$ (10)

The fitted mean model for Y_i(t) includes ${\overline{N}}_i$:

$${\mu }_i^{\star }(t)={\beta }_0+{\beta }_1{X}_i(t)+{\beta }_2{\overline{N}}_i={\mu }_i(t)-{\beta }_2\left[N_i(t)-{\overline{N}}_i\right].$$ (11)

Although ${\beta }_2\left[N_i(t)-{\overline{N}}_i\right]$ is not included in the fitted mean model, consistent estimation of β₂ is not hampered because ${\overline{N}}_i$ and $N_i(t)-{\overline{N}}_i$ are orthogonal. Therefore, in a linear model, a total average specification for surgeon volume provides a consistent estimate of the effect of cumulative surgeon experience.

It is important to note that for a non-linear model, ${\mu }_i(t)-{\mu }_i^{\star }(t)$ is not necessarily proportional to $N_i(t)-f\left[{\mathcal{N}}_i\left(T_j\right)\right]$. Therefore, in a non-linear model, a running average or total average specification for cumulative volume may not provide a consistent estimate of the effect of cumulative surgeon experience. In addition, if there is endogeneity in the exposure or event-time processes, then Assumptions (1) and (2) or working independence no longer assure that the estimating function in Equation (7) is unbiased because ${\mathit{x}}_{it}^{\star }$ is not equivalent to x_it .

2.6. Aggregate specifications for contemporaneous volume

Recall that $f\left[{\mathcal{N}}_i\left(T_j\right)\right]$ denotes a function of a volume measure ${\mathcal{N}}_i\left(T_j\right)$ for time j = 1, …, J. Consider the following specifications for $f\left[{\mathcal{N}}_i\left(T_j\right)\right]$ First, a yearly total— a total volume for each year:

$$f_3\left[{\mathcal{N}}_i\left(T_j\right)\right]=N_i\left(T_j\right)-N_i\left(T_{j-1}\right)=\sum _{s=1}^{T_j}d{N}_i(s)-\sum _{s=1}^{T_{j-1}}d{N}_i(s)=\sum _{s=T_{j-1}}^{T_j}d{N}_i(s).$$ (12)

Second, a yearly average—an average volume across the follow-up period:

$$f_4\left[{\mathcal{N}}_i\left(T_j\right)\right]=\frac{1}{J}\sum _{j=1}^J{f}_3\left[{\mathcal{N}}_i\left(T_j\right)\right]=\frac{1}{J}\sum _{s=1}^{T_J}d{N}_i(s)=\frac{J}{2}{f}_2\left[N_i\left(T_j\right)\right].$$ (13)

Figure 1(b) presents aggregate specifications for contemporaneous volume, along with non-aggregate volume (), for a hypothetical surgeon. Yearly total () and yearly average () represent aggregate measures that quantify contemporaneous surgeon experience at each calendar year. The yearly total and yearly average specifications appear to provide a poor summary of non-aggregate volume. Although non-aggregate volume increases steadily over time, yearly average volume is constant and yearly total volume decreases.

2.7. Summary

In this section, we focused on a marginal regression model to generate inference regarding the volume-outcome association. We used the recurrent marked point process framework to motivate specific assumptions that determine which longitudinal data analysis methods generate valid inference. We highlighted situations in which estimation of the volume-outcome association is identical using either aggregate or non-aggregate specification for cumulative volume. Although we focused on estimation and inference within the framework of GEE [6], identical issues arise within a mixed-model framework [7]. First, because volume is a time-dependent exposure, endogeneity in the event-time process may bias estimation of the volume-outcome association [19]. Second, because volume represents not only the time-dependent exposure of interest, but also the cluster size, Assumption (1) may be evaluated to determine whether cluster size is ‘informative’ [10–13]. In subsequent sections, we explore the impact of these issues on estimation and inference via a simulation study (Section 3) and motivating application (Section 4).

3. Simulation study

We designed a simulation study to emulate our motivating example: a multiyear volume-outcome study in which interest lies in the association between cumulative surgeon volume and patient outcomes among those who receive surgery [29]. Although the outcome in our motivating example is binary, we generated a continuous outcome in the simulation study to facilitate a direct comparison of marginal and conditional parameter estimates. The goal of the simulation study was to evaluate the potential for bias when estimating a volume-outcome association if:

1. Impact of endogeneity: The recurrent marked point process assumptions are violated, and/or

2. Impact of aggregation: Surgeon volume is specified using an aggregate measure.

We generated patient outcomes dependent on non-aggregate surgeon volume, but in aggregate analyses, we specified volume by using a yearly total and a yearly average volume, which are strategies frequently used in the applied literature [1, 21]. We also specified volume by using a running average and total average.

3.1. Parameters

At each of 1000 iterations, we generated data for a population of 10,000 surgeons at t = 1, …, 100 discrete time points [19]. We selected T = 100 to emulate a volume-outcome study conducted over a lengthy follow-up period. We generated a binary variable to indicate a surgery at time t such that the probability of a surgery depended on the previous outcome and current exposure:

$$\begin{gathered} d{N}_i\left(t\right)\left|{\mathcal{X}}_i\left(t\right),{\mathcal{N}}_i\left(t\right),{\mathcal{Y}}_i\left(t\right)=d{N}_i\left(t\right)\right|X_i\left(t\right),Y_i(t-1) \\ ~B\left\{\text{expit}\left[{\eta }_0+{\eta }_1{R}_i(t-1)+{\eta }_2{X}_i\left(t\right)\right]\right\}, \end{gathered}$$ (14)

where expit(·) = exp(·)/[1 + exp(·) and R_i(t − 1) denotes a residual for Y_i(t − 1) centered by its conditional expectation given X_i(t − 1). The parameter η₁ quantifies the extent to which Assumption (1) is violated. We considered η₁ = (log 1, log 2), which correspond to no association and a moderate association, respectively, between the previous outcome and the probability of a surgery. We specified an autoregressive exposure process:

$$\begin{gathered} X_i\left(t\right)\left|{\mathcal{X}}_i\left(t\right),{\mathcal{N}}_i\left(t\right),{\mathcal{Y}}_i\left(t\right)=X_i\left(t\right)\right|X_i(t-1),Y_i(t-1) \\ ~N\left[{\theta }_0{X}_i(t-1)+{\theta }_1{R}_i(t-1),v^2\left(1-{\theta }_0^2\right)\right]. \end{gathered}$$ (15)

The parameter θ₁ quantifies the extent to which Assumption (2) is violated. We considered θ₁ = (0, 0.1), which correspond to no association and a moderate association, respectively, between the previous outcome and current exposure.

To generate the mark process, we specified a marginal mean μ_i(t) = β₀ + β₁X_i(t) + β₂N_i(t) in which (β₁, β₂) = (−1, 0.05) represent moderate effects of exposure and volume. We generated surgeon-specific random intercepts and slopes γ_i = {γ_i0, γ_i1, γ_i2}, serial correlation W_i(t) and measurement error ∊_i(t) from independent Gaussian distributions. Therefore, the mark process was

$$\begin{gathered} Y_i\left(t\right)\mid {\mathcal{X}}_i\left(t\right),{\mathcal{N}}_i\left(t\right),{\mathcal{Y}}_i\left(t\right),{\mathcal{Z}}_i\left(t\right) \\ =Y_i\left(t\right)\mid X_i\left(t\right),N_i\left(t\right),Z_i\left(t\right) \\ ={\beta }_0+{\beta }_1{X}_i\left(t\right)+{\beta }_2{N}_i\left(t\right)+{\tilde{\gamma }}_{i0}\left(t\right)+{\tilde{\gamma }}_{i1}\left(t\right)X_i\left(t\right)+{\tilde{\gamma }}_{i2}\left(t\right)N_i\left(t\right)+{\tilde{W}}_i\left(t\right)+{ϵ}_i\left(t\right), \end{gathered}$$ (16)

where {Z_i(t) = {W_i(t), γ_i} denotes unmeasured error for the longitudinal process Y_i(t) and ${\mathcal{Z}}_i\left(t\right)=\left\{Z_i\left(s\right)\mid s⩽t\right\}$. Note that ${\tilde{\gamma }}_{i0}\left(t\right)$, ${\tilde{\gamma }}_{i1}\left(t\right)$, ${\tilde{\gamma }}_{i2}\left(t\right)$ and ${\tilde{W}}_i\left(t\right)$ were sequentially centered by their conditional expectation given dN_i(t) = 1 so that the marginal expectation of Y_i(t) was correctly specified.

From each simulated population, we sampled n = 300 surgeons and calculated non-aggregate cumulative volume N_i(t) as the total number of surgeries performed by a surgeon i through time t. We aggregated N_i(t) into four blocks corresponding to a total volume through year j = 1, …, 4. In aggregate analyses, we specified volume by using four measures:

1. running average volume [Equation (4)],

2. total average volume [Equation (5)],

3. yearly total volume [Equation (2)], and

4. yearly average volume [Equation (13)],

where (1) and (2) quantify cumulative experience and (3) and (4) quantify contemporaneous experience. We fit an IEE, a GEE assuming an exchangeable correlation structure, a linear mixed model with random intercepts (LMM-RI), and a linear mixed model with random intercepts, random exposure and volume effects, and an autoregressive correlation structure (LMM-RS). For the total average and yearly average specifications, a mixed model with random volume effects is not appropriate because volume is not time-dependent. We report mean point estimates for the volume-outcome association (β₂ = 0.05), mean standard error estimates, empirical standard error of point estimates, and estimated coverage of 95% confidence intervals.

3.2. Results

3.2.1. Impact of endogeneity.

Table II provides simulation results for a non-aggregate specification for cumulative volume. In the scenario that specifies no endogeneity (η₁ = log 1, θ₁ = 0), every method provides an approximately unbiased parameter estimate with acceptable confidence interval coverage. In the scenario that specifies endogeneity in the event-time process (η₁ = log 2, θ₁ = 0), an IEE provides an approximately unbiased parameter estimate with acceptable coverage. However, covariance-weighting methods provide a biased parameter estimate with reduced coverage. The relative bias in estimating β₂ is approximately 10% for GEE and LMM-RI. If there is also endogeneity in the exposure process (η₁ = log 2, θ₁ = 0.1), then covariance-weighting methods may provide substantially biased parameter estimates with poor coverage. The relative bias in estimating β₂ is approximately 24% for GEE and LMM-RI. A key observation is that endogeneity in the exposure process does not appear to negatively impact estimation of β₂ if there is no endogeneity in the event-time process (η₁ = log 1, θ₁ = 0.1).

Table II.

Simulation results for a non-aggregate specification for cumulative volume: mean of estimated regression coefficients (mean ${\widehat{\beta }}_2$), mean of standard error estimates (mean SE), empirical standard error of estimated regression coefficients (ESE ${\widehat{\beta }}_2$), and percent coverage of 95% confidence intervals (% coverage).

(η1, θ1)	Method	Mean ${\widehat{\beta }}_2$	Mean SE	ESE ${\widehat{\beta }}_2$	% coverage
(log 1, 0)	IEE	0.050	0.0020	0.0021	95
	GEE	0.050	0.0020	0.0020	95
	LMM-RI	0.050	0.0008	0.0020	52
	LMM-RS	0.050	0.0019	0.0020	95
(log 1,0.1)	IEE	0.050	0.0018	0.0017	95
	GEE	0.050	0.0018	0.0017	95
	LMM-RI	0.050	0.0007	0.0017	61
	LMM-RS	0.050	0.0019	0.0019	95
(log 2, 0)	IEE	0.050	0.0023	0.0022	95
	GEE	0.045	0.0022	0.0021	36
	LMM-RI	0.045	0.0009	0.0021	6
	LMM-RS	0.043	0.0022	0.0021	8
(log 2,0.1)	IEE	0.050	0.0029	0.0028	95
	GEE	0.038	0.0027	0.0027	1
	LMM-RI	0.038	0.0012	0.0027	0
	LMM-RS	0.034	0.0028	0.0031	0

Standard error estimates obtained via IEE are often greater than those obtained via GEE and LMM. This is not surprising; it is well-known that an IEE may be inefficient relative to a covariance-weighting method under non-independence correlation structures [30]. However, LMM-RI appears to underestimate the standard error. Recall that to generate the data, we specified surgeon-specific random effects and serial correlation. LMM-RI therefore misspecifies the within-surgeon correlation structure and provides inconsistent standard error estimates, whereas LMM-RS correctly specifies the correlation structure. Although the IEE and GEE misspecify the correlation structure, the standard errors are consistent, courtesy of the robust standard error estimator.

Note the contrast in the performance of LMM-RI and LMM-RS with respect to bias. Although LMM-RS is the correctly specified model, LMM-RI provides parameter estimates with a smaller amount of bias. For example, with η₁ = log 2 and θ₁ = 0.1, the mean estimates of β₂ obtained via LMM-RI and LMM-RS were 0.038 and 0.034, respectively. The difference is due to the different weighting scheme specified by the covariance models. Table III provides a subset of the covariance weight matrix from one simulated data set for (i) LMM-RI and (ii) LMM-RS. Of note are the larger off-diagonal elements for LMM-RS, which accentuate the bias incurred from violation of Assumption (1) or Assumption (2).

Table III.

Linear mixed model (LMM) covariance weights for simulated data.

(i) LMM-RI			(ii) LMM-RS
0.605	−0.014	−0.014	0.760	−0.403	−0.028
	0.605	−0.014		0.982	−0.391
		0.605			0.979

3.2.2. Impact of aggregation.

Table IV provides simulation results for a running average and total average specification for cumulative volume. In the scenario that specifies no endogeneity (η₁ = log 1, θ₁ = 0), if volume is specified using a running average, then both estimating equations provide an approximately unbiased parameter estimate with acceptable confidence interval coverage. Although the mixed model with random intercepts provides an approximately unbiased point estimate, coverage is reduced because the correlation model is misspecified and the standard error is underestimated. The mixed model with random volume effects underestimates the volume-outcome association and provides reduced coverage, possibly because the surgeon-specific volume effects are not properly estimated because of the lack of variability in within-surgeon volume measurements. If volume is specified using a total average, then every estimation method provides an approximately unbiased parameter estimate with acceptable coverage. These results show that, in this specific aggregate analysis, bias is not incurred from ignoring the serial structure of the event-time process.

Table IV.

Simulation results for aggregate specifications for cumulative volume: mean of estimated regression coefficients (mean ${\widehat{\beta }}_2$), mean of standard error estimates (mean SE), empirical standard error of estimated regression coefficients (ESE ${\widehat{\beta }}_2$), and percent coverage of 95% confidence intervals (% coverage).

		Running average				Total average
					%				%
(η1, θ1)	Method	Mean ${\widehat{\beta }}_2$	Mean SE	ESE ${\widehat{\beta }}_2$	coverage	Mean ${\widehat{\beta }}_2$	Mean SE	ESE ${\widehat{\beta }}_2$	coverage
(log 1,0)	IEE	0.050	0.0021	0.0020	96	0.050	0.0181	0.0184	94
	GEE	0.050	0.0021	0.0020	96	0.050	0.0179	0.0182	94
	LMM-RI	0.050	0.0008	0.0019	56	0.050	0.0180	0.0182	95
	LMM-RS	0.046	0.0019	0.0018	36
(log 2, 0)	IEE	0.053	0.0024	0.0024	78	0.090	0.0088	0.0091	1
	GEE	0.048	0.0023	0.0023	82	0.088	0.0085	0.0090	1
	LMM-RI	0.048	0.0009	0.0023	37	0.088	0.0084	0.0090	1
	LMM-RS	0.047	0.0022	0.0022	66
(log 2, 0.1)	IEE	0.056	0.0030	0.0031	53	0.098	0.0071	0.0071	0
	GEE	0.044	0.0028	0.0029	43	0.106	0.0065	0.0066	0
	LMM-RI	0.044	0.0013	0.0029	10	0.106	0.0063	0.0066	0
	LMM-RS	0.046	0.0028	0.0030	71

Table V provides simulation results for a yearly total and yearly average specification for contemporaneous volume. Results are provided for the scenario in which there is no endogeneity in either the exposure or event-time process. If volume is specified using a yearly total, then every estimation method underestimates the effect of cumulative experience and provides substantially reduced confidence interval coverage. The independence point estimate is on average half of the true value. All non-independence point estimates are on average approximately zero. If volume is specified using a yearly average, then every estimation method overestimates the effect of cumulative experience and provides reduced coverage. All point estimates are on average double the true value, which is expected in this case because the yearly average is half of the total average. These results show that substantial bias may be incurred from using an aggregate volume measure that is incongruous with the scientific question of interest.

Table V.

Simulation results for aggregate specifications for contemporaneous volume: mean of estimated regression coefficients (mean ${\widehat{\beta }}_2$), mean of standard error estimates (mean SE), empirical standard error of estimated regression coefficients (ESE ${\widehat{\beta }}_2$), and percent coverage of 95% confidence intervals (% coverage).

Volume specification	Method	Mean ${\widehat{\beta }}_2$	Mean SE	ESE ${\widehat{\beta }}_2$	% coverage
Yearly total	IEE	0.025	0.015	0.015	63
	GEE	0.003	0.016	0.016	16
	LMM-RI	0.003	0.006	0.016	2
	LMM-RS	0.008	0.011	0.011	4
Yearly average	IEE	0.099	0.036	0.036	72
	GEE	0.099	0.036	0.035	72
	LMM-RI	0.098	0.036	0.035	73

3.2.3. Impact of aggregation and endogeneity.

Table IV also provides simulation results for a running average and total average specification for cumulative volume in scenarios that specify endogeneity in the exposure and/or event-time processes. In the scenario that specifies endogeneity in the event-time process (η₁ = log 2, θ₁ = 0) if volume is specified using a running average, then every estimation method provides a biased estimate of the volume-outcome association with reduced confidence interval coverage. If volume is specified using a total average, then every estimation method provides a substantially biased parameter estimate with poor coverage. Positive bias is expected in this case because surgeon volume is positively associated with the outcome, which in turn is positively associated with occurrence of a subsequent event. Every estimation method performs slightly worse using either volume specification if there is also endogeneity in the exposure process (η₁ = log 2, θ₁ = 0.1). These results highlight the fact that if there is endogeneity in the underlying event-time process and an aggregate measure is used to specify cumulative volume, then an IEE may not guarantee consistent estimation of the effect of cumulative experience.

Biases incurred from aggregation and from endogeneity may be in the opposite direction. For example, comparing the results in Table IV for the running average specification with those presented in Table II shows that the amount of positive bias incurred from aggregation was constant across each estimation method, whereas negative bias was incurred from violation of Assumption (1). We performed additional simulation studies to examine the sensitivity of this result to the specified association between N_i(t) and Y_i(t) and that between Y_i(t) and N_i(t + 1). We specified all combinations for the sign of β₂ and η₁: (+, +); (−, −); (−, +); and (+, −). In each case, the biases incurred from aggregation and from endogeneity were in the opposite direction.

3.3. Summary

We explored the potential for bias when estimating the association between a non-aggregate specification for cumulative volume and patient outcomes if the recurrent marked point process assumptions are violated. We found that covariance-weighting methods may provide a biased estimate of the volume-outcome association if the assumptions are violated. We also explored the potential for bias when cumulative surgeon experience is specified using an aggregate volume measure. We found that an estimating equation estimator provides an unbiased estimate of the volume-outcome association when an aggregate measure of cumulative volume is used. However, every method may provide a biased estimate when an aggregate measure of contemporaneous volume is used. In addition, we explored the impact of endogeneity in the event-time process on estimation when using an aggregate measure of cumulative volume. We found that every method, including an independence estimation equation, may provide a biased estimate.

4. Application

According to the World Health Organization, lung cancer is the most common cause of cancer-related death in men, the second most common in women, and is responsible for 1.3 million deaths annually worldwide [31]. Early stage non-small cell lung cancer is optimally treated with pulmonary resection, for example, lobectomy (removal of a lobe of the lung) or segmentectomy (removal of an anatomic division of a particular lobe). We used the SEER-Medicare linked database (1992–2002) to explore the association between surgeon volume and 30-day patient mortality following lung resection. The database combines clinical information from population-based cancer registries in the USA with Medicare claims information [32]. Because the database excludes patients treated in a geographical region outside the SEER registry boundary and operated patients not insured by Medicare, SEER-Medicare volume is an undercount of the actual provider volume. For the purposes of illustration, we limited our focus to approaches to modeling provider volume and therefore ignored the effect of volume misclassification, which tends to bias the volume-outcome association toward the null [33].

4.1. Materials and methods

The outcome of interest was death from any cause within 30 days following resection. Information was available on resection date, patient demographic characteristics (gender, race, age, and Charlson comorbidity index), tumor characteristics (stage and histology), unique provider study number (surgeon and hospital), and provider characteristics (teaching hospital). Using the resection date and surgeon identifier, we calculated non-aggregate surgeon volume at each resection date, which quantifies cumulative experience. We also calculated aggregate specifications for surgeon volume: a running average and a total average volume, which quantify cumulative experience, and a yearly total and yearly average volume, which quantify contemporaneous experience.

To estimate the volume-outcome association, we modeled non-aggregate and aggregate surgeon volume as a continuous variable. We adjusted for gender, race, age (linear spline), Charlson comorbidity index, tumor stage and histology, indicator of teaching hospital, and yearly hospital volume (linear spline). We fit an IEE and a GEE assuming an exchangeable correlation structure. We also fit a GLMM with surgeon-specific random intercepts (GLMM-RI), a GLMM with surgeon-specific random intercepts and volume effects (GLMM-RS), and a hierarchical generalized linear model with surgeon-specific and hospital-specific random intercepts (HGLM). We completed all analyses by using R 2.8.0 [34].

4.2. Results

Following exclusion criteria described elsewhere [29], our data set consisted of 20,208 patients who underwent surgery by 1334 surgeons at 727 hospitals. The mean and median total surgeon volume (N.B., SEER-Medicare) were 11 and 3 patients, respectively. Approximately 5% of patients died within 30 days of surgery, a rate that was constant across the follow-up period. Figure 2 presents observed patient outcomes for three surgeons over the follow-up period. The surgeon in the top, middle, and bottom frame performed 10, 27, and 54 resections, respectively, over the study period that were captured by SEER-Medicare. For each surgeon, there appears to be an association between experience and patient mortality. Patients appear to be more likely to die if their surgeon is inexperienced. Although an aggregate measure of volume might classify these three surgeons differently, the apparent pattern in patient outcomes is similar across surgeons.

Figure 2.

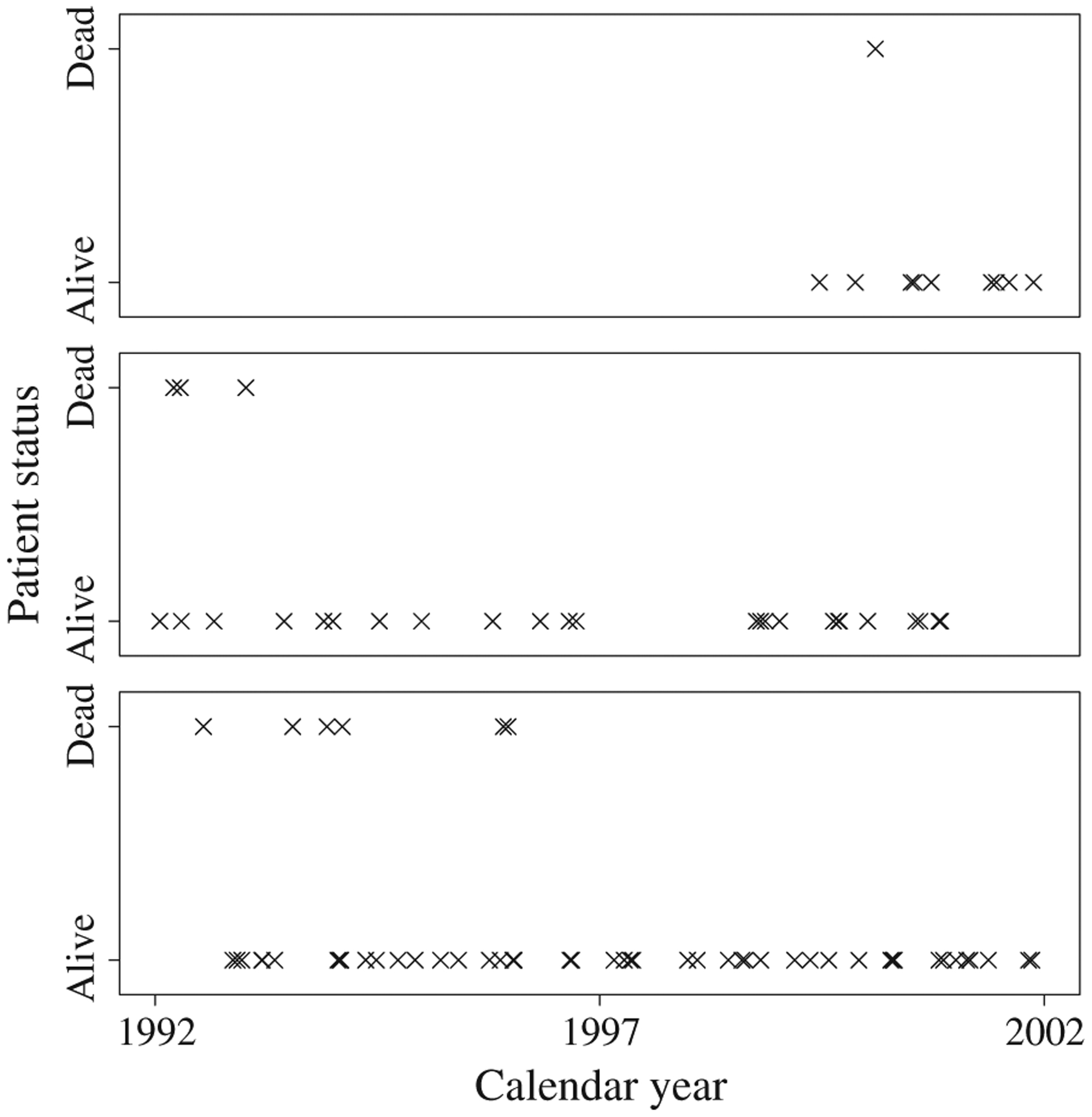
Observed patient outcomes for three surgeons from SEER-Medicare data.

4.2.1. Non-aggregate surgeon volume.

Table VI provides estimates of the odds ratio for 30-day patient mortality for non-aggregate surgeon volume. According to the IEE, a 10-patient increase in surgeon experience was associated with a −2.0% difference in the odds of 30-day patient mortality, 95% CI (−4.1%, +0.2%), which includes the null value of 0%. According to the GEE, a 10-patient increase in surgeon experience was associated with a −2.5% difference in the odds of 30-day patient mortality, 95% CI (−4.8%, −0.1%). These estimates quantified the effect of cumulative surgeon experience among a population of patients. According to the GLMM-RI, a 10-patient increase in surgeon experience was associated with a −2.6% difference in the odds of 30-day patient mortality, 95% CI (−5.0%, −0.2%). According to the GLMM-RS, a 10-patient increase in surgeon experience was associated with a −2.7% difference in the odds of 30-day patient mortality, 95% CI (−5.1%,−0.2%). These estimates quantified the effect of cumulative surgeon experience among a population of surgeons. According to the HGLM, a 10-patient increase in surgeon experience was associated with a −2.7% difference in the odds of 30-day patient mortality, 95% CI (−4.9%, −0.4%). This estimate quantified the effect of cumulative surgeon experience among a population of hospitals.

Table VI.

Estimated association between various specifications for surgeon volume and odds of 30-day patient mortality from SEER-Medicare data: odds ratio (OR) and 95% confidence interval (CI).

Volume specification	Method	OR	95% CI
Cumulative
Non-aggregate	IEE	0.980	(0.959, 1.002)
	GEE	0.975	(0.952, 0.999)
	GLMM-RI	0.974	(0.950, 0.998)
	GLMM-RS	0.973	(0.949, 0.998)
	HGLM	0.973	(0.951, 0.996)
Running average	IEE	0.980	(0.959, 1.001)
	GEE	0.974	(0.951, 0.998)
	GLMM-RI	0.974	(0.950, 0.998)
	GLMM-RS	0.973	(0.950, 0.998)
	HGLM	0.973	(0.950, 0.996)
Total average	IEE	0.980	(0.953, 1.008)
	GEE	0.970	(0.939, 1.002)
	GLMM-RI	0.967	(0.934, 1.002)
	HGLM	0.972	(0.944, 1.002)
Contemporaneous
Yearly total	IEE	0.935	(0.835, 1.046)
	GEE	0.916	(0.816, 1.028)
	GLMM-RI	0.917	(0.798, 1.053)
	GLMM-RS	0.933	(0.764, 1.139)
	HGLM	0.915	(0.806, 1.039)
Yearly average	IEE	0.897	(0.769, 1.047)
	GEE	0.845	(0.708, 1.009)
	GLMM-RI	0.834	(0.689, 1.010)
	HGLM	0.858	(0.729, 1.010)

Although the IEE is assured to provide a consistent estimator for the volume-outcome association, it may be preferable to generate inference by using a more efficient covariance-weighting method. This requires evaluation of the recurrent marked point process assumptions. To evaluate Assumption (1) we fit a Cox regression model, defining surgeons as clusters, for time between successive surgeries and adjusted for previous patient outcome. The estimated hazard rate ratio for a subsequent surgery associated with previous patient death was 1.014, 95% CI (0.945, 1.090). Thus, the hazard of a subsequent surgery among surgeons with a previous patient death were 1.4% higher than that among surgeons without a previous patient death, although this difference was not statistically significant (p = 0.710). Therefore, there was no evidence to suggest that Assumption (1) is violated.

Evaluating Assumption (2) is difficult in this application because six of the nine adjustment variables are patient specific and hence time dependent. However, our simulation results revealed that violation of Assumption (2) did not negatively impact estimation of the volume-outcome association if Assumption (1) is satisfied. Given that Assumption (1) appears to be satisfied, it may not be necessary to satisfy Assumption (2) in this application.

4.2.2. Aggregate surgeon volume.

Table VI also provides estimates for each aggregate volume measure: running average, total average, yearly total, and yearly average. The estimates obtained using a running average and total average specification for cumulative volume were similar to those obtained using non-aggregate volume with respect to effect size. However, unlike those obtained using non-aggregate volume, none of the differences obtained using a total average were statistically significant. The estimates obtained using a yearly total or yearly average specification revealed that an increase in contemporaneous surgeon experience was associated with a weak but non-significant decrease in the odds of 30-day patient mortality. For each estimation method, the estimated effect of contemporaneous experience was larger than the effect of cumulative experience. We obtained the largest association by using a yearly average specification for volume. However, none of these associations were statistically significant.

4.3. Summary

We used SEER-Medicare data to explore the association between surgeon volume and 30-day patient mortality following lung resection. Covariance-weighted methods revealed that cumulative surgeon experience as measured by non-aggregate surgeon volume was associated with a significant decrease in the risk of patient mortality following lung resection. Use of these methods required verification of recurrent marked point process assumption (1). There was no evidence to suggest that Assumption (1) was violated. A running average and total average specification for cumulative surgeon volume provided results similar to those obtained using non-aggregate surgeon volume. Contemporaneous surgeon experience as quantified by a yearly total or yearly average volume was not significantly associated with the risk of patient mortality.

5. Discussion

In this paper, we established the recurrent marked point process as a general framework from which to approach a longitudinal volume-outcome analysis. The recurrent marked point process framework motivates specific assumptions regarding the exposure and event-time processes to ensure that GEEs and GLMMs provide valid estimates of the volume-outcome association. We provided theoretical and empirical evidence that bias may be introduced when an aggregate volume measure is used to address a scientific question regarding the effect of cumulative surgeon experience. In our application, we found that spurious results may be obtained when surgeon volume is specified using an aggregate measure and the effect of cumulative surgeon volume is of primary interest.

Researchers interested in ‘informative’ cluster size suggest that a weighted estimating equation must be used to estimate the effect of exposure when cluster size is related to the outcome of interest [12–14, 16, 18]. We suggest that an unweighted estimating equation may be used to estimate a volume-outcome association. This contrast is due to an important difference between our setting and that of other researchers. These researchers defined cluster size as ‘ignorable’ if E[Y_i(t) | N_i(T), X_i(t)] = E[Y_i(t) | X_i(t)] and viewed cluster size as a nuisance variable. In their simulation studies, they generated cluster size by imposing a negative relationship between cluster size and a cluster-specific baseline risk, that is, a cluster-specific random intercept. Conversely, in a volume-outcome study, the expectation of Y_i(t) given N_i(t) is the target of inference and cluster size is the exposure of interest. In this case, cluster weighting may be problematic because N_i(t) would appear in μ_i(t) and in the cluster weights. We have addressed the ‘informative’ cluster size issue via an assumption regarding the endogeneity between past outcomes and occurrence of a subsequent event. Evaluation of Assumption (1) explicitly allows analysts to explore a mechanism for ‘informative’ cluster size, secondary to the volume-outcome association of interest.

We provided theoretical and empirical evidence that substantial bias may be incurred from selecting a volume measure that may be incongruous with the scientific question of interest. We focused on cumulative surgeon volume to capture the learning effect within a surgeon. The effect of contemporaneous volume may also be of interest to capture cross-sectional differences across surgeons based on their current practice. Recall the two hypothetical surgeons who both accumulated 100 patients during their career. The first surgeon achieved this experience in 5 years, whereas the second surgeon achieved this experience in 20 years. It is plausible that patient outcomes will improve over time for both surgeons. However, it is also plausible that patient outcomes may be relatively better for the first surgeon due to economy of scale; the first surgeon may be more likely to invest in equipment and staff to accommodate the larger number of patients treated per year. Establishment of the volume-outcome association for cumulative volume may suggest more investments in surgeon training to improve patient outcomes. Establishment of the association for contemporaneous volume may suggest more investment in infrastructure. It is possible that both effects are present and that both interventions are necessary to improve the overall quality of patient care.

In applications, both effects may be explored by including measures of cumulative and contemporaneous volume in the fitted mean model:

$$g\left[{\mu }_i\left(t\right)\right]={\beta }_0+{\beta }_1{X}_i\left(t\right)+{\beta }_2\underset{\text{Cumulative }}{\underbrace{N_i\left(T_{j-1}\right)}}+{\beta }_3\underset{\text{Contemporaneous }}{\underbrace{\left[N_i\left(t\right)-N_i\left(T_{j-1}\right)\right]}}.$$ (17)

We considered the model presented in Equation (17) in our application. According to an IEE, the odds ratios associated with a 10-patient increase in cumulative and contemporaneous surgeon volume were 1.002, 95% CI (0.815, 1.233) and 0.978, 95% CI (0.955, 1.003), respectively. According to a GEE, with an exchangeable correlation structure, the odds ratios associated with a 10-patient increase in cumulative and contemporaneous surgeon volume were 0.985, 95% CI (0.800, 1.213) and 0.974, 95% CI (0.948, 1.002), respectively. These results are similar to those obtained via separate models (Table VI). In practice, it may be difficult to separate the effects of cumulative and contemporaneous volume; collinearity may result in wide confidence intervals.

It may also be of interest to test for an interaction between N_i(T_{j − 1}) and N_i(t) − N_i(T_{j − 1}) to ascertain, for example, whether the effect of contemporaneous experience differs between surgeons with different levels of cumulative experience. We also considered this model in our application and found a positive interaction between cumulative and contemporaneous surgeon experience with respect to risk of 30-day mortality. For example, according to an IEE, a 10-patient increase in contemporaneous experience for a surgeon with a cumulative experience of 10 patients was associated with a −6.6% difference in the odds of 30-day patient mortality, 95% CI (−28%, +21%), whereas a 10-patient increase in contemporaneous experience for a surgeon with a cumulative experience of 40 patients was associated with a −3.7% difference in the odds of 30-day patient mortality, 95% CI (−24%, +22%).These results indicate that recent surgeon experience was more beneficial to patients treated by surgeons with less total experience. It may be difficult to identify interaction effects due to collinearity that may result in wide confidence intervals. However, both IEE and GEE indicate the possibility of an interaction between cumulative and contemporaneous experience (p = 0.054 and p = 0.043, respectively).

For the purposes of illustration, we only considered a linear term for cumulative surgeon volume in our application. However, there was evidence that the relationship between cumulative volume and 30-day patient mortality was non-linear. For example, in an IEE, a quadratic term for cumulative volume revealed a small but highly significant non-linear association (p = 0:013). Analysts must carefully specify the correct functional form for the volume measure they select [23]. There is a large amount of literature that urges caution when categorizing a continuous variable [35], which is a strategy frequently employed with provider volume.

An important limitation of our application, and of volume-outcome analyses in general, is the lack of information regarding surgeon volume prior to the start of follow-up, that is, previous experience. In our application, we assumed that surgeon volume was zero at the start of follow-up and effectively ignored any previous surgeon experience. Therefore, non-aggregate surgeon volume may not accurately represent cumulative surgeon experience, which may lead to improper estimation of the volume-outcome association. We recommend that analysts consider this important limitation to their volume-outcome analyses.

Analysis choices are often limited by the type or amount of information available to the analyst. In our application, we used the resection date and unique surgeon study number to calculate non-aggregate surgeon volume at each resection date. The information required to calculate non-aggregate surgeon volume is usually available for a volume-outcome analysis because volume-outcome data are typically collected using an administrative database. However, if specific dates are not available and only an aggregate volume measure is available, such as the total number of surgeries performed in a calendar year, then we recommend using a running average specification that includes cumulative volume through the previous year. In our simulation study and in our application, the running average specification provided a satisfactory approximation to non-aggregate surgeon volume and properly estimated the effect of cumulative surgeon experience.