Incorporating Longitudinal Biomarkers for Dynamic Risk Prediction in the Era of Big Data: A Pseudo-Observation Approach

Abstract

Longitudinal biomarker data are often collected in studies, providing important information regarding the probability of an outcome of interest occurring at a future time. With many new and evolving technologies for biomarker discovery, the number of biomarker measurements available for analysis of disease progression has increased dramatically. A large amount of data provides a more complete picture of a patient’s disease progression, potentially allowing us to make more accurate and reliable predictions, but the magnitude of available data introduces challenges to most statistical analysts. Existing approaches suffer immensely from the curse of dimensionality. In this paper we propose methods for making dynamic risk predictions using repeatedly measured biomarkers of a large dimension, including cases when the number of biomarkers is close to the sample size. The proposed methods are computationally simple, yet sufficiently flexible to capture complex relationships between longitudinal biomarkers and potentially censored events times. The proposed approaches are evaluated by extensive simulation studies and are further illustrated by an application to a dataset from the Nephrotic Syndrome Study Network.

1 |. INTRODUCTION

A key question in clinical practice is accurate prediction of patient prognosis. To this end, studies are increasingly measuring biomarkers repeatedly over time in order to dynamically update estimated survival probabilities. Improved information on prognosis aids in patient management, such as adjusting patient follow-up schedules, or prescribing appropriate medications. Commonly used approaches for dynamic risk predictions include 1) joint modelling (JM) of longitudinal and time-to-event data [1, 2, 3, 4, 5], and 2) landmarking [6, 7].

A JM approach requires specifying a complete joint distribution of the longitudinal response and the event times. For the longitudinal biomarker measurements, generalized linear mixed models are typically employed to describe the subject-specific longitudinal trajectories. Features of the estimated biomarker trajectories are then incorporated as time-varying covariates in a Cox regression model. In these approaches, calculation of predicted risk involves complicated integration over the marker processes. The computational burden of estimation increases exponentially with the dimensionality (p) of the biomarker data, which limits the JM approaches to studies with p < 5 longitudinal biomarker measurements [8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. As an alternative to the JM approach, a landmarking approach directly fits a Cox proportional hazards model to individuals still at risk at the landmark point. This technique is easy to apply in practice and can accommodate more longitudinal biomarkers than the JM approach, but still requires p ≪ n. For both JM and landmarking approaches, accurate predictions rely on correct specification of the functional forms linking biomarkers to the survival outcome.

As new technologies (e.g., genomics, proteomics, and metabolomics) have become available, studies are increasingly generating large numbers of biomarkers measured over time to study disease progression. This large amount of data provides a more complete picture of each patient’s physiologic reserve, but it also dramatically increases the difficulty of statistical modeling. In addition to the curse of dimensionality of the biomarkers, the relationship between biomakers and event times may be very complex, for example, (1) only a set of biomarkers are predictive for the event of interest (a variable selection problem), (2) some of the predictive biomarkers have non-linear effects and/or (3) interactions exist between some of the predictive biomarkers and measurement time. These settings offer substantial challenges for JM and landmarking approaches to biomarker discovery and dynamic risk prediction. The goal of this article is to provide simple and flexible tools for dynamically predicting risk when the number of longitudinal biomarkers is large and statistical relationships between biomarkers and risk are potentially complex.

Recently, [20] proposed partly conditional survival (PC) models to predict whether an event occurs in the next τ time units given covariate information and survival up to time s. Unlike the landmarking approach in [6, 7], the PC models reset the time origin to s and covariates at time s are regarded as baseline measures. They then model residual lifetime from s using a Cox proportional hazards regression model (PC_Cox) or a generalized linear model (PC_GLM). In PC_GLM, an individual’s residual survival time from s is dichotomized into a binary outcome depending on whether the residual survival time is larger or smaller than τ; an inverse censoring probability weighted method is used to correct for bias due to censoring prior to observing τ units of follow-up after time s. As shown in [20], both PC_Cox and PC_GLM have comparative performance to JM approaches, but have much simper computational steps at model fitting and risk prediction stages.

In this article we borrow ideas from the PC framework in [20] and develop a jackknife pseudo-observation approach to accommodate the censored nature of the data. The pseudo observations approach [21, 22, 23] provides an efficient and straightforward way to study the relationship between a survival outcome and covariates in the presence of censoring. It replaces censored survival outcomes by pseudo observations and reduces the complex survival analysis to a regression problem with numeric outcomes. Then standard regression techniques can be used. In this article we consider two analysis approaches applied to the regression problem 1) a generalized estimation equation analysis (GEE) [24] and 2) a random forest.

The rest of the article is organized as follows. In section 2 we introduce notation and develop our proposed methods. In section 3 we present simulation studies. In section 4 we illustrate our methods in an analysis of data from the Nephrotic Syndrome Study Network (NEPTUNE). Concluding remarks are given in Section 5.

2 |. PROPOSED RISK PREDICTION MODELS

2.1 |. Notation and data structure

Let T_i be the survival time and C_i be the independent censoring time for subject i, i = 1,…, n. We observe X_i = min(T_i, C_i) with censoring indicator, d_i = I (T_i ≤ C_i). For covariates, we use Z_i to denote the p-dimensional vector of time-invariant covariates for subject i and Y_i (s_ij) to denote the q-dimensional vector of time-varying biomarkers measured at time 0 ≤ s_ij ≤ X_i, i = 1,…, n; j = 1,…, m_i. For convenience, we denote the vector of longitudinal biomarker measurement times for subject i using ${\text{s}}_{i1}=\left\{s_{i1}=0,s_{i2},\cdots ,s_{i{m}_i}\right\}$ and let ${\tilde{Y}}_i=\left\{Y_i\left(s_{i1}\right),\cdots ,Y_i\left(s_{i{m}_i}\right)\right\}$. Unless subscripts on measurement times are needed for clarity, we will typically drop them to ease notational burden, simplifying this notation to s.

The pseudo-observations approach [21, 22, 23] provides an efficient way to study the relationship between a survival outcome and time-invariant covariates in the presence of censoring. To adapt the pseudo-observation approach to the dynamic prediction method where covariates are measured repeatedly over time, we treat each covariate measurement time, s, as a landmark time with X* = X − s denoting the remaining survival time from the landmark time. Table 1 shows a simple example of how to build a “stacked” dataset for three subjects with covariates measured every 6 months until the subject is removed from the study due to censoring or event occurrence. Subjects 1 and 2 experience events at 26 and 15 months, respectively, and subject 3 is censored at 10 months. Each survival time is converted into a sequence of remaining survival times from the landmark time points and then stacked along with the corresponding covariates into a single dataset. Table 1 also includes placeholders for pseudo survival probabilities that will be included in the stacked dataset. We introduce pseudo survival probabilities in Section 2.2.

TABLE 1.

A stacked dataset for 3 hypothetical subjects. Subject 1 dies at 26 months; subject 2 dies at 15 months and subject 3 is censored at 10 months. Here, s denotes landmark time, X* = X − s denotes the remaining survival time; δ is the censoring indicator for the remaining survival time; ${\widehat{S}}^{\tau }$ is the pseudo survival probability at τ months; Z is the time-constant covariate; Y is the time-varying covariate. Additional columns can be added for more covariates.

ID	s	X*	δ	${\widehat{S}}^{\tau }$	Z	Y
1	0	26	1	${\widehat{S}}_1^{\tau }(0)$	23	1.5
1	6	20	1	${\widehat{S}}_1^{\tau }(6)$	23	2.5
1	12	14	1	${\widehat{S}}_1^{\tau }(12)$	23	1.2
1	18	8	1	${\widehat{S}}_1^{\tau }(18)$	23	4.3
1	24	2	1	${\widehat{S}}_1^{\tau }(24)$	23	5.2
2	0	15	1	${\widehat{S}}_2^{\tau }(0)$	30	4.5
2	6	9	1	${\widehat{S}}_2^{\tau }(6)$	30	5.5
2	12	3	1	${\widehat{S}}_2^{\tau }(12)$	30	5.2
3	0	10	0	${\widehat{S}}_3^{\tau }(0)$	16	3.5
3	6	4	0	${\widehat{S}}_3^{\tau }(6)$	16	3.9

2.2 |. Dynamically computed pseudo probabilities

Suppose we are interested in dynamically estimating the probability of surviving τ units of time. That is, given a subject is alive at time s, we wish to estimate P (X* > τ|X > s), where X* = X − s is the remaining survival time from some landmark time, s. If there were no censored data, binary indicators I (X* > τ|X > s) would be observed for all subjects and landmark times, s, within subject. Hence, standard methods for modeling correlated binary endpoints, say generalized estimating equations, could be used to model P (X*> τ|X > s) in terms of Z and Y. However, these binary outcomes would not necessarily be observed for all landmark times when a subject is censored. Subject 3 in Table 1 is censored at 10 months, and hence does not have an observed value for I (X* > 12|X > s) for either of the two contributed rows of data from this subject that correspond to landmark times, s = 0 and s = 6 months. This (partially) missing data disrupts our ability to model correlated binary outcomes using standard software.

Our approach to handling the censored nature of the data is based on a jackknife method that has become popular in censored survival analysis literature for the analysis of restricted means [21, 22, 23]. We borrow similar ideas to construct pseudo survival probabilities that correspond to the correlated binary outcomes desired for dynamic risk prediction. Ultimately these pseudo survival probabilities, denoted by ${\widehat{S}}^{\tau }$ in Table 1, replace each of the binary indicators (observed and unobserved), as quantitative outcomes for analysis. Details of the pseudo probability calculations follow.

• Step 1.

  For a particular landmark time s, estimate P (X* > τ|X > s), using the (conditional) Kaplan-Meier survival estimate calculated using only those subjects remaining at risk at time s. Set aside the resulting survival estimate at time τ from this curve with label, ${\widehat{S}}^{\tau }(s)$.

• Step 2.

  For each subject i still at risk at time s, repeat this calculation without using subject i’s data. Hence, each subject will have a survival estimate for P (X* > τ|X > s) that specifically excludes them, labeled ${\widehat{S}}_{-i}^{\tau }(s)$.

• Step 3.
  For each subject i, the pseudo probability corresponding to surviving τ units from landmark time s becomes

  $${\widehat{S}}_i^{\tau }(s)=\tilde{n}{\widehat{S}}^{\tau }(s)-(\tilde{n}-1){\widehat{S}}_{-i}^{\tau }(s),$$ (1)

  where ñ is the number of subjects still at risk at time s.
• Step 4.

  Repeat steps 1–3 for each landmark time s.

• Step 5.

  The resulting calculated pseudo probabilities are formatted as the outcomes for analysis, following the example given in Table 1.

It is important to note that pseudo probabilities for patients at risk at landmark time s should be calculated and used in the analysis, regardless of whether or not I (X* > τ|X > s) was observable for the subject at landmark time s. However, as seen in the example given in Table 1, subjects not at risk at a particular landmark time do not contribute a pseudo probability for that time. The pseudo probability calculation in Step 1–4 also applies to studies with uncommon landmark times. In this case, the common landmark time s will be replaced by s_ij for subject i at the j^th time point. In sections 2.3 and 2.4 we describe two dynamic prediction modeling paradigms using the pseudo probabilities, ${\widehat{S}}^{\tau }$ in Table 1, as outcomes, and using Z, Y, and time s as predictor variables. For the GEE modeling paradigm described in sections 2.3, we assume common landmark times, as GEE requires a correlation matrix for the within-subject pseudo probabilities. This assumption is easily weakened for the random forest approach described in section 2.4.

2.3 |. Pseudo probability generalized estimating equation model

We first consider a generalized estimating equation (GEE) approach for dynamically estimating the probability of surviving τ subsequent time units. As mentioned in the introduction, dynamic prediction regression models are typically unstable unless the number of dynamic predictors incorporated in the model is small, say less than 5. The dynamic pseudo probability GEE regression model we consider takes the form

$$g\left[{\widehat{S}}_i^{\tau }\left(s_{ij}\right)\right]=\alpha B\left(s_{ij}\right)+\beta Z_i+\gamma Y_i\left(s_{ij}\right),i=1,\cdots ,n,j=1,\dots ,m_i,$$ (2)

where s_ij, j = 1,…, m_i are landmark times for individual i, B(s_ij) is a spline base function that captures nonlinear effects attributed to the landmark times and g(·) is a link function. If g(·) corresponds to a logit link function, the estimated dynamic probability of living at least τ subsequent time units is constrained to be between 0 and 1. Many statistical packages are available for fitting Model (2) using GEE methodology and obtaining estimates, $\widehat{\theta }$, of θ = (α, β, γ). In sections 3.1 and 4, we use the geese function from the geepack R package [25]. Use of this package requires specification of a working correlation matrix for the within-subject correlation between outcome measures (pseudo probabilities); we have used the default independence working correlation matrix throughout this manuscript. In performing inference on model parameters, sandwich methods for estimation of $Cov(\widehat{\theta })$ are typically employed that are robust to misspecification of the working correlation matrix. The geese package offers an approximate jackknife estimate, $\widehat{Cov}(\widehat{\theta })$, for $Cov(\widehat{\theta })$ [26, 27] that we have used in simulation and examples that follow.

Dynamic estimates for the probability of surviving τ time units can be quickly derived from the results of the GEE fit to model (2). For a new patient with H_o (s) = {B(s), Z_o, Y_o (s)}, the predicted probability of surviving the next τ time units is $g^{-1}\left({\widehat{\theta }}^T{H}_o\right)=\frac{\mathit{\text{exp}}\left({\widehat{\theta }}^T{H}_o\right)}{1+\mathit{\text{exp}}\left({\widehat{\theta }}^T{H}_o\right)}$ with estimated variance, $J\widehat{Cov}(\widehat{\theta }){\text{J}}^T$, obtained using the delta method, where J is the estimated Jacobian matrix of g⁻¹ (θ^T H_o). In particular, if using a logit link in Model (2),

$$J=\frac{\mathit{\text{exp}}\left(-{\widehat{\theta }}^T{H}_o\right)}{{\left(1+\mathit{\text{exp}}\left(-{\widehat{\theta }}^T{H}_o\right)\right)}^2}{H}_o$$

We refer to this approach as GEE.pseudo in the rest of the paper.

2.4 |. Pseudo-based random forest

Random forest (RF) methodology [28] has gained popularity in big data applications since (1) it is able to incorporate high dimensional biomarkers into estimated predictions, (2) it is not necessary to prespecify functional forms of biomarkers when using the algorithm, (3) interactions between biomarker processes are automatically embedded into predictions and (4) software is available for implementing these algorithms in the case of a single outcome (randomForest function from randomForest R package [28, 29]) or correlated outcomes (hrf function from htree R package [30, 31]). To our knowledge, RF methodology has not been applied to pseudo probabilities outcomes described in section 2.2 for dynamic prediction of censored survival outcomes. Because pseudo probabilities are correlated within individual, the hrf function from the htree package provides an RF algorithm suitable for our purposes. Importantly, RF methods for correlated data allow us to utilize information from substantially more dynamically measured predictors that the GEE method of section 2.3.

For those who are not well versed in RF terminology, we give a very brief primer to assist in understanding how to use the htree package to make dynamic predictions based on correlated pseudo probability outcomes. More advanced users of random forest methods may choose to skip ahead to section 2.4.2. Notation for the pseudo probability response variable and predictor variables in what follows is unchanged from section 2.3.

For simplicity, our primer first describes the special case with a single pseudo probability outcome contributed per subject (section 2.4.1) and the RF algorithm [28] that is the basis of the R package randomForest. We then describe how the hrf function in the htree package handles dependent outcomes, in our case pseudo probabilities contributed from the same subject, in section 2.4.2.

2.4.1 |. Random forest with single pseudo probability

Suppose for each of our n subjects we consider only the first pseudo probability, ${\widehat{S}}_i^{\tau }(0)$, as our outcome. The data from subject i, $i,\left[Z_i,{\widehat{S}}_i^{\tau }(0)\right]$, is referred to as a training sample in RF jargon, and our data consists of n training samples, $\left\{\left[Z_1,{\widehat{S}}_1^{\tau }(0)\right],\dots ,\left[Z_n,{\widehat{S}}_n^{\tau }(0)\right]\right\}$.

• Step 1.

  Draw a bootstrap sample of size n. I.e., randomly sample data pairs $\left[Z_i,{\widehat{S}}_i^{\tau }(0)\right]$, with replacement, from the i = 1,…, n subjects until the bootstrap sample is also of size n. In RF jargon, unique subjects who are represented in the bootstrap sample are called bagged, or collectively, the bagged sample. Subjects who do not make it into the bootstrap sample are called out of bag, or collectively, the out of bag sample.

• Step 2.
  For each bootstrap sample, a binary decision tree is built. An example binary decision tree is given in Figure 1. Each node in the tree reflects a decision point for traveling down the binary decision tree. The top node is often called the root node. Any node in the tree may become a parent node by splitting into two daughter nodes or become a terminal node, also called a leaf node. The number of terminal nodes in the tree is denoted by K, with Figure 1 showing a tree with K = 3. Each terminal node captures a partition, R_k of the data, k = 1,…, K. For example, in Figure 1, the first partition R₁ includes all black subjects with albumin < 3.8. The randomForest package has two parameters that influence whether a node splits or becomes terminal, the nodesize parameter and the maxnodes parameter. The nodesize parameter specifies the minimum number of individuals from the bootstrap sample that a terminal node must capture; the default is 5. The maxnodes parameter specifies the maximum number of terminal nodes allowed in the tree; if left unspecified, nodes continue to split until nodesize restrictions define the node as terminal. For parent nodes that split into daughter nodes, the process for defining the best split follows steps (a) through (c) below. Interestingly, rather than using all available predictors to choose the best split, an independently sampled subset of predictors is considered at each node, which improves processing speed considerably.

  1. Select a random subset of predictors, Z*, from Z. In the randomForest package, the default number of predictors in Z* is the number of predictors in Z divided by three (rounded down), which can be changed via the mtry parameter.
     The function, tuneRF, can be used to treat the number of sampled predictors in Z* as a tuning parameter, however, we have found reasonable operating characteristics using the default choice. The randomly selected predictors from this step are called input variables in RF jargon.
  2. Predictors (input variables) selected in step (a) are converted into binary variables that may or may not be used as daughter nodes of the node under consideration for a split. Dichotomous predictors are already in a suitable format for splitting into daughter nodes. For categorical predictors with I categories, the randomForest package dichotomizes the predictor by randomly splitting the I categories into two groups. This split varies across bootstrap samples of the original data (step 1 of algorithm). For each continuous or ordinal predictor, all possible thresholds from the observed data are considered for splitting individuals into low versus high valued groups. The resulting binary predictors that are generated from a single continuous/ordinal predictor are called split variables of that predictor. All binary variables defined in this step are compared for the best split from the parent node into daughter nodes.
  3. The best daughter nodes (or split) from a parent node under consideration is chosen from binary variables defined in step (b). Parent node selection borrows ideas from forward stepwise linear regression algorithms, in that the most favorable split is added to the existing tree based on further minimizing the sum of squared errors between observed and predicted outcomes in the data until each either the maxnode restriction is met or the nodesize restriction is met for all current terminal nodes of the tree.
     In our setting, for each node, k, the predicted outcome is the average of individual pseudo probabilities in the corresponding partition of the data, R_k. That is, define $n_R{}_{{}_k}$ to be the number of subjects in partition R_k. Then the predicted outcome for partition R_k is ${\overline{{\widehat{S}}^{\tau }(0)}}_{R_k}=\frac{1}{n_{R_k}}{\sum }_{i\in R_k}{\widehat{S}}_i^{\tau }\left(0\right)$ and sum of squared errors in partition k is $SS{E}_k={\sum }_{i\in R_k}{\left({\widehat{S}}_i^{\tau }(0)-{\overline{{\widehat{S}}^{\tau }(0)}}_{R_k}\right)}^2$. If nodesize and maxnode restrictions have not been met, and a further split for node k into daughter nodes k₁ and k₂ is possible, then the chosen split variable for node k minimizes SSE_k1 +SSE_k2. One node at a time is added to the existing tree such that after comparing all possible splits from all possible nodes, the overall SSE is minimized, where for K terminal nodes,

     $$SSE=\sum _{k=1}^K\sum _{i\in R_k}{\left({\widehat{S}}_i^{\tau }(0)-{\overline{{\widehat{S}}^{\tau }(0)}}_{R_k}\right)}^2,$$

     The tree is grown to the maximum size (i.e., until no further splits are possible for any of the terminal nodes) and not pruned back. This algorithm is sometimes described as a greedy recursive binary splitting algorithm.
• 3.
  Repeat step 1 (bootstrap step) and step 2 (tree growing step) until B decision trees are available; the RandomForest package default is B = 500 trees. Each of the b = 1,…, B trees have their own number of terminal nodes K_b, with corresponding partitions, R_bk, k = 1.…, K_b and τ-year survival probability estimates, ${\overline{{\widehat{S}}^{\tau }(0)}}_{R_{bk}}$, that apply to individuals who traverse the b^th tree and land in partition, R_bk. Define ${\overline{{\widehat{S}}^{\tau }(0)}}_{R_{b{k}_i}}$ as the estimated τ-year survival probability for individual i based upon traversing through the b^th decision tree and landing in partition $R_{b{k}_i}$ of that tree. Individual i’s final estimated τ-year survival probability aggregated across the B trees is

  $${\tilde{S}}_i^{\tau }(0)=\sum _{b=1}^B{\overline{{\widehat{S}}^{\tau }(0)}}_{R_{b{k}_i}},$$

  which we also call the fitted random forest model prediction for subject i.

FIGURE 1.

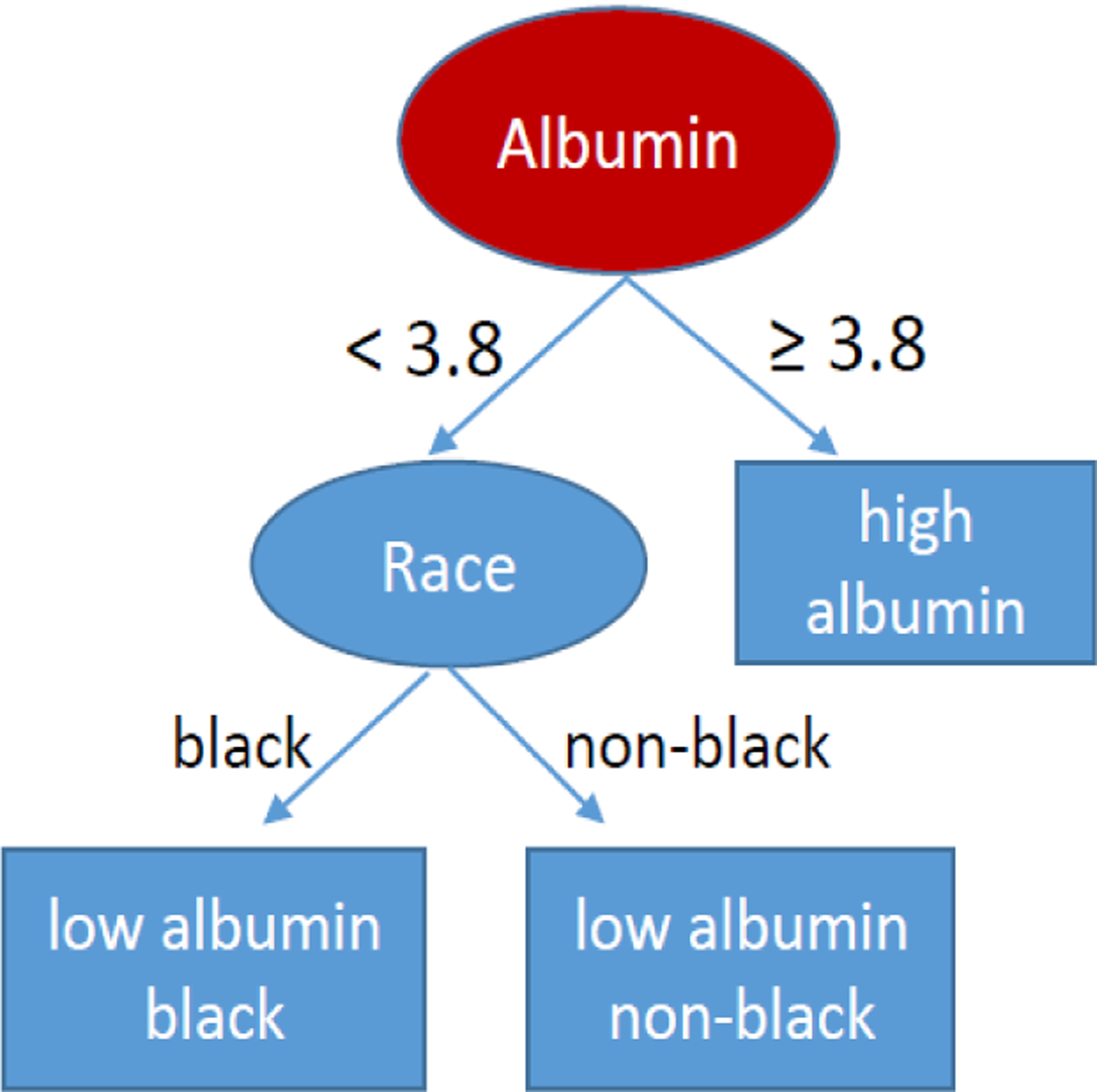
An example of a decision tree. The red circle is the root node. Ovals reflect parent nodes and rectangles reflect terminal (leaf) nodes.

2.4.2 |. Random forest with multiple correlated pseudo probabilities per individual

In the more general case, data from individual i is collected at timepoints s_ij, j = 1,…, m_i. Hence at time s_ij, subject i has time-varying biomarkers, Y_i (s_ij), time invariant predictors, Z_i, and pseudo probability outcome, ${\widehat{S}}_i^{\tau }\left(s_{ij}\right)$. An algorithm proposed by [32] modifies the bootstrap step (Step 1) from section 2.4.1 so that when individual i is sampled, only data $\left\{{\widehat{S}}_i^{\tau }\left(s_{ij}\right),Z_i,Y_i\left(s_{ij}\right)\right\}$ from a randomly selected measurement time s_ij is included in the bootstrap sample. Steps 2 (tree growing step) and 3 (aggregating estimates across trees), as described in section 2.4.1, remain unchanged. We refer to this approach as the RF.pseudo method is the rest of the manuscript.

The [32] approach for handling dependent outcomes has several strong advantages: (1) It restructures the data so that the randomForest package can be applied, which is elegant from a programming point of view. (2) Resampling of the data allows information from the dependent outcomes to be incorporated into predictions, as desired. (3) Technical proofs of consistency given in the original article by [28] that draw on theorems for independently distributed outcomes are able to be employed without further justification. And (4) Individuals with large numbers of measures, m_i, are not allowed to unduly dominate the algorithm at the expense of those with small numbers of measures.

One disadvantage of random forest methods, compared to more standard regression methods, is that the model underlying predictions cannot be written in terms of easily interpreted parameter estimates as in equation 2. And although we advocate open source code for fitted random forest models, few practitioners will be able to read and interpret the code, making it a bit of a black box approach for dynamic predictions.

One attempt to demystify fitted random forest models is to report variable importance summary statistics from a fitted random forest model. In the htree package, variable importance estimates for predictors (input variables) are calculated via the varimp_hrf function. The general idea is to compare model performance with and without the input variable under investigation. Of course predictions based on traversing trees in the fitted random forest model require all input variables to be specified. Hence, when calculating model performance without the input variable of interest, a random permutation of the observed input variables is reassigned to the training samples, eliminating any association between the predictor of interest and the training sample. It is common to randomly re-permute the input variable several times and average the corresponding model performance results; the nperm parameter for the varimp.hrf function defaults to 20 permutations of this nature.

Out of bag subjects feature prominently in estimating variable importance metrics. To briefly summarize how variable importance is calculated, consider the out of bag sample corresponding to the b^th (modified) bootstrap sample, recalling that these ℓ = 1,…, n_b out of bag subjects were those subjects not used to build the b^th decision tree. For out of bag subject ℓ, data from measurement time s_ℓj is $\left\{{\widehat{S}}_{\mathcal{l}}^{\tau }\left(s_{\mathcal{l}j}\right),Z_{\mathcal{l}},Y_{\mathcal{l}}\left(s_{\mathcal{l}j}\right)\right\}$, ℓ = 1,…, n_b,j = 1,…, m_ℓ, and the estimated τ-year survival probability for individual ℓ at time s_ℓj based upon traversing the b^th decision tree and landing in partition $R_{b{k}_i}$ is ${\overline{{\widehat{S}}^{\tau }\left(s_{\mathcal{l}j}\right)}}_{R_{b{k}_{\mathcal{l}}}}$. For the b^th decision tree, model fit in the out of bag sample is characterized by

$$MS{E}_b(Z)=\sum _{\mathcal{l}=1}^{n_b}\frac{1}{m_{\mathcal{l}}}\sum _{j=1}^{m_{\mathcal{l}}}{\left({\widehat{S}}_{\mathcal{l}}^{\tau }\left(s_{\mathcal{l}j}\right)-{\overline{{\widehat{S}}^{\tau }\left(s_{\mathcal{l}j}\right)}}_{R_{b{k}_{\mathcal{l}}}}\right)}^2,$$

where the summand is the average mean squared error seen for individual ℓ across follow-up windows, j = 1,…, m_ℓ. Denote $MS{E}_b(\tilde{Z})$ the value of MSE_b when the input variable of interest has been randomly permuted as described above, altering the estimated τ-year survival probabilities for individual ℓ at each time s_ℓj in the formula. The importance of the input variable under consideration is calculated as

$$\frac{{\sum }_{b=1}^B\left[MS{E}_b(\tilde{Z})-MS{E}_b(Z)\right]}{{\sum }_{b=1}^{B}MS{E}_b(Z)},$$

which measures the relative increase in MSE_b (Z) due to permuting the input variable under consideration. The htree package reports the percent increase in MSE (%IncMSE) based on this calculation, with larger values indicating more importance of the predictor. [33] noted that importance measures are able to assess the impact of an input variable in dynamic random forest predictions despite potentially complex functional relationships between the outcome and other predictors, a metric that is unavailable from more traditional regression models.

3 |. SIMULATIONS STUDIES

The proposed methods are evaluated in a variety of settings where three longitudinally measured biomarkers influence mortality. We will describe the latent biomarker processes, models and results momentarily. In each scenario, separate training and validation data sets are generated, with each including n = 200 subjects. The training data set is used to build a τ = 6-month dynamic risk prediction tool based on the existing PC_GLM method as well as the proposed GEE.pseudo and RF.pseudo methods described in this manuscript. Each generated validation subject’s follow-up windows are then filtered through the proposed algorithms to predict the probability of being event-free at time s + 6 given observed biomarker data up to time s. Performance of dynamic prediction algorithms in the validation data is summarized across 500 simulated iterations.

Latent non-linear continuous-time biomarker processes feature prominently in the simulations. Let N (a, b) and LN(a, b) denote the normal and lognormal distributions, respectively, with mean a and standard deviation b. For each individual i, i = 1,…, n, three true correlated latent biomarker processes follow

$$W_{1i}(t)={\alpha }_{1i}+{\gamma }_{i}t,W_{2i}(t)={\alpha }_{2i}+K_{L_{2i}}t+\frac{K_{D_{2i}}}{{\eta }_{2i}}\left(e^{-{\eta }_{2i}t}-1\right)\text{ and }{W}_{3i}(t)=I\left({\alpha }_{3i}+K_{L_{3i}}t+\frac{K_{D_{3i}}}{{\eta }_{3i}}\left(e^{-{\eta }_{3i}t}-1\right)>0\right),$$

where γ_i ~ (0, 0.1), η_2i ~ LN(−0.3, 0.5), η_3i ~ LN(−0.5, 0.5), $K_{L_{2i}}~\text{LN}(-1.2,0.5)$, $K_{L_{3i}}~\text{LN}(-1.5,0.5)$, $K_{D_{2i}}~\text{LN}(-0.4,0.5)$, $K_{D_{3i}}~\text{LN}(0.4,0.5)$ and α_i = (α_1i, α_2i, α_3i) follows a multivariate mean zero normal distribution with correlation matrix

$$\sum _{\alpha }=\left[\begin{array}{ccc}1& 0.3& 0.1\\ 0.3& 1& 0\\ 0.1& 0& 1\end{array}\right]$$

Both W_2i (t) and W_3i (t) are constructed from a combination of underlying growth and death processes [34, 35, 36, 37], with W_2i (t) reflecting a continuous process and W_3i (t) transformed to a Bernoulli process. Figure 2 illustrates continuous latent biomarker trajectories in 10 representative individuals for W_1i (t) (left panel), W_2i (t) (middle panel) and the process, ${\alpha }_{3i}+K_{L_{3i}}t+\frac{K_{D_{3i}}}{{\eta }_{3i}}\left(e^{-{\eta }_{3i}t}-1\right)$, that after transformation becomes the Bernoulli process, W_3i (t) (right panel).

FIGURE 2.

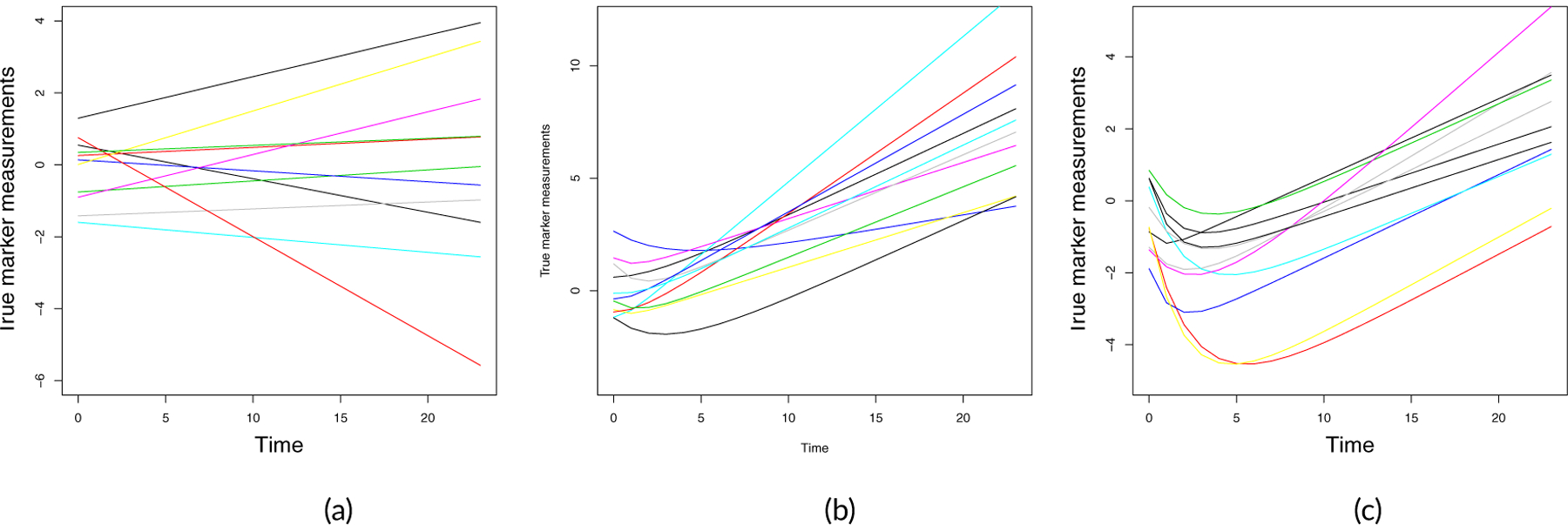
Simulated latent biomarker trajectories for 10 random subjects. Panel (a): W_1i (t). Panel (b): W_2i (t). Panel (c): Latent continuous process ${\alpha }_{3i}+K_{L_{3i}}t+\frac{K_{D_{3i}}}{{\eta }_{3i}}\left(e^{-{\eta }_{3i}t}-1\right)$ used to define the binary biomarker W_3i (t).

The continuous latent biomarker processes are measured with independent and identically distributed N(0, 0.5) random error at 6 month intervals, $s_i=\left\{0,6,12,\cdots ,s_{i{m}_i}\right\}$, where m_i in each case depends on the simulated censoring time for subject i. Uniform censoring times are independently generated to produce approximately 30 percent censoring. At measurement time s_ij the observed biomarker data is denoted Y_i (s_ij) = [Y_1i (s_ij),Y_2i (s_ij),Y_3i (s_ij)].

Survival times are linked to the latent longitudinal biomarkers via a piecewise exponential model assuming the rate is constant between two consecutive measurement times. In Simulation Study 1, the rate parameter in the exponential model is λ_i (s_ij) = 0.02 exp[0.5W_1i (s_ij) + 0.5W_2i (s_ij) + 0.5W_3i (s_ij) ] for time interval [s_ij, s_ij + 6). For additional complexity in Simulation Studies 2 and 3, the rate parameter includes an interaction term, i.e., λ_i (s_ij) = 0.02 exp[0.5W_1i (s_ij) + 0.5W_2i (s_ij) + 0.5W_3i (s_ij) − W_1i (s_ij) × W_2i (s_ij)].

Three performance metrics are used to evaluate the various dynamic risk prediction methods. The first metric is the area under the time-dependent receiver operating characteristic curve (AUC) [38], where a method that perfectly predicts survival status for a τ-length follow-up window has an AUC of 1.0, and methods with poor prediction have AUC values near 0.5. AUC estimates are obtained using the survivalROC package in R. The second metric is the prediction error (PE) [39, 40], or time-dependent Brier score, where smaller values indicate better precision in estimating the probability of surviving τ time units. In particular, an inverse weight approach estimates the average squared difference between observed and estimated survival probabilities at s_ij + τ amongst those at risk at s_ij using

$$PE\left(\tau ;s_{ij}\right)=\frac{1}{\tilde{n}}\sum _{i=1}^n\frac{I\left(s_{ij}<X_i\le s_{ij}+\tau \right){\left[{\tilde{S}}_i^{\tau }\left(s_{ij}\right)\right]}^2{d}_i}{\widehat{G}\left(X_i\mid s_{ij}\right)}+\frac{1}{\tilde{n}}\sum _{i=1}^n\frac{I\left(X_i>\tau \right){\left[1-{\tilde{S}}_i^{\tau }\left(s_{ij}\right)\right]}^2}{\widehat{G}\left(s_{ij}+\tau \mid s_{ij}\right)},$$

where ñ is the number of subjects still at risk at s_ij, Ĝ (·|s_ij) is the Kaplan-Meier censoring time survival estimate amongst subjects at risk at s_ij and the squared terms reflect observed minus estimated probabilities of surviving τ time units in the follow-up window starting at s_ij.

The last metric to evaluate prediction accuracy is the mean squared error (MSE). For individual i and at measurement time s, we can obtain the true 6-month survival probability from time s based on the data generating model. The MSE is the squared difference between the estimated 6-month survival probability and the true survival probability averaged across 200 subjects.

3.1 |. Scenarios evaluating a small number of longitudinal markers

With a small number of longitudinal biomarkers, we are able to compare performance of all three methods, PC_GLM, GEE.pseudo and RF.pseudo. In both Simulation Studies 1 and 2, the GEE.pseudo method, Model (2) took the form

$$\text{logit}\left[{\widehat{S}}_i^{\tau }\left(s_{ij}\right)\right]=\alpha B\left(s_{ij}\right)+{\gamma }_1{Y}_{1i}\left(s_{ij}\right)+{\gamma }_2{Y}_{2i}\left(s_{ij}\right)+{\gamma }_3{Y}_{3i}\left(s_{ij}\right),i=1,\cdots ,n,j=1,\dots ,m_i,$$

where B(s_ij) was taken to be a B-spline basis matrix with 3 degrees of freedom. As described in section 2.3, an independent working correlation was assumed with robust estimation of standard errors using the methods of [26] along with [27]. In RF.pseudo, the input variables for subject i at time s_ij include Y_i (s_ij) and s_ij. We implemented the RF.pseudo using the hrf function with default parameters.

Results for the above two simulation studies are shown in Tables 2 and 3. In the more simple case where the number of biomarkers is small and the relationship between the biomarkers and survival is correctly specified (Table 2), GEE.pseudo has very similar performance to PC_GLM, which indicates that the GEE.pseudo method is a competing alternative to the PC_GLM method. The nonparametric RF.pseudo approach performs slightly worse than the parametric approaches, PC_GLM and GEE.pseudo, in this case. We also increased correlations between the three biomarker measurements (i.e., from 0.3 to 0.6 and from 0.1 to 0.3 in Σ_α matrix), all three models performed similarly, or slightly better. However, conclusions remained the same (results not shown).

TABLE 2.

Simulation results comparing PC_GLM, GEE.pseudo and RF.pseudo in Simulation Study1 (n=200 in training data and n=200 in validation data; each with 30% censoring). AUC, PE and MSE are the averaged AUC, PE and MSE over 500 simulated data sets, respectively, and ESD is corresponding empirical standard error.

n0	s = 6	s = 12	s = 18	s = 24
	MSE (ESD)	MSE (ESD)	MSE (ESD)	MSE (ESD)
PCGLM	0.003 (0.002)	0.004 (0.002)	0.005 (0.003)	0.010 (0.009)
GEE.pseudo	0.003 (0.002)	0.004 (0.002)	0.005 (0.003)	0.010 (0.009)
RF.pseudo	0.010 (0.003)	0.014 (0.004)	0.019 (0.006)	0.028 (0.012)
	AUC (ESD)	AUC (ESD)	AUC (ESD)	AUC (ESD)
PCGLM	0.775 (0.04)	0.830 (0.04)	0.827 (0.06)	0.809 (0.09)
GEE.pseudo	0.775 (0.04)	0.830 (0.04)	0.827 (0.06)	0.810 (0.09)
RF.pseudo	0.752 (0.05)	0.805 (0.06)	0.798 (0.06)	0.761 (0.10)
	PE (ESD)	PE (ESD)	PE (ESD)	PE (ESD)
PCGLM	0.157 (0.02)	0.172 (0.02)	0.175 (0.03)	0.183 (0.05)
GEE.pseudo	0.157 (0.02)	0.172 (0.02)	0.175 (0.03)	0.184 (0.05)
RF.pseudo	0.165 (0.02)	0.192 (0.02)	0.200 (0.03)	0.215 (0.04)

TABLE 3.

Simulation results comparing PC_GLM, GEE.pseudo and RF.pseudo in Simulation Study 2(n=200 in training data and n=200 in validation data; each with 30% censoring). AUC, PE and MSE are the averaged AUC, PE and MSE over 500 simulated data sets, respectively, and ESD is corresponding empirical standard error.

n0	s = 6	s = 12	s = 18	s = 24
	MSE (ESD)	MSE (ESD)	MSE (ESD)	MSE (ESD)
PCGLM	0.058 (0.01)	0.080 (0.01)	0.079 (0.02)	0.061 (0.02)
GEE.pseudo	0.053 (0.01)	0.072 (0.01)	0.082 (0.02)	0.075 (0.03)
RF.pseudo	0.017 (0.01)	0.020 (0.01)	0.019 (0.01)	0.015 (0.01)
	AUC (ESD)	AUC (ESD)	AUC (ESD)	AUC (ESD)
PCGLM	0.674 (0.06)	0.809 (0.05)	0.844 (0.06)	0.845 (0.11)
GEE.pseudo	0.687 (0.06)	0.814 (0.05)	0.828 (0.07)	0.819 (0.12)
RF.pseudo	0.791 (0.05)	0.888 (0.04)	0.923 (0.04)	0.938 (0.08)
	PE (ESD)	PE (ESD)	PE (ESD)	PE (ESD)
PCGLM	0.185 (0.02)	0.186 (0.02)	0.157 (0.03)	0.110 (0.04)
GEE.pseudo	0.180 (0.02)	0.178 (0.02)	0.160 (0.03)	0.126 (0.05)
RF.pseudo	0.152 (0.02)	0.146 (0.02)	0.113 (0.02)	0.074 (0.03)

When an interaction is present (see Table 3), the RF.pseudo method that automatically incorporates complex relationships between predictors and outcomes performed substantially better than the PC_GLM and GEE.pseudo models that did not consider the interaction term. Similar conclusions were reached when the censoring rate was increased to 50% (see Table 4).

TABLE 4.

Simulation results comparing PC_GLM, GEE.pseudo and RF.pseudo in Simulation Study 2(n=200 in training data and n=200 in validation data; each with 50% censoring). AUC, PE and MSE are the averaged AUC, PE and MSE over 500 simulated data sets, respectively, and ESD is corresponding empirical standard error.

n0	s = 6	s = 12	s = 18	s = 24
	MSE (ESD)	MSE (ESD)	MSE (ESD)	MSE (ESD)
PCGLM	0.057 (0.011)	0.080 (0.014)	0.081 (0.021)	0.066 (0.035)
GEE.pseudo	0.051 (0.011)	0.073 (0.014)	0.091 (0.029)	0.089 (0.053)
RF.pseudo	0.018 (0.005)	0.022 (0.006)	0.022 (0.008)	0.017 (0.011)
	AUC (ESD)	AUC (ESD)	AUC (ESD)	AUC (ESD)
PCGLM	0.674 (0.063)	0.806 (0.052)	0.839 (0.081)	0.798 (0.214)
GEE.pseudo	0.694 (0.061)	0.812 (0.053)	0.808 (0.091)	0.742 (0.223)
RF.pseudo	0.787 (0.052)	0.882 (0.043)	0.918 (0.053)	0.895 (0.197)
	PE (ESD)	PE (ESD)	PE(ESD)	PE (ESD)
PCGLM	0.199 (0.024)	0.205 (0.028)	0.186 (0.043)	0.159 (0.082)
GEE.pseudo	0.191 (0.025)	0.197 (0.029)	0.199 (0.053)	0.197 (0.112)
RF.pseudo	0.165 (0.022)	0.163 (0.025)	0.135 (0.035)	0.106 (0.054)

3.2 |. Models with a large number of longitudinal markers

Simulation Study 3 is based on the same underlying data structure developed for Simulation Study 2. However, in this case, the truly useful biomarkers for predicting the event time are included for analysis along with a batch of n₀ biomarkers that are not associated with the event time. These n₀ biomarkers reflect random noise at each measurement time s_ij, i = 1, · · · , n, j = 1,…, m_i, with the observed data processes, Y_ki (s_ij) ~ N (0, 0.5), k = 4, · · · , 4 + n₀ and n₀ ∈ {50, 100, 150}. In this setting, only the RF.pseudo algorithm is able to process the large number of predictors and produce dynamic predictions. Table 5 shows that the RF.pseudo method has reasonably good performance, although not a strong as in Simulation Study 2 where the number of inputs, p, was smaller. This indicates that RF.pseudo is able to successfully draw information from the smaller set of useful biomarkers to make predictions over time. The performance measures improve as the number of random noise biomarkers included with the truly useful biomarkers decreases.

TABLE 5.

Simulation results of RF.pseudo in Simulation Study3 (n=200 in training data and n=200 in validation data; each with 30% censoring). AUC, PE and MSE are the averaged AUC, PE and MSE over 500 simulated data sets, respectively, and ESD is corresponding empirical standard error. n₀ is the number of noise markers that are not associated with the event outcome.

n0	s = 6	s = 12	s = 18	s = 24
	MSE (ESD)	MSE (ESD)	MSE (ESD)	MSE (ESD)
50	0.061 (0.01)	0.116 (0.02)	0.102 (0.03)	0.079 (0.03)
100	0.065 (0.01)	0.129 (0.03)	0.114 (0.03)	0.084 (0.03)
150	0.067 (0.02)	0.134 (0.03)	0.117 (0.03)	0.086 (0.03)
	AUC (ESD)	AUC (ESD)	AUC (ESD)	AUC (ESD)
50	0.664 (0.09)	0.756 (0.09)	0.778 (0.12)	0.749 (0.24)
100	0.628 (0.09)	0.707 (0.09)	0.717 (0.12)	0.688 (0.25)
150	0.602 (0.09)	0.675 (0.09)	0.690 (0.14)	0.642 (0.25)
	PE (ESD)	PE (ESD)	PE (ESD)	PE (ESD)
50	0.188 (0.03)	0.226 (0.04)	0.182 (0.04)	0.134 (0.05)
100	0.193 (0.03)	0.238 (0.04)	0.195 (0.04)	0.139 (0.05)
150	0.195 (0.03)	0.243 (0.04)	0.197 (0.05)	0.141 (0.05)

4 |. ANALYSIS OF NEPTUNE DATA

One of the goals of the Nephrotic Syndrome Study Network (NEPTUNE) was to understand factors leading to kidney failure, defined as the development of end-stage renal disease (ESRD) or estimated glomerular filtration rate (eGFR) decline by ≥ 40% from baseline [41, 42]. Our first example taken from this study focuses on dynamic prediction of 2-year kidney-failure-free survival based on risk factors that would be routinely available to most care givers. Our cohort is constrained to 174 subjects with proteinuria ≥ 0.5 g/d at the time of their first clinically indicated renal biopsy. Longitudinal data available for dynamic risk prediction from that point included clinical and demographic factors (e.g., diagnosis, presence of hypertension, gender, weight, age, race), urine measurements (e.g., urine albumin to creatinine ratio [UACR], urine protein to creatinine ratio [UPCR]), serum measurements (e.g., eGFR, triglycerides, albumin, creatinine, hematocrit, hemoglobin, CO₂, blood urea nitrogen[BUN]) and medication information.

In all, a mixture of 55 continuous and binary predictors are of interest, with updates to the 52 time-varying predictors measured at different times across subjects during the follow-up time ranging from 1.7 to 81 months. Of the PC_GLM, GEE.pseudo and RF.pseudo methods, only the RF.pseudo is able to simultaneously evaluate the large number of predictors for this analysis. Dynamically estimated probabilities of 2-year kidney-failure-free survival were estimated using 10-fold cross-validation to prevent model over-fitting based on the RF.pseudo method. The left panel of Figure 3 shows the time-dependent receiver operating characteristic (ROC) curve based on these estimated probabilities, with AUC= 0.86 and PE= 0.16 indicating very good prediction from the RF.pseudo algorithm.Variable importance was calculated using out of bag subjects, as described in section 2.4.2, with the top 12 featured predictors summarized in the right panel of Figure 3. The variable importance plot highlights several markers that have previously been linked to kidney failure (such as eGFR, serum creatinine, UPCR and UACR).

FIGURE 3.

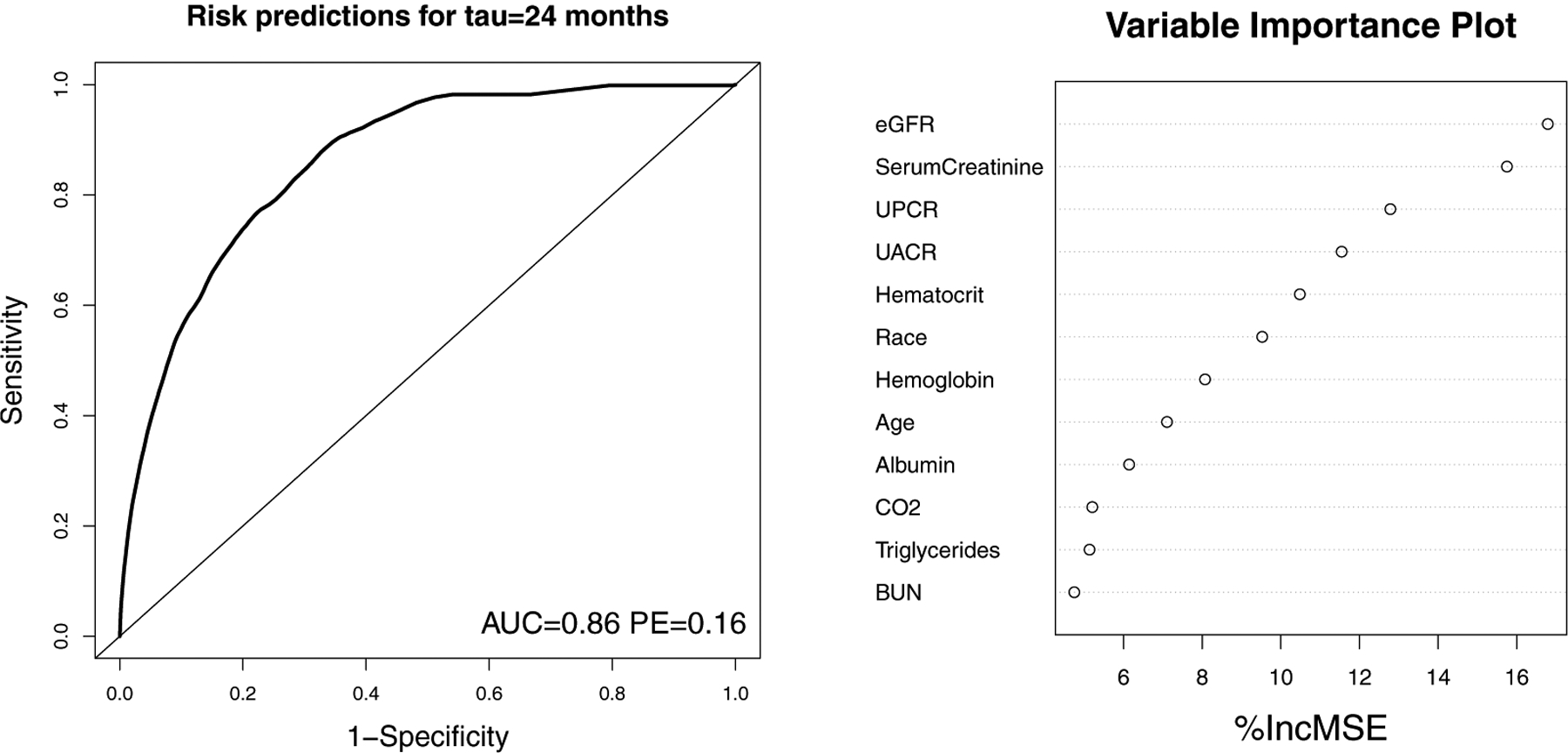
NEPTUNE Cohort Example 1 with Analysis Based on RF.pseudo Method. Left panel: Time-dependent receiver operating characteristic (ROC) curve for estimating 2-year kidney-failure-free survival probability based on 55 routinely collected predictors. Right panel: Variance important plot showing top 12 predictors. AUC: area under curve; PE: prediction error; %IncMSE: Percent increase in mean squared error when predictor is replaced with randomly permuted values in algorithm; eGFR: estimated glomerular filtration rate; UACR:urine albumin to creatinine ratio; UPCR: urine protein to creatinine ratio; BUN: blood urea nitrogen.

Our second example from the NEPTUNE cohort investigates three experimental urine biomarkers that are not routinely collected in clinical practice [epidural growth factor (EGF), monocyte chemoattractant protein-1 (MCP1) and tissue inhibitor of metalloproteinases-1 (TIMP1)], along with the top urine biomarker that emerged from the variable importance plot in our first example (UPCR from Figure 3, right panel); each biomarker is continuous, and the experimental biomarkers were measured at baseline, 12, 24 and 36 months. Two hundred and eleven subjects with proteinuria ≥ 0.5 g/d at the time of their first clinically indicated renal biopsy are available for this analysis. Because of the relatively smaller number of longitudinally measured biomarkers in this example, we are able to compare results from the existing method, PC_GLM, and our proposed methods, GEE.pseudo and RF.pseudo. For the GEE.pseudo method, Model (2) takes the form

$$\text{logit}\left[{\widehat{S}}_i^{\tau }\left(s_{ij}\right)\right]=\alpha B\left(s_{ij}\right)+{\gamma }_1{\text{EGF}}_i\left(s_{ij}\right)+{\gamma }_2\text{MCP}{1}_i\left(s_{ij}\right)+{\gamma }_3\text{TIMP}{1}_i\left(s_{ij}\right)+{\gamma }_4{\text{UPCR}}_i\left(s_{ij}\right),$$

i = 1, · · · , 211, j = 1,…, m_i, where B(s_ij) is a B-spline basis matrix with 3 degrees of freedom. An independent working correlation is assumed with robust estimation of standard errors, as previously described. For all methods, kidney-failure-free survival probabilities at τ = 12, 18, 24 and 30 months were estimated with 10-fold cross-validation to prevent model over-fitting.

Figure 4 displays time-dependent ROC curves, along with AUC and PE results for the three dynamic risk prediction methods, with τ varying across the four panels. In each panel, RF.pseudo outperforms the other methods with higher AUC values and equivalent or lower PE values. The GEE.pseudo and PC_GLM methods did not show a clear advantage over one another, with GEE.pseudo having better performance for τ = 24 and 30 months and PC_GLM having better performance at τ = 12 and 18 months.

FIGURE 4.

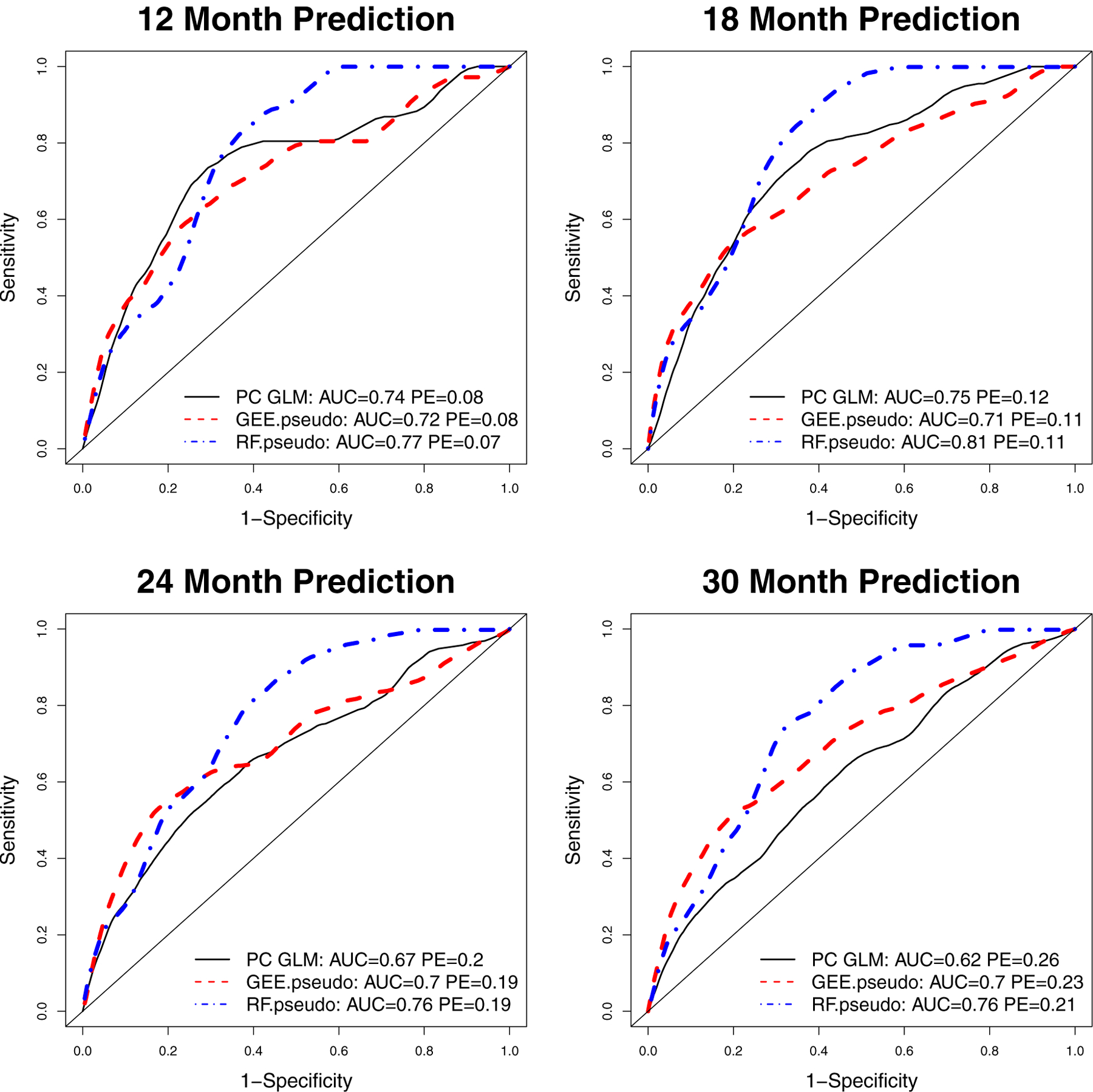
NEPTUNE Cohort Example 2 Comparing PC_GLM, GEE.pseudo and RF.pseudo Methods Using Four Longitudinal Urine Biomarkers. Time-dependent receiver operating characteristic (ROC) curves estimate kidney-failure-free survival probabilities at 12 months (top left panel), 18 months (top right panel), 24 months (bottom left panel) and 30 months (bottom right panel). AUC: area under curve; PE: prediction error. Preferred methods achieve higher AUC and lower PE.

5 |. DISCUSSION

The goal of this article is to provide simple and flexible tools for calculating dynamic risk predictions when the number of longitudinal biomarkers is large. We proposed methods for making dynamic risk predictions using repeatedly measured biomarkers of a large dimension. The main idea is to compute Jackknife pseudo-observations to replace the survival outcomes and then model these pseudo-observations as a function of the longitudinal marker measurements for risk predictions. Existing statistical methods (such as JM, landmarking, PC_Cox and PC_GLM in [20]) can not handle longitudinal data with a large dimension, p, especially when p > n. As illustrated in both simulation studies and the NEPTUNE data analysis, a key feature of the proposed RF.pseudo is its ability to select a small set of important markers when a large number of longitudinal markers are available. When the number of longitudinal markers is small, the proposed GEE.pseudo is a competing alternative to PC_GLM, and RF.pseudo could achieve better prediction accuracy when complexity relationships exist between markers and the survival outcome.

Another important feature of the proposed methods is their simplicity in computation. The two-stage strategy offers great flexibility to incorporate many features of longitudinal covariate history into the modelling. For example, fitted marker values can be used by modelling the longitudinal marker process up to the measurement time rather than the observed values; rates of changes in marker values can be included in the model as a covariate; changes from baseline (or nadir) could also be included in the model for the risk prediction. Compared to the popular randomForestSRC R package, which is the random forest method for survival data, pseudo.RF accounts for correlated data introduced by repeated measured within subjects. Furthermore, by using the pseudo probability as a quantitative response in the random forest, we can directly estimate the survival probability from the model.

KM estimates used in creating the pseudo values are subject to covariate-dependent censoring bias. In this case, we can replace the KM estimator by the inverse of probability of censoring weighted estimator for the survival function in computing the pseudo survival probabilities, which has been shown to reduce the bias in the parameter estimation [43, 44, 45]. The proposed methods can not automatically handle missing biomarker values. If biomarkers are measured at different time points, we can impute the missing data at pre-specified landmark times, using the Last Observation Carried Forward or the predicted random effects based on estimates from a linear mixed effects model as described in [20].

Abbreviations:

ABC

a black cat

DEF

doesn’t ever fret

GHI

goes home immediately