Fitting a naturally scaled point system to the ACMG/AMP variant classification guidelines

Abstract

Recently, we demonstrated that the qualitative American College of Medical Genetics and Genomics/ Association for Medical Pathology (ACMG/AMP) guidelines for evaluation of Mendelian disease gene variants are fundamentally compatible with a quantitative Bayesian formulation. Here, we show that the underlying ACMG/AMP “strength of evidence categories” can be abstracted into a point system. These points are proportional to Log(odds), are additive, and produce a system that recapitulates the Bayesian formulation of the ACMG/AMP guidelines. Strengths of this system are its simplicity and that the connection between point values and odds of pathogenicity allows empirical calibration of strength of evidence for individual data types. Weaknesses include that a narrow range of prior probabilities is locked in, and that the Bayesian nature of the system is inapparent. We conclude that a points-based system has the practical attribute of user friendliness and can be useful so long as the underlying Bayesian principles are acknowledged.

1. Introduction

Recently, we demonstrated that the qualitative American College of Medical Genetics and Genomics/ Association for Medical Pathology (ACMG/AMP) guidelines for the evaluation of Mendelian disease gene variants are fundamentally compatible with a quantitative Bayesian formulation (Richards et al., 2015; Tavtigian et al., 2018). However, actual use of that Bayesian formulation can be challenging for some users because of the required calculations. Through the following brief analysis, we further demonstrate a natural conversion from that Bayesian formulation into a points-based system.

2. Derivation of a points scale

Within the ACMG/AMP variant classification guidelines, thresholds for variant classification are defined by probabilistic boundaries that were set by community consensus (Plon et al., 2008; Richards et al., 2015). These are given in Table 1.

Table 1.

Variant classification categories and their probabilistic boundaries

Category	Posterior-Probability (PP) based boundaries
Pathogenic	PP > 0.99
Likely Pathogenic	0.99 ≥ PP > 0.90 †
Uncertain	0.10 ≤ PP ≤ 0.90
Likely Benign	0.001 ≤ PP < 0.10 †
Benign	PP < 0.001.

^†Note that the inequalities are symmetric around the broad Uncertain category.

With these community agreements in place, the strengths of the various ACMG/AMP rules for combining evidence criteria (Richards et al., 2015) can be expressed as odds in favor of pathogenicity via a single exponential equation (Tavtigian et al., 2018). Here we cite “equation 5“ from that publication, using the same variable definitions from that analysis:

$$OP=O_{\mathit{\text{PVSt}}}^{\left(\frac{N_{PSu}}{8}+\frac{N_{PM}}{4}+\frac{N_{PSt}}{2}+\frac{N_{\mathit{\text{PVSt}}}}{1}-\left[\frac{N_{BSu}}{8}+\frac{N_{BSt}}{2}\right]\right)}$$ equation 1:

where OP are the calculated odds of pathogenicity; O_PVSt are the odds of pathogenicity assigned to the “Very Strong” evidence of pathogenicity category; N_P and N_B are the number of invocations of a specific pathogenic or benign evidence strength level, respectively, by a specific classification rule; and Su, M, St, and VSt are “Supporting”, “Moderate”, “Strong”, and “Very Strong” strength of evidence strength level categories, respectively.

Does equation 1 imply a natural point system for variant classification?

Noting that by definition in our previous work $O_{\mathit{\text{PVSt}}}=O_{PSu}^8$, we can re-write equation 1 as:

$$OP=O_{PSu}^{\left(1N_{PSu}+2N_{PM}+4N_{PSt}+8N_{\mathit{\text{PVSt}}}-\left[1N_{BSu}+4N_{BSt}\right]\right)}.$$ equation 2:

Taking the Log₁₀ and then dividing by the Log₁₀ (O_PSu), we have:

$$\raisebox{1ex}{$Lo{g}_{10}(OP)$}\!\left/ \!\raisebox{-1ex}{$Lo{g}_{10}(O_{PSu})$}\right.=\mathbf{1}{N}_{PSu}+\mathbf{2}{N}_{PM}+\mathbf{4}{N}_{PSt}+\mathbf{8}{N}_{\mathit{\text{PVSt}}}-\left[\mathbf{1}{N}_{BSu}+\mathbf{4}{N}_{Bst}\right]$$ equation 3:

Inspecting the bolded integers 1, 2, 4, and 8 that emerge on the right side of equation 3, it is evident that the ACMG/AMP strength of evidence categories can be abstracted into a point system, given in Table 2. We emphasize that these points are proportional to Log(odds) rather than OP, and are therefore additive. Indeed, the odds corresponding to an individual rule for combining evidence criteria are easily retrieved, because $OP=O_{PSu}^{\left(\mathit{\text{Points}}\right)}$

Table 2.

Point values for ACMG/AMP strength of evidence categories

Evidence	Point Scale
Strength	Pathogenic	Benign
Indeterminate	0	0 §
Supporting	1	−1
Moderate	2	−2 †
Strong	4	−4
Very Strong	8	−8 †

^§Note is made that Richards et al did not specifically recognize indeterminate evidence. Nonetheless, if one thinks of the odds in favor of pathogenicity as a continuous variable, there exists a range that falls between Supporting Benign and Supporting Pathogenic. This is Indeterminate.

^†Note is also made that Richards et al did not specify benign evidence at the moderate or very strong levels. Nevertheless, the point system would readily support the addition of such criteria.

3. Derivation of point values for classification thresholds

While framing the ACMG/AMP evidence strength as OP expresses a Bayesian point of view, the actual application of Bayes’ rule arrives when a prior probability of pathogenicity (P₁) is combined with the OP to obtain a posterior probability of pathogenicity (P₂). Two relevant expressions of Bayes’ rule are:

$$P_2=\left(OP\times P_1\right)÷\left[\left(OP-1\right)\times P_1+1\right]$$ equation 4:

$$OP=\left[P_2\times \left(1-P_1\right)\right]÷\left[\left(1-P_2\right)\times P_1\right]$$ equation 5:

The ACMG/AMP classification criteria specify that if none of the criteria are met, a variant is VUS. This specification implies that the prior probability falls within the posterior probability range for VUS, which is 0.10 to 0.90. For BRCA1 and BRCA2, the empirically measured prior probability for the combination of missense substitutions, in-frame indels, and proximal splice junction variants is approximately 0.10 (Goldgar et al., 2004; Abkevich et al., 2004; Easton et al., 2007). Moreover, as the number of biologically relevant susceptibility genes included in gene panels increases, the average number of variants revealed by an individual test increases, which lowers their average prior probability. Yet it is important to recognize that if the generalized prior probability falls below the likely benign threshold, then unclassified sequence variants are a priori likely benign unless they are reported with evidence in favor of pathogenicity. Therefore, we chose to accept the ACMG/AMP assumption, with threshold-defining calculations based on a prior probability of 0.10, as before (Tavtigian et al., 2018). With a prior probability of 0.10 and posterior probability at the ACMG/AMP Likely Pathogenic threshold of 0.90, equation 5 shows that the OP threshold for Likely Pathogenic is >81:1. With the posterior probability at the Pathogenic threshold of 0.99, the OP threshold becomes >891:1. Similarly, the OP thresholds for Likely Benign and Benign are <1.00:1 and <0.00901:1, respectively.

Five of the six ACMG/AMP Likely Pathogenic Combining Criteria have strength equivalent to six pieces of supporting pathogenic evidence (Tavtigian et al., 2018, Table 1). This requirement for the equivalent of six of O_PSu implies that the exact value of O_PSu is $\sqrt[6]{81}=2.0801:1$; moreover, the expression $OP=O_{PSu}^{\left(\mathit{\text{Points}}\right)}$ can be employed to calculate the number of points required to reach the classification thresholds as simply Threshold=2.0801^(Points). Rounding up to the nearest integers, the ACMG/AMP thresholds for Pathogenic and Likely Pathogenic are 10 points and 6 points, respectively. Rounding down to the nearest integers, the thresholds for Likely Benign and Benign are −1 and −7 points, respectively. The resulting point-based categorical ranges are given in Table 3.

Table 3.

Point based variant classification categories

Category	Point ranges
Pathogenic	≥ 10
Likely Pathogenic	6 – 9 ¥
Uncertain	0 – 5
Likely Benign	−1 – −6 ¥
Benign	≤ −7

^¥Operationally, the prior probability should be understood to be infinitesimally greater than 0.10. This has two effects. First, it makes the posterior probability of the ACMG likely pathogenic combining rules infinitesimally greater than 0.90, so that the likely pathogenic rules work properly. A specific value of 0.102 would have the added benefit that 7 points would meet the IARC likely pathogenic threshold of 0.95. Second, it enforces a requirement for some evidence of benign effect for sequence variants to be classified as likely benign. One could also argue that the point threshold for likely benign should really be −2. This would match the ACMG rule “Likely Benign (ii)” rather than the simple numerical requirement that the posterior probability be <0.10.

4. Strengths, weaknesses, and relevance to recent literature

The principal strength of such a point system is that using it requires only addition and subtraction. The weakness is that the Bayesian nature of the system is hidden. Specific choices of prior probability, odds of pathogenicity, and posterior probability are locked in, and the very concepts of probabilities and odds are removed from view. It is important to reiterate, however, that the points described here are intentionally proportional to Log(odds), and simply a shorthand representation of equations 1–3. Consequently, the odds of pathogenicity can be calculated from any evidence combination, then combined with a prior probability using Bayes’ rule (i.e., equation 4). As strength of evidence increases in either the pathogenic or benign directions, the resulting posterior probabilities will asymptotically approach 1.00 or 0.00, respectively.

We know of multiple efforts that have developed or are developing point-based systems that are intended to contribute to sequence variant classification. One effort, “Sherloc” was developed by Invitae, Inc. with the intention to improve upon the precision of the ACMG/AMP guidelines (Nykamp et al., 2017). Sherloc captures a wide range of data, with scoring ranging from 5 Benign points to 5 Pathogenic points and explicitly accords 0 points to some (weak) data. The system focuses on separating the ACMG-AMP criteria into groups of criteria that are logically independent of each other. Then, within groups of related criteria, building data use patterns that choose the most appropriate data type and evidence strength while avoiding double-counting on non-independent data. On the pathogenic side, the basic Sherloc point scale is 1, 2, 3, 4, and 5. One point most often corresponds to an ACMG Supporting Pathogenic criterion, 5 points always corresponds to a Very Strong Pathogenic criterion, and in-between there is a trend of increasing ACMG evidence strength corresponding to increased points. The threshold for declaring a variant Likely Pathogenic is 4 points and Pathogenic is 5 points. While the Sherloc system focuses on rational use of the available data towards variant classification, neither the derivation of the point system nor the derivation of the classification thresholds are described.

A more recent effort involves standards for interpretation of copy number variants (Riggs et al., 2019). In this point system, total scores of 0.90 and 0.99 are the thresholds for likely pathogenic and pathogenic, respectively because “variants interpreted as pathogenic should have a 99% level of confidence and variants interpreted as likely pathogenic should have a 90% level of confidence”. That is, Riggs et al. considered that their score thresholds resemble probabilities of pathogenicity. Within this point system, individual pieces of evidence in favor of pathogenicity receive between 0.10 and 1.00 points, and all of the data for a single sequence variant are added together to arrive at a score for that variant. Focusing on the pathogenic side of the Riggs et al. system, we would point out three considerations. Firstly, as the Riggs et al. authors admit, there is no derived, fitted, trained, or otherwise calibrated connection between evidence types and the points accorded to them (Riggs et al. noted “that these numbers have not been statistically derived.”). This makes it difficult to calibrate a point scale. Secondly, since summing across the data for a single sequence variant can easily result in total scores that exceed 1.0, the thresholds of 0.90 and 0.99 cannot be considered as posterior probabilities. Thirdly, under Bayes’ rule (equation 4), conditional odds of 11.0:1 are required to move from a posterior probability of 0.90 to 0.99. Using the point system that we derived above, bridging that gap–moving from the threshold of likely pathogenic to pathogenic–requires 4 points, i.e., at least four supporting, or two moderate, or two supporting plus one moderate, or one strong piece of pathogenic evidence. Yet in both the Sherloc and Riggs et al. system, one element of supporting pathogenic evidence would be sufficient. This means that in these two points-based systems, the difference between likely pathogenic and pathogenic is very small; in all likelihood, either the likely pathogenic boundary is too strong or the pathogenic boundary too weak.

A common argument against classification based on point scales is that the scales and classification thresholds tend to be arbitrary. Of course, an arbitrary point-based classification system, if thoughtfully designed, may be operationally satisfactory. While the qualitative ACMG/AMP variant classification system itself has components that may be considered arbitrary, it was thoughtfully enough designed so that an internally consistent Bayesian formulation could be fitted to it. The point system derived here flows naturally from that Bayesian formulation. Indeed, upon examination of the Richards et al. combining rules (their Table 5), simply allowing one point for each invocation of supporting pathogenic evidence, two points for each invocation of moderate pathogenic evidence, etc., could lead one to propose this point system, with the same caveats about the strength of the rules Likely Pathogenic (i) and Pathogenic (iii) that we noted previously (Tavtigian et al., 2018).

In a more abstract sense depicted in Figure 1, the ACMG/AMP qualitative classification schema provided a scaffold that could be combined with Bayes’ rule to produce its Bayesian formulation. Bidirectional feedback between the qualitative classification schema and its Bayesian formulation, with a particular focus on empirical measurement of strength of evidence attributable to existing or new data types, should steadily improve the rigor of sequence variant classification. The point scale derived here automatically inherits these features.

Figure 1.

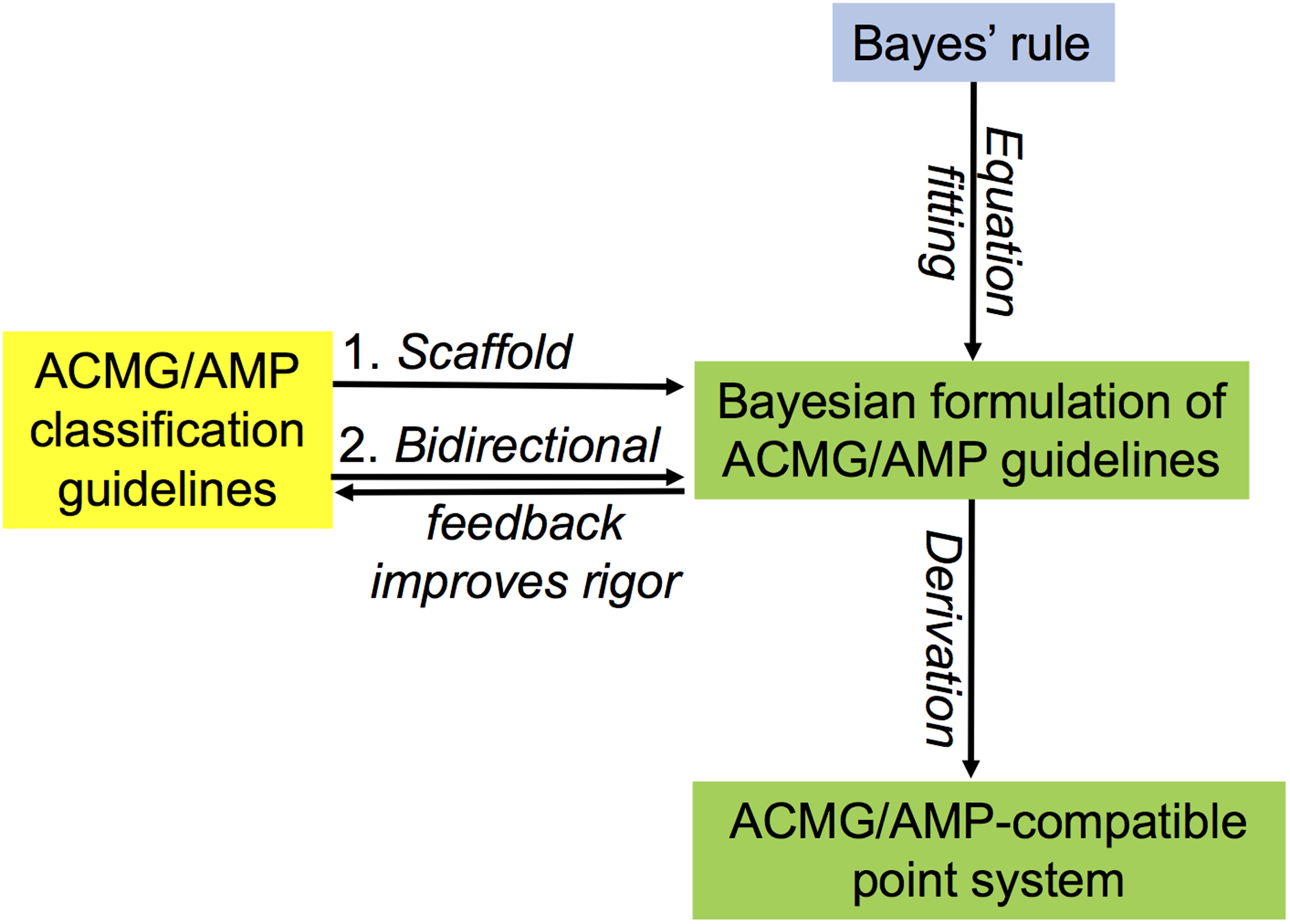
Schematic relationship among Bayes’ rule, the qualitative ACMG/AMP variant classification guidelines, the Bayesian formulation of those guidelines, and the point system derived here.

Variant interpretation is a new and rapidly developing science. All of us are learning and developing novel approaches at a rapid pace. Integration of mathematical, statistical, and computational techniques into our practices will benefit testing laboratories and, ultimately, patient care. Going forward, we recommend that developers of all variant evaluation schemes examine their proposed scoring scales, classification thresholds, and underlying logic to see how well they comport with a Bayesian probabilistic framework. This examination should assess how naturally they flow from the parent ACMG/AMP variant classification guidelines, which were pioneering and insightful and provide a solid foundation for future development efforts.