Granger causality analysis of rat cortical functional connectivity in pain

Abstract

Objective.

The primary somatosensory cortex (S1) and the anterior cingulate cortex (ACC) are two of the most important cortical brain regions encoding the sensory-discriminative and affective-emotional aspects of pain, respectively. However, the functional connectivity of these two areas during pain processing remains unclear. Developing methods to dissect the functional connectivity and directed information flow between cortical pain circuits can reveal insight into neural mechanisms of pain perception.

Approach.

We recorded multichannel local field potentials (LFPs) from the S1 and ACC in freely behaving rats under various conditions of pain stimulus (thermal vs. mechanical) and pain state (naive vs. chronic pain). We applied Granger causality (GC) analysis to the LFP recordings and inferred frequency-dependent GC statistics between the S1 and ACC.

Main results.

We found an increased information flow during noxious pain stimulus presentation in both S1→ACC and ACC→S1 directions, especially at theta and gamma frequency bands. Similar results were found for thermal and mechanical pain stimuli. The chronic pain state shares common observations, except for further elevated GC measures especially in the gamma band. Furthermore, time-varying GC analysis revealed a negative correlation between the direction-specific and frequency-dependent GC and animal’s paw withdrawal latency. In addition, we used computer simulations to investigate the impact of model mismatch, noise, missing variables, and common input on the conditional GC estimate. We also compared the GC results with the transfer entropy (TE) estimates.

Significance.

Our results reveal functional connectivity and directed information flow between the S1 and ACC during various pain conditions. The dynamic GC analysis support the hypothesis of cortico-cortical information loop in pain perception, consistent with the computational predictive coding paradigm.

1. Introduction

Pain is a unique and complex sensory experience that is triggered by external ascending signals, but at the same time is strongly shaped by internal cognitive and emotional variables. Pain perception is a dynamic process, which involves time-varying interaction and temporally-coordinated information processing among distributed cortical networks. At the cortical circuit level, pain experiences are encoded across distributed brain areas. Specifically, the primary somatosensory cortex (S1) is known to process stimulus-evoked information, such as location and timing (Bushnell et al., 1999; Vierck et al., 2013), while the anterior cingulate cortex (ACC) processes the aversive experience of pain (Rainville et al., 1997; Johansen et al., 2001; Bushnell et al., 2013; Bliss et al., 2016). However, functional dissection of these two cortical regions and identification of their functional connectivity during pain processing remain unclear.

In human studies, neural activities are often measured by functional magnetic resonance imaging (fMRI), magnetoencephalography (MEG) or electroencephalography (EEG) recordings. In animal studies, neural activities are measured by in vivo extracellular recordings or calcium imaging. The experience of pain is often associated with brain rhythms or neuronal oscillations at different frequencies (Ploner et al., 2017; Peng et al., 2018). For multisite recordings, investigation of the inter-regional local field potential (LFP) oscillatory coordination may provide important insight into the circuit mechanism in cognitive or behavioral tasks (Eto et al., 2011). Conventionally, the coordinated activity between different brain areas are quantified by cross-correlation or coherence, both of which are based on only second-order moment statistics. In the literature, various forms of causality-type measures have been developed to overcome the limitation of correlation or coherence (Cekic et al., 2018). Specifically, Granger causality (GC) is a useful tool to define “causal” functional connectivity in neurophysiological time series (Granger, 1069; Ding et al., 2006; Hu et al., 2011; Faes et al., 2012; Eichler, 2013; Stokes and Purdon, 2017). Several studies have used GC or its variants to study brain connectivity based on fMRI, MEG or EEG (Korzeniewska et al., 2003; Ploner et al.,, 2009; Cadotte et al., 2010; Hu et al., 2011; Gao et al., 2015). Due to its ease of implementation and interpretation, GC analysis can provide insight into the functional connectivity of brain network.

To date, several studies have been dedicated to GC analysis on human pain networks (Ploner et al.,, 2009; Liu et al., 2011; Zhang et al., 2012; Ning et al., 2018). However, most of human studies are limited by the lack of direct circuit-level measurements at high temporal resolution. Here we use a frequency-dependent GC analysis to characterize the directed information flow between the S1 and ACC based on the multi-site LFP recordings in freely behaving rats. The contributions of our paper are threefold. First, to the best of our knowledge, our work is the first systematic investigation of GC between the rat S1 and ACC during nociceptive or pain processing. Second, dynamic GC analysis revealed a cortico-cortical information loop, supporting the predictive coding hypothesis in pain perception. Third, we correlate dynamic GC measures with animal’s withdrawal time, and found negative correlation between direction-specific and frequency-dependent GC and animal’s paw withdrawal latency. Our results suggest that the directed information flow is elevated during pain stimulus presentation, and the chronic pain state further amplifies such conditions, especially at high gamma frequency band.

2. Materials and Methods

2.1. Experimental data

All experimental studies were performed in accordance with the National Institutes of Health (NIH) Guide for the Care and Use of Laboratory Animals to ensure minimal animal use and discomfort, and were approved by the New York University School of Medicine (NYUSOM) Institutional Animal Care and Use Committee (IACUC).

Male adult Sprague-Dale rats (250–300 g, Taconic Farms, Albany, NY) were used in our current study and kept at the new Science Building at NYUSOM, with controlled humidity, temperature and 12-h (6:30 a.m.–6:30 p.m.) light-dark cycle. Food and water were available ad libitum. Animals were given on average 10 days to adjust to the new environment before the initiation of experiments.

Noxious pain stimuli were used for freely exploring rats in a plastic chamber of size 38×20×25 cm³ on top of a mesh table. Two types of stimuli, thermal and mechanical, were used in the animal’s pain experiments. In the case of thermal pain, a blue (473 nm diode-pumped solid-state) laser with 250 mW intensity was delivered to the rat’s hindpaw; a 50 mW laser was also delivered in the same manner as a negative control. The laser stimulation was delivered in repeated trials (25–40) during 30–45 min. The stimulation was terminated by animal’s paw withdrawal. There was a small percentage of trials with withdrawal responses to 50 mW laser stimulations. In the case of mechanical pain, a pin prick (PP) with 30-gauge needle was delivered to the rat’s hindpaw. As a negative control, a non-noxious stimulus was also applied to the same hindpaw using a 2 g von Frey filament (VF) stimulation (for 3 s or until paw withdrawal). There was no withdrawal response to VF stimulation in the majority of trials. Two video cameras (60 frame per second) were used to continuously monitor the rat’s behavior during the course of experiment. Details are referred to previous publications (Zhang et al., 2017; Chen et al., 2017; Hu et al., 2018; Xiao et al., 2018; Xiao et al., 2019).

To produce chronic inflammatory pain, 0.075–0.1 ml of Complete Freund’s adjuvant (CFA) (mycobacterium tuberculosis, Sigma-Aldrich) was suspended in an oil-saline (1:1) emulsion, and injected subcutaneously into the plantar aspect of the hindpaw opposite to the paw that was stimulated by a blue laser, PP or VF. Namely, only a unilateral inflammation was induced, and nociceptive stimuli were delivered to the opposite paw of the injured foot. The summary of animals and experimental recordings used in the current study is shown in Table 1.

Table 1:

Summary of experimental trials in animal’s pain experiments

Animal	Thermal stimuli		Mechanical stimuli
	250 mW laser	50 mW laser	PP	VF
Naive rat 1	74	47	40	45
Naive rat 2	98	107	n/a	n/a
Naive rat 3	67	20	56	35
Naive rat 4	124	16	14	21
CFA rat 1	56	66	62	59

(PP: pin prick; VF: von Frey filament)

We used silicon probes (Buzsaki32, NeuroNexus) with 3D printed drive to record multi-channel (up to 64 channels) neural activities from the rat ACC and S1 areas simultaneously. The probe implant was on the contralateral side of the paw that received noxious stimulation. For surgery, rats were anesthetized with isoflurane (1.5%–2%). The skull was exposed and a 3 mm-diameter hole was drilled above the target region. The coordinates for the ACC and S1 implants were: ACC: AP 2.7, ML 1.4–2.0, DV 2.0, with an angle of 20° toward the middle line; S1: AP −1.5, ML 2.5–3.2, DV 1.5. The drive was secured to the skull screws with dental cement. The Plexon (Dallas, TX) data acquisition system was used to record in vivo extracellular neural signals at a sampling rate of 40 kHz. The raw signals were band-pass filtered (0.3 Hz–7.5 kHz).

2.2. LFP data preprocessing

The flow diagram of multichannel LFP data processing is shown in Fig. 1. Upon LFP data acquisition, we applied standard band-pass filtering (1–100 Hz), band-stop filtering (at 60 Hz), and down-sampling (at 200 Hz). The purpose of downsampling was to reduce the lag of autocorrelation in the subsequent model fitting. For all LFP channels, we applied a Z-score transformation in time at each trial with respect to the 5-s pre-stimulus baseline (Fig. 2A). Next, we either selected specific one channel from each brain region, or applied principal component analysis (PCA) to the observed multichannel LFP signals across trials (10 s duration centered at the stimulus onset).

Figure 1:

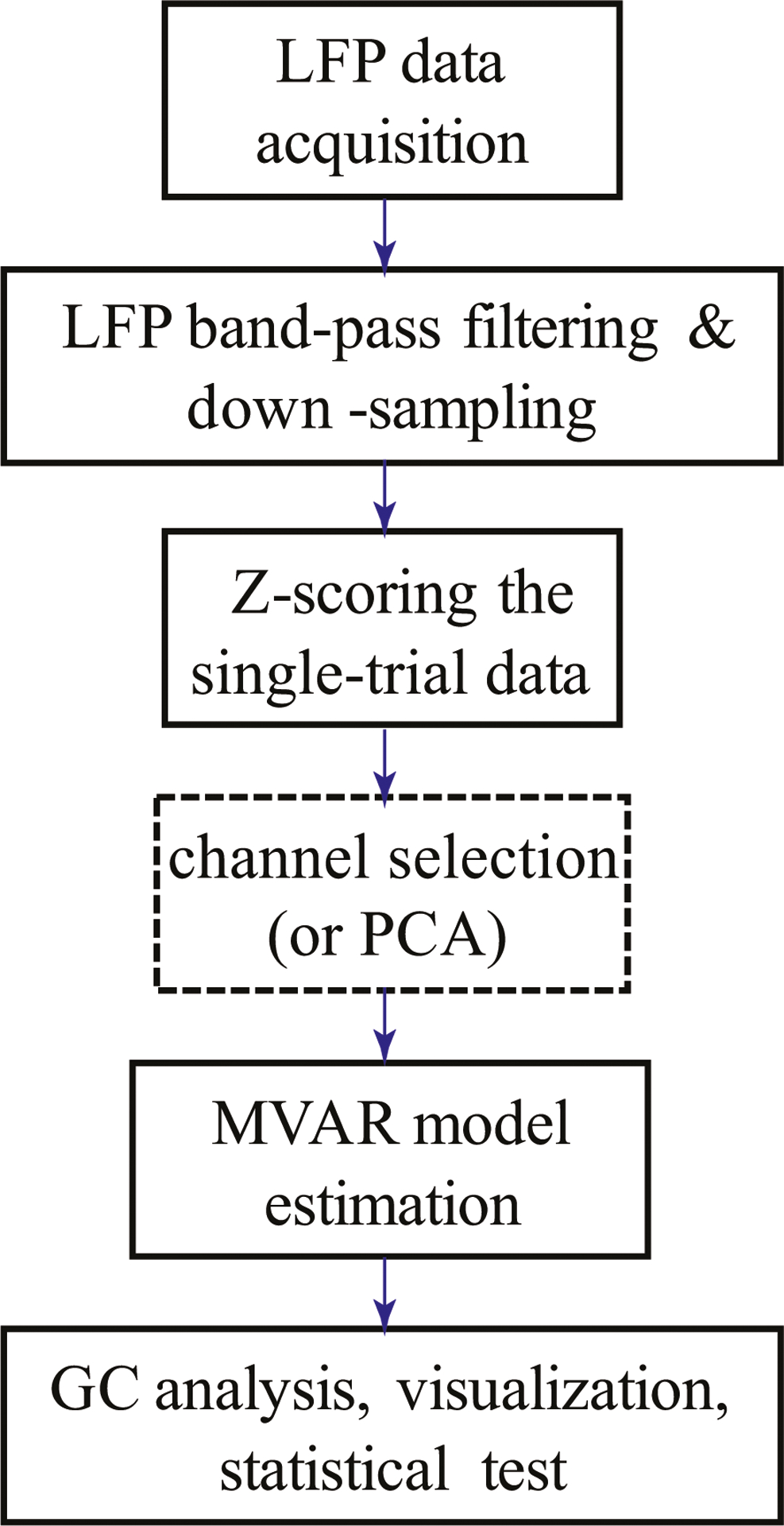
Schematic diagram of multichannel LFP data preprocessing and Granger causality (GC) analysis.

Figure 2:

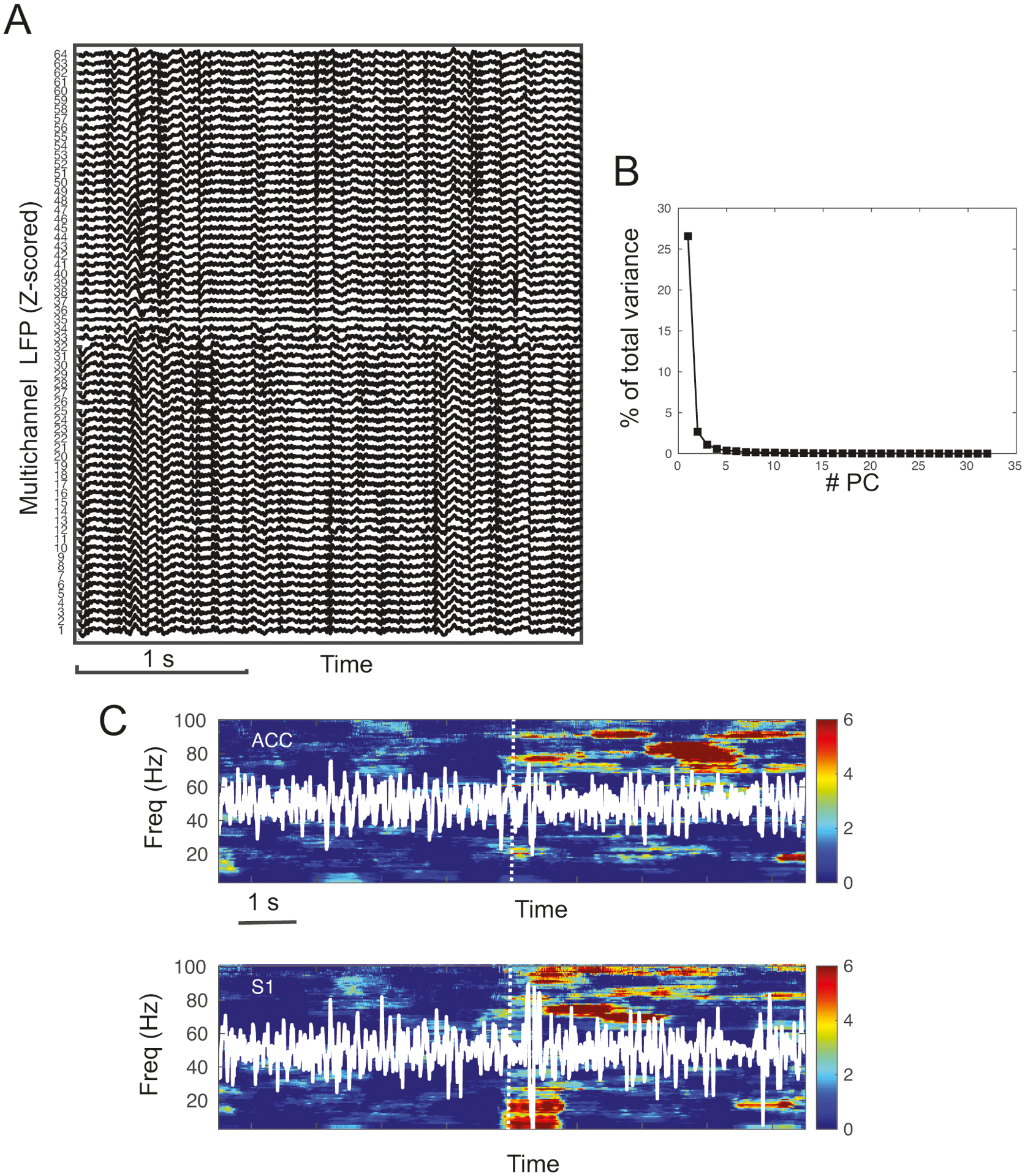
Experimental LFP data. (A) Snapshot of Z-scored multichannel LFP signals during spontaneous baseline. Channels #1–32 were implanted in the ACC, and Channels #33–64 were implanted in the S1. (B) PCA and the eigenspectrum showed that the dominant energy was concentrated in the 1st principal component (PC). (C) Z-scored spectrogram of LFP signals (white traces) from one S1 and one ACC channels. Warm color indicates an increase in spectral power. Vertical dotted lines show the onset of stimulus presentation. In this example, we observed a clear power increase in the S1 at theta and high gamma frequency bands, and in the ACC at high gamma frequency band.

For LFP channel selection, we first removed obvious artifact-corrupted channels. A simple cross-correlation or PCA analysis among remaining channels showed that the majority of LFP signals within one brain region were highly correlated (Fig. 2B). To test the sensitivity of channel selection, we also compared the Granger causality analysis results based upon either randomly selected channels or the dominant principal components derived from PCA (see Results section). Some experimental trials contaminated by large amplitude of noise or movement artifacts were excluded in our data analysis.

2.3. Time-frequency analysis

Multitapered spectral analyses for LFP spectrogram (e.g., Fig. 2C) were performed using the Chronux toolbox (chronux.org). Specifically, we chose a half-bandwidth parameter W such that the windowing functions were maximally concentrated within [−W,W]. We chose W > 1/T (where T denotes the duration) such that the Slepian taper functions were well concentrated in frequency and had bias reducing characteristics. In terms of Chronux function setup, we used the tapers setup [TW,N], where TW is the time-bandwidth product, and N = 2 × TW − 1 is the number of tapers. Mutually orthogonal taper functions produced independent spectral estimates. In spectrogram analyses, we used a moving window length of 500 ms. We used TW = 5. We further computed the Z-scored spectrogram, where the baseline was defined as the 5-s period before the stimulus onset.

2.4. Spectral Granger causality

Granger causality (GC) analysis can be conducted in both the time and frequency domains. For the ease of spectral interpretation, we used the frequency-based GC to represent the information flow between different brain regions at distinct frequency bands.

Let $\text{X}={\left[{\text{x}}_1,\dots ,{\text{x}}_M\right]}^{\top }\in {ℝ}^{M\times N}$ denote the augmented data matrix consisting of M time series, each with N samples. To investigate GC between M observed time series, we constructed a Kth-order multivariate or vector autoregressive (VAR) model as follows

$$\text{X}(t)=\sum _{k=1}^K\text{A}(k)\text{X}(t-k)+\text{W}(t)$$ (1)

where the individual noise process {W(t)} are zero mean and temporally uncorrelated (“white”).

To compute the frequency-domain GC, let X(ω) = H^f(ω)W^f(ω) denote the frequency-domain representation of Eq. (1), where the transfer function H^f(ω) is given as

$$H^f(\omega )={\left(1-\sum _{k=1}^K{A}^f(k)e^{-ik\omega }\right)}^{-1}$$ (2)

where $i=\sqrt{-1}$. In addition, we computed the power spectrum of {x_j} as follows

$$S_{x_j,x_j}(\omega )=H_{j,j}^f(\omega ){\Sigma }_{j,j}^f{H}_{j,j}^{f*}(\omega )+H_{j,i}^f(\omega ){\Sigma }_{i,i}^f{H}_{j,i}^{f*}(\omega )$$ (3)

where * denotes the conjugate transpose; the first and second terms represent the components of the spectrum of x_j induced by its own input noise process and x_i, respectively.

Geweke has defined the unconditional GC measure (Geweke, 1984)

$$\begin{gathered} f_{x_i\to x_j}(\omega )=\text{log}\frac{\left|S_{x_i,x_j}(\omega )\right|}{\left|H_{j,j}^f(\omega ){\Sigma }_{j,j}^f{H}_{j,j}^{f*}(\omega )\right|} \\ =\text{log}\frac{\left|H_{j,j}^f(\omega ){\Sigma }_{j,j}^f{H}_{j,j}^{f*}(\omega )+H_{j,i}^f(\omega ){\Sigma }_{i,i}^f{H}_{j,i}^{f*}\right|}{\left|H_{j,j}^f(\omega ){\Sigma }_{j,j}^f{H}_{j,j}^{f*}(\omega )\right|} \end{gathered}$$ (4)

And the total interdependence $f_{x_i,x_j}(\omega )$ is defined as (Cohne and Tsuchiya, 2018)

$$\begin{gathered} f_{x_i,x_j}(\omega )=\text{log}\frac{S_{x_i,x_i}(\omega )S_{x_j,x_j}(\omega )}{\left|\text{Q}(\omega )\right|} \\ =\text{log}\frac{S_{x_i,x_i}(\omega )S_{x_j,x_j}(\omega )}{S_{x_i,x_i}(\omega )S_{x_j,x_j}(\omega )-S_{x_i,x_j}(\omega )S_{x_i,x_j}^{*}(\omega )} \\ =-\text{log}\left[1-\frac{S_{x_i,x_j}(\omega )S_{x_i,x_j}^{*}(\omega )}{S_{x_i,x_i}(\omega )S_{x_j,x_j}(\omega )}\right] \\ =-\text{log}\left[1-C_{ij}(\omega )\right] \end{gathered}$$ (5)

where Σ denotes the noise covariance matrix, Q(ω) = H(ω)ΣH*(ω) denotes the spectral density matrix such that

$$Q_{ij}(\omega )=\left(\begin{array}{cc}{S}_{x_i,x_i}(\omega )& S_{x_j,x_i}(\omega )\\ S_{x_i,x_j}(\omega )& S_{x_j,x_j}(\omega )\end{array}\right)$$ (6)

and C_ij(ω) denotes the coherence between x_i and x_j.

To derive the conditional GC measure, Geweke further transformed the original full model to a reduced model such that (Geweke, 1984; Barnett et al., 2014)

$$\begin{gathered} f_{x_i\to x_j\mid x_k}(\omega )=f_{x_i{z}_k^{r(i)}\to z_j^{r(i)}}(\omega ) \\ =\text{log}\frac{\left|{\Sigma }_{j,j}^{r(i)}(\omega )\right|}{\left|G_{j,j}(\omega ){\Sigma }_{j,j}^f{G}_{j,j}^{f*}(\omega )\right|} \end{gathered}$$ (7)

where the original VAR model is rewritten in terms of time series {x_i,t}, $\left\{z_{j,t}^{r(i)}\right\}$, $\left\{z_{k,t}^{r(i)}\right\}$, and G_j,j(ω) is the new transfer function induced from the transformation (Stokes and Purdon, 2017). Note that in the case of bivariate time series, the unconditional GC is equivalent to the conditional GC.

We estimated the MVAR parameters from the least-squared estimation, and determined the VAR model order based on Akaike’s information criterion (AIC) or Bayesian information criterion (BIC). Upon fitting the MVAR, we further checked the statistical tests on VAR coefficients (“Wald statistic”), residual error (“whiteness”) and explained variance (R²). The complete process of model selection, model estimation, and statistical testing was conducted using a MATLAB toolbox (www.sussex.ac.uk/sackler/mvgc/) (Barnett et al., 2014). Gaussianity and wide-sense stationarity of signals were assumed in the GC analysis.

From the estimated MVAR parameters, we also derived the power spectrum $S_{x_j,x_j}(\omega )$, cross-spectrum $S_{x_i,x_j}(\omega )$. and coherence C_ij(ω). The directed transfer function (DTF) (Kaminski and Blinowska, 1991) and the partial directed coherence (PDC) (Baccal L and Sameshima, 2001) are alternative measures that are closely related to the GGC statistic, but they were not reported in the current investigation. A detailed comparison of these methods can be found in (Faes et al., 2012; Cekic et al., 2018; Olejarczyk et al., 2017).

2.5. Transfer entropy

Transfer entropy (TE) is an alternative measure of effective connectivity of brain areas based on information theory (Vicente et al., 2011). Unlike the GC analysis, which assumes a linear Gaussian model for the intrinsic dynamics of the signal and a linear interaction, TE does not require a model of the interaction and is inherently nonlinear. Specifically, let {X_t} and {Y_t} denote two random processes and the amount of information is measured using Shannon’s entropy; TE can be written as:

$$T_{X\to Y}=\mathcal{H}\left(Y_t\mid Y_{t-1:t-L}\right)-\mathcal{H}\left(Y_t\mid Y_{t-1:t-L},X_{t-1:t-L}\right)$$ (8)

where $\mathcal{H}(X)$ denotes the Shannon entropy of X. TE is also known as the conditional mutual information $\mathcal{I}(\cdot \mid \cdot )$, with the history of the influenced variable Y_t−1:t−L in the condition:

$$T_{X\to Y}=\mathcal{I}\left(Y_t;X_{t-1:t-L}\mid Y_{t-1:t-L}\right)$$ (9)

In the case of Gaussian variables, TE reduces to GC for VAR processes (Barnett, 2009).

Estimating TE requires the estimation of entropy or joint probability distribution of multi-variate random variables. The transfer entropy (TE) toolbox, is an open-source MATLAB toolbox for transfer entropy estimation (https://github.com/trentool/TRENTOOL3) (Lindner et al., 2011). Note that TE is merely defined in the time domain.

2.6. Computer simulations

The purpose of computer simulations is to investigate several statistical issues related to GC analysis, and compare the estimated results with the ground truth. Specifically, we generated simulated multivariate time series from three different VAR models (order K = 3) with predetermined statistical dependency. The three VAR models have different network topologies and directed functional connectivity, as visualized by graphs (Fig. 3A). In each graph, each variable is represented as a node, and the edge between nodes implies the pairwise statistical dependence. In each model, we generated 20 independent trials and N = 1000 samples per trial.

Figure 3:

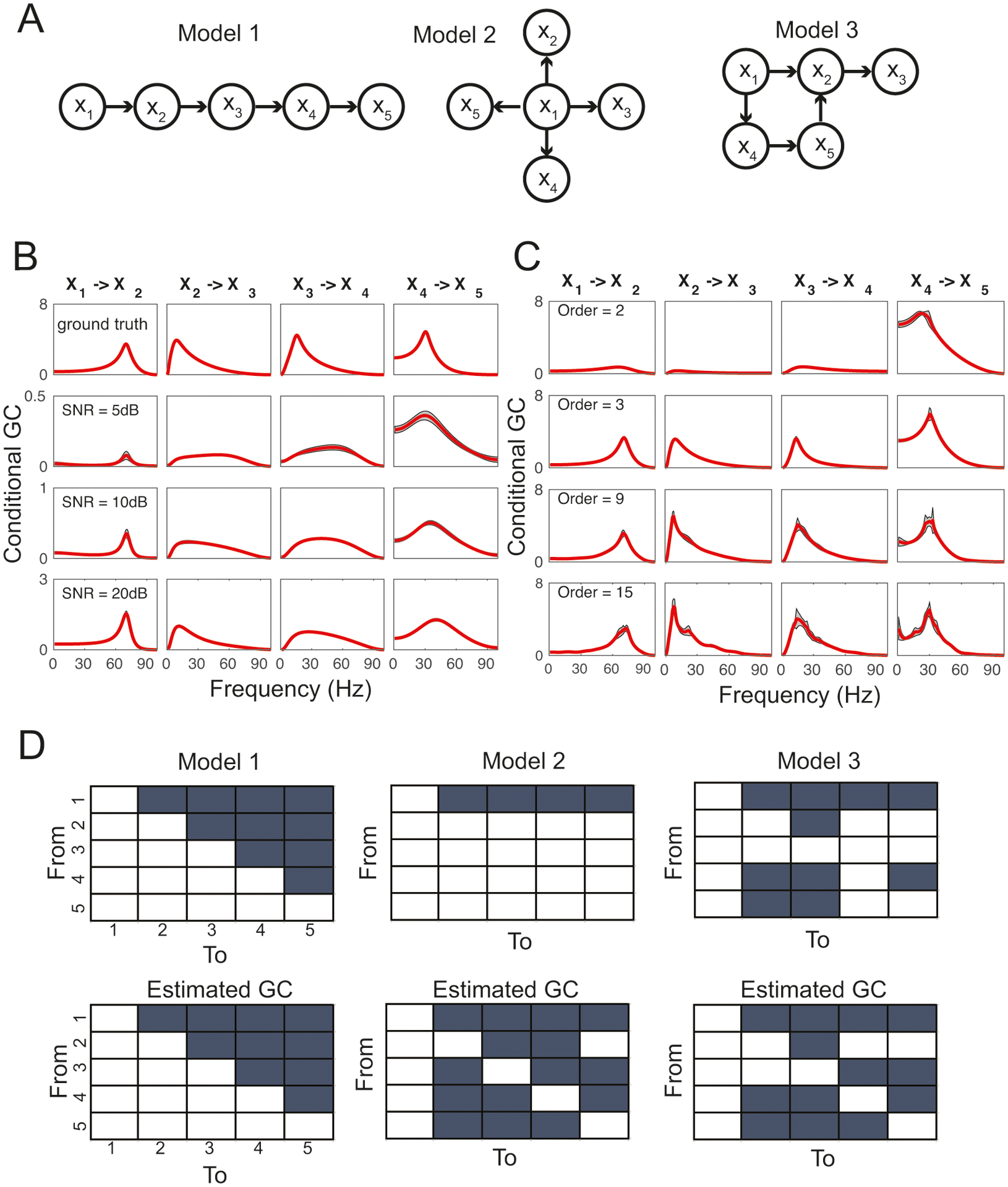
Computer simulation results. (A) Network connectivity. Arrow indicates the directed statistical dependence between two random variables. (B) Impact of different levels of SNR on the conditional GC estimates based on the simulated data from Model 1. Shaded area denotes the standard error of the mean (SEM) across trials. The first row shows the ground truth. (C) Impact of the model mismatch on the conditional GC estimates based on the simulated data from Model 1. Shaded area denotes SEM. (D) True (top) and estimated (bottom) pairwise directed functional connectivity based on two arbitrary nodes. Fill-in entry indicates the presence of directed GC.

Model 1.

The first model has a chain topology, as a described by the following equation:

$$\begin{gathered} \left[\begin{array}{c}{x}_{1,t}\\ x_{2,t}\\ x_{3,t}\\ x_{4,t}\\ x_{5,t}\end{array}\right]=\left[\begin{array}{ccccc}2r_1\text{cos}{\theta }_1& 0& 0& 0& 0\\ -r_2& 2r_2\text{cos}{\theta }_2& 0& 0& 0\\ 0& -r_3& 2r_3\text{cos}{\theta }_3& 0& 0\\ 0& 0& -r_4& 2r_4\text{cos}{\theta }_4& 0\\ 0& 0& 0& -r_5& 2r_5\text{cos}{\theta }_5\end{array}\right]\left[\begin{array}{l}{x}_{1,t-1}\hfill \\ x_{2,t-1}\hfill \\ x_{3,t-1}\hfill \\ x_{4,t-1}\hfill \\ x_{5,t-1}\hfill \end{array}\right] \\ +\left[\begin{array}{ccccc}-r_1^2& 0& 0& 0& 0\\ -r_2& -r_2^2& 0& 0& 0\\ 0& 0& -r_3^2& 0& 0\\ 0& 0& 0& -r_4^2& 0\\ 0& 0& 0& -r_5& -r_5^2\end{array}\right]\left[\begin{array}{l}{x}_{1,t-2}\hfill \\ x_{2,t-2}\hfill \\ x_{3,t-2}\hfill \\ x_{4,t-2}\hfill \\ x_{5,t-2}\hfill \end{array}\right]+\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& r_3& 0& 0& 0\\ 0& 0& r_4& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_{1,t-3}\hfill \\ x_{2,t-3}\hfill \\ x_{3,t-3}\hfill \\ x_{4,t-3}\hfill \\ x_{5,t-3}\hfill \end{array}\right]+\text{w} \end{gathered}$$

where w denotes a random variable drawn from a white Gaussian noise process with zero mean and diagonal covariance matrix Σ. In this model and the subsequent two models, we assumed r₁ = r₂ = r₃ = r₄ = r₅ = 0.9, and θ_i = 2πω_iΔ_t, where Δ_t = 0.05 s, and [ω₁, ω₂, ω₃, ω₄, ω₅] = [70, 8, 15, 30, 80] Hz are the oscillatory frequencies.

Model 2.

The second model has a tree topology, where the parent node sends the common input to four children nodes. The model is described by the following equation:

$$\begin{gathered} \left[\begin{array}{c}{x}_{1,t}\\ x_{2,t}\\ x_{3,t}\\ x_{4,t}\\ x_{5,t}\end{array}\right]=\left[\begin{array}{ccccc}2r_1\text{cos}{\theta }_1& 0& 0& 0& 0\\ -r_2& 2r_2\text{cos}{\theta }_2& 0& 0& 0\\ -r_3& 0& 2r_3\text{cos}{\theta }_3& 0& 0\\ -r_4& 0& 0& 2r_4\text{cos}{\theta }_4& 0\\ -r_5& 0& 0& 0& 2r_5\text{cos}{\theta }_5\end{array}\right]\left[\begin{array}{l}{x}_{1,t-1}\hfill \\ x_{2,t-1}\hfill \\ x_{3,t-1}\hfill \\ x_{4,t-1}\hfill \\ x_{5,t-1}\hfill \end{array}\right] \\ +\left[\begin{array}{ccccc}-r_1^2& 0& 0& 0& 0\\ -r_2& -r_2^2& 0& 0& 0\\ 0& 0& -r_3^2& 0& 0\\ 0& 0& 0& -r_4^2& 0\\ -r_5& 0& 0& -r_5& -r_5^2\end{array}\right]\left[\begin{array}{l}{x}_{1,t-2}\hfill \\ x_{2,t-2}\hfill \\ x_{3,t-2}\hfill \\ x_{4,t-2}\hfill \\ x_{5,t-2}\hfill \end{array}\right]+\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ r_3& 0& 0& 0& 0\\ r_4& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_{1,t-3}\hfill \\ x_{2,t-3}\hfill \\ x_{3,t-3}\hfill \\ x_{4,t-3}\hfill \\ x_{5,t-3}\hfill \end{array}\right]+\text{w} \end{gathered}$$

Model 3.

The third model has a loopy topology, as described by the following equation:

$$\begin{gathered} \left[\begin{array}{c}{x}_{1,t}\\ x_{2,t}\\ x_{3,t}\\ x_{4,t}\\ x_{5,t}\end{array}\right]=\left[\begin{array}{ccccc}2r_1\text{cos}{\theta }_1& 0& 0& 0& 0\\ -r_2& 2r_2\text{cos}{\theta }_2& 0& 0& -r_2\\ 0& -r_3& 2r_3\text{cos}{\theta }_3& 0& 0\\ -r_4& 0& 0& 2r_4\text{cos}{\theta }_4& 0\\ 0& 0& 0& -r_5& 2r_5\text{cos}{\theta }_5\end{array}\right]\left[\begin{array}{l}{x}_{1,t-1}\hfill \\ x_{2,t-1}\hfill \\ x_{3,t-1}\hfill \\ x_{4,t-1}\hfill \\ x_{5,t-1}\hfill \end{array}\right] \\ +\left[\begin{array}{ccccc}-r_1^2& 0& 0& 0& 0\\ -r_2& -r_2^2& 0& 0& -r_2\\ 0& -r_3& -r_3^2& 0& 0\\ -r_4& 0& 0& -r_4^2& 0\\ 0& 0& 0& -r_5& -r_5^2\end{array}\right]\left[\begin{array}{l}{x}_{1,t-2}\hfill \\ x_{2,t-2}\hfill \\ x_{3,t-2}\hfill \\ x_{4,t-2}\hfill \\ x_{5,t-2}\hfill \end{array}\right]+\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ r_2& 0& 0& 0& r_2\\ 0& 0& 0& 0& 0\\ r_4& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_{1,t-3}\hfill \\ x_{2,t-3}\hfill \\ x_{3,t-3}\hfill \\ x_{4,t-3}\hfill \\ x_{5,t-3}\hfill \end{array}\right]+\text{w} \end{gathered}$$

All models share the same parameter values and noise statistics.

2.7. Statistical tests

All GC analysis were conducted on a single-trial basis, and trial-averaged results were further summarized across sessions and animals. The mean and confidence intervals of frequency-dependent GC values were presented. All statistical tests were nonparametric tests (Mann-Whitney or rank-sum test, and signed-rank test), and p < 0.05 was used for the significance criterion.

3. Results

3.1. Simulated data

In the computer simulations, we investigated the impact of signal-to-noise ratio (SNR), model order mismatch, and missing variable on the GC estimate. In each scenario, we estimated the GC based on a single trial, and then computed the trial-average from 20 independent trials.

First, we considered the impact of varying SNR (5 dB, 10 dB, 15 dB, 20 dB) on the conditional GC estimate. By assuming the true model order, we added various amount of additive white (uncorrelated) Gaussian noise. We repeated the model estimation and conditional GC estimation. The result is shown in Fig. 3B and Table 2. With decreasing SNR, we observed several effects: (i) the magnitude of the conditional GC estimate reduced accordingly; (ii) the true positive (TP) rate decreased, and (iii) the false positive (FP) rate increased.

Table 2:

Estimation results of identified functional connectivity in computer simulated data under different levels of SNR.

SNR	Model 1		Model 2		Model 3
	TP	FP	TP	FP	TP	FP
5 dB	4/4	5/16	3/4	2/16	4/5	2/15
10 dB	4/4	4/16	3/4	1/16	4/5	1/15
15 dB	4/4	2/16	4/4	1/16	5/5	1/15
20 dB	4/4	1/16	4/4	0/16	5/5	0/15

Second, we considered the model mismatch issue, where the model order was different from the ground truth (i.e. K = 3). Using Model 1 as an illustration, we varied the model order from 2, 3, 9 to 15, and compared the estimated conditional GC with the ground truth. The result is shown in Fig. 3C. As seen from the figure, the conditional GC estimate was relatively robust with respect to the model order, even when the model order was overestimated. However, as the mismatch gap became larger, the estimation bias and variance increased accordingly.

Third, we considered the impact of missing variables on the conditional GC estimate. For Models 1–3, we selected two arbitrary paired variables and inferred their directed functional connectivity. In the case of two variables, the conditional GC is equivalent to the GC. We assumed the true model order in all computations. The result comparison between the ground truth and estimated GC results is shown in Fig. 3D. As seen in the figure, the parent node had a great impact on the FP of the GC relationship between two conditionally independent variables. In Model 2, all four children nodes {x₂, …, x₅} received common input from the parent node x₁, therefore, the chance of detecting FP among any pair of children nodes was very high.

3.2. Thermal pain in naive and chronic-pain treated rats

In experimental data analysis, we first examined the information flow between the S1 and ACC in thermal stimulus condition, where 250 mW (noxious stimulus) and 50 mW laser (the minimally painful stimulus as a negative control) stimulations were delivered to the rat’s hindpaw in an interleaved manner in each session. In each trial, we used a 1-s post-stimulus period as the pain condition and computed the GC measure; as comparison, we also computed the GC measure during 2-s pre-stimulus baseline.

The group average GC results are shown in Fig. 4A. We found that (i) in the S1→ACC direction, there was a peak in theta band (4–8 Hz) for both baseline and 50/250 mW laser stimulations, suggesting a continual directed information flow from the S1 to ACC. (ii) Comparing the baseline and 250 mW laser stimulation, there was an elevated GC measure in both theta and gamma (30–80 Hz) bands; this increase was more pronounced in 250 mW laser than 50 mW laser stimulation. (iii) In the ACC→S1 direction, we also observed an increase in GC at broadband frequencies during laser stimulations.

Figure 4:

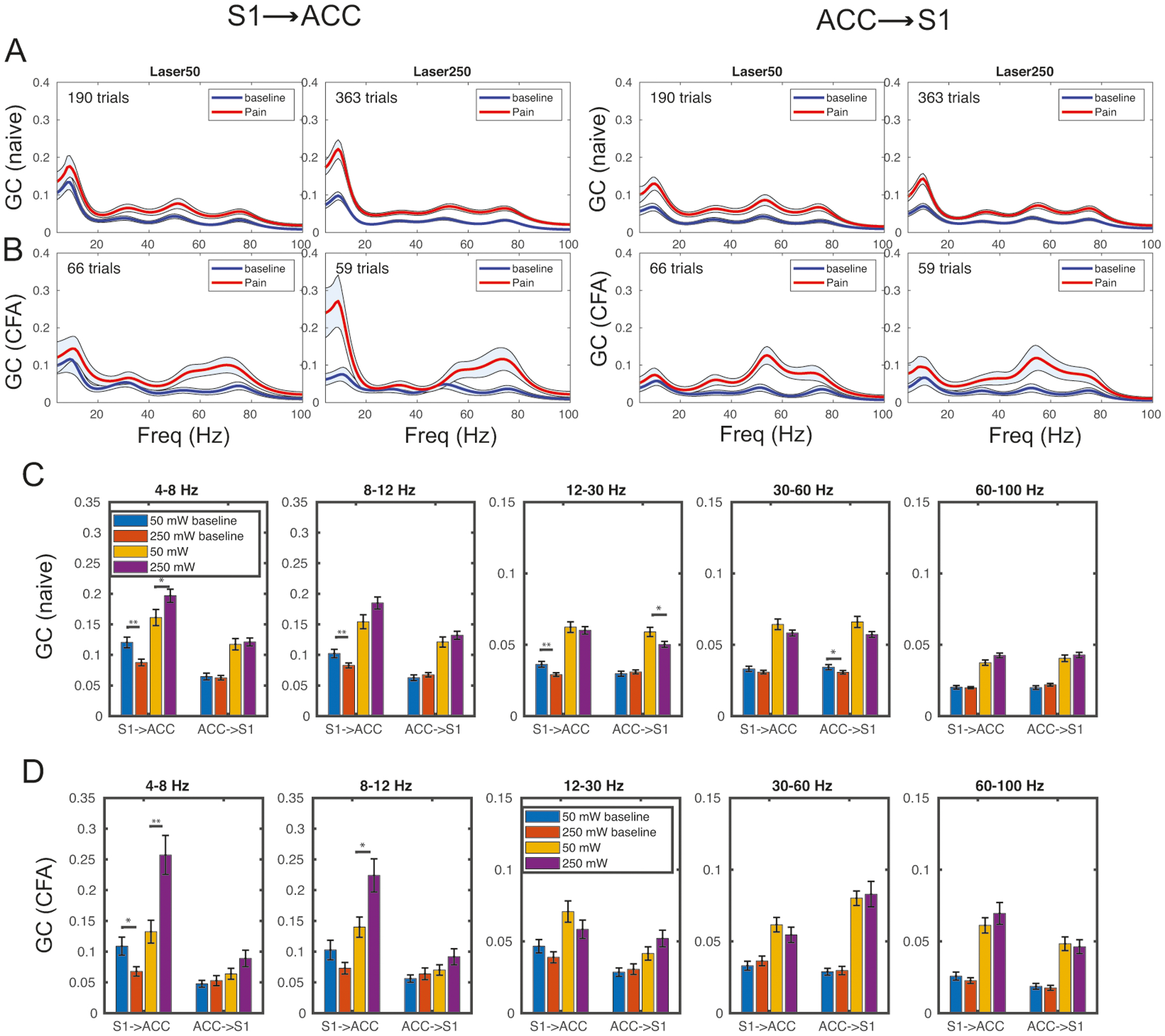
Granger causality (GC) analysis during thermal stimuli (250 mW vs. 50 mW laser) stimulations in naive and CFA rats. (A) Spectral GC estimates in both S1→ACC and ACC→S1 directions. Shaded areas denote the 95% confidence intervals. (B) Similar to panel A, except for CFA rats. (C,D) Population statistics of GC measures at different frequency bands. Rank-sum test: *, p < 0.05; **, p < 0.01.

In the chronic pain state, upon applying the same analysis to LFP recordings from the CFA rat (Fig. 4B), we found that (i) during 50 mW laser stimulation, there was a significant increase in GC at the gamma (50–80 Hz) band in the S1→ACC direction. (ii) During 250 mW laser stimulation, we observed a much larger increase in GC at the theta and gamma bands relative to the baseline, as well as compared to the same condition for the naive animals. (iii) In the ACC→S1 direction, we observed an elevated GC estimate in the gamma band for both 50 mW and 250 mW laser stimulations, which was much more pronounced than in naive animals. (iv) During 250 mW laser stimulation, the GC estimate in the ACC→S1 direction was more pronounced in the gamma than the theta band. Notably, the gamma-band GC peak was at ~55 Hz in the ACC→S1 direction, which was lower than the peak (~75 Hz) in the S1→ACC direction.

To directly compare the naive and chronic pain conditions, we also computed the averaged GC across specific frequency bands: theta (4–8 Hz), alpha (9–12 Hz), beta (12–30 Hz), low gamma (31–60 Hz), and high gamma (61–100 Hz). The results are summarized in Fig. 4C,D. There was a higher likelihood of significant GC difference (rank-sum test, p < 0.05) in the low-frequency than high-frequency band. Put together, these results suggest that there was an increasing GC trend in the S1→ACC direction at low frequency bands with increasing stimulus intensity.

3.3. Mechanical pain in naive and chronic-pain treated rats

Next, we examined the information flow between the S1 and ACC in the presence of mechanical stimuli, where PP (noxious stimulus) and VF (negative control) stimulations were delivered to the rat’s hindpaw in an interleaved manner.

The group average results are shown in Fig. 5A,B. We found that (i) in the S1→ACC direction, there was an increase in GC at the high gamma band during PP stimulation, while the GC increase was much lower during VF stimulation. (ii) In the ACC→S1 direction, there was a broadband increase in GC at both VF and PP stimulations, but the GC increase was more pronounced at the theta band. (iii) In the chronic pain state, surprisingly, there was no significant GC change in the S1→ACC direction, for both VF and PP stimulations; in contrast, there was an increased GC measure across broadband frequencies (4–70 Hz) in the ACC→S1 direction, for both VF and PP stimulations. (iv) During PP stimulations in the chronic pain state, the gamma-band GC peak was at ~78 Hz in the S1→ACC direction, and at ~58 Hz in the ACC→S1 direction.

Figure 5:

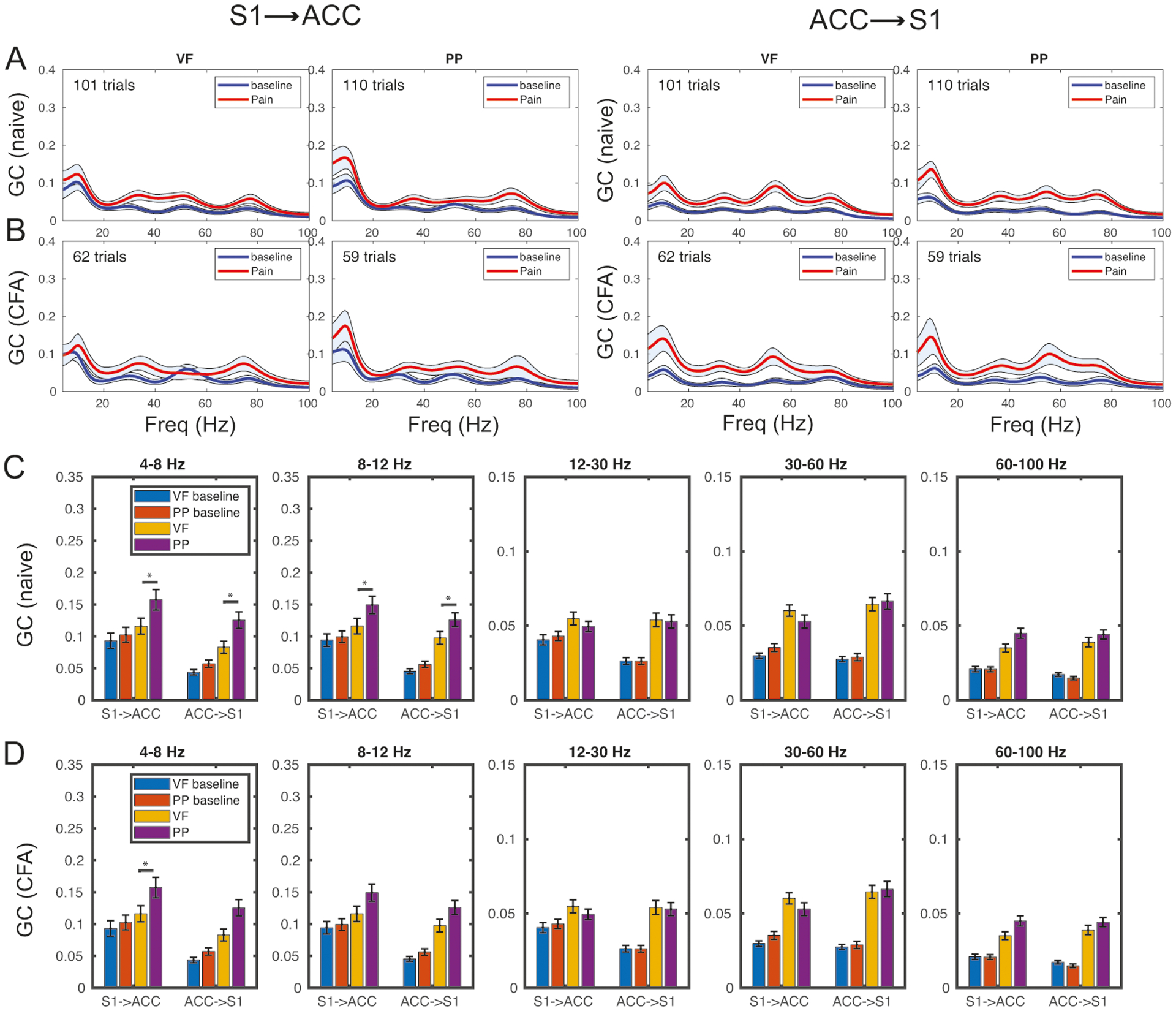
Granger causality (GC) analysis during mechanical stimuli (PP vs. VF) stimulations in naive and CFA rats. (A) Spectral GC estimates in both S1→ACC and ACC→S1 directions. Shaded areas denote the 95% confidence intervals. (B) Similar to panel A, except for CFA rats. (C,D) Population statistics of GC measures at different frequency bands. Rank-sum test: *, p < 0.05.

The group averaged GC comparison across all specific frequency bands are shown in Fig. 5C,D. Similarly, between VF and PP stimulations, there was a significantly increasing GC trend (rank-sum test, p < 0.05) in the S1→ACC direction at low frequency bands.

3.4. Assessment of channel selection

In the case of multichannel LFP recordings, LFP signals within one region were highly correlated. For 64-channel recordings (32 channels from the S1 and 32 from the ACC), estimating a 64×64×K (where K is the MVAR order) matrix in the MVAR model would be computationally intractable in the presence of small trial or sample size. In practice, for the purpose of MVAR estimation, we selected one or two channels from each region. We further investigated the impact of channel selection on GC estimate.

First, we compared the results between a 2 × 2 system (i.e., one ACC and one S1 channel) and a 4 × 4 system (i.e., two ACC and two S1 channels). To illustrate this effect, we selected one recording session during 250 mW laser and PP stimulations from a naive rat. For the 4 × 4 system, we derived four GC channel pairs in either the S1→ACC or ACC→S1 direction, and then conducted the group average. Figure 6 presents the results derived from different configurations of channel selection (Fig. 6).

Figure 6:

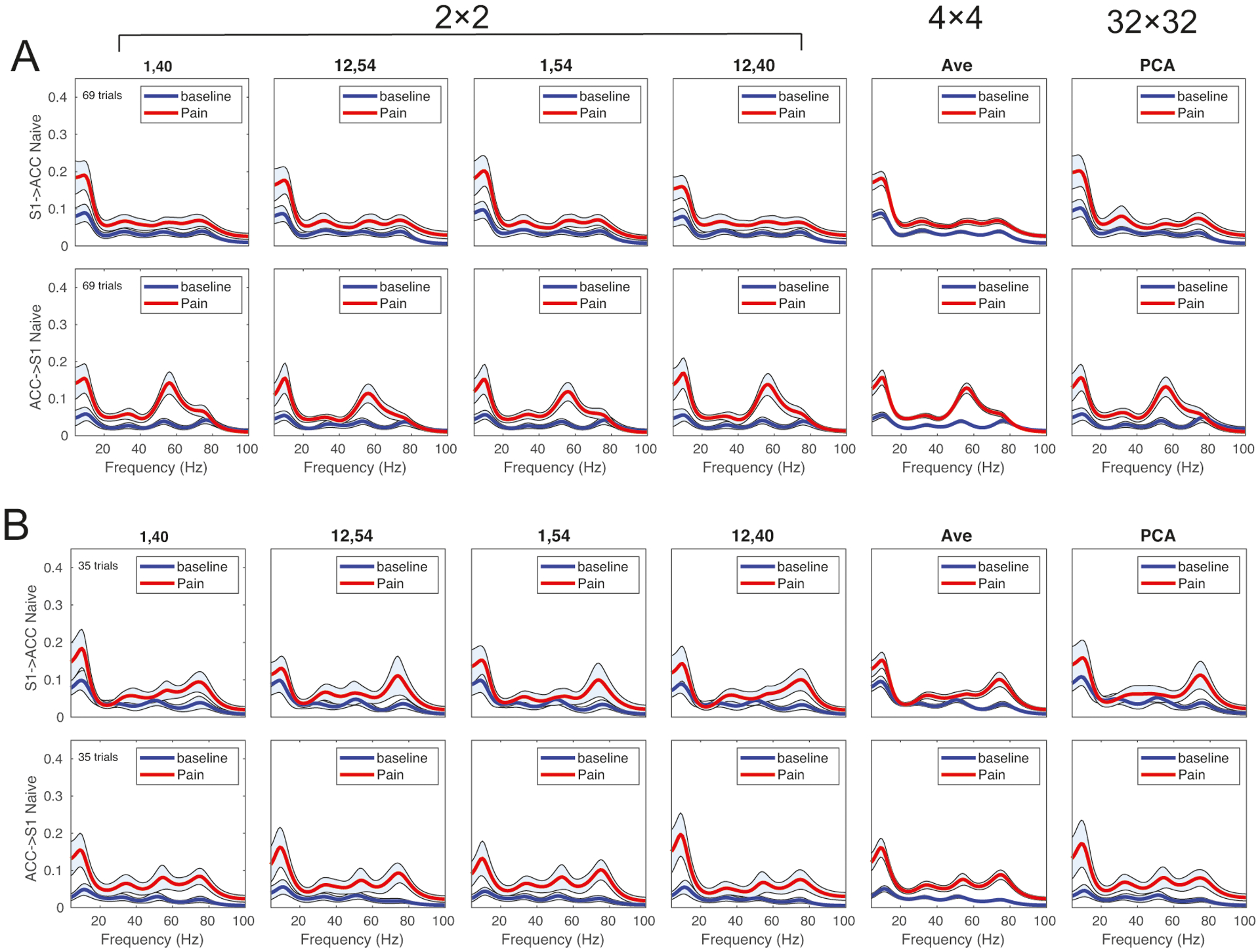
Assessment of channel selection and configuration for Granger causality analysis. The results of the first four columns were derived from a 2 × 2 system, with one channel from the S1 and the other from the ACC (channels #1 and #12 are ACC channels; channels #40 and #54 are S1 channels), whereas the result of the fifth column was derived from a 4 × 4 system. The result of the last column was derived from two PC1, each computed from PCA based on 32 channels within each region. (A) 250 mW laser stimulation. (B) PP stimulation.

Second, we computed the GC based on the dominant principal component (PC1) derived from PCA, one for each brain region (Fig. 2B). The purpose of PCA was to extract the component that explains the largest variance. The result derived from PCA was shown in Fig. 6 (last column). As seen in both thermal and mechanical pain conditions (from a naive rat), the derived GC measures were very similar. Taken together, these results suggest the consistency of GC analysis with respect to LFP channel selection. Furthermore, although we only illustrated this finding using a naive rat, this consistency also held for the CFA rat recording (results not shown).

3.5. Dynamic Granger causality analysis

Thus far, we have used a fixed interval to estimate the MVAR coefficients and derived the GC measures. To generalize the single-trial analysis to a time-varying manner (Ding et al., 2000; Cekic et al., 2018), we used a moving window of 1 s (step size 25 ms) to estimate the time-varying GC. For the sake of consistency, we used the same model order as before.

As an illustration, we selected one rat that underwent both laser and PP stimulations, before and after CFA—which produced a total of four pain conditions. Figure 7 shows the dynamic spectral GC estimates under four conditions (columns) at four frequency bands (rows). In 250 mW laser stimulations, we observed a sharp increase in GC (around the stimulus onset) at the theta, alpha+beta, low and high gamma bands. Interestingly, the GC in the S1→ACC direction generally showed a higher value than that in the ACC→S1 direction, except in the low gamma band. Comparing Fig. 7A with Fig. 7B, the overall GC trend remained similar, but the GC magnitude was higher in the chronic pain state, especially at the theta and high gamma bands in the S1→ACC direction. During PP stimulations, we observed more variability during the baseline, but the overall GC trend remained similar between pre and post-CFA conditions (Fig. 7C and Fig. 7D).

Figure 7:

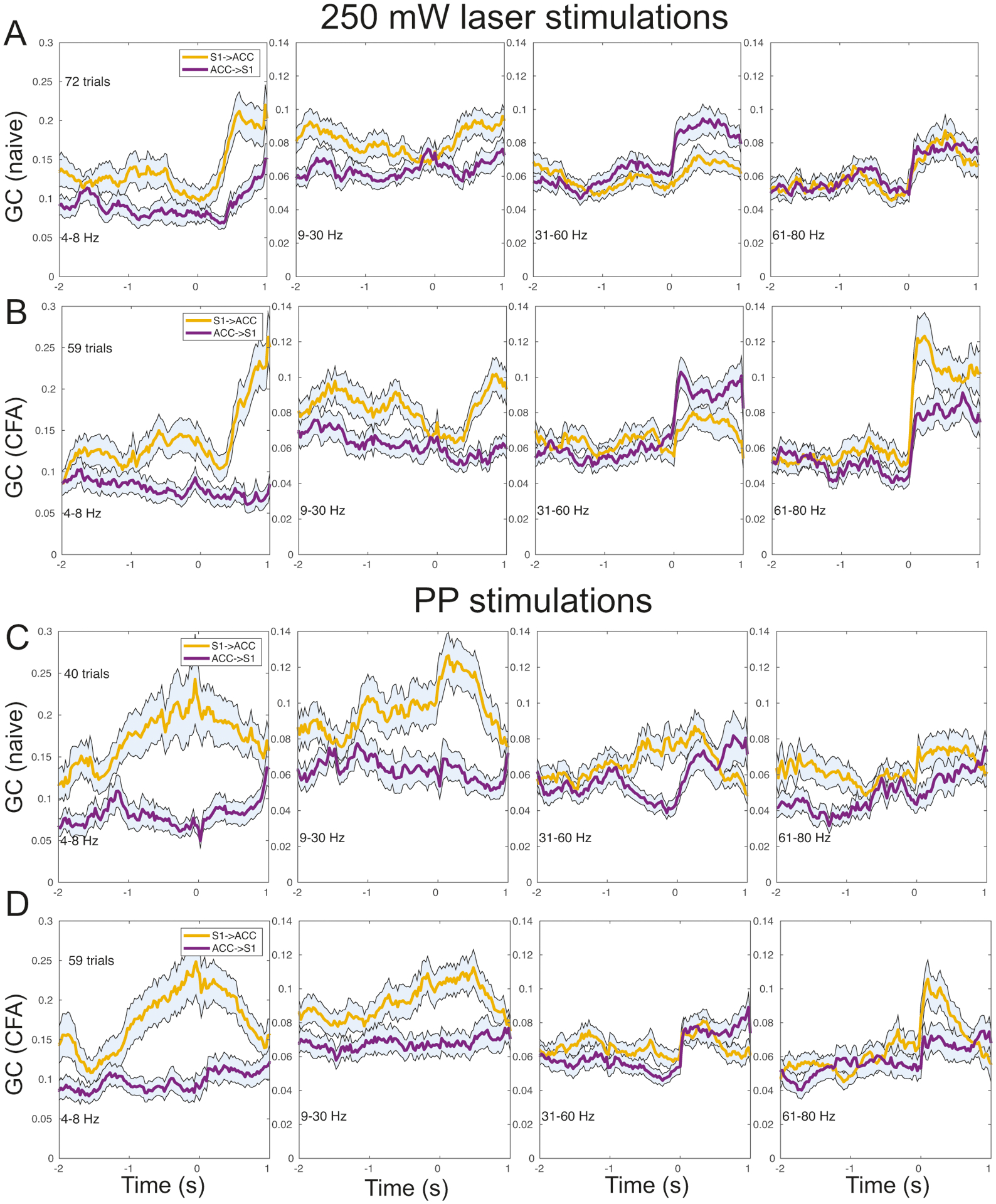
Illustration of dynamic Granger causality (GC) analysis based on one animal’s recordings before and after CFA. Time-varying GC estimates were derived from a moving window of 100 ms with a step size of 25 ms. Time 0 denotes the paw withdrawal onset. (A,B) Frequency-dependent GC measures in both S1→ACC and ACC→S1 directions at four frequency bands during 250 mW laser stimulations (A, naive condition before CFA; B, chronic pain condition after CFA). Shaded areas denote the 95% confidence intervals. (C,D) Similar to panels A and B, except for PP stimulations.

We further investigated the temporal relationship across different frequency bands. Motivated by the hypothesis of predictive coding in pain perception (Bastos et al., 2012; Ploner et al., 2017), we focused on the GC in the S1→ACC direction at high gamma band (61–80 Hz) and the ACC→S1 direction at low gamma band (31–60 Hz). As seen in single-trial examples (Fig. 8A), at around the withdrawal onset (time 0), the GC increased first in the S1→ACC direction, followed by the GC increased in the ACC→S1 direction at a lower frequency band. This temporal gap between two directions varied (~25–50 ms) across single trials, suggesting the possibility of an information loop within the predictive coding framework. Despite the trial variability, the temporal relationship was still visible in the trial-averaged plots (Fig. 8B).

Figure 8:

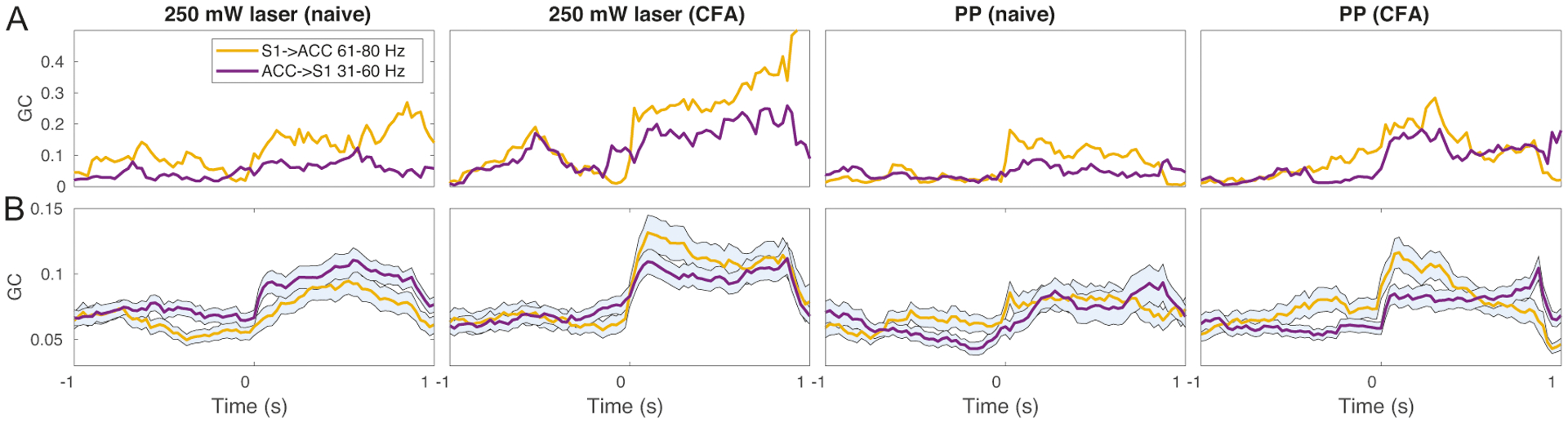
Temporal coordination of cross-frequency Granger causality (GC) between the S1→ACC (61–80 Hz, yellow) and ACC→S1 (31–60 Hz, blue) directions. (A) Representative single-trial examples during four pain conditions shown in Fig. 7. Time 0 denotes the paw withdrawal onset. As seen, the rise time of yellow trace appeared slightly earlier than the rise time of blue trace in each example. (B) Corresponding trial average during four pain conditions shown in Fig. 7. In all but one plots, the blue trace lagged behind the yellow trace in the rise time.

Next, we examined whether the dynamic GC statistics correlated with the paw withdrawal behavior. We computed the a moving window-averaged GC statistics (across frequency bands and in both directions), and further calculated the Spearman’s rank correlation between the log-GC value and the paw withdrawal latency. Specifically, the significance of rank correlation was assessed by at each step (25 ms) of the moving window—starting from the stimulus onset until 1 s after the withdrawal onset. For notation simplicity, we labeled time 0 as the withdrawal onset, and examined the time intervals that showed statistical significance in rank correlation. We systematically investigated the dynamic GC at various frequency bands and compared them with the paw withdrawal latency. In the S1→ACC direction, we found a significant negative rank correlation (p < 0.05) at specific frequency bands and specific temporal window: beta band ([0, 0.25] s, shaded area, Fig. 9B), and gamma band ([−0.075, −0.025] s, Fig. 9D). These results suggest that at the early stage of sensory processing, the information flow was the strongest at the high frequency bands from the S1 to ACC, and the significant temporal window appeared sooner in the gamma band than the other lower frequency bands.

Figure 9:

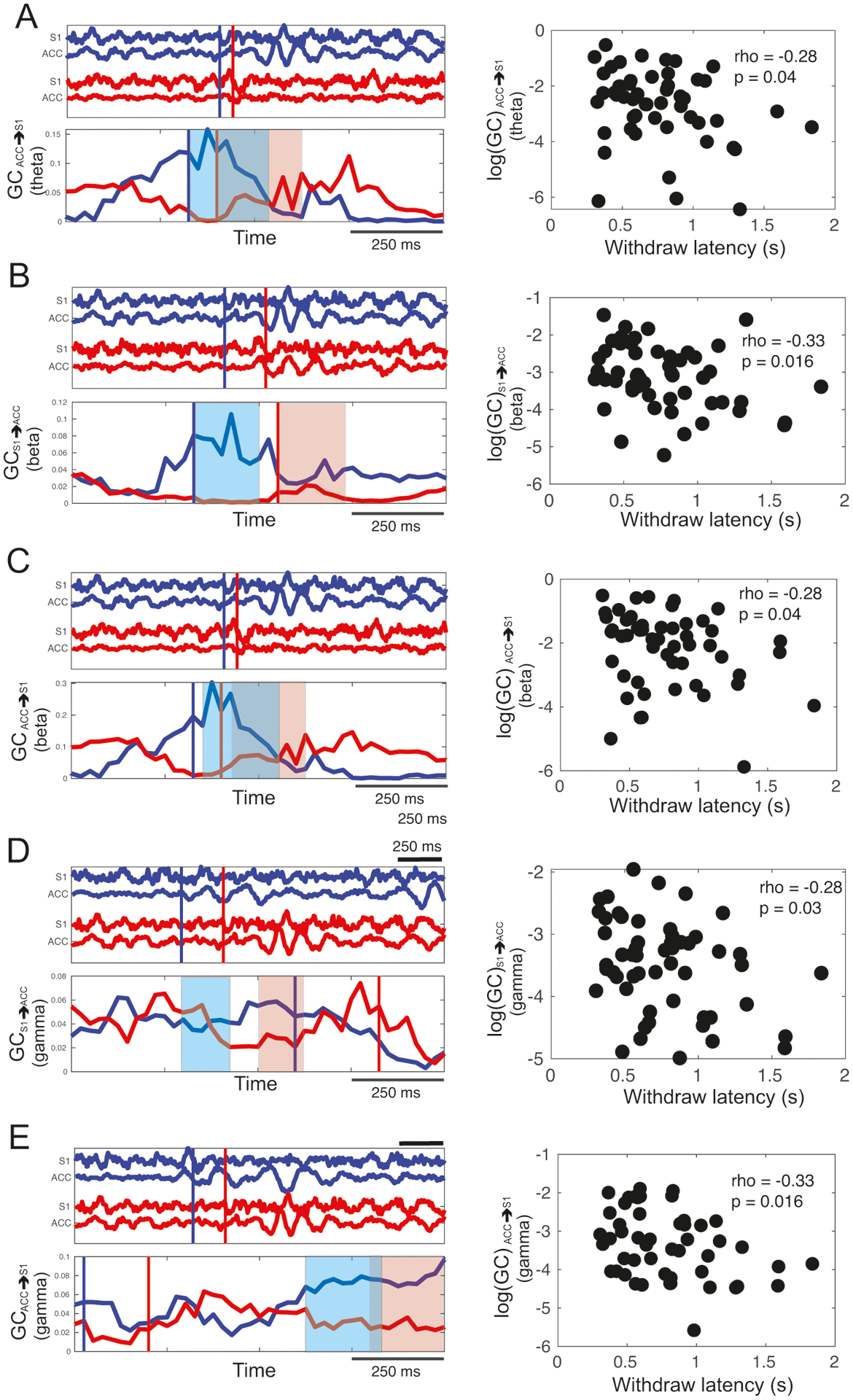
Left column: Two pairs of LFP signal trials (red and blue) from channels S1 and ACC (top part of every panel from A to E) with corresponding estimates of time-varying Granger causality (GC) (bottom part of every panel from A to E). In all panels the blue trials have a shorter withdrawal latency than the red trials. The vertical red and blue lines mark the animal’s paw withdrawal time from the respective trials. Note that time bar is different between the top and bottom plots. Right column: The scatter plot between the withdrawal latency and the log(GC) value computed within a specific moving window (i.e., the shaded area shown in the plots of time-varying GC). The Spearman’s rank correlation rho and p values (n = 54 trials) are shown. The results were illustrated for different frequency bands and directions: (A) GC_ACC→S1 at theta band. (B) GC_S1→ACC at beta band. (C) GC_ACC→S1 at beta band. (D) GC_S1→ACC at gamma band. (E) GC_ACC→S1 at gamma band.

In the ACC→S1 direction, we also found a significant negative rank correlation (p < 0.05) between the log-GC value and the paw withdrawal latency at specific frequencies and temporal window: theta band ([0, 0.25] s, Fig. 9A), beta band ([0.1, 0.35] s, Fig. 9C) and gamma band ([0.5, 0.75] s, Fig. 9E). Notably, the temporal window of significance shifted to a later time at the gamma band.

3.6. Comparison with the transfer entropy method

As a method comparison and consistency test, we used the transfer entropy (TE) measure to estimate the directed information flow using both simulated and experimental data.

In computer simulated data (Model 1), we found qualitative similar results between the GC and TE (Fig. 10). Specifically, both estimates varied depending on the number of sample size, and the estimate biases were quite large when the sample size was small. The GC estimates became more stable at around 4000 samples. In contrast, two TE estimates showed a rising trend with increasing sample size. The TE estimate between all variable pairs is shown in Table 3.

Figure 10:

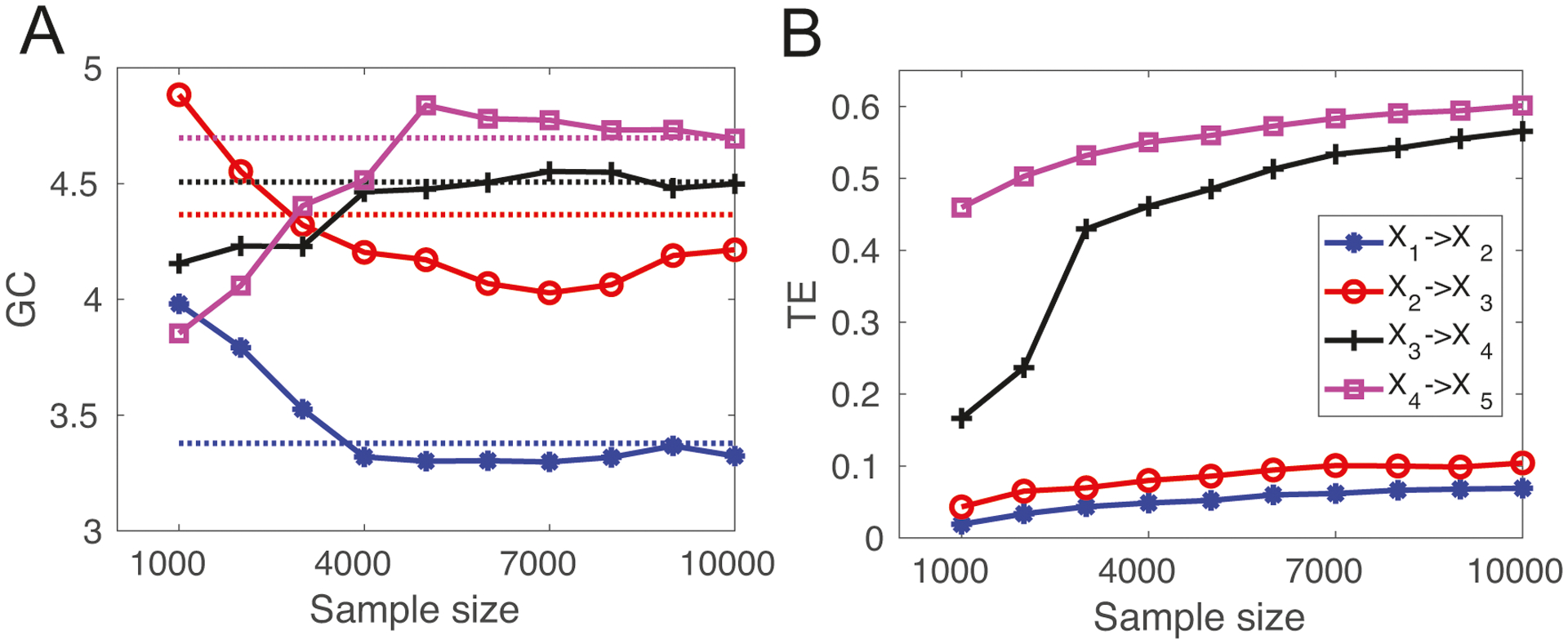
Comparison between the Granger causality (GC) and the transfer entropy (TE) method for computer simulated data (Model 1). (A) The estimated peak GC values with respect to the number of simulated samples. The horizontal dashed lines represent the respective ground truth values. With more samples, the GC estimates became more accurate. (B) The estimated TE with respect to the number of simulated samples.

Table 3:

The TE estimate between all paired variables for the computer simulated data (the numbers in bold font indicate TPs).

From╲To	1	2	3	4	5
1		0.069	−0.012	−0.008	0.001
2	0.008		0.104	0.057	0.093
3	−0.002	−0.013		0.566	0.384
4	0.001	−0.014	0.015		0.601
5	0.003	−0.007	−0.025	0.058

We further tested the TE using one experimental recording session during laser stimulations. We first applied the TE analysis to the broadband LFP signals. The results are shown in Fig. 11A. We found that the TE estimate was greater in 250 mW laser stimulation than in baseline, in both S1→ACC (signed-rank test, p = 0.0038, n = 72 trials) and ACC→S1 (p = 0.0295) directions. In contrast, the TE estimate showed no statistical difference between 50 mW laser stimulation and its own baseline (signed-rank test, p = 0.32 and p = 0.76, for the respective directions, n = 46 trials). In addition to the broadband LFP signals, we further band-pass filtered the LFP signals in the theta and gamma frequency bands, and repeated the TE estimation for those narrowband signals. In the theta band, we found a statistical significance between 250 mW laser and its baseline (Fig. 11B; p < 10⁻⁴ in the S1→ACC direction and p = 0.0435 in the ACC→S1 direction). However, no statistical difference was found for the gamma band (Fig. 11C).

Figure 11:

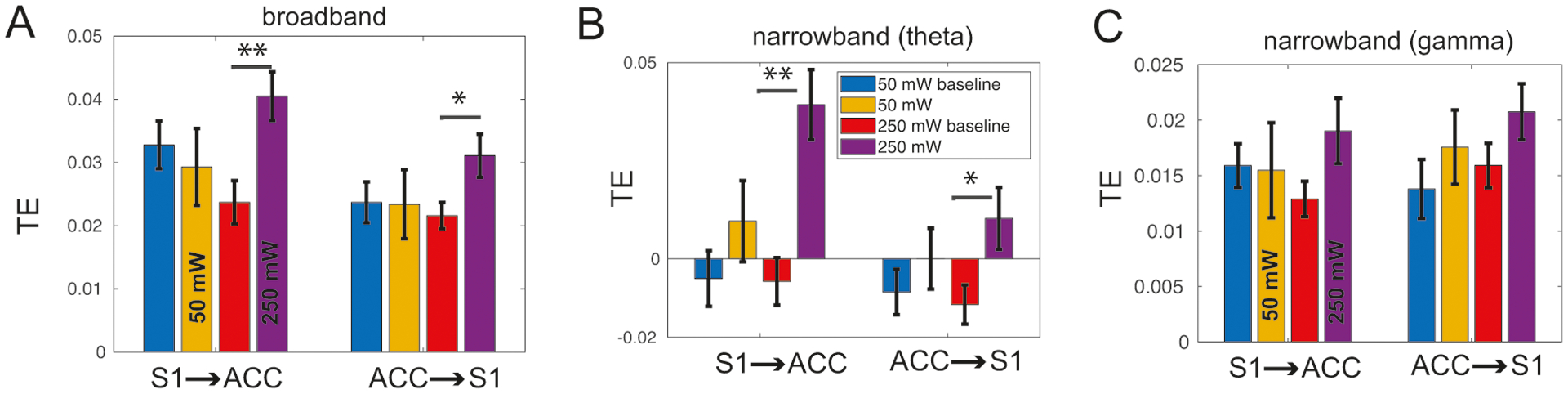
Comparison between the Granger causality (GC) and the transfer entropy (TE) method for experimental data. (A) The estimated TE in both S1→ACC and ACC→S1 directions during laser stimulations (50 mW, n = 46 trials; 250 mW, n = 72 trials). Signed-rank test: *, p < 0.05; **, p < 0.01. (B, C) Figure legend same as panel A, except for the narrowband signals filtered within the theta and gamma bands, respectively.

Put together, these results suggest that GC and TE methods tend to produce qualitatively similar outcome related to the information flow direction, but the TE method is not able to identify frequency-specific statistical dependency.

4. Discussion

4.1. Link to experimental evidence

Multiple lines of experimental evidence have pointed to a direct S1→ACC projection in central cortical pain circuits (Sesack et al., 1989; Sesack et al., 1992; Eto et al., 2011; Bliss et al., 2016; Tan et al., 2019). The nociceptive input to the ACC from the S1 is consistent with our functional connectivity and GC analysis. However, it remains experimentally unknown whether there is an indirect ACC→S1 pathway through the cortico-cortical feedback that modulates pain processing.

The GC increase in the theta band during stimulus presentation may be induced by the event-related potentials (ERPs) or evoked potentials (Pinheiro et al., 2016). Generally, the amplitude of ERP is larger when being evoked by noxious stimuli than non-noxious stimuli. In rodent experiments, ERPs are temporally associated with stereotyped pain behaviors—such as the paw withdrawal and licking (Deuis et al., 2017; Xiao et al., 2019). Our prior result has indicated that the peak ERP latency occurs sooner (~200–300 ms) in the S1 than in the ACC during 250 mW laser stimulations (Xiao et al., 2019). Therefore, although there was a GC peak at the theta band during baseline, the peak amplitude was much higher during noxious stimulus (e.g., 250 mW laser and PP) stimulations; the chronic pain state further amplifies this situation.

There was also a noticeable GC peak at the high gamma band during noxious nociceptive stimulation. In the literature, S1 gamma oscillations have been implicated in encoding the subjective pain intensity (Gross et al., 2007; Zhang et al., 2012). In the chronic pain state, CFA mice with inflammatory pain show elevated resting gamma activity and increased gamma power in response to sub-threshold stimuli, in association with nociceptive hypersensitivity (Tan et al., 2019), which may contribute to the increased information flow at high gamma band in both S1→ACC and ACC→S1 directions.

Chronic pain is known to induce anatomically non-specific increase in the aversive processing of the ACC (Zhang et al., 2017; Zhou et al., 2018). In chronic pain state, we observed the GC peak was at a higher frequency (~75 Hz) in the S1→ACC direction than in the ACC→S1 direction (at ~55 Hz). This observation was consistent in both thermal and mechanical pain conditions (Fig. 4B and Fig. 5B). This finding also supports the hypothesis of information-loop within the predictive coding framework (Bastos et al., 2012; Song et al., 2019a; Song et al., 2019b), such that the modulation frequency was higher in the bottom-up (high gamma) than in the top-down (low gamma or beta) pathways. While the S1→ACC projection represents a bottom-up nociceptive pathway, the ACC→S1 direction may represent a top-down pathway.

4.2. Distinction between thermal and mechanical pain responses

There are three main types of noxious stimuli: mechanical, thermal/cold, and chemical. To initiate a pain signal, the stimulus has to be above a threshold that would be sufficiently intense to cause damage to the tissues. Several human or nonhuman primate fMRI studies have shown that multiple brain regions, including the S1, ACC, secondary somatosensory cortex (S2), and prefrontal cortex (PFC), are activated during noxious heat and various forms of tactile stimuli (Disbrow et al., 1998; Chen et al., 2002; Chen et al., 2012; Bliss et al., 2016). At the single-cell level, modality-specific pain-modulated neurons have showed mixed selectivity in the S1 and ACC. In addition, the ACC is involved in signaling the unpleasantness associated with different types of acute pain (Bliss et al., 2016). However, the exact circuit mechanisms of modality-specific or stimulus-dependent cortical pain processing remain incompletely understood.

In rodent experiments, mechanical stimuli were shorter in duration and more focused in location. In our analysis, we have observed slightly different GC results between thermal and mechanical pain stimuli. Specifically, in dynamic GC analysis on some animals, we observed a sharper increase in gamma-band GC (Fig. 7) during thermal pain than during mechanical pain stimulations. However, we also observed a high degree of trial variability and subject variability, which might be contributed by the variability in pain behavior.

4.3. Limitation and future work

In model-based causality analysis, the data or model stationarity was assumed in the fixed interval or a moving window. In the presence of data non-stationarity, it is possible to adapt the state-space analysis or Kalman filter for online VAR model estimation (Havlicek et al., 2010; Blinowska, 2011; Cekic et al., 2018). In addition, the Granger causality has a limitation due to the effect of unobserved common input (Cohne and Tsuchiya, 2018), which was also confirmed in our computer simulations. Together, the non-stationarity, small sample size, low SNR, and common input would affect the GC estimate in experimental data analysis. In the context of pain perception, multiple and distributed brain circuits, including the PFC, orbitofrontal cortex (OFC), nucleus accumbens (NAc) and insular cortex, may interact with the S1 and ACC. However, simultaneous extracellular recordings of more than two brain regions would provide new research opportunities along this direciton.

The standard GC analysis has assumed the “time-lagged” causality and ignored the “instantaneous” (i.e., zero-lag) causality (Ding et al., 2006; Wen et al., 2013). While such instantaneous effect is less likely between the S1 and ACC given the cortico-cortical transmission delay, it is straightforward to adapt our current estimation framework to assess the frequency-dependent GC with instantaneous effects (Faes et al., 2013).

Thus far, we have focused on evoked acute pain in naive and chronic pain-treated animals. Spontaneous pain, unlike evoked pain triggered by noxious sensory stimuli, is primarily driven by internal processing. Spontaneous pain events may be induced by repeated noxious stimulations in naive animals, or may occur frequently in the chronic pain state (Bennett, 2012). Since there is a lack of ground truth in animal studies, identification of putative spontaneous pain events remains a challenge for potential GC analysis.

Finally, GC analysis only represents one of data-driven causal inference methods; the validity of any functional or effective connectivity depends on the context, and a priori plausibility (Marinescu et al., 2018). Therefore, the interpretation of GC should be also taken with caution, especially in the presence of unobserved common input. Several critical statistical issues and limitations have been discussed in the literature (Hu et al., 2011; Stokes and Purdon, 2017; Barnett et al., 2018). We believe that combining data-driven GC analyses with closed-loop experimental manipulations (Jazayeri and Afraz, 2017), such as optogenetic activation or inactivation of upstream circuits (Dale et al., 2018), can reveal new mechanistic insight into cortical pain processing.

4.4. Conclusion

In summary, we have applied GC analysis to examine the directed functional connectivity between the S1 and ACC during cortical pain processing. The increased directed information flow during noxious stimulus stimulation has supported experimental findings that the S1→ACC projection recruits pain-responsive ACC neurons to encode pain. Our LFP-based GC analysis has been purely driven by model-based inference. In the future, integrated studies of multimodal “causality” at fine temporal resolution are required to fully understand how information is temporally integrated from individual cortical nociceptive circuits and how such signal integration encodes the perception of pain.