Deformation-induced crystalline-to-amorphous phase transformation in a CrMnFeCoNi high-entropy alloy

In situ TEM experiments reveal the crystalline-to-amorphous phase transformation in an ultrafine-grained Cantor alloy.

Abstract

The Cantor high-entropy alloy (HEA) of CrMnFeCoNi is a solid solution with a face-centered cubic structure. While plastic deformation in this alloy is usually dominated by dislocation slip and deformation twinning, our in situ straining transmission electron microscopy (TEM) experiments reveal a crystalline-to-amorphous phase transformation in an ultrafine-grained Cantor alloy. We find that the crack-tip structural evolution involves a sequence of formation of the crystalline, lamellar, spotted, and amorphous patterns, which represent different proportions and organizations of the crystalline and amorphous phases. Such solid-state amorphization stems from both the high lattice friction and high grain boundary resistance to dislocation glide in ultrafine-grained microstructures. The resulting increase of crack-tip dislocation densities promotes the buildup of high stresses for triggering the crystalline-to-amorphous transformation. We also observe the formation of amorphous nanobridges in the crack wake. These amorphization processes dissipate strain energies, thereby providing effective toughening mechanisms for HEAs.

INTRODUCTION

High-entropy alloys (HEAs) consist of five or more elements in an equiatomic or near-equiatomic composition (1). Several HEAs have been shown to exhibit exceptional mechanical properties. For example, the CrMnFeCoNi Cantor alloy (2) demonstrates excellent mechanical properties at both room and cryogenic temperatures with the tensile strength up to ~1 GPa, ductility of ~60 to 70%, and fracture toughness exceeding ~200 MPa$\sqrt{\mathrm{m}}$ (3–7). Such a superior combination of strength, ductility, and toughness, as promoted by decreasing temperature (8, 9), stems from the synergy of several deformation mechanisms in the Cantor alloy, including dislocation slip and twinning at early stages (3, 10, 11) and crack bridging at late stages of deformation (12, 13).

The multiple principal elements in HEAs result in high configurational entropies, which were thought to be sufficient for the entropic stabilization of initial random solid solution phases against the formation of intermetallic compounds (14–18). However, recent studies indicated that entropic stabilization is often inadequate to maintain the initial phases of HEAs under thermomechanical loading. For example, a phase transformation from the face-centered cubic (FCC) to hexagonal close-packed (HCP) structure occurred when the Cantor alloy was deformed at high pressure (19, 20) or the CrFeCoNi HEA was deformed at cryogenic temperatures (21). Decomposition of the single-phase Cantor alloy occurred after prolonged annealing at intermediate temperatures (22) or under high-pressure torsion followed by annealing (23). Since most of these phase transformation phenomena have been previously observed in conventional alloys, it remains underexplored regarding how multiple principal elements in HEAs affect the emergence of new phase transformation pathways and products (24).

In the present study, we conduct in situ transmission electron microscopy (TEM) straining experiments to investigate the deformation-induced phase transformation in the Cantor alloy of CrMnFeCoNi at room temperature. We study two types of CrMnFeCoNi samples with the respective average grain size of 500 nm and 10 μm, referred to as ultrafine-grained (UFG) and coarse-grained (CG) Cantor alloys, respectively. Our in situ TEM straining experiments reveal an unexpected phenomenon of crystalline-to-amorphous phase transformation at the crack tip of UFG samples. This contrasts with the dominant plastic deformation mechanisms through crystalline defects at the crack tip of CG samples. Molecular dynamics (MD) simulations are performed to reveal the atomic bonding effects on the dislocation-mediated processes of crystalline-to-amorphous phase transformation. The mechanistic insights gained could be harnessed to enhance the toughening of HEAs.

RESULTS

Crystalline-to-amorphous phase transformation

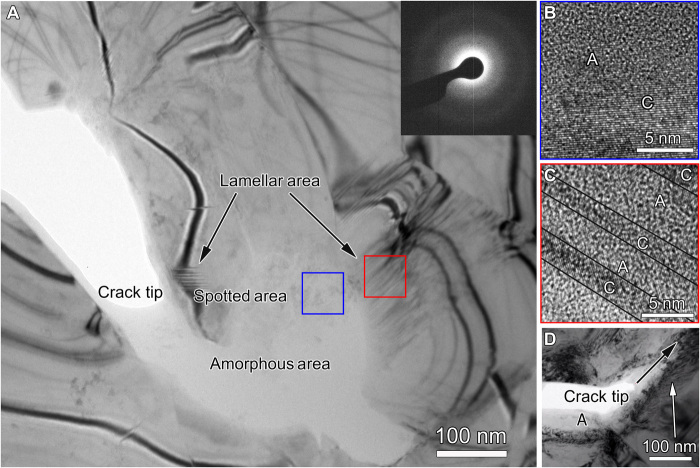
During in situ TEM tensile straining experiments, we observed the crystalline-to-amorphous phase transformation near the crack tip of a UFG Cantor alloy sample. Figure 1A presents a bright-field diffraction contrast TEM image near a crack tip. In addition to bending contours (i.e., equal inclination fringes) that are typically observed in crystalline specimens, this TEM image reveals three different types of areas near the crack tip, including the amorphous area with uniform bright contrast, the spotted area with dark spots randomly distributed within a bright contrast background, and the lamellar area with alternate bands of dark and bright contrast. In general, a crystalline structure gives rise to strong electron diffraction and thus results in relatively dark contrast in bright-field TEM images; however, an amorphous structure does not produce strong electron diffraction, thus making the amorphous area brighter than the crystalline one. The inset of diffraction pattern in Fig. 1A taken from the bright-contrast area further confirms the amorphous structure. Hence, the three different areas in Fig. 1A correspond to different combinations of crystalline and amorphous phases that yield different patterns of diffraction contrast. Such difference was further examined by high-resolution TEM (HRTEM) imaging. Figure 1B shows an HRTEM image taken from a spotted area (enclosed by a blue square in Fig. 1A). In this image, the region with an overall bright contrast exhibits random variations of local contrast, indicating an underlying disordered structure (marked by A); in contrast, the region with an overall dark contrast displays lattice fringes with fine parallel lines, indicating an underlying crystalline structure (marked by C). In such kind of spotted areas, the amorphous and crystalline regions are mixed together randomly, and the amorphous regions have a higher volume fraction than the crystalline regions. Figure 1C shows an HRTEM image of a lamellar area (enclosed by a red square in Fig. 1A), where the alternate bands of bright and dark contrast correspond to the amorphous and crystalline phases, respectively. The volume fractions of the crystalline and amorphous phases are comparable in the lamellar areas. In addition, the areas with uniform bright contrast in Fig. 1A display random variations of local contrast in their HRTEM images, thus confirming the only amorphous phase in these areas. Figure 1D presents a low-magnification TEM image of the overall crack-tip morphology. In this image, the black arrow points to the direction of crack propagation, and the white arrow indicates the dislocations in the wake of the propagating crack.

Fig. 1. Microstructures near a crack tip of a UFG Cantor alloy sample, from in situ TEM tensile straining experiment.

(A) TEM image showing all three types of amorphous, spotted, and lamellar areas near a crack tip. The inset of diffraction pattern is taken from the amorphous area. (B) HRTEM image of a spotted area taken from the blue square area in Fig. 1A, showing the coexistence of crystalline and amorphous regions, as marked by C and A, respectively. (C) HRTEM image of a lamellar area taken from the red square area in Fig. 1A. (D) Low-magnification TEM image of a crack tip captured during in situ straining experiment. The black arrow points to the direction of crack propagation. A high density of dislocations is indicated by the white arrow. An amorphous area in the crack wake is indicated by the symbol A.

Figure 2A shows the detailed analysis of a typical lamellar area containing the alternate crystalline and amorphous bands, with their respective average band thickness of ~1.7 and 2.3 nm. Fast Fourier transformation (FFT) analysis indicated that misorientations between the crystalline bands were all less than 1°. The inset of Fig. 2A shows the FFT pattern of a local area (enclosed by a white square in Fig. 2A) in a crystalline band marked by #3. One-dimensional inverse-FFT images in Fig. 2 (B and C) reveal the two different sets of planes within the crystalline band #3, respectively. Several dislocations, marked by the symbol ⊥, were identified near the boundary between the crystalline and amorphous bands.

Fig. 2. Analysis of a lamellar structure.

(A) HRTEM image of a typical lamellar area. Four crystalline bands are marked as 1, 2, 3, and 4. Inset is an FFT pattern from the squared area. The four spots (marked by red arrows) in the FFT pattern correspond to two different sets of planes (33). (B and C) One-dimensional Fourier-filtered image of the squared area in (A), showing each of the two sets of {111} planes. Dislocations are marked with the symbol ⊥.

Energy-dispersive x-ray spectroscopy was used to map elemental distributions near the crack tip. There were no appreciable compositional variations in the amorphous, spotted, and lamellar areas (table S1). The chemical composition of the five constituent elements remains nearly equiatomic. Hence, the crystalline-to-amorphous phase transformation results in no obvious changes of elemental distributions near the crack tip of the UFG Cantor alloy.

Figure 3 shows the time-series TEM images of a dynamic process of crystalline-to-amorphous phase transformation ahead of a crack tip. In Fig. 3A, a large crystalline region coexists with its surrounding amorphous region. This crystalline region had a length of ~8 nm along the crack extension direction and was separated to the crack tip by an amorphous region of ~3 nm long. Subsequent TEM imaging (Fig. 3, B to D) shows that the size of the crystalline region decreased, and meanwhile, the size of the amorphous region increased, while the crack tip propagated only by a small distance of ~1 nm. These TEM observations directly reveal the real-time process of crystalline-to-amorphous phase transformation ahead of a crack tip. These in situ TEM images were captured at the beginning and end of this in situ experiment (fig. S1), and they further corroborate the occurrence of crystalline-to-amorphous phase transformation.

Fig. 3. Crack-tip dynamic process of crystalline-to-amorphous transformation from in situ straining experiment.

(A) HRTEM image indicates the coexistence of amorphous and crystalline structures at time t = 7 s. The crystalline region is 3 nm in front of the crack tip and has a length of 8 nm along the crack propagation direction. (B to D) Time-series HRTEM images showing the decreasing crystalline region and the increasing amorphous region.

Amorphous nanobridges

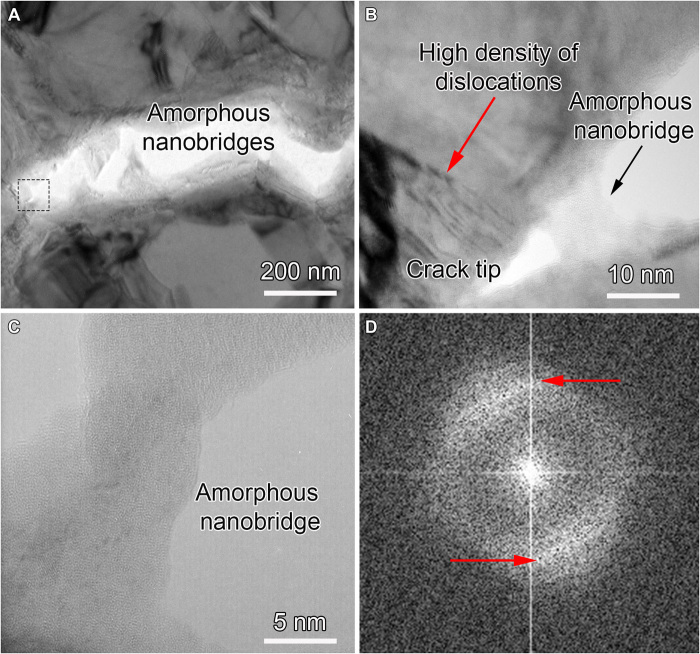
Previous studies have revealed the formation of crystalline nanobridges in the crack wake in the CG Cantor alloy, which hindered crack propagation and thus provided an extrinsic toughening mechanism (12, 13). In this work, nanobridging was observed during in situ TEM straining experiments for both the UFG (Fig. 4) and CG (fig. S2) Cantor alloys. In the CG samples, nanobridges retained the FCC crystal structure, consistent with the previous report. However, the UFG samples produced nanobridges with the amorphous structure. Figure 4A shows an example of nanobridges formed behind the crack tip in a UFG sample. Crack propagation was accompanied with widening between crack surfaces through elongation and fracture of these nanobridges. The hindrance to deform these nanobridges imposes an effective resistance to fracture by “shielding” the crack from the applied load. Figure 4B shows the HRTEM image of a newly formed amorphous nanobridge (enclosed by the square dashed box in Fig. 4A), at ~10 nm behind the crack tip. In addition to these amorphous nanobridges, dislocations were observed behind the crack tip, as indicated by the red arrow in Fig. 4B. Hence, both the amorphous nanobridges and the dislocations in crystalline regions provide ample sources of energy dissipation for an enhanced toughening response. Figure 4C presents the HRTEM image of an amorphous nanobridge at ~600 nm behind the crack tip. Compared with the crystalline nanobridges observed in CG samples (fig. S2A), the edges of these amorphous nanobridges were not parallel to any crystallographic planes because of their disordered atomic structures. Figure 4D shows the FFT image of the nanobridge area, confirming the amorphous structure. However, in contrast to the typical diffraction halo from a fully amorphous structure (25), which usually presents an axial symmetry, the intensity of the FFT pattern in Fig. 4D is not uniform. Two arcs with strong intensity are present, as indicated by red arrows. They can be associated with the interplanar distance of {111} planes in the parent FCC phase, indicating that some residual FCC regions remain.

Fig. 4. Amorphous nanobridges formed behind the crack tip.

(A) Low-magnification bright-field TEM image of a crack tip with nanoscale amorphous bridges. (B) Magnified TEM image of the boxed area in (A) showing a nanobridge with an amorphous structure behind the crack tip. The red arrow indicates an area with a high density of dislocations. (C) HRTEM image of an amorphous nanobridge that was ~600 nm behind the crack tip. (D) FFT pattern from an HRTEM image of the fractured amorphous bridge. The nonuniform intensity distribution is shown by two strong diffraction arcs (marked by red arrows) and thus demonstrates the existence of residual crystalline phases in the amorphous structure.

To assess the beam effect on amorphous nanostructures, we applied electron beam illumination to the amorphous nanobridges for a few minutes and observed the recrystallization of the amorphous phase. Figure S3 (A and B) shows a typical amorphous nanobridge and its FFT pattern, respectively, before electron beam illumination. The amorphous structure was transformed to the crystalline structure under electron beam illumination (fig. S3C). FFT patterns taken from the areas enclosed by the red and black squares are shown in fig. S3 (D and E), respectively. Diffraction spots from {111}, {200}, and {220} planes of the FCC structure are indicated by white arrows. These FFT patterns indicate that these two areas consist of a nanocrystalline FCC structure. The effect of electron beam illumination on crystallization was supported by the long-term stability of the amorphous structure, which was stored at room temperature for 3 months without crystallization. Hence, these results indicate that the near-tip high stress, as opposed to electron beam illumination, is the main driving force of formation of amorphous structures, and the electron beam effect can promote reverse transformation of the amorphous to crystalline structure in the present UFG Cantor alloy.

Atomistic modeling

To understand the atomistic mechanisms of deformation-induced crystalline-to-amorphous transformation, we performed MD simulations of tensile crack growth in a nanometer-thick thin film (fig. S4), which represents the thin-foil sample used by in situ TEM experiment. Since high-quality five-element interatomic potentials for HEAs are still under development (26), we used a binary Cu-Al potential (27) to construct a model FCC random solid solution for investigating the effects of alloying elements on crack-tip dislocation plasticity and solid-state amorphization. This potential uses an angular-dependent potential (ADP) formalism, which is a generalization of the traditional embedded atom method (EAM) formalism. The model FCC alloy based on this potential has an intrinsically high lattice resistance to dislocation glide, which arises because of strong angular-dependent bonding between Cu-Al atoms. Such high lattice resistance is not common in most model FCC alloy systems given by other EAM potentials. Hence, the present model system is well suited to reveal the crucial effects of high lattice resistance on dislocation motion and crystalline-to-amorphous transformation. Moreover, random concentration fluctuations in the model alloys, containing 10 or 15% Al atoms in the Cu matrix, allow local variations of pinning resistance to dislocation glide, which should be common in HEAs. To reveal the local pinning resistance, fig. S5 shows the nudged elastic band (NEB) result of glide of a screw dislocation in the model alloys under zero stress. It is seen that the minimum energy path of screw glide is rough with a series of fairly high-energy barriers that underlie the strong local pinning resistance to dislocation motion. Hence, these model alloys were used to investigate the impact of local pinning of dislocations in HEAs on crack-tip dislocation plasticity and resultant amorphization.

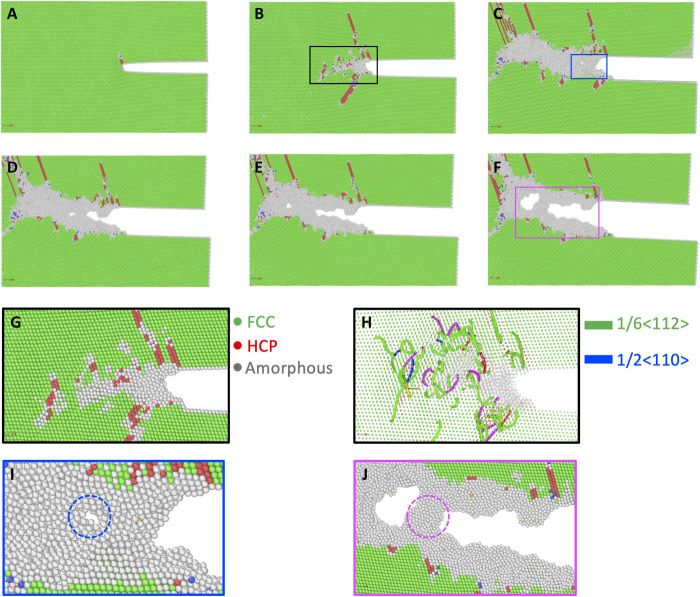
Figure 5 (A to F) shows MD snapshots of the simulated crack-tip responses in a model alloy containing 10% Al atoms in the Cu matrix, revealing the characteristic processes of strong dislocation pinning and crystalline-to-amorphous transformation. As the applied tensile load increased, a partial dislocation first emitted from the highly stressed crack tip (Fig. 5A). Subsequently, a number of dislocations, including both partial and full dislocations, nucleated on different slip planes near the crack tip (Fig. 5B). The existence of partial dislocations near the crack tip region was confirmed by TEM observations as shown in fig. S6. However, these dislocations were trapped near the crack tip, because of the intrinsically high lattice resistance that limits dislocation mobility. Such trapping response was further enhanced by mutual pinning and locking of dislocations on different slip systems, as plastic deformation became intensified near the crack tip with increasing load. Figure 5 (G and H) shows the magnified crack-tip region (enclosed by the black box) in Fig. 5B. It is seen that the interactions between densely tangled dislocations resulted in the onset of crystalline-to-amorphous transformation near the crack tip. In addition, the increased tensile load triggered an intense local thinning deformation of the amorphous film, resulting in the formation of a nanovoid ahead of the crack tip (Fig. 5C and the magnified crack tip region in Fig. 5I). Progressive nucleation, expansion, and coalescence of nanovoids in the crack-tip process zone led to crack propagation (Fig. 5, D to F). In particular, the amorphous nanobridge (e.g., Fig. 5F and the magnified crack tip region in Fig. 5J) formed in the crack wake. Such dynamic formation of amorphous nanobridges closely matched our in situ TEM observation. MD simulations with different initial crack orientations were also performed, as shown in fig. S7. Similarly, the crystalline-to-amorphous transformation occurred near the crack tip, through the development of dislocation tangles leading to the eventual transformation to the amorphous phase. The formation and elongation of amorphous nanobridges in the crack wake inhibit crack propagation. These processes provide the extrinsic toughening mechanism (12, 13), which complements the intrinsic toughening mechanisms of energy dissipation through dislocation plasticity and crystalline-to-amorphous transformation ahead of the crack tip.

Fig. 5. MD results of crack-tip amorphization in a model binary alloy.

(A to F) MD images showing the deformation-induced crystalline-to-amorphous transformation in a near-tip region (as extracted from the large simulation cell shown in fig. S5). The atomic structure visualization tool OVITO (43) is used for a common neighbor analysis, so as to identify the amorphous structure. Three types of atoms in local FCC (green), HCP (red), and amorphous (gray) structures are identified. (G and H) Magnified atomic images in the rectangle area in (B) with associated dislocation analysis, showing different types of dislocations near the crack tip. (I) Magnified image in the rectangle area in (C), showing the nucleation of a nanovoid ahead of crack tip. (J) Magnified image of the rectangle area in (F), showing the formation of an amorphous nanobridge during crack growth.

Note that the typical model FCC alloy systems based on traditional EAM potentials cannot readily produce the similar crack-tip processes of crystalline-to-amorphous transformation and amorphous nanobridge formation, as they are usually dominated by dislocation slip and deformation twinning near the crack tip. In contrast, for the present Cu-Al model system based on an ADP potential (27), the strong bonding between Cu-Al atoms gives rise to high pinning resistances to dislocation glide (fig. S5) and thereby promotes strong dislocation interactions (as shown in Fig. 5 and fig. S7), leading to crystalline-to-amorphous phase transformation. We also performed similar atomistic simulations with a different alloy composition of 85% Cu and 15% Al atoms. Figure S8 presents the NEB result showing high pinning resistance to dislocation glide, and fig. S9 displays the MD result of deformation-induced amorphization. These results further underscore the notion of strong lattice resistance to dislocation motion for promoting the trapping of crack-tip dislocations, leading to crystalline-to-amorphous transformation. In addition, we performed atomistic simulations for an equiatomic CrCoNi medium-entropy alloy with a recent EAM potential (figs. S10 and S11) (28). Deformation-induced amorphization at the crack tip occurred only in the CrCoNi samples after simulated annealing via Monte Carlo simulation (fig. S11), where a local chemical order (LCO) was developed (28). The LCO increases lattice resistance to dislocation motion and enhances crack-tip dislocation trapping, leading to crystalline-to-amorphous transformation. These results indicate that the effect of the LCO on lattice resistance is similar to that of the strong angular-dependent bonding between Cu-Al atoms in the Cu-Al potential. Hence, these MD results suggest that strong atomic bonding, which can be enhanced by the concentrated multicomponent alloying environment in HEAs, can play a critical role in the dislocation-mediated mechanisms of crystalline-to-amorphous phase transformation. This mechanism of solid-state amorphization warrants further study when the high-quality interatomic potential for the Cantor alloy becomes available in the future.

DISCUSSION

Two main routes have been used to obtain the amorphous structures in metallic materials. One is rapid solidification for retaining dynamic disorder in a fast-cooling liquid phase until a solid phase forms. The other is destabilization of a crystalline solid phase into a disordered one, which is known as solid-state amorphization (29, 30). Various processing methods have been developed to produce the amorphous phases from their crystalline counterparts (30), including cold rolling (29, 31), high-pressure torsion (32, 33), ball milling (34), and electrical charging (35). These processes usually introduce a high density of dislocations (between 10¹⁷ and 10¹⁸/m²) that act as precursors of amorphization in metallic materials (29, 31, 32, 36). Since our in situ straining experiments were conducted at room temperature and a fairly low strain rate (~1 × 10⁻⁴/s), the effect of thermal heating should be insignificant during amorphization. The observed structural disordering can be mainly attributed to extensive dislocation plasticity, leading to crystalline-to-amorphous phase transformation.

To estimate the deformation-induced dislocation densities involved in amorphization, we analyzed the spotted and lamellar areas near the crack tip of a UFG sample. The near-tip areas of a CG sample were also analyzed for comparison. Only crystalline areas along the <110> zone axis of electron beam were chosen to estimate local dislocation densities (34), based on the inverse FFT taken from HRTEM images. The area of each region analyzed was ~45 nm², and multiple positions (>5) of each type of areas were analyzed. The dislocations at phase boundaries were not counted to reduce the error of the estimate. Since only two sets of planes can be observed along the 〈110〉 zone axis, the estimated local dislocation density should represent a lower bound (33). The mean dislocation density in the spotted (5.6 × 10¹⁷/m²) and lamellar areas (2.8 × 10¹⁷/m²) of the UFG sample is nearly one order of magnitude higher than that in the near-tip areas (7.6 × 10¹⁶/m²) of the CG sample. This result indicates that the relatively low dislocation density near the crack tip of the CG sample has not reached the critical density needed for amorphization in the Cantor alloy. Our results suggest that the critical dislocation density for crystalline-to-amorphous transformation is approximately 5.6 × 10¹⁷/m² (as estimated from the spotted area in the UFG sample) for the Cantor alloy. On the other hand, when the average grain size was reduced from 10 to 0.5 μm (fig. S10), the volume fraction of grain boundaries increased notably. These grain boundaries acted as effective barriers to dislocation slip and therefore raised flow stresses to facilitate the accumulation of a high density of dislocations in the UFG sample. Since high-angle grain boundaries usually provide stronger resistance to dislocation motion than low-angle grain boundaries, they could be more effective in promoting dislocation accumulation and resultant amorphization. However, no experimental result is currently available to compare the effects of low-angle and high-angle grain boundaries on crack-tip amorphization because of the low fraction of low-angle grain boundaries (~2%) in the UFG samples. Hence, the intrinsically high lattice resistance to dislocation slip in an HEA such as the Cantor alloy, in conjunction with the grain boundary-enhanced trapping of dislocations in the UFG sample, could eventually raise the local dislocation density to the critical value for triggering solid-state amorphization near the crack tip.

In our atomistic simulations, a rapid increase in dislocation density occurred near the crack tip under increasing load, similar to our experimental observations. The simulated near-tip amorphization processes resulted from the running balance between the increasing stress and resistance to dislocation glide at the crack tip. Namely, the accumulation of a high density of dislocations is driven by the high near-tip stresses and, more importantly, by the high lattice resistance to dislocation glide originating from multiple principal elements in the Cantor alloy. Because of the limited simulation cell size, the effect of grain boundaries in UFG samples could not be directly studied by MD. Nonetheless, the necessity of the UFG microstructure for amorphization can be directly recognized from experiment, since there is no crack-tip amorphization in the CG Cantor alloy. Compared to CG samples, grain boundaries in UFG samples are closer to the crack tip and could impose a long-range constraining effect through dislocations in between the crack tip and grain boundaries. This would increase the resistance to dislocation glide and enhance the trapping of crack-tip dislocations, thereby promoting crystalline-to-amorphous transformation near the crack tip.

In addition, our in situ TEM observations revealed that the crystalline and amorphous structures coexisted in the spotted and lamellar areas near the crack tip of the UFG sample. These areas reflect the transition processes of crystalline-to-amorphous phase transformation. In lamellar areas, the volume fractions of the crystalline and amorphous structures were comparable. However, in spotted areas, only a small amount of the crystalline structure (less than 10%) remained. The decreasing volume fraction of the crystalline structure indicates that the structural evolution should follow the sequence from the lamellar areas to spotted areas. The formation mechanism of lamellar areas has not been clearly understood. While grains in the material presented different orientations, the crystalline/amorphous phase boundaries (Fig. 2) in lamellar structures were always approximately parallel to {100} planes, as observed in HRTEM images taken from several lamellar areas. This result indicates that the formation of the lamellar structure has neither direct connection with deformation twinning that involve twin boundaries (33) nor any special stress field at crack tips. Note that Moiré fringes and specimen thickness fringes also present layer-by-layer morphology. The period of a Moiré fringe pattern is a constant and lattice images present in a whole Moiré fringe area (37). In contrast, the lamellar structure in Fig. 2 did not have a constant period and presented no lattice fringes at the white band areas, clearly indicating that the lamellar structure is not Moiré fringes. The possibility of the lamellar morphology being thickness fringes can also be excluded because thickness fringes normally have periods that are at least one order of magnitude larger than that shown in Fig. 2 (38).

As reported by previous studies (12, 13), nanobridging at crack tips in HEAs hinders crack propagation and therefore toughens HEAs. Since the amorphous phase is at a higher energy state than the crystalline counterpart, the dissipation of some extra energy is needed in the amorphization processes both ahead of the crack tip and in nanobridges behind the crack tip in the UFG Cantor alloy. Such extra energy consumption is expected to contribute to toughening of this alloy. Although previous studies demonstrated that surface diffusion can play a critical role in nanoscale deformation (39), this process unlikely has a major impact on the formation of amorphous nanobridges that involves the structural disordering through local atomic displacements but warrants further study in the future. A large-scale amorphous structure might have a detrimental effect on the toughness because of its limited capacity of plastic deformation due to a lack of slip systems. However, it has been reported that the small-scale amorphous structure with its size on the order of 100 nm could actually undergo extensive ductile deformation by necking (40). From our in situ TEM observations, the widths of the amorphous nanobridges were less than 100 nm (see Fig. 4B), and the nanobridges usually exhibited large tensile deformation before failure (Fig. 4, A and C). It is therefore expected that these amorphous bridges experienced ductile deformation and therefore did not really have any detrimental effect on the toughness of the UFG Cantor alloy. While strength and ductility are the global mechanical properties controlled by their bulk responses, fracture toughness originates from the resistance to crack initiation and propagation that is more closely related to the local microstructure and evolution. Therefore, the near-tip mechanisms revealed in this work, including the crystalline-to-amorphous phase transformation and formation of amorphous nanobridges, could be generally applicable to the toughening of other UFG HEAs.

In conclusion, we have found the deformation-induced crystalline-to-amorphous phase transformation in the UFG Cantor alloy. The structural evolution exhibits a sequence of formation of the crystalline, lamellar, spotted, and amorphous patterns in TEM images that arise from different proportions and organizations of the crystalline and amorphous structures. The crack-tip high stresses, high lattice and grain boundary resistances to dislocation slip, and resulting accumulation of high-density dislocations are essential to the observed solid-state amorphization, thereby dissipating energy and resisting crack propagation. The formation of nanoscale amorphous bridges in the crack wake can further hinder crack propagation. Hence, the collective effects of crystalline-to-amorphous phase transformation and the formation of amorphous nanobridges may enable strong toughening of HEAs. These toughening effects need to be quantitatively evaluated by direct experimental measurements of fracture toughness in the future (12).

MATERIALS AND METHODS

Material processing and sample preparation

To obtain the CG Cantor alloy, ingots with an equiatomic CrMnFeCoNi were prepared by arc-melting a mixture of pure metals [purity > 99.99 weight % (wt %)] in a Ti-gettered high-purity argon atmosphere. The ingots were remelted four times to ensure chemical homogeneity. The melted alloys were then drop-cast into a mold. The drop-cast ingots were solution-treated for 48 hours at 1473 K under a high-purity argon atmosphere. After that, the ingots were cold rolled to sheets having a final thickness of ~2 mm and then sliced into coupons with dimensions of 100 mm by 100 mm by 2 mm. After cold rolling, the samples were annealed in a vacuum furnace at 850°C for 2 hours to obtain a mean grain size of ~10 μm.

To obtain the UFG Cantor alloy (41), a mixture of pure metals (purity > 99.7 wt %) of equiatomic CrMnFeCoNi was melted and solidified in a magnetic levitation melting furnace in a high-purity nitrogen atmosphere, resulting in an ingot with a diameter of 110 mm and a height of 90 mm. Although the ingot was melted only once, chemical homogeneity of the as-cast sample was achieved as evidenced by scanning electron microscopy energy dispersive spectroscopy (EDS) data. The ingot was solution-treated at 1100°C for 2 hours and then hot forged at 1000°C to a perch with a final diameter of 30 mm. The perch was further cold rolled to sheets with final thickness of 1 mm. To obtain fully recrystallized specimens with ultrafine grains, the cold-rolled sheets were annealed at 650°C for 30 min to obtain a mean grain size of ~500 nm.

Samples were cut into rectangular pieces (3 mm by 3 mm by 0.5 mm) using a Accutom-50 diamond saw. They were then grounded with SiC papers down to a thickness of ~100 μm. The twin jet polishing technique was used to further polish the surface of the samples to get electron-transparent regions in the middle of the foils for TEM observation and in situ tensile straining experiments. The solution used for twin jet polishing was 6 volume % perchloric acid in methanol. The polishing process was conducted at ~−30°C with a voltage of 20.5 V.

Each sample was glued on a rectangular copper holder with a thickness of around 100 μm. The copper holder comprised two holes, serving as loading pins for the Gatan cooling strain holder, and a circular window in the center to transmit the electron beam. This method is similar to those used in a previous study (12).

Structural characterization and in situ tensile straining experiments

In situ TEM tensile tests were carried out in a JEM 3000F and JEM 2200FS operating at 300 and 200 kV, respectively, using a Gatan cooling strain holder at room temperature. Only samples that were well attached to the copper holder without pollution, rotation, or bending during the experiments were used for detailed TEM investigation. Displacement was controlled manually through a trigger switch, leading to an axial constant strain rate of ~1 × 10⁻⁴/s within each pulse. During the holding period, the specimen maintained at a strained state at a certain displacement. During the tensile experiments, regions in front of the crack tip were observed. Quantitative compositional analysis and elemental mapping were conducted using EDS operated in an aberration-corrected Themis-Z scanning transmission electron microscope equipped with ChemiSTEM (Super-X) EDS detectors. Compositional mapping used a beam current of 200 pA and sufficiently long data collection time to ensure >100,000 counts to minimize statistical errors.

Atomistic modeling

Figure S4 shows the atomic configuration of a free-standing thin film with a precrack. The thin film has dimensions of 42.4 nm by 33.8 nm by 4.1 nm and contains a total of ~600,000 atoms. A periodic boundary condition is imposed in the Y-[111] direction, while the surfaces along the X-$\left[11\overline{2}\right]$ and Z-$\left[1\overline{1}0\right]$ directions are maintained traction free. A precrack with a length of 14 nm is created at the sample edge by removing three layers of atoms on the flat (111) plane. A uniaxial tensile load is applied in the Y-[111] direction at a constant strain rate of 1 × 10⁸/s, while both the X-$\left[11\overline{2}\right]$ and Z-$\left[1\overline{1}0\right]$ directions are traction free. MD simulations at a low temperature of 5 K were performed with an ADP potential of Cu-Al (27) and Ni-Co-Cr (28) using Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (42). The visualization tool OVITO (43) was used to perform common neighbor analysis, so as to clearly identify the amorphous structure and its evolution during the simulations. Three categories of atoms, including FCC, HCP, and other structure orders, were identified in the simulated structures. Atoms with other structural order usually belong to the amorphous structure induced by crack-tip plastic deformation. At an annealing temperature of 650 K, the structure was relaxed to lower the potential energy by element rearrangement for the Ni-Co-Cr alloy through Monte Carlo algorithm implemented by LAMMPS (24, 28). The simulation cell of the NEB calculation in fig. S5 or S8 has dimensions of 16 nm by 10 nm by 6 nm and contains a total of ~83,000 atoms. Periodic boundaries are applied in the X-〈112〉 and Z-〈110〉 directions, while the surface is traction free in the Y-〈111〉 direction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/14/eabe3105/DC1