Abstract
Background
During the COVID-19 pandemic, authorities must decide which groups to prioritise for vaccination in a shifting social–epidemiological landscape in which the success of large-scale non-pharmaceutical interventions requires broad social acceptance. We aimed to compare projected COVID-19 mortality under four different strategies for the prioritisation of SARS-CoV-2 vaccines.
Methods
We developed a coupled social–epidemiological model of SARS-CoV-2 transmission in which social and epidemiological dynamics interact with one another. We modelled how population adherence to non-pharmaceutical interventions responds to case incidence. In the model, schools and workplaces are also closed and reopened on the basis of reported cases. The model was parameterised with data on COVID-19 cases and mortality, SARS-CoV-2 seroprevalence, population mobility, and demography from Ontario, Canada (population 14·5 million). Disease progression parameters came from the SARS-CoV-2 epidemiological literature. We assumed a vaccine with 75% efficacy against disease and transmissibility. We compared vaccinating those aged 60 years and older first (oldest-first strategy), vaccinating those younger than 20 years first (youngest-first strategy), vaccinating uniformly by age (uniform strategy), and a novel contact-based strategy. The latter three strategies interrupt transmission, whereas the first targets a vulnerable group to reduce disease. Vaccination rates ranged from 0·5% to 5% of the population per week, beginning on either Jan 1 or Sept 1, 2021.
Findings
Case notifications, non-pharmaceutical intervention adherence, and lockdown undergo successive waves that interact with the timing of the vaccine programme to determine the relative effectiveness of the four strategies. Transmission-interrupting strategies become relatively more effective with time as herd immunity builds. The model predicts that, in the absence of vaccination, 72 000 deaths (95% credible interval 40 000–122 000) would occur in Ontario from Jan 1, 2021, to March 14, 2025, and at a vaccination rate of 1·5% of the population per week, the oldest-first strategy would reduce COVID-19 mortality by 90·8% on average (followed by 89·5% in the uniform, 88·9% in the contact-based, and 88·2% in the youngest-first strategies). 60 000 deaths (31 000–108 000) would occur from Sept 1, 2021, to March 14, 2025, in the absence of vaccination, and the contact-based strategy would reduce COVID-19 mortality by 92·6% on average (followed by 92·1% in the uniform, 91·0% in the oldest-first, and 88·3% in the youngest-first strategies) at a vaccination rate of 1·5% of the population per week.
Interpretation
The most effective vaccination strategy for reducing mortality due to COVID-19 depends on the time course of the pandemic in the population. For later vaccination start dates, use of SARS-CoV-2 vaccines to interrupt transmission might prevent more deaths than prioritising vulnerable age groups.
Funding
Ontario Ministry of Colleges and Universities.
Introduction
The COVID-19 pandemic has imposed a massive global health burden as waves of SARS-CoV-2 infection move through populations around the world.1 Empirical analyses and mathematical models have shown that non-pharmaceutical interventions—such as physical distancing, handwashing, and mask wearing—are effective in reducing the COVID-19 case incidence.2, 3, 4 However, pharmaceutical interventions are highly desirable given the socioeconomic costs of lockdowns and physical distancing. Dozens of vaccines are in development,5 and model-based analyses are exploring the question of which groups should get COVID-19 vaccines first.6, 7, 8
When vaccines become widely available, we will face a very different epidemiological landscape from the early pandemic.9 Many populations will already have had one or more waves of COVID-19. As a result of natural immunity, the effective reproduction number R eff (the average number of secondary infections produced per infected person) will be reduced from its original value of R 0≈2·2 in the absence of pre-existing immunity.10 Epidemiological theory tells us that as R eff (or R 0) declines towards 1, the indirect benefits of vaccines that reduce transmission become stronger. For instance, if R 0≈1·5, such as for seasonal influenza, only an estimated 33% of the population needs immunity for transmission to die out in a homogeneously mixing population.11, 12 This effect was evidenced by the strong suppression of influenza incidence in Australia in the spring of 2020 due to non-pharmaceutical interventions targeted against COVID-19.13
Research in context.
Evidence before this study
Whether to vaccinate individuals who cause the most transmission or those who are at highest risk of death is relevant to prioritising COVID-19 vaccination. We searched PubMed and medRxiv using the terms COVID-19, vaccin*, model, and priorit* up to Sept 24, 2020, with no date or language restrictions. We identified four preprints on mathematical models of COVID-19 vaccine prioritisation that explored the conditions under which different age groups should be vaccinated first. We did not find any coupled social–epidemiological models that captured feedback between social dynamics and epidemic trajectories.
Added value of this study
The dynamic interaction between SARS-CoV-2 epidemics and the population response through scalable non-pharmaceutical interventions will continue to have a large role in the course of the pandemic, both before and after vaccines become available. Therefore, social–epidemiological models can be useful. Our social–epidemiological model identifies the conditions under which we can prevent more COVID-19 deaths by prioritising older individuals first versus other strategies designed to interrupt transmission. In this study, we explored how the best vaccination strategy depends on a wide range of social–epidemiological and vaccine programme parameters. We identified clear and interpretable conditions that determine how well COVID-19 vaccines can interrupt transmission and reduce mortality.
Implications of all the available evidence
Antibody seroprevalence surveys before the onset of vaccination could ascertain a population's level of pre-existing SARS-CoV-2 immunity. In populations where seropositivity is high due to previous pandemic waves, population-specific models can help vaccine prioritisation decisions by determining whether vaccinating to interrupt transmission might prevent more deaths than prioritising individuals older than 60 years.
This effect has stimulated a literature comparing the vaccination of groups that are responsible for most transmission with the vaccination of groups that are most susceptible to serious disease as a result of infection. Natural immunity to SARS-CoV-2 is likely to continue to rise in many populations on account of further infection waves. Given these likely changes to the epidemiological landscape before the vaccine becomes available, we suggest the question of which groups to prioritise for vaccination is worthy of investigation in the context of COVID-19.
The social landscape will also look very different when vaccines become available. This aspect is crucial to understanding the pandemic. Scalable non-pharmaceutical interventions are often one of the few available interventions when a novel pathogen emerges. Flattening the COVID-19 epidemic curve was possible through a sufficient response by populations willing to adhere to public health recommendations. Therefore, pandemic waves are not simply imposed on populations—they are a creation of the population response to the pathogen. They exemplify coupled social–epidemiological systems in which disease dynamics and behavioural dynamics interact with one another.14
Approaches to modelling coupled social–epidemiological dynamics vary.15, 16, 17, 18, 19 Some models have used evolutionary game theory to model this two-way feedback in a variety of coupled human–environment systems.14, 20, 21, 22, 23, 24, 25 Evolutionary game theory captures how individuals learn social behaviours from others while weighing risks and benefits of different choices. In this framework, individuals who do not adopt non-pharmaceutical interventions can free-ride on the benefits of reduced transmission generated by individuals who do adopt non-pharmaceutical interventions.15
In this study, our objective was to compare projected COVID-19 mortality under four strategies for the prioritisation of COVID-19 vaccines: older individuals first, children first, uniform allocation, and a novel strategy based on the contact structure of the population. We use an age-structured model of SARS-CoV-2 transmission, including evolutionary game theory, to model population adherence to non-pharmaceutical interventions and changes to mobility patterns. We use scenario and sensitivity analyses to identify how strategy effectiveness responds to possible changes in the social–epidemiological landscape that could occur before and after vaccines become available.
Methods
Model structure and parameterisation
We developed an age-structured SEPAIR (susceptible, exposed, presymptomatic, asymptomatic, symptomatic, removed) model with ages in 5-year increments. Upon infection, individuals enter a latent period in which they are infected but not yet infectious (exposed). After the latent period, individuals become presymptomatically infectious, and then either symptomatically or asymptomatically infectious, before finally entering the removed compartment when their infectiousness ends. We did not explicitly model testing or contact tracing, although we assume infected individuals are ascertained at some rate. Transmission occurs through an age-specific contact matrix, susceptibility to infection is age-specific, and we include seasonality because of changes in contact patterns throughout the year.
Statistical analysis
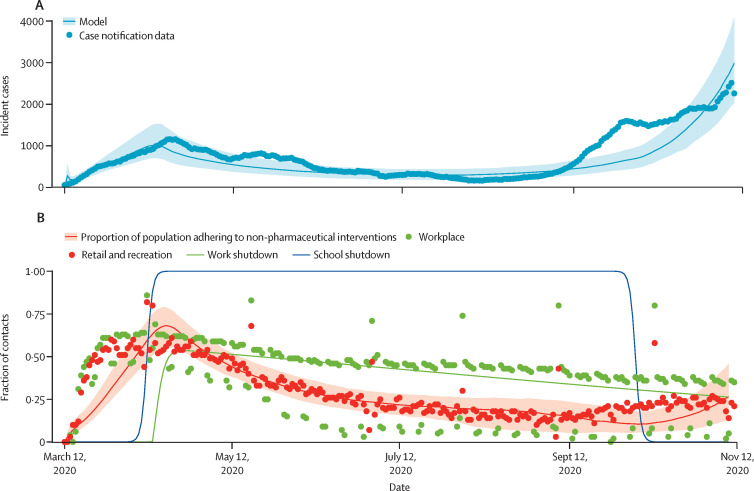
To infer model parameters, we used a Bayesian particle filtering approach to fit the model to Ontario COVID-19 case notifications (stratified by age and time), Ontario seroprevalence data, and Ontario mobility data. Using seroprevalence data ensured that our estimates of transmission were not biased by case under-reporting. Remaining model parameter values were fixed with use of Ontario demographic and mortality data, and literature on COVID-19 serial interval and incubation periods. Details of our model structure, parameterisation, data sources, and model fits are provided in the appendix (pp 1–11). The posterior distributions for predicted case notifications and adherence to non-pharmaceutical interventions are compared with the corresponding empirical data in figure 1 .
Figure 1.
COVID-19 case numbers and proxy for adherence to non-pharmaceutical interventions
(A) COVID-19 case incidence by date of report in Ontario. Dots show the 7-day running average of case notification data, and the line represents the ascertained case incidence from best fitting models (with 95% credible intervals represented by the shaded region). (B) Each dot represents the proportional reduction in time spent at retail and recreation destinations and workplaces on the given date, compared with the 5-week average on corresponding days of the week 1 year ago, according to Google mobility data. Lines show the proportion of the population adhering to non-pharmaceutical interventions (with 95% credible intervals represented by the shaded region) as well as workplace and school shutdown curves from the fitted model. Methods and data sources are provided in the appendix (pp 1–11).
Non-pharmaceutical intervention scenarios
In our scenarios, both schools and workplaces are closed when the number of ascertained active cases surpasses 50%, 100%, 150%, 200%, or 250% of the peak ascertained active cases that occurred during the first wave (the shutdown threshold), and are reopened again when cases fall below that threshold. We use social learning dynamics derived from evolutionary game theory to model individual adherence to non-pharmaceutical interventions.14, 20, 21, 22 Individuals interact with other individuals at a specified rate and switch between adherence and non-adherence to non-pharmaceutical interventions, including mobility restrictions, by comparing the cost of practicing non-pharmaceutical interventions against the cost of not practicing non-pharmaceutical interventions, and thereby being subject to an increased risk of infection according to the prevalence of ascertained cases. Both school and workplace closure and population adherence to non-pharmaceutical interventions reduce transmission according to a specified efficacy (appendix pp 1–5).
Vaccine scenarios
We considered two dates for the onset of vaccination: Jan 1 and Sept 1, 2021. These dates correspond to the end dates of a two-dose course of vaccination lasting 2 weeks. We assumed it was possible to vaccinate 0·5%, 1·0%, 1·5%, 2·5%, or 5·0% of the population per week (the vaccination rate). Our baseline scenario assumed a vaccine with 75% efficacy, in all ages, against both disease and transmissibility.
In the oldest-first strategy, the vaccine is administered to individuals aged 60 years or older first. After all individuals in this group are vaccinated, the vaccine is administered uniformly to individuals of other ages. The youngest-first strategy is similar, except that the vaccine is administered to individuals younger than 20 years of age first. In the uniform strategy, the vaccine is administered to all age groups uniformly from the very start. The contact-based strategy allocates vaccines according to the relative role played by different age groups in transmission. This strategy tends to prioritise ages 15–19 year first, 20–59 year second, and gives least priority to older or younger ages (appendix pp 4, 12). The oldest-first strategy targets a vulnerable age group, while the other three strategies are designed to interrupt transmission. We also report on sensitivity analyses that explore the effects of vaccine efficacy assumptions and a higher R 0, ascertainment rate, or social learning rate, and that incorporate dynamics of vaccinating behaviour.
Role of the funding source
The funder of the study had no role in study design, data collection, data analysis, data interpretation, or writing of the report.
Results
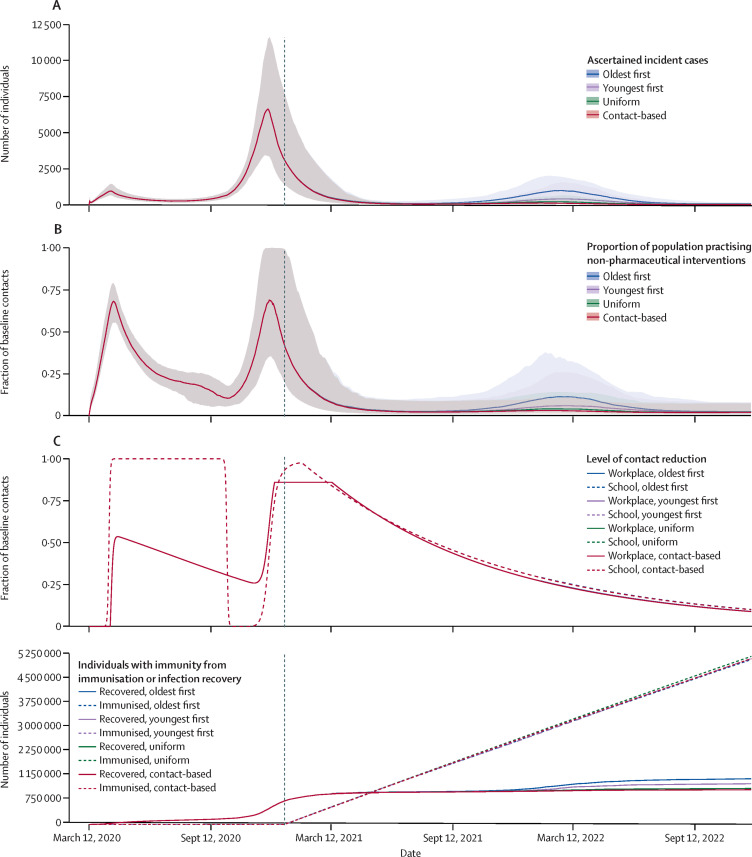
The model reproduces two or more pandemic waves from March, 2020, onward, not only with respect to COVID-19 cases but also population adherence to non-pharmaceutical interventions and periods of school and workplace closure (figure 2 ; appendix pp 14–15).
Figure 2.
Effect of interaction of social and epidemiological dynamics on pandemic waves and vaccine strategy effectiveness over time
(A) Number of ascertained incident COVID-19 cases. (B) Proportion of the population practising non-pharmaceutical interventions. (C) Level of school and workplace closure (note that curves for different vaccination strategies overlap). (D) Number of individuals with natural or vaccine-derived immunity. Predictions are based on the Ontario population size (14·6 million), with vaccination beginning on Jan 1, 2021 (as indicated by the dashed vertical line in the graphs), shutdown occurring at 200% of peak cases in the first wave, and a vaccination rate of 0·5% of the population per week. Other parameter values are provided in the appendix (pp 1–11).
The effects of the four vaccination strategies on COVID-19 cases and COVID-19-related deaths depends on when the vaccine becomes available and how quickly the population can be vaccinated. For most parameter values governing the vaccination rate and shutdown threshold, vaccinating people aged 60 years or older first prevents the most deaths out of all four strategies if vaccination begins on Jan 1, 2021, although the uniform or contact-based strategies prevent the most deaths if vaccination begins on Sept 1, 2021, and the vaccination rate ranges from 1% to 2·5% of the population per week. The model predicts that 72 000 deaths (95% credible interval 40 000–122 000) would occur in Ontario from Jan 1, 2021, to March 14, 2025, in the absence of vaccination, and the oldest-first strategy would reduce COVID-19 mortality by 90·8% on average (followed by 89·5% in the uniform, 88·9% in the contact-based, and 88·2% in the youngest-first strategies) at a vaccination rate of 1·5% of the population per week. 60 000 deaths (31 000–108 000) would occur from Sept 1, 2021, to March 14, 2025, in the absence of vaccination, and the contact-based strategy would reduce COVID-19 mortality by 92·6% on average (followed by 92·1% in the uniform, 91·0% in the oldest-first, and 88·3% in the youngest-first strategies), at vaccination rate of 1·5% per week.
We identified three regimes for model dynamics, and explored them through plots of infection incidence over time, percentage reduction in mortality under all four strategies (as they depend on the vaccination rate and shutdown threshold), and number of deaths prevented (as a function of the shutdown threshold and the vaccination rate).
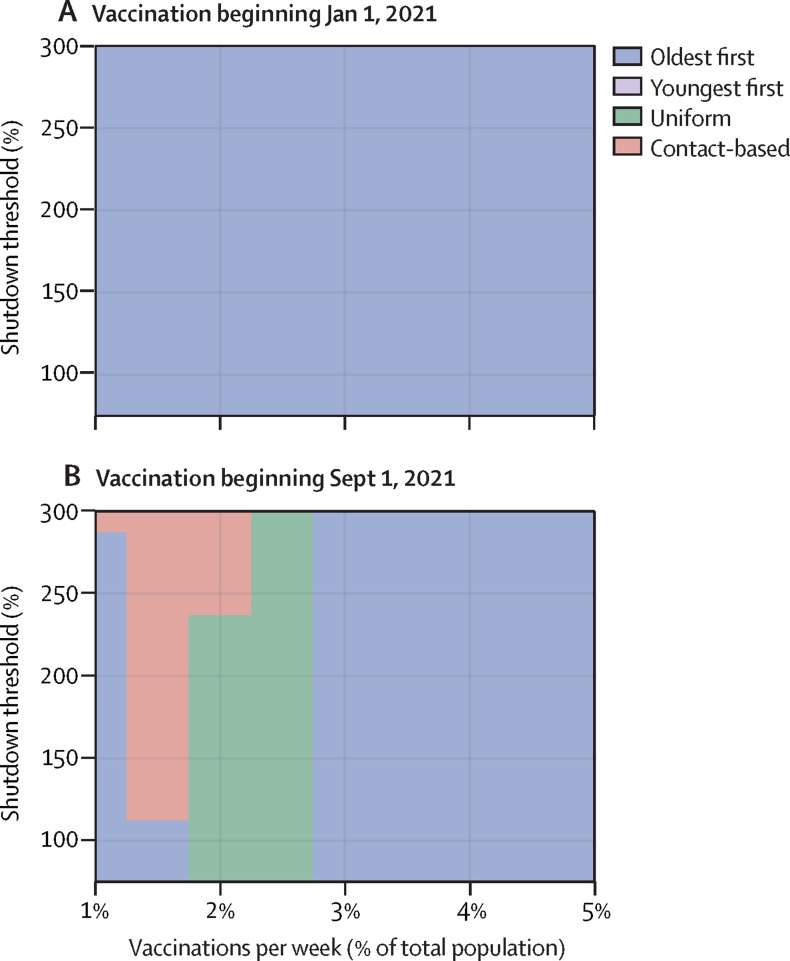
In the first regime, vaccination starts on Jan 1, 2021, and the vaccination rate is relatively high (≥1·0% of the population per week). A third wave in the autumn of 2021 or winter of 2022 is thereby prevented (figure 3A ; appendix p 13). In this regime, enough people are vaccinated sufficiently far in advance to prevent a third wave, but the oldest-first strategy prevents more deaths than the other strategies (Figure 4, Figure 5 ).
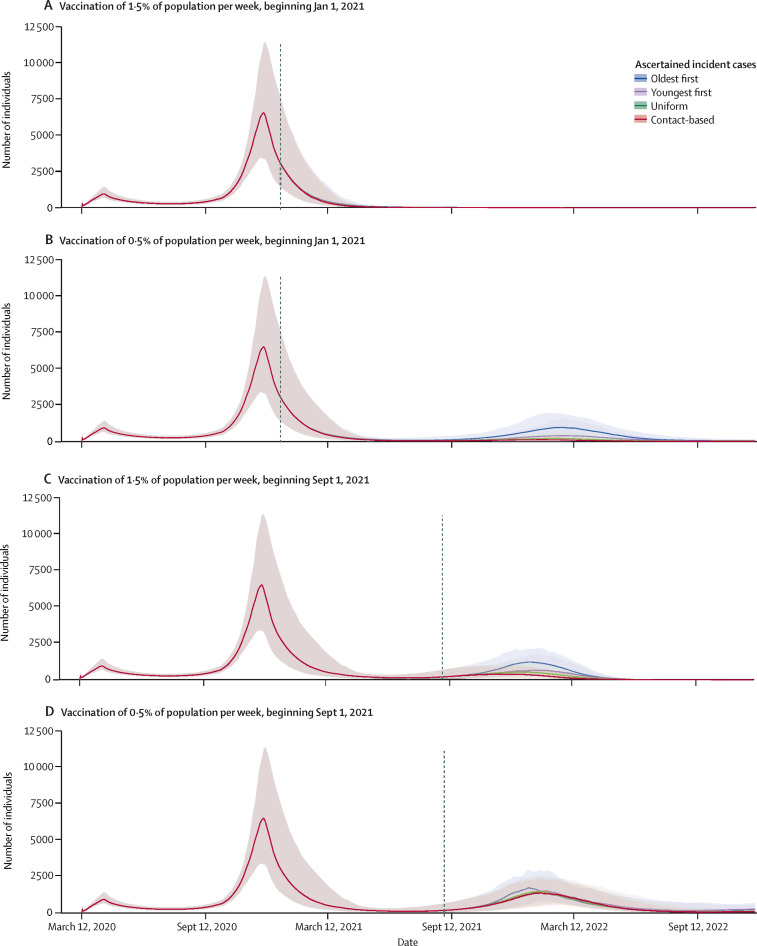
Figure 3.
Incident cases by vaccination strategy across three model regimes
Projections of ascertained incident COVID-19 cases if vaccination begins in January (A, B) or September (C, D), and if the rate of vaccination is 1·5% (A, C) or 0·5% (B, D) of the population per week. These scenarios represent three main model regimes: timely vaccination (A), partial vaccination and indirect protection (B, C), and slow and late vaccination (D). Projections are based on the Ontario population size of 14·6 million and shutdown occurring at 200% of peak cases in the first wave. Other parameter values are provided in the appendix (pp 1–11).
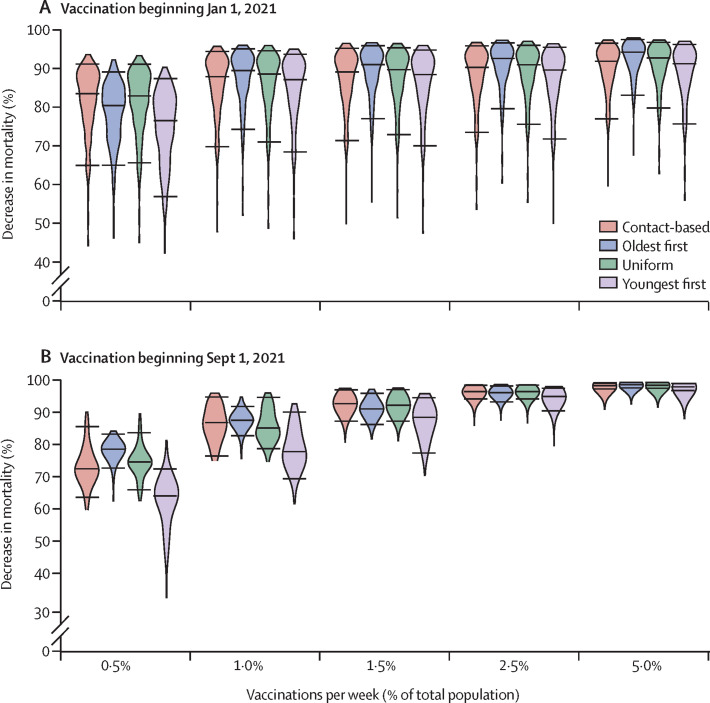
Figure 4.
Effects of vaccination strategy and start date on percentage reduction in mortality
Violin plots of the percentage reduction in mortality under the four vaccine strategies, relative to no vaccination, as a function of the vaccination rate, for vaccination beginning on Jan 1, 2021 (A), and Sept 1, 2021 (B). Horizontal lines represent the median values and 95% credible intervals of posterior model projections. Projections are based on the Ontario population size of 14·6 million and shutdown occurring at 200% of peak cases in the first wave. Other parameter values are provided in the appendix (pp 1–11). The projected number of deaths in the absence of vaccination was 72 000 (95% credible interval 40 000–122 000) from Jan 1, 2021, to March 14, 2025, and 60 000 (31 000–108 000) from Sept 1, 2021, to March 14, 2025.
Figure 5.
Best strategies for preventing deaths according to shutdown threshold and vaccination rate for vaccinations beginning in January (A) and September (B), 2021
Each parameter combination on the plane is colour coded according to which of the four strategies prevented the most deaths, on average, across all model realisations. Shutdown threshold is the number of active cases as a percentage of peak cases in the first wave. Other parameter values are provided in the appendix (pp 1–11).
In the second regime, either vaccination starts early (Jan 1, 2021) but the vaccination rate is low (≤0·5% of the population per week; Figure 2, Figure 3, Figure 4), or vaccination starts late (Sept 1, 2021) but the vaccination rate is high (≥1·5% of the population per week; Figure 3, Figure 4; appendix p 14). In this intermediate scenario, a sufficient proportion of the population is vaccinated for indirect protection from the vaccine to become important during the third wave, but not enough individuals are vaccinated to completely prevent it. As a result, the uniform and contact-based strategies are more effective than the oldest-first strategy, but the youngest-first strategy does worst of all (Figure 2, Figure 4, Figure 5). However, as the vaccination rate becomes very high, the effectiveness of all four strategies converges because the entire population is vaccinated quickly (figure 4B).
In the third regime, vaccination starts late (Sept 1, 2021) and the vaccination rate is relatively low (≤1·0% of the population per week; figure 3D; appendix p 15). This scenario does not allow enough time for indirect protection from vaccination to become strong. As a result, the oldest-first strategy prevents more deaths than the other three strategies (Figure 4, Figure 5). Overall mortality is higher for all strategies compared with the other two regimes on account of the delayed rollout of the vaccine. The relative performance of the strategies in these three regimes is generally unchanged across the full range of values for the shutdown threshold (appendix pp 16–17).
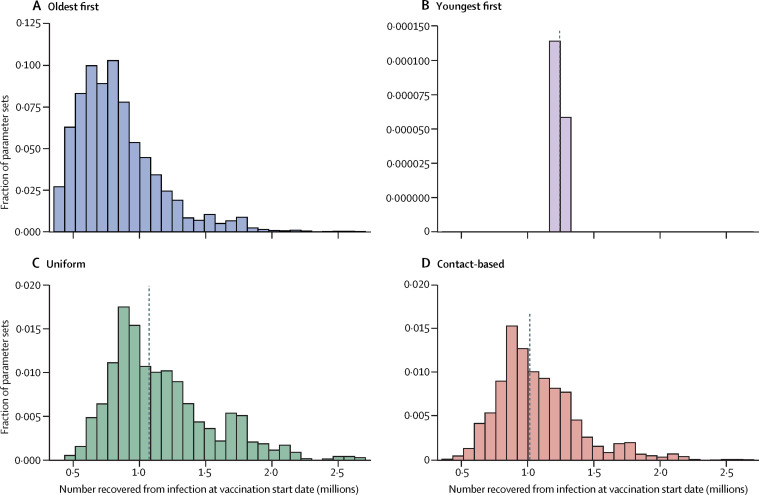
Frequency histograms across all stochastic model realisations showing what percentage of the population has natural immunity at the start of a vaccine programme, when a particular strategy was shown to work best, illustrate the role of indirect protection (figure 6 ). In simulations in which the oldest-first strategy did best, the percentage of the population with natural immunity tends to be relatively low. This finding is expected because indirect protection from vaccines is weaker when few people have natural immunity upon which vaccine indirect protection can build. However, when the uniform or contact-based strategy does best, more simulations exhibit a high level of natural immunity at the start of vaccination. We note that the variance in these histograms is high, which underscores the role of other factors in the model, such as timing and interaction between social and epidemiological dynamics. Similarly, if we plot the percentage reduction in mortality for hypothetical vaccination start dates ranging from Sept 1, 2020, to Sept 1, 2021, the transmission-interrupting strategies become relatively more effective than the oldest-first strategy for later vaccination start dates, because herd immunity has time to increase before the start of the vaccine programme (appendix p 18).
Figure 6.
Effect of pre-existing natural immunity on the effectiveness of transmission-interrupting strategies
Frequency histogram of the proportion of the population with natural immunity for each strategy, taken from simulations where that strategy reduced mortality most effectively, for oldest-first (A), youngest-first (B), uniform (C), and contact-based strategies (D). The most effective strategy is defined as the one that reduced mortality the most across the largest number of model realisations. Vertical dashed lines denote median values of the distribution. Other parameter values are provided in the appendix (pp 1–11).
We also studied how the best strategy changes depending on vaccine efficacy (ranging from 40% to 90%) in people aged 60 years and older and people younger than 60 years (appendix p 19). For January vaccine availability, the oldest-first strategy is best, even when vaccine efficacy is lower in those aged 60 years and older than in those younger than 60 years. For September vaccine availability, the uniform or contact-based strategies do best, except when vaccine efficacy in those aged 60 years or older is at least 5% higher than vaccine efficacy in those younger than 60 years.
We modelled the dynamics of vaccinating behaviour after vaccines become available (appendix pp 4, 20–23). Because of a lack of empirical data, we explored a wide range for the social learning rate and the perceived relative cost of vaccination versus infection. The results suggest that a sufficiently high perceived cost of vaccination allows the uniform or contact-based strategies to outperform the oldest-first strategy, especially for January vaccine availability, except when the vaccine social learning rate is also high (appendix pp 20). Vaccine refusal increases as the vaccine cost rises (appendix pp 21–23). Because vaccine refusal in the targeted age group forces vaccination of other age groups instead, it makes all strategies behave more like the uniform strategy, although age-specific behaviours could change these predictions.
We ran simulations with R 0=2·5 for December, 2020, onward and found that the oldest-first strategy was more effective more effective than the other three strategies across a broader region of parameter space for September availability, particularly at higher vaccination rates (appendix pp 24). This finding is expected because indirect protection is less effective when R 0 is higher. We also ran simulations with 30% higher and lower ascertainment for December, 2020, onward to capture potential changes to COVID-19 testing and found that it had little effect on which strategy was most effective (appendix pp 25–26). Similarly, higher or lower social learning rates for non-pharmaceutical interventions had little effect on the predictions (appendix pp 27–28).
We also analysed a scenario in which the vaccine efficacy against disease can be greater than the vaccine efficacy against infectivity. We found that increasing the efficacy against disease up to 95%, while holding the efficacy against infectivity constant at 75%, led to a slight improvement in the effectiveness of all four strategies, especially for the oldest-first and uniform strategies (appendix p 29). We generated results for our baseline scenario, but using a more stringent acceptance threshold for our Bayesian particle filtering algorithm, and found that our results were qualitatively unchanged (appendix p 30). Finally, in a special case of the model in which social dynamics are held fixed, the model fit to the epidemic curve worsens and the region of parameter space where the contact-based or uniform strategies are most effective expands (appendix pp 31–32)
Discussion
Our social–epidemiological model suggests that if a vaccine against SARS-CoV-2 becomes available sufficiently late in the pandemic, use of such vaccines to interrupt transmission might prevent more deaths from COVID-19 than use of the vaccines to target those aged 60 years and older, depending on when the vaccine becomes available and how quickly the population can be vaccinated. These results are driven by the fact that the vaccine might only become available after populations have had one or more waves of immunising infections. As a result, the effective reproduction number, R eff, could be significantly closer to 1 than the basic reproduction number R 0≈2·2 that applies to susceptible populations. In this regime, vaccines that reduce transmission have disproportionately large indirect protective effects.11
The Google mobility data that we used as a proxy for adherence to non-pharmaceutical interventions closely mirror the COVID-19 case notification data over the period used for fitting (figure 1). A heightened perception of COVID-19 infection risk stimulates the adoption of non-pharmaceutical interventions,26 which in turn reduces SARS-CoV-2 transmission,2, 3 exemplifying a coupled social–epidemiological dynamic. This mirroring might represent convergence between social and epidemiological dynamics, which has been predicted for strongly coupled systems.27 Moreover, the fit of the social submodel to the mobility data is as good as the fit of the epidemic submodel to case notification data, despite the fact that our social model consists of substantially fewer equations and a similar number of parameters to that of our epidemiological model. This shows how modelling population behaviour during a pandemic can be accomplished with relatively simple models.
Several studies have used compartmental models to study prioritisation of age groups for COVID-19 vaccination.6, 7, 8 These models vary widely in terms of study populations, representation of population heterogeneity, interventions, and assumptions about when vaccination starts. Similar to our results, Matrajt and colleagues8 found that the level of pre-existing immunity strongly dictates outcomes: when pre-existing immunity is high, strategies that distribute the vaccine more evenly across age groups can be more effective than prioritising older age groups. Buckner and colleagues7 found that targeting individuals aged 60 years and older is best for reducing mortality. They assumed that vaccination begins in December, 2020, and they base initial conditions on case notifications in the USA in that month. Similarly, Bubar and colleagues6 showed that vaccinating those aged 60 years and older works best for reducing mortality for vaccine programmes starting in July, 2020, in Belgium, or August, 2020, in New York City. Our results are consistent with those of Bubar and colleagues6 and Buckner and colleagues7 and for the scenario of January, 2021, vaccine availability. However, we found that more deaths could be prevented by first vaccinating other age groups for vaccinations starting in September, 2021. Such a late vaccine start date was not analysed in the aforementioned studies,6, 7 although their findings might change if the models were reinitialised to accommodate vaccination starting in September, 2021.
The under-performance of the youngest-first strategy occurs because in populations with strong age-assortative mixing,28 the indirect benefits of vaccination are wasted if vaccination is first concentrated in specific age groups before being extended to the rest of the population, whereas the oldest-first strategy is less affected by this because the COVID-19 case fatality rate is higher in people aged 60 years or older.
Our analysis was limited by its focus on prioritisation of age groups. We did not model other sources of heterogeneity, such as geography, socioeconomic status, sex, or race—all of which are important determinants of disease burden in this highly unequal pandemic. We did not model outbreaks in long-term care facilities, where the dynamics of transmission and indirect protection differ from those of the general population. Similarly, we did not distinguish health-care or other essential workers. However, many of these individuals are working-age adults, and thus vaccinating them first among other working adults is consistent with our uniform and contact-based strategies. For our baseline analysis, we assumed that the vaccine blocks transmission as well as it prevents COVID-19 disease. However, in general, vaccines have differing efficacy in this regard.29 These differences can reduce the relative benefits of strategies intended to interrupt transmission. We used a single population model, but interpopulation mobility can influence transmission dynamics: a large influx of infectious persons from another population can weaken the indirect protection afforded by vaccines.
We used changes to baseline time spent at retail and recreational outlets to represent population adherence to non-pharmaceutical interventions. Such mobility data is an imperfect proxy for adherence to non-pharmaceutical interventions and will not capture mask use or handwashing. We did not have high-resolution mobility data on these practices, although, in future, it might be possible to infer information about these practices by combining information from phone surveys with online social media data. Our simple ascertainment process in the model was designed to implicitly capture the effects of SARS-CoV-2 PCR testing, contact tracing, and isolation. However, without explicitly representing them, it is impossible for us to study combined strategies of vaccination and testing, tracing, and isolation, or to anticipate how specific changes to these practices would influence our findings.
Finally, the model was parameterised with data from Ontario, Canada. The projected effect of the four vaccine strategies might differ in settings with different epidemiological or social characteristics. For instance, the emergence of a more transmissible strain of SARS-CoV-2 would weaken the indirect protection provided by a vaccine that reduces transmission. At the same time, we note that our findings rely upon a robust epidemiological effect that occurs when R eff becomes sufficiently small. Therefore, the only thing that might change in other settings is the timing of the switch to vaccine strategies that interrupt transmission.
We opted for a coupled social–epidemiological model on account of the importance of interactions between population behaviour and disease dynamics for the control of COVID-19 in the absence of preventive pharmaceutical interventions. Our model generated significantly different projections in our sensitivity analysis in which population behaviour was assumed to be constant (appendix pp 31–32), which is similar to conventional approaches to transmission modelling. Our social model is less complicated than our epidemiological model and, despite this, the coupled social–epidemiological model fitted population-level behaviour as readily as it fitted the epidemic curve. Predicting behaviour is fraught with uncertainty, but so is predicting an epidemic curve. Moreover, digital data on behaviour and sentiment that can be used to model social dynamics are increasingly available.30 Thus, we suggest a role for more widespread use of social–epidemiological models during pandemics.
To apply these results to COVID-19 pandemic mitigation, large-scale seroprevalence surveys before the onset of vaccination could ascertain the level of a population's natural immunity. Age-structured compartmental models could be initialised with this information to generate population-specific projections. In populations in which SARS-CoV-2 seropositivity is high because of wave of cases in autumn or winter, 2020, vaccinating to interrupt transmission might reduce COVID-19 mortality more effectively than targeting vulnerable groups.
Data sharing
All empirical data used in this study are publicly available and have been cited in the Article or its appendix. The simulation code is available online.
Acknowledgments
Acknowledgments
This study was funded by a COVID-19 Rapid Research Grant from the Ontario Ministry of Colleges and Universities.
Contributors
MA and CTB conceptualised the study. All authors designed the model. PCJ developed and analysed the model and generated figures. PCJ and CTB wrote the first draft of the manuscript and accessed and verified the data. All authors revised the manuscript critically for important intellectual content, and read and approved the final version of the manuscript. All authors had full access to all the data in the study, and the corresponding author had final responsibility for the decision to submit for publication.
Declaration of interests
MA and CTB report Discovery Grants from the Natural Sciences and Engineering Council of Canada (NSERC) and a Tri-agency Institutional Programs Secretariat NFRF Exploration Grant, outside the submitted work. MA and CTB report a grant from the NSERC Alliance program for COVID-19 modelling research. PCJ declares no competing interests.
Supplementary Material
References
- 1.Miller IF, Becker AD, Grenfell BT, Metcalf CJE. Disease and healthcare burden of COVID-19 in the United States. Nat Med. 2020;26:1212–1217. doi: 10.1038/s41591-020-0952-y. [DOI] [PubMed] [Google Scholar]
- 2.Anderson SC, Edwards AM, Yerlanov M, et al. Estimating the impact of COVID-19 control measures using a Bayesian model of physical distancing. medRxiv. 2020 doi: 10.1101/2020.04.17.20070086. published online April 22. (preprint, version 1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Peak CM, Kahn R, Grad YH, et al. Individual quarantine versus active monitoring of contacts for the mitigation of COVID-19: a modelling study. Lancet Infect Dis. 2020;20:1025–1033. doi: 10.1016/S1473-3099(20)30361-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tuite AR, Fisman DN, Greer AL. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ. 2020;192:E497–E505. doi: 10.1503/cmaj.200476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lurie N, Saville M, Hatchett R, Halton J. Developing COVID-19 vaccines at pandemic speed. N Engl J Med. 2020;382:1969–1973. doi: 10.1056/NEJMp2005630. [DOI] [PubMed] [Google Scholar]
- 6.Bubar KM, Kissler SM, Lipsitch M, Cobey S, Grad Y, Larremore DB. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. medRxiv. 2021 doi: 10.1101/2020.09.08.20190629. published online Jan 8. (preprint, version 3). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Buckner JH, Chowell G, Springborn MR. Dynamic prioritization of COVID-19 vaccines when social distancing is limited for essential workers. medRxiv. 2020 doi: 10.1101/2020.09.22.20199174. published online Dec 17. (preprint, version 5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Matrajt L, Eaton J, Leung T, Brown ER. Vaccine optimization for COVID-19: who to vaccinate first? medRxiv. 2020 doi: 10.1101/2020.08.14.20175257. published online Dec 15. (preprint, version 3). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Saad-Roy CM, Wagner CE, Baker RE, et al. Immune life history, vaccination, and the dynamics of SARS-CoV-2 over the next 5 years. Science. 2020;370:811–818. doi: 10.1126/science.abd7343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hilton J, Keeling MJ. Estimation of country-level basic reproductive ratios for novel coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLOS Comput Biol. 2020;16 doi: 10.1371/journal.pcbi.1008031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Anderson RM, May RM. Oxford University Press; Oxford: 1992. Infectious diseases of humans: dynamics and control. [Google Scholar]
- 12.Dushoff J, Plotkin JB, Viboud C, et al. Vaccinating to protect a vulnerable subpopulation. PLoS Med. 2007;4:e174. doi: 10.1371/journal.pmed.0040174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Australian Government. Department of Health Australian influenza surveillance report and activity updates. Dec 2, 2020. https://www1.health.gov.au/internet/main/publishing.nsf/Content/cda-surveil-ozflu-flucurr.htm
- 14.Pedro SA, Ndjomatchoua FT, Jentsch P, Tcheunche JM, Anand M, Bauch CT. Conditions for a second wave of COVID-19 due to interactions between disease dynamics and social processes. Front Phys. 2020;8 [Google Scholar]
- 15.Reluga TC. Game theory of social distancing in response to an epidemic. PLOS Comput Biol. 2010;6 doi: 10.1371/journal.pcbi.1000793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Salathé M, Bonhoeffer S. The effect of opinion clustering on disease outbreaks. J R Soc Interface. 2008;5:1505–1508. doi: 10.1098/rsif.2008.0271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Funk S, Gilad E, Watkins C, Jansen VAA. The spread of awareness and its impact on epidemic outbreaks. Proc Natl Acad Sci USA. 2009;106:6872–6877. doi: 10.1073/pnas.0810762106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Verelst F, Willem L, Beutels P. Behavioural change models for infectious disease transmission: a systematic review (2010–2015) J R Soc Interface. 2016;13 doi: 10.1098/rsif.2016.0820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Funk S, Salathé M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interface. 2010;7:1247–1256. doi: 10.1098/rsif.2010.0142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc Biol Sci. 2005;272:1669–1675. doi: 10.1098/rspb.2005.3153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Innes C, Anand M, Bauch CT. The impact of human–environment interactions on the stability of forest–grassland mosaic ecosystems. Sci Rep. 2013;3 doi: 10.1038/srep02689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bury TM, Bauch CT, Anand M. Charting pathways to climate change mitigation in a coupled socio-climate model. PLOS Comput Biol. 2019;15 doi: 10.1371/journal.pcbi.1007000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Amaral MA, de Oliveira MM, Javarone MA. An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. arXiv. 2020 doi: 10.1016/j.chaos.2020.110616. http://arxiv.org/abs/2008.05979 published online Nov 26. (preprint, version 2). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao S, Stone L, Gao D, et al. Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020. Ann Transl Med. 2020;8:448. doi: 10.21037/atm.2020.03.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Alam M, Ariful Kabir KM, Tanimoto J. Based on mathematical epidemiology and evolutionary game theory, which is more effective: quarantine or isolation policy? J Stat Mech. 2020;2020 [Google Scholar]
- 26.Wise T, Zbozinek TD, Michelini G, Hagan CC, Mobbs D. Changes in risk perception and self-reported protective behaviour during the first week of the COVID-19 pandemic in the United States. R Soc Open Sci. 2020;7 doi: 10.1098/rsos.200742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sigdel R, Anand M, Bauch CT. Convergence of socio-ecological dynamics in disparate ecological systems under strong coupling to human social systems. Theor Ecol. 2019;12:285–296. [Google Scholar]
- 28.Prem K, Cook AR, Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLOS Comput Biol. 2017;13 doi: 10.1371/journal.pcbi.1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hodgson SH, Mansatta K, Mallett G, Harris V, Emary KRW, Pollard AJ. What defines an efficacious COVID-19 vaccine? A review of the challenges assessing the clinical efficacy of vaccines against SARS-CoV-2. Lancet Infect Dis. 2021;21:E26–E35. doi: 10.1016/S1473-3099(20)30773-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Salathé M, Bengtsson L, Bodnar TJ, et al. Digital epidemiology. PLOS Comput Biol. 2012;8 doi: 10.1371/journal.pcbi.1002616. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All empirical data used in this study are publicly available and have been cited in the Article or its appendix. The simulation code is available online.