Abstract
How do children allocate their attention? There is too much information in the world to encode it all, so children must pick and choose. How do they organize their sampling to make the most of the learning opportunities that surround them? Previous work shows infants actively seek intermediately predictable information. Here we employ eye-tracking and computational modeling to examine the impact of stimulus predictability across early childhood (ages 3–6 years, n = 72, predominantly Non-Hispanic White, middle- to upper-middle-income), by chronological age and cognitive ability. Results indicated that children prefer attending to stimuli of intermediate predictability, with no differences in this pattern based on age or cognitive ability. The consistency may suggest a robust general information-processing mechanism that operates across the lifespan.
Infants and young children face the remarkable task of learning about the world by extracting relevant information from a complex environment. To do so, attentional resources must be allocated carefully to stimuli that provide the most useful information. Substantial research has shown that young children track and learn from contingencies and statistical regularities in their environment (Fiser & Aslin, 2001, 2002a, 2002b; Saffran, Aslin, & Newport, 1996; Tarabulsy, Tessier, & Kappas, 1996). Yet, there is still relatively little research quantifying how the statistical properties of incoming information impact attention.
Early work in this area proposed that infants preferentially attend to stimuli that are moderately discrepant from the infant’s prior knowledge (Kinney & Kagan, 1976). Similarly, early theoretical work in the area of curiosity suggested that an optimal level of complexity may drive exploration (Berlyne, 1960). In line with these theories, recent work showed that in both visual and auditory domains, 8-month-old infants’ attention is best captured by information with intermediate predictability relative to previous observations (Kidd, Piantadosi, & Aslin, 2012, 2014). In these studies, infants viewed or listened to sequences of events, and eye-tracking was used to measure the event at which infants terminated attention to the sequence. The predictability of events in a sequence was quantified using an ideal learner model (see Experiment and Modeling Approach). Results revealed a U-shaped function relating stimulus predictability and attentional preferences (termed the “Goldilocks Effect”) such that infants were more likely to look away from stimulus events that were either highly predictable or highly unpredictable, and were more likely to attend to stimuli of intermediate predictability, both at the group and individual levels (Kidd, Piantadosi, & Aslin, 2012, 2014; Piantadosi, Kidd, & Aslin, 2014). These findings are in line with the long-standing theory that children construct knowledge by seeking material that is just beyond mastery (Piaget, 1970). No study, however, has examined the impact of stimulus predictability on attention post-infancy.
Extending investigation of this phenomenon into childhood is a critical next step for understanding whether the U-shaped pattern observed in infants represents a robust information-processing mechanism that operates beyond infancy. Early childhood is a time of rapid learning and development across higher-order skill domains. Higher-order cognitive abilities, such as executive functions, emerge and begin to differentiate (Anderson, 2002; Carlson, 2005; Zelazo et al., 2003). Specifically, between the ages of 2 and 6 years old, children experience rapid gains in their ability to regulate attention, including skills such as selective attention and attention switching (for a review, see Garon, Bryson, & Smith, 2008). It is possible that maturation in executive functioning abilities across the early developmental period relate to changes in attentional mechanisms that support information processing efficiency, such as the Goldilocks effect. Furthermore, in the United States, formal teaching and learning typically begin during early childhood, underscoring the importance of deepening our understanding of environmental factors and cognitive processes that contribute to optimal information-seeking behavior, attention, and learning during this developmental period. Finally, characterizing the impact of predictability on attention preferences in early childhood lays a foundation for investigating this phenomenon in clinical populations with characteristic deficits in attention and executive functioning, such as autism spectrum disorder and attention deficit/hyperactivity disorder (Craig et al., 2016), as these developmental disorders are commonly diagnosed in the early childhood period (Maenner et al., 2020; Visser et al., 2014).
The present study involved exploratory analyses quantifying the impact of predictability on visual attention in children ages 3–6 years, and additionally explored whether there is a shift in the impact of predictability on attention preferences with maturation across this age range. In addition to examining potential changes in attention allocation strategies with age, the present study also explored whether children’s attentional preferences shift with increases in cognitive ability. For the purpose of the present study, three brief measures of nonverbal cognitive abilities were selected that were potentially most relevant to implicit visual attentional preferences and predictability, due to their reliance on visual attention skills and lack of verbal or social content. Specifically, measures consisted of two tasks measuring executive functioning skills (including selective attention/inhibitory control, and set shifting) and one measuring visual processing speed.
Given the rapid development of higher-order cognitive abilities across early childhood, it would be reasonable to expect that with increasing age and cognitive maturity, children might show a general shift toward preferring more complex, or less predictable, stimuli. This pattern of results would suggest that neural development or accumulated experience play a role in shaping attentional preferences for predictability. However, findings of consistency in the impact of predictability on attention across the age range of children in the study (3–6 years old), and across levels of nonverbal cognitive ability, would provide support for the hypothesis that the drive to prioritize attentional resources for information at an intermediate level of predictability may represent a more automatic, low-level phenomenon.
Experiment and Modeling Approach
Many prior attempts to examine visual attention to stimuli varying in complexity or predictability have lacked a quantitative definition of complexity. The present study utilizes a formalized definition based on previous work by Kidd et al. (2012, 2014), in which the predictability values of sequential events were estimated according to an ideal learner model. This model represents a formal theory for how a learner might track incoming statistics and use this observed information to form probabilistic expectations about what sort of events are likely to occur in the future. The model thus allows us to compute how predictable or surprising an ideal learner would find an event to be, according to the model’s probabilistic expectations. Events that differ substantially from what the ideal learner model expected are very surprising, while events that are in line with the model’s expectations are very predictable. Previous work has employed similar probabilistic models for understanding learning (Griffiths & Tenenbaum, 2006; Téglás et al., 2011; Tenenbaum, Griffiths, & Kemp, 2006). Here, we calculate predictability by taking the negative log probability of each event according to this model. This negative log probability value, also called “surprisal,” represents the information content of each stimulus event and quantifies the number of bits of information required for an ideal learner to encode the new stimulus based on previously observed stimuli (Shannon, 1948).
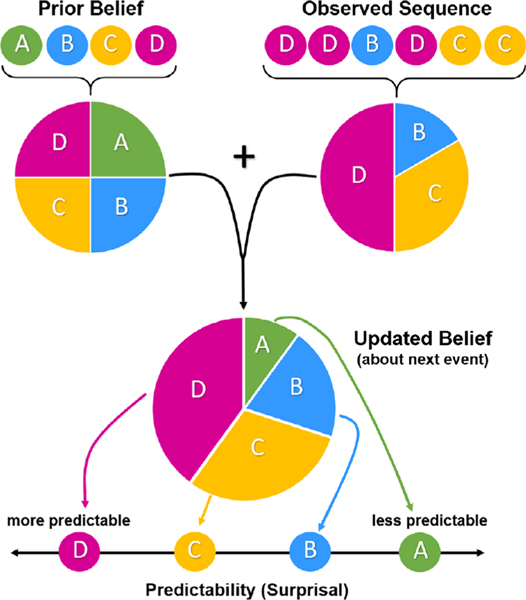
To further illustrate, imagine there are four possible visual events that can be observed by an ideal learner (see Figure 1). In this case, we assume a flat, uninformative prior belief before observing any stimuli, representing the learner’s belief that each event has an equal chance of occurring in the absence of direct evidence at the onset (i.e., events A, B, C, and D are equally likely). After observing each stimulus event, the ideal learner updates their belief about the true probability of each of the four events. After observing the six events depicted in Figure 1, the updated belief would be that a D event is most likely to occur next in this sequence, C and B events have intermediate probabilities of occurring next, and an A event is relatively unlikely to occur next. Therefore, if a D event is observed next, this stimulus event will have a low surprisal value (high predictability), whereas an A event occurring next would have a high surprisal value (low predictability). This example represents a unigram version of the ideal observer model, but we can employ the same method to investigate whether children also track transitional statistics about incoming stimuli.
Figure 1.
Schematic of the ideal learner model. A uniform prior is combined with observed events to form expectations about the likelihood of upcoming events.
In the present experiment, eye-tracking was used to measure at which event in the sequence children looked away from the display. While many previous studies measure attentional preferences with mean looking time, the present study instead measured the likelihood that children looked away at each event to capture children’s real-time attentional behavior as informational content changes as the sequence unfolds. This allowed for characterization of children’s attentional behavior as a function of stimulus predictability, according to both unigram and transitional versions of ideal observer models. Previous work showed that both unigram and transitional statics predicted infants’ attentional preferences (Kidd, Piantadosi, & Aslin, 2012, 2014). Therefore, both unigram and transitional models were tested in the present study.
Method
Participants
In all, 75 children ages 3;2–6;11 years were enrolled in the study between May 2018 and April 2019. Three participants did not yield sufficient usable eye-tracking data (see Procedure) and were excluded from analyses. The final sample included 72 children (49 males and 23 females), with a roughly equal distribution of participants across the age span (Mage = 4.8 years, SD = 1.1; see Supporting Information for age distribution). Children were majority Non-Hispanic White (92%) from predominantly middle- to upper-middle-income families (93% with annual household income over $55,000) and were recruited from local hospitals and community events in the greater Rochester, NY area. Participants were screened for caregiver-reported developmental, learning, or mental health concerns, vision and motor deficits, and neurological problems. All procedures were approved by the university’s Institutional Review Board and informed consent for participation was obtained from each child’s legal guardian. Participants received financial compensation for participation. Study procedures took place across two visits.
Attention Preference Eye-Tracking Task
The present study aimed to test how the predictability of visual sequences of events in the environment influences attention preferences in young children. This task was based on similar tasks used with infants (Kidd et al., 2012, 2014), and was adapted for children ages 3–6 years.
Stimuli
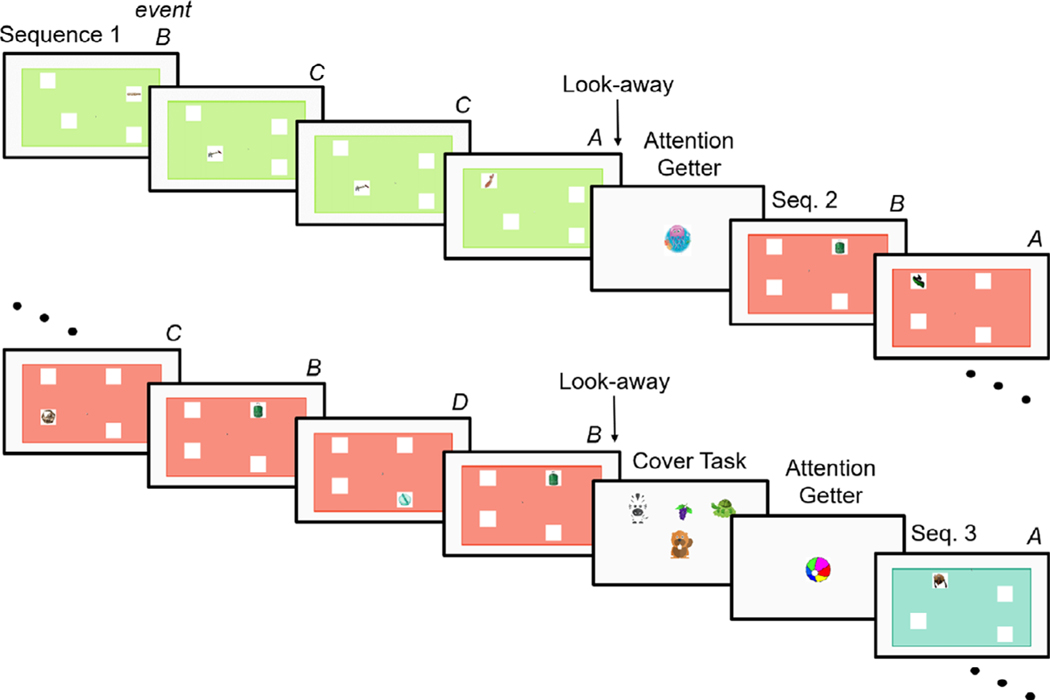
Children were presented with visual displays depicting sequences of events varying in predictability (Figure 2). The displays featured a large, colored rectangle with four windows. Each window was located in one of the four quadrants of the rectangle, and its position within the quadrant was randomized on each sequence to one of four locations within the quadrant. Novel objects were animated to pop in and out of the windows, one after another in sequence. Objects consisted of real images of unique, unfamiliar objects that were not easily nameable (to reduce semantic content). Each object was unique to each window. No objects were repeated across event sequences. The number of possible objects (4) was chosen to be within the range children in the study’s age range are reasonably able to track (Alvarez & Franconeri, 2007). Each event in the sequence lasted 1,000 ms (500 ms “pop-out,” 500 ms “pop-in”). Events were presented sequentially with no overlap or delay. Stimuli for the eye-tracking task were programmed in Python (see Kid Experimental Library in Python; KELPY, https://github.com/piantado/kelpy).
Figure 2.
Example of progression of eye-tracking task.
Procedure
This task was conducted using a table-mounted Tobii Pro T60XL eye-tracker (Tobii Technology, Inc., Falls Church, VA) in a partially darkened room. Experimenters and caregivers were directly outside of the room while the task was completed. Children were seated with their eyes approximately 23 in. from the monitor. At this viewing distance, the 24-in. LCD screen was subtended 24 × 32 degrees of visual angle. A five-point calibration procedure was conducted at the onset of the experiment.
Participants were presented with the same set of 32 sequences of events, each consisting of 30 possible events. The objects and sequence order were randomized across participants. Sequences varied in the probabilities of each of the four objects appearing in their respective windows, ranging from very simple (e.g., A, A, A, A, A, …) to more varied (e.g., A, B, D, A, C, . . .; see Supporting Information for details and full sequences. Full sequences also available at https://github.com/cubitl/attentionpredictability). Child-friendly music with no words was played quietly in the background to maintain participants’ engagement with the task, which was unrelated to the unfolding of visual event on the screen and thus not expected to systematically influence behavior event-to-event.
The primary outcome measure for each sequence was the probability value of the specific event at which the child looked away from the area covered by the colored rectangle (a “look-away”). Each sequence of events continued until either (a) the participant met the look-away criterion (i.e., gaze directed outside of the viewing area continuously for > 1,000 ms) or (b) 30 s, the maximum duration of a sequence. Before the start of each new sequence, an attention-attracting stimulus was displayed on the screen until the child fixated on the center of the screen for 1,000 ms, at which point the next sequence was initiated. Children were prompted to take brief breaks between sequences as necessary to facilitate successful completion of the task. The amount of time children spent completing this task varied based on the amount of time they looked at the sequences as well as time required for breaks and ranged from 12 to 34 min. To maintain engagement, a simple cover task was inserted randomly between sequences of the main task. Children were only given instructions related to the cover task, and were informed they may also see other pictures appear on the screen that were different from the cover task. Importantly, children were never explicitly instructed to look at or attend to the screen.
Sequences were discarded prior to analysis if (a) the participant looked continuously for the full 30 s (11.8%), as the final event of the sequence in this case does not represent the point at which children stopped attending, (b) the participant looked for fewer than four events within a sequence, since so few observations is likely insufficient to establish expectations about the distribution of events in the sequence (18.0%), or (c) a false look-away (the eye-tracker temporarily stopped tracking the eyes while the child was still looking at the screen due to child movement), other equipment failure, or experimenter error (6.8%) occurred.
Participants yielded an average of 20.3 (SD = 4.5) useable sequences out of 32 possible sequences. Children attended to useable sequences for an average of 12.2 events (SD = 7.0) per sequence before looking away (see Supporting Information for details). Importantly, participants were not expected to look for all 30 items within a sequence, as the key outcome of interest was the predictability of the event at which participants looked away.
Measures of Cognitive Ability
Three cognitive measures from the NIH Toolbox Cognition Battery (Weintraub et al., 2013) were used to assess key areas of cognitive functioning, including attention, inhibitory control, set shifting, and processing speed (Anderson, 2002; Zelazo et al., 2013). Tasks included the Flanker Inhibitory Control and Attention Test (Flanker; selective visual attention, inhibitory control), the Dimensional Change Card Sort (DCCS; set shifting), and Picture Comparison Processing Speed (PCPS; processing speed). These tasks have been validated in young children in this age range, and have been shown to be sensitive to developmental changes in cognitive functions (Weintraub et al., 2013; Zelazo et al., 2013). Tasks were administered via a 9.7 in. touchscreen tablet at the second study visit.
For all three cognitive measures, analyses utilized the Uncorrected Standard Score, which represents a child’s score compared to the population mean across ages 3–85 years, facilitating comparison of cognitive ability across children of different ages. Performance data for all three measures indicated substantial variability in performance within the study sample, despite screening for developmental delays (see Supporting Information for performance data). For participants whose completion of the tasks was discontinued based on low performance on the practice trials (Flanker, n = 7; DCCS, n = 13), no standard scores were calculated. These participants were not included in analyses utilizing the tasks for which they did not receive scores.
Analytic Approach
Modeling and data analytic methods used to quantify predictability and examine the impact of predictability on attention preferences are based on methods used in previous studies of attentional preference in infants (Kidd et al., 2012, 2014). The probability value of each event in a sequence was quantified according to the ideal learner model using a Markov Dirichlet-Multinomial model, a probabilistic model that uses counts of observed events to calculate a posterior distribution for an underlying multinomial distribution of events (see Supporting Information for details). We built both a unigram and transitional version of the model to test both types of probabilistic expectations.
To examine the nature of the relation between predictability and attention preferences, the surprisal value (predictability) of each event was then compared with children’s probability of looking away from that event to yield the linking function. For visualizations of the linking function, a Generalized Additive Model (GAM; Hastie & Tibshirani, 1990) was fit to the data to visually examine the shape of a continuous linking function between predictability and likelihood of looking away. Separate GAM functions were fit to the data to address each unique question. Importantly, these modeling methods do not attempt to force the linking function to fit a specific shape; rather, the shape of linking function is free to vary, allowing us to detect any potential pattern relating stimulus predictability and children’s likelihood of looking away (e.g., preference for novelty, preference for familiarity, preference for intermediate predictability, no impact of predictability on children’s attention).
To test the significance of the impact of predictability on look-away likelihood, Cox regression was used to account for the fact that once the child looks away they provide no more data on that sequence (Hosmer, Lemeshow, & May, 2008; Klein & Moeschberger, 2005). The Cox regression controls for the baseline distribution of look-aways in the sample and accounts for the number of events into the sequence that the look-away occurred (as children are naturally more likely to look away the further they are into the sequence). Linear and quadratic surprisal terms were included in the regression as predictors of look-away likelihood. Surprisal was centered and standardized before being squared. Model fit comparisons were conducted using the Akaike information criterion (AIC; Akaike, 1974).
Results
Unigram and Transitional Models for Full Sample
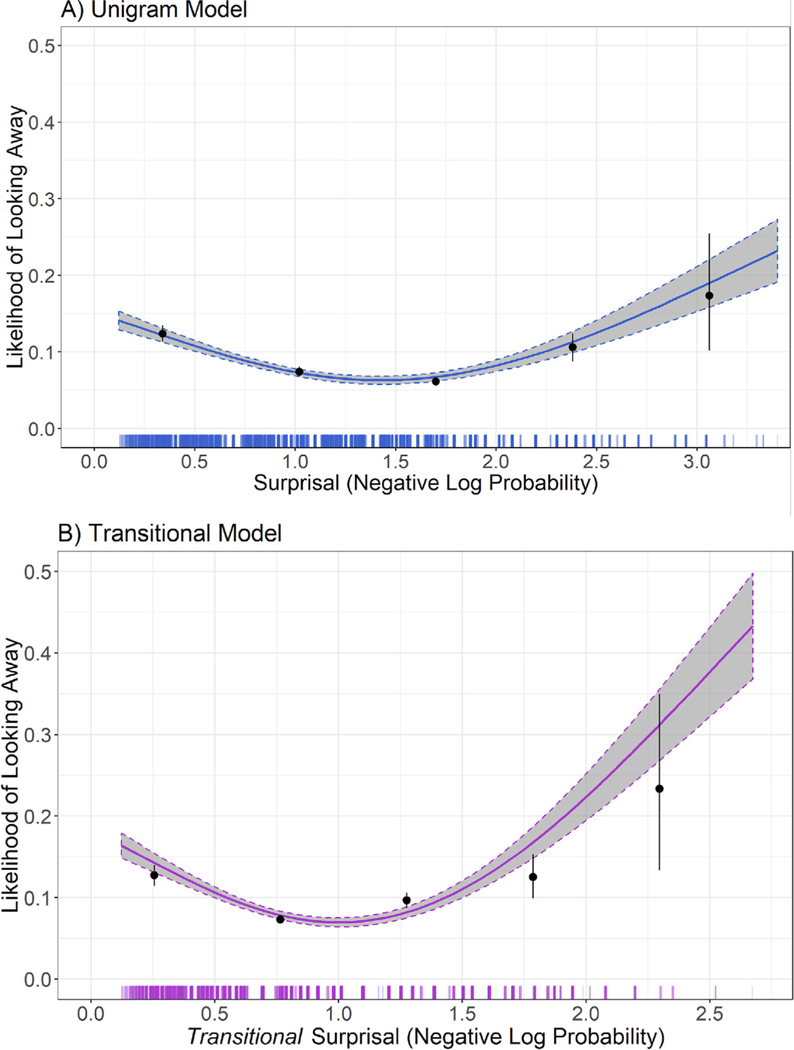
The Cox regression for the unigram model (Table 1) yielded a significant quadratic effect (β = .061, z = 3.729, p = .0001) indicating a significant U-shaped association between predictability (surprisal) and attentional preferences, where children were most likely to continue attending to stimuli of intermediate predictability, and most likely to look away from stimuli of either relatively high or relatively low predictability (Figure 3A). The size of this effect was exp(β) = 1.063, which means that with each increase in squared surprisal by 1 standard deviation from the mean, the likelihood of looking away increased by a factor of 1.063. While this is a relatively small effect, it is highly significant (p = .0001). The linear effect of surprisal was also significant (β = −.071, z =2.942, p = .003), which indicates that the U-shaped function is not symmetrical around the mean, shifted toward lower surprisal values.
Table 1.
Cox Regression of the Effect of Predictability on Attention Preferences
| Covariate | Coef (β) | exp (β) | SE (β) | z | p |
|---|---|---|---|---|---|
| Unigram model | |||||
| Linear surprisal | −.071 | 0.931 | .024 | −2.942 | .003** |
| Quadratic surprisal | .061 | 1.063 | .016 | 3.729 | .0001*** |
| Transitional model | |||||
| Linear surprisal | −.054 | 0.948 | .024 | −2.238 | .03* |
| Quadratic surprisal | .058 | 1.060 | .013 | 4.428 | 1 × 10−5*** |
Note. For each regression model, linear and quadratic effects were entered simultaneously. Surprisal was centered and standardized to have a mean of 0 and a standard deviation of 1 before being squared.
p ≤ .05.
p ≤ .01.
p ≤ .001.
Figure 3.
Look-away likelihood as a function of (A) unigram and (B) transitional surprisal (predictability). Curves represent the fit of a Generalized Additive Model (with 95% confidence intervals) linking predictability to probability of looking away. Low values on the y-axis indicate increased attentional preference, whereas low values on the x-axis indicate increased predictability (decreased surprisal). Dots represent raw data binned into 5 bins (± SE) equally spaced across the x-axis. Vertical lines on the x-axis represent count of data points collected at each predictability value.
Results from the Cox regression for the transitional model (Table 1) showed a similar overall pattern as the unigram model, yielding significant quadratic (β = .058, z = 4.428, p < .0001) and linear (β = −.054, z = −2.238, p = .03) effects of surprisal (Figure 3B). The size of the quadratic effect was also relatively small (exp(β) = 1.060) but highly significant (p < .0001). The fits of the unigram and transitional models were compared using AIC values to understand whether either model better explained the relation between predictability and attention preferences. The absolute difference between AIC values for the unigram (AIC = 18,351.3) and transitional (AIC = 18,350.7) models was < 2, which is considered strong evidence of no difference in model fit (Burnham & Anderson, 2004).
To examine the potential impact of other task-related factors that could influence look-away likelihood, additional Cox regression analyses were conducted with these factors as covariates. Covariates were selected based on task-related factors examined in infants (Kidd et al., 2012), and included whether this was the first appearance of the item in the sequence, whether this event was the same as the previous event (repeated event), and the sequence number (indexing how far into the experiment the child was). Results from these analyses indicated that even when including these covariates, the quadratic surprisal term remained significant for both unigram and transitional models, and there was no difference in model fit between unigram and transitional models (see Supporting Information for details).
Taken together, these results suggest that young children are also tracking the statistics of both single events and pairs of events in their environment, and that there is a U-shaped association between predictability (surprisal) and attentional preferences such that children are least likely to look away for events of intermediate predictability.
Developmental Trajectory
The present study also explored potential changes in the impact of predictability on attention preferences across early childhood, which was done by examining changes based on both chronological age and cognitive ability level. Because analyses utilize group-level data, to maximize the ability to detect any possible differences with maturation, the sample was divided into two groups based on median splits for both chronological age and cognitive ability analyses.
Chronological Age
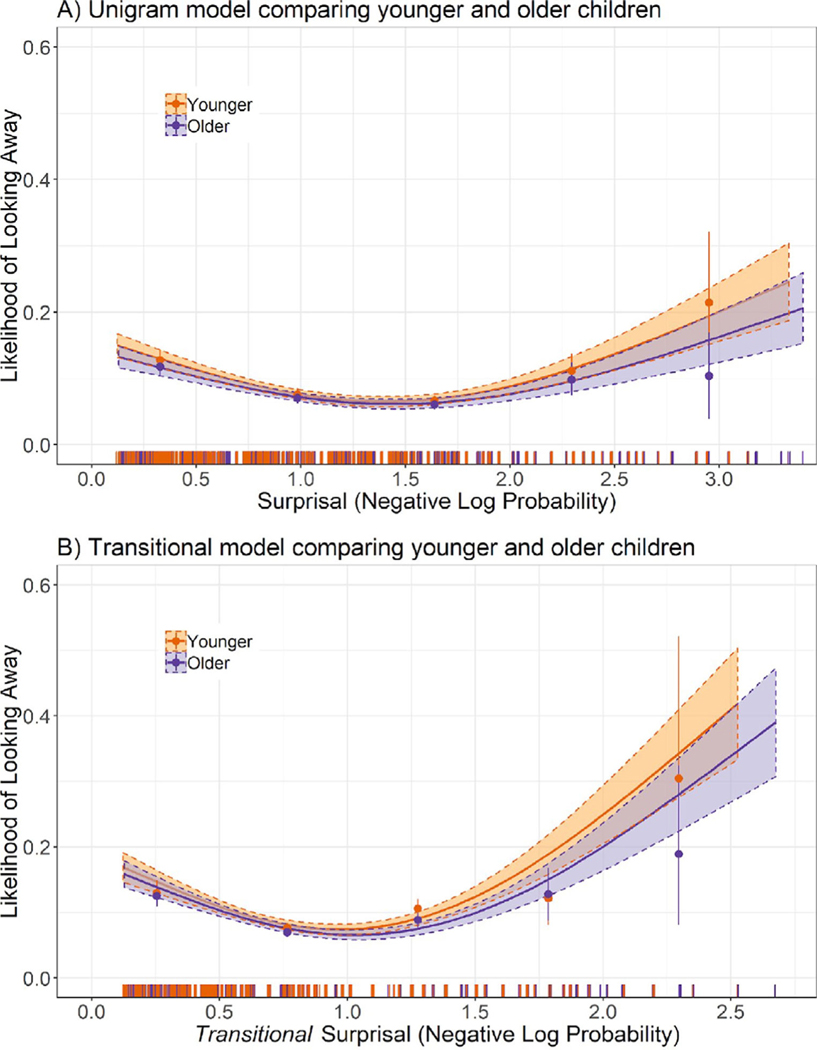
The sample was divided into two equal-sized groups based on a median split of chronological age (Younger [3.12–4.61 years, n = 36], Older [4.62–6.95 years, n = 36]). Younger and older children yielded a similar average number of useable sequences (M (SD) for Younger = 20.4 (4.6); Older = 20.1 (4.4)). Additionally, younger and older children attended to each useable sequence for a similar average of number of events before looking away (M (SD) for Younger = 11.7 (6.7); Older = 12.7 (7.4)). Separate GAMs for each age group were plotted to examine the association between predictability and attention preferences for each group according to both the unigram and transitional models (Figure 4). Visualization of these curves indicates overlap of 95% confidence intervals of the two GAMs across the length of the x-axis for both the unigram and transitional models, indicating no significant differences in the shape of the function linking attention preferences and predictability based on age. These results suggest that the U-shaped association between predictability and attention preferences is relatively stable across the age range of 3–6 years.
Figure 4.
Look-away likelihood as a function of (A) unigram and (B) transitional surprisal (predictability) for younger and older groups. The curves represent the fit of separate Generalized Additive Models for each age group (with 95% confidence intervals), linking predictability to probability of looking away separately for each group. Dots represent raw data binned into 5 bins (± SE) equally spaced along the x-axis. Vertical lines on the x-axis represent count of data points collected at each predictability value.
Cognitive Ability
In all, 69 out of the 72 children who yielded useable data on the eye-tracking task also completed at least one of the selected subtests from the NIH Toolbox Cognition Battery. Analyses utilized participants’ Uncorrected Standardized Scores, which represent each child’s performance compared to the general population mean and do not correct for age. Children were grouped into two roughly equal-sized groups based on a median split of task performance as measured by Uncorrected Standard Scores (“Lower Ability” included participants below and including the median; “Higher Ability” included participants above the median). Groups were created separately for each of the three measures, including Flanker (Lower Ability, n = 33; Higher Ability, n = 31), DCCS (Lower Ability, n = 26; Higher Ability, n = 31), and PCPS (Lower Ability, n = 33; Higher Ability, n = 35). For each measure, separate GAMs for Lower Ability and Higher Ability groups were plotted to examine the association between predictability and attention preferences for each group according to unigram and transitional models (Figure 5). Visualization of these curves indicates overlap of 95% confidence intervals of the two GAMs across the length of the x-axis for all measures, for both the unigram and transitional models. These findings indicate no significant differences in the shape of the function linking attention preferences and predictability based on cognitive ability, suggesting that the U-shaped association between predictability and attention preferences does not change significantly with increases in nonverbal cognitive abilities tested.
Figure 5.
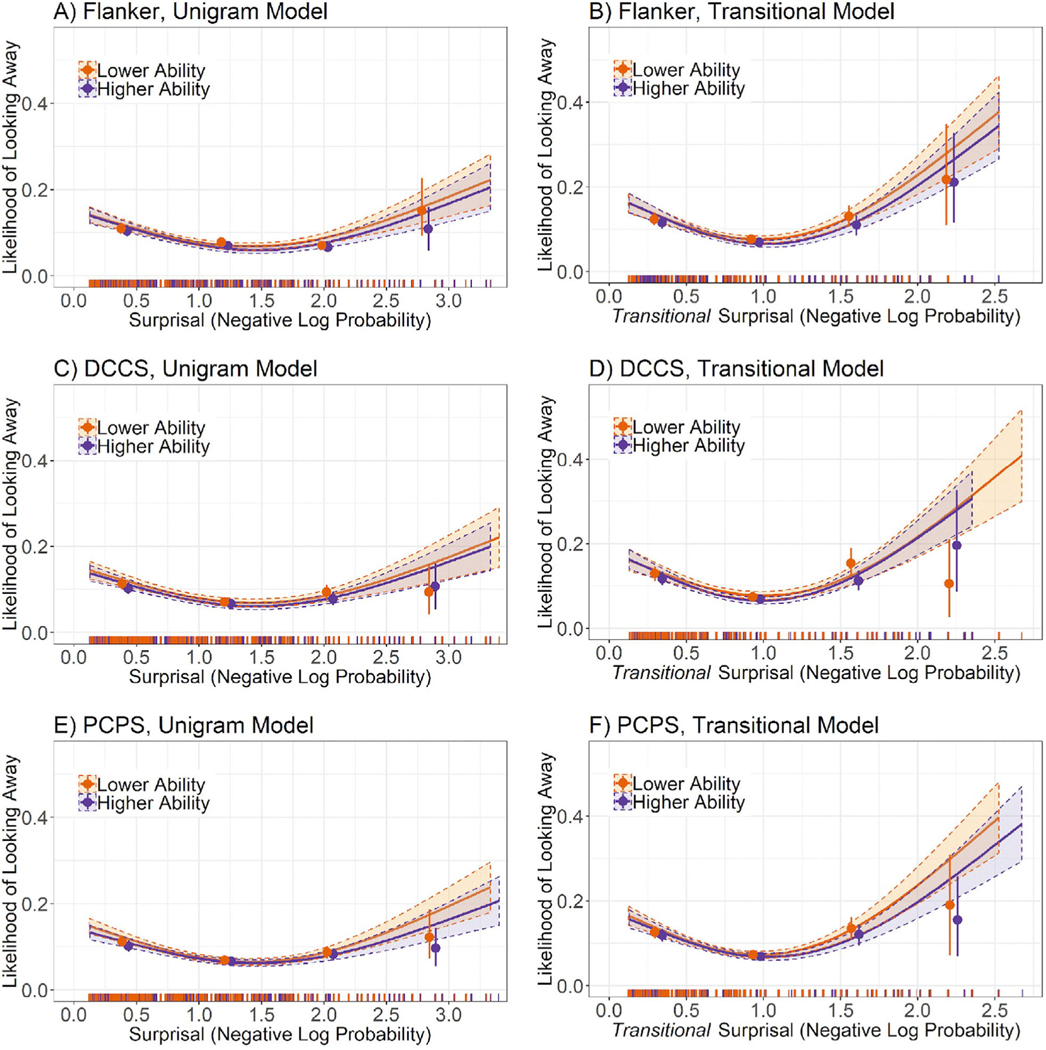
Look-away likelihood as a function of (A, C, E) unigram and (B, D, F) transitional surprisal (predictability) for Lower Ability and Higher Ability groups for NIH Toolbox tasks. Measures included Flanker Inhibitory Control and Attention Test (Flanker), Dimensional Change Card Sort (DCCS), and Picture Comparison Processing Speed (PCPS). Curves represent the fit of separate Generalized Additive Models (with 95% confidence intervals) linking predictability to probability of looking away separately for each group. Dots represent raw data binned into 5 bins (± SE) equally spaced along the x-axis. Vertical lines on the x-axis represent count of data points collected at each predictability value.
Discussion
The present study quantified the impact of predictability on visual attentional preferences in young children, and examined the developmental trajectory of this phenomenon across early childhood. Consistent with previous findings in infants, results revealed a U-shaped association between predictability and attention such that young children were most likely to maintain attention to stimuli of intermediate complexity and were more likely to terminate attention to highly predictable or highly unpredictable stimuli. Results also provided preliminary evidence that a “Goldilocks effect” may be consistent across development in 3- to 6-year-old children, both by chronological age and cognitive ability. This is the first evidence that the Goldilocks effect extends beyond infancy, suggesting that this attentional preference may be preserved across childhood and perhaps the lifespan.
Furthermore, this U-shaped association was significant for both unigram and transitional models of predictability, suggesting that children tracked both types of statistics in a task with minimal demands. It is likely that the optimal model of environmental probability impacting attention allocation would change based on task demands or in contexts where prior learning indicates certain statistics are more informative than others. Additionally, consistent with findings in infants (Kidd et al., 2012, 2014), the size of this effect for both models was small, though highly significant. This is expected, as many other stimulus factors also impact visual attention (e.g., salience, movement; Itti & Koch, 2001). The predictability of visual stimuli may also have greater influence on attention preferences in a task where tracking statistical properties of events improves performance.
Taken together, these findings contribute to our understanding of how statistical properties of information in the environment influence attentional patterns and subsequent learning across development. Young children are tracking probabilistic visual information in their environment and preferentially attending to intermediately predictable information. This implicit attentional strategy may serve as a domain-general mechanism prioritizing information that is optimal for learning, thereby maximizing cognitive efficiency in the complex natural environment. Given the sociocultural homogeneity of the present study sample, it will be critical for future work to examine this phenomenon in more diverse populations to better understand the generalizability of these findings. Another limitation of this work is that age and cognitive ability differences were examined cross-sectionally. Furthermore, median splits on age and cognitive ability were used in the present study due to the paradigm and group-level analyses conducted, as they maximized our ability to observe any possible shift in attentional behavior with maturation. It may be valuable for future studies to explore potential subtle developmental changes in this attentional mechanism by estimating individual linking functions, as has been done in infants (Piantadosi et al., 2014). To draw meaningful conclusions from this sort of analysis would require collecting significantly more data from each individual, perhaps even using a variety of tasks or stimuli. However, to fully characterize the impact of predictability on attention across the lifespan, it will be important to extend this work to a broader age range and to examine individual developmental trajectories of this phenomenon.
Our findings have important implications for ongoing work in curiosity and learning, and the interaction of these processes across development. The present study demonstrated that in the absence of an explicit goal, young children across a range of ages beyond infancy and across cognitive ability levels track the statistical properties of incoming information, and modulate their attention to prioritize information that is intermediately predictable based on their prior observations. These results are consistent with long-standing theories in exploration and curiosity suggesting that learners select material that is neither too simple nor too complex, and therefore potentially optimal for learning (Berlyne, 1960). Our results demonstrate that across early childhood, an attentional preference for intermediate predictability is an organizing principle that guides what information children sample in their environment, contributing to our understanding of curiosity-driven learning processes (Kidd & Hayden, 2015; Oudeyer & Smith, 2016). Because the present paradigm did not directly measure learning, it will be important for future work to examine the impact of this attentional mechanism on downstream learning. Open questions remain as to whether learners vary in the extent to which predictability of incoming information impacts their learning, and which aspects of learning are facilitated by this phenomenon.
Findings from the present study also suggest next steps in efforts to identify neural systems involved in attention, curiosity, and learning. Consistency in the attentional preference for intermediate predictability across development suggests that this phenomenon may be related to basic neural processes, such as mechanisms striving to maintain optimal arousal of the neural system (Aston-Jones & Cohen, 2005; Cools & D’Esposito, 2011; McGinley, David, & McCormick, 2015; Yerkes & Dodson, 1908). Future work examining possible neural underpinnings of this attentional preference could aid in linking the role of this attentional preference to other aspects of cognition (Turk-Browne, Scholl, & Chun, 2008).
Finally, predictability of visual events in a sequence is just one of many aspects of stimulus complexity, and this phenomenon has only been examined in highly controlled, laboratory-based experimental tasks. Additional work is necessary to gain a more sophisticated understanding of the combined impact of various types of complexity on how children allocate attention in the natural environment. It will also be important to explore other environmental factors that may impact the optimal level of predictability for capturing attention (e.g., distracting environments, social interactions). Continued work in this area will deepen our understanding of typical cognitive development, and provide a foundation for exploring potential deviations from this process in developmental disorders (e.g., autism spectrum disorder, attention deficit/hyperactivity disorder).
Supplementary Material
Appendix S1. Supporting information includes additional details regarding 1) participant age distribution, 2) sequences used in the experiment, 3) number of events seen by participants in each sequence, 4) participants’ performance on cognitive measures, 5) the analytic approach, and 6) additional analyses that include task-related covariates.
Acknowledgments
We thank Steve Piantadosi for help with data analysis; Tonya Bortz, Emily Ballou, Shannon Cahalan, and Holly Palmeri for help with stimulus development and data collection; and Yim Register and Amanda Yung for help with task programming and data processing. This work was supported by a Ruth L. Kirschstein National Research Service Award from the National Institute of Mental Health (F31 MH113269) to Laura S. Cubit, the National Institute on Deafness and Other Communication Disorders (R21 DC016165; PI: Loisa Bennetto), Google (Faculty Research Award; PI: Celeste Kidd), and the Jacobs Foundation (Early Career Research Fellowship; PI: Celeste Kidd).
Footnotes
Supporting Information
Additional supporting information may be found in the online version of this article at the publisher’s website:
Contributor Information
Laura S. Cubit, University of Rochester and Children’s Hospital of Philadelphia.
Rebecca Handsman, University of Rochester and Children’s National Medical Center.
Loisa Bennetto, University of Rochester.
Rebecca Canale, University of Rochester and Yale University.
Celeste Kidd, University of California, Berkeley.
References
- Akaike H.(1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723. 10.1007/978-1-4612-1694-0_16 [DOI] [Google Scholar]
- Alvarez GA, & Franconeri SL (2007). How many objects can you track?: Evidence for a resource-limited attentive tracking mechanism. Journal of Vision, 7, 14. 10.1167/7.13.14 [DOI] [PubMed] [Google Scholar]
- Anderson P.(2002). Assessment and development of executive function (EF) during childhood. Child Neuropsychology, 8, 71–82. 10.1076/chin.8.2.71.8724 [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, & Cohen JD (2005). An integrative theory of locus coeruleus-norepinephrine function: Adaptive gain and optimal performance. Annual Review of Neuroscience, 28, 403–450. 10.1146/annurev.neuro.28.061604.135709 [DOI] [PubMed] [Google Scholar]
- Berlyne DE (1960). Conflict, arousal, and curiosity. New York, NY: McGraw-Hill Book. [Google Scholar]
- Burnham KP, & Anderson DR (2004). Multimodel inference: understanding AIC and BIC in model selection. Sociological Methods & Research, 33, 261–304. 10.1177/0049124104268644 [DOI] [Google Scholar]
- Carlson SM (2005). Developmentally sensitive measures of executive function in preschool children. Developmental Neuropsychology, 28, 595–616. 10.1207/s15326942dn2802_3 [DOI] [PubMed] [Google Scholar]
- Cools R, & D’Esposito M.(2011). Inverted-U–shaped dopamine actions on human working memory and cognitive control. Biological Psychiatry, 69, e113–e125. 10.1016/j.biopsych.2011.03.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig F, Margari F, Legrottaglie AR, Palumbi R, De Giambattista C, & Margari L.(2016). A review of executive function deficits in autism spectrum disorder and attention-deficit/hyperactivity disorder. Neuropsychiatric Disease and Treatment, 12, 1191. 10.2147/NDT.S104620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiser J, & Aslin RN (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychological Science, 12, 499–504. 10.1111/1467-9280.00392 [DOI] [PubMed] [Google Scholar]
- Fiser J, & Aslin RN (2002a). Statistical learning of higher-order temporal structure from visual shape sequences. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28, 458–467. 10.1037/0278-7393.28.3.458 [DOI] [PubMed] [Google Scholar]
- Fiser J, & Aslin RN (2002b). Statistical learning of new visual feature combinations by infants. Proceedings of the National Academy of Sciences of the United States of America, 99, 15822–15826. 10.1073/pnas.232472899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garon N, Bryson SE, & Smith IM (2008). Executive function in preschoolers: A review using an integrative framework. Psychological Bulletin, 134, 31. 10.1037/0033-2909.134.1.31 [DOI] [PubMed] [Google Scholar]
- Griffiths TL, & Tenenbaum JB (2006). Optimal predictions in everyday cognition. Psychological Science, 17, 767–773. 10.1111/j.1467-9280.2006.01780.x [DOI] [PubMed] [Google Scholar]
- Hastie TJ, & Tibshirani RJ (1990). Generalized additive models. Boca Raton, FL: Chapman and Hall/CRC Press. [Google Scholar]
- Hosmer D, Lemeshow S, & May S.(2008). Applied survival analysis: Regression modeling of time to event data (2nd ed.). Hoboken, NJ: Wiley. [Google Scholar]
- Itti L, & Koch C.(2001). Computational modelling of visual attention. Nature Reviews Neuroscience, 2, 194. 10.1038/35058500 [DOI] [PubMed] [Google Scholar]
- Kidd C, & Hayden BY (2015). The psychology and neuroscience of curiosity. Neuron, 88, 449–460. 10.1016/j.neuron.2015.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidd C, Piantadosi ST, & Aslin RN (2012). The Goldilocks effect: Human infants allocate attention to visual sequences that are neither too simple nor too complex. PLoS One, 7, e36399. 10.1371/journal.pone.0036399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidd C, Piantadosi ST, & Aslin RN (2014). The Goldilocks effect in infant auditory attention. Child Development, 85, 1795–1804. 10.1111/cdev.12263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinney DK, & Kagan J.(1976). Infant attention to auditory discrepancy. Child Development, 47, 155–164. 10.2307/1128294 [DOI] [PubMed] [Google Scholar]
- Klein JP, & Moeschberger ML (2005). Survival analysis: techniques for censored and truncated data (2nd ed.). New York, NY: Springer-Verlag. [Google Scholar]
- Maenner MJ, Shaw KA, Baio J, Washington A, Patrick M, DiRienzo M, … Dietz PM (2020). Prevalence of autism spectrum disorder among children aged 8 years—autism and developmental disabilities monitoring network, 11 sites, United States, 2016. MMWR Surveillance Summaries, 69, 1. 10.15585/mmwr.ss6904a1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley MJ, David SV, & McCormick DA (2015). Cortical membrane potential signature of optimal states for sensory signal detection. Neuron, 87, 179–192. 10.1016/j.neuron.2015.05.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oudeyer P-Y, & Smith LB (2016). How evolution may work through curiosity-driven developmental process. Topics in Cognitive Science, 8, 492–502. 10.1111/tops.12196 [DOI] [PubMed] [Google Scholar]
- Piaget J.(1970). Structuralism. New York, NY: Harper & Row. [Google Scholar]
- Piantadosi ST, Kidd C, & Aslin R.(2014). Rich analysis and rational models: Inferring individual behavior from infant looking data. Developmental Science, 17, 321–337. 10.1111/desc.12083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saffran JR, Aslin R, & Newport E.(1996). Statistical learning by 8-month-old infants. Science, 274, 1926–1928. 10.1126/science.274.5294.1926 [DOI] [PubMed] [Google Scholar]
- Shannon C.(1948). A mathematical theory of communication. Bell Systems Technical Journal, 27, 379–423. 10.1002/j.1538-7305.1948.tb01338.x [DOI] [Google Scholar]
- Tarabulsy GM, Tessier R, & Kappas A.(1996). Contingency detection and the contingent organization of behavior in interactions: Implications for socioemotional development in infancy. Psychological Bulletin, 120, 25–41. 10.1037/0033-2909.120.1.25 [DOI] [PubMed] [Google Scholar]
- Téglás E, Vul E, Girotto V, Gonzalez M, Tenenbaum JB, & Bonatti LL (2011). Pure reasoning in 12-month-old infants as probabilistic inference. Science, 332, 1054–1059. 10.1126/science.1196404 [DOI] [PubMed] [Google Scholar]
- Tenenbaum JB, Griffiths TL, & Kemp C.(2006). Theory-based Bayesian models of inductive learning and reasoning. Trends in Cognitive Sciences, 10, 309–318. 10.1016/j.tics.2006.05.009 [DOI] [PubMed] [Google Scholar]
- Turk-Browne NB, Scholl BJ, & Chun MM (2008). Babies and brains: Habituation in infant cognition and functional neuroimaging. Frontiers in Human Neuroscience, 2, 16. 10.3389/neuro.09.016.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visser SN, Danielson ML, Bitsko RH, Holbrook JR, Kogan MD, Ghandour RM, … Blumberg SJ (2014). Trends in the parent-report of health care provider-diagnosed and medicated attention-deficit/hyperactivity disorder: United States, 2003–2011. Journal of the American Academy of Child and Adolescent Psychiatry, 53, 34–46. 10.1016/j.jaac.2013.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weintraub S, Dikmen SS, Heaton RK, Tulsky DS, Zelazo PD, Bauer PJ, … Gershon RC (2013). Cognition assessment using the NIH Toolbox. Neurology, 80, S54–S64. 10.1212/WNL.0b013e3182872ded [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yerkes RM, & Dodson JD (1908). The relation of strength of stimulus to rapidity of habit-formation. Journal of Comparative Neurology and Psychology, 18, 459–482. 10.1002/cne.920180503 [DOI] [Google Scholar]
- Zelazo PD, Anderson JE, Richler J, Wallner-Allen K, Beaumont JL, & Weintraub S.(2013). II. NIH Toolbox Cognition Battery (CB): Measuring executive function and attention. Monographs of the Society for Research in Child Development, 78, 16–33. 10.1111/mono.12032 [DOI] [PubMed] [Google Scholar]
- Zelazo PD, Müller U, Frye D, Marcovitch S, Argitis G, Boseovski J, … Sutherland A.(2003). The development of executive function in early childhood. Monographs of the Society for Research in Child Development, 68, 10.1111/j.0037-976X.2003.00261.x [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Supporting information includes additional details regarding 1) participant age distribution, 2) sequences used in the experiment, 3) number of events seen by participants in each sequence, 4) participants’ performance on cognitive measures, 5) the analytic approach, and 6) additional analyses that include task-related covariates.