Nonlinear Neural Network Based Forecasting Model for Predicting COVID-19 Cases

Abstract

The recent COVID-19 outbreak has severely affected people around the world. There is a need of an efficient decision making tool to improve awareness about the spread of COVID-19 infections among the common public. An accurate and reliable neural network based tool for predicting confirmed, recovered and death cases of COVID-19 can be very helpful to the health consultants for taking appropriate actions to control the outbreak. This paper proposes a novel Nonlinear Autoregressive (NAR) Neural Network Time Series (NAR-NNTS) model for forecasting COVID-19 cases. This NAR-NNTS model is trained with Scaled Conjugate Gradient (SCG), Levenberg Marquardt (LM) and Bayesian Regularization (BR) training algorithms. The performance of the proposed model has been compared by using Root Mean Square Error (RMSE), Mean Square Error (MSE) and correlation co-efficient i.e. R-value. The results show that NAR-NNTS model trained with LM training algorithm performs better than other models for COVID-19 epidemiological data prediction.

Introduction

The first instance of novel coronavirus, which is also known as the Wuhan Virus or COVID-19, was reported in the middle of December 2019 [1]. The human-to-human transition of nCov or COVID-19 raises the infected cases exponentially in this early stage. The World Health Organization (WHO) has issued a worldwide health emergency on 30 January 2020 because of this COVID-19 [2]. Morbidity and mortality rates for the COVID-19 infection are unknown at an advanced stage [3], particularly for young and old people. To control the widespread of the COVID-19, government authorities took preventative actions and enforced curfew or shutdown infested cities in the most of the world. This helps the public authorities to implement social distance among the people to prevent the spread of this novel virus. Therefore, predicting COVID-19 cases with multi parameters is an extreme need in this current scenario in terms of social and community health aspects [4].

In this scenario, any single prediction model is not adequate for COVID-19 prediction with high accuracy [5]. In the existing works [6–9], researchers have used neural networks with multi-layered perceptron, regression model and vector autoregression model for forecasting the epidemiological cases of COVID-19 in India. Autoregression is basically a time series model, which utilizes the observations from the previous time steps as input to any regression equation for predicting the significance of the next time step. This process is simple, which results the accurate forecast on a given range of time series problems. Generally, data mining and machine learning models are used for predicting COVID-19 [10–12] and data are collected and processed from various sources in the secured process [13–37]. Deep learning techniques are also used to identify the confirmed COVID-19 disease from the X-ray dataset [38]. This pandemic prediction can be based on different variables including the influence of natural aspects, infection rate, confinement effect, age, gender and many more. Most of the researches used above mentioned methods and variables for the prediction of COVID-19 [39–41]. Multivariate evidence revealed that the epidemics condition with COVID-19 has an optimistic and important impact on online shopping [42]. Burstyn et al. [43] have analysed clinical time series data besides SARS-CoV-2 epidemiologic illness to identify the common cause for COVID-19. The authors of [44–46] have identified the clinical diagnosis factors for epidemic using the Bayesian approach.

Iwendi et al. [47] have proposed an adjusted random forest model supported through AdaBoost calculation for the prediction of COVID-19 cases. This model is used to monitor the COVID-19 affected people with many details like geographical location, health condition, travel history and segment information to expect the seriousness of the case and the conceivable result, recuperation or passing. The traditional forecasting models, such as ARIMA [7, 9], regression models [10, 11] and Bayesian approaches [43] are often not very helpful in decision making activities for the epidemics as these are failed to support long term prediction. In addition, sometimes, these models misinterpret information due to underfitting and overfitting problems. These techniques are mainly helpful in predicting short-range trends and values. The overfitting problem is one of the key issues, when developing a neural network based forecasting model. This problem occurs, when a model learned the noise or random fluctuations in the training data to some extent that negatively affects the performance of the model. This is a very common problem for non-parameter and non-linear prediction models.

In [48], authors have proposed an ensemble of convolutional neural networks with a combination of different activation functions. This scheme produces more accurate results than the standard activation function. Maguolo et al. [49] have proposed a weighted resampling based transfer learning algorithm that combines efficient data with the data labelled in its target domain, and then, this scheme integrates the learned classifiers with the integrated data. A novel model has been proposed by Nanni et al. [50], which combines static and dynamic activation functions. This scheme replaces all activation layers of a Convolutional Neural Network (CNN). However, this scheme is slow.

In this paper, a novel nonlinear autoregressive neural network time series model has been developed for forecasting COVID-19 cases. The proposed methodology can support a predictive tool for assessing the current status of COVID-19 infection and can help government and healthcare officials to take accurate decisions to reduce mortality and control the spread of this disease. The proposed NAR-NNTS model consists of an input layer, a hidden layer and an output layer. It combines the default two-layer feed-forward Backpropagation (BP) algorithm with the sigmoid activation function in the hidden layer and a linear activation function in the output layer. The output of NAR-NNTS model is provided back to the input layer of the network with delays. This proposed model can find patterns between the non-linear past variables and can predict future variables. To evaluate the performance of the proposed NAR-NNTS, it is trained by adjusting neural network configuration parameters, such as different training algorithms, number of Hidden neurons (H) and Initial Weight (IW). It helps to reduce the overfitting problem and improves the prediction accuracy. The benchmark performance measure like RMSE, R-value and MSE are used to assess the time series forecasting model. Here, RMSE value is the selection criterion for choosing the best prediction model. The main contributions of the proposed work can be summarized as follows:

1. The proposed NAR-NNTS is based on neural network and it can able to identify the uncertainty in the COVID-19 dataset.

2. NAR-NNTS is trained with different training algorithms and network configuration parameters to avoid overfitting problem. Therefore, it is also suitable for small datasets.

3. The proposed scheme has the potential to provide a predictive tool for assessing the current status of COVID-19 infection and enable government and health workers to make better decisions to reduce mortality.

The rest of the paper is organized into different sections. Section 2 describes the proposed methodology for forecasting COVID-19 cases. Section 3 represents the results and discussions of the proposed work, and finally, Sect. 4 summarizes the entire paper with some future works.

Proposed Scheme

The decision making systems for the rapidly spreading COVID-19 epidemic need to deal with high uncertainty. Generally, the epidemiological data of COVID-19 vary in the number of confirmed, recovered and death cases. Furthermore, COVID-19 is an ongoing outbreak in India. India is the second largest country in terms of population. In India, the prevalence of COVID-19 is very high, and state-of-the-art hospital facilities are not available everywhere in India. Therefore, forecasting of CVOID-19 death can be helpful for the government officials to control this pandemic by making appropriate decisions.

NAR-NNTS is a time series neural network model for estimating future values of the input variable. It can be suitable for the nonlinear dataset and predicts future values based on the historical background using a re-feeding mechanism. The predicted value can be used as an input for future predictions using forward-looking points [51–53]. NAR-NNTS model is generated by specifying values for network configuration parameters, such as feedback delays, number of neurons in the hidden layer, training algorithms and activation functions. These parameters depend only on the problem domain, and finding the optimal values of these parameters is a challenging task. Then, it accomplished in an open-loop network based on the actual target values as feedback, and thus, makes the training with high accuracy. After training, the model open-loop is converted into a closed-loop, and a new predicted value is given back as input into the feedback network.

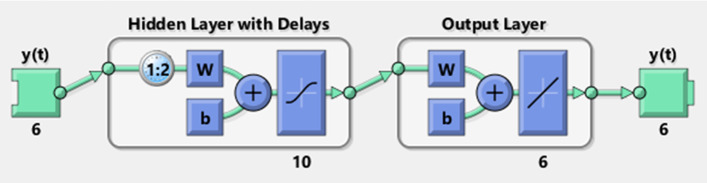
The design of NAR-NNTS network is shown in Fig. 1. It consists of input layer of $n$ time point, output layer and hidden layer, which consist of pre-defined number of neurons. The performance of the training network is based on the BP algorithm, and uses a descent time step ahead. BP algorithm is the elementary building block of the neural network. It is used to effectively train the neural network through the chain rule system. In other words, it performs a backward pass, while adjusting the weights and biases of the model to improve its accuracy. BP algorithm provides a low error rate and high accuracy during the prediction.

Fig. 1.

Design of NAR-NNTS network

Equation (1) represents the mathematical form of NAR in which the new predicted values are denoted as time series $y\left(\mathit{ts}\right)$ and historical observation values are represented as $y\left(ts-1\right)$, $y\left(ts-2\right)$, …, $y\left(ts-d\right)$.

$$y=\sigma \left(\epsilon \right)=\left\{\begin{array}{cc}1\hfill & \text{if}\epsilon \ge h\\ h\hfill & \text{if}\epsilon <h\end{array}\right)\text{where}\epsilon =\sum _{i=0}^y{w}_i{y}_i$$ 1

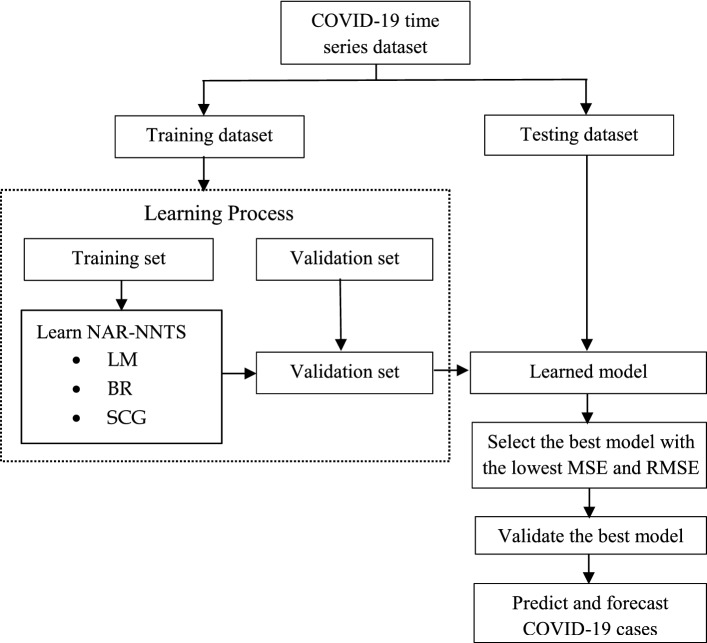
The output value i.e. $y\left(\mathit{ts}\right)=\sigma \left(\epsilon \right)$ is achieved after the threshold excitation level $h$, which can be determined by the activation function $\sigma$. The inputs are $y\left(ts-1\right),y\left(ts-2\right),\dots .,y\left(ts-d\right)$ and $w_1,w_2,\dots ,w_n$ are the weights that transform input data within the network's hidden layers. Here, $d$ is the time delay. The training algorithm is used to determine the optimal weights and bias values of the proposed NAR-NNTS. The identification of the most suitable training algorithm for a given dataset is a challenging task. To address this issue, this NAR-NNTS model has been proposed by three different algorithms, namely LM, SCG and BR. All these algorithms are well suited for non-linear and small time-series datasets. Figure 2 shows the processing steps of the proposed methodology.

Fig. 2.

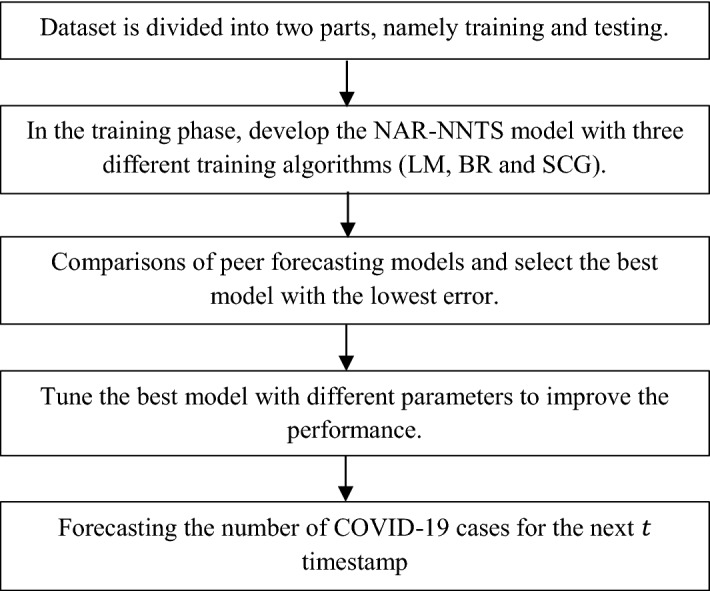
Processing steps in the proposed methodology

In the proposed work, COVID-19 data has made for forecasting by using three separate training algorithms [54–57] as discussed below:

1. LM training algorithm is commonly used for nonlinear data and optimization problems. It provides a nonlinear least-square minimization as a solution, which shows the minimization function defined in the following Eq. (2). LM is a supervised algorithm, and it is mostly suited for the nonlinear time-series datasets.

   $$f\left(x\right)=\frac{1}{2}\sum _{j=1}^m{r}_j^2\left(x\right)$$ 2

   where $x$ is the input vector, $r_j$ is the model residuals (residual is nothing but the error in the predictions), and it is assumed that $m\ge n$, where $m$ is the records in the dataset and $n$ is the number of parameters.
2. BR is used to update the weights and bias values of the model based on LM optimization. This reduces squared error and weights, and then, determines the correct combination of them to develop the generalized model. BR algorithm has two variables defined as $\alpha$ and $\beta$, which are known as Bayesian hyper-parameters. These parameters are used to show whether the training algorithm depends on the minimum weight or the minimum error or both [51–53]. Equation (3) represents the function of the BR training algorithm.

   $$C\left(i\right)=\alpha S_w+\beta S_e$$ 3

   where $S_e$ is the sum of squared error, $S_w$ is the sum of squared weight, and $\alpha$ and $\beta$ are constants, where $\alpha +\beta =1$.
3. SCG is completely automated, which does not include any important parameters and depend on application. For each execution, the appropriate phase size is used in Conjugate Gradient Backpropagation (CGB) and Broyden–Fletcher–Goldfarb–Shanno memory less quasi-Newton algorithm (BFGS) is used to reduce the path scan time-consumption [51–53]. A training algorithm for the feed-forward neural networks is a part of the conjugate gradient methods. During the first epoch, SCG scans the path that allows the unbiased function to be minimized as quickly as possible, instead of scanning a path to obtain the interval value for use. Figure 3 shows the workflow of the proposed forecasting model for COVID-19 cases.

   $$x_{i+1}=x_i+{\alpha }_i{g}_i$$ 4

Fig. 3.

The entire workflow of the proposed methodology

In Eq. (4), $i$ represents the $i\text{th}$ variable, $x$ denotes connection weights, ${\alpha }_i$ is to regulate the indefiniteness of the Hessian matrix and $g_i$ is a function of ${\alpha }_i$ i.e., the Hessian matrix of the error function.

All three training algorithms are well suited for non-linear and small datasets. The fastest training function is generally LM learning algorithm, however, it is not efficient for a large network. SCG learning algorithm is the best for a large network and the requirement of memory is relatively less than LM. BR learning algorithm spends more time than LM and SCG to learn, but generalization capability is very high and avoids overfitting and underfitting issues even for a small dataset. The proposed methodology comprises of the following steps:

1. Data Collection: In this step, data are collected from the reliable and authenticate data source.

2. Splitting the Dataset: Here, dataset is divided into 70:15:15 percent of data into a training set, validation set and testing set, respectively.

3. Model Development: The third step is responsible for mainly four works:

4. To configure NAR-NNTS model with different network setup parameters.

5. To design the proposed algorithm using LM, SCG and BR learning algorithms.

6. To train the model with a different set of parameters and ensemble training algorithm.

7. At last, an average value is taken for forecasting.

• 4.Validate the Model: Here, RMSE and R-value are used to validate the proposed NAR-NNTS model.
• 5.Forecasting: In this step, $t$ timestamp value is forecasted for COVID-19 epidemiological data.

Results and Discussions

This section discusses the results of the NAR-NNTS model with different training algorithms.

Overview of Dataset

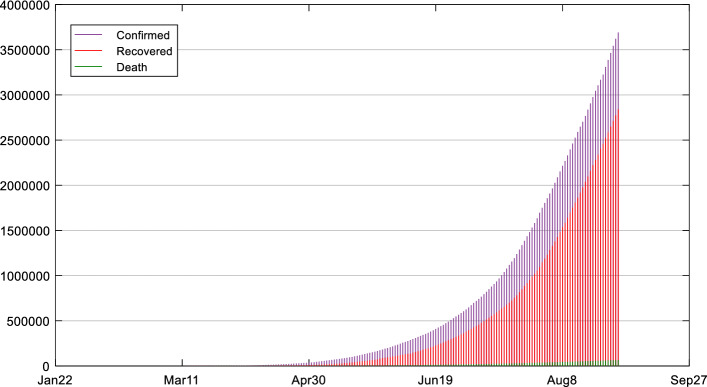
An empirical study is carried out to assess the efficiency of the proposed methodology to forecast the COVID-19 pandemic. COVID-19 epidemiological data for India is downloaded from [58]. Datasets are taken from January 2020 to August 2020 time series that contains cumulative confirmed, recovered and death cases [59]. Figure 4 shows the graphical representation of the COVID-19 time series dataset. Sometimes, the default values of the parameters are used to start the initial flow. The parameters are optimized for the selection of the best model based on the dataset and increase the forecasting accuracy. The values of the neural network parameters like training algorithm, number of neurons in the hidden layer and feedback delays are completely depended on the dataset. There is no benchmark values of these parameters.

Fig. 4.

Graphical representation of COVID-19 dataset

Qualitative Performance Measures

The performance of the proposed NAR-NNTS model has been analyzed with three different training algorithms using the following measures [53–56]:

1. Root mean square error is a polynomial counting rule. It represents the error-index, which is used to compare different forecasting models. This is the square root of the square differences measured between prediction and actual observation.

   $$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(P_i-A_i\right)}^2}$$ 5

   where $n$ is the number of samples, $P$ is the predicted value and $A$ is actual value.
2. Mean square error is defined as the variance between predicted and actual values (average). The model having low MSE values is better. If the MSE value is 0.00, it denotes no error value occurs in the prediction model.

   $$MSE=\frac{1}{n}\sum _{i=1}^n{\left(P_i-A_i\right)}^2$$ 6

   where $n$ is the number of samples, $P$ is the predicted value and $A$ is the actual value.
3. Correlation co-efficient value i.e. R-value is used to measure the relationship between the actual and the predicted values. If $R$ is 1, there is a close relationship, and when $R$ is 0, then, there is a random relationship.

   $$R=\frac{n\left(\sum PA\right)-\left(\sum P\right)\left(\sum A\right)}{\sqrt{(n\sum P^2-{(\sum P)}^2[n\sum A^2-{(\sum A)}^2]}}$$ 7

   where $n$ is the number of samples, $P$ is the predicted value and $A$ is the actual value.

Experimental Setup

Matlab toolbox 2019 is used to implement the proposed NAR-NNTS forecasting model. The experiments are executed on the on a Dell OptiPlex 7070 desktop, which has 16 GB RAM, 2 TB SSD, 3.0 GHz Intel Core i7 9700 eight core and Windows 10 as operating system. NAR-NNTS forecasting model with different training algorithms run iteratively for COVID-19 epidemiological dataset until the convergence of loss function or maximum iteration reached. Table 1 shows the parameter settings for three different training algorithms of NAR-NNTS, namely LM, BR and SCG. These parameters are used to analyze the performance of the model using the training, validation and testing dataset as per the following aspects.

1. Forecasting error of NAR-NNTS model for MSE.

2. The complexity of NAR-NNTS model lies on the neuron count and the hidden layer.

3. Convergence speed (epoch) of NAR-NNTS model and training time of the NAR-NNTS model.

4. Accuracy of the NAR-NNTS model is evaluated by RMSE and R-value.

Table 1.

Parameter settings for different NAR-NNTS training algorithms

Parameter	LM	BR	SCG
Training (maximum iteration)	1000	1000	1000
Objective performance	0	0	0
validation of failures (maximum)	2	2	2
Original error value i.e., $\mu$	0.001	N/A	0.005
Maximum $\mu$	1e10	N/A	1e10

Performance Analysis of NAR-NNTS Model

The performance measures, namely RMSE, MSE and R-value have been used in this work to assess the model. Three different NAR-NNTS models are constructed as mentioned below with appropriate neural network configuration parameter for COVID-19 dataset:

1. Confirmed case model

2. Recovered case model

3. Death case model

Table 2 illustrates the performance of NAR-NNTS model for confirmed cases with three different training algorithms in the training, validation and testing phases. The error measure i.e., MSE is used in this work to select the best prediction model for COVID-19 confirmed case prediction. As shown the values of Table 2, NAR-NNTS model with LM is the best prediction model. This is because it has a less MSE value compared to the other two training methods used for evaluation purposes.

Table 2.

MSE value of the NAR-NNTS model with different training algorithms (confirmed cases)

Algorithm	Training MSE	Validation MSE	Testing MSE
LM	4,227,568.42	15,200,807.45	5,286,473.29
BR	8,375,333.84	0	23,628,016.84
SCG	50,705,416.88	147,483,647.5	10,280,507.55

Table 3 illustrates the performance of NAR-NNTS model for recovered cases with three different training algorithms in the training, validation and testing phases. Although MSE value in validation phase is zero for BR validation phase, MSE of all three phases are high. Therefore, it is concluded that LM training algorithm is the best for the recovered case prediction.

Table 3.

MSE value of the NAR-NNTS model with different training algorithms (recovered cases)

Algorithm	Training MSE	Validation MSE	Testing MSE
LM	3,204,290.32	25,514,125.9	3,002,158.38
BR	31,806,366.9	0	34,820,470.44
SCG	64,161,317.4	3,028,286.04	14,748,364.08

Table 4 shows the performance of NAR-NNTS model for death cases with three different training algorithms in the training, validation and testing phases. Based on the MSE values of the three phases for the death case prediction model, NAR-NNTS with LM training algorithm outperformed the other two training algorithms.

Table 4.

MSE value of the NAR-NNTS model with different training algorithms (death cases)

Algorithm	Training MSE	Validation MSE	Testing MSE
LM	1165.11	89,014.74	1317.5
BR	36,604.248	0	339,501.04
SCG	600,824.8	484,634.38	528,707.21

Table 5 shows the performance of NAR-NNTS model for confirmed cases with LM, SCG and BR training algorithms in the training, validation and testing phases. The accuracy measure i.e., R-value is used as the selection criterion for selecting the best prediction model. It is observed that the NAR-NNTS model with LM is the best model for confirmed case prediction.

Table 5.

Performance evaluation of NAR-NNTS model with different training algorithms (confirmed cases)

Algorithm	Training R-value	Validation R-value	Testing R-value
LM	1	0.99999	1
BR	0.99998	0.0	0.99993
SCG	0.99034	0.98782	0.99366

Table 6 illustrates the performance evaluation of NAR-NNTS with three different training algorithms with the training, validation and testing phases. Based on R-value, the NAR-NNTS model with LM is the best prediction model for COVID-19 recovered cases. This is because R-value is much closer to 1, when compared to the other two training algorithms taken for evaluation. Furthermore, in three phases, R-value is equal to 1 for LM training algorithm, which signifies that it is the most suitable algorithm and this model fits the data exactly in all three phases.

Table 6.

Performance evaluation of NAR-NNTS model with different training algorithms (recovered cases)

Algorithm	Training R-value	Validation R-value	Testing R-value
LM	1	1	1
BR	0.99996	0.00	0.99996
SCG	0.998183	0.99921	0.99801

Table 7 shows the performance evaluation of NAR-NNTS with three different training algorithms in the training, validation and testing phases. Based on R-value, the NAR-NNTS model with LM is the best prediction model for COVID-19 death cases. The main reason for this is because R-value is much closer to 1, when compared to the other two training algorithms taken for study.

Table 7.

Performance evaluation of NAR-NNTS model with different training algorithms (death cases)

Algorithm	Training R-value	Validation R-value	Testing R-value
LM	0.9999	0.9999	0.99999
BR	0.99974	0.0	0.99996
SCG	0.999125	0.99897	0.99934

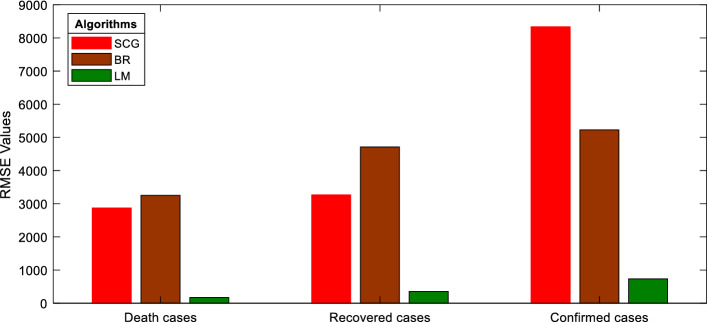
Tables 8, 9 and 10 illustrate the overall performance evaluation of the proposed NAR-NNTS with three different training algorithms. The error measures like MSE value, RMSE value and accuracy measure R-value are used separately to select the best model for COVID-19 confirmed, recovered and death case prediction. In all the cases, it has been observed that the NAR-NNTS model with LM is the best prediction model because it has less MSE value and RMSE value, and R-value is much closer to 1, when compared to the other two training algorithms taken for the study. The lowest RMSE values for the prediction of the confirmed cases, recovered cases and death cases are 2870.241, 3251.696 and 174.64, respectively. RMSE is used as a performance indicator to select the best model for forecasting. Therefore, LM training algorithm has performed well in all three phases of NAR-NNTS model compared to other algorithms.

Table 8.

Overall performance results of NAR-NNTS model (confirmed cases)

Algorithm	MSE	RMSE	R-value
LM	8,238,283.053	2870.241	1
BR	10,667,783.56	3266.157	0.666663
SCG	69,489,857.31	8336.058	0.999060

Table 9.

Overall performance results of NAR-NNTS model (recovered cases)

Algorithm	MSE	RMSE	R-value
LM	10,573,524.87	3251.696	1
BR	22,208,945.78	4712.637	0.66666
SCG	27,312,655.84	5226.151	0.998473

Table 10.

Overall performance results of NAR-NNTS model (death cases)

Algorithm	MSE	RMSE	R-value
LM	30,499.11667	174.64	0.99998
BR	125,368.4293	354.074	0.666567
SCG	538,055.4633	733.5226	0.99914

Selection and Validation of the Best Model with the Lowest RMSE

Commonly, RMSE is used as a standard key performance measure to assess the time series prediction. Figure 5 represents the RMSE value for NAR-NNTS with three training algorithms, namely LM, BR and SCG for COVID-19 confirmed, recovered and death cases, respectively. NAR-NNTS with LM training algorithm is the best model for forecasting COVID-19 confirmed cases, recovered cases and death cases.

Fig. 5.

Comparison of RMSE values for different NAR-NNTS training algorithm

It can be easily observed from Fig. 5, Tables 8, 9 and 10 that the proposed NAR-NNTS with LM model is always a good fit for the pandemic COVID-19 datasets. It is witnessed that NAR-NNTS model has excellent fit and a good forecasting accuracy for pandemic COVID -19 data in a short-range.

Forecast Model Result for COVID-19

The COVID-19 pandemic data forecasting using NAR-NNTS model can be helpful for the public health professionals and government authorities to develop disease control programme and early warning systems. Table 11 shows the predicted number of COVID-19 cases (confirmed, death and recovered cases) for India using NAR-NNTS with LM.

Table 11.

Predicted value of COVID-19 cases in India using NAR-NNTS with LM

Date	Confirmed	Recovered	Death
1-Sep	3,762,977	2,903,147	66,234.27
6-Sep	4,128,523	3,220,774	70,965.61
13-Sep	4,640,288	3,665,452	77,589.48
20-Sep	5,152,053	4,110,129	84,213.36
27-Sep	5,663,819	4,554,807	90,837.24
4-Oct	6,175,584	4,999,485	97,461.11
11-Oct	6,687,349	5,444,162	104,085
18-Oct	7,199,114	5,888,840	110,708.9
25-Oct	7,710,879	6,333,518	117,332.7
1-Nov	8,222,644	6,778,195	123,956.6
8-Nov	8,734,409	7,222,873	130,580.5
15-Nov	9,246,175	7,667,551	137,204.4
22-Nov	9,757,940	8,112,228	143,828.2
29-Nov	10,269,705	8,556,906	150,452.1
6-Dec	10,781,470	9,001,584	157,076
13-Dec	11,293,235	9,446,262	163,699.9
20-Dec	11,805,000	9,890,939	170,323.8
27-Dec	12,316,766	10,335,617	176,947.6
3-Jan	12,828,531	10,780,295	183,571.5

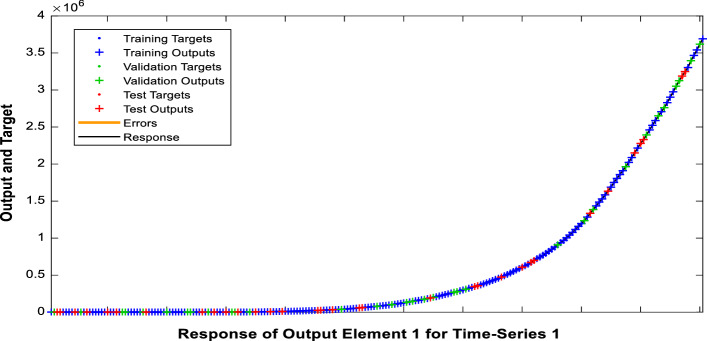
Figure 6 shows the time series response plot for confirmed cases using NAR-NNTS with LM training algorithm. Here, x-axis represents the response output and y-axis represents the target output. It also shows which time points are selected for training, testing and validation phases. The experimental result shows that NAR-NNTS model with LM training algorithm outperformed other models, and it produces higher prediction accuracy. This approach reduces the overfitting problem and improves prediction accuracy. MSE value of the validation set in the proposed model is lower than the training set for confirmed case and recovered case prediction using LM training algorithm, which indicates that there is no overfitting issue and it has a high degree of model generalization.

Fig. 6.

Time series response plots for the confirmed cases using LM training algorithm

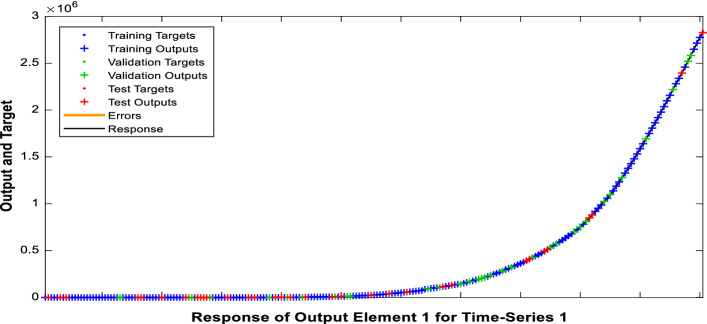
Figure 7 illustrates the time series response plot for recovered cases using NAR-NNTS with LM training algorithm. Here, the x-axis and y-axis represent the response output and target output, respectively. The experimental result shows that NAR-NNTS model with LM training algorithm outperformed other models in terms of prediction accuracy and model fit.

Fig. 7.

Time series response plots for the recovered cases using LM training algorithm

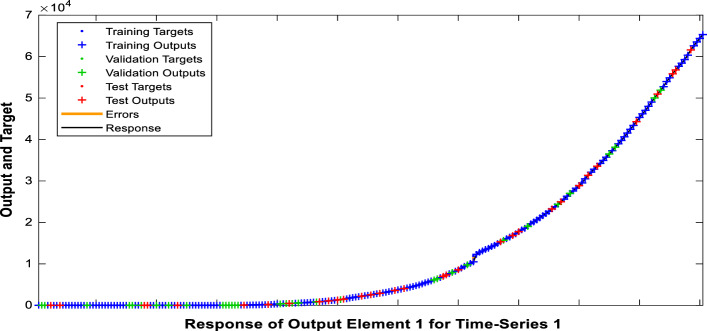
Figure 8 illustrates the time series response plot for the death cases using NAR-NNTS with LM training algorithm. Here, the x-axis represents the response output and the y-axis represents the target output. Based on the prediction accuracy and model fit, NAR-NNTS model with LM training algorithm is the best prediction model. It is clearly known from Figs. 6, 7 and 8 that the actual and target output values are exactly fitted into the model without any significant error for COVID-19 cases because of low RMSE value of the proposed NAR-NNTS model.

Fig. 8.

Time series response plots for the death cases using LM training algorithm

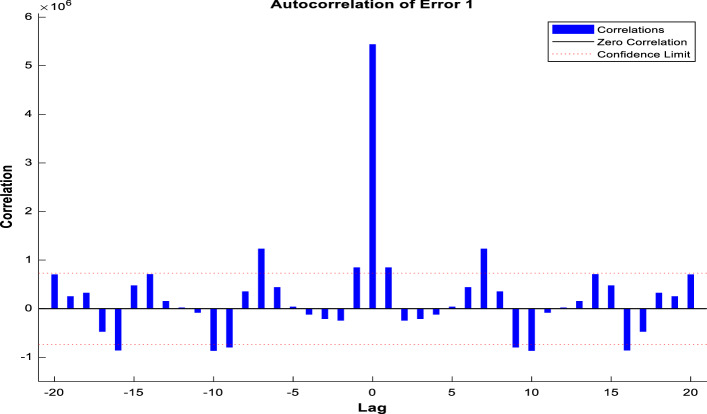
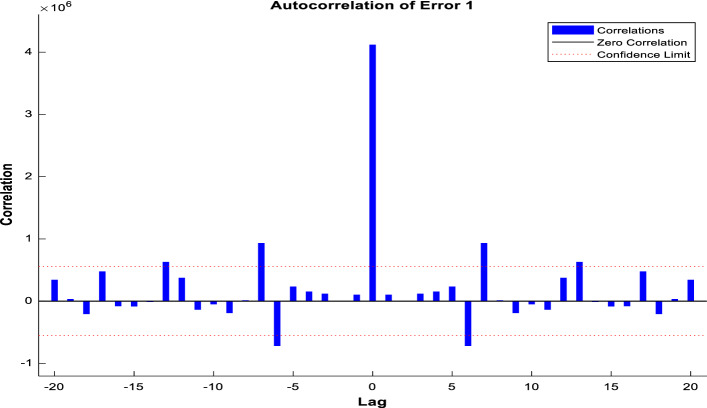
Figure 9 displays the correlation plot for confirmed cases with varying degrees of lag. Here, the x-axis represents the lag values and the y-axis represents the correlation values for confirmed cases. In this model, most of the lines fall into 95% confidence limits. Generally, an error autocorrelation plot is used to indicate how much the predicted value of the model is related to its actual value.

Fig. 9.

Autocorrelation of error for the confirmed cases using LM training algorithm

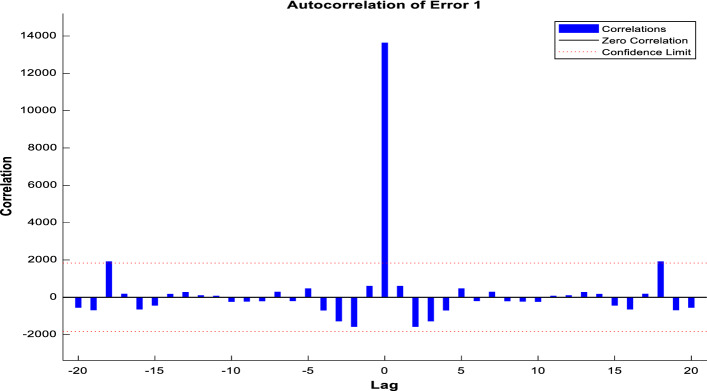
Figure 10 displays the correlation plot for the recovered cases with respect to the degrees of lag. Here, the x-axis and the y-axis represent the lag values and the correlation values for confirmed cases, respectively. In the proposed model, most of the lines fall into the 96% confidence limits.

Fig. 10.

Autocorrelation of error for the recovered cases using LM training algorithm

Figure 11 shows the correlation plot for the death cases with varying degrees of lag. Here, the x-axis represents the lag values and the y-axis represents the correlation values for confirmed cases. In the proposed model, most of the lines fall into the 99% confidence limits. The autocorrelation plots are illustrated in Figs. 6, 7 and 8. Here, value zero occurs at zero lag, which represents a good prediction model. This is due to the low RMSE value of the proposed NAR-NNTS model with LM training algorithm.

Fig. 11.

Autocorrelation of error for the death cases using LM training algorithm

Figure 12a shows the plot of target vs. output in the training phase, whose R-value is 0.9999. Figure 12b shows the plot of target vs. output in the validation phase, whose R-value is 1. Figure 12c shows the plot of target versus output in the testing phase, whose R-value is 1. Figure 12d shows the overall performance of NAR-NNTS forecasting model for the confirmed cases.

Fig. 12.

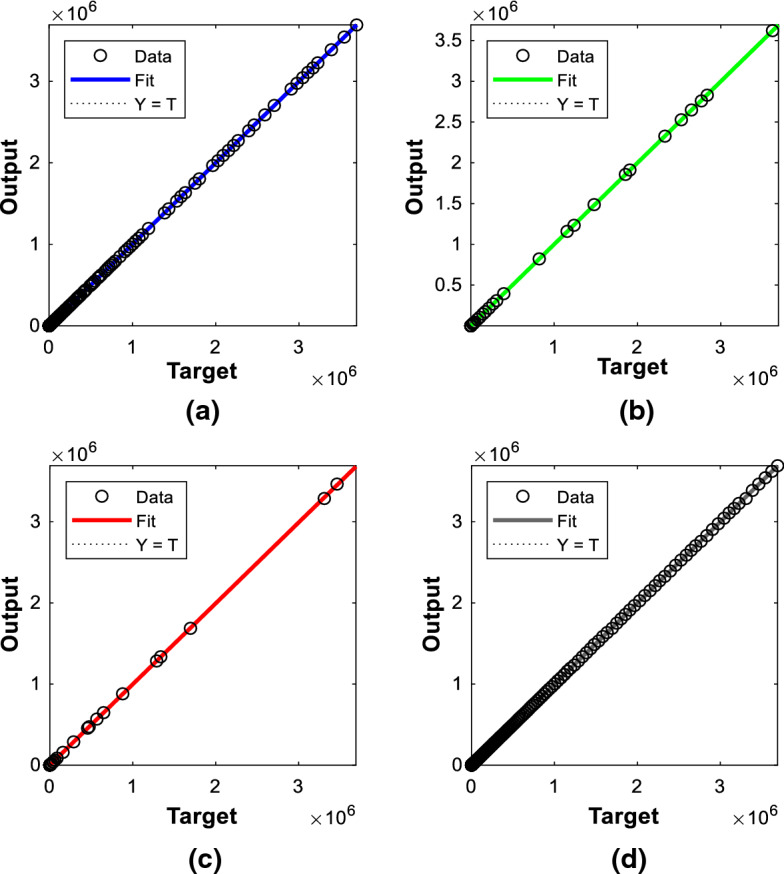
Regression plot for the confirmed cases: a training, b validation, c testing, d all

Figure 13a shows the plot of the target with respect to the output in the training phase of the recovered case prediction model, whose R-value is 1. Figure 13b shows the plot of target vs. output in the validation phase, whose R-value is 1. Figure 13c shows the target plot with respect to the output in the testing phase, whose R-value is 1. Figure 13d shows the overall performance of NAR-NNTS forecasting model for the recovered cases.

Fig. 13.

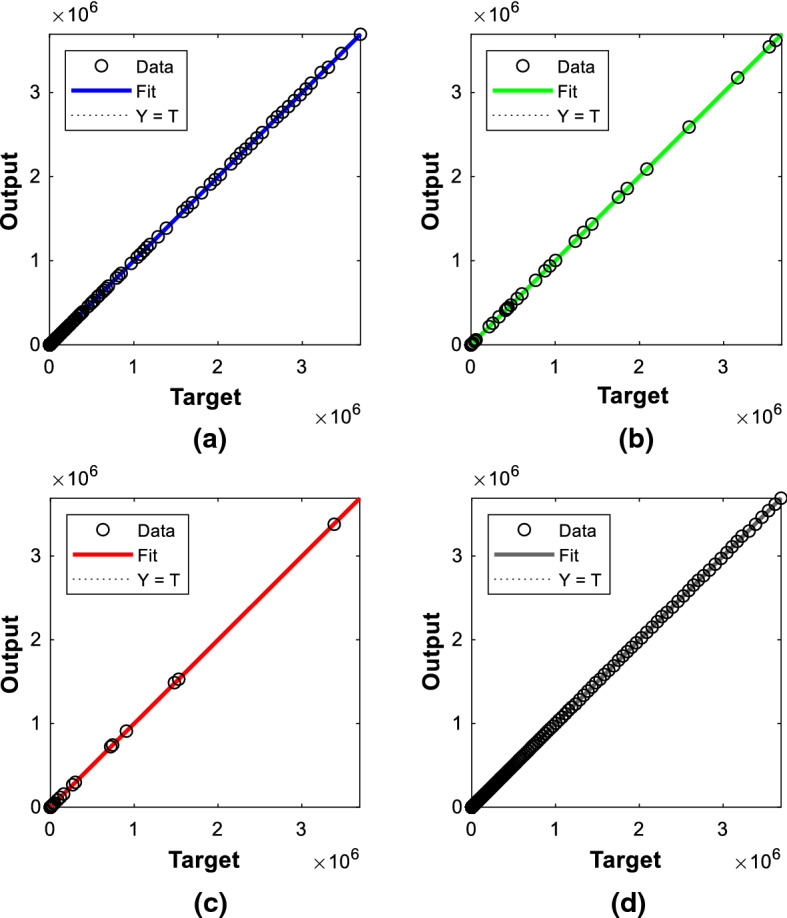
Regression plot for recovered cases: a training, b validation, c testing, d all

Figure 14a shows the plot of target vs. output in the training phase of the death case prediction model, whose R-value is 0.99998. Figure 14b shows the plot of target vs. output in the validation phase, whose R-value is 0.99999. Figure 14c shows the target plot with respect to the output in the testing phase, whose R-value is 0.99999. Figure 14d shows the overall performance of NAR-NNTS forecasting model for the death cases.

Fig. 14.

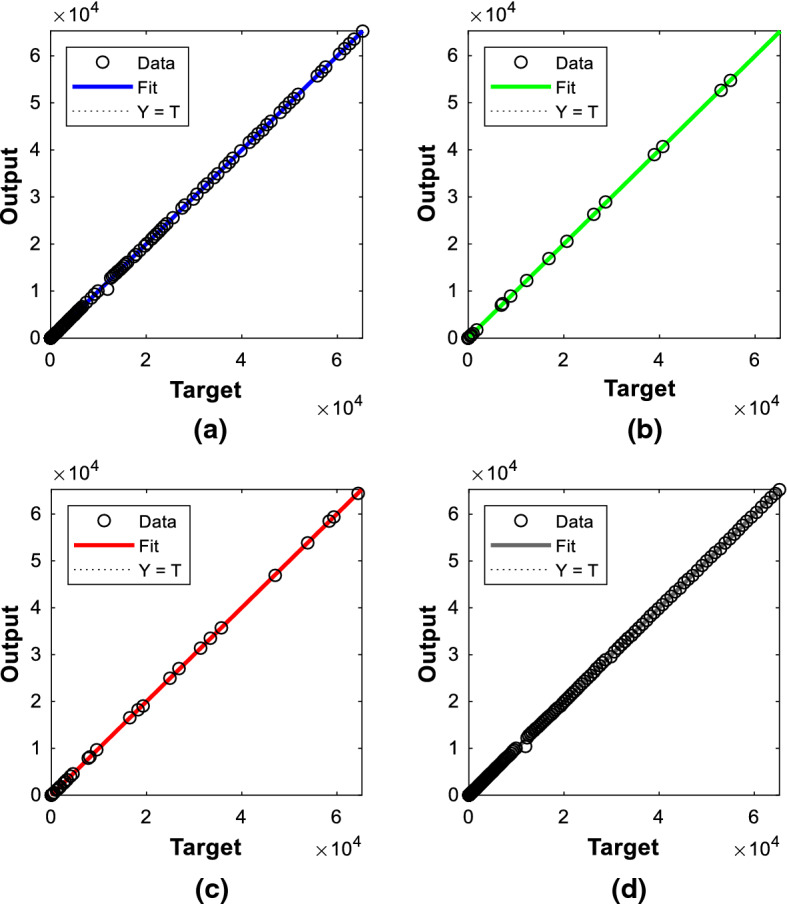
Regression plot for the death cases: a training, b validation, c testing, d all

The prediction of COVID-19 confirmed cases and recovered cases in the proposed NAR-NNTS is the best for LM training algorithm. This is because the predicted data are fitted into the model without any deviation at all the stages of model development. In the case of death case prediction, one or two predicted values are not fitted into the model. This is because there is a significant increase in the RMSE value over the predictive model of the remaining two cases.

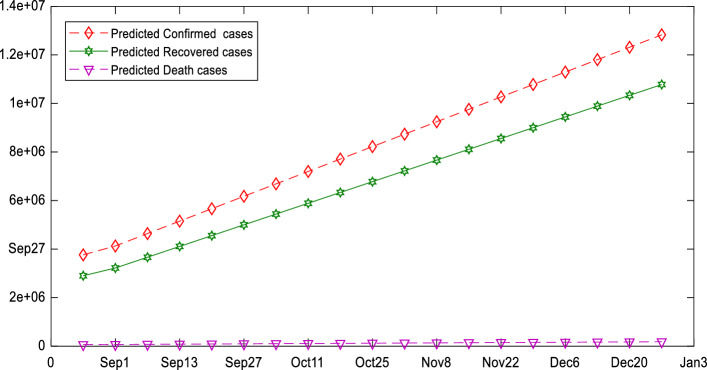
Figure 15 shows the prediction values of the confirmed, recovered and death cases of India using the proposed NAR-NNTS with LM training algorithm. Here, the x-axis represents the time periods and the y-axis represents the predicted case values. In this empirical work and analysis, NAR-NNTS with LM training algorithm is the optimal model for the COVID-19 time series dataset. It supports better prediction accuracy compared to BR and SCG training algorithms. Based on the time series analysis of the COVID-19 dataset, it has been seen that all types of predicted COVID-19 cases can be increased steadily till December 2020. Therefore, all preventive and precautionary measures recommended by the WHO and the Government of India should be carefully followed. This is the best way to avoid the worst-case scenario of COVID-19 spread.

Fig. 15.

COVID-19 predicted cases for India

Conclusion and Future works

The epidemiological data forecasting model always plays an important role in planning preventive measures for infectious diseases, such as SARS, dengue, Ebola virus and many more. Because of the non-linear nature of COVID-19 time-series database, forecasting is a challenging task. In this paper, a methodology has been proposed for precise and reliable COVID-19 forecast, which ensembles a collection of three different training algorithms for NAR_NNTS model. Experiments have been conducted on the COVID-19 outbreak dataset for India to evaluate the proposed methodology. The results show that the proposed NAR-NNTS with LM training algorithm and optimized network configuration parameter produce better results. The proposed scheme is suitable for the government officials to control COVID-19 by taking appropriate decisions. The main issue of the proposed method is that it consumes much time. In the future, a novel technique can be developed to identify COVID-19 patients in less time. Moreover, a combination of different training algorithms and activation functions for the proposed NAR-NNTS can be designed to assess the improvement of the model in terms of performance.