Patient-Specific Computational Hemodynamics of Intracranial Aneurysms from 3D Rotational Angiography and CT Angiography: An In Vivo Reproducibility Study

Abstract

BACKGROUND AND PURPOSE:

Patient-specific simulations of the hemodynamics in intracranial aneurysms can be constructed by using image-based vascular models and CFD techniques. This work evaluates the impact of the choice of imaging technique on these simulations.

MATERIALS AND METHODS:

Ten aneurysms, imaged with 3DRA and CTA, were analyzed to assess the reproducibility of geometric and hemodynamic variables across the 2 modalities.

RESULTS:

Compared with 3DRA models, we found that CTA models often had larger aneurysm necks (P = .05) and that most of the smallest vessels (between 0.7 and 1.0 mm in diameter) could not be reconstructed successfully with CTA. With respect to the values measured in the 3DRA models, the flow rate differed by 14.1 ± 2.8% (mean ± SE) just proximal to the aneurysm and 33.9 ± 7.6% at the aneurysm neck. The mean WSS on the aneurysm differed by 44.2 ± 6.0%. Even when normalized to the parent vessel WSS, a difference of 31.4 ± 9.9% remained, with the normalized WSS in most cases being larger in the CTA model (P = .04). Despite these substantial differences, excellent agreement (κ ≥ 0.9) was found for qualitative variables that describe the flow field, such as the structure of the flow pattern and the flow complexity.

CONCLUSIONS:

Although relatively large differences were found for all evaluated quantitative hemodynamic variables, the main flow characteristics were reproduced across imaging modalities.

Degradative biologic processes in the arterial wall that lead to growth and rupture of intracranial aneurysms¹ have been related to intra-aneurysmal hemodynamics.^2–4 CFD simulations have been used to gain insight into the patient-specific hemodynamics and could potentially assist rupture-risk assessment^5–9 and treatment planning.^10–16

Vascular models can be constructed through segmentation of 3DRA and CTA images. Compared with CTA, 3DRA produces images with higher contrast, higher spatial resolution, and lower visibility of bone,^17–19 which lead to better segmentation results²⁰ and superior anatomic accuracy.^21–23 However, acquisition of 3DRA images involves the introduction of a catheter into the cerebral vasculature to locally inject contrast agent, making it more invasive than CTA, in which contrast is injected in a peripheral vein.^24,25 As a result of this trade-off, 3DRA is often used before and during treatment, whereas CTA is often used for diagnosis and follow-up studies.²⁶

To the best of our knowledge, the reproducibility of hemodynamic simulations based on in vivo images from different modalities is yet unknown. Previous studies did show that among all input parameters of the modeling pipeline, the vascular geometry has the greatest impact on its output.^27,28 Because the choice of imaging technique may affect the vascular geometry, it could give rise to differences in hemodynamic predictions. To investigate this issue, we conducted a study comparing simulations with 3DRA- and CTA-based vascular models of 10 aneurysms.

Materials and Methods

Patient Population

Clinical data were obtained at the department of radiology of the Academic Medical Center, Amsterdam, the Netherlands, for a study including 108 patients imaged with both 3DRA and CTA within a 3-day interval.²⁹ Approval from the institutional review board was obtained for review of anonymized medical records and images. As part of this study, the quality of CTA images was rated by 2 experienced clinicians. From a subgroup of 80 patients with the highest quality images, 4 patients with 10 aneurysms were randomly chosen for our study (Table 1).

Table 1:

Clinical information of patient population

Patient			Aneurysm
No.	Sex	Age (yr)	No.	Side	Location	Rupture
1	F	45	1	Right	MCA M1-M2	Yes
			2	Left	MCA M1-M2	No
2	F	74	3	Left	ICA	Yes
3	F	37	4	Right	MCA M1	No
			5	Right	MCA M1	No
			6	Right	MCA M1-M2	No
4	F	43	7	Left	MCA M1	No
			8	Right	MCA M1	No
			9	Right	MCA M1-M2	Yes
			10	Midline	BA tip	No

Imaging Protocols

3DRA images were acquired with a single-plane angiographic unit (Integris Allura Neuro; Philips Healthcare, Best, the Netherlands). Nonionic contrast agent (320 mg I/mL of iodixanol, Visipaque; GE Healthcare, Cork, Ireland) was injected through a 6F catheter positioned in the ICA or VA. One hundred images were acquired during a 240° rotational run in 8 seconds with 15–21 mL of contrast agent at 3 mL/s. A 3D image of the region of interest was reconstructed with a 256 × 256 × 256 matrix on a dedicated workstation.

CTA images were acquired with a 4-section spiral CT scanner (Somatom, Sensation 4; Siemens, Erlangen, Germany). Eighty to 100 mL of nonionic contrast agent (320 mg I/mL of iodixanol, Visipaque) was injected in a cubital vein at a rate of 4 mL/s. Scanning delay was automatically adjusted by a bolus-tracking technique. Parameters were set as follows: 120 kV, 250 mAs, 4 × 1 mm detector collimation, pitch of 0.875, section thickness of 1.3 mm, increment of 0.5 mm, 512 × 512 matrix, H30f reconstruction kernel.²⁹

Vascular Modeling

Patient-specific vascular models were constructed from the image datasets by using a completely automatic geodesic active regions segmentation algorithm.²⁰ This approach drives the evolution of geometric deformable models toward the vascular boundaries on the basis of minimal local curvature (internal force) and a combination of region-based information and image-gradient maps (external force). Region-based information is used to initialize the model and prevents the leakage of the evolving front when the image gradient is weak. The accuracy of the segmentation algorithm was recently investigated for both 3DRA and CTA.²⁰ In a study of 10 clinical datasets, the technique compared favorably with other techniques, showing a high overlap with respect to the ground truth (91.13% and 73.31% for 3DRA and CTA, respectively) and an error distance to the ground truth close to the in-plane resolution (0.40 and 0.38 mm, respectively).

The segmentation process outputs a surface mesh representing the vascular boundaries. Subsequently, postprocessing operations were applied manually to separate touching vessels, extrude poorly segmented in- and outlets, smooth the surface, and improve the mesh quality. Operations were executed with ReMESH, Version 2.0 (IMATI-GE/CNR, Genova, Italy).³⁰

From this point on, we will refer to vascular models obtained from 3DRA or CTA images and their corresponding CFD simulations as 3DRA and CTA models, respectively.

Blood Flow Modeling

Unstructured meshes containing tetrahedral and prismatic elements were created with ICEM CFD, Version 11.0 (ANSYS, Canonsburg, Pennsylvania). Element sizes ranged between 0.1 and 0.2 mm, with smaller elements in high curvature regions. Three prismatic boundary layers with a total thickness of approximately 0.15 mm covered the vessel wall to locally ensure an accurate definition of the velocity gradient. On average, meshes consisted of 0.4 million nodes and 1.5 million elements.

Transient CFD simulations were created with CFX, Version 11.0 (ANSYS), which uses a finite volume approach to solve the Navier-Stokes equations. Blood was modeled as an incompressible Newtonian fluid (ρ = 1060 kg/m³, μ = 0.004 Pa · s). The vessel wall was assumed to be rigid with a no-slip boundary condition. A straight inlet extension was added to the image-based vasculature, and a parabolic velocity profile was imposed at the inlet of the extension. Because patient-specific flow information was not available, a flow rate waveform from a healthy volunteer acquired with phase-contrast MR imaging described the pulsatile flow conditions at the inlet. This waveform was scaled to obtain a physiologically realistic mean WSS of 1.5 Pa near the inlet of the 3DRA model.³¹ To prevent hemodynamic discrepancies further downstream due to a difference in inflow conditions, we chose an equal inflow rate for the corresponding CTA model. We will elaborate on this modeling choice further in the “Discussion”. Traction-free boundary conditions were prescribed at all outlets. Time steps were chosen to be 0.003 seconds around peak systole, when the time-derivative of the flow rate was relatively large, and 0.02 seconds elsewhere. To reduce initial transients, we computed 2 complete cardiac cycles and data of the second cardiac cycle were stored and analyzed.

Data Analysis

Quantitative geometric and hemodynamic variables were measured in both models. Unless otherwise stated, the time-averaged flow field was analyzed. The aneurysm neck area and the volume of the aneurysm were measured to quantify features of the aneurysm geometry. The distribution of flow was described by measuring the flow rate in the parent vessel just proximal to the aneurysm, the flow rate into the aneurysm, and their ratio to normalize the flow rate into the aneurysm. The WSS plays an important role in the development of aneurysms.³ We, therefore, measured the mean WSS on a segment of the parent vessel just proximal to the aneurysm, the mean WSS on the aneurysm wall, and their ratio to normalize the WSS on the aneurysm wall. Normalized measurements were included to differentiate discrepancies in hemodynamic patterns from scaling of hemodynamic variables as a result of differences in vessel size and differences in flow divisions at proximal bifurcations. Furthermore, we evaluated 2 WSS-derived quantitative variables that have been associated with a clinical history of rupture: the portion of aneurysm wall under low WSS (< 0.4 Pa) at end diastole⁸ and the maximum WSS on the aneurysm wall at peak systole.^5,9 In addition to the latter, 2 other measures of high WSS were evaluated: the 90th percentile value of the WSS on the aneurysm at peak systole and this percentile normalized by the mean WSS on the aneurysm at peak systole.

For each variable, the relative difference between the 2 models with respect to the 3DRA model was determined. The mean and SE of this difference over all 10 cases were calculated. The number of cases for which the value in the CTA model was lower than that in the 3DRA model was determined for each variable. The Wilcoxon signed rank test was used to test the significance of the differences between the 2 models. Differences were considered statistically significant for P ≤ .05.

The intra-aneurysmal flow field was characterized using qualitative variables that have been proposed by Castro et al⁵ and Cebral et al,⁶ namely the location and size of the impingement region on the aneurysm wall; the size of the inflow jet in the aneurysm; and the flow complexity, stability, and pattern type in the aneurysm. Data were obtained by 2 independent observers through inspection of streamlines color-coded with the magnitude of the velocity and color maps of the WSS and the OSI. The OSI describes the oscillatory nature of the WSS during the cardiac cycle with 0 and 0.5 representing minimum and maximum oscillation, respectively.³² The hemodynamic results were examined for the flow field at end diastole and peak systole and for the time-averaged flow field. Agreement between the 2 imaging modalities and agreement between the 2 observers were tested with free-marginal κ statistics.³³ Agreement was categorized as poor (κ < 0.20), fair (0.20 < κ < 0.40), moderate (0.40 < κ < 0.60), good (0.60 < κ < 0.80), or excellent (κ ≥ 0.80).

Results

Main Observations

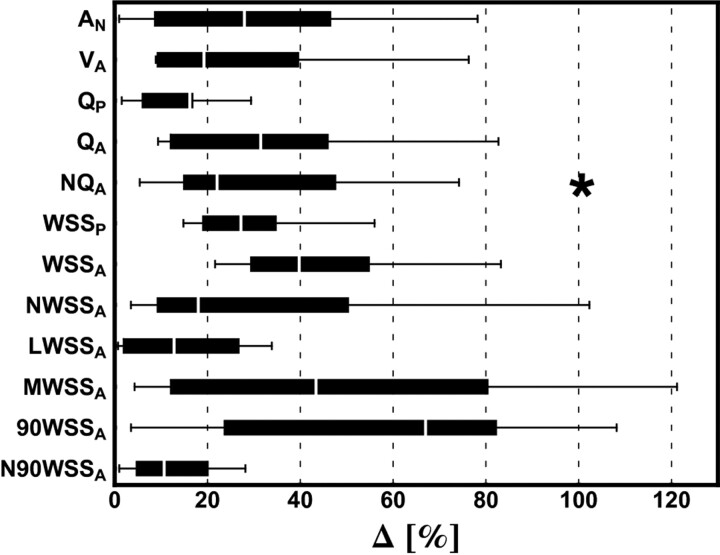
The flow rate in the parent vessel, measured just proximal to the aneurysm, differed by 14.1 ± 2.8% (mean ± SE) due to geometric differences in proximal bifurcations that affected their flow splits (On-line Table). In some cases, bifurcations to smaller vessels, such as the ophthalmic artery or the anterior choroidal artery, were missing in the CTA model but were successfully reconstructed in the 3DRA model. Naturally, these variations gave rise to differences in the flow split. Most of the missing small vessels were <1 mm in diameter (measured in the 3DRA model), whereas the smallest vessels in 3DRA models were approximately 0.7 mm in diameter. The segmentation algorithm failed to preserve these vessels due to the lower spatial resolution of CTA and the presence of bone tissue near vascular structures.

The lower spatial resolution of CTA also made it difficult for the segmentation algorithm to distinguish vascular structures that were in close proximity to each other. As a result, the aneurysm neck was significantly wider in CTA models (Δ = 33.0 ± 8.3%, P = .05). This affected the flow split at the aneurysm neck, which is reflected in a 35.9 ± 9.8% difference in the normalized inflow into the aneurysm. The difference in mean WSS on the aneurysm wall was relatively large (Δ = 44.2 ± 6.0%, P = .43). However, the difference slightly decreased after normalization, and this variable was found to be significantly higher in CTA models (Δ = 31.4 ± 9.9%, P = .04). Regarding the 2 variables that have been associated with rupture, the differences were relatively large for the maximum WSS on the aneurysm wall at peak systole (Δ = 47.9 ± 11.9%, P = .85) and relatively small for the portion of aneurysm wall under low WSS (< 0.4 Pa) at end diastole (Δ = 13.7 ± 4.0%, P = .11). As an alternative to quantify high WSS on the aneurysm, N90WSS gave relatively small differences between both modalities (Δ = 12.6 ± 4.0%, P = .85).

Overall, differences in geometric and hemodynamic variables appeared to be relatively large and varied considerably from one aneurysm to another (Fig 1). However, the main blood flow characteristics were often the same for the 3DRA and CTA models. Excellent agreement was found between the 3DRA and CTA models for all evaluated qualitative variables (κ-values ranging from 0.9 to 1.0) with the interobserver variability being slightly higher (κ-values ranging from 0.8 to 1.0) (Table 2). We qualitatively assessed the OSI distributions to be moderately similar; although corresponding regions of high OSI could often be recognized, there were clear differences in more detailed features.

Fig 1.

Boxplot showing the distribution of differences for each geometric and hemodynamic variable among the 10 aneurysms. Outliers, marked with an asterisk, are defined as data points that are >1.5 times the interquartile range above the upper or below the lower quartile.

Table 2:

Intermodality and interobserver agreement for qualitative hemodynamic variables

Variable	No. of Categories	κmodality		κobserver
		κ	Agreement	κ	Agreement
Impingement location	3	0.95	Excellent	0.76	Good
Impingement region size	2	1	Excellent	1	Excellent
Jet size	2	1	Excellent	1	Excellent
Flow complexity	2	0.9	Excellent	1	Excellent
Flow stability	2	0.9	Excellent	0.81	Excellent
Flow pattern type	3	0.95	Excellent	0.76	Good

Representative Cases

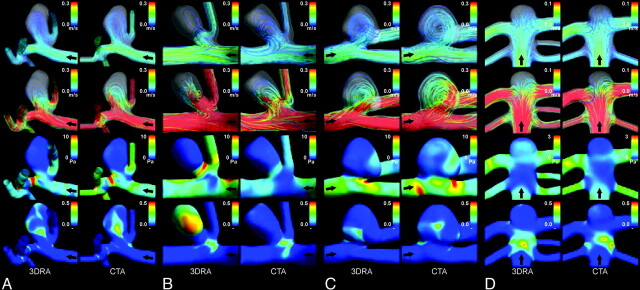
To shed more light on the output of our experiments and to better understand the relationship between geometric and hemodynamic differences, we present 4 representative cases for further discussion. Numeric data are provided in the On-line Table and visualizations of the hemodynamic simulations are presented in Fig 2.

Fig 2.

Visualizations of hemodynamic results for aneurysms 1 (A), 6 (B), 9 (C), and 10 (D). The view was chosen to most clearly present the main hemodynamic features. Displayed are streamlines color-coded with the velocity magnitude representing the flow fields at end diastole (row 1) and peak systole (row 2), the time-averaged WSS magnitude (row 3), and the OSI (row 4). Black arrows indicate the direction of flow.

Aneurysm 1 was located on the MCA M1-M2 and had ruptured before image acquisition. The flow rate in the parent vessel and the inflow into the aneurysm were similar (16.1% and 9.9%, higher in the CTA model, respectively). Also, agreement was found for all studied qualitative variables. The mean WSS on the aneurysm wall was 61.9% larger in the CTA model. After normalization to the WSS on the parent vessel wall, this difference was 20.2%.

Aneurysm 6 was located on the MCA M1-M2 and was unruptured at the moment of image acquisition. Compared with the other 9 cases, the 24.5% lower flow rate in the parent vessel of the CTA model was a relatively large difference. By measuring the outflow through all outlets, we could deduce 2 main geometric sources: First, the geometric difference in the bifurcation from the ICA to the ACA and MCA led to a larger outflow through the ACA in the CTA model. Second, the outflow through the branching vessels near the 2 proximal aneurysms was relatively much larger. Aneurysm 6 had a more complex flow pattern in the 3DRA model. It appears that the aneurysm shape in this model was more bottle-necked than that in the CTA model, which disrupted the inflow and created a high WSS area at the neck. When we reviewed the evolution of the WSS distribution over the cardiac cycle, the 3DRA model clearly showed a shift of the impingement region on the aneurysm wall, whereas the impingement region in the CTA model was spatially static. This instability of flow in the 3DRA model was also apparent from the large region on the aneurysm wall with high OSI values.

Aneurysm 9 was located on the MCA M1-M2 and had ruptured before image acquisition. In the CTA model, the flow rate into the aneurysm was 34.2% larger and the mean WSS on the aneurysm wall was 54.8% larger. Geometrically, the main difference between the 2 models was the 66.0% larger aneurysm neck area in the CTA model. This effectively led to the partial elimination of a bulge at the distal end of the neck, which was apparent in the 3DRA model. After the split at the aneurysm neck, the main flow jet detached from the aneurysm wall and created a second impingement region farther up the aneurysm sac. As a result, the bulge formed a relatively large region of low flow and low WSS. Due to the partial elimination of the bulge, this low-flow region was much less pronounced in the CTA model.

Aneurysm 10 was located on the basilar tip and was unruptured at the moment of image acquisition. We found relatively small differences of <35% for all quantitative hemodynamic variables. For all qualitative hemodynamic variables, both observers found agreement between the 2 models. We did recognize the imaging artifacts reported by Jou et al,³⁴ in which the top of the basilar tip aneurysm appeared to be flattened in the 3DRA image and, thus, in the 3DRA-model. However, besides a slight disruption in the curve of the main flow jet at the aneurysm top, which slightly increased the WSS magnitude at that location, no major hemodynamic differences were observed between the 2 models.

Discussion

The purpose of this study was to assess the impact of the imaging technique on image-based computational hemodynamic simulations of intracranial aneurysms. To this end, we conducted a study comparing simulations with 3DRA- and CTA-based vascular models of 10 aneurysms. Although relatively large discrepancies—exceeding normal physiologic variation³⁵—were found between 3DRA and CTA models for quantitative hemodynamic variables, the visual categorization of flow characteristics was mostly reproduced across modalities and observers.

Hemodynamic simulations are believed to be sensitive to the geometry of image-based vascular models,^27,28 which in turn depends on a number of aspects, including the imaging technique, image quality, segmentation algorithm, and manual postprocessing of surface meshes. To investigate the sensitivity of hemodynamic simulations to the latter, Cebral et al²⁷ let 3 modelers each reconstruct vascular models of 4 aneurysms and compared the computed hemodynamics. With results similar to those of our current study, they found that the differences in geometry did not alter the main flow characteristics in most cases. In the same work, they reported that small vessels branching off the parent vessel did not cause substantial differences in the intra-aneurysmal flow patterns, and Dempere-Marco et al³⁶ came to the same conclusion after comparing rigid and nonrigid wall conditions. However, as demonstrated by Castro et al,³⁷ including an anatomically realistic parent vessel in the vascular model instead of a straight extrusion did prove essential to reproduce the main flow characteristics.

Besides the vascular geometry, the impact of the flow-rate waveform has also received much attention.^{27,35,38–40} Hoi et al⁴¹ found differences in ICA and VA waveform shapes between young and older adults but concluded on the basis of a CFD study³⁹ of the carotid bifurcation that the computed hemodynamics are relatively robust to the assumed waveform shape in comparison with assumptions made on the time-averaged flow rate, and especially in comparison with geometry-related uncertainties. Venugopal et al³⁸ similarly stressed the relative importance of the assumed flow rate and the outflow ratios in comparison with the assumed heart rate. Other studies evaluated the intra-aneurysmal hemodynamics during rest and exercise conditions, which essentially combined the change in waveform shape, flow rate, and heart rate. Bowker et al³⁵ found that the overall flow patterns did not significantly change with a heart rate increase from 70 to 121 beats per minute and a flow-rate increase of 8%. However, Jiang and Strother⁴⁰ increased the heart rate from 60 to 150 beats per minute and the flow rate 21% and reported that the overall flow patterns did change significantly. Both studies observed large variations in hemodynamic changes for different aneurysm geometries, which raises the interesting question of whether hemodynamic differences between 3DRA and CTA models would change under exercise conditions. The results presented in the current work are based on rest flow conditions, and caution is warranted with generalizations across physiologic conditions. Future investigation may provide additional value by comparing 3DRA and CTA models for exercise flow conditions.

To describe the main flow characteristics, Castro et al⁵ introduced and studied qualitative hemodynamic variables. In a data base of 62 cases, these authors found that ruptured aneurysms had complex unstable flow patterns, small impingement regions, and small inflow jet sizes, whereas unruptured aneurysms had simple stable flow patterns, large impingement regions, and large inflow jet sizes. Our study showed that these variables are mostly independent of the choice for 3DRA or CTA for construction of the vascular model. We, therefore, suggest that CTA might suffice for risk assessment based on predicted hemodynamics.

As part of the present study, we compared quantitative variables that have been correlated to aneurysmal rupture to illustrate the potential variability due to the choice of imaging technique. Jou et al⁸ studied 26 aneurysms at the ICA and observed that the portion of the aneurysm dome with a WSS lower than 0.4 Pa at end diastole was significantly higher in ruptured aneurysms. We evaluated this variable for our 10 aneurysms and found a 13.7% difference between the 3DRA and CTA models (Δ = 13.7 ± 4.0%, P = .11). Castro et al⁵ studied 26 aneurysms at the anterior communicating artery and observed that the maximum WSS on the aneurysm at peak systole was significantly higher in ruptured aneurysms. We found a 47.9% difference between the 3DRA and CTA models (Δ = 47.9 ± 11.9%, P = .85). As an alternative measure of high WSS, we proposed the 90th percentile value of the WSS normalized by the mean WSS on the aneurysm at peak systole, which had a higher reproducibility (Δ = 12.6 ± 4.0%, P = .85).

To prevent the difference in the inflow rate propagating to the intra-aneurysmal hemodynamics, we chose to impose the same inflow rate on the 3DRA and the CTA models. Because patient-specific data were unavailable, the inflow rate was estimated on the basis of the inlet diameter so that the WSS near the inlet was 1.5 Pa. Inlets of cerebral vascular models are usually located on either the ICA or the VA, which both run through the skull base. For 3DRA segmentation, proximity of vasculature to bone poses no difficulty. However, in CTA images, the intensity values of bone and contrast agent overlap; this overlap makes it challenging for the algorithm to segment near-bone vasculature. As a result, CTA models are anatomically less accurate in the lower parts of the ICA and VA²⁰ and, therefore, should not be used to estimate the inflow rate. In our study, we found that the inlet area of the CTA model was, in 8 of 10 cases, smaller (Δ = 20.0 ± 3.5%, P = .11), which would lead to a significantly smaller inflow rate (Δ = 29.3 ± 5.2%, P = .05). Instead, we chose to obtain a physiologic estimation of the inflow rate on the basis of the 3DRA model and used the same value for both models.

In this study, a 4-section CT scanner was used to acquire the CTA data. However, the development of CT scanners is advancing rapidly and 16-, 64-, or even 320-section CT scanners are widespread or will become available soon. With the increasing number of detector rows, larger volumes are covered in a single rotation and scanning times are reduced. Also, the use of thinner sections leads to a higher out-of-plane resolution. However, the in-plane spatial resolution mainly depends on the detector geometry and the convolution kernel and is not substantially improved in 16- or 64-section CTA.⁴² Although some increase in anatomic accuracy has been found,⁴³ the minimal improvement in spatial resolution will not substantially resolve the issues brought forward in this study, such as the omission of small vessels, the widening of the aneurysm neck, and the bone-related segmentation issues.

Conclusions

The purpose of this study was to assess the impact of the imaging technique on image-based computational hemodynamic simulations of intracranial aneurysms. We addressed this by conducting a study comparing simulations with 3DRA- and CTA-based vascular models of 10 aneurysms. Differences in quantitative hemodynamic variables were relatively large, with mean values varying from 14.1% for the flow rate in the parent vessel to 44.2% for the mean WSS on the aneurysm sac. However, for qualitative variables such as the flow pattern and the flow complexity, we found excellent agreement (κ ≥ 0.9) between both image modalities. Although hemodynamic simulations should ideally be available to clinicians at all stages of the patient care cycle and throughout all imaging modalities, currently one can possibly reliably approximate and refer to only the main flow characteristics.

Abbreviations

3DRA

3D rotational angiography

ACA

anterior cerebral artery

A_N

aneurysm neck area

BA

basilar artery

CFD

computational fluid dynamics

CTA

CT angiography

Δ

relative difference between the 3DRA and CTA models with respect to the 3DRA model

ICA

internal carotid artery

LWSS_A

the portion of aneurysm wall under low WSS (<0.4 Pa) at end diastole

M

number of cases for which the value in the CTA model was lower than in the 3DRA model

MCA

middle cerebral artery

MCA M1

MCA M1 segment

MCA M1-M2

MCA M1-M2 bifurcation

MWSS_A

maximum WSS on the aneurysm wall at peak systole

NQ_A

Q_A/Q_P

NWSS_A

WSS_A/WSS_P

N90WSS_A

90WSS_A normalized by the mean WSS on the aneurysm at peak systole

OSI

oscillatory shear index

Q_A

flow rate into the aneurysm

Q_P

flow rate in the parent vessel just proximal to the aneurysm

SE

standard error

VA

vertebral artery

V_A

aneurysm volume

90WSS_A

90th percentile value of the WSS on the aneurysm at peak systole

WSS

wall shear stress

WSS_A

mean WSS on the aneurysm wall

WSS_P

mean WSS on a segment of the parent vessel just proximal to the aneurysm