Racial residential segregation and economic disparity jointly exacerbate COVID‐19 fatality in large American cities

Abstract

The disproportionately high rates of both infections and deaths among racial and ethnic minorities (especially Blacks and Hispanics) in the United States during the COVID‐19 pandemic are consistent with the conclusion that structural inequality can produce lethal consequences. However, the nature of this structural inequality in relation to COVID‐19 is poorly understood. Here, we hypothesized that two structural features, racial residential segregation and income inequality, of metropolitan areas in the United States have contributed to health‐compromising conditions, which, in turn, have increased COVID‐19 fatalities; moreover, that these two features, when combined, may be particularly lethal. To test this hypothesis, we examined the growth rate of confirmed COVID‐19 cases and deaths in an early 30‐day period of the outbreak in the counties located in each of the 100 largest metropolitan areas in the United States. The growth curves for cases and deaths were steeper in counties located in metropolitan areas where Blacks and Hispanics are residentially segregated from Whites. Moreover, the effect of racial residential segregation was augmented by income inequality within each county. These data strongly suggest that racial and economic disparities have caused a greater death toll during the current pandemic. We draw policy implications for making virus‐resilient cities free from such consequences.

We examined whether racial residential segregation and income inequality jointly predict the growth rate of both COVID‐19 cases and deaths in the first 30‐day period of county‐wise outbreaks. We predicted that the progression of the virus spread would be faster in counties located in MSAs with a high level of Black‐White and Hispanic‐White segregation. Second, we also predicted that this effect of segregation should be augmented for counties higher in income inequality. That is, the impact of COVID‐19 would be the greatest when high segregation is combined with high income inequality.

It has become increasingly clear that the rate of fatalities during the current COVID‐19 pandemic caused by SARS‐CoV‐2 is relatively higher for racial and ethnic minorities in the United States, especially Blacks and Hispanics.a For instance, Blacks and Hispanics are almost three times more likely to be infected by the coronavirus than Whites. ¹ The disproportionate suffering of minority groups is likely due to many social structural factors, including unequal distribution of wealth and other societal resources, such as adequate housing and access to health care and other social services. ² , ³ , ⁴ Furthermore, racial biases in medical treatment at hospitals and clinicsb may be relevant. Such factors highlight the structural inequality that exists in many metropolitan areas of the United States.

Here, we focused on two central aspects of this inequality, systemic racism (racial residential segregation) and social class disparity (income inequality), which are inherently related. For example, when racial and ethnic minorities are residentially segregated, income inequality often results in the area. ⁵ Our aim was to achieve greater conceptual clarity by combining the spatial variable racial residential segregation with the nonspatial, economic variable income inequality. These two structural factors combined may illustrate the extent of deepening poverty among some communities in the United States and its lethal effects during the pandemic.

Below, we explore the hypothesis that metropolitan areas become more vulnerable to COVID‐19 if wealth is unevenly distributed in these areas and, as a consequence, poverty is concentrated in certain communities. Concentrated poverty, in turn, will result in a deprivation of many social, medical, and community‐related resources in these communities. ⁶ , ⁷ These communities may not have adequate access to medical and social services; suffer from congested housing and compromised hygienic conditions; ³ , ⁸ and lack availability of healthy foods. ⁹ , ¹⁰ , ¹¹ Over time, residents in these communities may develop medical conditions that compromise immunity, including obesity, diabetes, and cardiovascular problems. ¹² , ¹³ , ¹⁴ In addition, residents in these communities may be more likely to work in essential service jobs, leaving no option to work at home; they thus have a higher risk of being exposed to the virus while working. ¹⁵ They may also have difficulty accessing adequate COVID‐19 testing and medical treatment. All these conditions, when extant, make the residents more vulnerable to infectious diseases, such as COVID‐19.

We propose that poverty becomes concentrated through two processes. The first involves racial residential segregation (“segregation” hereafter), which refers to the extent to which households of two racial or ethnic groups—typically, Whites and a minority group (e.g., Blacks, Hispanics, or Asians)—are clustered into racial enclaves above and beyond the level expected by chance alone. ¹⁶ , ¹⁷ , ¹⁸ Metropolitan areas high in segregation contain more and larger enclaves of both Whites and minorities. A large body of literature in sociology and demography ⁶ , ¹⁹ , ²⁰ , ²¹ , ²² shows that when Blacks are segregated, poverty is concentrated in the segregated Black enclaves, reflecting significant wealth disparity (more than seven‐fold) between Whites and Blacks. ²³ In their classical contribution to this literature, American Apartheid: Segregation and the making of the underclass, Massey and Denton (1993) observed, “Because of racial segregation, a significant share of black America is condemned to experience a social environment where poverty and joblessness are the norm (Page 2).” ²¹ The economic consequence of segregation may also apply to Hispanics because of an equally stark wealth disparity between Whites and Hispanics. ²³ Our first prediction, then, is that the negative impacts of COVID‐19 are greater in metropolitan areas that segregate the two minority groups (Blacks and Hispanics).

The second process by which poverty is concentrated in certain segments of metropolitan areas involves income inequality. When income inequality of a given area is high, it can affect all racial groups in the area. First, this factor may exacerbate the poverty of the segregated enclaves of the minority groups since these groups are also disadvantaged in income, relative to Whites. ²⁴ Second, it may also lend itself to White enclaves that are as poor. ²⁵ Although residential segregation based on income is lower among Whites than in Blacks, ²⁶ , ²⁷ , ²⁸ poor White enclaves may still exist due to the dramatic loss of economic standings among Whites without college degrees over the last few decades. ²⁹ , ³⁰ Hence, the poor White enclaves, together with the poor minority enclaves, will form larger areas suffering from poverty and the relative deprivation of social, medical, and community‐related resources. Accordingly, we anticipated that segregation's adverse effects would be exacerbated by income inequality in the area.

Numerous prior studies have investigated segregation and income inequality as correlates of health outcomes. A growing body of research shows that segregation is linked to chronic illnesses (e.g., hypertension, diabetes, and systemic inflammation) and greater mortality, particularly among racial minorities. ¹² , ¹³ , ¹⁴ , ³¹ Likewise, the evidence shows that the unequal distribution of income is associated with poor health outcomes, such as obesity and cardiovascular diseases; ² , ³² it has also been linked to reduced well‐being and higher all‐cause mortality. ³³ , ³⁴

However, one important shortcoming of the current literature is that it largely ignores the two factors' possible joint, or interactive, effects. One important exception comes from Nuru‐Jeter and LaVeist, ³⁵ who showed that Black–White segregation attenuates the effect of income inequality in predicting greater all‐cause mortality among Blacks. They interpreted the pattern as reflecting higher social cohesion in segregated Black communities, which may serve as a protective factor against economic disparity (for a similar argument, see Ref. 36). However, it is unclear whether such a protective effect extends to COVID‐19–related outcomes. Indeed, social cohesion could conceivably contribute to the spread of infectious disease by increasing social contact with a wider range of individuals in the community. ³⁷ More generally, as argued above, when metropolitan areas are high in both racial segregation and income inequality, more and larger enclaves will be impoverished and, thus, more vulnerable to the disease. We thus tested whether the combination of the two facets of structural inequality (i.e., segregation and income inequality) exacerbates the negative impacts of COVID‐19.

We focused on the 100 largest American metropolitan statistical areas (MSAs) ³⁸ during the current pandemic. MSA refers to a single contiguous geographic region consisting of a city (or cities) and surrounding communities that are connected by social and economic factors. ³⁹ This area typically encompasses multiple counties. Our analytic unit was each of the 577 counties subsumed under the 100 largest MSAs. All measures except for segregation, including a measure of income inequality (Gini), daily counts of COVID‐19 cases or deaths, as well as all control variables, were assessed at the county level. Segregation was assessed at the MSA level. Segregation typically occurs across city and county boundaries within a larger MSA, which would make counties or cities too granular to characterize the dispersal of different racial and ethnic groups within a single interconnected region for social and economic activity. ⁴⁰

A critical challenge in cross‐area comparisons—including the current one—stems from the fact that the counties can vary on a variety of factors, including those directly influencing the reported numbers of cases and deaths. Counties may vary in the availability of COVID‐19 diagnostic tests, as well as the diagnostic criteria in classifying symptoms and deaths as being COVID‐19–related or not. To address these potential biases, we followed our earlier work ³⁷ , ⁴¹ and tested the growth rate of both confirmed COVID‐19 cases and deaths in the first 30 days of county‐wise outbreaks in our main analysis, which was supplemented by a robustness check comprising a test of an even shorter period of 15 days: any confounding variables are unlikely to vary systematically within such a short period and thus are unlikely to influence the growth rate of cases and deaths. ³⁷ , ⁴¹ We also controlled for population size, population density, median income, percent of population over 65 years of age, and the proportion of Blacks, Hispanics, and Asians in each county.

In summary, we examined whether the MSA‐level racial segregation and the county‐level income inequality jointly predict the growth rate of both COVID‐19 cases and deaths in the first 30‐day period of the county‐wise outbreaks. We predicted that the progression of the disease would be faster in counties located in racially segregated MSAs. Second, we also predicted that this effect of segregation should be augmented for counties higher in income inequality. That is, the spread of COVID‐19 would be the fastest when high segregation is combined with high income inequality.

Methods

Sample and data

We retrieved daily reports of COVID‐19 confirmed cases and deaths from a public repository updated daily by the Johns Hopkins University Center for Systems Science and Engineering.c Our results are based on data from January 22, 2020 through June 20, 2020, before the second nationwide outbreak began. The cumulative daily counts of confirmed cases and deaths were available for each of the 577 counties nested under the 100 MSAs we examined. Some MSAs were composed of only one county (e.g., Bakersfield, CA, was composed of Kern county), but others included multiple counties (e.g., Pittsburgh, PA, includes seven counties: Allegheny, Fayette, Washington, Westmoreland, Butler, Beaver, and Armstrong). We determined which counties belong to each of the MSAs using the Office of Management and Budget Bulletin on the White House website.d Following prior work, ³⁷ , ⁴¹ we analyzed the data of the first 30 days of the outbreak of each county, with Day 1 defined as the day when at least 20 confirmed cases or at least 1 death was reported in the county for the analyses on cases and deaths, respectively. The exact number of cases used as a cutoff, 20, is arbitrary. Prior work used both 100 and 20. ³⁷ , ⁴¹ Unlike in these two studies (which compared countries), the current study focused on a cross‐county variation. To maximize the number of the counties included in the analysis, we adopted the smaller of the two criteria used in the past for our main analysis, followed by a robustness check that used the 100‐case cutoff. In order to ensure that the estimate of the growth rate is robust, counties were excluded from the analysis if less than 15 days of data were available. This resulted in a total of 535 and 495 counties for the analyses of cases and deaths, respectively.

We used a dissimilarity index of segregation. It quantifies segregation as the degree of deviation from a random residential distribution of two social groups within a given geographic area. ¹⁶ This index is available for Black–White segregation, Hispanic–White segregation, and Asian–White segregation based on the 2005–2009 Census data. ^{38 ,} e The index takes values from 0 to 100. It reflects the percentage of one group that would have to be relocated to attain the same spatial dispersion as the second group. Values of 60 or above are considered to show a “high” degree of segregation. ⁵ On average, the Black–White segregation was higher (M = 58, SD = 10.1) than either the Hispanic–White segregation (M = 46, SD = 8.2) or the Asian–White segregation (M = 45, SD = 6.7) across the 100 MSAs, P < 0.001. There was no significant difference between the latter two indices of segregation, P = 0.313.

To quantify income inequality, we obtained the Gini coefficient for each county. The Gini coefficient is a measure of income inequality based on dispersion of household income across the entire income distribution within a given geographic area. Gini coefficients were estimated from the American Community Survey, a large‐scale survey conducted by the U.S. Census Bureau.f We obtained the most recent 5‐year estimate of Gini coefficients (“Gini” hereafter) available in 2018.

We included several covariates. The first were the proportions of Blacks, Hispanics, and Asians in each county (called Black, Hispanic, and Asian shares, respectively). These minority share variables help us assess whether the growth of the number of cases and deaths might depend on the proportion of each minority group in the area. Population size and population density were included since both of these variables could increase the speed of the spread of the disease. The proportion of elderly adults (over 65 years old) was included because, generally, mortality goes up as a function of age. Median household income was included to adjust for the overall economic status of each county. The above data were taken from the U.S. Census Bureau Website.g The MSA‐level correlations among the covariates, including segregation and Gini, are reported in Figure S1 (online only). To compute the MSA‐level correlations, the pertinent county scores for all variables except for segregation (which was measured at the MSA‐level) were averaged to yield the MSA‐level scores. The county‐level correlations among them, except for segregation (which was measured at the MSA‐level), are given in Figure S2 (online only).

In addition, different states instituted lockdowns at different times after the outbreak. Hence, in a set of supplementary analyses, we additionally controlled for the number of days the state‐wide lockdown was in effect for each county during the 30‐day period of interest. Dates for state‐imposed stay‐at‐home orders were obtained from the Wall Street Journal.h

Statistical analyses

We used a three‐level linear mixed model analysis implemented with the lme4 package in R ⁴² for analyses on both confirmed cases and deaths. Infectious disease trajectories are approximately exponential in their initial phases. ⁴³ Thus, the number of both confirmed cases and deaths was natural‐log–transformed first and then subjected to linear mixed models with restricted maximum likelihood estimation. At level 1, the natural log of the cumulative number of either cases or deaths of the counties on each day was regressed on day (varying from 1 through 30), which was centered. The main effect of day is necessarily positive and shows the rate of growth of the cases or deaths. The effect of day on cases and deaths was assessed in each county. The county level constitutes level 2. We had several predictors at level 2, that is, Gini, population size, population density, median income, percentage of older adults, and Black, Hispanic, and Asian share. Finally, the counties were nested under relevant MSAs, which constituted level 3. The MSAs varied in the degree of segregation. Three measures of segregation were tested in separate analyses, that is, Black–White segregation, Hispanic–White segregation, and Asian–White segregation.

We analyzed whether the growth rate of cases or deaths across the days in each county (the effect of day) would vary in magnitude as a function of the segregation of the MSA in which the county was located (as indicated by the day × segregation interaction), and the multiplicative effect of income inequality and segregation (as indicated by the day × Gini × segregation interaction). The hypothesis that the growth was particularly fast when a high level of income inequality is combined with a high level of segregation would be supported if this three‐way interaction proved significant. Furthermore, we tested whether the growth rate of cases or deaths varied as a function of the Black, Hispanic, and Asian shares. This analysis sheds light on whether certain minority groups were impacted disproportionately, as suggested by public health data. This analysis enabled us to examine the racial disparity of the current pandemic in the United States, even though data for the daily cumulative counts of cases and deaths separated by race are currently unavailable.

Each model estimated a random intercept and a random slope across days for the MSAs and for the counties nested under the MSAs to allow for heterogeneity in growth curves across counties and MSAs. Because our maximal model did not converge, we dropped the intercept–slope covariance. ^{44 ,} i The day variable was centered, so the main effects can be interpreted as the effects at the mean day of the growth curve. Total population was natural‐log–transformed to reduce skewness. All predictors in the model (except day) were Z‐scored. Post‐hoc comparisons of the estimate of slopes across different conditions (high or low segregation, and high or low Gini) were carried out using the emmeans function in R, with P values adjusted for multiple comparisons using the Tukey's method. The data and R code for the present study are made available at: https://osf.io/qm697/?view_only = c30e3ce756904c529c36feb2e028958b.

Results

Confirmed cases

We first tested the effect of Black–White segregation on the growth rate of confirmed cases. As presented in Table 1, the day × segregation interaction was significant, b = 0.009, P < 0.001. Counties located in MSAs with high Black–White segregation showed faster growth of confirmed cases. Although the day × Gini interaction was not significant, b = 0.001, P = 0.511, the three‐way interaction involving day, segregation, and Gini proved significant, b = 0.003, P = 0.013. The growth rate was higher for counties with high Gini (+1 SD) located in MSAs with high segregation (+1 SD), as compared with the remaining three conditions (high in Gini/low in segregation, low in Gini/high in segregation, and low in Gini/low in segregation). This difference was statistically significant for the high Gini/low segregation and low Gini/low segregation conditions, slope difference = 0.023, Z = 4.767, P < 0.001; slope difference = 0.020, Z = 3.811, P < 0.001, respectively. It was marginal for the low Gini/high segregation condition, slope difference = 0.007, Z = 2.359, P = 0.085. The pattern is illustrated in the left panel of Figure 1A.

Table 1.

Regression coefficients for confirmed COVID‐19 cases for the Black‐White (left), Hispanic‐White (middle), and Asian‐White segregation (right) models during the first 30 days of county‐wise outbreaks

Predictor	b	t	P	b	t	P	b	t	P
Intercept	4.514	100.120	<0.001***	4.523	100.608	<0.001***	4.523	93.686	<0.001***
Variables of Interest
Day	0.070	31.768	<0.001***	0.070	33.761	<0.001***	0.071	29.460	<0.001***
Segregation	0.166	3.604	<0.001***	0.167	3.683	<0.001***	0.061	1.209	0.229
Day × Segregation	0.009	3.936	<0.001***	0.010	4.806	<0.001***	0.003	1.114	0.268
Gini	0.019	0.770	0.441	0.023	0.949	0.343	0.032	1.339	0.181
Day × Gini	0.001	0.658	0.511	0.001	0.595	0.552	0.002	1.356	0.176
Segregation × Gini	0.031	1.507	0.132	0.006	0.293	0.769	−0.029	−1.278	0.202
Day × Segregation × Gini	0.003	2.497	0.013*	0.003	2.483	0.013*	−0.001	−0.501	0.617
Minority Share
Black Share	0.132	4.634	<0.001***	0.131	4.605	<0.001***	0.134	4.647	<0.001***
Day × Black Share	0.007	4.809	<0.001***	0.007	5.043	<0.001***	0.007	4.686	<0.001***
Hispanic Share	0.069	2.233	0.026*	0.047	1.542	0.124	0.062	1.933	0.054 +
Day × Hispanic Share	0.005	3.279	0.001**	0.003	2.304	0.022*	0.005	2.857	0.005**
Asian Share	−0.032	−1.226	0.221	−0.036	−1.373	0.170	−0.040	−1.502	0.134
Day × Asian Share	0.002	1.338	0.182	0.002	1.205	0.229	0.001	0.950	0.342
Covariates
Natural Log of Population Size	0.789	27.565	<0.001***	0.798	28.028	<0.001***	0.800	27.912	<0.001***
Day × Natural Log of Population Size	0.034	22.506	<0.001***	0.035	23.179	<0.001***	0.035	22.795	<0.001***
Median Income	0.025	0.864	0.388	0.017	0.601	0.548	0.031	1.045	0.296
Day × Income	0.001	0.659	0.510	0.001	0.329	0.742	0.001	0.838	0.403
Population Density	0.067	2.941	0.003**	0.080	3.461	0.001**	0.087	4.078	<0.001***
Day × Population Density	0.003	2.438	0.015*	0.003	2.521	0.012*	0.004	3.803	<0.001***
Proportion Elderly	0.007	0.247	0.805	0.006	0.216	0.829	0.013	0.470	0.638
Day × Proportion Elderly	0.000	0.288	0.773	0.000	0.235	0.814	0.001	0.525	0.600

^*** P < 0.001.

^** P < 0.01.

^* P < 0.05.

⁺ P < 0.10.

Figure 1.

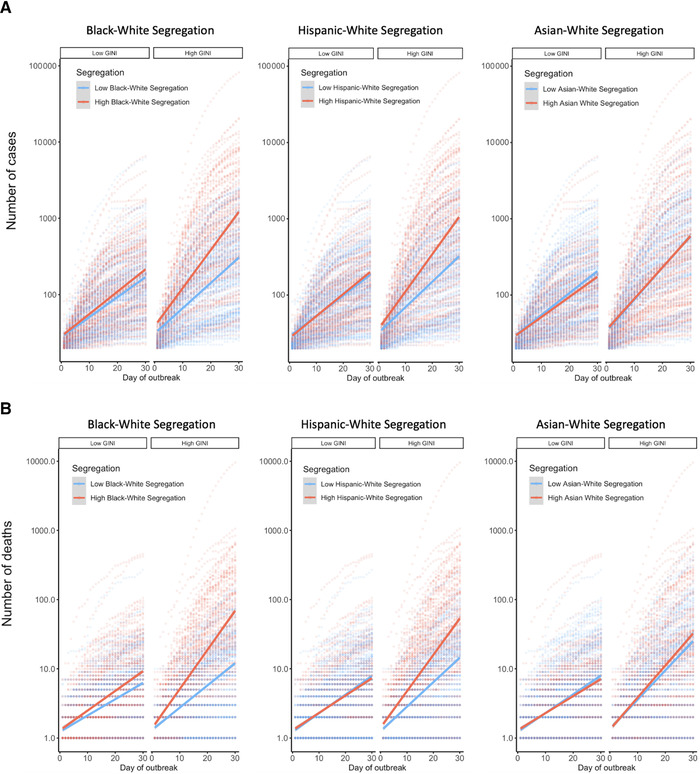
The growth of confirmed COVID‐19 cases (A) and deaths (B) on a log‐scale during the first 30 days of the county‐wise outbreaks. The growth trend of each of the 535 counties (case analysis) and 495 counties (death analysis) under the 100 largest U.S. metropolitan areas is plotted with dotted lines, as a function of high versus low Gini (median split) and high versus low racial segregation (median split). The solid lines in the figure are the best fit line across all data points within each of the conditions defined by the combination of Gini and segregation.

We ran a comparable analysis with Hispanic–White segregation (see Table 1). The day × segregation interaction was significant, b = 0.010, P < 0.001. Counties located in MSAs with high Hispanic–White segregation showed faster growth of confirmed cases. Although the day × Gini interaction was not significant, b = 0.0008, P = 0.552, the three‐way interaction involving day, segregation, and Gini was significant, b = 0.003, P = 0.013. The growth rate was higher for counties with high Gini (+1 SD) located in MSAs with high segregation (+1 SD), compared with the remaining three conditions. This difference was statistically significant for the high Gini/low segregation and low Gini/low segregation conditions, slope difference = 0.026, Z = 5.721, P < 0.001; slope difference = 0.022, Z = 4.528, P < 0.001, respectively. It was marginal for the low Gini/high segregation condition, slope difference = 0.007, Z = 2.311, P = 0.095. Among the latter three conditions, counties with high segregation/low Gini also had larger growth rate than the remaining two conditions, P < 0.05. The center panel of Figure 1A illustrates the pattern.

We also ran the identical model with Asian–White segregation (see Table 1). Unlike in the first two models, there was no significant effect of Asian–White segregation on the growth of cases, b = 0.003, P = 0.268 (the right panel of Fig. 1A). As in the prior analyses, the interaction between day and Gini was not significant, b = 0.002, P = 0.176. There was no three‐way interaction between day, segregation, and Gini, b = −0.001, P = 0.617.

Did the covariates demonstrate effects? First, we tested whether the growth of the number of cases depends on the share of each minority group in each county. Across the three segregation models, there was a significant interaction between day and Black share, b = 0.007, P < 0.001 (Black–White segregation model), b = 0.007, P < 0.001 (Hispanic–White segregation model), b = 0.007, P < 0.001 (Asian–White segregation model). A similar trend is evident for Hispanics. The day × Hispanic share interaction was significant in all the three models, b = 0.005, P = 0.001 (Black–White segregation model), b = 0.003, P = 0.022 (Hispanic–White segregation model), b = 0.005, P = 0.005 (Asian–White segregation model). The Asian share had no effect. Across the three models, both population size and population density of the counties predicted both a faster increase and a larger number of confirmed cases, P < 0.05.

Deaths

We performed the same set of three‐level mixed effects linear regressions predicting the growth rate of deaths of the counties nested under the MSAs. As shown in Table 2, the Black–White segregation model showed a significant day × segregation interaction, b = 0.012, P < 0.001. Counties located in MSAs with high Black–White segregation showed faster growth of deaths. The interaction between day and Gini was not significant, b = 0.003, P = 0.180. As in the analysis of confirmed cases, the three‐way interaction involving day, segregation, and Gini proved significant, b = 0.007, P < 0.001. The growth rate was significantly higher for counties with high Gini (+1 SD) located in MSAs with high segregation (+1 SD), compared with the remaining three conditions (low in Gini/high in segregation, high in Gini/low in segregation, and low in both), slope difference = 0.020, Z = 4.110, P < 0.001; slope difference = 0.038, Z = 5.847, P < 0.001; slope difference = 0.030, Z = 4.198, P < 0.001, respectively. The latter three conditions did not differ from each other, P > 0.10. This is illustrated in the left panel of Figure 1B.

Table 2.

Regression coefficients for COVID‐19 deaths for the Black‐White (left), Hispanic‐White (middle), and Asian‐White segregation (right) models during the first 30 days of county‐wise outbreaks

Predictor	b	t	P	b	t	P	b	t	P
Intercept	1.311	23.987	<0.001***	1.325	23.761	<0.001***	1.320	22.474	<0.001***
Variables of Interest
Day	0.067	23.759	<0.001***	0.068	22.860	<0.001***	0.068	21.787	<0.001***
Segregation	0.210	3.724	<0.001***	0.185	3.196	0.002**	0.125	1.962	0.052 +
Day × Segregation	0.012	4.099	<0.001***	0.009	2.993	0.003**	0.006	1.871	0.064 +
Gini	0.091	2.039	0.042*	0.090	2.040	0.042*	0.111	2.512	0.012*
Day × Gini	0.003	1.343	0.180	0.004	1.728	0.085 +	0.005	2.321	0.021*
Segregation × Gini	0.049	1.360	0.175	0.063	1.661	0.097 +	−0.017	−0.423	0.672
Day × Segregation × Gini	0.007	4.124	<0.001***	0.006	3.140	0.002**	0.001	0.525	0.600
Minority Share
Black Share	0.145	3.179	0.002**	0.142	3.102	0.002**	0.142	3.029	0.003**
Day × Black Share	0.007	2.977	0.003**	0.007	3.070	0.002**	0.007	2.777	0.006**
Hispanic Share	0.027	0.583	0.560	−0.018	−0.403	0.687	0.021	0.429	0.668
Day × Hispanic Share	0.001	0.239	0.812	−0.002	−0.819	0.413	0.000	0.166	0.868
Asian Share	−0.069	−1.602	0.110	−0.069	−1.599	0.111	−0.084	−1.935	0.054 +
Day × Asian Share	0.001	0.529	0.597	0.001	0.377	0.706	−0.000	−0.036	0.971
Covariates
Natural Log of Population Size	0.678	13.981	<0.001***	0.689	14.257	<0.001***	0.700	14.323	<0.001***
Day × Natural Log of Population Size	0.039	16.547	<0.001***	0.040	16.893	<0.001***	0.041	16.890	<0.001***
Median Income	0.130	2.654	0.008**	0.113	2.293	0.022*	0.155	3.097	0.002**
Day × Income	0.003	1.125	0.261	0.002	0.849	0.396	0.004	1.654	0.099 +
Population Density	0.096	2.413	0.016*	0.095	2.372	0.018*	0.127	3.400	0.001**
Day × Population Density	0.002	0.852	0.395	0.002	1.242	0.215	0.005	2.635	0.009**
Proportion Elderly	0.057	1.290	0.198	0.055	1.255	0.210	0.069	1.540	0.124
Day × Proportion Elderly	0.003	1.198	0.232	0.003	1.273	0.204	0.004	1.581	0.115

^*** P < 0.001.

^** P < 0.01.

^* P < 0.05.

⁺ P < 0.10.

The Hispanic–White segregation model showed a parallel pattern (see Table 2). The day × segregation interaction was significant, b = 0.009, P = 0.003, indicating greater growth rate of COVID‐19 deaths for segregated MSAs (the center panel of Fig. 1B). The day × Gini interaction was marginally significant, b = 0.004, P = 0.085. The three‐way interaction involving day, segregation, and Gini was significant, b = 0.006, P = 0.002. The growth rate was significantly higher for counties with high Gini (+1 SD) located in MSAs with high segregation (+1 SD), as compared with the remaining three conditions (low in Gini/high in segregation, high in Gini/low in segregation, and low in both), slope difference = 0.019, Z = 3.691, P = 0.001; slope difference = 0.030, Z = 4.486, P < 0.001; slope difference = 0.026, Z = 3.533, P = 0.002, respectively. The latter three conditions did not differ significantly, P > 0.20.

In the third model, we tested the Asian–White segregation (see Table 2). The effect of segregation on the rate of increase in deaths was marginal, b = 0.006, P = 0.064. However, the day × Gini interaction was significant, b = 0.005, P = 0.021. Counties with more income inequality had a steeper increase in deaths attributed to COVID‐19. The three‐way interaction involving day, segregation, and Gini was negligible, b = 0.001, P = 0.600 (see the right panel of Fig. 1B).

Did the covariates demonstrate effects on the growth rate of deaths? First, across the three models, we found clear evidence that counties with higher Black share reported a greater rate of increase in deaths, b = 0.007, P = 0.003 (Black–White segregation model), b = 0.007, P = 0.002 (Hispanic–White segregation model), b = 0.007, P = 0.006 (Asian–White segregation model). There was virtually no evidence that the share of either Hispanics or Asians had any effects. As in the analysis of confirmed cases, population size also predicted a greater rate of increase in deaths and a larger total number of deaths, P < 0.001. The effect of population density was also similar, though compared with the analysis of confirmed cases, it was much weaker.

Robustness checks and additional analyses

To check the robustness of the findings above, we carried out several variations on the main analysis. In the first variation, we additionally controlled for the potential effects of state‐wide lockdowns. We computed the number of days during the 30‐day period after the state‐wide lockdown.j When this variable was entered as an additional covariate, it predicted a less‐steep increase of cases, b = −0.006, P < 0.001 (Black–White segregation model), b = −0.005, P < 0.001 (Hispanic–White segregation model), b = –0.005, P < 0.001 (Asian–White segregation model); it also predicted a less‐steep growth of deaths, b = –0.004, P = 0.023 (Black–White segregation model), b = −0.004, P = 0.024 (Hispanic–White segregation model), b = −0.003, P = 0.052 (Asian–White segregation model). The key effects in our main analysis reported above, however, were unchanged (see Tables S1 and S2, online only).

In the second variation, we analyzed only the first 15 days (instead of 30 days) of county‐wise outbreaks. The focus on the shorter period may be desirable because various confounding factors, particularly reporting biases, are less likely to change systematically if the period is shorter; however, one downside of this analysis is that the data are reduced in half, thus making the estimation of growth curves less reliable compared with the 30‐day analysis. The day × segregation interaction (Blacks and Hispanics) remained significant for both cases and deaths. The day × Gini × segregation interaction (Blacks and Hispanics) remained significant for deaths, although it was no longer significant for cases (Tables S3 and S4, online only).

In the third variation, we used 100 cases (rather than 20 cases) to define the first day of county‐wise outbreaks for the analysis of cases; this alternate cutoff is equally reasonable and has been used in prior work. ⁴¹ Under this condition, our previously observed effects were unchanged (Table S5, online only).

In a fourth variation, because Black–White and Hispanic–White segregation were positively correlated (r = 0.59, P < 0.0001), we averaged the two indices to form a single index of segregation. When we ran the standard models reported in the main analyses, all effects replicated, and the three‐way interactions were highly significant for both cases and deaths (Tables S6 and S7, online only).

Discussion

In the present work, we showed that the growth rate of COVID‐19 cases and deaths was higher for MSAs that exhibit greater Black–White or Hispanic–White segregation. Furthermore, this effect of residential racial segregation was exacerbated by income inequality in the area. The effect demonstrated in our analyses above is not trivial. For example, were the Detroit metro area less racially segregated on the Black–White axis so that it was at the same level as Albuquerque, NM, and were the counties included in Detroit metro area more economically equal (e.g., at the level of Ionia county of Grand Rapids, MI), our model shows that the Detroit metro area would have suffered only 45.4% of the deaths reported by the end of the 30‐day study period (744 predicted deaths, compared with 1639 actual deaths).

Both racial segregation and income inequality have been the focus of research in the areas of sociology, demography, and public health, ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ although few studies have evaluated racial segregation and income inequality together. Our work demonstrates that combining the two factors shows a synergistic effect on infections and deaths during the COVID‐19 pandemic. Compared with White communities, segregated Black and Hispanic communities, given the racial disparity in net wealth, ²³ are more likely deprived of a wide range of social, medical, and other related resources. High income inequality exacerbates the poverty of segregated minority enclaves, while also resulting in impoverished White enclaves. ⁶ , ²² , ²⁵ The combination of segregation and income inequality yields larger areas plagued with poverty and deprived of social, medical, and community‐level resources within a metropolitan area. Such communities are thereby more vulnerable to infectious diseases, such as COVID‐19. Conversely, reduced income disparity may buffer the malignant effect of segregation.

The joint effects of segregation and income inequality may begin to explain why COVID‐19 has had a disproportionate impact on the members of racial or ethnic minorities, especially among Blacks and Hispanics. Over many decades, the segregation of Black communities has been enforced, particularly strictly, in many large American cities, ⁵ , ²¹ consistent with a higher mean of the dissimilarity index of segregation for Blacks than for either Hispanics or Asians. Our current findings are in line with the suggestion that the “hypersegregation” ¹⁸ in American cities is a fundamental root cause of racial disparity in educational attainment, socioeconomic status, and health. ⁵ , ¹⁸ Indeed, the spread of the disease was faster in counties with a higher share of both Blacks (in the analyses of both cases and deaths) and, to some degree, Hispanics (only in the analysis of cases). Nevertheless, as race‐stratified daily counts of cases or deaths at the county‐level are not available at present, the data we used in the present study included counts of confirmed cases and deaths from entire counties. Therefore, it is currently impossible to be specific about any race‐specific patterns.

It is unknown exactly how much impact segregation and income inequality have had on Whites, particularly, Whites not plagued with poverty. At present, approximately 50% of all cases and deaths in the United States have been among the White population.k Furthermore, in our analysis, we found that minority shares did not always predict increased growth of deaths. This suggests that the lethal consequences of structural inequality may be widely shared across the entire area, not strictly limited to the minority groups alone.

What about Asians? There was weak evidence for the day × segregation interaction for deaths, but not for cases. Unlike that for Blacks and Hispanics, this effect was not moderated by income inequality (see Tables 1 and 2). Despite the prejudice and stereotypes Asians and Asian Americans often contend with, ⁴⁹ , ⁵⁰ their median household wealth is no different from American Whites. ²⁴ Hence, White–Asian segregation may be less likely to result in the concentration of poverty in Asian enclaves.

Recently, Kraus and colleagues ⁵¹ found that representative samples of Americans estimated the current average wealth of Blacks to be 90% of the current average wealth of Whites in 2016. The respondents also estimated the average wealth of Blacks to be, approximately a half‐century earlier, in the early 1960s, 50% of the average wealth of Whites. The correct percentages, however, are 10% and 5%, respectively. Thus, most Americans fail to register the great wealth disparity between Whites and minority groups, such as Blacks and Hispanics, and indeed suggest instead progress toward racial equality, which remains unrealized. Kraus and colleagues suggest that the optimistic picture of racial progress is false in economic domains and self‐deceiving; it may in fact perpetuate racism by blinding many individuals to racism that remains pervasive. In the present case, false optimism could make it even more difficult for Americans to realize the role of segregation in the devasting human toll during the COVID‐19 pandemic.

Over the course of the COVID‐19 pandemic, the United States has suffered exceptionally: as of January 2021, it leads the world in the total numbers of both infections and deaths. There are many contributing causes of this suffering: some historical (e.g., the absence of mandatory BCG (tuberculosis vaccination) policy during the 20th century ⁴¹ ), and some psychological (e.g., the United States is especially high in social openness, which has been linked to an increased infection risk ³⁷ ). It is also hard to dismiss the absence of effective political leadership as a crucial factor. ⁵² Our work here adds social structure as another fundamental dimension: systemic racism (owing to segregation, particularly pronounced in the United States, compared with many countries) and social class disparity (as revealed in income inequality, also particularly extreme in the United States compared with many countries). Importantly, the confluence of the two factors is evident in the data we have provided.

Some limitations of our analyses must be noted. First, as stated above, the county‐wise statistics did not stratify the daily count of either infections or deaths by race. Future work must test the growth rate of both confirmed cases and deaths separately for different ethnic groups. Second, segregation is multidimensional, and the current dissimilarity measure of segregation ¹⁶ might not capture this construct in its entirety. ¹⁷ Similarly, Gini is only one way to study income inequality, and it does not take into account the spatial distribution of wealth. ²⁷ Future work may use alternate measures of segregation and income inequality, such as income segregation, which has also been shown to predict health‐related outcomes. ⁵³ It will also be informative for future research to examine within‐race income inequality and its consequences on health outcomes. Third, the current analysis did not include all racial minority groups that have suffered disproportionately (e.g., Native Americans); this is a major omission that must be rectified in future work in which sufficient care must be taken to differentiate the varying historical reasons for segregation of different minority groups. Fourth, our work is limited to the United States. It is unknown if a similar dynamic might exist in other countries that are also severely affected by COVID‐19. Fifth, a substantial amount of variance is unaccounted for by the two axes of structural inequality alone; future work must address this gap to achieve a fuller picture of the pandemic's social dynamics from multidisciplinary perspectives. Sixth, as important as pandemics are, there is more to social life than the consequences of virus infection; future work must test whether the adverse effect of segregation and income inequality generalize to other domains, such as life satisfaction and the community's well‐being. ³⁴

Despite these limitations, our work provides the first evidence that racial residential segregation and income inequality yield a synergistic effect of producing a “lethal spiral” that leads to a greater number of fatalities during a pandemic. We hasten to add that our work does not suggest (or imply) that segregated Black/Hispanic enclaves should be stigmatized for spreading infections during a pandemic. These enclaves are often plagued with an assortment of adverse health conditions because of the existing structural inequality that, in turn, renders them particularly vulnerable to infectious diseases. Much effort is needed to eliminate discriminatory institutional practices that reinforce segregation and economic disparity. Such effort would be indispensable for making cities both virus‐resistant and virus‐resilient in our era of rapid‐spreading infectious diseases. ⁵⁴

Competing interests

There are no competing interests to declare.

Supporting information

Table S1. Regression coefficients for confirmed COVID‐19 cases for the Black (left), Hispanic (middle), and Asian (right) segregation models, after controlling for the potential effect of lockdowns (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S2. Regression coefficients for COVID‐19 deaths for the Black (left), Hispanic (middle), and Asian (right) segregation models, after controlling for the potential effect of lockdowns (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S3. Regression coefficients for confirmed COVID‐19 cases for the Black (left), Hispanic (middle), and Asian (right) segregation models (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S4. Regression coefficients for COVID‐19 deaths for the Black (left), Hispanic (middle), and Asian (right) segregation models (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S5. Regression coefficients for confirmed COVID‐19 cases for the Black (left), Hispanic (middle), and Asian (right) segregation models (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S6. Regression coefficients for confirmed COVID‐19 cases with Black and Hispanic segregation combined as a single segregation index (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Table S7. Regression coefficients for COVID‐19 deaths with Black and Hispanic segregation combined as a single segregation index (^*** P < 0.001, ^** P < 0.01, ^* P < 0.05, ⁺ P < 0.10).

Figure S1. Correlation matrix of the predictors included in the present analysis.

Figure S2. Correlation matrix of the county‐level predictors included in the present analysis.