Potential impact of COVID‐19 on ongoing clinical trials: a simulation study with the neurological Yale Global Tic Severity Scale based on the CANNA‐TICS study

Abstract

The COVID‐19 pandemic has manifold impacts on clinical trials. In response, drug regulatory agencies and public health bodies have issued guidance on how to assess potential impacts on ongoing clinical trials and stress the importance of a risk‐assessment as a pre‐requisite for modifications to the clinical trial conduct. This article presents a simulation study to assess the impact on the power of an ongoing clinical trial without the need to unblind trial data and compromise trial integrity. In the context of the CANNA‐TICS trial, investigating the effect of nabiximols on reducing the total tic score of the Yale Global Tic Severity Scale (YGTSS‐TTS) in patients with chronic tic disorders and Tourette syndrome, the impact of the two COVID‐19 related intercurrent events handled by a treatment policy strategy is investigated using a multiplicative and additive data generating model. The empirical power is examined for the analysis of the YGTSS‐TTS as a continuous and dichotomized endpoint using analysis techniques adjusted and unadjusted for the occurrence of the intercurrent event. In the investigated scenarios, the simulation studies showed that substantial power losses are possible, potentially making sample size increases necessary to retain sufficient power. However, we were also able to identify scenarios with only limited loss of power. By adjusting for the occurrence of the intercurrent event, the power loss could be diminished to different degrees in most scenarios. In summary, the presented risk assessment approach may support decisions on trial modifications like sample size increases, while maintaining trial integrity.

Abbreviations

BSWP

Biostatistics Working Party

CBD

Cannabidiol

CMH

Cochran‐Mantel‐Haenszel

CTD

chronic tic disorder

EMA

European Medicines Agency

FDA

Food and Drug Administration

GCP

good clinical practice

HMA

Heads of Medicines Agency

THC

tetrahydrocannabinol

TS

Gilles de la Tourette syndrome

TTS

total tic score

YGTSS

Yale Global Tic Severity Scale

1. INTRODUCTION

The COVID‐19 pandemic does not only affect public health and daily living, but also has manifold impacts on clinical trials. In response, drug regulatory agencies and public health bodies have issued guidance and recommendations on how to assess potential impacts of the COVID‐19 pandemic on ongoing clinical trials and on potential mitigation measures. In Europe, the Clinical Trials Expert Group of the European Commission, supported by the European Medicines Agency (EMA), the Clinical Trials Facilitation and Coordination Group of the Heads of Medicines Agencies (HMA) and the Good Clinical Practice (GCP) Inspectors' Working Group have published general guidance on the management of clinical trials during the COVID‐19 pandemic. ¹ Additionally, the Biostatistics Working Party (BSWP) issued a Points to Consider document on the implications of COVID‐19 on methodological aspects of ongoing clinical trials. ² The Food and Drug Administration (FDA) provides “Statistical Considerations for Clinical Trials During the COVID‐19 Public Health Emergency”. ³

These documents discuss the role of a risk‐assessment and modifications to the clinical trial conduct—if deemed necessary, as has also been emphasized in recent publications. ⁴ , ⁵ While Kunz et al. discuss adaptive designs as an approach to modify ongoing trials to react to specific impacts of the COVID‐19 pandemic, ⁵ Großhennig and Koch caution against hasty changes of the original plans. ⁶ The BSWP recommends the “risk‐assessment of the impact of: (i) COVID‐19 potentially affecting trial participants directly and (ii) COVID‐19 related measures affecting clinical trial conduct on trial integrity and interpretability.” Based on this risk assessment, the guidance lists the need to adjust the trial sample size as a potential follow‐up consideration together with “recommendations of additional measures when completing the trial after the pandemic.” Additionally, the FDA lists the “modifications to the […] ascertainment of trial endpoints” as one option to address the impact of COVID‐19 on trial integrity.

Here, we investigate the above mentioned recommendations with regard to the ongoing CANNA‐TICS trial (ClinicalTrials.gov identifier NCT03087201). This multicenter, randomized, double‐blind, placebo controlled, parallel‐group trial aims to demonstrate that the treatment with the cannabis extract Nabiximols is superior to placebo in reducing tics and comorbidities in adult patients with chronic tic disorders (CTD) and Gilles de la Tourette syndrome (TS). The primary endpoint was defined as the Total Tic Score (TTS) of the Yale Global Tic Severity Scale (YGTSS), ⁷ a semi‐structured interview assessing the severity of motor and phonic tics (range, 0‐50). In addition, the Global Score (GS, range 0‐100) of the YGTSS was defined as a secondary endpoint calculated by the sum of the YGTSS‐TTS and the impairment score (0‐50) assessing patients' self‐esteem, family life, social acceptance, and function at school or at work. As a primary endpoint, a dichotomization of the continuous change from baseline compared to 13 weeks after treatment initiation is used measured as the proportion of patients with a reduction in the YGTSS‐TTS of at least 30%. At the beginning of the COVID‐19 pandemic, the primary endpoint had been already fully assessed for the majority of patients. However, some patients had been recruited and assessed at baseline, before the pandemic, but measurements after 13 weeks of treatment had to be completed during the COVID‐19 pandemic. Another small number of patients were planned to be recruited during (or after) the pandemic. As recommended by Meyer et al., ⁴ Degtyarev et al., ⁸ and Hemmings, ⁹ we will use the estimands framework as outlined in the ICH E9 addendum on estimands and sensitivity analyses ¹⁰ to describe and investigate the impact of the COVID‐19 pandemic. In the ICH E9 addendum, estimands are defined as a “precise description of the treatment effect reflecting the clinical question posed by a given clinical trial objective,” and characterized by the attributes treatment, population, variable of interest, (strategies for handling) intercurrent events and the population‐level summary. For defining the clinical question of the trial, intercurrent events need to be considered for precisely defining the treatment effect that is to be estimated and a variety of strategies for handling intercurrent events have been proposed. Applying the treatment policy strategy, “the value for the variable of interest is used regardless of whether or not the intercurrent event occurs.” ¹⁰ This reflects a different clinical question as compared to the hypothetical strategy, which would envisage a scenario where the intercurrent event would not occur.

Applying this framework and using intercurrent events for describing and investigating, the COVID‐19 pandemic may affect the ongoing trial in two ways:

1. Implementation of social distancing measures: Public health measures such as social distancing or complete lockdowns can affect mental health and increase anxiety. This has been shown to increase the severity of tics of patients with CTD and TS. ¹¹ In a clinical trial, this would imply a potential increase in the YGTSS‐TTS due to the COVID‐19 pandemic in patients recruited before the start of the COVID‐19 pandemic and assessed at 13 weeks during the pandemic. On the other hand, the same measures transform the extent to which tics interfere with normal functioning. This is however more likely to influence the YGTSS‐GS (used here as a secondary endpoint) than the YGTSS‐TTS. ¹² Thus, the assessment of the baseline value pre‐pandemic and of the primary endpoint during‐pandemic could influence the interpretability of the primary endpoint. On one hand, patients are less exposed to social events, and therefore less impact on functioning may be anticipated. ¹³ On the other hand, social distancing measures might increase anxiety and thereby the severity of symptoms. ¹³ Consequently, for this simulation study, we consider the implementation of social distancing measures by the local or state authority as the intercurrent event and model the effect on the YGTSS‐TTS not as a fixed but as a random variable, allowing it to vary between patients. Without loss of generality, however, we expect the intercurrent event to lead to a worsening of the score on average (as an improvement will be modeled with the second intercurrent event of interest, see below);

2. Change in assessment method: The YGTSS is designed to be assessed via a personal interview. Due to the COVID‐19 pandemic, this ascertainment method has been changed to an assessment via a video‐call due to the change in access rules by participating hospitals. This change is in line with the call for an increased use of telemedicine and video‐conferencing technology for treating and diagnosing patients with movement disorders. ¹⁴ , ¹⁵ This change in the assessment method from baseline to primary endpoint measurement might influence the interpretability of the primary endpoint, for example, due to the different psychological state of the subjects undergoing a visit in a clinic versus connecting from their own house, leading to a different assessment of their own symptoms. ¹⁶ While no specific evidence comparing in‐person versus remote assessment of the YGTSS exists, conflicting evidence can be found from other neurological and psychiatric conditions. On the one hand, there is some support to the interchangeability of in person and remote assessment for some of the most widely used scales for depression ¹⁶ and remote assessment of the YGTSS is used as a pre‐defined standard procedure in the EMTICS trial. ¹⁷ On the other, there is some evidence suggesting that the physical distance from the clinician can decrease anxiety, ¹⁸ or that patients might be more or less prone to admit severity of symptoms depending on the modality of assessment. ¹⁹

Since both events potentially affect the interpretability of the primary endpoint, they qualify as intercurrent events, which are defined in the Addendum to the ICH E9 guideline ¹⁰ as “Events occurring after treatment initiation that affect either the interpretation or the existence of the measurements associated with the clinical question of interest.” These intercurrent events were not known to exist at the planning stage of the study, and it may be argued that any newly defined estimand that incorporates these events does not strictly correspond to the original aim of the study. For determining a strategy for handling the intercurrent events, Degtyarev et al. ⁸ propose (in the setting of oncology) to choose the strategy most in line with the original study objective. Whereas, a hypothetical strategy would be based on the assumption that the intercurrent events will not occur in the future (eg, due to the world being COVID‐19‐free, or social distancing measures being revoked), choosing the treatment policy strategy is based on the belief that the intercurrent events will also be of relevance in the future. While both the hypothetical and treatment policy strategy have some merits for the interpretation of the trial outcome, in our analysis we decided to handle both intercurrent events by a treatment policy strategy and target the marginal risk difference between treatment groups, because social distancing measures and changes in assessment methods might be relevant at least in the near future. As an additional estimand of interest, we propose to use a hypothetical strategy for the intercurrent events.

Following the recommendations issued by EMA and FDA, the impact of the two intercurrent events on the trial should be assessed as part of a risk assessment, before deciding on potential follow‐up actions. For this purpose, we designed a simulation study based on the planning assumptions of the CANNA‐TICS trial, allowing to modify the proportion of patients impacted by the COVID‐19 pandemic and the distribution of the effects of the intercurrent events on the outcome.

The methodological approach outlined in the subsequent chapters can serve as a basis for discussion for assessing the impact of intercurrent events in similar clinical trial settings, where some patients are recruited pre‐pandemic and assessed during‐pandemic and a change from baseline value on neurological scales serves as the primary endpoint.

Therefore, first we briefly introduce the CANNA‐TICS trial as a motivating example and outline the simulation model, the simulated scenarios and the trial analysis methods. Here, we investigate the impact of the intercurrent events using both the responder criterion, dichotomizing the change in YGTSS‐TTS, and the continuous change in YGTSS‐TTS as endpoints. Subsequently, we present the results for the simulated scenarios separately for the continuous and the dichotomized endpoint and discuss the consequences of our findings.

2. OBJECTIVES

This paper discusses an example of how COVID‐19 related intercurrent events may affect an ongoing study. We aim to quantify the effect of such intercurrent events on the power of the study (see section “Simulation assumptions” for a justification and elaboration on the choice of outcome).

3. METHODS

To investigate the impact on the power of an ongoing trial, we designed a simulation study motivated by the running CANNA‐TICS trial. For better identification of the impact of the intercurrent events, we simplified some aspects of the trial for the simulation study as outlined below. First, we introduce the details of the CANNA‐TICS trial and thereafter describe the design of the simulation study.

3.1. The CANNA‐TICS trial

The CANNA‐TICS trial is the motivating example for the investigation of the impact of the COVID‐19 pandemic on ongoing trials.

3.2. Background

CANNA‐TICS is a multi‐center, randomized, double‐blinded, phase‐III trial to demonstrate that the cannabis extract nabiximols is efficacious in reducing tic severity in patients with TS or CTD. N = 96 patients with TS or CTD were planned to be randomized in a 2:1 ratio to receive either nabiximols or placebo. Nabiximols contains THC (Tetrahydrocannabinol) and cannabidiol (CBD) and is administered as an oral spray. Treatment is administered at an individual dose, which patients may select within the first 4 weeks of treatment, according to a fixed schedule for optional dose increases. This 4‐week titration period is followed by 9 weeks of stable treatment at the individually selected dose.

3.3. Primary endpoint

The primary endpoint to evaluate efficacy is a dichotomous responder criterion, defined as having at least 30% reduction in YGTSS‐TTS after 13 weeks of treatment as compared to baseline. Here, relative change was defined as the difference between the YGTSS‐TTS measured at week 13 and at baseline, divided by the baseline value.

3.4. Analysis

The analysis is planned to be conducted by means of a Cochran‐Mantel‐Haenszel test stratified for center for the risk difference at the two‐sided significance level of 5%, claiming superiority if the risk difference for response is significantly greater than 0. The analysis is planned to follow the intention to treat principle, that is, all randomized patients are planned to be analyzed as randomized, irrespective of whether they were actually treated or not. For patients with missing responder status, the primary endpoint is planned to be imputed as non‐responder.

The original study planning pre‐dates the publication of the ICH E9 addendum on estimands and sensitivity analyses. For the sake of simplicity, no intercurrent events in addition to the above‐mentioned COVID‐19 related intercurrent events will be discussed and included in the simulation study.

3.5. Sample size

The sample size of n = 96 subjects was chosen as follows in the original study planning. Based on data from a previous randomized study ²⁰ responder proportions of 29% and 1% were assumed. Under these assumptions, an exact Fisher test would have at least 90% power to demonstrate a difference at the two sided significance level of 5% if n = 75 subjects (50:25 in the treatment arms, respectively) are included. In order to account for potential drop‐outs under the assumption of data Missing At Random, which would lead to a diminished difference in responder proportions due to non‐responder imputation, sample size was increased to a total of n = 96 (64:32).

3.6. Recruitment status

The trial is ongoing. The exact beginning of the pandemic and its potential influence is hard to define. At the time when political measures such as social distancing were officially put in place there was already a broad public awareness of the pandemic. For the purpose of this article, we make the following simplifying assumptions that approximate the status of CANNA‐TICS: n = 77 subjects were recruited and had finished the study before the pandemic and n = 19 subjects had been recruited before the pandemic but will have their measurements during the pandemic.

3.7. Simulation‐study

For investigating the potential impact of the above outlined intercurrent events on the power of the ongoing clinical trial, we designed a simulation study, where the magnitude of the impact of the intercurrent event and the proportion of affected patients can be varied. In the following sections, the data generating model of our simulation study is outlined, followed by the detailed specification of the investigated scenarios and the analysis methods used for analyzing each simulated trial. The simulation study was conducted using the R programming language.

3.8. Simulation assumptions

For the simulation study, we assume the alternative hypothesis that the treatment is effective in reducing YGTSS‐TTS. We did not consider the null hypothesis, because under the assumed circumstances (ie, perfectly double‐blinded study and the intercurrent event being independent from treatment assignment), the presence of the intercurrent event only affects variance and does not increase type‐1‐error. In a real trial, these assumptions may be violated and the robustness toward such violation should be challenged by careful sensitivity analyses. However, for the purpose of this investigation, we found that the major interest could be on power.

Under the alternative hypothesis and in line with the sample size planning of CANNA‐TICS, we assume that the relative change, calculated as the difference between the YGTSS‐TTS measured at week 13 and baseline divided by the baseline score, follows different normal distributions in the treatment groups. For patients receiving placebo we assume that the change follows a normal distribution with mean −0.025 and standard deviation of 0.12, whereas for patients receiving nabiximols a mean of −0.16 and a standard deviation of 0.25 is assumed (see Figure 1A). These assumptions were used to derive the planning assumptions of the CANNA‐TICS study, and are based on a previous trial, in which 24 patients with TS or CTD had been randomized to 6 weeks of THC or placebo medication in a 1:1 ratio (drop‐out rate 17%: THC n = 3 drop‐outs, placebo n = 1 drop‐out). ²¹ In light of the small sample size of 24 patients, the assumption of a normally distributed change in YGTSS‐TTS was considered more robust than simply assuming responder probabilities based on the observed responder proportions. Based on these assumptions, the expected responder proportions can be calculated from the normal distributions (and correspond to the area under the respective normal curves left from the vertical −30% threshold as indicated in Figure 1A) as 1% in the placebo group and 29% in the nabiximols group. Simplifying the clinical trial setting, we do not consider missing data in our simulation and we assume an envisaged sample size of 75 patients to achieve a 90% power to show a difference between treatment groups regarding the responder criterion. Further, we assume that 10% of the patients are affected by the intercurrent events and that misclassification could take place, categorizing some patients to be affected, who are not, and vice versa. In line with the sample size calculation of the CANNA‐TICS trial, we omit center as a factor.

FIGURE 1.

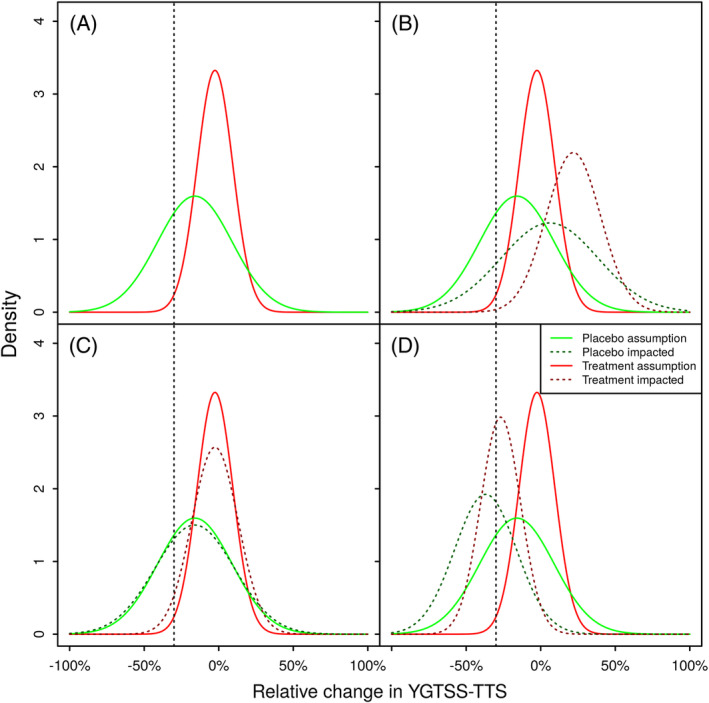
Potential impacts of the intercurrent event on the distribution of relative change in YGTSS‐TTS from 13 weeks. Panel (A) depicts the planning assumptions for the relative change in YGTSS‐TTS, corresponding expected response rates are 1% for the Placebo group and 29% for the Treatment group. Panel (B) exemplifies scenario (i) leading to an increase at the YGTSS‐TTS at the second visit, and a decrease in the expected response rates to 0% for the Placebo group and 14% for the Treatment group. Panel (C) exemplifies scenario (ii) introducing additional variability, but not changing the expected YGTSS‐TTS. Due to in increased variability, the expected response rates increase to 4% for the Placebo group and 30% for the Treatment group. Panel (D) exemplifies scenario (iii) leading to a decrease of the YGTSS‐TTS at the second visit, and an increase in the expected response rates to 41% for the Placebo group and 62% for the Treatment group

3.9. Data generating model

For a fixed sample size n = 75 and fixed proportions of patients affected by the intercurrent events p _affected , the number of patients (not) affected was calculated as

$$n_{\mathit{\text{unaffected}}}=\mathit{\text{round}}\left(n*\left(1-p_{\mathit{\text{affected}}}\right)\right)\text{and}{n}_{\mathit{\text{affected}}}=n-n_{\mathit{\text{unaffected}}}.$$

The variable ${\mathit{\text{affected}}}_i=\left\{\begin{array}{c}0\mathrm{i}\in \left\{1,\dots ,n_{\mathit{\text{unaffected}}}\right\}\\ 1\mathrm{i}\in \left\{n_{\mathit{\text{unaffected}}}+1,\dots ,n\right\}\end{array}\right.$ denotes whether a patient is affected by the intercurrent event in question. This approach was preferred to simulating the variable affected _i as a Bernoulli variable with success probability p _affected to reflect the clinical trial setting, where we assume that the proportion of affected patients (or at least an upper bound) can be estimated based on the start of the pandemic with sufficient precision, and thus avoid an (unnecessary) source of additional variability.

The treatment allocation treat _i  ∼ Ber(p _treat ) for each patient i ∈ {1, …, n} was simulated as Bernoulli distributed variables with fixed probability $p_{\mathit{\text{treat}}}=\frac{2}{3}$ to receive the active treatment. This approach simplifies the stratified block‐randomization used for the CANNA‐TICS trial. For each patient, a baseline value Y _0,i  ∼ N(25, 6.5)_[14,50] from a truncated normal distribution was simulated. ²² Here, the lower boundary of 14 is a simplification of the inclusion criteria requiring a score of at least 14 for patients with TS and 10 for those with CTD and the upper boundary of 50 reflects the maximal value of the YGTSS‐TTS. Based on previous data, for patients receiving placebo and nabiximols treatment the relative change from baseline to week 13 was assumed to be approximately normal distributed with

$${\mathit{\text{change}}}_i{\left|{\hspace{0.17em}}_{{\mathit{\text{treat}}}_i=0}=\frac{Y_{1,i}-Y_{0,i}}{Y_{0,i}}\right|}_{{\mathit{\text{treat}}}_i=0}~N\left(-0.025,0.12\right)$$

for placebo patients, and

$${\mathit{\text{change}}}_i{\left|{\hspace{0.17em}}_{{\mathit{\text{treat}}}_i=1}=\frac{Y_{1,i}-Y_{0,i}}{Y_{0,i}}\right|}_{{\mathit{\text{treat}}}_i=1}~N\left(-0.16,0.25\right)$$

for patients treated with nabiximols. From these, the underlying, potentially unobserved YGTSS‐TTS scores after 13 weeks, unaffected by intercurrent events, were calculated as

$$Y_{1,i}=Y_{0,i}+{\mathit{\text{change}}}_i*Y_{0,i}=Y_{0,i}+\frac{Y_{1,i}-Y_{0,i}}{Y_{0,i}}*Y_{0,i.}.$$

For modeling the impact of the intercurrent event on the score at week 13, we decided on a multiplicative effect influencing the score that would have been observed in absence of the intercurrent event. Additionally, we assume that the intercurrent event affects the patients' outcomes heterogeneously (eg, patients living alone being differently affected by social distancing as compared to patients not living alone). Therefore, a random factor from a normal distribution truncated at 0 and 2 was simulated for each patient, C _i  ∼ N(μ, σ)_(0,2) with pre‐defined mean μ and standard deviation σ .

Using this factor, the observed scores were calculated as $Y_{1,i}^{*}=Y_{1,i}*{\left(C_i\right)}^{{\mathit{\text{affected}}}_i}$, making sure that for unaffected patients, the observed score equals the underlying score. Here, μ > 1 indicates an increase in $Y_{1,i}^{*}$ in expectation, whereas μ < 1 corresponds to a decrease in $Y_{1,i}^{*}$ in expectation. In contrast, μ = 1 does not change the expectation of $Y_{1,i}^{*}$, but influences the variability. This increases the variance of $Y_{1,i}^{*}$, which in turn influences the expectation of the dichotomized responder criterion as we shall see in the subsequent section. Based on the observed value $Y_{1,i}^{*}$, the observed relative change is calculated as ${\mathit{\text{change}}}_i^{*}=\frac{Y_{1,i}^{*}-Y_{0,i}}{Y_{0,i}}$, and the responder criterion is calculated as

$${\mathit{\text{responder}}}_i=\left\{\begin{array}{c}0{\mathit{\text{change}}}_i^{*}<0.3\\ 1{\mathit{\text{change}}}_i^{*}\ge 0.3\end{array}\right.$$

To assess the robustness of our simulations, we explored a range of similar models, including an additive effect of the intercurrent events on the observed YGTSS‐TTS scores (see Appendix A in Data S1). In a real clinical trial setting, the exact onset date of the COVID‐19 pandemic could be difficult/impossible to define correctly for each center as official measures might have been implemented gradually by local authorities, public debates about planned official measures might have had an effect prior to implementation. This could result in misclassification in defining affected and unaffected patients. For modeling this uncertainty, and increasing the applicability of the simulation study findings to settings, where misclassification can occur, also misclassification of patients was considered (see Appendix B in Data S1).

3.10. Simulation scenarios

Three different scenarios of interest are investigated to reflect

1. the intercurrent event leading to an expected increase in the YGTTS‐TTS in affected patients as motivated by intercurrent event (1), for example, modeling a worsening of the disease due to public health measures (see Figure 1B),

2. the intercurrent event not changing the expected value of the YGTTS‐TTS in affected patients, but increasing the variability, for example, modeling a change in measurement methods and replacing the standard method by a less precise method (see Figure 1C), and

3. the intercurrent event leading to an expected decrease in the YGTTS‐TTS in affected patients as motivated by intercurrent event (2), for example, modeling a change in measurement methods and replacing the standard method by a less sensitive method (see Figure 1D).

To illustrate the effect of the intercurrent events on the distribution of the relative change in affected patients, Figure 1 compares for all three scenarios the distributions for the unaffected relative change change _i |treat _i = 0 and change _i |treat _i = 1 for both treatment groups, and the distribution of the relative change affected by the intercurrent event ${\mathit{\text{change}}}_i^{*}\left|{\mathit{\text{treat}}}_i=0\right.$ and ${\mathit{\text{change}}}_i^{*}\left|{\mathit{\text{treat}}}_i=1\right.$. Panel B reflects scenario (i), where C _i  ∼ N(1.25, 0.1) leads to an increase in the expected YGTSS‐TTS at week 13/13 weeks, shifting the distributions to the right and increasing the variance, which leads to (unequally) decreased response rate as compared to the original assumption. Notably, the response rate in the placebo group decreases less than the nabiximols response rate as compared to the planning assumptions, decreasing the true difference between treatment groups. In contrast, Panel C reflects scenario (ii), where C _i  ∼ N(1, 0.1) leads to an increase in the variance of the relative change, increasing the mass of the distributions on the left of the responder threshold, which leads to (unequally) increased response rates as compared to the original assumption. Notably, the placebo response rate increases more than the nabiximols response rate, decreasing the difference between treatment groups. Panel D reflects scenario (iii), where C _i  ∼ N(0.75, 0.1) leads to a decrease in the expected YGTSS‐TTS at week 13/13 weeks, shifting the distributions to the left and increasing the variance, which leads to (unequally) increased response rates as compared to the original assumption.

Notably, in all scenarios, the difference in expected response rates based on the affected distributions between treatment groups decreases as compared to the unaffected scenario, where the difference is 29% − 1% = 28%. However, this does not necessarily translate into a decrease in power as the variance of a binary variable is highest for the success probability of 0.5 and decreases approaching the limits of 1 and 0. Hence, in scenario (iii), we expect a decrease in power for comparing the groups regarding the responder criterion due to a decrease in difference between treatment groups and both response rates approaching 0.5. Regarding the continuous relative change, the resulting distribution in the trial will be a mixture of the original and shifted distributions for the respective treatment groups, which increases the variance. Resulting means and variances will be determined partly by the distribution of C _i , and partly by the proportion of affected patients (eg, the weight of the shifted distribution in the mixture).

For a detailed investigation of the impact of the intercurrent event, these scenarios were translated into the data‐generating model using the model parameter specifications outlined in the above section and referenced in Tables 1 and 2. Different settings were simulated varying the proportion of affected patients and the distribution of the factor affecting the YGTSS‐TTS measured after 13 weeks. For each parameter combination, 10,000 trials were simulated and analyzed. The number of simulation runs was chosen to achieve a standard error for the estimated empirical power of at most 0.005, resulting in a half‐width of the 95% confidence interval of at most 0.01.

TABLE 1.

Empirical power for responder analysis

		Empirical responder proportion (SE)		Empirical Power original a (SE)		Empirical Power updated b (SE)				Bias of (SE)
Distribution of C i	$p_{{\mathit{\text{affected}}}^{\#}}$ c	Placebo	Active	Fisher's exact test	Chi2 test	Fisher's exact test	Chi2 test	CMH d test	Exact CMH d test	CMH pooled risk difference
N(0.75, 0.1)[0,2]	0.1	0.049 (0)	0.321 (0.001)	0.912 (0.003)	0.947 (0.002)	0.783 (0.004)	0.835 (0.004)	0.885 (0.003)	0.842 (0.004)	0 (0)
	0.2	0.094 (0.001)	0.359 (0.001)	0.911 (0.003)	0.943 (0.002)	0.675 (0.005)	0.731 (0.004)	0.802 (0.004)	0.751 (0.004)	0 (0)
N(0.9, 0.1)[0,2]	0.1	0.02 (0)	0.3 (0.001)	0.913 (0.003)	0.946 (0.002)	0.889 (0.003)	0.927 (0.003)	0.924 (0.003)	0.892 (0.003)	−0.001 (0)
	0.2	0.03 (0)	0.314 (0.001)	0.911 (0.003)	0.947 (0.002)	0.864 (0.003)	0.907 (0.003)	0.907 (0.003)	0.873 (0.003)	0 (0)
N(1, 0.1)[0,2]	0.1	0.013 (0)	0.29 (0.001)	0.91 (0.003)	0.948 (0.002)	0.901 (0.003)	0.94 (0.002)	0.935 (0.002)	0.898 (0.003)	0 (0)
	0.2	0.015 (0)	0.29 (0.001)	0.911 (0.003)	0.946 (0.002)	0.893 (0.003)	0.933 (0.002)	0.927 (0.003)	0.891 (0.003)	0 (0)
N(1.1, 0.1)[0,2]	0.1	0.01 (0)	0.28 (0.001)	0.91 (0.003)	0.945 (0.002)	0.904 (0.003)	0.939 (0.002)	0.933 (0.002)	0.902 (0.003)	0.001 (0)
	0.2	0.011 (0)	0.275 (0.001)	0.912 (0.003)	0.947 (0.002)	0.888 (0.003)	0.933 (0.002)	0.925 (0.003)	0.887 (0.003)	0.001 (0)
N(1.25, 0.1)[0,2]	0.1	0.01 (0)	0.274 (0.001)	0.913 (0.003)	0.948 (0.002)	0.891 (0.003)	0.934 (0.002)	0.928 (0.003)	0.891 (0.003)	0.001 (0)
	0.2	0.009 (0)	0.258 (0.001)	0.913 (0.003)	0.948 (0.002)	0.858 (0.003)	0.912 (0.003)	0.91 (0.003)	0.864 (0.003)	0.001 (0)
N(1.5, 0.1)[0,2]	0.1	0.01 (0)	0.268 (0.001)	0.911 (0.003)	0.946 (0.002)	0.878 (0.003)	0.924 (0.003)	0.922 (0.003)	0.88 (0.003)	0.003 (0)
	0.2	0.009 (0)	0.245 (0.001)	0.914 (0.003)	0.949 (0.002)	0.826 (0.004)	0.892 (0.003)	0.891 (0.003)	0.842 (0.004)	0.002 (0)

Note: Assumed distribution without COVID‐19 impact: ${\mathit{\text{change}}}_i{\left|{\hspace{0.17em}}_{{\mathit{\text{treat}}}_i=0}~N\left(-0.025,0.12\right),{\mathit{\text{change}}}_i\right|}_{{\mathit{\text{treat}}}_i=1}~N\left(-0.16,0.25\right)$. Baseline distribution: Y _0,i ~N(25, 6.5)_[14,50] . Corresponding expected responder proportions, placebo group: 1%, treatment group: 29%. Monte‐Carlo Standard Errors, estimated proportions and estimated bias are rounded to 3 decimals.

^a responder as dependent variable.

^b responder ^* as dependent variable.

^c Fixed proportion of patients affected by the intercurrent event.

^d Cochran‐Mantel‐Haenszel test stratified for affected ^* .

TABLE 2.

Empirical power for continuous analysis of YGTSS‐TTS

		Empirical distributions of change *				Empirical Power (SE)			Bias (SE)
		Placebo group		Treatment group
Distribution of C i	p affected a	Mean (SE)	Standard deviation (SE)	Mean (SE)	Standard deviation (SE)	ANCOVA original b	ANCOVA updated c	ANCOVA c COVID‐19 factor d	ANCOVA c COVID‐19 factor d
N(0.75, 0.1)[0.2]	0.1	−0.048 (0)	0.139 (0)	−0.18 (0)	0.252 (0)	0.734 (0.004)	0.673 (0.005)	0.713 (0.005)	0 (0)
	0.2	−0.073 (0)	0.156 (0)	−0.202 (0)	0.255 (0)	0.731 (0.004)	0.623 (0.005)	0.697 (0.005)	0 (0)
N(0.9, 0.1)[0,2]	0.1	−0.034 (0)	0.125 (0)	−0.168 (0)	0.249 (0)	0.731 (0.004)	0.714 (0.005)	0.714 (0.005)	0 (0)
	0.2	−0.044 (0)	0.13 (0)	−0.177 (0)	0.249 (0)	0.733 (0.004)	0.698 (0.005)	0.705 (0.005)	0 (0)
N(1, 0.1)[0,2]	0.1	−0.025 (0)	0.123 (0)	−0.16 (0)	0.25 (0)	0.733 (0.004)	0.724 (0.004)	0.72 (0.004)	0 (0)
	0.2	−0.025 (0)	0.126 (0)	−0.16 (0)	0.251 (0)	0.731 (0.004)	0.716 (0.005)	0.709 (0.005)	0 (0)
N(1.1, 0.1)[0,2]	0.1	−0.016 (0)	0.127 (0)	−0.152 (0)	0.253 (0)	0.731 (0.004)	0.713 (0.005)	0.715 (0.005)	0 (0)
	0.2	−0.006 (0)	0.134 (0)	−0.143 (0)	0.259 (0)	0.734 (0.004)	0.695 (0.005)	0.706 (0.005)	0 (0)
N(1.25, 0.1)[0,2]	0.1	−0.002 (0)	0.143 (0)	−0.141 (0)	0.264 (0)	0.738 (0.004)	0.682 (0.005)	0.724 (0.004)	0 (0)
	0.2	0.024 (0)	0.163 (0)	−0.118 (0)	0.277 (0)	0.731 (0.004)	0.641 (0.005)	0.705 (0.005)	0 (0)
N(1.5, 0.1)[0,2]	0.1	0.021 (0)	0.188 (0)	−0.121 (0)	0.29 (0)	0.733 (0.004)	0.569 (0.005)	0.71 (0.005)	0 (0)
	0.2	0.072 (0)	0.238 (0)	−0.076 (0)	0.327 (0)	0.735 (0.004)	0.491 (0.005)	0.695 (0.005)	0 (0)

Note: Assumed distribution without COVID‐19 impact: ${\mathit{\text{change}}}_i{\left|{\hspace{0.17em}}_{{\mathit{\text{treat}}}_i=0}~N\left(-0.025,0.12\right),{\mathit{\text{change}}}_i\right|}_{{\mathit{\text{treat}}}_i=1}~N\left(-0.16,0.25\right)$. Baseline distribution: Y _0,i ~N(25, 6.5)_[14,50] . Corresponding expected responder proportions, placebo group: 1%, treatment group: 29%. Monte‐Carlo Standard Errors, estimated proportions and estimated bias are rounded to 3 decimals.

^a Fixed proportion of patients affected by the intercurrent event.

^b change as dependent variable, adjusted for baseline YGTSS‐TTS.

^c Change*as dependent variable, adjusted for baseline YGTSS‐TTS.

^d Change* as dependent variable, adjusted: Adjusted for affected ^* and baseline YGTSS‐TTS.

3.11. Trial analysis and performance criteria

The data from the simulated trials were analyzed both using the primary responder criterion and the continuous change in YGTSS‐TTS potentially influenced by the occurrence of the intercurrent event, to investigate the impact of the intercurrent events on the power of the trial under the planning assumptions. For the binary responder endpoint, Fisher's exact test (via R function fisher.test) and a Chi² test without continuity correction were used (via R function chisq.test). For the continuous change in YGTSS‐TTS, an ANCOVA model with change in YGTSS‐TTS from baseline ${\mathit{\text{change}}}_i^{*}$ as dependent variable is applied as an estimator (via R function aov) with treatment treat _i and baseline YGTSS‐TTS Y _0,i as independent variables.

As in practice analyses might be considered that adjust for the presence of the intercurrent event by including a respective factor, also a stratified Cochran‐Mantel‐Haenszel test without continuity correction, an exact Cochran‐Mantel‐Haenszel test (via R function mantelhaen.test) incorporating the binary variable encoding the occurrence of the intercurrent event, affected ^* , and an ANCOVA model (via R function aov) with the additional binary variable affected ^* included as independent variable, are applied as additional estimators. For the stratified analysis, the pooled risk difference was estimated using the Cochran‐Mantel‐Haenszel estimator. ²³

It should be noted, that for the responder criterion, stratified analyses do not necessarily address the originally intended treatment policy estimand anymore. While Permutt argues that for continuous outcome analyses via analysis of covariance methods adjusting for covariates does not change the target of estimation, ²⁴ for binary variables the marginal effect does not necessarily equal the (weighted sum of the) conditional effects within the strata. ²⁵ In case risk differences are truly heterogeneous between strata, the weighted sum of the conditional risk differences equals the marginal risk difference only if the weights of the effect in each stratum equal the proportion of patients within the respective stratum. Since the intercurrent event could be interpreted as a covariate, as it is unaffected by treatment allocation in our data generating mechanism and corresponds directly to the recruitment time, which is measurable at baseline, in this situation adjusting the continuous analysis indeed does not change the estimand. Please note that this does not hold generally, if the occurrence of the intercurrent event is associated with treatment allocation.

For estimating the empirical power initially envisaged in absence of the intercurrent events, the underlying trial data not influenced by the intercurrent event, change _i and responder _i calculated based on change _i , are used.

Based on the simulated trials and the results of the analysis models, the empirical responder proportions and the empirical distributions of the relative change in both treatment arms were calculated. Additionally, the empirical power was calculated as the proportion of simulations, where the respective two‐sided P‐value of the overall treatment effect in the analysis model was smaller than 5%, suggesting superiority of the experimental treatment over control. For all aforementioned variables, respective Monte‐Carlo standard errors were calculated. Since misclassification can bias the estimates for the analyses adjusted for affected ^* , for these estimators only also bias (as compared to the estimated marginal risk difference) and root mean squared error together with Monte Carlo standard errors are calculated. ²⁶

4. RESULTS

The following sections display the results of the above‐described simulation study separately for the dichotomized responder criterion and for the analysis of the change in YGTSS‐TTS as a continuous endpoint.

4.1. Dichotomized endpoint

The results of the simulation study for the dichotomized responder criterion show that the impact of the intercurrent events on the power depends on the magnitude of the effect of the intercurrent event on the YGTSS‐TTS measured at the second time point and on the proportion of affected patients (see Table 1). As could be expected, the simulated power using only the unaffected values for Fisher's exact test was circa 91% in all scenarios; the power of the Chi² test was slightly higher in all scenarios.

In general, both intercurrent events lead to a decrease in power in all investigated scenarios, increasing (the mean of C is larger than 1) or reducing (the mean of C is smaller than 1) the observed YGTSS‐TTS on average. This effect is more pronounced for larger proportions of affected patients. By introducing additional variability only without changing the YGTSS‐TTS in expectation (mean of C equals 1), the power of both Fisher's exact test and the Chi² test is slightly reduced for a scenario with 20% of the patients being affected. For scenarios with only 10% of the patients being affected, no relevant difference is observed.

Overall, for proportions of affected patients of 20%, the decrease in power was smaller than 12% as compared to the intended power. Moreover, in all but the extreme scenarios, the difference between actual power in presence of the intercurrent event and the intended power was smaller than 5%.

The observed responder proportions for both treatment groups in presence of the intercurrent event depend on the mean of the factor C. A mean smaller than 1 leads to higher responder proportions in both treatment groups, whereas and a mean larger than 1 leads to a decrease in responder proportions in both treatment groups.

Interestingly, for a reduced YGTSS‐TTS (if the mean of C is smaller than 1), the difference in proportions does not change substantially, but the increase in reference proportion leads to a power loss. On the other hand, for increased scores (if the mean of C is larger than 1), the difference in proportions diminishes, but the decrease in power is small since the reference proportions decreases. In the extreme scenario with a mean of 1.5 for C, the reference proportion is but 0.1% as compared to 1% in the underlying distribution, which compensates part of the power loss of a diminished difference in treatment groups of 23.5 percentage points as compared to 28 percentage points in the underlying distribution.

The effect of adjustment for the occurrence of the intercurrent event using a stratified Cochran‐Mantel‐Haenszel test on the power are heterogeneous:

1. If the expected YGTSS‐TTS is decreased, using the stratified analysis compensates for some of the power loss, but the intended power is not fully recovered.

2. If the variability is increased only, or the expected YGTSS‐TTS is increased, using the stratified analysis does not increase the power as compared to the unadjusted analysis.

Due to the low proportion and the small strata, the assumptions of the approximate tests are possibly not fulfilled, and an exact test might be of higher interest. Here, the stratified exact test shows a slightly higher power in the extreme scenarios, when the YGTSS‐TTS is strongly increased or reduced, and the proportion of affected patients is higher. For the CANNA‐TICS trial, where 10% of the patients were assumed to be affected, the power in the worst case using Fisher's exact test was still 79%. It is important to note that pooling the strata‐specific risk differences via the Cochran‐Mantel‐Haenszel estimator estimates the marginal risk difference with negligible bias.

For deciding about potential modifications of the ongoing trial and potentially increasing the sample size, the simulations results provide the basis for calculating the number of additional patients needed to recover the originally planned power. Based on the empirical responder proportions ${\widehat{p}}_{\mathit{\text{Placebo}}}$ and ${\widehat{p}}_{\mathit{\text{Active}}}$ for each scenario in Table 1, and assumed true responder proportions p _{Placebo, add} and p _{Active, add} of patients additionally recruited during the pandemic, the number of additional patients n _add can be calculated as follows. Using the initial sample size n , for any given number of additional patients n _add the expected responder proportions combining the original n patients and the additional n _add can be calculated as

$$p_{\mathit{\text{Active}},\mathit{\text{combined}}}=\frac{n*{\widehat{p}}_{\mathit{\text{Active}}}+n_{\mathit{add}}*p_{\mathit{\text{Active}},\mathit{add}}}{\left(n+n_{\mathit{add}}\right)}\text{and}$$

$$p_{\mathit{\text{Placebo}},\mathit{\text{combined}}}=\frac{n*{\widehat{p}}_{\mathit{\text{Placebo}}}+n_{\mathit{add}}*p_{\mathit{\text{Placebo}},\mathit{add}}}{\left(n+n_{\mathit{add}}\right)}$$

Taking into account the randomization ratio p _treat , for any given number of additional patients n _add the power of the extended trial can be calculated based on the statistical test of choice (eg, Fisher's exact test). Applying this to a range of potential additional sample sizes results in a graph n _add  → power(n _add ), from which the additional sample size to recover the original power (or another power of choice) can be derived (see Data S1). This approach does not account for slightly increased variance of the Binominal variable using the pooled responder proportions in contrast to the sum of two binomial variables. However we considered this negligible in the presented case. Alternatively, power could be calculated based on a simulation study, simulating the responder status from different binominal distributions for originally planned and additional patients.

This approach can be followed both (a) to derive the additional sample size for single scenarios (eg, C _i  ∼ N(0.9, 0.1)_[0,2]) or (b) to derive the additional sample size for a range of scenarios by first investigating each scenario separately and secondly choosing the maximum resulting sample size. Importantly, careful consideration is needed regarding the assumed responder proportions for the additional patients, which are recruited during the pandemic, and on the question, whether the newly recruited patients fundamentally differ from the patients recruited before the start of the pandemic.

4.2. Continuous endpoint

Similar to the dichotomized responder criterion, the results of the simulation study for the continuous change in YGTSS‐TTS show that the impact of the intercurrent events on the power depends on the magnitude of the effect of the intercurrent event on the YGTSS‐TTS measured at the second time point and on the proportion of affected patients (see Table 2). In all scenarios, the power of the ANCOVA analysis using the unaffected values change _i as dependent variable was circa 74%. Contrary to common conception, here the power using the dichotomized value is higher than using the continuous value, because unequal variances are simulated in the underlying distribution for change _i for both treatment groups. ²⁷

In general, both intercurrent events lead to a decrease in power in all investigated scenarios, increasing (if the mean of C is larger than 1) or reducing (if the mean of C is smaller than 1) the observed YGTSS‐TTS on average. This effect is more pronounced for larger proportions of affected patients. Also, by introducing additional variability only without changing the YGTSS‐TTS in expectation (mean of C equals 1), the power of the ANCOVA model is slightly reduced.

Overall, for proportions of affected patients of 20%, the largest decrease in power was 15% as compared to the intended power. However, in all but the extreme scenario where the expected YGTSS‐TTS score at the second visit is increased by a 1.5‐fold, the difference between actual power in presence of the intercurrent event and the intended power was smaller than 10%.

The observed distributions of relative change depend on the mean of the factor C, a mean smaller than 1 decreasing the means of both treatment groups, and a mean larger than 1 increasing the means of both treatment groups. Overall, the difference in means of the distributions between the treatment and control group does not change substantially. More importantly, however, the intercurrent event increases the standard deviation of both distributions, which leads to the decreased power. This effect is more pronounced if the intercurrent events lead to an increase in the expected YGTSS‐TTS.

The results of the effect of adjustment for the occurrence of the intercurrent event, that is, using the same ANCOVA model additionally adjusted for the presence of the intercurrent event, on the power depend on the impact of the intercurrent event:

1. If the expected YGTSS‐TTS is reduced or increased, using the additional covariate compensates for some of the power loss, but the intended power is not fully recovered.

2. If the variability is increased only, using the additional covariate slightly decreases the power as compared to the unadjusted analysis.

For the CANNA‐TICS trial, where 10% of the patients were assumed to be affected, in the worst scenario the power for secondarily analyzing the YGTSS‐TTS as a continuous variable using the unadjusted ANCOVA model is 58%, and 71% using the adjusted ANCOVA model. As expected, in our simulation study without an association between the treatment allocation and the occurrence of the intercurrent event, the adjusted estimator shows no bias in estimating the average treatment effect.

5. DISCUSSION

In this paper, we introduced the CANNA‐TICS trial as an example of how COVID‐19 related intercurrent events may affect an ongoing study. To quantify the effect of such intercurrent events on the power of the study, we conducted a simulation study varying the proportion of affected patients, both for a binary responder criterion and the underlying continuous variable. In the following, we discuss the implications of the results of the simulation study first for the CANNA‐TICS trial and then from a more general perspective. Thereafter, we discuss limitations of our approach and finally highlight our main conclusions.

5.1. The CANNA‐TICS trial

Interpreting the results of our simulation study in the light of the CANNA‐TICS trial, only simulation results using a proportion of affected patients of 10% are relevant. For this situation, the impact of the intercurrent events handled by a treatment policy strategy on the power are judged to be minor. Only in extreme scenarios, where the magnitude of the effect of the intercurrent event on the YGTSS‐TTS measured at the second visit is large, a notable decrease is observed. Still, due to the high original power, in these scenarios the power is judged to be sufficiently large. Additionally, any increase in sample size would add complexity to the interpretation of the study results. Patients (willing to be) recruited during the pandemic could differ systematically from patients previously recruited. In particular, it would not be obvious that the baseline scores of newly recruited patients (which would be impacted by the pandemic) were comparable to scores of patients recruited prior to the pandemic. Therefore, in the risk assessment for the CANNA‐TICS trial, weighting the decrease in power against the additional complexity inherent in an increase in sample size, it was decided not to modify the originally planned sample size and not to include additional patients to retain the originally planned power. However, at least for the intercurrent event of a change in YGTSS‐TTS assessment (from personal to video), post‐hoc studies for a within‐patient comparison of the assessment methods could be conducted to investigate the potential impact in more detail and to facilitate the interpretation of the results of the CANNA‐TICS trial. In case a hypothetical strategy instead of a treatment policy strategy were to be used, it would be even more important to investigate whether statistical methods used for estimating the hypothetical estimand are in line with the directly observed effect of video assessment as compared to personal assessment of YGTSS‐TTS.

5.2. General interpretation

In contrast to the CANNA‐TICS trial, where the proportion of affected patients was relatively low, in different clinical trial settings the power loss could be substantial, depending on the proportion and magnitude of the effects of the intercurrent events. In principle, by adjusting for being affected by the intercurrent event, the power loss could be diminished. However, caution is needed on several aspects. In practice it may be impossible to adjust/stratify for being affected by the pandemic. In the example of the CANNA‐TICS trial, for the change of assessment method, the occurrence of the intercurrent event could be directly observed. For other intercurrent events such as the introduction of social distancing measures by local state authorities, unambiguous definition might be more difficult and misclassification could take place. In these cases, the power gain by adjusting might be small or disappear entirely. Additionally, careful consideration is needed, as an adjusted estimator might not be a suitable estimator for the estimand applying a treatment policy strategy for handling COVID‐19 related intercurrent events, as it could be subject to bias or small sample issues. Here, the collapsibility of the effect measure needs to be taken into account. While for the risk difference, the marginal difference can be expressed as (any) weighted sum of the stratum‐specific risk differences under the assumption of a common true risk difference, this does not automatically hold for heterogeneous risk differences and depends on the weights. ²⁵ Since the intercurrent events typically truly modify the risk difference, as depicted in Figure 1, care is needed in combining the stratum‐specific risk differences when the marginal effect is targeted.

In general, it is important to note that the difference of the observed distribution of the continuous YGTSS‐TTS as compared to the assumed distribution in absence of the intercurrent events, and thus the differences between observed responder proportions do not represent a bias. By definition the observed proportions are an unbiased estimate of an estimand that applies a treatment policy strategy for the marginal effect. In contrast, it rather reflects the fact that the intercurrent event could not be considered at the planning stage.

The approach of the simulation study applied to the YGTSS‐TTS in patients with CTD and TS could be applied similarly in related situations. As trialists struggle to assess the impact of the COVID‐19 pandemic on their trials, and regulators discourage analyses that entail a risk of unblinding data, ² a simulation approach offers a relevant alternative. While in our example the literature on the YGTSS‐TSS did not allow us to select a priori between scenarios (i), (ii), and (iii), more evidence may be or soon become available for other outcome measurement tools, allowing to limit the range of credible scenarios and draw more specific conclusions.

Our specific approach is particularly relevant where a responder criterion is used. In trials for disorders of the central nervous system, dichotomizing the outcome based on relative reduction from baseline is often seen as a way to identify patients whose condition substantially improves during a clinical trial. This is endorsed in several regulatory guidelines. ²⁸ , ²⁹ , ³⁰ For the YGTSS‐TTS specifically, dichotomization around relative values for the decrease close to/similar to the one chosen for this study have been demonstrated to optimally correlate with a positive response on the clinician‐rated Clinical Global Impression. ²²

Furthermore, the outlined approach could also be followed for sample size calculations at the study planning stage for taking expected intercurrent events and the planned strategies for handling directly into account, or as a basis for sample‐size re‐estimations.

Kunz et al. ⁵ discuss early stopping as one option for handling trials potentially affected by the COVID‐19 pandemic that are far advanced in the recruitment and follow‐up of patients. While this could be considered if only a hypothetical strategy for handling all COVID‐19 related intercurrent events was of interest, careful consideration is needed if also a treatment policy strategy was of interest for at least some of the relevant COVID‐19 related intercurrent events, as in the example presented above.

5.3. Limitations

As with most simulation studies, there is an identification‐generalization trade‐off. To allow modeling and better identification of the effect of the occurrence of the intercurrent events on the power, a number of simplifications and assumptions were made for the simulation study, which affect the generalizability of the findings. While the simplifications were plausible for the clinical context of the CANNA‐TICS trial, this cannot automatically be assumed for different clinical settings.

It is important to note that in this simulation study, the effects of the two investigated intercurrent effects were considered separately to allow an unambiguous interpretation of the simulation results, while in practice, both effects could occur simultaneously.

In our example, we simplified the clinical situation by assuming that all patients had been recruited, but the primary endpoint was not assessed for some of the patients. In ongoing clinical trials, this situation will often be more complex, as also new patients are recruited during the pandemic. For those patients, both baseline value and primary endpoint would be affected (but not necessarily in the same way), which would add another level of complexity. In principle, the same approach as outlined in this paper could be applied to investigate potential impacts on the power of the trial, by using different distributions for patients recruited before and during the pandemic.

Additionally, we decided to use a multiplicative model for the impact of the intercurrent event, reflecting one plausible scenario, where the potential impact depends on the patient's YGTSS‐TTS score. The robustness of the results was checked using an additive model (see Data S1). However, in a different clinical context, a different model could be more plausible and the results of this paper would need to be applied with caution.

The occurrence of the investigated intercurrent events were assumed to be independent from the treatment allocation, patient characteristics and post‐baseline measurements, and the results cannot automatically be extrapolated to situations, where the occurrence of the intercurrent event is correlated with the treatment assignment, post‐baseline measurements or patient characteristics. While this assumption can be reasonably made for the pandemic‐related intercurrent events (at least for trials with constant randomization ratio), it likely does not hold in general and caution is needed in extrapolating the findings of this article.

Additionally, for the simulation study, we assumed no missing data to simplify the interpretation. Taken together, under these assumptions, type‐I‐error rate inflation and biased estimation of the treatment policy estimand would not occur using the un‐stratified Chi² test and Fisher's test for the responder criterion or the ANCOVA model adjusted for baseline for the continuous endpoint, and consequently the focus of our simulation study was on power only.

In this simulation study, the intercurrent events have been handled using a treatment policy strategy. Depending on the intercurrent events in other clinical scenarios and the scientific question of interest, a different strategy, for example, a hypothetical strategy, ⁴ could be of primary interest. The COVID‐19 pandemic‐related intercurrent events might also affect or necessitate changes to other attributes of the estimands, as outlined by Degtyarev et al. ⁸ with special focus on oncology. An extensive risk assessment should incorporate all estimands attributes in the considerations.

6. CONCLUSIONS

The COVID‐19 pandemic impacts ongoing clinical trials in manifold ways. Drug regulatory agencies and public health bodies were quick to respond by issuing guidance documents reflecting on the statistical considerations for ongoing clinical trials. As one of the most important aspects, a risk assessment was recommended to investigate impacts of the pandemic on the ongoing trial before deciding on potential follow‐up actions. As an exemplary approach to conduct a risk assessment without unplanned data analyses, in this article, we discussed an example of how COVID‐19 related intercurrent events may affect the power of an ongoing study and quantified the potential impact using a simulation study as a pre‐requisite for potential sample size increases. Our simulation study based on the YGTSS‐TTS used for defining the primary endpoint in the CANNA‐TICS trial shows that substantial power losses are possible, potentially making sample size increases necessary to retain sufficient power. On the other hand, we identified situations where the power loss is small. In these situations, it should be carefully evaluated, whether the increase in complexity by recruiting additional patients, which would as well be affected by the pandemic and thus could differ systematically from the patients recruited prior, would be justified.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

AUTHOR CONTRIBUTIONS

Florian Lasch: Conceptualization, Methodology, Software, Formal analysis, Writing ‐ Original Draft. Lorenzo Guizzaro: Writing ‐ Review & Editing, Lukas Aguirre Dávila: Writing ‐ Review & Editing. Kirsten R Müller‐Vahl: Writing ‐ Review & Editing. Armin Koch: Writing ‐ Review & Editing.

DISCLAIMER

The views expressed in this article are the personal views of the authors and may not be understood or quoted as being made on behalf of or reflecting the position of the agencies or organizations with which the authors are affiliated.

Supporting information

DATA S1 Supporting information

Lasch F, Guizzaro L, Aguirre Dávila L, Müller‐Vahl K, Koch A. Potential impact of COVID‐19 on ongoing clinical trials: a simulation study with the neurological Yale Global Tic Severity Scale based on the CANNA‐TICS study. Pharmaceutical Statistics. 2021;20:675–691. 10.1002/pst.2100

DATA AVAILABILITY STATEMENT

The simulation code that support the findings of this study is available from the corresponding author upon reasonable request.