Marginal Mark Regression Analysis of Recurrent Marked Point Process Data

Summary.

Longitudinal studies typically collect information on the timing of key clinical events and on specific characteristics that describe those events. Random variables that measure qualitative or quantitative aspects associated with the occurrence of an event are known as marks. Recurrent marked point process data consist of possibly recurrent events, with the mark (and possibly exposure) measured if and only if an event occurs. Analysis choices depend on which aspect of the data is of primary scientific interest. First, factors that influence the occurrence or timing of the event may be characterized using recurrent event analysis methods. Second, if there is more than one event per subject, then the association between exposure and the mark may be quantified using repeated measures regression methods. We detail assumptions required of any time-dependent exposure process and the event time process to ensure that linear or generalized linear mixed models and generalized estimating equations provide valid estimates. We provide theoretical and empirical evidence that if these conditions are not satisfied, then an independence estimating equation should be used for consistent estimation of association. We conclude with the recommendation that analysts carefully explore both the exposure and event time processes prior to implementing a repeated measures analysis of recurrent marked point process data.

1. Introduction

A point process may be defined as a random system of events that occur in space and time (Cox and Isham, 1980). Specific examples include a Poisson process, a Markov process, and a marked point process. Historically, the study of point processes developed from renewal theory; application focused on life tables (Daley and Vere-Jones, 2002). Recent applications include telecommunications, image analysis, and stereology. Modern theoretical research of marked point processes has centered on model construction via a conditional intensity. Current methodological research focuses on testing the underlying assumptions of a marked point process, such as independence (Guan, 2006) and separability (Schoenberg, 2004).

Longitudinal marked point process data consist of possibly recurrent events, with the outcome (or mark) and possibly exposure measured only when an event occurs. These types of data are common in the current biomedical literature. Examples include determining the effect of patient characteristics on total cost following hospitalization for pediatric injury (Yang et al., 2007) and evaluating the effect of surgeon experience on patient mortality following coronary artery bypass graft (Glance et al., 2005). In our motivating example the recurrent event is a live birth and the relationship between maternal exposures such as cigarette smoking and infant characteristics such as birth weight is of primary scientific interest (Hardy, 2003).

The defining characteristic of recurrent marked point process data is that the outcome exists if and only if an event occurs. For example, birth weight exists if and only if a birth occurs. In a traditional repeated measures analysis the times at which exposure and outcome are measured are usually specified in advance by the study protocol and often comprise a limited number of equally spaced observation times common to all participants. This conventional design assumes that each subject has a potential measurement at each observation time, although attrition may lead to missing data. In a marked point process setting measurement times are not specified in advance and may vary substantially between subjects. In addition, subjects may not have more than one observation time and the outcome is not defined for subjects who do not experience an event. A secondary characteristic is that a time-dependent exposure of interest may be either available throughout follow-up or collected if and only if an event occurs.

There are several features of longitudinal marked point process data that present interesting challenges. First, correlation may be induced within subjects by repeatedly collecting information on the same subjects over time. This requires application of appropriate longitudinal data analysis methods, which account for within-subject dependence. Second, endogeneity may exist between past outcomes and current exposure. For example, giving birth to an infant with low birth weight may cause a mother to cease cigarette smoking. Third, endogeneity may exist between past outcomes and occurrence of a subsequent event. For example, a mother may reconsider or delay a future pregnancy if she gave birth to a low birth weight infant. Ignoring these endogenous processes may lead to spurious conclusions (Louis et al., 2006). Therefore, analysts must consider these relationships prior to implementing an analysis of recurrent marked point process data.

The seminal work of Liang and Zeger (1986) introduced estimating equations as a general method to obtain inference from either continuous or discrete longitudinal data. Their generalized estimating equation (GEE) approach adopts a semiparametric model by specifying only the marginal mean and covariance of repeated measurements. A complete multivariate probability model is not uniquely identified and therefore a likelihood function is not available. Semiparametric methods are attractive because estimates of regression coefficients and standard errors are valid under minimal model assumptions.

An estimator for the effect of a time-independent exposure obtained via a GEE is consistent regardless of the assumed covariance structure (Liang and Zeger, 1986). However, care is required when evaluating the effect of a time-dependent exposure and attention must be given to factors that lead to inclusion or exclusion of observations (Pepe and Anderson, 1994; Pan, Louis, and Connett, 2000). Pepe and Anderson commented that an independence estimating equation (IEE) is assured to provide a consistent estimate of the marginal regression coefficient for a time-dependent exposure. However, a covariance-weighted estimating equation or linear mixed model (LMM) analysis requires an additional assumption regarding the association between current outcome and past, current, and future exposure. Substantial bias may result if this assumption is not satisfied and a nonindependence working covariance structure is used (Diggle et al., 2002). Furthermore, endogenous exposures may require specialized causal methods if cross-sectional associations are not of interest.

A large amount of literature exists that discusses missing data for predetermined observation times (Little and Rubin, 2002). Recent research has focused on mechanisms that influence observing data, i.e., a stochastic measurement process that determines if and when outcomes are to be recorded (Lipsitz et al., 2002; Lin, Scharfstein, and Rosenheck, 2004; Fitzmaurice et al., 2006; Sun, Tong, and He, 2007). The statistical issue is similar between the “missing data” and “observing data” setting and essentially reduces to an assumption regarding ignorable missing data mechanisms. In these situations an IEE may provide biased estimates, whereas a properly specified likelihood analysis is valid. Taken together these examples illustrate that situation-specific assumptions determine whether simple unweighted methods are appropriate, or whether more elaborate likelihood-based methods are required.

In this article, we consider situations in which the primary target of inference is a marginal mean regression model that quantifies the association between a time-dependent exposure and an outcome of interest among individuals who experience an event. Our goal is to articulate the assumptions required for consistent marginal regression analysis of recurrent marked point process data. We detail conditions required of the exposure and event time processes to ensure that commonly used repeated measures regression methods such as LMMs and GEEs provide valid cross-sectional estimation. We relax these assumptions so that they can be evaluated whether exposure is available throughout follow-up or collected if and only if an event occurs. In addition, we explore the potential for bias if these conditions are not satisfied.

In Section 2, we motivate and detail requisite assumptions for generating valid inference from recurrent marked point process data. In Section 3, we evaluate via simulation the potential for bias if these assumptions are not satisfied. In Section 4, we describe a motivating example, the Collaborative Perinatal Project (Hardy, 2003), and illustrate an analysis of recurrent marked point process data. The analysis goal is to quantify the effect of maternal cigarette smoking on infant birth weight. We provide concluding discussion in Section 5. In the Appendix, we weaken the assumption of “joint exogeneity” required by the assumptions in Section 2.

2. Statistical Methods

We assume that an outcome exists if and only if an event occurs and therefore limit our focus to observations collected in discrete time. However, it is straightforward to generalize the model to allow continuous times (Lipsitz et al., 2002; Tsiatis and Davidian, 2004).

2.1. Notation

Let X_i (t) and Y_i (t) denote the exposure and outcome, respectively, observed for independent subjects i = 1, … , n at discrete calendar times t = 1, … , T. Note that T represents the end of follow-up. Similarly let N_i (t) denote the total number of events for subject i through time t. We use the following notation to denote the complete history of each variable ascertained retrospectively at time $t:{\mathcal{X}}_i(t)=\left\{X_i(s)|s\le t\right\}$, ${\mathcal{N}}_i(t)=\left\{N_i(s)|s\le t\right\}$, and ${\mathcal{Y}}_i(t)=\left\{Y_i(s)|s\le t\right\}$. In addition we use the notation dN_i (t) = N_i (t) − N_i (t − 1) such that dN_i (t) = 1 indicates an event at time t.

2.2. Framework

We adopt assumptions regarding time ordering to characterize the underlying biological process for X_i (t), N_i (t), and Y_i (t). Specifically, we assume that X_i (t) ≺ N_i (t) ≺ Y_i (t), where ≺ denotes time ordering (Tsiatis and Davidian, 2004). Figure 1 presents the underlying framework for recurrent marked point process data for a single subject i (Louis et al., 2006). The process X_i (t) depicts a quantitative time-dependent exposure of interest and the process N_i (t) depicts the total number of events through time t. Note that Y_i (t) is observed only when N_i (t) increases, which indicates an event.

Figure 1.

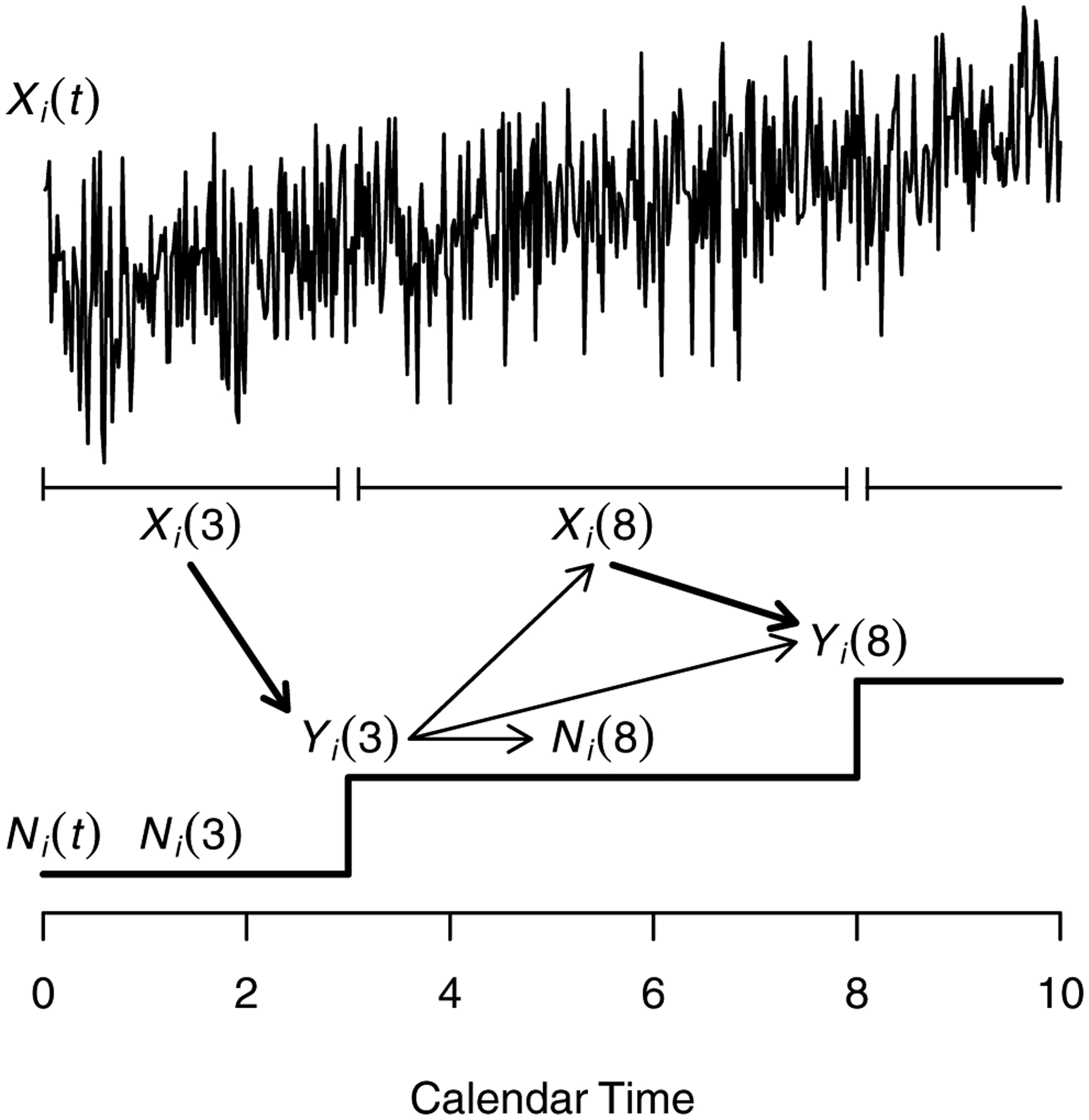
Underlying framework for recurrent marked point process data.

In Figure 1, the relationships X_i (3) → Y_i (3) and X_i (8) → Y_i (8) represent the cross-sectional association of interest. Other relationships represented in Figure 1 may bias estimation of this association or its significance. First, the relationship Y_i (3) → Y_i (8) represents the correlation that may be induced between observations collected on the same subject. Second, the relationship Y_i (3) → X_i (8) represents the endogeneity that may exist between past outcomes and current exposure. Third, the relationship Y_i (3) → N_i (8) represents the endogeneity that may exist between past outcomes and occurrence of a subsequent event.

2.3. Target of Inference

For regression modeling of longitudinal data with a time-dependent exposure, the primary consideration is specifying a target of inference. We focus on situations in which interest lies in a marginal model that quantifies the association between exposure and the average outcome among individuals who experience an event:

$${\mu }_i(t)=\text{E}\left[Y_i(t)|d{N}_i(t)=1,{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)\right]={\mathit{x}}_{it}\mathit{\beta }.$$

Note that x_it includes the relevant components of the exposure and event time processes. Parameters β quantify the association between these components and the average outcome. Note also that dN_i (t) = 1 is explicitly required in μ_i (t) because otherwise Y_i (t) would not exist. Because μ_i (t) does not condition on the entire exposure and event time processes, or on past outcomes, it is known as a partly conditional mean (Pepe and Couper, 1997). However, μ_i (t) does condition on the history of the exposure and event time processes, which may specify a lag relationship between these processes and the mark process. This specification may be required to more accurately characterize the latency in the underlying biological process. Depending on the biological context μ_i (t) may also condition on a partial history of the exposure or event time processes. In this case the model would focus on E[Y_i (t) | dN_i (t) = 1, z_it], where z_it denotes a user-chosen subset of $\left\{{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)\right\}$.

This target of inference is useful when primary interest lies in describing the marginal association between a full or partial history of the exposure process and the mark process among those who experience an event. It may also be used to predict a future outcome as a function of the observed exposure and event time processes. In addition, this model may be reduced to a cross-sectional model to characterize the cross-sectional association between exposure at a single time point and the average outcome among individuals who experience an event.

2.4. Assumptions

As one aspect of model checking, we detail two conditions required of the exposure and event time processes. Suppose that primary scientific interest lies in estimating the marginal association between a time-dependent exposure X_i (t) and an outcome Y_i (t) among individuals who experience an event, i.e., dN_i (t) = 1. To ensure consistency of a GEE estimator or a likelihood-based estimator, it is sufficient to assume that for all t′ > t:

$$Y_i(t)\perp N_i\left(t\prime \right)|{\mathcal{X}}_i(t),{\mathcal{N}}_i(t),d{N}_i(t)=1,$$ (1)

$$Y_i(t)\perp X_i\left(t\prime \right)|{\mathcal{X}}_i(t),{\mathcal{N}}_i(t\prime ),d{N}_i(t)=1.$$ (2)

If either of these conditions is not satisfied, then an IEE is the only estimating equation option that may be used for consistent estimation of β.

The main idea behind these assumptions is to factor the joint distribution of the exposure and event time processes given the mark process:

$$\left[N_i\left(t\prime \right),X_i\left(t\prime \right)|Y_i(t)\right]=\left[N_i\left(t\prime \right)|Y_i(t)\right]\times \left[X_i\left(t\prime \right)|N_i\left(t\prime \right),Y_i(t)\right].$$

Assumption (1) implies that the event time process is exogenous with respect to the mark process. Assumption (2) implies that the exposure process is exogenous with respect to the mark process given the event time process. This is similar to a full covariate conditional mean assumption (Pepe and Anderson, 1994; Pepe and Couper, 1997). The similarity between these assumptions is intuitive because both X_i (t) and N_i (t) may be conditioned on as covariates in the analysis of Y_i (t).

We illustrate the importance of these assumptions by examining the estimating function for estimation of β. Let w_itt′ denote the (t, t′) element of the inverse of a working covariance matrix V_i. In a recurrent marked point process setting the estimating function is:

$$\begin{gathered} {\mathcal{U}}_{\beta }(\mathit{\beta })=\sum _{i=1}^n{\mathit{X}}_i^T{\mathit{V}}_i^{-1}\left({\mathit{Y}}_i-{\mathit{\mu }}_i\right)\mathit{d}{\mathit{N}}_i \\ =\sum _{i \\ =1}^n\sum _{t\prime =1}^T\sum _{t=1}^T{\mathit{x}}_{it\prime }{w}_{itt\prime }\left(Y_i(t)-{\mu }_i(t)\right)d{N}_i(t)d{N}_i\left(t\prime \right). \end{gathered}$$ (3)

Consistency of $\widehat{\mathit{\beta }}$ relies on the assumption that the estimating function is unbiased, i.e., $\text{E}\left[{\mathcal{U}}_{\beta }(\mathit{\beta })\right]=0$. Examine the expectation of each summand of ${\mathcal{U}}_{\beta }(\mathit{\beta })$ via iterated expectation:

$$\begin{gathered} \text{E}\left[{\mathit{x}}_{it\prime }{w}_{itt\prime }\left(Y_i(t)-{\mu }_i(t)\right)d{N}_i(t)d{N}_i\left(t\prime \right)\right] \\ ={\text{E}}_{X,N}[{\text{E}}_Y[{\mathit{x}}_{it\prime }{w}_{itt\prime }(Y_i(t)-{\mu }_i(t))d{N}_i(t)d{N}_i\left(t\prime \right)|{\mathcal{X}}_i(T),{\mathcal{N}}_i(T)]] \\ ={\text{E}}_{X,N}[{\mathit{x}}_{it\prime }{w}_{itt\prime }({\text{E}}_Y[Y_i(t)|d{N}_i(t)=1,d{N}_i\left(t\prime \right)=1,{\mathcal{X}}_i(T),{\mathcal{N}}_i(T)]-{\mu }_i(t))d{N}_i(t)d{N}_i\left(t\prime \right)]. \end{gathered}$$

Note that w_itt′ may be nonzero and x_it′ may include future exposures and events. Therefore, conditioning on the entire exposure and event time processes may be required to bring x_it′w_itt′ outside the conditional expectation above. If assumptions (1) and (2) are satisfied, then the partly conditional mean μ_i (t) is equivalent to a full conditional mean:

$$\begin{gathered} {\mu }_i(t)=\text{E}\left[Y_i(t)|d{N}_i(t)=1,{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)\right] \\ =\text{E}\left[Y_i(t)|d{N}_i(t)=1,{\mathcal{X}}_i(T),{\mathcal{N}}_i(T)\right]. \end{gathered}$$

Therefore, the estimating function is unbiased provided that the regression model for μ_i (t) is correctly specified and that assumptions (1) and (2) are satisfied. If working independence is assumed, then V_i is a diagonal matrix, i.e., w_itt′ = 0 (t ≠ t′). Hence the estimating function reduces to:

$${\mathcal{U}}_{\beta }(\mathit{\beta })=\sum _{i=1}^n\sum _{t=1}^T{\mathit{x}}_{it}{w}_{itt}\left(Y_i(t)-{\mu }_i(t)\right)d{N}_i(t).$$ (4)

In this case $\text{E}\left[{\mathcal{U}}_{\beta }(\mathit{\beta })\right]=0$ if the assumed marginal regression model is correctly specified; assumptions (1) and (2) are not required. To generalize the model to allow continuous times, the sums indexed by calendar time in equations (3) and (4) need only be replaced by integrals.

2.5. Empirical Evaluation of Assumptions

Empirically evaluating assumptions (1) and (2) is generally possible using the observed data. Suppose that t′ > t. To evaluate assumption (1) analysts may use standard recurrent event methods to assess the relationship between past outcomes and occurrence of a subsequent event. Let λ_i (t′) denote the hazard of an event by time t′ for subject i. Analysts may model λ_i (t′) given Y_i (t) using a Cox regression model:

$$\begin{gathered} \text{log}{\lambda }_i\left(t\prime |d{N}_i(t)=1,Y_i(t),{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)\right) \\ =\text{log}{\lambda }_0\left(t\prime \right)+{\eta }_1{Y}_i(t)+{\mathit{\eta }}_2{\mathcal{X}}_i(t)+{\mathit{\eta }}_3{\mathcal{N}}_i(t). \end{gathered}$$ (5)

Note that η₁ quantifies the association between past outcomes and the hazard of a subsequent event. Therefore, a hypothesis test of η₁ = 0 may be used to formally evaluate assumption (1). This test is valid because it directly evaluates the conditional dependence between past outcomes and occurrence of a subsequent event (see Figure 2).

Figure 2.

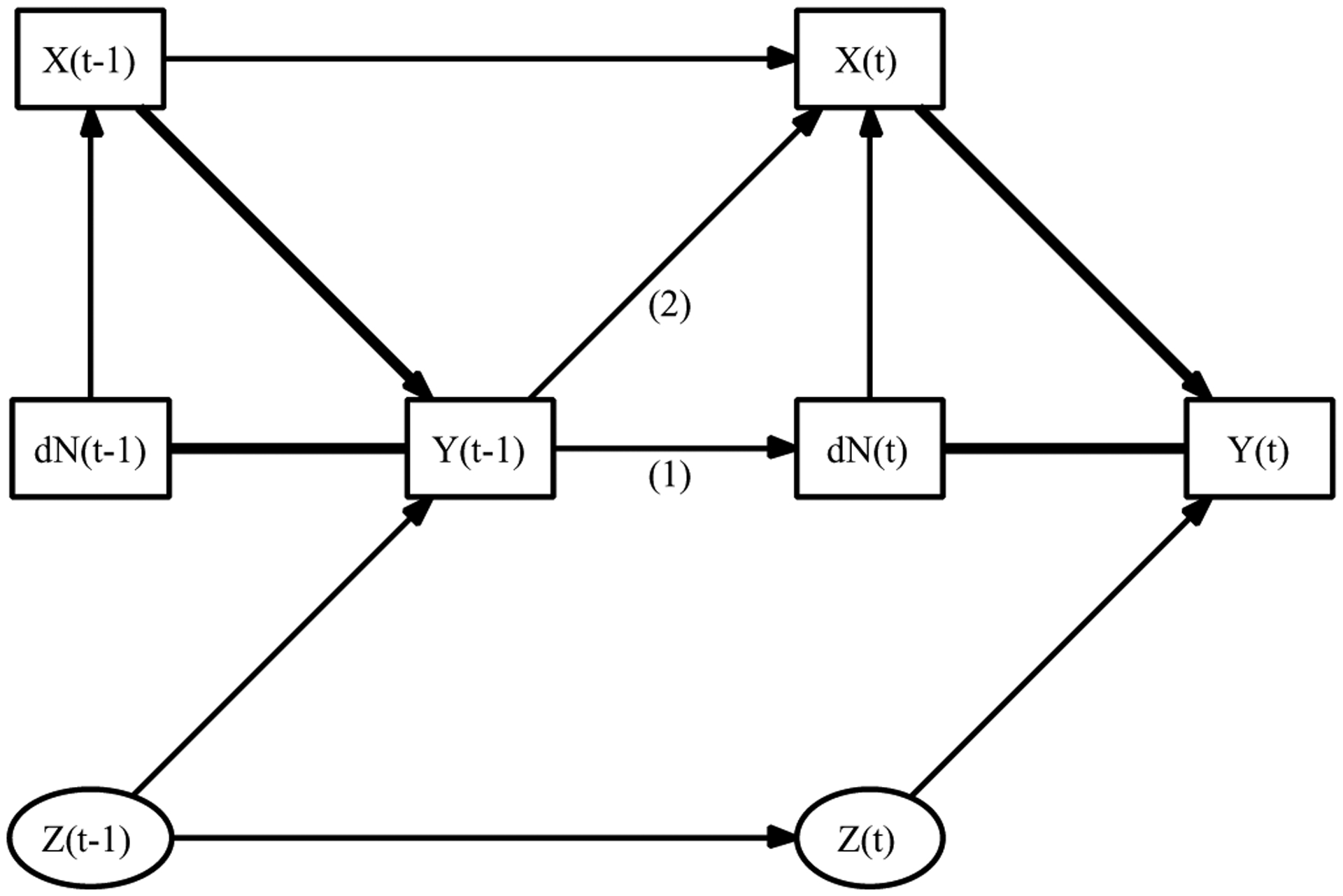
Directed acyclic graph representing conditional dependence relationships for the data generated in our simulation study; Zi (t) represents unmeasured error for the longitudinal process Y_i (t).

To evaluate assumption (2) analysts may use standard regression methods to assess the relationship between past outcomes and current exposure. Specifically, analysts may model X_i (t′) given Y_i (t) using a regression model that is appropriate for the distribution of X_i (t′). Let g denote the link function specified by this regression model:

$$\begin{gathered} g\left(\text{E}\left[X_i\left(t\prime \right)|d{N}_i(t)=1,Y_i(t),{\mathcal{X}}_i(t),{\mathcal{N}}_i\left(t\prime \right)\right]\right) \\ ={\theta }_0+{\theta }_1{Y}_i(t)+{\mathit{\theta }}_2{\mathcal{X}}_i(t)+{\mathit{\theta }}_3{\mathcal{N}}_i\left(t\prime \right). \end{gathered}$$ (6)

Because past exposures are likely associated with both past outcomes and current exposure, past exposures confound the association between past outcomes and current exposure. Therefore, in this model it is important to adjust for ${\mathcal{X}}_i(t)$. Note that θ₁ quantifies the association between past outcomes and current exposure. Therefore, a hypothesis test of θ₁ = 0 may be used to formally evaluate assumption (2). This test is valid because it directly evaluates the conditional dependence between past outcomes and current exposure (see Figure 2).

Model (6) requires that X_i (t′) be ascertained for all subjects, including those who do not experience an event at time t′, i.e., dN_i (t′) = 0. In the Appendix, we detail assumption (2^★), which is a weaker assumption that can be evaluated in situations in which X_i (t′) is ascertained only when dN_i (t′) = 1. In our application maternal cigarette smoking was ascertained if and only if a birth occurred. Hence in our application we empirically evaluate assumption (2^★).

3. Simulation Study

We performed a simulation study to evaluate the potential for bias if assumption (1) is not satisfied. We did not exclusively examine departures from assumption (2) because it is well known that if the exposure process is endogenous, then covariance-weighting methods do not provide a consistent estimate of the cross-sectional parameter (Pepe and Anderson, 1994). We designed our simulation study to emulate our motivating example: a continuous exposure process to represent a maternal exposure, an event time process to represent a live birth, and a continuous mark process to represent an infant birth outcome.

3.1. Parameters

At each of 1000 iterations we generated an exposure, event time, and mark process for a population of 10,000 individuals at t = 1, … , 5 discrete calendar times. We specified an autoregressive exposure process: X_i (t) ~ N(θ₀X_i (t − 1), $v^2\left(1-{\theta }_0^2\right)$), where X_i (0) = 0. The parameter θ₀ quantifies the amount of autocorrelation in the exposure process. We generated a binary variable to indicate an event at time t such that the probability of an event depended on the previous outcome and current exposure: dN_i (t) ~ B(expit(η₀ + η₁R_i (t − 1) + η₂X_i(t))). Instead of simply using Y_i (t − 1) to specify the probability of an event, we used a residual centered by the conditional expectation of Y_i (t − 1):

$$R_i(t-1)=Y_i(t-1)-\text{E}\left[Y_i(t-1)|d{N}_i(t-1)=1,X_i(t-1),{\gamma }_i\right],$$

where R_i (0) = 0. Under this specification an event was likely to occur if the difference between the observed and expected previous outcome was large. The parameter η₁ quantifies the extent to which assumption (1) is violated. We considered three values for η₁: log 1, log 2, and log 4 such that a standard deviation increase in R_i (t) corresponded to an event odds ratio of 1.0, 2.2, and 4.8, respectively. In each scenario η₂ = −η₁.

To generate the mark process we specified a marginal mean μ_i (t) = β₀ + β₁X_i (t). In each scenario β₀ = 1 and β₁ = − 1. We also specified unit-specific random intercepts and slopes γ_i = {γ_i0, γ_i1} ~ N₂(0, D), serial correlation W_i (t) ~ N(ρW_i(t − 1), τ²(1 – ρ²)), and measurement error ϵ_i(t) ~ N(0, σ²), where W_i (0) = 0. Therefore, the mark process was:

$$Y_i(t)={\beta }_0+{\beta }_1{X}_i(t)+{\tilde{\gamma }}_{i0}(t)+{\tilde{\gamma }}_{i1}(t)X_i(t)+{\tilde{W}}_i(t)+{ϵ}_i(t),$$

where ${\tilde{\gamma }}_{i0}(t)$, ${\tilde{\gamma }}_{i1}(t)$, and ${\tilde{W}}_i(t)$ were sequentially centered by their conditional expectation given dN_i (t) = 1. This was required so that the marginal expectation of Y_i (t) was correctly specified given dN_i (t) = 1.

From each simulated population we sampled n = 300 units and fit an ordinary least squares regression model using first events, an IEE, a GEE assuming an exchangeable correlation structure, and a LMM with random intercepts. We selected the following values for the nuisance parameters: θ₀ = ρ = 0.9, υ² = τ² = 1.5, D₀₀ = 0.5², D₁₁ = 0.2², and σ² = 1.

Figure 2 presents a graphical summary of our simulation study. Boxes enclose observed variables and ovals enclose unobserved variables Z_i (t) = {γ_i, W_i (t)}. Directed arrows represent causal relationships and bold directed arrows represent the cross-sectional association of interest. Bold segments between the event time and mark process indicate that an outcome is observed if and only if an event occurs. The arrows labeled (1) and (2) indicate the relationships that violate assumptions (1) and (2), respectively.

3.2. Results

Table 1 provides mean intercept and slope estimates across 1000 iterations, mean squared error (MSE), and estimated coverage of 95% confidence intervals for each scenario. If assumption (1) is satisfied (η₁ = log 1), then every method provides approximately unbiased parameter estimates with appropriate confidence interval coverage. However, ordinary least squares using first events has a higher MSE due to reduced sample size. If assumption (1) is not satisfied (η₁ ≠ log 1), then an IEE provides approximately unbiased parameter estimates with appropriate confidence interval coverage. However, covariance-weighting methods provide biased parameter estimates with reduced confidence interval coverage. Restricting to first events also performs poorly if assumption (1) is not satisfied.

Table 1.

Simulation results evaluating departures from assumption (1)

η1	Method	Mean estimate		MSE × 10		Coverage (%)
		${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$
log l	First	0.999	−1.002	0.081	0.057	95	94
	IEE	1.000	−1.002	0.071	0.044	95	95
	GEE	0.999	−1.000	0.065	0.031	95	96
	LMM	0.999	−1.000	0.065	0.031	95	94
log 2	First	0.879	−1.043	0.234	0.081	74	92
	IEE	0.996	−1.000	0.076	0.053	94	94
	GEE	0.778	−1.030	0.564	0.046	24	91
	LMM	0.785	−1.029	0.530	0.045	26	89
log 4	First	0.806	−1.099	0.479	0.188	53	82
	IEE	0.995	−1.002	0.095	0.072	93	93
	GEE	0.673	−1.075	1.156	0.105	4	78
	LMM	0.688	−1.072	1.056	0.099	5	76

Although bias is not substantial for GEE and LMM slope estimates if assumption (1) is violated, it increases if assumption (2) is also violated. We performed a second simulation study in which we included R_i (t − 1) in the autoregressive exposure process: X_i (t) ~ N(θ₀X_i (t – 1) + θ₁R_i (t − 1), $v^2\left(1-{\theta }_0^2\right)$). The parameter θ₁ quantifies the extent to which assumption (2) is violated. For η₁ = log 4 and θ₁ = 0.1 the mean slope estimate obtained via GEE and LMM was −1.206 and −1.196, respectively. For both methods the estimated confidence interval coverage of β₁ was 10%. Therefore, if both assumptions are violated, then covariance-weighting methods provide substantially biased parameter estimates with poor confidence interval coverage. We did not observe an interaction effect on the performance of these methods resulting from a violation of both assumptions.

4. Application

The Collaborative Perinatal Project was a landmark national prospective epidemiological study conducted between 1959 and 1965 (Hardy, 2003). Motivation for launching the study included unacceptably high levels of maternal and infant mortality and interest in linking maternal lifestyle and pregnancy exposures to infant neurological conditions such as cerebral palsy, epilepsy, and mental retardation. Epidemiological analyses focused on risk factors for poor pregnancy outcomes, including the effects of specific drugs and other exposures such as cigarette smoking. At the conclusion of the study, the sample consisted of 48,197 women with up to six births per woman.

We limited our focus to the cross-sectional association between maternal cigarette smoking and infant birth weight. We restricted our analysis to births that were recorded prospectively at sites that selected 100% of eligible women, which yielded four sites for analysis: Harvard, Buffalo, Minnesota, and Philadelphia. Our sample consisted of 8403 women with up to three births per woman. Among all infants in our sample, approximately 10% were of low birth weight, defined as birth weight less than 2500 g.

4.1. Evaluating the Scientific Question

We obtained cross-sectional point estimates by fitting a separate ordinary least squares regression model to first (n₁ = 8403), second (n₂ = 1951), and third (n₃ = 527) births. In each model, we adjusted for site such that Harvard served as the reference group and for maternal race such that white mothers served as the reference group. We also obtained longitudinal point estimates by including all births in a single regression model and specifying various structures for within-subject correlation. We considered an IEE, a GEE assuming an exchangeable correlation structure, and a LMM with random intercepts. In these models we also adjusted for birth order such that first births served as the reference group.

Table 2 provides cross-sectional and longitudinal point estimates and standard errors. According to each cross-sectional model maternal cigarette smoking is associated with a significant decrease in infant birth weight. The difference in mean infant birth weight of babies born to smokers and that of babies born to nonsmokers among women with a first, second, and third birth is: −163 g, 95% CI: (−187, −140); −174 g, 95% CI: (−222, −125); and −179 g, 95% CI: (−277, −82), respectively. A weighted average of these point estimates (weighted by number of births η_t★) is −166 g. The IEE reveals that the difference in mean infant birth weight of babies born to smokers and that of babies born to nonsmokers is −165 g, 95% CI: (−187, −143). This estimate corresponds well to the cross-sectional point estimates and is consistent with the weighted average of the cross-sectional estimates. However, results obtained via GEE and LMM are surprisingly not consistent with the cross-sectional results. These methods estimate the effect of maternal cigarette smoking on infant birth weight to be −158 g, 95% CI: (−180, −136). This estimate is greater than every cross-sectional point estimate and is more than a half standard deviation greater than the IEE point estimate.

Table 2.

Results from the Collaborative Perinatal Project: Coefficient (standard error)

	Cross-sectional models						Longitudinal models
	First		Second		Third		IEE		GEE		LMM
Smoke	−163	(12)	−174	(25)	−179	(50)	−165	(11)	−158	(11)	−158	(11)
Site
Buffalo	47	(22)	−67	(49)	113	(137)	30	(20)	38	(19)	38	(21)
Minnesota	41	(18)	−29	(45)	96	(106)	33	(17)	37	(16)	37	(17)
Philadelphia	−74	(24)	−118	(53)	−146	(113)	−84	(26)	−83	(26)	−84	(22)
Race
Black	−204	(23)	−180	(53)	−110	(113)	−196	(26)	−198	(26)	−199	(22)
Other	−186	(37)	−186	(83)	−249	(198)	−189	(31)	−184	(30)	−184	(36)
Birth
Second							58	(12)	57	(12)	57	(12)
Third							42	(24)	63	(22)	63	(21)

4.2. Evaluating Assumptions

This disparity in the longitudinal results may exist because assumptions (1) and (2^★) may not be satisfied. To evaluate assumption (1) we fit a Cox regression model for time from first until second birth. We censored women who did not experience a second birth. In this model, we included an indicator of low birth weight for first births. We adjusted for cigarette smoking at their first birth, site, and maternal race. This model revealed that mothers who initially gave birth to a low birth weight infant delayed a second pregnancy. The hazard of a second birth among women who initially gave birth to a low birth weight infant was approximately 16% lower than that among women who initially gave birth to an infant of normal birth weight, 95% CI: (1.7%, 28%). This difference was statistically significant (p = 0.03). Therefore, there is evidence to suggest that assumption (1) is violated.

We fit a logistic regression model for cigarette smoking among women who experienced a second birth to evaluate assumption (2^★). In this model, we included an indicator of low birth weight for their first birth. We adjusted for cigarette smoking at their first birth because previous smoking status may confound the association between previous birth weight and current smoking status. We also adjusted for site and maternal race. This model revealed that among mothers with identical smoking status at their first birth, those who initially gave birth to a low birth weight infant were more likely to subsequently smoke cigarettes. Among women who experienced a second birth, the odds of cigarette smoking for women who initially gave birth to a low birth weight infant were approximately 21% higher than that for women who initially gave birth to an infant of normal birth weight, although this difference was not statistically significant (p = 0.41). Therefore, there is evidence to suggest that assumption (2^★) is violated.

5. Discussion

In this article, we presented recurrent marked point process data and its defining characteristic: an outcome exists if and only if an event occurs. We also described the challenging features of recurrent marked point process data: correlation may be induced within subjects, endogeneity may exist between past outcomes and current exposure, and endogeneity may exist between past outcomes and occurrence of a subsequent event. To overcome these challenges we detailed assumptions required of the exposure and event time processes to ensure that existing longitudinal analysis methods provide a valid estimate of the marginal association between a time-dependent exposure and outcome of interest among individuals who experience an event. Our theoretical and empirical results showed that covariance-weighting methods such as GEEs and LMMs provide biased parameter estimates if these assumptions are not satisfied. In our motivating example to quantify the effect of maternal cigarette smoking on infant birth weight, we demonstrated that inappropriate application of these methods may lead to spurious results.

Our simulation results are in contrast to previously published results (Lipsitz et al., 2002). Lipsitz and colleagues found that if measurement times depend on past outcomes, then incorrectly specifying the covariance between clustered outcomes results in biased regression estimates and hence recommend caution when using an IEE. We found that an IEE provides consistent regression estimates and recommend caution when using covariance-weighting methods. This difference arises because there is an important distinction between our setting and that of Lipsitz and colleagues. They assume that subjects have a potential measurement at every time. Conversely, we assume that a measurement is available if and only if an event occurs. The implication of this distinction is that the target of inference differs between our setting and that of Lipsitz and colleagues. They seek to generate inference regarding an average response in a population of individuals, i.e., E[Y_i (t) | X_i (t)], whereas we seek to generalize to a population of individuals who experience an event, i.e., E[Y_i (t) | dN_i (t) = 1, X_i(t)]. Analysts must decide which target of inference is appropriate to their specific context to ensure valid application of the estimation method they select.

In certain simulation scenarios we found that although an IEE provides consistent parameter estimates, it may be less efficient than a GEE (see Table 1). This is not surprising given that it is well known that an IEE may be inefficient relative to a covariance-weighted GEE under nonindependence correlation structures (Liang and Zeger, 1986; Mancl and Leroux, 1996). Therefore our results illustrate the bias/efficiency tradeoff. For example, analysts may decide to implement a GEE and accept a small amount of bias due to departures from assumptions (1) and (2) if the efficiency gain is large. An alternative method is a generalized method of moments estimator (Lai and Small, 2007). This estimator retains the attractive consistency of an IEE for a time-dependent exposure and may be substantially more efficient than an IEE given an additional assumption regarding the type of time-dependent exposure.

Although the methods we presented are not specifically designed to generate causal inference, a longitudinal data analysis may provide evidence of a causal association by establishing the temporal association between exposure and outcome. However, there are several challenges associated with generating causal inference from observational data. A challenge specific to recurrent marked point process data is that modification of the exposure may impact not only the outcome of interest, but also occurrence of an event. In a recurrent marked point process setting an outcome is measured if and only if an event occurs. Therefore, it may be difficult to disentangle the causal effect of exposure on outcome from the effect of exposure on occurrence of an event. A g-computation algorithm (Robins, Greenland, and Hu, 1999) could be used to provide causal estimates of the effect of exposure on outcome, but would require specification of additional assumptions regarding the effect of exposure on occurrence of an event.

We recommend that analysts who undertake a repeated measures analysis of recurrent marked point process data carefully identify any factors that may influence the exposure and event time processes. Identification of these factors may be based on prior scientific knowledge. Alternatively, it may be based on the observed data. In Section 2.6, we outlined several approaches to empirically explore these factors; we provided an example in Section 4.2. Only after these factors have been identified may analysts choose appropriate statistical techniques to validly answer their scientific questions.

Appendix

In this Appendix, we show that we can weaken the assumption of “joint exogeneity” required by assumptions (1) and (2) given in Section 2.4. Let ${\mathit{x}}_{it}=\left\{{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)\right\}$ (or a partial history, as appropriate) and recall that ${\mu }_i(t)=\text{E}[Y_i(t)d{N}_i(t)=1,{\mathcal{X}}_i(t),{\mathcal{N}}_i(t)]=\text{E}\left[Y_i(t)|d{N}_i(t)=1,{\mathit{x}}_{it}\right]$. Examine the expectation of each summand of ${\mathcal{U}}_{\beta }(\mathit{\beta })$ given in equation (3):

$$\begin{gathered} \text{E}\left[{\mathit{x}}_{it\prime }{w}_{itt\prime }\left(Y_i(t)-{\mu }_i(t)\right)d{N}_i(t)d{N}_i\left(t^{\prime }\right)\right] \\ =\text{P}\left(d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1\right)\times \text{E}\left[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}\left(Y_i(t)-{\mu }_i(t)\right)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1\right]\propto \text{E}\left[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}\left(Y_i(t)-{\mu }_i(t)\right)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1\right] \\ ={\text{E}}_{{\mathit{x}}_{it}}[{\text{E}}_{{\mathit{x}}_{i{t}^{\prime }},Y_i(t)|{\mathit{x}}_{it}}[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}\left(Y_i(t)-{\mu }_i(t)\right)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1,{\mathit{x}}_{it}]] \\ ={\text{E}}_{{\mathit{x}}_{it}}[{\text{E}}_{{\mathit{x}}_{i{t}^{\prime }}|{\mathit{x}}_{it}}[{\text{E}}_{Y_i(t)|{\mathit{x}}_{i{t}^{\prime }},{\mathit{x}}_{it}}\times [{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}\left(Y_i(t)-{\mu }_i(t)\right)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1,{\mathit{x}}_{it},{\mathit{x}}_{i{t}^{\prime }}]]] \\ ={\text{E}}_{{\mathit{x}}_{it}}[{\text{E}}_{{\mathit{x}}_{it\prime }|{\mathit{x}}_{it}}[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}({\text{E}}_{Y_i(t)|{\mathit{x}}_{i{t}^{\prime }},{\mathit{x}}_{it}}\times [Y_i(t)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1,{\mathit{x}}_{it},{\mathit{x}}_{i{t}^{\prime }}]-{\mu }_i(t))]] \end{gathered}$$

Assume (2^★): Y_i(t) ⊥ x_it′ | x_it, dNi (t) = 1, dNi (t′) = 1 :

$$={\text{E}}_{{\mathit{x}}_{it}}[{\text{E}}_{{\mathit{x}}_{i{t}^{\prime }}|{\mathit{x}}_{it}}[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}({\text{E}}_{Y_i(t)|{\mathit{x}}_{it}}\times [Y_i(t)|d{N}_i(t)=1,d{N}_i\left(t^{\prime }\right)=1,{\mathit{x}}_{it}]-{\mu }_i(t))]].$$

Using assumption (1) we obtain:

$$\begin{gathered} ={\text{E}}_{{\mathit{x}}_{it}}[{\text{E}}_{{\mathit{x}}_{i{t}^{\prime }}|{\mathit{x}}_{it}}[{\mathit{x}}_{i{t}^{\prime }}{w}_{it{t}^{\prime }}({\text{E}}_{Y_i(t)|{\mathit{x}}_{it}}\left[Y_i(t)|d{N}_i(t)=1,{\mathit{x}}_{it}\right]-{\mu }_i(t))]] \\ =0\text{ by definition of }{\mu }_i(t). \end{gathered}$$

In assumption (2^★) we assume that Y_i (t) ⊥ x_it′ | x_it′, dN_i (t) = 1, dN_i (t′) = 1. This is a weaker assumption regarding the endogeneity between past outcomes and current exposure than assumption (2). In particular, assumption (2^★) can be evaluated in situations in which x_it′ is ascertained only when dN_i (t′) = 1, whereas evaluation of assumption (2) requires x_it′ be ascertained for all strata defined by N_i (t′). This includes subjects who have not been observed to experience an event at time t′, i.e., dN_i (t′) = 0.