Abstract

Unsupported donor–acceptor complexes of noble gases (Ng) with group 13 elements have been theoretically studied using density functional theory. Calculations reveal that heavier noble gases form thermodynamically stable compounds. The present study reveals that no rigid framework is necessary to stabilize the donor–acceptor complexes. Rather, prepyramidalization at the Lewis acid center may be an interesting alternative to stabilize these complexes. Detailed bonding analyses reveal the formation of two-center–two-electron dative bonding, where Ng atoms act as a donor.
Introduction
Noble gases (Ng) having a complete outer electronic shell exist as individual atoms. They are not likely to be involved in chemical bonding. Extreme conditions such as strong oxidizing agents, such as F2, or extreme activation by laser irradiation, electric discharge, etc. are required, and the products are trapped in low-temperature matrices. After the first synthesis of xenon compounds by Bartlett1 and Hoppe2 in 1962, many compounds featuring Ng–X (X = halogen, oxygen, sulfur, nitrogen, and carbon) bonds have been isolated and characterized.3 The chemistry of krypton and other noble gases has been thoroughly reviewed.4−6
Noble-gas compounds are generally metastable and readily dissociate into their atomic form. The bonding situation in the stable compound, NgF2, is described as three-center–four-electron bonds,7 where terminal fluorine atoms also participate in the bond formation. Similar bonding situation has also been described in Au+–Ng–F–.8 The other possibility of three-center–four-electron bond formation is through donor–acceptor interaction, as pointed by Mück et al.9 Such a bonding situation can describe the experimentally synthesized compounds such as HArF10 and HKrF,11 which were prepared by the photolysis of HF in argon and krypton matrices. However, calculations reveal that both HArF and HKrF molecules are metastable due to exothermic dissociation into free Ng and HF.12 To overcome the problem of dissociation, Mück et al. have theoretically proposed the use of a rigid cage, such as a push–pull cryptand ligand, which contains both donor (D) and acceptor (A) sites.9 Their calculations reveal that the dissociation process, A–Ng–D = Ng + AD (A = acceptor and D = donor), is endergonic (ΔG > 0), indicating that the cryptand-encapsulated noble-gas compounds are thermodynamically stable.
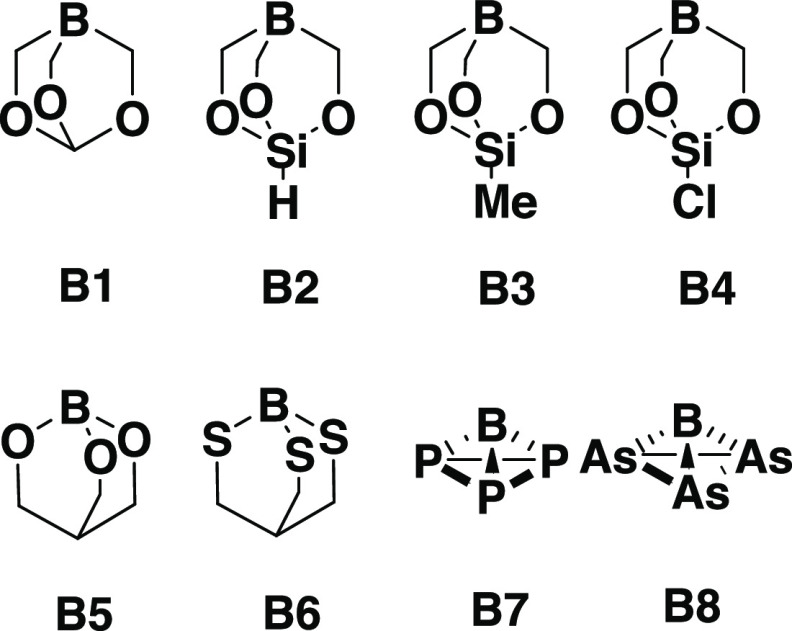
Is there a possibility of formation of thermodynamically stable noble-gas compounds featuring donor–acceptor interactions without the use of steric protection? Is it possible for the noble gases to form a usual two-center–two-electron bond? To answer these questions, we have carried out quantum chemical calculations on donor–acceptor complexes between noble gases and group 13 elements (Scheme 1). The bond dissociation energies (BDEs) of BH3–Ng complexes are very low, which might be due to the requirement of large preparation energy by planar boron acceptors to achieve pyramidal conformation upon complexation with noble gases. We, therefore, envisioned that prepyramidalized boron center (B1–B8, Scheme 1) will be effective to stabilize such donor–acceptor complexes. It should be noted that Mück et al. have also used a prepyramidalized acceptor center in their study.9 The strategy of using prepyramidalized boron center has been utilized by Borthakur et al. in stabilizing unsupported transition metal boron donor–acceptor complexes.13 Recently, our group has reported pyramidal tricoordinate boron centers (B7–B8, Scheme 1) stabilized by pnictogens.14 Our calculation revealed that P3B and As3B molecules are global minima with extreme pyramidalization at the boron center with enhanced Lewis acidity.15 Therefore, these prepyramidalized boron centers are quite likely to form stable Ng–B donor–acceptor complexes. Herein, we have carried out density functional calculations to investigate the possibility of formation of donor–acceptor complexes between experimentally known prepyramidalized boron centers (B1–B6)13 and our previously proposed molecules B7–B8.14
Scheme 1. Pyramidal Lewis Acidic Boron Centers Considered in This Study.
Computational Details
All of the structures were fully optimized without any symmetry constraints at the BP86-D3(BJ)/def2-TZVPP level.16 This theory includes third generation of Grimme’s empirical dispersion with the Becke–Johnson damping function.17 This method is known to produce very good geometries, and the dispersion correction produces bond dissociation energies with least mean deviation.18 Harmonic frequency calculations were also performed to understand the nature of the stationary state. All structures were found to be at their local minima with all real values of the Hessian matrix. All of these calculations were performed using the GAUSSIAN 16 suite of program.19 All energies are zero-point- and thermal-corrected. Basis set superposition error (BSSE) is not considered as it is reported that while using DFT-D methods with triple zeta quality basis set, BSSE correction can be avoided.20 The electronic structures of these molecules were analyzed using natural bond orbital (NBO) analyses,21 quantum theory of atoms in molecules (QTAIM),22 and electron localization function (ELF)23 at the BP86-D3(BJ)/def2-TZVPP level. QTAIM and ELF analyses were performed using Multiwfn program code.24 Charge decomposition analysis (CDA)25 was performed using Multiwfn program code. The force constant k was calculated using the compliance program code.26
To investigate the effect of dispersion on the molecular geometry, bond dissociation energy, and electronic structure, some of the molecules were optimized at BP86 functional without D3 correction.
Results and Discussion
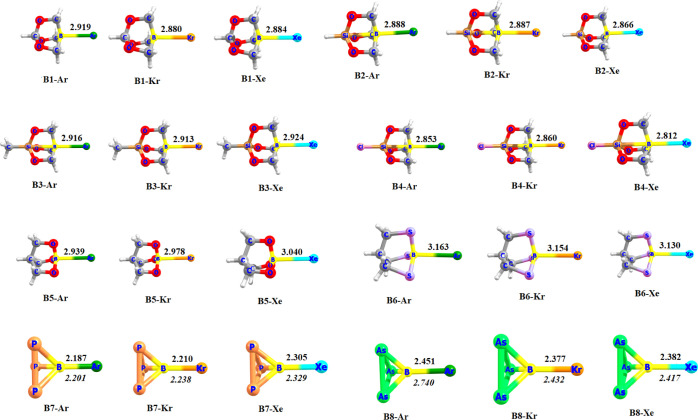
Figure 1 shows the optimized geometries of the donor–acceptor complexes. Lighter noble gases He and Ne form very weak complexes, and hence are not discussed in the text. However, heavier noble gases Ar, Kr, and Xe form stronger complexes, and hence are emphasized throughout the text. With noble gases Ar, Kr, and Xe, B–Ng bond lengths are slightly longer than single bonds in comparison to the self-consistent radii of Pyykkö,27 which might be due to the dative nature of these bonds. The shortest B–Ng distances are found for the B7 adducts, while the longest ones are found for the B6 adduct. B8 also forms a stronger B–Ng interaction as revealed by their bond distances, bond dissociation energies, and force constant values (Table 1). However, the B–Ng bonds of the B8–Ng adducts are slightly weaker than that of B7 but stronger than the rest. Dispersion plays a major role in these molecules as evident from Figure 1 and Table 1. Pure BP86/def2-TZVPP without D3 correction resulted in longer B–Ng bonds with lower bond dissociation energies for B7 and B8 molecules.
Figure 1.
BP86-D3(BJ)/def2-TZVPP optimized geometries of the donor–acceptor complexes. Bond lengths are in Å. Values in italics refer to the BP86/def2-TZVPP level.
Table 1. Wiberg Bond Index (WBI), Force Constant (k in mDyne Å–1), Difference in Pyramidalization Angle at B (ΔθB, in Degrees), and Bond Dissociation Energies (kJ mol–1) of the Donor–Acceptor Complexesa.
| molecule | bond | wib | force constant (k) | difference (ΔθB) | BDE |
|---|---|---|---|---|---|
| B1–X | B–Ar | 0.071 | 0.0281 | 0.6 | 5.8 |
| B–Kr | 0.134 | 0.0234 | 1.5 | 9.6 | |
| B–Xe | 0.240 | 0.0312 | 3.3 | 16.7 | |
| B2–X | B–Ar | 0.078 | 0.0172 | 0.9 | 6.2 |
| B–Kr | 0.134 | 0.0257 | 1.5 | 10.4 | |
| B–Xe | 0.253 | 0.0230 | 2.7 | 18.4 | |
| B3–X | B–Ar | 0.071 | 0.0262 | 0.6 | 6.7 |
| B–Kr | 0.134 | 0.0177 | 1.2 | 10.4 | |
| B–Xe | 0.221 | 0.0107 | 2.4 | 18.0 | |
| B4–X | B–Ar | 0.086 | 0.0350 | 0.6 | 7.5 |
| B–Kr | 0.145 | 0.0238 | 1.2 | 11.7 | |
| B–Xe | 0.284 | 0.0343 | 2.9 | 20.0 | |
| B5–X | B–Ar | 0.053 | 0.0251 | 0.6 | 4.4 |
| B–Kr | 0.083 | 0.0189 | 0.9 | 6.2 | |
| B–Xe | 0.137 | 0.0194 | 1.5 | 10.0 | |
| B6–X | B–Ar | 0.049 | 0.0322 | 0.1 | 5.8 |
| B–Kr | 0.085 | 0.0247 | 0.2 | 9.2 | |
| B–Xe | 0.167 | 0.0242 | 1.2 | 15.9 | |
| B7–X | B–Ar | 0.395 (0.381) | 0.314 (0.237) | 9.9 (9.9) | 20.0 (8.3) |
| B–Kr | 0.536 (0.516) | 0.445 (0.362) | 12.9 (12.9) | 35.9 (21.0) | |
| B–Xe | 0.667 (0.650) | 0.512 (0.443) | 15.9 (15.9) | 61.5 (40.9) | |
| B8–X | B–Ar | 0.226 (0.125) | 0.099 (0.025) | 6.0 (3.3) | 9.6 (0.5) |
| B–Kr | 0.397 (0.362) | 0.206 (0.162) | 10.5 (9.9) | 21.7 (6.5) | |
| B–Xe | 0.591 (0.566) | 0.557 (0.454) | 15.3 (15.3) | 44.3 (22.8) |
Values within parentheses refer to the BP86/def2-TZVPP level.
The bond strengths are measured in terms of their Wiberg bond indices (WBI) as well as their force constant, k, values. Table 1 contains some important numerical data of the donor–acceptor complexes. The WBI values as well as the force constant values increase from Ar to Xe. Similarly, the bond dissociation energy (BDE) values also increase from Ar to Xe. The lowest BDE value is found for the B5–Ar complex, while the highest value is found for the B7–Xe complex, reaching a maximum value of 61.5 kJ mol–1. There is a dramatic increase in WIB, k, and BDE for the complexes with B7 and B8. The increase in all of these parameters with B7 and B8 can be rationalized by the fact that both these acceptor molecules feature a highly pyramidalized boron center.14 The high degree of pyramidalization imparts higher Lewis acidity to the boron center,14 which in turn helps in stronger dative bond formation with the noble gases. The change in pyramidalization angle at B (ΔθB), measured as the difference in pyramidalization angle at B in the free acid and in the donor–acceptor complex, is maximum with B7 and B8, for which higher BDE values were found. This implies that B7 and B8 are more flexible to form stronger donor–acceptor complexes. A good correlation has been found between the change in pyramidalization angle (ΔθB) and BDE values (Figure 2).
Figure 2.
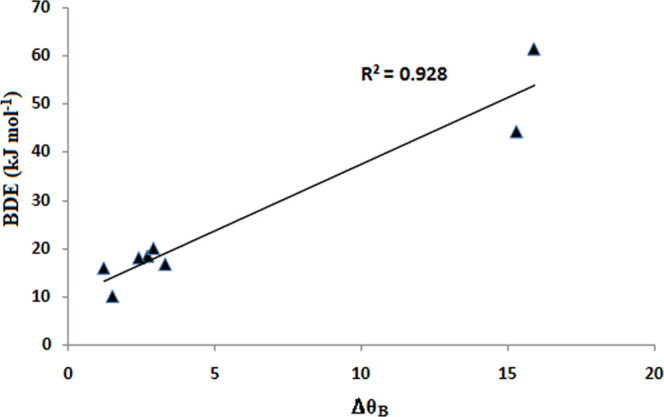
Correlation plot between change in pyramidalization angle (ΔθB) and BDE values for the complexes with xenon.
We then turned our attention to investigate the electronic structure of the complexes. Figure 3 shows the frontier Kohn–Sham molecular orbital as well as the density difference plot of the complexes. The Ng–B bonding molecular orbitals are located at either HOMO-10 or HOMO-11 with a larger contribution from the Ng (80–83%) p orbital, indicating the Ng → B donor–acceptor two-center–two-electron bond. The density difference plot also reveals the same phenomenon. The density increment zone (red) is located at the B center, while the depletion zone (blue) is located at Ng gases. Thus, the bonding situation is exactly of donor–acceptor type as expected. To quantify the donor–acceptor interaction, we have carried out charge decomposition analyses25 of the adducts. As the fragments are closed-shell species, the application of CDA to quantify charge donation/back-donation will be appropriate. Table 2 contains the numerical data. The CDA results clearly quantify that there is significant donation from the Ng fragment to the empty orbitals on B. The amount of donation increases for B7 and B8 complexes compared to others. This indicates that the boron atoms in B7 and B8 are better acceptors. The repulsive terms are all negative, indicating reduced closed-shell repulsion.25Table 2 also contains the magnitude of charge transfer |q| from Ng to the Lewis acidic boron centers. The values of |q| are found to be higher, with B7 and B8 indicating their stronger accepting ability.
Figure 3.
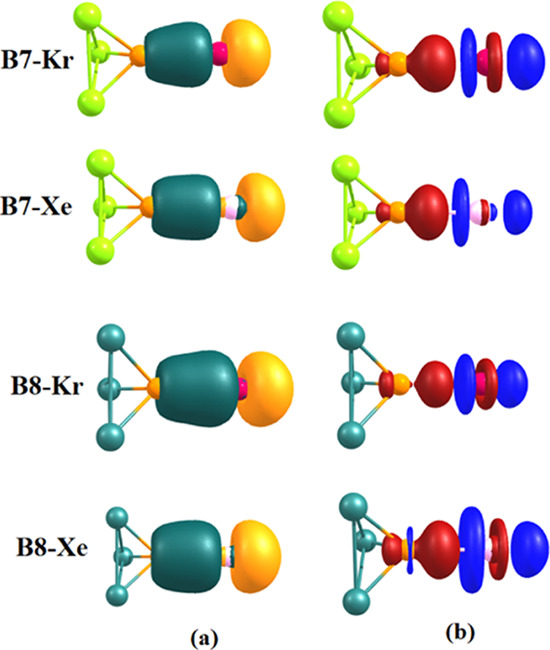
(a) Bonding molecular orbital of the complexes featuring Ng → B dative bond and (b) density difference plot of the donor–acceptor adducts (red = density increment, blue = density depletion).
Table 2. Charge Decomposition Analysis (CDA) Results of the Adductsa.
| molecules | donation (d) | repulsion (r) | residue (Δ) | |q| |
|---|---|---|---|---|
| B1–Ar | 0.032 | –0.304 | –0.020 | 0.043 |
| B1–Kr | 0.021 | –0.301 | –0.021 | 0.083 |
| B1–Xe | 0.011 | –0.307 | –0.023 | 0.154 |
| B2–Ar | 0.042 | –0.303 | –0.019 | 0.049 |
| B2–Kr | 0.016 | –0.311 | –0.021 | 0.084 |
| B2–Xe | 0.021 | –0.308 | –0.021 | 0.166 |
| B–Ar | 0.039 | –0.309 | –0.020 | 0.044 |
| B3–Kr | 0.034 | –0.301 | –0.023 | 0.078 |
| B3–Xe | 0.012 | –0.302 | –0.018 | 0.143 |
| B4–Ar | 0.043 | –0.303 | –0.019 | 0.054 |
| B4–Kr | 0.039 | –0.313 | –0.021 | 0.091 |
| B4–Xe | 0.023 | –0.304 | –0.024 | 0.187 |
| B5–Ar | 0.029 | –0.306 | –0.020 | 0.033 |
| B5–Kr | 0.024 | –0.307 | –0.022 | 0.053 |
| B5–Xe | 0.017 | –0.303 | –0.021 | 0.089 |
| B6–Ar | 0.022 | –0.304 | –0.018 | 0.033 |
| B6–Kr | 0.015 | –0.301 | –0.019 | 0.058 |
| B6–Xe | 0.020 | –0.310 | –0.020 | 0.117 |
| B7–Ar | 0.147 | –0.300 | –0.002 | 0.273 |
| B7–Kr | 0.175 | –0.311 | –0.001 | 0.387 |
| B7–Xe | 0.210 | –0.301 | –0.002 | 0.507 |
| B8–Ar | 0.094 | –0.310 | –0.013 | 0.158 |
| B8–Kr | 0.136 | –0.305 | –0.011 | 0.285 |
| B8–Xe | 0.186 | –0.306 | –0.010 | 0.446 |
Here, donation means donation from Ng to empty orbital of B. The magnitude of charge transfer |q| is also tabulated. Back-donation from BR3 fragment to Ng gases is zero in all cases.
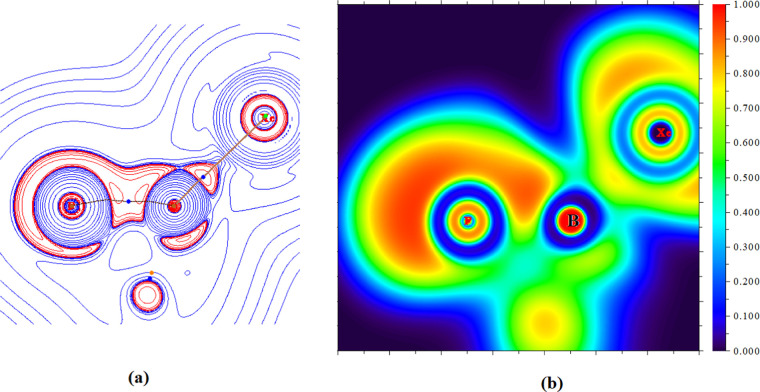
The bonding in these adducts is further analyzed using quantum theory of atoms in molecules (QTAIM)22 and electron localization function (ELF).23Figure 4 shows the Laplacian plot of electron density and electron localization function in the P–B–Xe plane for the B7–Xe molecule as a representative case. QTAIM reveals a bond path (Figure 4a) and an associated (3, −1) bond critical point22 between B–Xe atoms, which indicates the bonding interaction between the pair of atoms. ELF analyses (Figure 4b) also reveals localization of a significant amount of electron density between the B and Xe atomic basins.
Figure 4.
(a) Laplacian plot of electron density (red = charge concentration, blue = charge depletion) and (b) electron localization function in the P–B–Xe plane of the B7–Xe molecule.
Table 3 contains the topological parameters of electron density for the B–Ng bond. There is a significant electron density, ρ, at the B–Ng bond critical points, which increases with heavier noble gases. The B7–Xe adduct has the highest electron density (0.065 au) at the B–Xe bond critical point among all of the studied compounds. It should be noted that the calculated BDE for this adduct was also found to be highest (Table 1). The Laplacian of electron density, ∇2ρ, is positive in all cases, and the total electronic energy density, H(r), is negative, suggesting that these bonds should be described as polar with significant covalency.28 Significant values of electron localization function (ELF) are also observed.
Table 3. Calculated Electron Density ρ, Laplacian of Electron Density ∇2ρ, Local Electronic Energy Density H(r), and ELF Values at the B–Ng Bond Critical Pointa.
| molecule | bond | ρ | ∇2ρ | H(r) | ELF |
|---|---|---|---|---|---|
| B1–X | B–Ar | 0.010 | 0.029 | –0.001 | 0.051 |
| B–Kr | 0.015 | 0.030 | –0.002 | 0.101 | |
| B–Xe | 0.021 | 0.028 | –0.002 | 0.198 | |
| B2–X | B–Ar | 0.011 | 0.031 | –0.001 | 0.052 |
| B–Kr | 0.015 | 0.031 | –0.002 | 0.095 | |
| B–Xe | 0.022 | 0.029 | –0.002 | 0.197 | |
| B3–X | B–Ar | 0.010 | 0.030 | –0.001 | 0.048 |
| B–Kr | 0.014 | 0.031 | –0.000 | 0.088 | |
| B–Xe | 0.019 | 0.028 | –0.001 | 0.172 | |
| B4–X | B–Ar | 0.012 | 0.032 | –0.003 | 0.058 |
| B–Kr | 0.016 | 0.032 | –0.003 | 0.103 | |
| B–Xe | 0.024 | 0.029 | –0.003 | 0.225 | |
| B5–X | B–Ar | 0.009 | 0.024 | –0.002 | 0.043 |
| B–Kr | 0.011 | 0.024 | –0.001 | 0.075 | |
| B–Xe | 0.014 | 0.021 | –0.002 | 0.144 | |
| B6–X | B–Ar | 0.007 | 0.021 | –0.002 | 0.035 |
| B–Kr | 0.010 | 0.023 | –0.003 | 0.064 | |
| B–Xe | 0.014 | 0.024 | –0.003 | 0.139 | |
| B7–X | B–Ar | 0.047 (0.045) | 0.029 (0.028) | –0.022 (−0.019) | 0.262 (0.268) |
| B–Kr | 0.057 (0.054) | 0.004 (0.004) | –0.032 (−0.028) | 0.342 (0.358) | |
| B–Xe | 0.065 (0.062) | –0.030 (−0.026) | –0.037 (−0.033) | 0.516 (0.526) | |
| B8–X | B–Ar | 0.029 (0.017) | 0.040 (0.035) | –0.005 (−0.000) | 0.218 (0.107) |
| B–Kr | 0.043 (0.039) | 0.018 (0.023) | –0.014 (−0.011) | 0.385 (0.361) | |
| B–Xe | 0.058 (0.054) | –0.014 (−0.007) | –0.026 (−0.022) | 0.552 (0.545) |
All bond critical point values are in au. Values within parentheses refer to the BP86/def2-TZVPP level.
Conclusions
Quantum chemical calculations have been carried out to propose a design strategy to realize the formation of unsupported donor–acceptor complexes between noble gases with group 13 Lewis acids. The bonding feature shows the hitherto unexplored two-center–two-electron-type interaction. Calculations reveal that heavier noble gases form stable donor–acceptor complexes with sizable bond dissociation energies. This study also highlights the fact that prepyramidalization of the Lewis acidic center is an interesting strategy to realize stable donor–acceptor complexes of noble gases. Detailed bonding analyses reveal the donor–acceptor interaction in these molecules, where noble gases act as electron pair donors. Topological analyses within the realm of QTAIM and ELF reveal that these bonds have significant covalent character and are polar. The results presented in this study will shed light on the possibility of realizing unsupported donor–acceptor complexes of noble gases in future, and experimental realization is yet to be achieved.
Acknowledgments
A.K.G. thanks the Science and Engineering Research Board (SERB), Government of India, for providing financial assistance in the form of a project (Project no. ECR/2016/001466).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c00543.
Cartesian coordinates of all of the molecules along with their total energies in au (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bartlett N. Xenon hexafluoroplatinate (V) Xe+[PtF6]−. Proc. Chem. Soc. 1962, 197–236. 10.1039/PS9620000197. [DOI] [Google Scholar]
- Hoppe R.; Dähne W.; Mattauch H.; Rödder K. M. Fluorination of xenon. Angew. Chem., Int. Ed. 1962, 1, 599 10.1002/anie.196205992. [DOI] [Google Scholar]
- a Greenwood N. N.; Earnshaw A.. Chemistry of the Elements; Butterworth-Heinmann: Oxford, 2001; p 888. [Google Scholar]; b Frohn H. J.; Bardin V. V. Preparation and reactivity of compounds containing a carbon-xenon bond. Organometallics 2001, 20, 4750. 10.1021/om010490j. [DOI] [Google Scholar]; c Pettersson M.; Lundell J.; Khriachtchev L.; Isoniemi E.; Räsänen M. HXeSH, the First Example of a Xenon–Sulfur Bond. J. Am. Chem. Soc. 1998, 120, 7979. 10.1021/ja981032d. [DOI] [Google Scholar]; d Khriachtchev L.; Tanskanen H.; Lundell J.; Pettersson M.; Kiljunen H.; Räsänen M. Fluorine-Free Organoxenon Chemistry: HXeCCH, HXeCC, and HXeCCXeH. J. Am. Chem. Soc. 2003, 125, 4696. 10.1021/ja034485d. [DOI] [PubMed] [Google Scholar]; e Khriachtchev L.; Isokoski K.; Cohen A.; Räsänen M.; Gerber R. B. A Small Neutral Molecule with Two Noble-Gas Atoms: HXeOXeH. J. Am. Chem. Soc. 2008, 130, 6114. 10.1021/ja077835v. [DOI] [PubMed] [Google Scholar]
- Lehmann J. F.; Mercier H. P. A.; Schrobilgen G. J. The chemistry of krypton. Coord. Chem. Rev. 2002, 233–234, 1–39. 10.1016/S0010-8545(02)00202-3. [DOI] [Google Scholar]
- Gerber R. B. Formation of novel rare-gas molecules in low-temperature matrices. Annu. Rev. Phys. Chem. 2004, 55, 55–78. 10.1146/annurev.physchem.55.091602.094420. [DOI] [PubMed] [Google Scholar]
- Grochala W. Atypical compounds of gases, which have been called ‘noble’. Chem. Soc. Rev. 2007, 36, 1632. 10.1039/b702109g. [DOI] [PubMed] [Google Scholar]
- Collins G. A. D.; Cruickshank D. W. J.; Breeze A. Bonding in krypton difluoride. J. Chem. Soc., Faraday Trans. 1974, 70, 393. 10.1039/f29747000393. [DOI] [Google Scholar]
- a Belpassi L.; Infante I.; Tarantelli F.; Visscher L. The Chemical Bond between Au(I) and the Noble Gases. Comparative Study of NgAuF and NgAu+ (Ng = Ar, Kr, Xe) by Density Functional and Coupled Cluster Methods. J. Am. Chem. Soc. 2008, 130, 1048. 10.1021/ja0772647. [DOI] [PubMed] [Google Scholar]; b Breckenridge W. H.; Ayles V. L.; Wright T. G. Evidence for Emergent Chemical Bonding in Au+–Rg Complexes (Rg = Ne, Ar, Kr, and Xe). J. Phys. Chem. A 2008, 112, 4209. 10.1021/jp711886a. [DOI] [PubMed] [Google Scholar]
- Mück L. A.; Timoshkin A. Y.; Hopffgarten M. V.; Frenking G. Donor Acceptor Complexes of Noble Gases. J. Am. Chem. Soc. 2009, 131, 3942–3949. 10.1021/ja805990h. [DOI] [PubMed] [Google Scholar]
- a Khriachtchev L.; Pettersson M.; Runeberg N.; Lundell J.; Räsänen M. A stable argon compound. Nature 2000, 406, 874. 10.1038/35022551. [DOI] [PubMed] [Google Scholar]; b Khriachtchev L.; Pettersson M.; Lignell A.; Räsänen M. A More Stable Configuration of HArF in Solid Argon. J. Am. Chem. Soc. 2001, 123, 8610. 10.1021/ja016197s. [DOI] [PubMed] [Google Scholar]
- Pettersson M.; Khriachtchev L.; Lignell A.; Räsänen M.; Bihary Z.; Gerber R. B. HKrF in solid krypton. J. Chem. Phys. 2002, 116, 2508. 10.1063/1.1434992. [DOI] [Google Scholar]
- Chen Y. L.; Hu W. P. Rate Constant Calculation for HArF → Ar + HF and HKrF → Kr + HF Reactions by Dual-Level Variational Transition State Theory with Quantized Reactant State Tunneling. J. Phys. Chem. A 2004, 108, 4449. 10.1021/jp049740a. [DOI] [Google Scholar]
- Borthakur B.; Das S.; Phukan A. K. Strategies toward realization of unsupported transition metal–boron donor–acceptor complexes: an insight from theory. Chem. Commun. 2018, 54, 4975–4978. 10.1039/C8CC02027B. [DOI] [PubMed] [Google Scholar]
- Kalita A. J.; Rohman S. S.; Kashyap C.; Ullah S. S.; Guha A. K. Stabilization of neutral tricoordinate pyramidal boron: Enhanced Lewis acidity and profound reactivity. Polyhedron 2020, 175, 114193 10.1016/j.poly.2019.114193. [DOI] [Google Scholar]
- a Mikhailov B. M.; Bubnov Y. M.. Organoboron Compounds in Organic Synthesis; Harwood Academic: New York, 1984. [Google Scholar]; b Mikhailov B. M.; Smirnov V. N. 1-boraadamantane and its conversion to 1-hydroxyadamantane. Russ. Chem. Bull. 1973, 22, 2124. 10.1007/BF00929432. [DOI] [Google Scholar]; c Kaszynski P.; Pakhomov S.; Gurskii M. E.; Erdyakov S. Y.; Starikova Z. A.; Lyssenko K. A.; Antipin M. Y.; Young V. G. Jr.; Bubnov Y. N. 1-Pyridine- and 1-Quinuclidine-1-boraadamantane as Models for Derivatives of 1-Borabicyclo[2.2.2]octane. Experimental and Theoretical Evaluation of the B–N Fragment as a Polar Isosteric Substitution for the C–C Group in Liquid Crystal Compounds. J. Org. Chem. 2009, 74, 1709–1720. 10.1021/jo802504c. [DOI] [PubMed] [Google Scholar]
- a Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]; b Perdew J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- a Becke A. D.; Johnson E. R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101–154109. 10.1063/1.2065267. [DOI] [PubMed] [Google Scholar]; b Johnson E. R.; Becke A. D. A post-Hartree–Fock model of intermolecular interactions. J. Chem. Phys. 2005, 123, 024101–024107. 10.1063/1.1949201. [DOI] [PubMed] [Google Scholar]; c Johnson E. R.; Becke A. D. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections. J. Chem. Phys. 2006, 124, 174104–174109. 10.1063/1.2190220. [DOI] [PubMed] [Google Scholar]
- Hirao H. Which DFT Functional Performs Well in the Calculation of Methylcobalamin? Comparison of the B3LYP and BP86 Functionals and Evaluation of the Impact of Empirical Dispersion Correction. J. Phys. Chem. A 2011, 115, 9308–9313. 10.1021/jp2052807. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, revision A.03; Gaussian, Inc.: Wallingford, CT, 2016.
- Boys S. F.; Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. 10.1080/00268977000101561. [DOI] [Google Scholar]
- Reed A. E.; Weinhold F.; Curtiss L. A. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
- Bader R. W. F.Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, 1990. [Google Scholar]
- a Silvi B.; Savin A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. 10.1038/371683a0. [DOI] [Google Scholar]; b Becke A. D.; Edgecombe K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. 10.1063/1.458517. [DOI] [Google Scholar]
- Tian L.Multiwfn: A Multifunctional Wavefunction Analyzer (version 3.1). http://Multiwfn.codeplex.com (accessed May 22, 2015). [DOI] [PubMed]
- Dapprich S.; Frenking G. Investigation of Donor-Acceptor Interactions: A Charge Decomposition Analysis Using Fragment Molecular Orbitals. J. Phys. Chem. A 1995, 99, 9352–9362. 10.1021/j100023a009. [DOI] [Google Scholar]
- a Brandhorst K.; Grunenberg J. Efficient computation of compliance matrices in redundant internal coordinates from Cartesian Hessians for nonstationary points. J. Chem. Phys. 2010, 132, 184101–184107. 10.1063/1.3413528. [DOI] [Google Scholar]; b Brovarets O. O.; Zhurakivsky R. O.; Hovorun D. M. DPT tautomerization of the long A·A* Watson-Crick base pair formed by the amino and imino tautomers of adenine: combined QM and QTAIM investigation. J. Mol. Model. 2013, 19, 4223–4237. 10.1007/s00894-013-1880-2. [DOI] [PubMed] [Google Scholar]
- Pyykkö P. Additive Covalent Radii for Single-, Double-, and Triple-Bonded Molecules and Tetrahedrally Bonded Crystals: A Summary. J. Phys. Chem. A 2015, 119, 2326–2337. 10.1021/jp5065819. [DOI] [PubMed] [Google Scholar]
- Cremer D.; Kraka E. Chemical Bonds without Bonding Electron Density — Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond?. Angew. Chem. Int. Ed. 1984, 23, 627. 10.1002/anie.198406271. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.