Highly Deformable, Ultrathin Large-Area Poly(methyl methacrylate) Films

Abstract

Poly(methyl methacrylate) (PMMA) is a glassy engineering polymer that finds extensive use in a number of applications. Over the past decade, thin films of PMMA were combined with graphene or other two-dimensional materials for applications in the area of nanotechnology. However, the effect of size upon the mechanical behavior of this thermoplastic polymer has not been fully examined. In this work, we adopted a homemade nanomechanical device to assess the yielding and fracture characteristics of freestanding, ultrathin (180–280 nm) PMMA films of a loaded area as large as 0.3 mm². The measured values of Young’s modulus and yield strength were found to be broadly similar to those measured in the bulk, but in contrast, all specimens exhibited a quite surprisingly high strain at failure (>20%). Detailed optical examination of the specimens during tensile loading showed clear evidence of craze development which however did not lead to premature fracture. This work may pave the way for the development of glassy thermoplastic films with high ductility at ambient temperatures.

1. Introduction

Polymers in the form of nanoscale thin films are attracting increasing attention as ideal structural materials of sensors or actuators in soft robotics or flexible/wearable electronic systems.¹⁻³ As these applications require components to withstand mechanical loadings, like traction or bending, the development of robust and reliable industrial products requires deep knowledge of the mechanical behavior of all involved materials, especially at the length scale relevant for such applications, that is, microscale and nanoscale. Indeed, at these length scales, the mechanical properties of materials can be significantly different. As expected from the reduced probability of finding larger defects in smaller volumes, many inorganic materials⁴ or metals⁵ showed an improvement of their mechanical strength at the nanoscale. In contrast, polymers were reported to show either an improvement or an even significant reduction of their mechanical performances (such as Young’s modulus) with decreasing thickness.⁶⁻⁸ Thus, the existence of conflicting reports in the literature⁹ requires a more extensive investigation of the mechanical behavior of thin and ultrathin polymeric films.

Testing specimens with a characteristic length in the order of micrometers/nanometers poses many challenges, which have been addressed in the past decades with the development of specific experimental setups.¹⁰ In the case of polymer nanofilms, these, for example, include nanoindentation,^11,12 buckling metrology,^13,14 bulge tests,¹⁵ or elastocapillary bending.¹⁶ These have been proven as effective methods for the derivation of meaningful mechanical properties, such as strength and stiffness. However, most of them rely on an indirect estimation of the mechanical properties, which is based on the application of analytical models relying on assumptions, require a supporting substrate, and do not enable a full understanding of the mechanical behavior of specimens, including failure processes.¹⁷ In this scenario, the use of tensile tests appears as the most straightforward approach to deeply investigate both elastic and plastic mechanical behavior of materials even at the nanoscale.¹⁸ Since the handling of a completely freestanding polymer film with less than 300 nm is extremely difficult, most of the tensile testing devices reported in the literature rely on the presence of a water layer to support the polymer film during testing.^7,19 Nevertheless, the liquid layer can play a role in the observed polymer behavior.²⁰

Herein this paper, we applied a custom-made tensile testing platform (Figure 1), recently proposed by some of the authors,²¹ to perform in situ optical microscopy mechanical characterization of freestanding poly(methyl methacrylate) (PMMA) nanoscale thin films. PMMA nanoscale thin films are widely used in the emerging two-dimensional materials technology,^22,23 also in combination with graphene or graphene-based materials; however, limited data about the full stress–strain curve of sub-micrometer thick PMMA samples are currently available in the literature that thus represents the motivation of our study.

Figure 1.

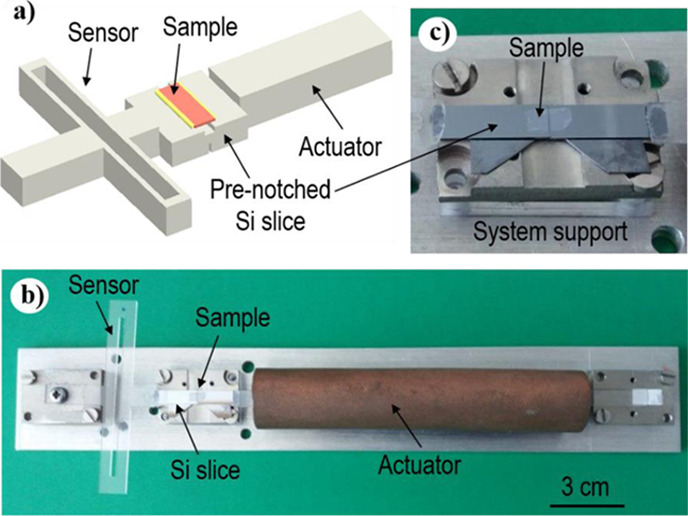
(a) Tensile testing platform for the mechanical characterization of nanoscale thin films, consisting of a thermal actuator, a flexible structure with the load sensing function (i.e., a load sensor), and a double pre-notched Si slice supporting the sample to be tested (not scaled). During the test (b), the actuator is covered with a copper shield to guarantee homogeneous heat distribution over the actuating beam. The actuating beam and the sensor are glued to opposite sides of a pre-notched Si slice. Before the test, preserving the film intact, the Si slice is carefully fractured, thus resulting in two blocks separated by a gap of a few micrometers [zoomed view (c)].²¹

2. Results and Discussion

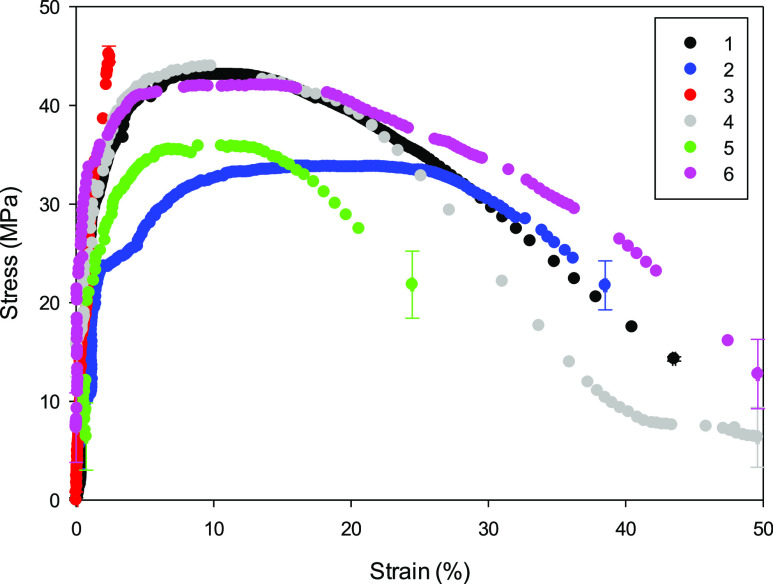
Figure 2 presents the stress–strain curves derived from PMMA films with the width in the range of 2.5–3 mm and the thickness ranging from 180 to 280 nm (Figure S1).

Figure 2.

Stress–strain curves of PMMA films with the thickness ranging between 180 and 280 nm (see Table 1).

Different from other common mechanical testing systems reported in the literature, which require the film to be supported, for example, by a compliant substrate¹³ or water,²⁴ here, the specimen is completely freestanding while loaded uniaxially. Its gauge length corresponds to the width (about 120 μm) of the pre-notch located on the top side of a silicon slice, where the specimen is decoupled from the substrate. Elsewhere, the specimen is instead in contact with the substrate with no evidence of slippage (more details can be found in the Supporting Information, Figure S2).

Compared to the bulk mechanical properties, both the strength and Young’s modulus (Table 1) herein derived for PMMA (41 ± 5 MPa and 2.6 ± 1.1 GPa, respectively) are in good agreement with bulk values (40–80 MPa and 1.8–3.3 GPa, respectively), while the strain at maximal stress is significantly higher (12 ± 3%) than the typical value of a few percent,²² which causes PMMA to be usually considered a brittle material. Indeed, in all tests (curve no. 3 was not fully recorded), at the end of the initial linear region, the stress–strain curve shows a plastic-like plateau, where thus the highest level of stress keeps more or less constant over a further strain increment.

Table 1. Overview of the Mechanical Properties of PMMA Films with Nanoscale Thicknesses.

specimen no.	thickness [nm]	strength [MPa]	strain at maximum stress (%)	E [GPa]
1	246 ± 25	43	10	3.2
2	254 ± 12	34	17	2.0
3	276 ± 30	48		2.3
4	180 ± 13	44	10	1.1
5	187 ± 9	36	11
6	180 ± 14	42	13	4.4
	ave.	41 ± 5	12 ± 3	2.6 ± 1.1

In order to get further insight into the mechanism enabling such high strain capability, it is useful to inspect the specimen appearance in the plateau and post-plateau regime. Figure 3 reports a sequence of images showing an area of a PMMA freestanding specimen, as observed in real time by using an optical microscope. The film appears quite transparent and enables to visualize at the right- or left-hand side few vertical lines corresponding to the underlying silicon substrate (i.e., a few micrometers off from the film). Already at the yield stress (corresponding to the red-framed picture), the specimen shows crazes that develop perpendicular to the main load direction (full-size pictures are reported in Figures S3–S7). At this stage, crazes result to be well confined within horizontal bands which can be clearly recognized on the specimen. With the further increase of displacement (blue-, green-, purple-, or pink-framed panels of Figure 3), crazes continue to grow and widen, thus causing a subsequent softening of the stress–strain curve, which finally leads to the specimen failure upon crack initiation and coalescence.

Figure 3.

Stress–strain curve of a 200 nm thick PMMA film. Each of the highlighted points in the curve corresponds to an optical microscopy image of a freestanding specimen during the tensile test. The sequence of images reveals the development of crazes (indicated by the arrows and initially almost confined within horizontal bands), which allows nanoscale PMMA films to accommodate large deformation (>10%) prior to fracture. Scale bar: 5 μm.

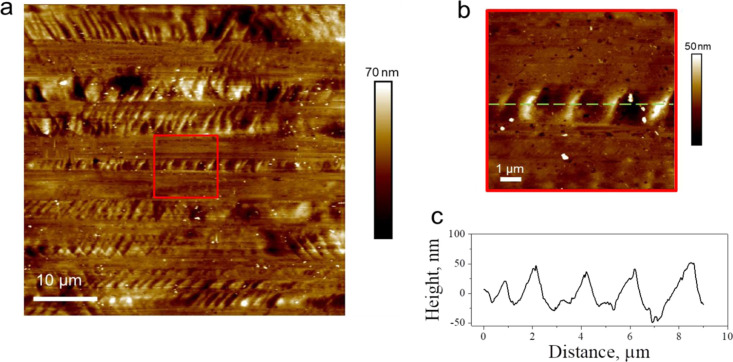
In the past, the occurrence of crazing was observed in polymeric thin films provided with both brittle²⁵ and ductile⁹ behavior. In the case of PMMA, non-fibrillated crazes were previously reported in macroscopic specimens under tensile loading, although not associated with the high deformation capability that we found in our experiments.²⁶ Crazes usually nucleate at defects or impurities at the surface or within the material,²⁷ which are likely to be present in our specimens as a consequence of the preparation method (commonly implemented during graphene production and manipulation). In general, the preparation process is known to play a significant role on the mechanical properties of thin-film materials by promoting, for example, specific chain conformation or solvent residuals.⁹ In our specimens, we can exclude the presence of solvent residuals as thermal annealing was performed before the transfer of the PMMA films on our testing platform. However, it is interesting to notice that our investigated PMMA films reproduced the morphology of the copper foil that we used in the first fabrication steps as a sacrificial substrate. This latter was characterized by a striated pattern with nanoscale roughness (Figure 4), which corresponds to the horizontal bands visible in the PMMA film of Figure 3. In the past, it was already reported that the application of wrinkle patterns on thin films can modify their mechanical response.²⁸ On the other hand, a recent study²⁹ on PMMA films with a thickness comparable with that of our specimens but fabricated from spin-coating on a smooth substrate, such as mica, reported a typical fracture strain of a few percent, with no evidence of crazing.

Figure 4.

Topographical investigation of the copper foil adopted as a sacrificial substrate in the production of PMMA films: AFM height images at different magnification scales of the sample (a,b) and the height profile along the dashed line (c). The morphology is characterized by alternated flat and undulated bands with a root-mean-square peak-to-valley value (R_q) of 18 nm. It is interesting noting that the striated pattern is reproduced in the PMMA films, as revealed by visible bands which are clearly aligned along the longitudinal axis of the tensile specimens (Figures 3 and S3–S7).

Thus, our experimental data and the examination of the current literature suggests that the striated pattern originating from the copper foil could be mainly responsible for the resulting high ductility of our PMMA films.

3. Conclusions

The mechanical characterization of polymer films with a thickness much smaller than 1 μm poses many technological challenges, which require the development of specific mechanical testing platforms. In this paper, we applied a novel custom-made tensile testing system to derive the mechanical behavior of freestanding PMMA films of nanoscale thicknesses. The real-time observation of the specimen during testing showed the formation of crazes that accompanied an unexpected high ductility of these films, which could thus possess several interesting applications where a large toughness modulus is required. The topographical investigation of the copper foil substrates used for the PMMA deposition provided evidence of an undulated regular pattern, which was reproduced by the freestanding films, too. Such correlation could reveal the engineering of wrinkling patterns on deposition substrates as a possible strategy to enhance and control the mechanical properties, such as ductility and toughness, of nanoscale films.

4. Materials and Methods

4.1. Thin-Film Preparation

A solution of PMMA (Sigma-Aldrich, M_w 350,000) in anisole was spin-coated on a strip of a 30 μm thick copper foil (C. Colombos & Co.). Then, the copper substrate was thermally annealed at 150 °C for about 20 min to remove any solvent residuals. After that, the PMMA film on copper was inserted in a transfer device, where copper was etched away using a 0.1 M aqueous solution of ammonium persulphate (APS). Afterward, the floating PMMA film was rinsed with distilled water slowly inserted in the transfer device until the full replacement of the APS solution. Finally, by gradually reducing the water level, the floating PMMA layer was deposited onto a pre-notched ⟨110⟩ single-crystal silicon slice (Figure 1). After the deposition, the specimen was dried at 40 °C for some hours under vacuum to remove the excess of water.

4.2. Thin-Film Thickness Measurement

The thickness of the PMMA film was measured through atomic force microscopy (AFM) with a Dimension Icon (Bruker) instrument, operating in the PeakForce Tapping mode using ScanAsyst-Air probes (stiffness 0.2–0.8 N/m, frequency ∼80 kHz). The film was scratched without damaging the substrate (more details are available in the Supporting Information, Figure S1). The average depth of the scratch below the mean surface plane, corresponding to the film thickness, was measured using the cross-section analysis of the NanoScope Analysis software. Several different scratches (performed in an area far enough from the gauge length) were measured for each film to allow statistical analysis of data.

4.3. Mechanical Characterization

After the production and thickness measurement, the silicon slice with the PMMA sample on top was transferred to the mechanical testing platform (Figure 1). Here, the silicon slice was connected on one side to a thermal actuator in order to apply load/displacement and on the other side to a calibrated spring with the load sensing function (i.e., a load sensor). As explained in an earlier report of the authors,²¹ before the tensile test, the silicon slice was cautiously fractured, leading to two blocks connected by an intact freestanding PMMA film. The platform then enabled a relative displacement between the actuator and the load sensor. Then, the actuator was activated, and the silicon block connected to the actuator moved, thus stretching the specimen. This latter, in turn, depending on its mechanical strength, pulled the silicon block connected to the load sensor, causing a deformation which can be used to estimate the traction force. The tensile specimen deformation was observed in real-time via optical microscopy, and pictures were taken in order to capture the gap between the two silicon blocks opening during the test. Such pictures were processed through a custom-made image correlation routine in order to derive the displacement of both the load sensor and the actuator. The load sensor displacement was then multiplied by its stiffness (evaluated experimentally) in order to derive the force experienced by the specimen, which was later divided by the specimen cross-sectional area in order to provide the stress. The strain was instead calculated as the difference between the load sensor and actuator displacement, divided by the initial gauge length.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c00016.

• Details about the procedure followed to measure the PMMA film thickness by AFM; 250 nm thick PMMA film deposited onto a silicon slice and connected to the tensile testing platform; deformations appearing only in areas where the film is detached from the Si substrate; measurement of the displacement induced in the sample by the application of an axial force; and 200 nm thick PMMA film under strains of 6, 17, 25, 30, and 43% (PDF)

The authors declare no competing financial interest.