Methodological evaluation of bias in observational coronavirus disease 2019 studies on drug effectiveness

Abstract

Background and objective

Observational studies may provide valuable evidence on real-world causal effects of drug effectiveness in patients with coronavirus disease 2019 (COVID-19). As patients are usually observed from hospital admission to discharge and drug initiation starts during hospitalization, advanced statistical methods are needed to account for time-dependent drug exposure, confounding and competing events. Our objective is to evaluate the observational studies on the three common methodological pitfalls in time-to-event analyses: immortal time bias, confounding bias and competing risk bias.

Methods

We performed a systematic literature search on 23 October 2020, in the PubMed database to identify observational cohort studies that evaluated drug effectiveness in hospitalized patients with COVID-19. We included articles published in four journals: British Medical Journal, New England Journal of Medicine, Journal of the American Medical Association and The Lancet as well as their sub-journals.

Results

Overall, out of 255 articles screened, 11 observational cohort studies on treatment effectiveness with drug exposure–outcome associations were evaluated. All studies were susceptible to one or more types of bias in the primary study analysis. Eight studies had a time-dependent treatment. However, the hazard ratios were not adjusted for immortal time in the primary analysis. Even though confounders presented at baseline have been addressed in nine studies, time-varying confounding caused by time-varying treatment exposure and clinical variables was less recognized. Only one out of 11 studies addressed competing event bias by extending follow-up beyond patient discharge.

Conclusions

In the observational cohort studies on drug effectiveness for treatment of COVID-19 published in four high-impact journals, the methodological biases were concerningly common. Appropriate statistical tools are essential to avoid misleading conclusions and to obtain a better understanding of potential treatment effects.

Introduction

With a growing number of publications on potential therapeutic candidates for coronavirus disease 2019 (COVID-19) treatment, high-quality observational studies have added value to the assessment of drug benefit in the real-world health-care setting [1,2]. However, the observational study design has important limitations and poses several challenges in the data analysis, particularly regarding the time-dependent nature of the data [3]. Ignorance of methodological biases in observational studies with time-to-event analysis may lead to distorted results and false conclusions on the exposure–outcome associations [4,5]. The aim of this article is to review the observational studies on evaluation of drug effectiveness in individuals with COVID-19 with regard to the presence of three methodological biases referred to as immortal time bias, confounding and competing risk bias. This work also aims to give recommendations on avoiding these biases.

In contrast to randomized clinical trials, in observational cohort studies a drug of interest is often prescribed after initiation of a study, e.g. later during follow-up. Immortal time typically occurs when there is a delay or waiting period between cohort entry and the time of the first prescription, which is falsely accounted for as drug-exposed time. Hence, exposed participants must survive the initial time period to receive treatment if they are not assigned to the unexposed cohort [5,6]. Exclusion or misclassification of observation time often leads to immortal time bias and consequently to artificial overestimation or underestimation of drug effectiveness [6,7].

Control of both time-fixed and time-varying confounding is crucial because of the lack of randomization in observational real-world data [8]. In contrast to time-fixed confounding bias, time-varying confounding is commonly encountered in longitudinal observational studies [[9], [10], [11]]. In clinical epidemiology, treatment exposures are often time-varying and the values of potential confounders may change during the observational period, leading to time-varying confounding [12,13]. A lack of control of confounding may lead to biased estimates of treatment effects and causal misinterpretation [11,14].

Another issue that is often observed in observational studies with survival or time-to-event analysis is the competing risk bias. By definition, a competing risk is an event that modifies the chance of occurrence of the primary event of interest and can occur when a patient is at risk of more than one type of event [15].

Competing risk events are frequently observed in hospital epidemiology when the follow-up ends with hospital discharge. In turn, hospital discharge is a competing risk for the hospital death that is often the outcome of interest [7,16]. In survival analyses, the survivor function and the hazard function are the two most common methods for representation of survival data. In the presence of competing risks, the naïve Kaplan–Meier estimator takes the competing risks as censored observations. As a result the Kaplan–Meier analysis overestimates cumulative risks and produces upwards-biased estimates [[16], [17], [18]]. Furthermore, the causal treatment effects cannot be completely assessed if the measures of association are reported only for the event of interest [7,17,18]. The key recommendations to address all the three methodological biases are listed as summary points in Box 1 .

BOX 1. Summary points.

• •Time zero, time of treatment initiation and end of follow-up should be clearly described in the research methods. To avoid immortal time bias, follow-up time and treatment status should be properly accounted by the design or statistical methods.
• •To avoid competing risk bias, a competing risk analysis has to be performed to describe results on all cause-specific hazards and visualized using cumulative hazard functions. If there is no follow-up beyond hospital discharge, the discharge has to be handled as a ‘competing event’ in the statistical analysis.
• •Immortal time bias, time-fixed confounding and competing risk bias can be addressed simultaneously by applying a cause-specific Cox regression for an event of interest and a competing event with the inclusion of treatment as a time-dependent covariate.
• •If robust time-varying clinical data are available and applicable, time-varying confounding should be addressed using a marginal structural Cox model or other g-methods for causal inference.
• •Data analysis should be performed in a stepwise manner, starting from simple straightforward methods to increased model complexity.

Alt-text: BOX 1

Methods

Study selection, inclusion and exclusion criteria

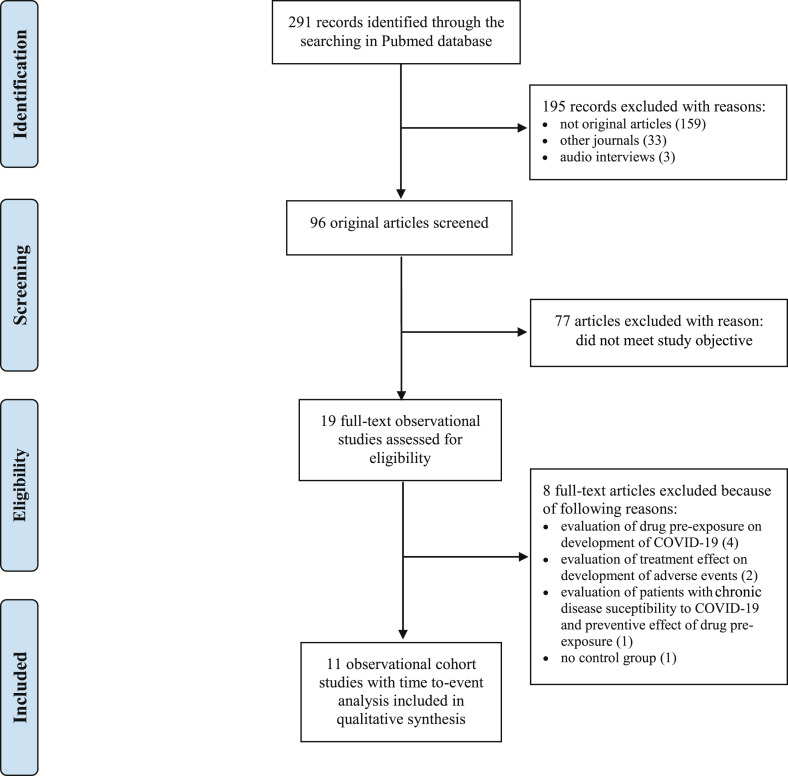
A literature search of observational studies on drug effectiveness in hospitalized patients with COVID-19 was performed in four journals: the British Medical Journal (The BMJ), the New England Journal of Medicine (NEJM), the Journal of the American Medical Association (JAMA), and The Lancet. Also, their sub-journals were selected. These journals were chosen because they are the leading and most cited medical journals with high impact factors. This review required original retrospective observational cohort studies with primary data including time-to-event data analysis. As a result, comments, correspondence, opinions, researcher letters and audio interviews were excluded. The inclusion criteria were hospitalized patients diagnosed with COVID-19. Both single-centre and multicentre studies were included. The literature search included studies that investigated drug effectiveness alone or in combination with standard therapy. Studies that focused on drug preventive rather than therapeutic effects were excluded. Articles that investigated the adverse effects of drug therapy only were not included either. The selection included studies with a comparative control group in which patients either received standard therapy or no treatment. Studies with different time-dependent clinical outcomes, such as in-hospital mortality, overall survival and survival without transfer to the intensive care unit (ICU), were selected for our review. Finally, the study selection was limited to articles published between the start of the pandemic in December 2019 and 23 October 2020. The selection procedure of our literature search is shown in the Preferred Reporting Items for Systematic Reviews and Meta-analyses (PRISMA) flow diagram (Fig. 1 ).

Fig. 1.

Flow diagram of the identified studies in the systematic literature review.

Data sources and search strategy

The systematic literature review was performed in the PubMed database on 23 October 2020. The review was conducted according to the PRISMA guidelines for reporting systematic reviews [19]. The list of keywords and detailed search strategy are described in the Supplementary material (Tables S1 and S2).

Methodological bias assessment

The assessment of biases was performed independently by all three authors. Each observational study was reviewed in-depth to determine the possible presence of immortal time bias, confounding bias and competing risk bias by screening the Methods as well as the Results section. The design, methods and statistical techniques were evaluated. Studies were considered to be susceptible to the immortal time bias if the time period before treatment allocation was not addressed in the analysis and, as a result, time-dependent drug exposure was statistically handled as a time-fixed exposure. The susceptibility to both time-fixed and time-varying confounding biases was evaluated. The occurrence of time-fixed confounding biases was determined if baseline covariates were not adjusted. However, the evaluation of correctness, adequacy and effectiveness of the applied adjustment methods and the degree of residual confounding were outside the scope of this review. The time-varying confounders were evaluated by examining the presence of time-dependent treatment and time-varying covariates. Studies were considered vulnerable to time-varying confounding bias if sophisticated statistical methods for controlling of time-dependent confounders were not applied. Studies were considered as being susceptible to competing risk bias if follow-up of patients was ensured only until discharge and individuals who were discharged alive were censored at the time of discharge for quantifying the probability of experiencing the event of interest. To identify whether the biases were addressed, the study methodology (i.e. study design and applied analytical methods) and results were evaluated. In addition, the supplementary materials of the included articles were checked.

Results

Out of 255 articles screened, 11 observational cohort studies on the drug effectiveness for COVID-19 treatment in hospitalized patients were included; six articles from The Lancet and its sub-journals, three articles from the Journal of the American Medical Association and its sub-journals as well as one from the British Medical Journal and one from the New England Journal of Medicine (Table 1 ) [[20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30]]. These observational studies investigated the effectiveness of drugs such as anakinra, azithromycin, chloroquine or hydroxychloroquine, methylprednisolone and tocilizumab. These drugs were administered alone or in combination with standard therapy. All of these studies were susceptible to at least one of the three discussed types of bias (Fig. 2 ). The results and examples of the identified biases are given in the following sections.

Table 1.

Characteristics of included studies and their features of immortal time bias

First author [reference]	Journal title abbreviation	Study baseline (time zero)	Start of treatment exposure	Susceptibility to immortal time bias	Accounted for bias		Methods addressed immortal time bias
					Primary analysis	Secondary analysis
Biran [20]	Lancet Rheumatol	admission to ICU	early in ICU	yes	no	no	not reported
Cavalli [21]	Lancet Rheumatol	admission to hospital	day zero (different time scales for treated and untreated patients)	yes a	no	no	not reported
Geleris [22]	N Engl J Med	24 hours after admission to hospital	within 48 hours or during follow-up period	yes	no	yes	landmark analysis
Guaraldi [23]	Lancet Rheumatol	admission to tertiary hospital	at time of hospital admission up to 24 hours	yes	no	no	not reported
Gupta [24]	JAMA Intern Med	admission to hospital	within 2 days of ICU admission	yes	no	yes	nested target trial emulation analysis
Huet [25]	Lancet Rheumatol	admission to hospital	day zero (different time scales for treated and untreated patients)	yes a	no	no	not reported
Kuderer [26]	Lancet	start of follow-up not clearly defined	start of treatment not clearly defined	start of follow-up, start of treatment is not clearly defined	n/a	n/a	not reported
Mahévas [27]	BMJ	admission to hospital	within 48 hours, more than 48 hours or during follow-up	yes	no	yes	target trial emulation analysis (mimicking an ITT and an as-treated)
Mehra [28]	Lancet	start of follow-up not clearly defined	within 48 hours after diagnosis established	start of follow-up is not clearly defined	n/a	n/a	not reported
Rosenberg [29]	JAMA	admission to hospital	at any time during hospitalization	yes	no	yes	sensitivity analysis with time-dependent treatment status
Wu [30]	JAMA Intern Med	admission to hospital	start of treatment not clearly defined	start of treatment is not clearly defined	n/a	n/a	not reported

Abbreviations: ICU, intensive care unit; ITT, intention-to-treat analysis; n/a, not available.

Journal title abbreviations: BMJ, the British Medical Journal; JAMA, the Journal of the American Medical Association; JAMA Intern Med, the Journal of the American Medical Association Internal Medicine; N Engl J Med, the New England Journal of Medicine; Lancet, The Lancet; Lancet Rheumatol, The Lancet Rheumatology.

^aTreatment was artificially converted to a time-fixed exposure.

Fig. 2.

The summary of biases for the included studies.

Occurrence of immortal time bias

Overall, eight studies were susceptible to immortal time bias [[20], [21], [22], [23], [24], [25],27,29]; in the three remaining studies, the start of the follow-up and/or the start of treatment exposure administration were not clearly defined [26,28,30]. In two of these studies, treatment was artificially converted into a time-fixed exposure by using different time scales for the treated and untreated cohorts, i.e. for the untreated group the start of follow-up was at time zero whereas for the exposed cohort the start of follow-up was set at the time of treatment [21,25]. As a result, artificial conversion of the time scale made the evaluation of the treatment impossible because of starting events before follow-up. It is likely that the three studies with unclear start of treatment administration are also susceptible to immortal time bias (Table 1) [26,28,30].

To account for immortal time bias, four studies performed sensitivity analyses and included the results in the secondary analyses or in the supplementary materials [22,24,27,29]. To address the immortal time bias, methods such as the landmark analysis [22], the target trial emulation analysis [24,27] and the time-dependent Cox regression analysis [29] were performed (Table 1). For instance, Rosenberg et al. accounted for delayed treatment start by using the time-dependent Cox proportional hazards model in their sensitivity analysis. The resulting hazard ratio for in-hospital mortality corrected for the immortal time bias increased in all treatment groups. In particular, for the group treated with hydroxychloroquine in combination with azithromycin it increased from 1.35 (95% CI 0.76–2.40) to 1.83 (95% CI 1.02–3.28) and for hydroxychloroquine alone from 1.08 (95% CI 0.63–1.85) to 1.46 (95% CI 0.84–2.55), respectively [29].

Occurrence of confounding bias

Out of the 11 studies susceptible to confounding, nine studies used methods to account for the time-fixed confounding bias [20,[22], [23], [24], [25], [26], [27], [28], [29]]; the two remaining studies showed results from the crude (unadjusted) analysis only [21,30]. The most frequently used methods to control for time-fixed confounding were adjustment in a regression model or stratification. Seven studies applied the propensity score weighting methods for confounding adjustment (Table 2 ).

Table 2.

Characteristics of included studies and their features of time-fixed and time-varying confounding bias

First author [reference]	Type of exposure	Susceptibility to time-fixed/time-varying confounders	Accounted for time-fixed confounding bias	Accounted for time-varying confounding bias		Methods controlling for confounding bias
				Primary analysis	Secondary analysis	Time-fixed	Time-varying
Biran [20]	time-dependent exposure	yes/yes	yes	no	no	semiparametric multivariate methods: regression models, PS matched analysis and PS covariate adjustment	not reported
Cavalli [21]	time-fixed exposure at day zero	yes/no	no	no	no	n/a	not reported
Geleris [22]	time-dependent exposure	yes/yes	yes	no	yes	stratification; semiparametric multivariate methods: regression models, PS matched analysis and PS covariate adjustment, IPW	landmark approach
Guaraldi [23]	time-dependent exposure	yes/yes	yes	no	no	stratification; semiparametric multivariate methods: regression models	not reported
Gupta [24]	time-dependent exposure	yes/yes	yes	no	yes	semiparametric multivariate methods: regression models and IPW	by conducting the nested target trial emulation approach and using IPW
Huet [25]	time-fixed exposure at day zero	yes/no	yes	no	no	semiparametric multivariate methods: regression model	not reported
Kuderer [26]	unclear defined	yes/unclear	yes	unclear	n/a	semiparametric multivariate methods: regression models	not reported
Mahévas [27]	time-dependent exposure	yes/yes	yes	no	yes	standardization; semiparametric multivariate methods: regression models, PS and IPTW	by conducting the target trial emulation approach and using IPTW
Mehra [28]	unclear defined	yes/unclear	yes	unclear	n/a	semiparametric multivariate methods: regression models, PS matched analysis	not reported
Rosenberg [29]	time-dependent exposure	yes/yes	yes	no	yes	by design: hospital-stratified random sampling; at analysis stage: semiparametric multivariate methods: regression models	time-dependent Cox regression
Wu [30]	unclear defined	yes/unclear	no	unclear	n/a	n/a	not reported

Abbreviations: IPW, inverse probability weighting; IPTW, inverse probability of treatment weighting; PS, propensity score.

In contrast to the time-fixed confounding bias, the time-varying confounding bias was less recognized. In eight studies where the exposure was time-varying (see Immortal time bias section), we presume that treatment initiation was caused by evolving clinical characteristics of the patient, which led to time-varying confounding (Table 2) [[20], [21], [22], [23], [24], [25],27,29]. In these studies, treatment exposure was analysed as a baseline covariate and, as a result, time-varying confounding was not addressed. For instance, covariates such as blood cell count as well as biochemical, coagulation and inflammatory parameters were more likely routinely collected and influenced the subsequent decisions on drug administration and on the outcome.

The time-varying confounding was controlled and secondary results were presented by four studies. For example, in the study conducted by Geleris et al. the landmarking analysis was based on the value of time-varying exposure at the landmark point (24 and 48 hours), after which the time-varying exposure may change value [22]. In the studies conducted by Gupta et al. and Mahévas et al. an observational target trial emulation methodology was used and appropriate adjustment methods, like inverse probability weighting, were applied [24,27]. In the study conducted by Rosenberg et al. a time-dependent Cox model that accounted for time-dependent treatment was used [29].

Occurrence of competing risk bias

Several time-to-event primary outcomes were investigated in the studies, such as development of acute respiratory distress syndrome, admission to ICU, administration of invasive mechanical ventilation, in-hospital death or 30-day in-hospital mortality, survival without transfer to ICU and overall survival. These end points were studied as a single event, or as a composite end point of several events (Table 3 ).

Table 3.

Characteristics of included studies and their features of competing risk events

First author [reference]	Primary end point/outcome	Competing event	Competing risk analysis		Cause-specific regression analysis for competing event	Graphical representation of survival curves
			In primary analysis	In secondary analysis
Biran [20]	in-hospital mortality	discharge alive	no	no	no	event-free survival probabilities; i.e. KM plot a for overall survival
Cavalli [21]	overall survival (at day 21), MV-free survival	discharge alive, discharge without need for MV	no	no	no	event-free survival probability; i.e. KM plots for overall survival and MV free survival
Geleris [22]	intubation or death without intubation as a composite endpoint	discharge alive without need for intubation	no	no	no	event-free survival probability; i.e. KM plot
Guaraldi [23]	composite of IMV or death, in-hospital death	discharge alive without need for IMV	no	no	no	cumulative incidence probabilities for MV or death, and death alone; i.e. 1–KM
Gupta [24]	in-hospital death (30-day mortality)	discharge alive	no	yes b	no b	cumulative incidence probabilities for mortality; i.e. 1–KM
Huet [25]	admission to ICU for IMV or death as a composite endpoint	discharge alive before ICU or without need for IMV	no	no	no	event-free survival probabilities; i.e. KM plots for event-free of IMV, death, and IMV or death
Kuderer [26]	30-day all-cause mortality	discharge alive	no	no	no	forest plot for 30-day all-cause mortality
Mahévas [27]	survival without transfer to ICU (at day 21)	no competing event	not necessary, CR is addressed by extended follow-up		no competing risk bias	event-free survival probability; i.e. KM plot for survival without ICU admission
Mehra [28]	in-hospital mortality	discharge alive	no	no	no	forest plot for in-hospital mortality
Rosenberg [29]	in-hospital mortality	discharge alive	no	no	no	cumulative incidence probabilities for in-hospital mortality; i.e. 1–KM
Wu [30]	development of ARDS and death among those with ARDS	discharge alive among those with ARDS	no	no	no	event-free survival probability; i.e. KM plots for overall survival

Abbreviations: ARDS, acute respiratory distress syndrome; CR, competing risk; ICU, intensive care unit; IMV, invasive mechanical ventilation; MV, mechanical ventilation; KM, Kaplan–Meier.

^aThe KM curves provided for the secondary end point (overall survival).

^bDischarge was addressed by keeping discharged patients in the risk set and not treating them as randomly censored. Keeping discharged patients in the risk set targets at estimating a sub-distribution hazard. This approach is not appropriate if the treatment is time-dependent.

All in all, ten out of the eleven studies seemed to be susceptible to competing risk bias because a follow-up ended with hospital discharge and discharged patients were censored in probability analyses [[20], [21], [22], [23], [24], [25], [26],[28], [29], [30]]. In nine out of the ten studies, the classical Kaplan–Meier method was applied to display the treatment effect and to compare survival probabilities between the treatment and control groups [[20], [21], [22], [23], [24], [25],27,29,30]. In one study, performed by Mahévas et al., the competing event of discharge alive for the primary outcome (survival without transfer to ICU) was addressed by the extension of follow-up for discharged patients, and the corrected Kaplan–Meier curves were presented in the supplementary material [27].

All of the studies used a regression model (logistic regression and/or the Cox proportional hazard regression model) to quantify the treatment effect for the primary event of interest. The Cox proportional hazards model provides a correct estimate of the treatment effect on the event of interest. Nonetheless, the regression analysis is incomplete if the hazard ratio for the competing event is not reported. Only in one sensitivity analysis, conducted by Gupta et al., discharge was addressed by keeping discharged patients in the risk set and not treating them as randomly censored. As a result, the adjusted hazard ratio of the event of interest shifted from 0.71 (95% CI 0.56–0.92) to 0.72 (95% CI 0.56–0.93). Keeping discharged patients in the risk set is targeted at estimating a sub-distribution hazard [31]. We remark that this approach is not appropriate if the treatment is time-dependent [24].

Discussion

Since the number of studies on COVID-19 treatment effectiveness and the speed of publishing new data in journals has drastically increased [32], unbiased results from observational studies are extremely important as a complement to randomized controlled trials. The methodological challenges in studying observational COVID-19 data and performing statistical analysis on drug effectiveness has been described in detail elsewhere [33,34]. However, our review has demonstrated that methodological issues such as immortal time bias, confounding bias and competing risk bias are commonly found in articles published in high-impact medical journals.

To our knowledge, for treatment effectiveness assessment, the best practice is to perform analysis in a stepwise manner, starting from simple straightforward methods to increased model complexity. To ensure a complex approach and enhance confidence, the results from simple and extended models should be presented side by side [35]. This approach can be used to address time-to-treatment, confounders, and competing risks issues. For details on the proper statistical techniques and analysis of time-to-event data in observational studies, we highly recommend the guidance of Kragh Andersen et al. [36].

As the primary step, a complete competing risk analysis should be presented that includes a cause-specific Cox regression analysis for the event of interest and for all competing events [7,33,36,37]. An initial model should include baseline covariates, further, time-fixed confounders need to be adjusted. This analysis provides insights into the effect of treatment and covariates on each event type separately [38]. To account for non-randomized treatment administration and reduce the effects of confounding, the model can be extended using more complex procedures, such as propensity score-based methods. Further, to estimate the causal treatment effect, more sophisticated analysis for time-varying confounders, such as g-methods (i.e. the inverse probability of treatment weighted marginal structural models, g-computation formula and g-estimation of structural nested models) must be applied [8,10]. For instance, in the excellent study by Ursino et al., the g-computation approach was applied to evaluate the potential treatment effect of corticosteroids and interleukin antagonists like tocilizumab and anakinra [39]. In addition, we refer to the textbook of Hernán et al. for the detailed tutorial on causal inference and g-methods [40].

In the presence of competing risks, we discourage the use of Kaplan–Meier plots for effect visualization because of the high risk of potentially misleading conclusions. Instead, cumulative cause-specific hazards can be calculated and should be plotted for the events of interest and for the competing events [41]. This method allows us to account for competing events and to display treatment exposure differences [16]. More generally, the multistate methodology offers several advantages for survival data analysis with multiple outcomes. A multistate model allows us to evaluate the time dynamics of disease progression by describing the occurrence of the events as transitions between different states [42]. This also makes it possible to visualize primary outcomes of interest and competing events simultaneously over a time period in a single plot [43].

The article by Lapadula et al. presents an appropriate analysis on antiviral treatment assessment in patients with COVID-19 [44]. In their study, the landmark analysis was applied to estimate survival rates conditional on a landmark time (7 days after intubation) to adjust for immortal time bias. The exposure was modelled to each treatment (remdesivir, hydroxychloroquine and lopinavir/ritonavir) as time-dependent covariates. The competing risk bias was addressed by estimation of two cause-specific hazard functions: for the event of interest such as in-patient hospital death and for the competing event such as discharge, respectively. As a result, the competing risk analysis showed that remdesivir was significantly associated with hospital discharge (hazard ratio 2.25; 95% CI 1.27–3.97) and with a non-significantly lower mortality (hazard ratio 0.73; 95% CI 0.26–2.1). Moreover, the cumulative hazard plots were used to visualize potential treatment effects [44]. This example addresses all three methodological biases and clearly demonstrates the need to study competing events.

With our study, we assessed the presence of methodological biases and provided recommendations. Several study limitations are noteworthy, such as the inclusion of only four journals and their sub-journals. As a result, we cannot extend the results obtained to other journals. Another limitation is that an incomplete or unclear description of the study methodology or/and results in the investigated publications could have resulted in incorrect interpretation of the analyses.

Conclusions

Immortal time bias, confounding bias and competing risk bias alone or in combination were present in all of the 11 reviewed observational studies on treatment effectiveness evaluation for hospitalized patients with COVID-19. These biases may have led to a severe overestimation or underestimation of COVID-19 treatment effectiveness estimates. As a result, the drugs may appear to be either more effective or conversely to have little to no effect. In fact, making valid causal inferences from real-world observational data is a demanding task that requires high-quality data and adequate statistical methods as well as clinical knowledge and statistical expertise.

Even though every study has its unique features, which should be addressed in a tailor-made analysis, the summary points (Box 1) and the following recommendations could be taken into account to prevent or decrease the occurrence and the severity of the methodological biases. To overcome immortal time bias, time-dependent treatment exposures should be included in the Cox regression model as a time-dependent variable [45]. In the presence of time-varying confounders, a marginal structural Cox model can be used and estimated using inverse probability of treatment weights [8]. In the competing risks setting, the cause-specific hazard ratios could also be obtained from the time-dependent Cox regression model. Furthermore, treatment effects should be visualized with cumulative hazard functions for the event of interest and all competing events [37,46]. Finally, corrected estimates should be reported as primary findings in the primary results section.

Transparency declaration

The authors declare no conflicts of interest. This study has been funded by the German Research Foundation (DFG) with project grant WO 1746/5-1.

Editor: L. Leibovici

Appendix A. Supplementary data

The following is the Supplementary data to this article: