Abstract
Radiologists, and doctors in general, need relevant information for the quantification and characterization of pulmonary structures damaged by severe diseases, such as the Coronavirus disease 2019 (COVID-19). Texture-based analysis in scope of other pulmonary diseases has been used to screen, monitor, and provide valuable information for several kinds of diagnoses. To differentiate COVID-19 patients from healthy subjects and patients with other pulmonary diseases is crucial. Our goal is to quantify lung modifications in two pulmonary pathologies: COVID-19 and idiopathic pulmonary fibrosis (IPF). For this purpose, we propose the use of a three-dimensional multiscale fuzzy entropy (MFE3D) algorithm. The three groups tested (COVID-19 patients, IPF, and healthy subjects) were found to be statistically different for 9 scale factors (). A complexity index (CI) based on the sum of entropy values is used to classify healthy subjects and COVID-19 patients showing an accuracy of , a sensitivity of , and a specificity of . Moreover, 4 different machine-learning models were also used to classify the same COVID-19 dataset for comparison purposes.
Keywords: Computed tomography, COVID-19, Multiscale entropy, Texture analysis
1. Introduction
Coronavirus disease 2019 (COVID-19), a highly infectious disease, is caused by a new coronavirus called SARS-CoV-2 [13], [34]. The SARS-CoV-2 infection leads to pulmonary interstitial damages, which may cause severe pneumonia, acute respiratory distress syndrome, multiple organ failure, and death [3], [7], [13], [34]. Currently, the gold standard diagnostic test for COVID-19 is a real-time reverse transcription polymerase chain reaction (RT-PCR) of the viral nucleic acid [7], [13], [34]. However, many studies have demonstrated the importance of using chest computed tomography (CT) in the management of COVID-19 patients [7], [33], [34]. Recent studies have found that chest CT have higher sensitivity values compared to RT-PCR when diagnosing COVID-19 [1], [14]. According to [1], chest CT has a sensitivity of , with RT-PCR as a reference standard. Besides, a study conducted on 51 COVID-19 patients [16] revealed that diagnosing through chest CT only misses of the positive cases.
The severity and the time course of the disease may lead to different CT patterns in COVID-19 patients. The main hallmarks of CT manifestations of COVID-19 are ground glass opacities (GGO), and consolidated pulmonary opacities [2]. Li et al. reported that these two features were both present in of their COVID-19 patients dataset [16]. GCO are present in most of the patients with a predominantly bilateral distribution in the posterior, subpleural, and peripheral lung areas [2], [7], [34]. GGO is defined as a hazy area of increased opacity within which pulmonary vessels remain visible. There can be several causes of GGO such as partial filling of air spaces, interstitial thickening, partial collapse of alveoli, increased capillary blood volume, or a combination of these [10]. This CT feature is considered to be one of the earliest visible CT manifestation as well as the most common imaging findings [34]. As the time gap between the first symptoms and the chest CT execution increases, so does the frequency of consolidation, and bilateral and peripheral lung disease. Other features like linear opacities and crazy-paving pattern can also appear [2].
Image texture analysis has been proposed as an alternative approach to the more traditional visual methods, for disease quantification. Texture analysis may improve the diagnosis and monitoring of pulmonary diseases [4], [8], [25], [26]. So far, several works have described typical CT imaging features [7], [13], [28], [33], [34], but they do not always indicate the complete information regarding the patients or CT imaging parameters [12]. Recently, a segmentation and classification scheme has been proposed for identification of pulmonary regions affected by COVID-19 among normal ones on CT images [6]. Besides, several works based on neural networks and machine learning techniques have been proposed to classify COVID-19 [17], [29], [30], [31], [32].
In [30], public datasets of X-rays and CT scans were used to classify COVID-19 cases and No Findings (healthy) cases, having a total of 510 images. Their feed-forward neural network based on texture features shows a validation accuracy of . To feed this neural network the authors used a 129 vector composed by gray-level co-occurrence matrix and based features, and local binary patterns [20], [21].
Wang et al. [32] proposed the use of a three-dimensional deep neural network called DeCoVNet. The authors used a large dataset of COVID-19 and non-COVID-19 CT volumes. Besides, they also used a data augmentation technique to increase their dataset. They report accuracy values of [32].
Other approaches have also been used with successful results. For example, in [17] the authors combined COVID-19 images with images generated using generative adversial network (GAN) and classified up to 4 classes (COVID-19, normal, pneumonia bacterial, and pneumonia virus cases). After obtaining the dataset, they used neural networks already proposed: AlexNet [15], GoogLeNet [27], and ResNet18 [11]. When classifying COVID-19 and normal cases, the validation accuracy reported is , , and , respectively [17].
Another interesting method used in this application is the FGCNet [31]. The authors use CT slices chosen by radiologists to classify COVID-19 cases. Their work involved a preprocessing stage, obtaining gray-scaled and increased contrast images that are posteriorly down-sampled [31]. Their network is based on convolutional neural network (CNN) to obtain a representation at the image level, and on graph convolutional network (GCN) to obtain a relation-aware representation. A data augmentation stage is also performed in their work. The authors report a mean accuracy of and a mean sensitivity of [31].
We herein propose the application of a newly developed textural analysis method for CT scans [9] based on three-dimensional multiscale fuzzy entropy (MFE3D) determination. This quantitative analysis is first applied to CT scans of COVID-19 patients, to determine pulmonary textual changes. Then, the results are compared to those obtained from healthy subjects and idiopathic pulmonary fibrosis (IPF) patients, another pulmonary disease for which quantification is not an easy task [9].
2. Materials and methods
The extremely recent MFE3D algorithm that we propose to use in our work has previously been tested on synthetic data for validation purposes, having already shown interesting results in CT scans texture analysis (for details see [9]).
2.1. Clinical dataset
The total clinical dataset, processed in this study, is composed of CT scans from 51 patients diagnosed with COVID-19, 26 healthy subjects, and 26 IPF patients, making a total of 103 subjects. The population characteristics for each group as well as the detailed description of the CT scans features are shown in Table 1 and Table 2 , respectively. The data regarding IPF disease goes inline with the disease's incidence since IPF typically affects elderly males [24].
Table 1.
Population characteristics of COVID-19 patients, healthy subjects, and idiopathic pulmonary fibrosis (IPF).
| Subjects | Mean age (years) | Gender |
|
|---|---|---|---|
| Male (%) | Female (%) | ||
| Healthy subjects | |||
| IPF patients | |||
| COVID-19 patients | |||
Table 2.
Clinical dataset CT features (kVp – kiloVolt peak).
| Reconstruction matrix | pixels |
| Tube voltage (% of subjects) | 100 kVp (37.9%) |
| 120 kVp (62.1%) | |
| Mean pixel spacing | mm |
| Mean number of scans per patient | units |
| Slice thickness (% of subjects) | mm () |
| mm () | |
| mm () | |
| Total collimation width (% of patients) | mm () |
| mm () |
The CT images were collected by the University Hospital of Rennes, France (IRB approval following the Declaration of Helsinki - approval number of 19.6). IPF-diagnosed patients were diagnosed with stable IPF (according to multidisciplinary discussions) and were recruited at the competence center for rare pulmonary diseases, Department of Respiratory Medicine, University Hospital of Rennes, France. Neither infection nor exacerbation was encountered in the preceding 8 weeks to their first appointment. The subjects that underwent chest CT scans to rule out other pathologies were considered healthy if the scans, verified by an expert radiologist, confirmed the absence of any abnormal structures of the lungs parenchyma [9]. For the COVID-19 dataset, the suspected patients, admitted to the regional emergency departments of COVID-19 (University Hospital of Rennes, France) between March 26 and April 17 of 2020, were considered as possible candidates. These patients were assessed using a non-contrast chest CT scan and all underwent RT-PCR testing for SARS-CoV-2. The retrospectively confirmed cases were included in the dataset.
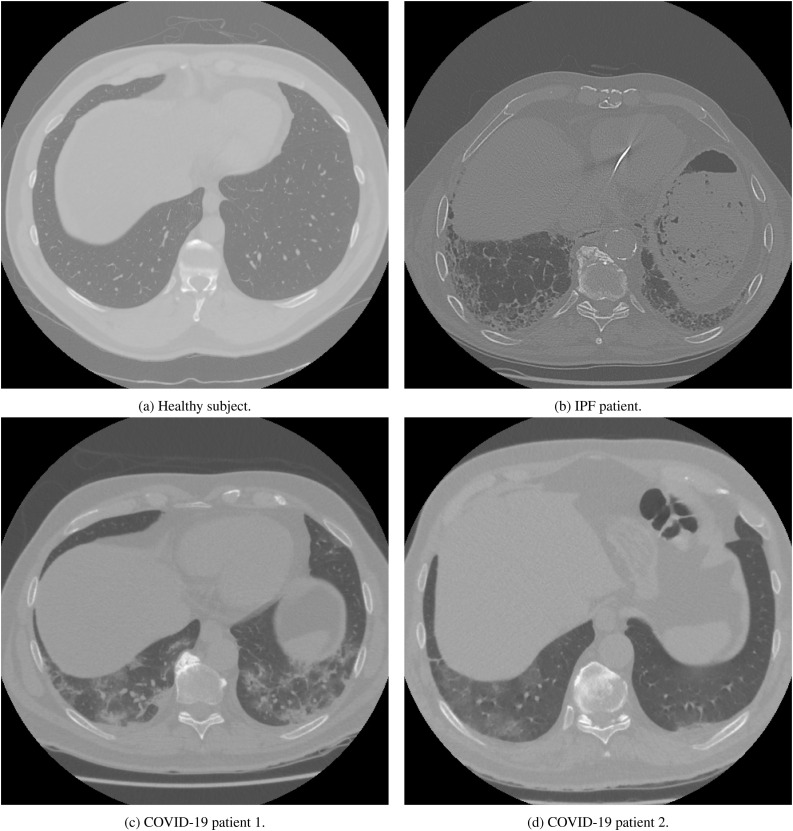
Fig. 1 shows typical examples of chest CT in the basal area of the lungs for each group. The control group is represented in Fig. 1a by a 53 years old healthy subject with normal lung structure. In Fig. 1b, a CT scan from a diagnosed patient with IPF (78 years old) is represented and shows honeycombing and reticular pattern which are two typical features of IPF patients in CT scans. Fig. 1c and Fig. 1d show CT scans of two patients diagnosed with COVID-19 with ages of 56 and 72 years, respectively. Fig. 1c shows ground glass opacities and some consolidation. In Fig. 1d, consolidation is mainly visible.
Fig. 1.
CT scans examples of a healthy person (a), idiopathic pulmonary fibrosis (IPF) (b), and Coronavirus disease 2019 (COVID-19) patients (c and d).
2.2. Segmentation of the region of interest
As mentioned earlier, one of the most common features present in CT images of pulmonary regions affected by COVID-19 is GGO. This feature, caused by the presence of COVID-19, is mainly predominant in posterior, subpleural, and peripheral lung regions with a bilateral distribution [34], [7]. On the other hand, IPF affects basal, subpleural, and peripheral lung regions [24]. Hence, the motivation is to segment volumes from these regions according to both diseases incidence.
Therefore, we selected CT scans from the basal and peripheral lung areas that were posteriorly segmented to a region of interest (ROI). The ROI volumes used for entropy analysis had voxels and were chosen based on the process detailed in [9]. This process searches for a cube (with an edge of 50 voxels) using a bottom-up approach to guarantee that the volume corresponds to a basal and peripheral region. Given the slice thickness (see Table 2), the final volumes represent a region of the lung with a height up to 62.5 mm. All the ROI volumes were taken from the right lung as an arbitrary choice. Volumes from the left lungs were not considered to avoid data correlation.
2.3. Entropy determination
The algorithm applied in this work relies on two main steps. The first step is to determine the fuzzy entropy on the original region of interest (ROI) using a three-dimensional fuzzy entropy (FuzEn3D) [9]. This algorithm divides the volume into smaller three-dimensional templates of size , , where corresponds to the size of the edge of the cubes to be compared, i.e., the embedding dimension. Afterwards, a fuzzy exponential function, controlled by parameters tolerance () and fuzzy power (), is used to determine a similarity degree between the templates. Finally, the entropy value is determined by a relation between the average similarity degree obtained for two consecutive embedded dimensions ( and ).
Consider a given volume, , of dimensions W L H (W-width, L-length, H-height). To determine its entropy value, cubic templates of edge sizes and , both with the same starting voxel (), must be compared. The total number of three-dimensional templates that can be obtained is [9].
In order to simplify the mathematical notation, two volumetric templates of edge size , with different starting voxels, can be defined using U and U . For comparison purposes of the templates, the distance between the two templates ( and ), , is defined as the infinity norm distance between them and used in the exponential fuzzy function to obtain the similarity degree as it follows [9]:
| (1) |
The variable represents the tolerance parameter, chosen as a percentage of the standard deviation of the original data, and is the fuzzy power parameter [9].
Once the similarity degree is computed for all the possible templates (excluding self-matches) then, the average of all similarity degrees is defined as follows [9]:
| (2) |
The previous steps are repeated for () - edged three-dimensional templates, allowing to determine the entropy value as the natural logarithm of the ratio between and [9]:
| (3) |
According to the recently validated algorithm [9], the embedding dimension (), tolerance (), and fuzzy power () parameters used to determine entropy values were , , and , where SD(U) stands for the standard deviation of the original volume. The maximum downsampling scale applied in this analysis is . These parameters were previously obtained using synthetic volumes [9], allowing us to compare the three different conditions in this study (healthy, IPF-suffering, and COVID-19-suffering patients). Otherwise, the comparison between the two pathologies would be much harder. Even if these parameters might not be the optimal ones, these ones allow an adequate and consistent analysis.
The second main step that this processing procedure relies on corresponds to the application of a coarse-graining procedure to produce different downsampled volumes, in order to obtain information across several scale factors (). The number of voxels for each downsampled volume, , is determined by the relation where represents the degree of downsampling and , , and the original volume width, length, and height, respectively (in this study voxels). The computation of FuzEn3D is then repeated for each downsampled volume (see equation (4)).
| (4) |
The described data processing results in a total of 10 entropy values for each volume (one for each scale factor). The entropy computation was performed on MATLAB R2019® software. The full description of the algorithm can be found in [9].
2.4. Complexity index
Based on [5], we also propose the use of a score for the multiscale entropy values. This score is unique for each ROI and is computed as a complexity index (CI). It is defined as the sum of the entropy values for a certain interval of scale factors, i.e.:
| (5) |
For this work, as described below, and were chosen, therefore, . Moreover, the CI was used to classify the healthy subjects and COVID-19 patients using a threshold (of 1.74 to maximize the accuracy). The receiver operating characteristic (ROC) analysis was also performed.
2.5. Statistics
Once the multiscale fuzzy entropy values were obtained for each scale factor, the normality of the groups was assessed using the Shapiro-Wilk test (for ). When the distribution of the three groups was found to be normal, the one-way ANOVA parametric test was performed. Otherwise, a Kruskal-Wallis test was used to find if the groups were statistically significantly different. Afterwards, to perform a pairwise comparison, the post-hoc Tukey's honestly significant difference test was used. A similar procedure was considered for the CI values to verify the existence of statistical differences. The statistical analysis was also performed on MATLAB R2019® software considering a statistical significance for .
2.6. Classification approaches
For comparison purposes, the MFE3D entropy values of to and the CI values were used as features for several classifiers. Due to the rise of entropy for the last two-scales, probably associated with the extremely low size of the down-sampled volumes, the last two scale factors values were not used as features.
The classifiers used were: support vector machine (SVM) with a linear and a radial basis function (rbf) kernel, a k-nearest neighbors (kNN) algorithm, and finally, a neural network using the Multi-layer Perceptron (MLP) classifier.
The regularization parameter was set to for the linear-SVM and for the rbf-SVM. The gamma parameter was set to for the rbf-SVM since the number of features is 9. For the kNN algorithm, the number of neighbors used was , using the Manhattan distance definition. The MLP network used 4 hidden layers, with 40 neurons each, using a quasi-Newton based optimizer, with ReLu activation, and a learning rate of .
The classification approaches used a split of for the train and test dataset. In addition, within the train dataset, we also used a k-fold technique with , obtaining the validation scores.
Similarly to the threshold classifier using the complexity index, these different classification approaches were used to classify healthy, and COVID-19 cases. In the Results and Discussion section, these are compared in terms of accuracy, area under the curve (AUC), and sensitivity. The mean values and best cases of accuracy, AUC, and sensitivity of the validation and test datasets are shown.
The classifiers models were implmented using Python® 3.7.4 and the library scikit-learn 0.24.1. [22].
3. Results and discussion
3.1. Entropy determination
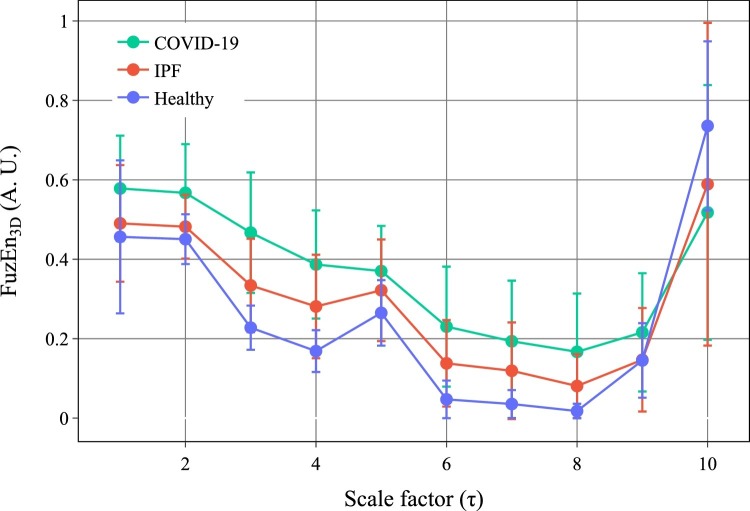
The results obtained for the MFE3D values are presented in Fig. 2 . The entropy values are depicted as mean standard deviation for each scale factor () and group. Fig. 2 shows different values for FuzEn3D for each group and at each scale factor, allowing a direct comparison between previously obtained results [9] and the new COVID-19 data. Except for , COVID-19 group FuzEn3D mean values are higher, with a significant difference, than both healthy and IPF groups. Furthermore, the three groups follow a decreasing behavior of their entropy values up to . The rise observed for and occurs due to the small size of the downsampled coarse-grained volumes. Given that the original volumes have a size of voxels, for the volume has voxels resulting in a structure with few similarities between its voxels, leading to higher values of entropy.
Fig. 2.
Mean and standard deviation for the tridimensional fuzzy entropy values for healthy subjects, idiopathic pulmonary fibrosis (IPF), and coronavirus disease 2019 (COVID-19) patients. Results for the scale factors to are shown.
For , the entropy increase can be explained by the blood vessels that have a size between 2-4 mm [23]. When considering the mean pixel spacing value, these vessels will be represented up to around pixels. For , they are averaged and represented only by 1.1 pixels. We hypothesize that this introduces slight three-dimensional texture modifications, leading to a more irregular structure and, therefore, a relative increase of the system's entropy value [9].
3.2. Statistics
The normality of the entropy values distribution was assessed using Shapiro-Wilk test for a statistical significance of (Table 3 ). The results show that only for the scale factor , the three groups, healthy subjects, IPF, COVID-19 patients, follow a normal distribution for p-values of 0.125, 0.601, and 0.054, respectively. For the remaining scale factors, at least one group does not follow a normal distribution.
Table 3.
Normality test assessment using Shapiro-Wilk (W) statistics and a statistical significance of (*) for healthy subjects, idiopathic pulmonary fibrosis (IPF), and coronavirus disease 2019 (COVID-19) patients.
| Scale factor () | Healthy subjects |
IPF patients |
COVID-19 patients |
|||
|---|---|---|---|---|---|---|
| 1 | * | |||||
| 2 | ||||||
| 3 | * | * | * | |||
| 4 | * | * | * | |||
| 5 | * | * | ||||
| 6 | * | * | * | |||
| 7 | * | * | * | |||
| 8 | * | * | * | |||
| 9 | * | * | ||||
| 10 | * | * | ||||
For , the normality assumption is verified, therefore the one-way ANOVA test was used to verify the existence of a statistical difference between the groups. For the remaining scales, the Kruskal-Wallis test was performed. The statistical test and the corresponding p-values are presented in Table 4 .
Table 4.
One-way ANOVA (F) and Kruskal-Wallis (H) statistics for and for and , respectively, to assess statistical differences between the three groups for (**) and for (*).
| Scale factor () | Test statistics | |
|---|---|---|
| 1 | ** | |
| 2 | ** | |
| 3 | ** | |
| 4 | ** | |
| 5 | ** | |
| 6 | ** | |
| 7 | ** | |
| 8 | ** | |
| 9 | * | |
| 10 | ** | |
The null hypothesis of both one-factor ANOVA and Kruskal-Wallis is rejected with a significant level of 0.01, for most of the scales (9 out of 10). This means that the population median of the groups is different, confirming the discriminatory nature of FuzEn3D. For the case of one-factor ANOVA (), the populations of each group do not have the same mean value. The previous results only determine the existence of a statistical difference between the groups. To evaluate which specific groups are statistically different from each other, a post hoc test for pairwise comparison is applied. With that in mind, a Tukey's honestly significant difference test was performed to assess multiple comparisons of the groups. Table 5 summarizes the results for healthy, IPF, and COVID-19 groups.
Table 5.
Tukey's honestly significant difference test of the possible comparison pairs (Healthy (H) VS. IPF; Healthy VS. COVID; and, IPF VS. COVID). Statistical significance for (**) and for (*).
| Scale factor () |
-Value |
||
|---|---|---|---|
| H-IPF | H-COVID | IPF-COVID | |
| 1 | 0.330 | 0.000** | 0.040* |
| 2 | 0.502 | 0.000** | 0.002** |
| 3 | 0.003** | 0.000** | 0.002** |
| 4 | 0.001** | 0.000** | 0.010* |
| 5 | 0.100 | 0.000** | 0.163 |
| 6 | 0.001** | 0.000** | 0.023* |
| 7 | 0.001** | 0.000** | 0.015* |
| 8 | 0.002** | 0.000** | 0.031* |
| 9 | 0.942 | 0.101 | 0.040* |
| 10 | 0.093 | 0.005** | 0.754 |
From the results obtained using Tukey's test, we can observe that the null hypothesis is rejected in many cases, confirming that the distributions show mean ranks (mean values for ) that are statistically significantly different from each other (please see also Table 6 ). Special attention should be given to the cases of . For these scale factors, the null hypothesis is rejected for all the groups combinations with a significance level of . Moreover, in one case () the three combinations are statistically significant for .
Table 6.
Mean estimates using Tukey's test for Healthy subjects, IPF, and COVID-19 patients. Estimation of the mean values for , and estimation of the mean ranks for the remaining scale factors.
| Scale factor () | Mean estimates |
||
|---|---|---|---|
| Healthy subjects | IPF patients | COVID-19 patients | |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
Nevertheless, the most significant result is the direct comparison between healthy and COVID-19 groups. The null hypothesis is rejected, in 9 out of 10 scales, for significance level of , making MFE3D a discriminatory metric between healthy subjects and COVID-19 patients. For to and , the group of COVID-19 patients is statistically different from the group of healthy subjects.
3.3. Complexity index
The CI was defined based on the sum of the entropy values from scale factors . Scales 9 and 10 were not included because they present a different behavior compared with the lower scale factors. Fig. 3 presents the box-histogram plot of the CI distributions for each group. The healthy subjects have a mean CI of , IPF patients have , and COVID-19 patients have .
Fig. 3.
Box-histogram plot of the complexity index for the healthy, IPF patients, and COVID-19 groups.
From the CI distributions, we can see that COVID-19 patients’ values increase up to 5.2 while the highest value for the healthy group is lower than 2.2 (excluding outliers). Moreover, the spread of the CI in the case of COVID-19 patients is much larger than the one of the healthy group. Even when comparing with the IPF group, COVID-19 patients exhibit higher CI. The distribution results of the CI shows that it can be a good indicator for fast screening of COVID-19 patients.
Besides, the normality of the CI values for the three groups was assessed to further analyze the statistical differences between them. Using a Shapiro-Wilk (W) test (with a significance level of ) we obtained for the healthy subjects and , for the IPF patients and , and finally, for the COVID-19 patients and . Given that the CI values of two groups do not follow a normal distribution, we proceeded to the Kruskal-Wallis analysis obtaining and . This implies that there is a statistical difference between the three groups for . When performing Tukey's test, the mean ranks were estimated, leading to , , and for healthy subjects, IPF, and COVID-19 patients, respectively. Moreover, for the three comparisons Healthy-IPF, Healthy-COVID-19, and IPF-COVID-19 the respective p-values were: , , and . For the first two comparisons, the groups are statistically different for , and the third is statistically different for . Therefore, we can conclude that the estimated mean rank of CI for COVID-19 patients is statistically significantly higher than for the other two groups.
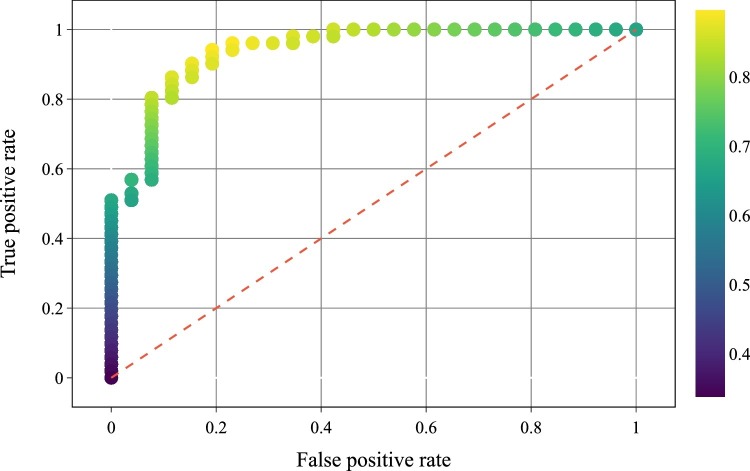
To proof the screen capabilities of the CI metric, a simple classifier based on a fixed threshold was implemented to classify the subjects as healthy subjects or as COVID-19 patients. The receiver operating characteristic (ROC) curve of this classifier was plotted by changing the decision threshold from 0 to 5.2 with steps of 0.01 (please see Fig. 4 ).
Fig. 4.
ROC curve of the threshold classifier to detect COVID-19 patients. The color-scale indicates the global accuracy of the classifier.
This simple classifier can achieve an accuracy of 0.896 with a sensitivity of 0.961 and a specificity of 0.769 for a decision threshold of 1.74. The area under the ROC curve achieved by this system was 0.940. The high sensitivity value shows the ability to determine that the subject has COVID-19 given that the subject is infected.
As mentioned previously, COVID-19 disease has some CT hallmark features that will modify the image texture. These features introduce variability in the lungs’ CT scans which explains higher entropy values for COVID-19 patients compared to healthy subjects. However, it is not only important to differentiate COVID patients from healthy subjects but also other pulmonary diseases with similar CT features. So far, this analysis has shown the potential to discriminate both cases using MFE3D. On the other hand, this dataset is not balanced or considering the incidence of both diseases which can be a drawback in the design of a classifier. The dataset is also quite small and should be larger to make sure that the conclusions regarding the considered sample still apply to the population. Another major drawback is the fact that the settings and features of the CT scans are not uniform which can result on some texture differences that are not being considered. Furthermore, as mentioned earlier, since it is necessary to differentiate COVID-19 patients from other pulmonary pathologies a more robust classifier can be used and include, for example, a dataset of IPF patients.
3.4. Classification approaches
Herein, texture-based features are used to classify COVID-19 cases. Previous studies have also used texture-based features to obtain an automated system to detect COVID-19. The novelty here is that volumetric data is analysed and then, through a multiscale entropy algorithm and complexity index, these texture-based features are obtained.
Table 7 shows the accuracy of the classifiers. For the best classifiers, MLP and kNN, a validation accuracy of and is reported, respectively. In addition, the kNN classifiers has the best test accuracy (), and the MLP neural network has the second best test accuracy of . Therefore, when using a neural network an high accuracy value can be achieved. Based on this, in the future, it can be interesting to explore more options in terms of neural networks approaches to classify volumetric HRCT data.
Table 7.
Accuracy of the classifiers for healthy and COVID-19 cases using MFE3D and CI values as features.
| MLPC | SVM-rbf | kNN | SVM-linear | ||
|---|---|---|---|---|---|
| Validation | Mean (%) | ||||
| Best (%) | |||||
| Test | Mean (%) | ||||
| Best (%) |
When analyzing the AUC values in Table 8 , the MLP neural network demonstrates to have the highest mean AUC () for the validation dataset, revealing the effectiveness of the model in detecting COVID-19 disease. For the test dataset, this value decreases which can result from slight overfitting and from the unbalanced dataset. For the test dataset, the kNN shows the best mean AUC value ().
Table 8.
Area under the curve (AUC) of the classifiers for healthy and COVID-19 cases using MFE3D and CI values as features.
| MLPC | SVM-rbf | kNN | SVM-linear | ||
|---|---|---|---|---|---|
| Validation | Mean | ||||
| Best | |||||
| Test | Mean | ||||
| Best |
Another parameter of major importance is the sensitivity to detect COVID-19 (Table 9 ). The two classifiers with the highest mean validation sensitivity are the MLP neural network and kNN with and , respectively. This reveals that in case someone is infected there is a high probability to detect it and classify the case correctly. This value is of extremely importance since a recent study stated that the RCT-PCR test has a sensitivity of around which is lower than the presented classifiers [18]. Nevertheless, there is still space to improve this results. One of the drawbacks of this work and that can explain why the average test accuracy is above the is that an unbalanced dataset is used. Another disadvantage is that the dataset is only composed by 77 subjects.
Table 9.
Sensitivity of the classifiers for healthy and COVID-19 cases using MFE3D and CI values as features.
| MLPC | SVM-rbf | kNN | SVM-linear | ||
|---|---|---|---|---|---|
| Validation | Mean (%) | ||||
| Best (%) | |||||
| Test | Mean (%) | ||||
| Best (%) |
In [30], the validation accuracy in classifying COVID-19 and healthy subjects was higher than when full images are used as features for their feed-forward network. Nevertheless, when using texture-based features the validation accuracy is , as mentioned earlier [30]. With the neural network used in our study with 9 texture-based features, we were able to reach similar accuracy. Nonetheless, a supplementary study, with a larger dataset, would be useful to take further conclusions.
The accuracy reported in [32] was . They also classify COVID-19 and non-COVID-19 cases. If we consider our mean test accuracy, our kNN approach outperforms their results. In addition, the MLP classifier achieves similar performance using a smaller dataset (see Table 7). However, when considering the best value of accuracy, our approaches outperform their method.
In addition, using FGCNet [31], a mean accuracy of and a mean sensitivity of can be achieved. Using GAN and neural networks, the authors of [17] achieved accuracy values superior to . Although the best cases of our classifier can reach accuracy, the mean value of our approaches are not as good.
The extreme good values shown in [17] can also be explained by the fact that the test dataset only contains 18 images, compared to the 130 images of the train dataset, which corresponds to a dataset split of . In fact Wang et al. [31] compares ResNet and the GoogLeNet with FCGNet and they report accuracy values of and , respectively.
As mentioned earlier, our dataset is too small but the approach of using texture-based features, from three-dimensional CT data, in addition with other classification approaches, namely, with AlexNet [15], GoogLeNet [27], and ResNet18 [11], and the FGCNet [31] can be of great interest.
4. Conclusions
With this work, we have demonstrated that the entropy analysis of CT data can contain relevant information concerning the pulmonary condition of COVID-19 patients. The presented work showed significant statistical differences (p-values 0.01) between the entropy values of 9 out of 10 scales when comparing healthy subjects with COVID-19 patients. The presented technique can be used for COVID-19 patients screening, with improvements on the response time compared to traditional diagnosis methods, allowing for fast patients isolation. Just the distribution of a simple uni-dimensional metric, like the CI, could be used to signalize potential COVID-19 patients with high sensitivity () even using a simple threshold classifier.
When applying different classifiers to our full dataset, we show that a mean accuracy of is achieved. The classification approaches used can achieve similar or superior results to other literature classification methods. Although some techniques based on deep learning show better results [31], [30], [17], our method used less features. Furthermore, our methodology is based on a statistical analysis of texture-based features. A simple score as the CI reached similar accuracy values, using only one feature and a threshold classifier as the more sophisticated classification models used.
In the future, after these preliminary results, it should be interesting applying this validated method in larger public datasets. Furthermore, since the disadvantages of this method is that we use an unbalanced and small dataset, the correction of this issue could lead to an improvement of both the statistical tests and machine learning results.
Even though machine-learning and deep learning can reveal very helpful, these techniques can involve an huge amount of training time and data to obtain desirable results. Besides, overfitting is one of the main issues that can occur in classification models. For clinical practitioners can also be very difficult to interpret this type of models and their results. However, statistical approaches are very common in medical sciences. Therefore, a model based on a statistical assessment provides more insight for the specialists, being easier for them to interpret the results. This method also allows to select the best features to use in a machine learning or deep learning system instead of using a huge number of features that can lead to high computational cost and overfitting issues.
Future work based on this evidence can also be the development of a classification system based in other more successful deep learning strategies. by expanding the number of variables. Moreover, by increasing the number of subjects, a more complete analysis can be performed, and eventually, could use the complexity index or some similar score to quantify the extent of the diseases.
Finally, it has been reported that recovered COVID-19 patient might present a reduced lung function [19]. The findings detailed in this work open the possibility to assess and quantify the lung function of recovered COVID-19 patients. This could be achieved by comparing the CT scans before and after recovery to confirm the extent of pulmonary damages.
Authors’ contribution
Andreia S. Gaudêncio: Conceptualization, Methodology, Software, Formal Analysis, Writing – Original Paper, Writing – Review and Editing. Pedro G. Vaz: Conceptualization, Methodology, Software, Formal analysis, Writing – Original Paper, Writing – Review and Editing. Mirvana Hilal: Conceptualization, Writing – Review and Editing. Guillaume Mahé: Resources, Writing – Review and Editing. Mathieu Lederlin: Resources, Writing – Review and Editing. Anne Humeau-Heurtier: Conceptualization, Supervision, Writing – Review and Editing. João M. Cardoso: Conceptualization, Supervision, Writing – Review and Editing.
Acknowledgments
This work was supported by FCT - Fundação para a Ciência e Tecnologia under the project UID/04559/2020 to fund the activities of LIBPhys-UC – Laboratory for Instrumentation, Biomedical Engineering and Radiation Physics and the project PTDC/EMD-TLM/30295/2017 European Regional – Development Fund (PT-COMPETE 2020).
Acknowledgments
Declaration of Competing Interest
The authors report no declarations of interest.
Footnotes
This work was supported by FCT – Fundação para a Ciência e Tecnologia under the project UID/04559/2020 to fund the activities of LIBPhys-UC – Laboratory for Instrumentation, Biomedical Engineering and Radiation Physics and the project PTDC/EMD-TLM/30295/2017 European Regional – Development Fund (PT-COMPETE 2020).
References
- 1.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., Tao Q., Sun Z., Xia L. Correlation of chest CT and RT-PCR testing for coronavirus disease 2019 (COVID-19) in china: a report of 1014 cases. Radiology. 2020;296:E32–E40. doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bernheim A., Mei X., Huang M., Yang Y., Fayad Z.A., Zhang N., Diao K., Lin B., Zhu X., Li K., Li S., Shan H., Jacobi A., Chung M. Chest CT findings in coronavirus disease-19 (COVID-19): relationship to duration of infection. Radiology. 2020;295:200463. doi: 10.1148/radiol.2020200463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cheng Z., Qin L., Cao Q., Dai J., Pan A., Yang W., Gao Y., Chen L., Yan F. Quantitative computed tomography of the coronavirus disease 2019 (COVID-19) pneumonia. Radiol. Infect. Dis. 2020 doi: 10.1016/j.jrid.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Colombi D., Bodini F.C., Petrini M., Maffi G., Morelli N., Milanese G., Silva M., Sverzellati N., Michieletti E. Well-aerated lung on admitting chest CT to predict adverse outcome in COVID-19 pneumonia. Radiology. 2020 doi: 10.1148/radiol.2020201433. 201433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Costa M., Goldberger A. Generalized multiscale entropy analysis: application to quantifying the complex volatility of human heartbeat time series. Entropy. 2015;17:1197–1203. doi: 10.3390/e17031197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dey N., Rajinikanth V., Fong S.J., Kaiser M.S., Mahmud M. Social group optimization–assisted kapur’s entropy and morphological segmentation for automated detection of COVID-19 infection from computed tomography images. Cogn. Comput. 2020 doi: 10.1007/s12559-020-09751-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of chest CT for COVID-19: comparison to RT-PCR. Radiology. 2020 doi: 10.1148/radiol.2020200432. 200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gao N., Tian S., Li X., Huang J., Wang J., Chen S., Ma Y., Liu X., Guo X. Three-dimensional texture feature analysis of pulmonary nodules in CT images: lung cancer predictive models based on support vector machine classifier. J. Digit. Imaging. 2019;33:414–422. doi: 10.1007/s10278-019-00238-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gaudêncio A.S.F., Vaz P.G., Hilal M., Cardoso J.M., Mahe G., Lederlin M., Humeau-Heurtier A. Three-dimensional multiscale fuzzy entropy: validation and application to idiopathic pulmonary fibrosis. IEEE J. Biomed. Health Inform. 2020 doi: 10.1109/jbhi.2020.2986210. 1-1. [DOI] [PubMed] [Google Scholar]
- 10.Hansell D.M., Bankier A.A., MacMahon H., McLoud T.C., Müller N.L., Remy J. Fleischner society: glossary of terms for thoracic imaging. Radiology. 2008;246:697–722. doi: 10.1148/radiol.2462070712. [DOI] [PubMed] [Google Scholar]
- 11.He K., Zhang X., Ren S., Sun J. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016:770–778. [Google Scholar]
- 12.Hope M.D., Raptis C.A., Henry T.S. Chest computed tomography for detection of coronavirus disease 2019 (COVID-19): don’t rush the science. Ann. Intern. Med. 2020 doi: 10.7326/m20-1382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jalaber C., Lapotre T., Morcet-Delattre T., Ribet F., Jouneau S., Lederlin M. Chest CT in COVID-19 pneumonia: a review of current knowledge. Diagn. Interv. Imaging. 2020;101:431–437. doi: 10.1016/j.diii.2020.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim H., Hong H., Yoon S.H. Diagnostic performance of CT and reverse transcriptase-polymerase chain reaction for coronavirus disease 2019: a meta-analysis. Radiology. 2020 doi: 10.1148/radiol.2020201343. 201343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Krizhevsky A., Sutskever I., Hinton G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012;25:1097–1105. [Google Scholar]
- 16.Li Y., Xia L. Coronavirus disease 2019 (COVID-19): role of chest CT in diagnosis and management. Am. J. Roentgenol. 2020;214:1280–1286. doi: 10.2214/ajr.20.22954. [DOI] [PubMed] [Google Scholar]
- 17.Loey M., Smarandache F., Khalifa N.E.M. Within the lack of chest COVID-19 x-ray dataset: a novel detection model based on GAN and deep transfer learning. Symmetry. 2020;12:651. doi: 10.3390/sym12040651. [DOI] [Google Scholar]
- 18.Long C., Xu H., Shen Q., Zhang X., Fan B., Wang C., Zeng B., Li Z., Li X., Li H. Diagnosis of the coronavirus disease (COVID-19): rRT-PCR or CT? Eur. J. Radiol. 2020;126:108961. doi: 10.1016/j.ejrad.2020.108961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mo X., Jian W., Su Z., Chen M., Peng H., Peng P., Lei C., Chen R., Zhong N., Li S. Abnormal pulmonary function in COVID-19 patients at time of hospital discharge. Eur. Respir. J. 2020;55 doi: 10.1183/13993003.01217-2020. 2001217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ojala T., Pietikainen M., Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002;24:971–987. doi: 10.1109/tpami.2002.1017623. [DOI] [Google Scholar]
- 21.Ojala T., Pietikäinen M., Harwood D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996;29:51–59. doi: 10.1016/0031-3203(95)00067-4. [DOI] [Google Scholar]
- 22.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M., Duchesnay E. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
- 23.Pienn M., Burgard C., Payer C., Avian A., Urschler M., Stollberger R., Olschewski A., Olschewski H., Johnson T., Meinel F.G., Bálint Z. Healthy lung vessel morphology derived from thoracic computed tomography. Front. Physiol. 2018;9 doi: 10.3389/fphys.2018.00346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Raghu G., Remy-Jardin M., Myers J.L., Richeldi L., Ryerson C.J., Lederer D.J., Behr J., Cottin V., Danoff S.K., Morell F., Flaherty K.R., Wells A., Martinez F.J., Azuma A., Bice T.J., Bouros D., Brown K.K., Collard H.R., Duggal A., Galvin L., Inoue Y., Jenkins R.G., Johkoh T., Kazerooni E.A., Kitaichi M., Knight S.L., Mansour G., Nicholson A.G., Pipavath S.N.J., Buendía-Roldán I., Selman M., Travis W.D., Walsh S.L.F., Wilson K.C. Diagnosis of idiopathic pulmonary fibrosis. an official ATS/ERS/JRS/ALAT clinical practice guideline. Am. J. Respir. Crit. Care Med. 2018;198:e44–e68. doi: 10.1164/rccm.201807-1255st. [DOI] [PubMed] [Google Scholar]
- 25.Scalco E., Rizzo G. Texture analysis of medical images for radiotherapy applications. Br. J. Radiol. 2017;90 doi: 10.1259/bjr.20160642. 20160642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sørensen L., Nielsen M., Petersen J., Pedersen J.H., Dirksen A., de Bruijne M. Chronic obstructive pulmonary disease quantification using CT texture analysis and densitometry: results from the Danish lung cancer screening trial. Am. J. Roentgenol. 2020;214:1269–1279. doi: 10.2214/ajr.19.22300. [DOI] [PubMed] [Google Scholar]
- 27.Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A. Going deeper with convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015:1–9. [Google Scholar]
- 28.Tenda E.D., Yulianti M., Asaf M.M., Yunus R.E., Septiyanti W., Wulani V., Pitoyo C.W., Rumende C.M., Setiati S. The importance of chest ct scan in covid-19. Acta Med. Indones. 2020;52:68–73. [PubMed] [Google Scholar]
- 29.Toğaçar M., Ergen B., Cömert Z. COVID-19 detection using deep learning models to exploit social mimic optimization and structured chest x-ray images using fuzzy color and stacking approaches. Comput. Biol. Med. 2020;121:103805. doi: 10.1016/j.compbiomed.2020.103805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Varela-Santos S., Melin P. A new approach for classifying coronavirus COVID-19 based on its manifestation on chest x-rays using texture features and neural networks. Inf. Sci. 2021;545:403–414. doi: 10.1016/j.ins.2020.09.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang S.H., Govindaraj V.V., Górriz J.M., Zhang X., Zhang Y.D. Covid-19 classification by FGCNet with deep feature fusion from graph convolutional network and convolutional neural network. Inf. Fusion. 2021;67:208–229. doi: 10.1016/j.inffus.2020.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang X., Deng X., Fu Q., Zhou Q., Feng J., Ma H., Liu W., Zheng C. A weakly-supervised framework for COVID-19 classification and lesion localization from chest CT. IEEE Trans. Med. Imaging. 2020;39:2615–2625. doi: 10.1109/tmi.2020.2995965. [DOI] [PubMed] [Google Scholar]
- 33.Wei J., Xu H., Xiong J., Shen Q., Fan B., Ye C., Dong W., Hu F. 2019 novel coronavirus (COVID-19) pneumonia: serial computed tomography findings. Korean J. Radiol. 2020;21:501. doi: 10.3348/kjr.2020.0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ye Z., Zhang Y., Wang Y., Huang Z., Song B. Chest CT manifestations of new coronavirus disease 2019 (COVID-19): a pictorial review. Eur. Radiol. 2020 doi: 10.1007/s00330-020-06801-0. [DOI] [PMC free article] [PubMed] [Google Scholar]