Statistical methods for time-dependent variables in hematopoietic cell transplantation studies

Abstract

The interaction of clinically important yet time-dependent events such as infection and acute graft-versus-host disease (GVHD) on hematopoietic cell transplant outcomes is of particular interest to transplant physicians. Clinically, the development of these events is unknown at the time of transplant, however, both events place the patient at risk of morbidity and mortality. Furthermore, the occurrence of one may affect the risk for the development of the other (i.e. GVHD results in increased immunosuppression resulting in infection). While these risks can be determined using traditional Cox modeling, due to their time-varying effects on the outcome, it is challenging to graphically display the patient’s expected clinical status over time. Landmark analysis is one of the commonly used methods to present time-dependent variables graphically. It can be a useful tool for describing an outcome of interest with time-dependent variables. In this paper, we review the basic concepts of time-dependent variables, and describe a landmark study with a single landmark time point and a dynamic landmark study with multiple landmark time points. We illustrate these methods with a hematopoietic cell transplantation data set with infections.

Introduction

A time-dependent variable occurs in hematopoietic cell transplantation (HCT) studies when a value of a variable changes over time. For example, the patient’s infection status after HCT is a time-dependent variable. At any time post HCT, a patient’s current infection status at time t has two values, infected or not infected, or rather, no infection before time t and infection before time t. These infections are often a cause of death and after getting infections patients often show worse outcomes compared to before getting infections (Ustun et al, 2018; Abidi et al., 2019). Furthermore, infectious events and their impact often occur early after HCT and interact with other time dependent events such as neutrophil engraftment and GVHD. Thus, the analysis result of such time-dependent variables provides important information on the patient’s prognosis depending on their time-varying status after HCT. There are several methods to deal with time-dependent variables. The Cox model (Cox, 1972) allows one to include time-dependent variables and provides a hazard ratio as a summary measure to compare two groups. A multi-state model can describe how a patient’s clinical status evolves over time, and can be used for time-dependent variables which can be represented by a state, such as development of an infection (Logan BR, 2013). The traditional landmark study with a single landmark time point can also be used to fit time-dependent variables. In the landmark study, one can draw Kaplan-Meier (KM) curves or cumulative incidence functions (CIF) based on the value of the time-dependent variable at the given single landmark time point, restricting to the cohort of patients still at risk for the outcome at the landmark time. However, choosing a best landmark time point may not be clear in practice, particularly when events and changes in the status of time-dependent covariates occur at similar times. For example, infections (time dependent covariate) and acute GVHD (outcome of interest) occur mostly within day 100 after HCT. In addition, the analysis results may considerably change depending on landmark time point chosen. To overcome this limitation of a single landmark study, a dynamic landmark study was proposed to allow several landmark time points within one model (Van Houwelingen, 2006; Van Houwelingen and Putter, 2008). Thus, one can display KM and CIF based on the status of the time-dependent variable at various landmark time points that were examined in the dynamic landmark study. In this paper, we review statistical methods for time-dependent variables and their applications to an HCT dataset with viral infections (Ustun et al, 2018).

Time-dependent variables

There are two types of variables in survival and competing risks data analyses: time-independent (fixed) variables and time-dependent variables. While a time-independent variable such as gender and race does not change over time, time-dependent variables such as development of acute GVHD or infections after HCT may change value over time. For example, if a patient experienced a viral infection at day 100 after HCT, the patient’s viral infection history status before day 100 would be “not infected” but the patient’s viral infection history status after day 100 would be “infected”. Thus, the patient’s viral infection status changed at day 100 after HCT. Unlike time-independent variables, one needs to account for such changes of time-dependent variables in the analysis.

There are several ways to handle time-dependent variables. The Cox model can evaluate the effect of time-dependent variables on the outcome. Their overall effects can be represented as the hazard ratio. Note that the Cox model is given by the hazard function

$$\lambda (t\mid X(t))={\lambda }_0(t)exp(\beta X(t)),$$

where time-dependent variable 𝑋(𝑡) represents a patient’s clinical status at time 𝑡, 𝜆₀(𝑡) is an unspecified baseline hazard function, and 𝛽 is an unknown parameter of interest. Thus, the effect of a time-dependent variable X(𝑡) on a particular outcome of interest can be interpreted as the hazard ratio (HR), exp(𝛽). For example, suppose that the time-dependent variable for a viral infection history was coded as 0 until the patient experienced a viral infection, and 1 after the patient experienced a viral infection, and that the HR for death associated with this time dependent variable was 2. This means that patients with a history of viral infection at any time point t have twice the risk of death compared to patients without a history of viral infection at the same time point.

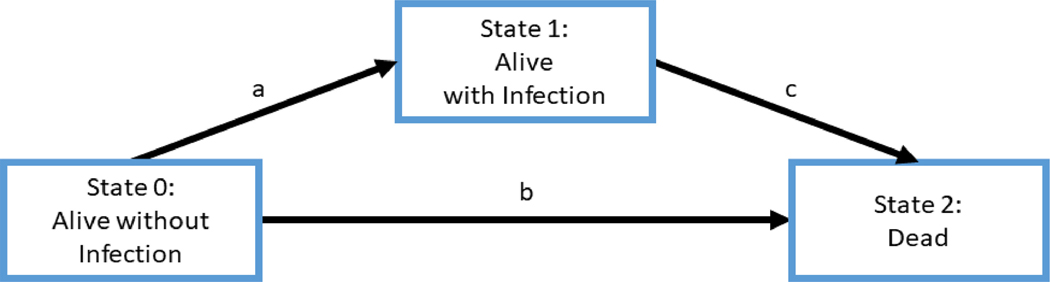
Multi-state models have also been used to handle time-dependent variables (Logan ,2013; Andersen and Keiding, 2007), by treating them as a separate clinical state. Figure 1 shows an example of a multi-state model where interest is in modeling overall survival and infection after HCT. There are three states in this multi-state model: Alive without infection (State 0), Alive with infection (State 1), and Dead (State 2). All patients are at State 0 at time of HCT. Patients change their status from State 0 to State 1 if they get infected. When infected patients at State 1 die, their status moves from State 1 to State 2. If patients without infection die, their status switches from State 0 to State 2. By estimating transition intensities at each time point, the multi-state model can estimate transition probabilities between states and predict an outcome of interest over time for survival and competing risks data. Multi-state models are flexible and powerful to handle time-dependent variables which can be represented as a distinct clinical state. They typically estimate a different set of parameters (hazard ratios) for each transition intensity. Thus, if there are several states in the model, it may be difficult to fit all of the different models and summarize covariate effects on the outcome of interest such as death.

Figure 1:

An example of a multi-state model with three states

Graphical representation of survival probabilities or cumulative incidences is helpful for investigators to easily visualize the findings from the analysis. For a time-independent categorical variable, KM estimates and CIF are most commonly used to display survival and competing risks outcomes, respectively. However, a graphical representation using KM curves or CIF for time-dependent variables is problematic because their values change over time. The simplistic, albeit incorrect plan, is to attempt is to classify patients using infection status after HCT (at any time) and draw KM curves or CIF from the time of transplant as if infection status is determined at the time of transplant. More specifically, if a patient becomes infected at some point after HCT, he/she would belong to the infection group. If a patient did not get infected by the last follow-up or a pre-specified follow-up time-point, he/she would belong to the no-infection group. Then, they would apply KM curves or CIF by treating such grouping as a fixed variable at HCT. However, this is not statistically correct because treating an infection as a fixed variable at time of HCT uses “post”-HCT information to classify patients “at time of HCT” and thus it does not reflect its time-dependent structure. In reality, all patients belong to the no-infection group at time of HCT, and at the time of HCT we do not know who will get infected or not. Their infection status changes over the course of treatment and recovery after HCT. Note also that fitting a Cox proportional hazards model with a time-dependent covariate only provides information about the relative effect on the hazard attributable to changes in the value of the time-dependent covariate (e.g. prior infection vs. not infected), but it does not lend itself to graphical depictions of absolute risk such as KM curves or CIF. A Simon–Makuch plot (Simon and Makuch, 1984) is often used to draw survival type of plots for time-dependent covariates. It displays survival curves for fictional patients who either never develop an infection or have experienced an infection at time of HCT. However, it is unclear whether these curves reflect clinically realistic quantities. (Putter and van Houwelingen, 2017).

Overview of a landmark study at a single time point:

In a landmark study with a single time point, one needs to select a reasonable landmark time point of interest for the study (Anderson et al., 1983; Dafni et al., 2001; Østgård et al. 2018 ). For example, evaluating the impact of infections on overall survival is often of interest. The status for time-dependent variables is determined by whether patients have experienced infections before the landmark time point, which makes the time-dependent variable time-independent at the landmark time point. Depending on whether they get infected before the landmark time point, the patients still alive at the landmark time are decomposed into two groups: no infection and infection groups. The patients who died before the time of landmark are excluded from the analysis and they are analyzed according to their infection status at the landmark time even if any subsequent changes in infection status happen (Anderson et al. 1983). To graphically display the outcome, one can use KM curves or CIF using the status of the time-dependent variable at the landmark time point.

In practice, choosing a best landmark time point might not be easy and appropriate for some outcomes. For example, assume one studies the impact of infection on acute GVHD. In a single landmark study, events of acute GVHD that occurred before the landmark time point do not contribute to the analysis. In addition, changes in the infections that occurred after the landmark are not considered. Thus, compared with studying a late landmark time point, the analysis at an early landmark time point considers more acute GVHD cases, but fewer infections because the number of patients who experienced acute GVHD before an early landmark time point is smaller than those before a late landmark time point and the number of patients who got infected before an early landmark time point is larger than those before a late landmark time point, and vice versa. These make it hard to choose a best landmark time point in particular because most infections and acute GVHD occur within 100 days after HCT in general. Therefore, investigating a single landmark point within 100 days after HCT may reflect a limited aspect of the data.

In such cases, it is desirable to investigate multiple landmark time points instead, where a dynamic landmark study can be used.

Overview of dynamic prediction using multiple landmark time points:

The dynamic landmark study (Van Houwelingen and Putter, 2008) examines the impact of time-dependent variables on the outcome at several landmark time points of interest. Consider an infection as a time-dependent variable for overall survival. Multiple landmark time points can be chosen based on clinical importance of such time points. Let a landmark time point be $t_{LM}$ and the end of study time be τ. Suppose there are 𝑚 landmark time points, $t_{LM}=t_1,\dots ,t_m$. At each landmark time 𝑠, let the values of the 𝑝 time-dependent covariates be $X{(s)}^T=\left(X_1(s),\dots ,X_p(s)\right)$. Then a hazard function for the dynamic landmark study is

$$\lambda (t\mid X(s),s)={\lambda }_0(t\mid s)exp\left(X{(s)}^T\beta (s)\right)\mathrm{ f}o\mathrm{r }s=t_{LM}\le t\le \tau ,$$ (1)

where 𝛽(𝑠) represents the log hazard ratios at landmark time 𝑠 corresponding to the time-dependent covariates 𝑋(𝑠). Van Houwelingen and Putter (2008) used the log hazard ratio 𝛽(𝑠) = 𝛽₀ + 𝛽₁𝑠 to smooth out the log hazard ratio as a function of landmark time 𝑠. The log hazard ratio 𝛽(𝑠) allows time-varying effects to reflect potential covariate effect changes over different landmark time points such as increasing or decreasing or mixed patterns depending on the function form of 𝛽(𝑠). When covariate effects are the same across different landmark time points, 𝛽(𝑠) can also be a constant over time.

To conduct the dynamic landmark analysis, one stacks data sets at landmark time points of interest, where data at a given landmark time point t consist of patients who were available at time t. Thus, patients who had follow-up up to a certain time point are included in data sets for all landmark time points before that time. This induces correlation within the dataset, since a single patient’s data can appear multiple times across different landmark time points at which they are at risk. The marginal Cox model (Lin and Wei, 1989; Lee et al, 1992) can be used to account for this correlation and obtain standard errors by the sandwich variance estimators using the standard statistical software such as SAS and R. At each landmark time point, one can calculate Kaplan-Meier estimates or CIF or covariate-adjusted survival probabilities/CIF to graphically display the outcome after treating the status of a time-dependent variable at each of the landmark time points as a fixed variable.

Example of the dynamic landmark study:

In this section, we apply a dynamic landmark study to the HCT data set that Ustun et al. (2018) studied. Its study population included 7128 patients receiving first alloHCT for acute myeloid leukemia, acute lymphoblastic leukemia, and myelodysplastic syndrome between January 2008 and December 2012.The percentage of patients who experienced a fungal infection by day 100 and a viral infection by day 100 was 8% and 44%, respectively. The numbers of patients who died by 100 day and experienced acute GVHD were 1059(15%) and 2847 (39%), respectively.

First, we examined a fungal infection as a time-dependent variable for overall survival. Six landmark time points were chosen at 15, 30, 45, 60, 75, and 90 days after HCT.

Table 1 shows the total number of patients who are considered in each landmark time point. When a landmark time point increases, the total number of patients decreases because patients died or were censored over the course after HCT. The number of patients in each fungal infection group also may change at each landmark time point as more patients may become infected.

Table 1:

total number of patients at each landmark time point

Landmark point	day 15	day 30	day 45	day 60	day 75	day 90
# of deaths	84	202	365	566	738	919
# of total	7044	6926	6763	6562	6390	6209
No fungal infection	6876	6667	6461	6229	6045	5851
fungal infection	168	259	302	333	345	358

Figure 2 includes plots for overall survival probabilities in fungal infection group and no fungal infection group based on the six landmark time points at day 15, 30, 45, 60, 75, 90. All patients who died or were censored before each landmark time point were excluded from the analysis for each landmark analysis. A fungal infection status was determined as the patient’s fungal infection history up to each landmark time point. The two KM curves were created based on patients’ fungal infection status up to each landmark time point. At any landmark time point, the “not infected” group has higher overall survival probability than the “infected” group with p-value <.0001. As a landmark time point increases, the gap between the two groups’ survival probabilities decreases.

Figure 2:

Plots of landmark studies using multiple landmark time points for overall survival

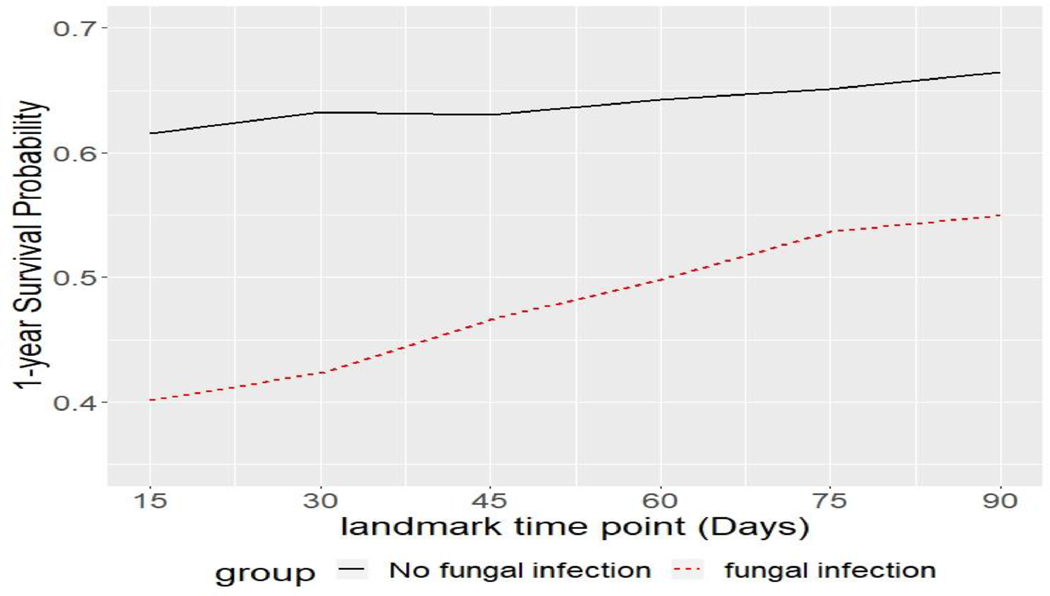
Figure 3 shows a summary plot for 1-year survival probabilities post landmark time point of fungal infection group and no fungal infection group across the six landmark time points. The gap between the two groups’ 1-year survival probabilities decreases as landmark time points increase, which is consistent with the trend in Figure 2.

Figure 3:

Plot for 1-year survival probability post landmark time points

We also fitted the model (1) to the data, where the unit for t is a month. The parameters of the final model, their standard errors, and p-values are reported in Table 2. The estimate of landmark time points, −0.060 (p<.001) indicates the hazard of death for each landmark analysis decreases over time. There is an interaction between landmark time points and fungal infection (p-value = 0.001). The sign for the interaction is negative (−0.131), which means as landmark time points moves forward, the difference in the hazard ratio between infection group and no-infection group is reduced. For example, we can interpret the risk of death for patients with fungal infection is exp(0.697 − 0.131 ∗ 30/30) = 1.761 times higher compared to those without fungal infection(p<.001) at the landmark time point with 30 days. At the landmark time point with 90 days, the risk of death for patients with fungal infection is exp(0.697 − 0.131 ∗ 90/30) = 1.355 times higher compared to those without fungal infection. We also fitted the Cox model with a time-dependent variable. The estimates for the Cox model are similar with those of the dynamic landmark study because the magnitude of the interaction is relatively small; however, the Cox model did not capture changes in the impact of a fungal infection on overall survival (OS) over time. Any given time point, the risk of death for patients with the fungal infection is exp(0.697) = 2 times higher than those without fungal infection (p<.001). In addition to fungal infection, age, Karnofsky score at transplant, donor/recipient HLA match, year of transplant 2010–2012, and Donor/Recipient CMV status are significant in the both final models.

Table 2:

Estimated parameters for the fungal infection on overall survival

		Dynamic landmark		Cox model
$\widehat{\beta }$	variable	$\widehat{\beta }$ (SE)	p-value	$\widehat{\beta }$ (SE)	p-value
${\widehat{\beta }}_0$	Fungal infection	0.697 (0.114)	<.001	0.697 (0.051)	<.001
	Age <=20 (reference)
	Age 21–40	0.356 (0.062)	<.001	0.349 (0.057)	<.001
	Age 41–50	0.509 (0.064)	<.001	0.497 (0.060)	<.001
	Age 51–60	0.645 (0.060)	<.001	0.649 (0.055)	<.001
	Age > 60	0.771 (0.060)	<.001	0.744 (0.056)	<.001
	Karnofsky score at transplant >=90(reference)
	Karnofsky score at transplant <90	0.250 (0.036)	<.001	0.265 (0.033)	<.001
	Karnofsky score at transplant Missing	0.194 (0.125)	0.120	0.208 (0.113)	0.065
	Donor/recipient HLA match HLA-identical siblings (reference)
	Donor/recipient HLA match 8/8 unrelated	0.043 (0.042)	0.306	0.067 (0.041)	0.105
	Donor/recipient HLA match <=7/8 unrelated	0.246 (0.060)	<.001	0.300 (0.056)	<.001
	Donor/recipient HLA match Cord blood	0.353 (0.050)	<.001	0.408 (0.047)	<.001
	Donor/recipient HLA match Other	0.282 (0.083)	0.001	0.314 (0.079)	<.001
	Year of transplant 2008–2009 (reference)
	Year of transplant 2010–2012	−0.109 (0.034)	0.001	−0.134 (0.032)	<.001
	Donor/Recipient CMV status −/− (reference)
	Donor/Recipient CMV status Any positive	0.146 (0.038)	<.001	0.143 (0.036)	<.001
	Donor/Recipient CMV status Missing	0.003 (0.134)	0.983	0.070 (0.126)	0.582
	Landmark time points	−0.060 (0.004)	<.001
${\widehat{\beta }}_1$	Fungal infection*Landmark time points	−0.131 (0.041)	0.001

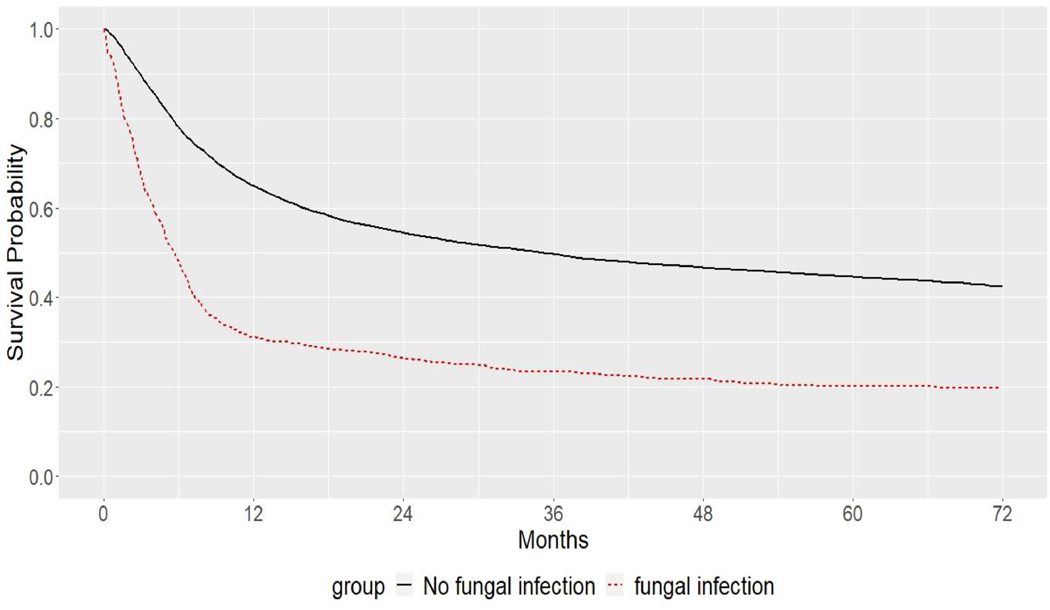
Figure 4 shows the Simon-Makuch plot. It attempts to display survival-type curves for fictional patients who either never develop a fungal infection or have experienced a fungal infection at time of HCT. When the hazards of death from infection and no-infection are equal, the two curves are the same (Simon and Makuch, 1984). Figure 4 shows two distinct curves, which means the fungal infection group is riskier than the no-fungal infection group.

Figure 4.

Simon-Makuch plot for the fungal infection in overall survival

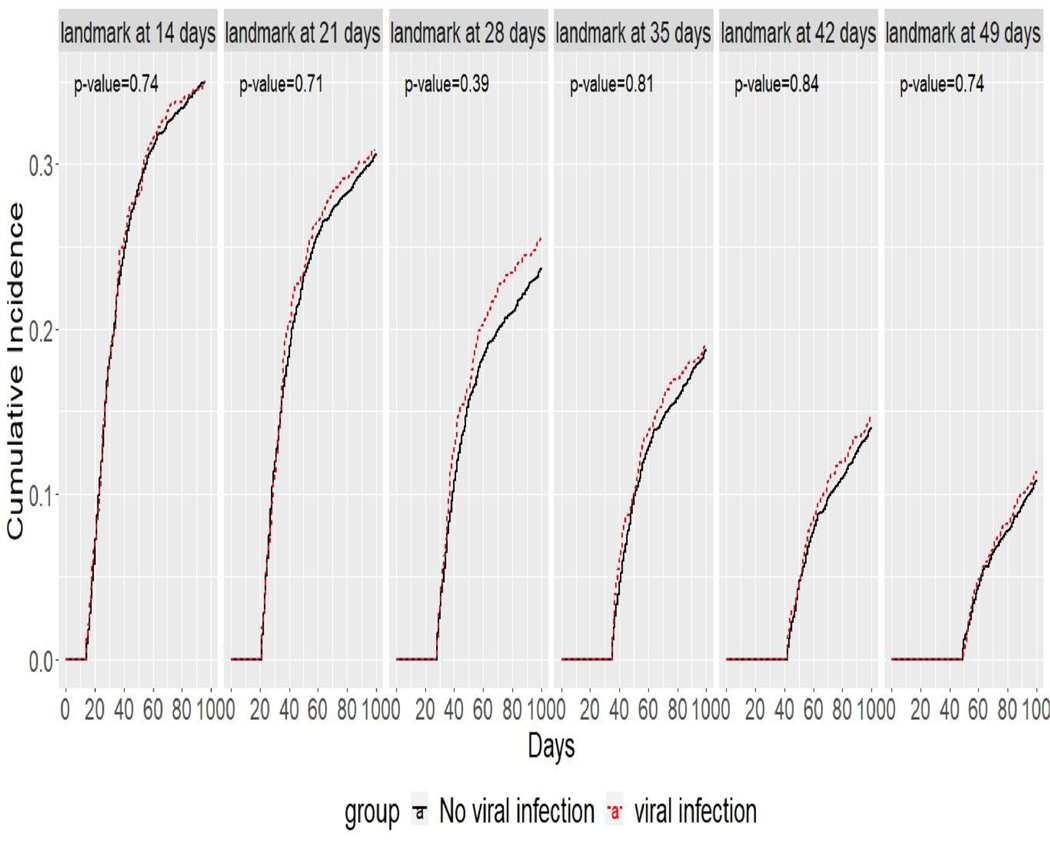
The second example considered an impact of viral infections on development of acute GVHD using the dynamic landmark study with six landmark time points at day 14, day 21, day 28, day 35, day 42, and day 49. Since death before acute GVHD is a competing event to acute GVHD, similarly to model (1), we conducted the dynamic landmark analysis by fitting the marginal Fine-Gray model (Zhou, Fine, Latouche, Labopin, 2012). Similarly to other dynamic prediction models for competing risks data (Nicolaie, Van Houwelingen, De Witte, and Putter, 2013a, 2013b), we considered acute GVHD and death-free patients at each landmark time point. Table 3 shows the total number of patients who were considered in each landmark time point. Figure 5 shows cumulative incidence plots to compare the viral infection group and the no-viral infection group at the six landmark time points. For all landmark time points, the cumulative incidence rates for the “infected” group are close to those for the “not infected” group.

Table 3:

total number of patients at each landmark time point

Landmark	day 14	day 21	day 28	day 35	day 42	day 49
# of death	69	113	173	259	340	423
# of acute GVHD	328	815	1363	1720	1978	2126
Total	6731	6200	5592	5149	4810	4579
No Viral infection	6197	5318	4473	3874	3457	3155
Viral infection	534	882	1119	1275	1353	1424

Figure 5:

cumulative incidence plots for acute GVHD in viral infection group and no viral infection group

Table 4 reports estimates of the final model. The parameter estimates for 𝛽₁which correspond to the interaction between the landmark times and all covariates, including viral infections, were set to zero because none of the interactions between the landmark time points and all covariates were significant. The negative estimate of landmark time points, −1.021 (p<.001) indicates that patients who survive event-free to later landmark timepoints have a lower subsequent incidence of acute GVHD. The effect of a viral infection was not significant for acute GVHD at the significance level 0.01. Therefore, we can interpret that there are no significant effects of a viral infection on development of acute GVHD. In addition, age, donor/recipient HLA match, ATG/CAMPATH as conditioning or GVHD prophylaxis, and landmark time points are significant in the final model. SAS codes for two examples are provided in the Supplementary material.

Table 4:

Estimated parameters for acute GVHD based on dynamic landmark model

parameters and their standard errors
Variables
	${\widehat{\beta }}_0$ (SE)	p-value
Viral infection	0.035 (0.057)	0.541
Age <= 20 (reference)
Age 21–40	0.243 (0.080)	0.002
Age 41–50	0.259 (0.086)	0.003
Age 51–60	0.291 (0.080)	<.001
Age > 60	0.452 (0.077)	<.001
Donor/recipient HLA match HLA-identical siblings (reference)
Donor/recipient HLA match 8/8 unrelated	0.481 (0.062)	<.001
Donor/recipient HLA match <=7/8 unrelated	0.739 (0.085)	<.001
Donor/recipient HLA match Cord blood	0.507 (0.069)	<.001
Donor/recipient HLA match Other	0.343 (0.124)	0.006
ATG/CAMPATH as conditioning or GVHD prophylaxis No ATG or CAMPATH (reference)
ATG/CAMPATH as conditioning or GVHD prophylaxis At least one	−0.408(0.053)	<.001
Landmark time points	−1.021(0.032)	<.001

Conclusion

The interplay of concurrent time-dependent competing risks such as infection on HCT outcomes is clinically important for a clinician at the bedside. In the patient with a new infection but not yet experiencing GVHD, will infection impact future GVHD development? If the patient develops GVHD, what is the likelihood of developing an infection? How do both of these events impact overall survival or impact relapse? Estimating the effect of such time dependent variables on the outcome is challenging because the value of time dependent variables changes over the course of post-HCT follow-up. The dynamic landmark study provides a useful tool for understanding clinical time-dependent variables on the outcome by examining multiple landmark time points. The advantage of the dynamic landmark approach is that it can easily incorporate any type of information about the patient history. Using landmark time points allows graphical display of the impact of time-dependent covariates on the outcome over time. Compared with the Simon-Makuch plot, it has a clinically-relevant interpretation. The dynamic landmark analysis uses patients who were infected by previous landmark time points when analyzing next landmark time points if they are still available at next landmark time points. This may impose difficulty on distinguishing the impact of cases for time-dependent covariates (e.g, infections) that occurred at different time points on the outcome. The number of events for the outcome and the number of cases/non-cases for time-dependent variables (e.g. infection vs. no-infection) are also crucial for the dynamic landmark analysis. Multi-state model also requires the large number of events and sample size to model transition probabilities for all states because one needs to fit multiple models for transition intensities between states and thus estimate a large number of parameters (van Houwelingen and Putter, 2008). Lack of any of these may result in unstable modeling. The Cox model with time-dependent variables can be considered to some degree as a dynamic landmark study with infinitely many landmark time points and without an interaction with time. Thus, if the parameter for landmark time points 𝛽₁ is zero, that is, no interaction with time, the dynamic landmark study may produce similar results to the Cox model. Although the dynamic landmark analysis investigates the impact of time-dependent variables at pre-specified multiple time points, it allows a graphical display of the analysis results for time-dependent variables, which may be helpful to clinicians.

Highlights.

• The basic concepts of time-dependent variables

• The impact of a time-dependent variable can be accessed using traditional Cox modeling but it is challenging to graphically display

• Description of a landmark study with a single landmark time point and a dynamic landmark study with multiple landmark time points