Abstract
Reduced models of neuronal spiking activity simulated with a fixed integration time are frequently used in studies of spatio-temporal dynamics of neurobiological networks. The choice of fixed time step integration provides computational simplicity and efficiency, especially in cases dealing with large number of neurons and synapses operating at a different level of activity across the population at any given time. A network model tuned to generate a particular type of oscillations or wave patterns is sensitive to the intrinsic properties of neurons and synapses and, therefore, commonly susceptible to changes the time step of integration. In this study, we analyzed a model of sharp-wave activity in the network of hippocampal area CA3, to examine how an increase of the integration time step affects network behavior and to propose adjustments of intrinsic properties neurons and synapses that help minimize or remove the damage caused by the time step increase.
Keywords: Integration time sensitivity, Network dynamics, Sharp waves, Hippocampus
1. Introduction
The understanding of spatio-temporal dynamics and critical mechanisms causing the formation of specific types of neuronal activity in the brain, observed in neurobiological experiments, relies on numerical simulations of very large-scale networks involving dynamical models of neurons and synapses connected in accordance with the anatomical structure of studied neurobiological networks [1–3]. To deal with large numbers of neurons and synapses in such studies the network model is frequently designed using reduced nonlinear models of neuronal spiking activity, see for example [4–10] and references therein. The parameter space studied in such networks usually includes parameters controlling the intrinsic dynamics of neurons, synapses and background noise. Such models successfully capture the details of neuronal network activity of various specific networks and the activity changes observed in experiments and explain such changes using detailed parametric analysis of network dynamics [11–14]. Although the computational efficiency of such models is very high and modern computational means are getting more and more powerful, the needs for realistic network simulations, dealing with multiple time scales governing the behavior of the studied neuronal networks and detailed analysis of such behavior in the space of multiple network parameters still require further improvement of computational efficiency in such models. The improvement is also needed for real-time simulation implementations of bio-inspired neuronal networks to be utilized in robotics, prosthetics and other devices [15–17]. One of the promising approaches to speed up network computation is to increase the time step of the simulations. However, a simple significant increase of the time step affects model dynamics strongly, rendering it unusable. In this work, we consider modifications of a reduced model that are capable of rendering its dynamics less susceptible to time step increases, and demonstrate it with an example of an Adaptive-Exponential Integrate and Fire network model used to capture sleep-related dynamics in the hippocampus.
Sleep is known to be beneficial for memories, in particular as a stage in which the brain is not processing input but can freely elaborate on recently learned memories, in a process called memory consolidation [18]. Oscillatory activity found in different brain regions during sleep has been shown to be influential in the process of memory consolidation and the presence and coordination of rhythms with different frequencies and time scales is hypothesized to be necessary for memory consolidation to occur [19–26]. Hence, studies of oscillations observed in the brain at various stages of sleep are very important for understanding of mechanisms of memory formation and consolidation. One of the essential rhythms within sleep oscillations is given by sharp-wave ripple (SWR) complexes. These are short-lived (with duration of 50–100 ms) events observed in hippocampal activity during stages of quiet wake and slow wave sleep. These events are detected in the traces in the local field potential (LFP) measured across layers in hippocampal area CA1, where they appear as a strong deflection in stratum radiatum followed by fast (>150 Hz) oscillations in stratum pyramidale. The strong deflection is caused by inputs from hippocampal are CA3 that projects its activity onto the pyramidal cells of CA1. Therefore, sharp waves are formed by the overall activity of CA3 pyramidal cells that evoke ripples through the activation of CA1 inhibitory neurons, generating fast transient local oscillations.
In this work, we used a recently developed model of SWR activity in CA3 and CA1 [27–29], and focused on sharp wave activity in CA3. The model has been fit to biological data (average firing rate, cell spiking properties, distribution of event occurrences in time, fraction of excitatory and inhibitory cells spiking in each event, ripple frequency, sharp waves size [29]) and used to study the dynamical mechanisms underlying ripples in CA1 [30] and sharp waves in CA3, in particular the spiking activity within CA3 sharp waves has been studied as a function of synaptic changes induced by learning activity [28]. Other biophysically realistic models of either CA3 sharp waves, CA1 ripples or CA3-CA1 sharp wave ripples in general use a variation of the Integrate and Fire model [31–33], apart from highly complex multicompartmental models of CA1 only activity that suggest CA1 ripples could emerge from electrical coupling between interneurons [34,35]. Our model included 2800 neurons aggregating the two regions, and the model equations were solved using a standard 1-step Euler integration algorithm. The complex dynamics of SWRs in the biological hippocampus as well as the co-existence of multiple spatial scales (i.e., fine resolution necessary to describe a single SWR event and large-scale network dynamics controlling multiple co-existing SWRs), require scaling computational networks to a size similar to the actual biological size of a human hippocampus (about 16 million pyramidal cells have been estimated in the CA1 area alone [36]). Therefore, new strategies are necessary to accelerate the computer simulations of network activity in this CA3-CA1 network.
We found highly nonlinear effects induced into the CA3 network activity by a large increase in the integration time step, from 0.001 to 0.5 ms. We looked for the range of integration step sizes that maintained consistency of the network activity features. We further manipulated the network parameters to achieve qualitatively similar patterns of activity in the network solved with very large step size and a fine step size. In particular, we focused on preserving the emergence of the sharp waves in CA3 activity, and in maintaining their exponentially distributed in-between times.
2. Network model structure
2.1. Cells: equations and parameters
We model sharp wave activity in the hippocampal area CA3 using a network of 240 basket cells and 1200 pyramidal cells. Each cell type is modeled as one Adaptive-Exponential Integrate and Fire neuron [8]. All cells in the same population have the same intrinsic parameters, but different inputs (I (t)), which introduce heterogeneity within both excitatory and inhibitory neuron populations. The inputs are separated in a deterministic component, a noise component and a synaptic component. In the deterministic part of the input, every cell receives a different direct current (IDC) term, fixed for the duration of the simulation, with values selected from a Gaussian distribution (with parameters different for the two cell types). In the noise component of the input, every cell receives an independent Ornstein–Uhlenbeck process [37] (OU-process, ηt), with cutoff at 100 Hz, which roughly resembles a single-pole filtered white noise. This noisy input is added to put the single cells in a state of noise-driven spiking, which is considered a good representation of in vivo cell activity [38–41]. The standard deviation of the OU process (β) controls the size of the noisy fluctuations in the sub-threshold voltage of the cells, and is fixed within each cell type. Parameters of the deterministic and noisy input component are chosen to have cells in a noise-driven spiking regime, rather than a deterministic spiking regime perturbed by noise. For each neuron, the equations are
| (1) |
| (2) |
with spike reset conditions at the threshold
| (3) |
and input current that include DC bias, noise and synaptic inputs.
| (4) |
| (5) |
The intrinsic parameters of the neuron models are presented in Table 1.
Table 1.
CA3 cells intrinsic parameters.
| Cell type | C [pF] | gL [nS] | EL [mV] | a | b [pA] | Δ[mV] | τw [ms] | Vt [mV] | Vr [mV] | Vthr [mV] |
|---|---|---|---|---|---|---|---|---|---|---|
| Pyramidal | 200 | 7 | −58 | 2 | 40 | 2 | 120 | −50 | −46 | 0 |
| Interneuron | 200 | 10 | −70 | 2 | 10 | 2 | 30 | −50 | −58 | 0 |
CA3 cells input parameters:
The level of noise in the network was set by a coefficient β = 80 for pyramidal cells and β = 90 for interneurons. The baseline voltage of the cells, was controlled with constant input IDC. Values of IDC were selected from Gaussian distributions with mean 24 (pA) and standard deviation 30% of the mean for pyramidal cells, and mean 130 (pA) and standard deviation 30% of the mean for interneurons.
Synaptic currents were modeled with double exponential functions, where one exponential captures the rise and the other one the decay of the synaptic conductance probability variable s(t). For every cell n we had
| (6) |
where Ei and Ee stand for reverse potential of inhibitory and excitatory synapses, respectively. In simulations we used Ei = −80 mV and Ee = 0 mV, and
| (7) |
The constant F is a normalization coefficient, set so that every spike in the double exponential within parentheses peaks at one, and for each gate type it is a function of the time constants of rise and decay. H(·) represents the Heaviside function, and tK are the spike times of pre-synaptic cell j. The time scales of rise (τR) and decay (τD), expressed in ms, are given in Table 2, together with parameters controlling the strength of synapses (and hence the gj→n values), introduced in Section 2.2.
Table 2.
CA3 synaptic parameters.
| Synapse type | τR [ms] | τD [ms] | μ [nS] | σ [nS] |
|---|---|---|---|---|
| AMPA (Py→Py) | 0.5 | 3.5 | 34/Npy | 0.4 μ |
| AMPA (Py→Int) | 0.5 | 3 | 77/Npy | 0.4 μ |
| GABAA (Int→Int) | 0.3 | 2 | 54/Nint | 0.4 μ |
| GABAA (Int→Py) | 0.3 | 3.5 | 55/Nint | 0.4 μ |
2.2. Network connectivity
The model represents CA3 as a one-dimensional network. To build connections within CA3, we populated connection matrices across the different sub-population of excitatory and inhibitory neurons. For excitatory connections from and to pyramidal cells, we first select a radius of about a third of all pyramidal cells in the network around the matrix diagonal (which corresponds to a radius around the pre-synaptic cell). Outside of this radius, no connections are formed. Within this radius, we shape a non-uniform probability of connection, depending on the distance between the pre-synaptic cell and the post-synaptic cell (distance in terms of their indexes in the 1D network). Specifically, we scale the decay of probability of connection with distance using a cosine function: if x is the index distance within the network, y = arctan (kx)/arctan (x) imposes the decay probability p(y) = Pcos(4y), where P is the peak probability (P = 1 in our case) and k = 2 is a parameter controlling the decay of connection probability within the radius. As a result, the probability of connection along the diagonal is higher for cells with indexes nearby the presynaptic cell and decreases progressively with cell index distance.
For excitatory connection from pyramidal cells to interneurons, since the two populations have different sizes, we first identify an approximate diagonal to attribute to the connection matrix, so that every pre-synaptic pyramidal cell is assigned an inhibitory neuron spanning the whole connectivity matrix. Around that diagonal, we choose a radius about a third of the post-synaptic population (interneurons). Outside of that radius, no synapses were formed. Within that radius, we used the same distance driven scaling with the function p(y) = P cos (4y) with P = 1 and y = arctan(kx) /arctan (x),. where x is the distance (in cell index within the interneuron population) between the post-synaptic interneuron and the diagonal interneuron point for a given pre-synaptic pyramidal cell, and k = 2 controls the decay connection probability within the radius of non-zero synapses.
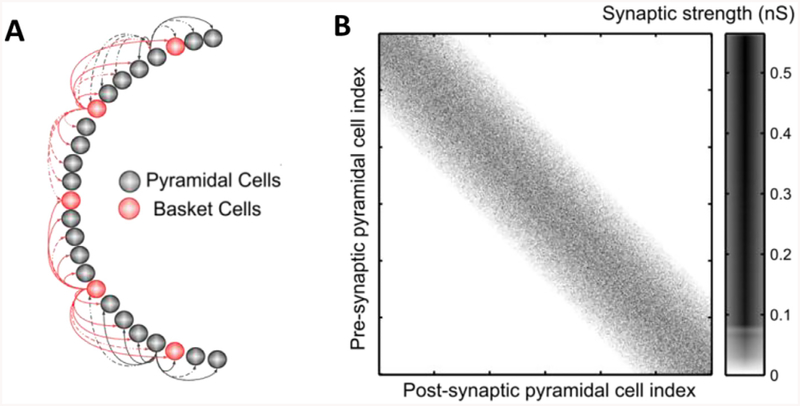
For inhibitory connections to both pyramidal cells and interneurons, we identified the connection matrix diagonal and consider a radius about one third of the post-synaptic network. Within the radius, the probability of connection was uniform (P = 0.7) in both inhibitory projections to excitatory cells and to interneurons. Once synapses presence was established according to the aforementioned probabilities, synaptic weights for all synapse types were sampled from Gaussian distributions with variance (σ) given by a percent of the mean (μ). Parameters μ and σ used in the simulations are given in Table 2. It is to note that the mean here declared was normalized by the total number of cells in the pre-synaptic population before the variance to the mean was introduced in the distribution (NPY and NInt, respectively). Since the excitatory and inhibitory populations are of different sizes, a direct comparison of the parameter values or their magnitudes would not account for the effective values used in the simulations. One example of connection matrix for CA3 pyramidal cells is reported in Fig 1.
Fig. 1. Model connectivity.
A. Schematic of the model of CA3, with pyramidal cells (gray) and interneurons (red), note that the network is arranged in one layer. B. Example of synaptic connections between CA3 pyramidal cells in one simulation. Pre-synaptic cell index is on the -axis. Note the higher density along the diagonal, decreasing toward the outermost part of the matrix. Also note that the synaptic weights (in nS) are not distributed with any topological preference. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.3. Stochasticity of network activity
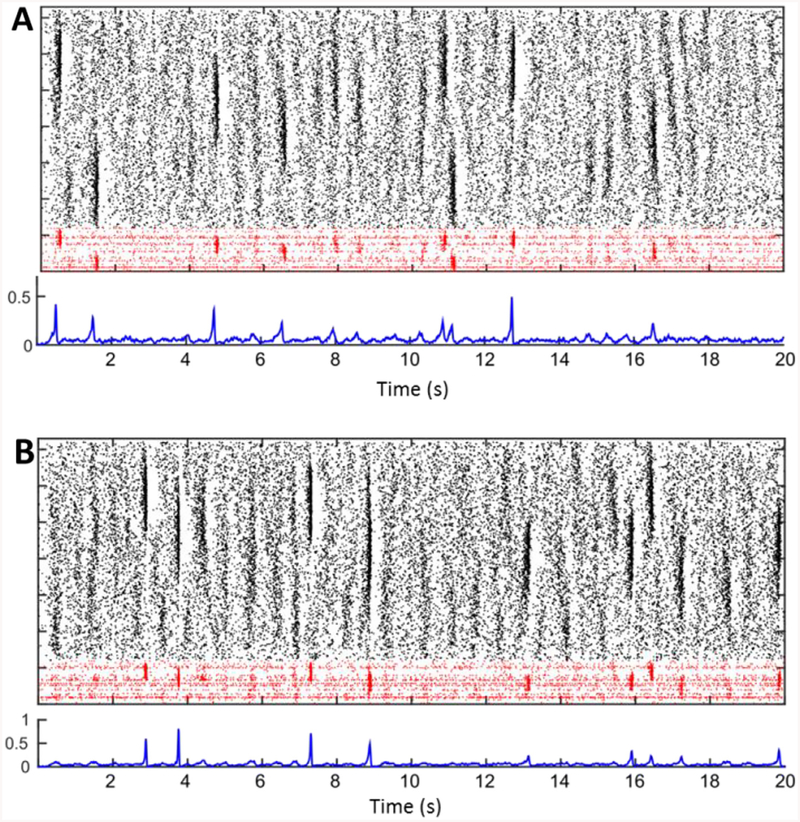
For every different simulation, we selected a new specific network connections pattern, new direct current values assigned to each cell, and delivered newly generated OU-processes traces to each neuron during each second of a simulation. To represent network activity, we studied the spike patterns in rastergrams (marking spikes by cell index in time) and the overall probability of spiking in the pyramidal cell population, which was found by finding the total spike counts in windows of 30 ms length, slid every 10 ms, and dividing the spike count by the size of the pyramidal cell population (1200). Whenever a sharp wave event was present in CA3, this spiking probability measure would show a rapid (highly nonlinear) rise to a peak and an abrupt decline back to baseline right after the peak. Rastergrams show how stochastic the emergence, size and location of each sharp wave can be in a simulation, and the probability of spiking traces capture the dynamics of increased firing leading up to a full blown sharp wave, which can start up to a full 150 ms earlier than the sharp wave peak (Fig 2). We interpret this peak as a measure of how synchronous the sharp wave event is. The model was solved using a one-step Euler method, with integration step 0.001 ms.
Fig. 2. Examples of CA3 network activity in the original model.
A. Top plot: spiking activity in one example simulation of CA3. The rastergram shows in black dots marking spikes of pyramidal cells, and in red interneurons. On the y-axis different cells are stacked by cell index, and on the x-axis time is in seconds. The line below shows the probability of spiking for CA3 pyramidal cells in windows of 30 ms. Note that high-spiking events appear as darker regions in the rastergram and as peaks of the spiking probability. The lower two plots represent a separate example of CA3 activity, generated by one new sample of connection matrix, heterogeneity DC values and ever-changing independent noise traces. Note that sharp-wave occurrence, size, and synchrony vary in time and across simulations. B. Same as A, but with a new instantiation of network connectivity, input noise and heterogeneity parameters. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.4. Instability of network dynamics
The rastergrams of network activity show complex dynamics of response to the input noise, including the formation and development of various sharp wave (SW) events. The input noise clearly plays a critical role in generating the complex distribution of activity patterns in the rastergrams, however the dynamical features of the network are also critical to the formation and shaping of SW. To evaluate the main contributors to the generation of the events we studied if SW were triggered exclusively by the input noisy patterns or if network dynamics also contributes the initialization of events. It is known that noise can lead to onset of synchronization that leads to event formation through the increase of reliability of spike timing of neurons [42]. One of the ways to evaluate this effect in the network is to check if the network activity in SW generation is locked to input-driven patterns. Such an analysis can be done adopting the Auxiliary System Method developed in studies of generalized synchronization of chaos [43]. This method can tell if the response dynamics of a dynamical system driven with complex signals is stable or not using an auxiliary system, which is a replica of the response system. Simulating response and the auxiliary systems, driven by the same inputs, but started with slightly different initial conditions one can detect if both systems converge to the same patterns of activity, in the case of stable response, or the initial deviations between the systems grow in time indicating the instability of the response dynamics.
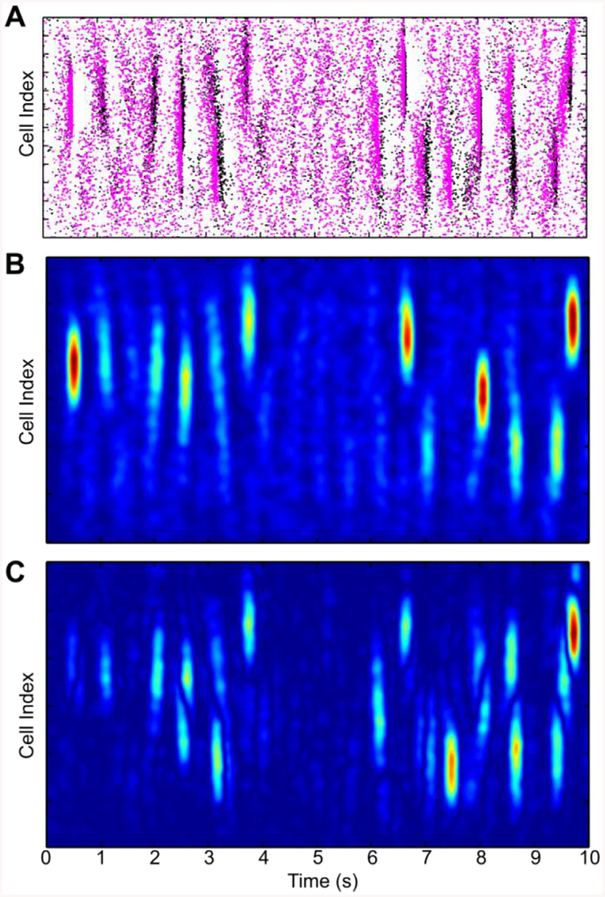
The results of the auxiliary system analysis in application to the CA3 network are presented in Fig 3, where rastergrams of the network spiking of response system (the original network, Eqs. (1)–(5)) are indicated by black dots, while spikes of the auxiliary network are shown as magenta dots on the same plot (Fig 3A). Since the timing of individual spikes is extremely sensitive to the intrinsic dynamics of neurons we do not expect onset precise synchronization between the networks at the level of individual spikes. Therefore, we focus on the analysis of spatio-temporal patterns of averaged spiking activity of the networks. We obtain such averaged activity by computing a 2-D cross-correlation of spikes both in time and in cell positions using Hanning window WH(i) = 0.5 (), where i = 0,1,..N−1. Index i represents the time sample, for convolving in time with (N = NT = 400), or cell number for computing convolution along the cell positions with (N = NP = 80). The smoothed field of network activity patterns given by black dots is presented in Fig 3B the dynamics of perturbation computed as the difference of such fields in two identical networks shows that the errors given by absolute value of the perturbations grow in time, see Fig 3C. Note the Z-scales in the intensity plots of Fig 3B and C are the same.
Fig. 3. Network activity is sensitive to initial conditions.
A. Rastergrams illustrating dynamics of PY cells spiking (black and red dots) generated by two identical networks in response to the same noisy inputs, but started at slighly different initial conditions. B. Smoothed activity field of the first network shown in A with black dots. C. Evolution of the deviations (errors) between network illustrated with the smoothed network fields demonstrate the increase of the perturbations in the network with time. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The increase of perturbations with time during a simulation indicates that network activity in the regime of generation of SW is not fully controlled by the noise inputs and that the network dynamics shows instability in its response behavior. Such instability supports variability in the network activity patterns and affects timing and shape of individual SW events. In application to our study, changing only the time step of a simulation, even if maintaining the network dynamics exactly the same, would introduce a slight perturbation of the solution at every step of integration. The instability we found in the network implies that, even in the ideal situation of same exact inputs, two identical SW networks with different integration steps could show differences in their activity responses. In the focus of our research goals it implies that criteria for matching of the SW dynamics with increasing step size should capture the capability of generation of SW events with proper characteristics of the individual events (e.g. like spiking rate profiles and fraction of neurons involved), rather than precise replication of the detailed structure of the spatio-temporal pattern generated in the response to the same sets of input patterns resampled in accordance with the step size.
3. Modification of the model to perform larger step simulations
To make model suitable for large step simulation we explicitly rewrite it in the form of a map using Euler 1-step integration method and changing the reset conditions for better control of spiking events. The equations will be of the form
| (8) |
| (9) |
where input currents are also in discrete-time with time interval h:
| (10) |
Note that the main difference between this map model and the map obtained by using fixed step Euler scheme of the original model is a modified reset condition, which now takes two steps (iterations) because of an extra condition for shaping the spike in the waveform of vn. In the Euler scheme of original model the reset to Vr will take place at vn ≥ Vthr. The shaping of spike by enforcing a step to value 40 mV (in the new map model) helps to maintain the consistency of spiking waveform at large values of h. We will discuss the effect of the spike shaping in the next section.
3.1. Noise in discrete time model
To integrate the solution, we also introduce noise in discrete time (ηn), by producing a discretized noise trace, binned with a given time step, that shows the core property of an OU-process, namely a single pole spectrum. This method follows closely strategies developed to introduce noise conductances to cell voltages in vitro through dynamic-clamp experiments [38,41,44]. To obtain such trace for a 1 s time of simulation, we first construct the noise representation in the frequency domain as a complex-valued function, assigning a norm and a phase to each frequency bin. Note that the frequency axis is binned according to the frequency resolution of the trace, which depends on the duration of the noise trace, in our case 1s and the integration time step considered: df = 1/(T + dt). To each frequency bin, we assign a complex value with phase sampled normally across the unit circle and norm the value at the given frequency bin f of a theoretical power spectrum of an OU-process, given by ; where f* is the location of the frequency single-pole filter, in our case 100 Hz.
The complex trace on the frequency axis is then transformed to obtain a conjugate symmetric complex function, which is the representation in Fourier space of our noise sample. The inverse Fourier transform (function ifft in Matlab, The Math-Works) of this trace is the OU-sample of length 1 s at the given integration time step. Since in our model we introduce a scaling parameter β which controls for the standard deviation of the noise, we further normalize the noise trace by its sample-depending standard deviation, which gives us ηn.
3.2. Discrete time models of synaptic connection
In discrete time, the synapse rise and fall equations can be simplified using the known property that the derivative of an exponential is still an exponential. In fact, the synaptic gates (variables s in the equations) can be separated in two separate decay and rise terms (pr and pd), and their difference (appropriately normalized by F) will constitute the variable s. The separate terms have a straightforward ODE regulating their time evolution, which is given by , where t0 was the last pre-synaptic spike time; which is the same as (for h the integration step) pn+1 = pne−h/τ. At every time step, we hence can follow the evolution of the rise and fall portion of the synaptic gate, and have sn+1 = g(pr,n+1 − pd,n+1). This method has been introduced in [45]. Note that this choice of discretization, while exact (which can be rarely said for discretized ODE solutions) shows explicitly the perils of using larger integrations steps: the rise and fall of a synaptic gate on different time scales could erase each other if the integration time step is too large. We keep our analysis for integration steps up to 0.5 ms, which is smaller than all the decay times of synapses in the network.
3.3. Pyramidal cell activity when changing integration step
It is meaningful to start our evaluation of the effect of changing integration step size on cell dynamics from the spiking response to a step of current. In fact, experimental measurements that characterize a cell basic biophysical properties measure its response to step currents on f-1 curves (frequency-current curves) [38]. The response of a cell to a step of current is shaped by intrinsic dynamics (for example, having a bursting response rather than a fast spiking one). It is known that the Adaptive Exponential 1ntegrate and Fire, the type of equation our cell models are based upon, can show quite a large set of different behaviors across parameter regimes [8,46].
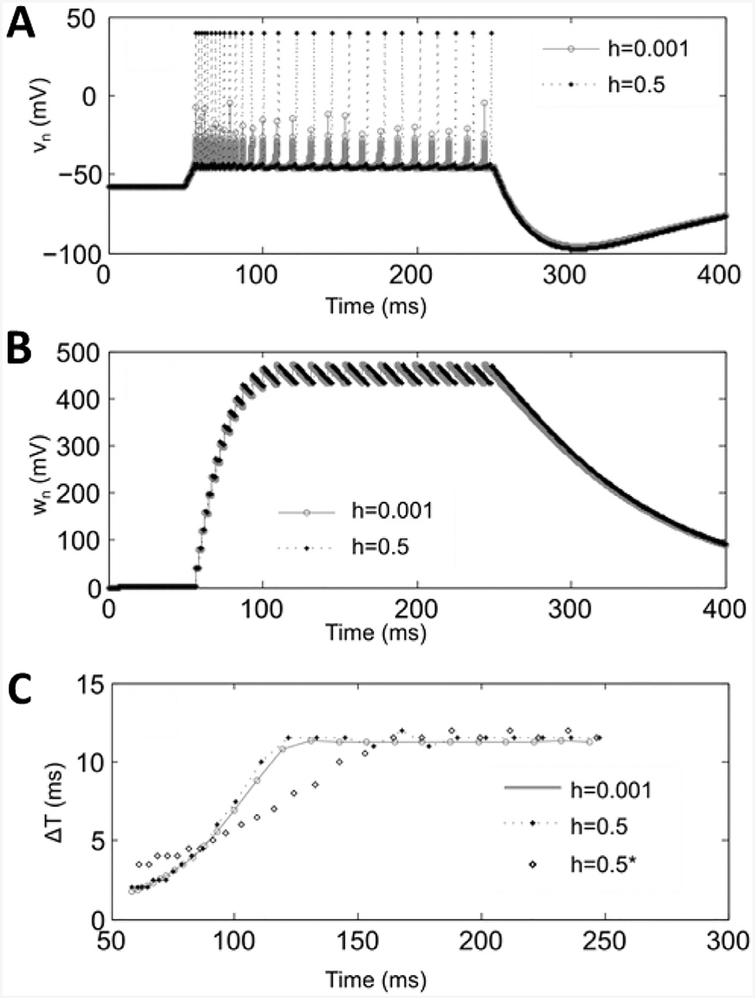
Consider the effects of increasing the integration step size on the dynamics of a single CA3 pyramidal cell, activated by a rectangular pulse of injected current In. We set the parameters of the map to be the same as in the original model with the new parameter Vth = −43.5. Waveforms vn and wn illustrating a response activity evoked by a rectangular pulse of amplitude A = 450 started at tSTART=50 ms and terminated at tEND=250 ms are presented in Fig. 4A and B, where the waveforms were computed for original model with h = 0.001 and map model with h = 0.5.
Fig. 4. Comparison of single cell activity with different integration steps.
A–B. Waveforms of vn and wn computed for the original model, Eqs. (1)–(3), with h = 0.001 and the map, Eqs. (8) and (9), with h = 0.5 with the same set of parameter values except for Vth = −43.5. Panel C shows spike timing of the corresponding activity patterns plotted on the plane representing moments of spikes and proceeding inter-spike interval. Case h = 0.5* correspondes to the spike timing obtained using the original model, Eqs. (1)–(3), simulated with stime step 0.5 ms.
Dynamics of the spike timing in the activity patterns of each waveform is shown in Fig. 4C, which presents each spike as a point in the plane (Ts, ΔTs), where Ts is the time of the s-spike and ΔTs = Ts – Ts-1. If all spikes in of comparing activity patterns overlap, then dynamics of the patterns match. To evaluate the fitness of two comparing spike patterns S1 {T1,1, …, T1,M} and S2 {T2,1, …, T2,M} we design a cost function as follows. For each spike point T1,k of S1 we find the nearest neighbor spike T2,l in sequence S2 in the plane, i.e. the point that give the minimum value of the distance computed as . Then, for each nearest neighbor pairs we compute the mismatch between spikes as ϵT1,k = | ΔT2,l − ΔT1,k |, which characterizes error in local inter-spike intervals (ISI). We also compute the number spikes in S2, which were not selected as the nearest neighbors and normalize it to total number of spikes in S2, to get the value ϵS2,1. We repeat the same calculations with sequence of spikes S2 to get ϵT2,n and ϵS1,2. To evaluate patterns mismatch we compute total error as
| (11) |
where 〈..〉 means averaging over all spikes in the sequence. Note that total error ϵ, representing the mismatch between two patterns, in our case does not include mismatch in simultaneous firing of the comparing nearest neighbor spikes directly. This allows us to deal with the cases of tonic spiking settled in the case of depolarizing DC input, when spikes in compared models can have some phase shift despite the precise matching of the spiking rate. The coefficient 0.2 in equation for ϵ is a weight, which is selected empirically to get a better consistency in changes of cost function shape, ϵ vs a parameter of the map.
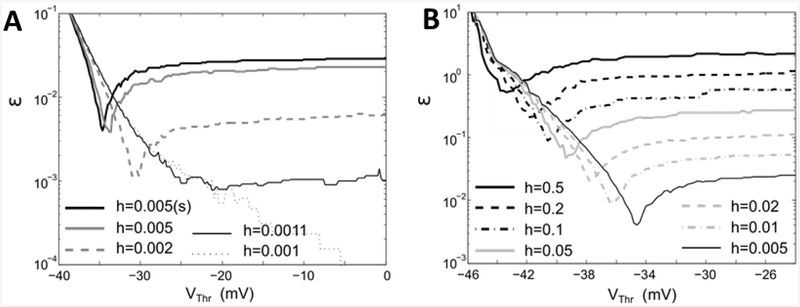
Using ϵ as a measure of mismatch between comparing patterns of spiking activity in the models evoked by the same input, we consider how accuracy of the original model evolve as we change the size of h focusing on the analysis of cost function ϵ(Vthr). The results of such analysis is shown in Fig 5A. One can see that even a small change of h (e.g. 10%) significantly increases the value of errors ϵ in the original model, where Vthr = 0. The presented plots also show that if the value of h increases beyond 10%, than for a given value of h one can find an optimal value of Vthr, which minimizes the deviation of spiking patterns from the original model, Eqs. (1)–(3), computed with h = 0.001 and Vthr = 0. Fig 5A also shows that the use of additional spike shaping iteration, Eqs. (8)–(9), affects the optimal values of Vthr. Compare plots for h = 0.005 and h = 0.005(s), where (s) indicates the use of spike shaping condition.
Fig. 5. Shapes of cost function (Eq. 11) computed for different values of h.
A. Original model, Eqs. (1)–(3), with rectangular pulse size A = 450 integrated with fixed step Euler scheme B. Modified map, Eqs. (8) and (9), simulated with A = 450. For comparison panel A includes a plot computed for modified map with h = 0.005 and A = 450 labled as h = 0. 005(s).
A typical change of cost function in modified map with increasing value of h is illustrated in Fig. 5B, where the plots of ϵ(Vth) were computed for the spike patterns evoked by rectangular pulse of amplitude A = 450 and the other parameters are the same as in Fig. 4. The plots show that errors grow and optimal value of Vth moves down as the values of h increases.
3.4. CA3 network activity when changing integration step
To compare the simulation outcomes when changing integration step, we kept unchanged the specific network connection matrix and assignment of direct current value to each cell in the network. For the input noise received by each cell, we froze each trace sampled at the highest rate (h = 0.001) and down-sample the trace to the new integration step. Within these constrains, we run copies of the “same” simulation for integration steps progressively increasing (Fig 6).
Fig. 6. Integration step affects network dynamics.
Increasing the integration step (h) leads to loss of sharp wave activity in the network: four examples. Across the different integration steps, all connections and heterogeneity DC values were kept identical, to test whether new integration steps would lead to different overall network patterns.
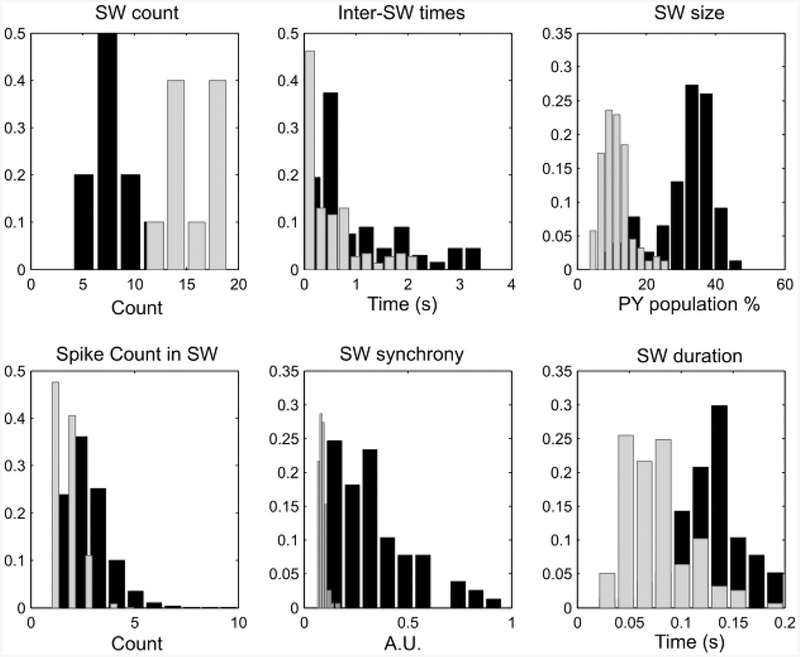
In Fig 6, examples show how for a network of CA3 pyramidal and basket cells, increasing step size affects the presence of spontaneous sharp wave activity. To test specifically what changed in network dynamics, we created an initial pool of ten simulations, each 10 s long, for the finest integration step (h = 0.001 ms). We run a copy of each simulation in this group where we only changed the integration step to h = 0.5 ms. We then compared a number of biologically relevant characteristics of the SW events in the original model (h = 0.001 ms) and in the large integration step case (h = 0.5). In each simulation, we counted the number of SW detected (SW count), the duration of times in between two successive SW (inter-SW times), the fraction of pyramidal cell population which spiked at least once in each SW (SW size), the number of spikes emitted by cells during a SW (spike count in SW), the peak value reached during a SW of the 30ms-windowed probability of spiking for pyramidal cells (SW synchrony, i.e. the peak values of the blue lines in Fig 2) and the duration of SW events (SW duration). Across all simulations, we pooled these values to create histograms of the statistics (Fig 7). It is to note that the statistical distributions of these properties were carefully introduced in the original model to resemble known biologically quantified SW properties [47–49], so it is important that they are preserved in solutions for larger integration steps.
Fig. 7. Integration step affects the statistics of SW properties.
Panels show histograms of SW properties with data collected across 10 simulations, each 10 s long. Histograms of the statistics for the small integration step (h = 0.001 ms, black bars) and for the large integration step (h = 0.5 ms, gray bars). SW count: count of SW in each simulation. Inter-SW times: time in between the end of a SW and the beginning of the next one. SW size: fraction of the pyramidal cell population which spikes at least once in the SW. Spike Count in SW: number of spikes released by the pyramidal cells active during SW. SW synchrony: peak height of the probability of spiking of the pyramidal cell population (in 30 ms time bins). SW duration: time between start and end of each SW.
As can be seen in Fig 7, increasing the size of integration step led to too many SWs. This might seem to contrast with our observation in Fig 6, where we show that increasing the integration step led to loss of SW. In fact, this apparent contradiction can be reconciled by a small technical point. The automatic detection of SW events is based on the time evolution of the network-wide probability of spiking of pyramidal cells (blue lines in Fig 2), binned in 30 ms windows and sampled every 10 ms (pE(t)), which we use to compute the SW synchrony, given by the peak value of this probability during a SW. If a network activity profile with no sharply defined SW event is passed through the algorithm, the “ghosts” of SW activity might lead the probability measure to occasionally cross the detection threshold, which is given by pTh = bE + 2σ, where bE is the baseline of pyramidal cell activity, found as the mean value of all pE(t) values that are below the sum of mean and standard deviation of pE(t). As a consequence, the baseline is close to the mean of pE(t) but always below it. The threshold pTh is reached when crossing the sum of baseline and σ, which is the standard deviation of pE(t). Hence, every simulation has its own baseline and threshold, and simulations without any SW synchronous enough to drive the creation of a meaningful threshold can detect as SW events which are not synchronous or large. This is exactly the case with the h = 0.5 ms simulations, as can be verified in the “SW synchrony” panel of Fig 7, showing all the SW detected in the large integration step case (in red) tightly packed near zero synchrony.
Other discrepancies in the h = 0.5 simulations are given by SW which are too small (SW size panel) and last about half the appropriate duration (SW duration panel). Overall, increasing the time step without any form of adjustment led to a dramatic loss of SW-like behavior in the model activity. We believe that this is due to the loss of excitatory propagation in the network, because increasing the step size hyper-synchronizes some sparse spikes, which cannot accumulate in time on their shared targets, therefore losing the slowly building excitatory activity which precedes every SPW by about 50–100 ms (biologically consistent).
Since larger integration steps caused the CA3 network activity to lose (for the most part) the ability to start sharp waves, even when preserving all other network properties as connectivity, initial conditions and frozen noise, we chose to adjust some parameters to test whether we could recover the SPW spontaneous emergence. Since we thought that excitatory synaptic transmission was affected in the larger integration step cases, we investigated the effects of strengthening two network parameters which we knew enhanced the likelihood of SW activity in the network when simulated at a fine time step: the strengths of excitatory synapses and the standard deviation of the noise delivered to excitatory cells (both mechanisms efficient at promoting spiking in the CA3 population).
Specifically, in each of the original 10 simulations (blue histograms in Fig 5) we multiplied all the pyramidal-to-pyramidal synaptic connections by a non-dimensional scaling factor Gα which varied between 1 and 1.04. Also, we multiplied the factor β which scales the contribution of the noise current to pyramidal cells (see the system of equations introduced in section Cells: equations and parameters) by a factor Bα which varied between 1 and 1.05. As a result, these values were either unaltered (at scaling 1) or slightly increased. The two scaling operations were carried out independently, generating a two-dimensional parameter space in which, for every combination of Gα and Bα, we run the 10 simulations with integration step h = 0.5 ms.
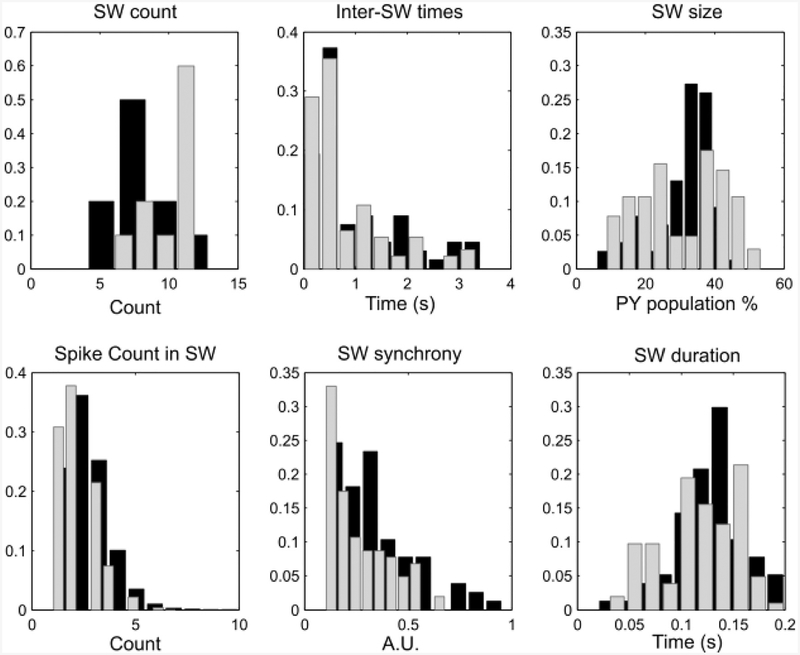
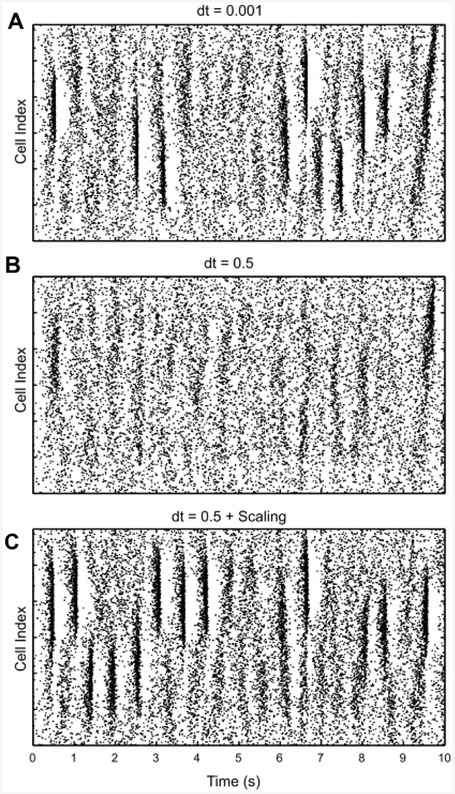
We pooled data from simulations to compare SW properties in the original model solved with small integration step and the modified models solved with large integration step. We used the same properties that we introduced in Fig 7: SW count, size, duration, synchrony, the Inter-SW times and the cell spike count during SW events. When comparing across all possible scaling combinations, we found one which performed the best in terms of matching the distributions of these properties in the pool of simulations. It was given by Gα = 1.025 and Bα = 1.04, and the resulting statistics are shown in Fig 8. In Fig 9 we show one example of the rastergrams for the same simulation in the original model, increased integration step and modified model conditions.
Fig. 8. Adjustments to simulations parameters rescue the SW dynamics with large integration step.
In the panels, computed as in Fig. 7, we should a comparison between data pooled by simulation of the original model (black bars) solved with h = 0.001 ms and the modified model (gray bars) solved with h = 0.5 ms. Note that while not perfectly overlapping, all distributions lie in overlapping ranges and show similar trends.
Fig. 9. Example of recovered network activity at large h.
Shown is one simulation solved at h = 0.001 ms (A), the same network at h = 0.5 ms without any other changes (B). C. The same network (h = 0.5) with re-scaled excitatory connections and excitatory noise size.
4. Conclusions
We have studied how an ODE-based phenomenological model of spiking neuron, known as Adaptive Exponential Integrate and Fire Model, can be modified into a form of discrete-time model (a map) that tolerates simulations with large time step and supports proper behavior of network dynamics in generation of sharp-wave oscillations modeling CA3 region of hippocampal network. We have demonstrated that dynamics of oscillations produced by considered network models is very sensitive to the variation of parameters of the neurons and synapses forming the network, changes in the noise and time step of simulations used in Euler scheme of integration. To achieve reliable operation of network in the regime of sharp-wave generation the integration step should be set at very small values ~0.001 ms, which makes difficult to apply this model for detailed analysis of large-scale network dynamics.
Since noise plays a critical role in the initiation of sharp waves in this model, it has to be properly modified to support proper network activity as the integration step changes. We have shown that even for the same noisy inputs (frozen noise) used in the simulations the response behavior of the network model is very sensitive to small variations in initial conditions indicating that although the network reacts to various noisy events in inputs whose coherency can evoke a sharp wave, the network dynamics has intrinsic instability. This instability hampers the tuning of the model to achieve behavior matching between models simulated with different step size h. Therefore, tuning of the model with large time step is done by matching the spiking response activity in the individual neurons. We have shown the most appropriate parameter to adjust here is the value of threshold level. The correction of model behavior using tune up of the threshold level provides a better control of the spike generation mechanism in the integrate and fire type of models and allows one significantly increase the size of time step keeping proper dynamics and characteristics of network behavior. A similar approach has been also successfully used recently for control of sampling in a map-based model of spiking neuron [50]. The results of this study have demonstrated that it could be used to deal with the large time step simulation in other reduced models of spiking neurons.
Additional parameter turning with increase of time step has to be done at the level of network simulation. This is mostly needed to properly balance the effects of noise and synaptic inputs on the network responsivity. We used strengths of the synaptic connections as control parameters of the network tuning. Because of intrinsic instability of the network dynamics capable of sharp-wave generation, the only working indicator of the similarity between the networks was statistical analysis of the SW events. This analysis includes distributions of SW count, Inter-SW times, SW size, Spike count in SW, SW synchronization and SW durations, which were kept within biological constrains [49].
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grant Number (IIS-1724405), the National Institute of Health (grant 1RF1MH117155) and the Office of Naval Research (MURI: N00014-16-1-2829). NR also appreciate partial support from ONR grant N00014-16-1-2252.
Abbreviations:
- CA3, CA1
Cornus Ammonis area (1 and 3, respectively). Anatomic sub-regions of the hippocampus
- SWR
sharp-wave ripples. Hippocampal events in area CA3 and CA1, tied to sleep-dependent memory consolidation
References
- [1].Dayan P, LF A Theoretical neuroscience. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- [2].Graham B, Gillies A, Willshaw D Principles of computational modelling in neuroscience. Cambridge University Press; 2011. [Google Scholar]
- [3].Shepherd GM. The synaptic organization of the brain. 5th ed. Oxford; New York: Oxford University Press; 2004. [Google Scholar]
- [4].Brette R, Rudolph M, Carnevale T, Hines M, Beeman D, Bower JM et al. Simulation of networks of spiking neurons: a review of tools and strategies. J Comput Neurosci 2007;23:349–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yavuz E, Turner J, Nowotny T. GeNN: a code generation framework for accelerated brain simulations. Sci Rep 2016;6:18854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Izhikevich EM. Which model to use for cortical spiking neurons? IEEE Trans Neural Netw 2004;15:1063–70. [DOI] [PubMed] [Google Scholar]
- [7].Izhikevich EM. Simple model of spiking neurons. IEEE Trans Neural Netw 2003;14:1569–72. [DOI] [PubMed] [Google Scholar]
- [8].Touboul J, Brette R. Dynamics and bifurcations of the adaptive exponential integrate-and-fire model. Biol Cybern 2008;99:319–34. [DOI] [PubMed] [Google Scholar]
- [9].Rulkov NF. Timofeev I. Bazhenov M. Oscillations in large-scale cortical networks: map-based model. J Comput Neurosci 2004;17:203–23. [DOI] [PubMed] [Google Scholar]
- [10].Jin X. Furber SB. Woods JV. Efficient modelling of spiking neural networks on a scalable chip multiprocessor. In: Neural networks, 2008 1JCNN 2008 (1EEE World Congress on Computational 1ntelligence) 1EEE international joint conference on. 1EEE; 2008. p. 2812–19. [Google Scholar]
- [11].Bazhenov M Rulkov NF. Timofeev 1. Effect of synaptic connectivity for long-range synchronization of fast cortical oscillations. J Neurophysiol 2008;100:1562–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Komarov M Krishnan G. Chauvette S. Rulkov N. Timofeev 1. Bazhenov M. New class of reduced computationally efficient neuronal models for large-scale simulations of brain dynamics. J Comput Neurosci 2018;44:1–24. [DOI] [PubMed] [Google Scholar]
- [13].Assisi C. Stopfer M, Laurent G. Bazhenov M. Adaptive regulation of sparseness by feedforward inhibition. Nat Neurosci 2007;10:1176–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Kee T Sanda P. Gupta N. Stopfer M, Bazhenov M. Feed-forward versus feedback inhibition in a basic olfactory circuit. PLoS Comput Biol 2015;11:e1004531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Dura-Bernal S, Chadderdon GL, Neymotin SA, Francis JT, Lytton WW. Towards a real-time interface between a biomimetic model of sensorimotor cortex and a robotic arm. Pattern Recognit Lett 2014;36:204–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Zbrzeski A Bornat Y. Hillen B, Siu R, Abbas J. Jung R. et al. Bio-inspired controller on an FPGA applied to closed-loop diaphragmatic stimulation. Front Neurosci 2016;10:275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Westphal A Rulkov N. Ayers J. Brady D. Hunt M. Controlling a lamprey-based robot with an electronic nervous system. Smart Struct Syst 2011;8:39–52. [Google Scholar]
- [18].Diekelmann S Born J. The memory function of sleep. Nat Rev Neurosci 2010;11:114–26. [DOI] [PubMed] [Google Scholar]
- [19].Molle M Born J. Slow oscillations orchestrating fast oscillations and memory consolidation. Progr Brain Res 2011;193:93–110. [DOI] [PubMed] [Google Scholar]
- [20].Rasch B Born J. About sleep’s role in memory. Physiol Rev 2013;93:681–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Achermann P Borbely AA. Low-frequency (< 1Hz) oscillations in the human sleep electroencephalogram. Neuroscience 1997;81:213–22. [DOI] [PubMed] [Google Scholar]
- [22].Schwindel CD. McNaughton BL. Hippocampal-cortical interactions and the dynamics of memory trace reactivation. Progr. Brain Res 2011;193:163–77. [DOI] [PubMed] [Google Scholar]
- [23].Sirota A Csicsvari J. Buhl D. Buzsáki G. Communication between neocortex and hippocampus during sleep in rodents. Proc Natl Acad Sci USA 2003;100:2065–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Staresina BP, Bergmann TO, Bonnefond M, van der Meij R, Jensen O, Deuker L, et al. Hierarchical nesting of slow oscillations, spindles and ripples in the human hippocampus during sleep. Nat Neurosci 2015;18:1679–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Sutherland gR. McNaughton B. Memory trace reactivation in hippocampal and neocortical neuronal ensembles. Curr Opin Neurobiol 2000;10:180–6. [DOI] [PubMed] [Google Scholar]
- [26].Walker MP. Stickgold R. Sleep, memory, and plasticity. Annu Rev Psychol 2006;57:139–66. [DOI] [PubMed] [Google Scholar]
- [27].Malerba P, Jones MW, Bazhenov M Defining the synaptic mechanisms that tune CA3-CA1 reactivation during sharp-wave ripples. biorxiv.org 2017. [Google Scholar]
- [28].Malerba P, Tsimring K. Bazhenov M. Learning-induced sequence reactivation during sharp-wave ripples: a computational study. Advances in the mathematical sciences SD University of California, Department of Medicine, La Jolla, CA, USA. Springer 1nternational Publishing; 2017. [Google Scholar]
- [29].Malerba P Bazhenov M. Circuit mechanisms of hippocampal reactivation during sleep. Neurobiol Learn Mem 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Malerba P Krishnan GP, Fellous JM. Bazhenov M. Hippocampal CA1 ripples as inhibitory transients. PLoS Comput Biol 2016;12:e1004880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Memmesheimer RM. Quantitative prediction of intermittent high-frequency oscillations in neural networks with supralinear dendritic interactions. Proc Natl Acad Sci USA 2010;107:11092–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Taxidis J Coombes S. Mason R. Owen MR. Modeling sharp wave-ripple complexes through a CA3-CA1 network model with chemical synapses. Hippocampus 2012;22:995–1017. [DOI] [PubMed] [Google Scholar]
- [33].Omura Y„ Carvalho MM„ Inokuchi K„ Fukai T„ A lognormal recurrent network model for burst generation during hippocampal sharp waves. J Neurosci 2015;35:14585–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Traub RD „ Bibbig A. A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon-axon gap junctions between pyramidal neurons. J Neurosci 2000;20:2086–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Traub RD„ Schmitz D„ Jefferys JG„ Draguhn A, High-frequency population oscillations are predicted to occur in hippocampal pyramidal neuronal networks interconnected by axoaxonal gap junctions. Neuroscience 1999;92:407–26. [DOI] [PubMed] [Google Scholar]
- [36].West MJ, Gundersen HJ. Unbiased stereological estimation of the number of neurons in the human hippocampus. J Comp Neurol 1990;296:1–22. [DOI] [PubMed] [Google Scholar]
- [37].Uhlenbeck GE, Ornstein LS. On the theory of the Brownian motion. Phys Rev 1930;36:823. [Google Scholar]
- [38].Fernandez FR„ Broicher T„ Truong A„ White JA„ Membrane voltage fluctuations reduce spike frequency adaptation and preserve output gain in CA1 pyramidal neurons in a high-conductance state. J Neurosci 2011;31:3880–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Atallah BV, Scanziani M. Instantaneous modulation of gamma oscillation frequency by balancing excitation with inhibition. Neuron 2009;62:566–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Pouille F, Marin-Burgin A, Adesnik H, Atallah BV, Scanziani M. Input normalization by global feedforward inhibition expands cortical dynamic range. Nat Neurosci 2009;12:1577–85. [DOI] [PubMed] [Google Scholar]
- [41].Broicher T„ Malerba P„ Dorval AD„ Borisyuk A, Fernandez FR„ White JA„ Spike phase locking in CA1 pyramidal neurons depends on background conductance and firing rate. J Neurosci 2012;32:14374–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Mainen ZF„ Sejnowski TJ„ Reliability of spike timing in neocortical neurons. Science 1995;268:1503–6. [DOI] [PubMed] [Google Scholar]
- [43].Abarbanel HD „ Rulkov Nf„ Sushchik MM„ Generalized synchronization of chaos: the auxiliary system approach. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 1996;53:4528–35. [DOI] [PubMed] [Google Scholar]
- [44].Fernandez FR„ Malerba P„ Bressloff PC, White JA„ Entorhinal stellate cells show preferred spike phase-locking to theta inputs that is enhanced by correlations in synaptic activity. J Neurosci 2013;33:6027–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Pervouchine DD, Netoff TI, Rotstein HG, White JA, Cunningham MO, Whittington MA, et al. Low-dimensional maps encoding dynamics in entorhinal cortex and hippocampus, Neural computation. 18 (2006) 2617–50. [DOI] [PubMed] [Google Scholar]
- [46].Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol 2005;94:3637–42. [DOI] [PubMed] [Google Scholar]
- [47].Buzsaki G Hippocampal sharp wave-ripple: a cognitive biomarker for episodic memory and planning, Hippocampus. 25 (2015) 1073–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Mizuseki K, Buzsaki G. Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep 2013;4:1010–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Csicsvari J„ Hirase H, Mamiya A„ Buzsáki G„ Ensemble patterns of hippocampal CA3-CA1 neurons during sharp wave-associated population events. Neuron 2000;28:585–94. [DOI] [PubMed] [Google Scholar]
- [50].Rulkov NF„ Neiman AB„ Control of sampling rate in map-based models of spiking neurons. Commun Nonlinear Sci Numer Simul 2018. [Google Scholar]