Revisiting physical distancing threshold in indoor environment using infection-risk-based modeling

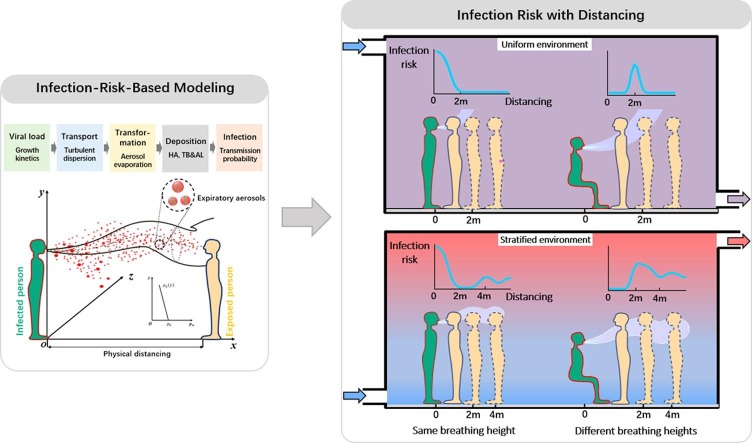
Graphical abstract

Abstract

Physical distancing has been an important policy to mitigate the spread of the novel coronavirus disease 2019 (COVID-19) in public settings. However, the current 1–2 m physical distancing rule is based on the physics of droplet transport and could not directly translate into infection risk. We therefore revisit the 2-m physical distancing rule by developing an infection-risk-based model for human speaking. The key modeling framework components include viral load, droplets dispersion and evaporation, deposition efficiency, viral dose-response rate and infection risk. The results suggest that the one-size-fits-all 2-m physical distancing rule derived from the pure droplet-physics-based model is not applicable under some realistic indoor settings, and may rather increase transmission probability of diseases. Especially, in thermally stratified environments, the infection risk could exhibit multiple peaks for a long distance beyond 2 m. With Sobol’s sensitivity analysis, most variance of the risk is found to be significantly attributable to the variability in temperature gradient, exposure time and breathing height difference. Our study suggests there is no such magic 2 m physical distancing rule for all environments, but it needs to be used alongside other strategies, such as using face cover, reducing exposure time, and controlling the thermal stratification of indoor environment.

1. Introduction

The novel coronavirus disease 2019 (COVID-19) pandemic has caused significant deaths and economic loss globally (WHO, 2020a). To contain and control the first and second waves of infection, non-pharmaceutical interventions have become the main strategies due to limited antiviral medications and absence of vaccines. Maintaining physical distancing has been considered to be effective at reducing transmission of SARS-CoV-2 virus. The so-called ‘social distancing rules’ have been implemented in many countries in the on-going pandemic. World Health Organization (WHO) advises health care personnel and other staff to maintain a 3-foot (1-m) distance away from a person showing symptoms of respiratory disease (WHO, 2020b), which is followed in countries like China, Denmark, France and Singapore (BBC, 2020). The US Centers for Disease Control and Prevention (CDC) recommends a 6-foot (2-m) separation (CDC, 2020), as being seen in Canada, Spain and UK (Qian and Jiang, 2020). In other countries such as Australia and Germany (BBC, 2020, Qian and Jiang, 2020), a 1.5-m distancing rule is recommended in public places. The definition of 1–2 m physical distancing can be traced back to many earlier studies (Wells, 1934, Turner et al., 1941), in which most of the exhaled droplets (>100 μm) was found to land within 1–2 m. However, the previous research now seems oversimplified from the following aspects:

1) The droplets embedded in a cloud of exhaled airflow in fact contain those visible to the naked eye (millimeters), and invisible ones in the micron scale. Previous droplet dispersion observation work was insufficient to capture smaller droplets and the observation field was set at a few feet to the source (Wells, 1934, Turner et al., 1941). Those small droplets could easily travel long distances with exhaled jet or indoor airflow, and cause short- or long- range airborne transmission (Liu et al., 2017a). Current social distancing rules for COVID-19 are based primarily on the assumption that SARS-CoV-2 is transmitted in large droplets only, but it has been understood that the aerosol transmission cannot be excluded and become much recognized recently (Anderson et al., 2020, Morawska and Cao, 2020). 2) Coughing has been identified as the manifest symptom of respiratory diseases, such as influenza (Lindsley et al., 2010), SARS (Breugelmans et al., 2004), and the novel COVID-19 (Sohrabi et al., 2020), so research on the spread modes prior to the current pandemic has mainly focused on violent expiratory events like sneezing and coughing (Liu et al., 2017b, Wei and Li, 2015). Most recently, (Li et al., 2020a) suggested that 79% of the actual infected cases were infected by individuals with “mild, limited, or no symptoms”. Droplets generated from normal speaking by an asymptomatic infected person are increasingly considered to be responsible for infectious disease transmission, and may even lead to highly probable outbreak events (Buonanno et al., 2020, Stadnytskyi et al., 2020). It is of practical importance to clarify the physical distancing in view of speaking rather than coughing droplets, especially in public places where more asymptomatic infected individuals may be present. 3) In most studies, indoor air is assumed to be well mixed. However, in the indoor space with displacement ventilation (DV) (Gil-Lopez et al., 2017), under-floor air distribution (UFAD) (Wang et al., 2011), and/or displacement nature ventilation (DNV) (Brandan, 2012), the air is likely not well mixed and a vertical thermal stratification exists, especially large enclosed space, e.g., airport terminals (Gil-Lopez et al., 2017) and a rebuilt Fangcang hospital (Liu et al., 2020b), among others. Previous studies found that the exhaled small droplets and droplet nuclei could be locked up at people’s breathing zone by the thermal stratification, and travel a long distance along the exhalation direction, increasing the range of cross infection (Qian et al., 2006, Liu et al., 2019). This suggests that the physical distancing in indoor environments could be complicated by its airflow and temperature distribution. 4) Owing to the directionality of exhaled airflow, the relative postures of infected and exposed individuals are important factors in determining cross-infection risk (Bjørn and Nielsen, 2002, Liu et al., 2019), such as seated and standing passengers in public vehicles, standing doctors and seated or bed-lying patients in hospital wards, and children and adults in public places. In this connection, the relative postures influence the individual’s exposure to the exhaled aerosols generated by the infector. 5) The current definition of physical distancing only looks at how far respiratory droplets of different sizes could travel physically, but does not represent the exposure to virus-laden droplets nor the infection risk of the susceptible individuals. The disease transmission is a combined action of respiratory droplets transport, viral kinetics and dose-response effects. The current recommended physical distancing of 3–6 feet (1–2 m) is mostly based on droplet transport physics, but somehow does not address the potential exposure and risk estimation, possibly generating an underappreciated potential infection risk for the susceptible individuals.

Due to the complication of the transmission risk of infectious disease, the distancing rules need to take account of multiple factors including viral load, indoor ventilation, expiratory airflow and viral dose-response rate. In this study, an infection-risk-based model is used to quantify the relationship between infection risk and physical distancing within a short distance range. The key processes in the model include viral kinetics, droplet dispersion and transformation with exhalation air and deposition in respiratory system. The infection risk is assessed using the dose-response models for viruses. The infection risk by aerosol transmission during speaking is quantified under various scenarios, i.e., with or without thermal stratification, commonly seen relative postures of infected and exposed individuals in public places and exposure time. The infection risks due to close contact (direct/indirect) and large respiratory droplets by coughs or sneezes or droplets of saliva are not included in this study.

2. Methods

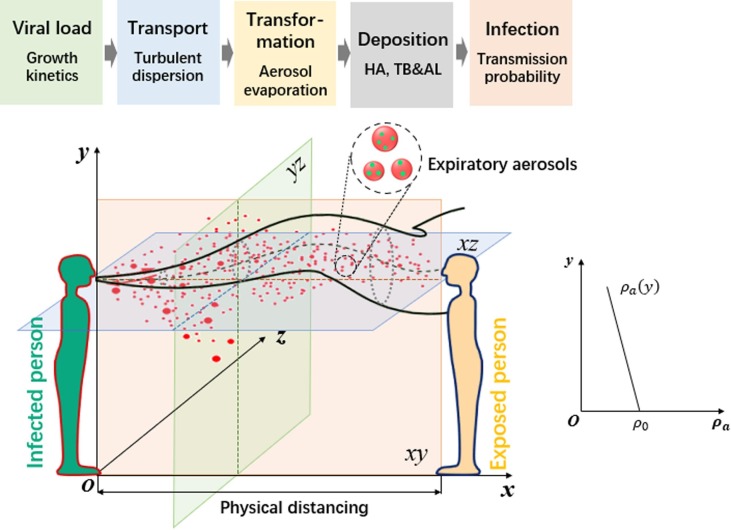
The goal here is to establish a risk-based physical distancing assessment model between the infected and susceptible individuals, which necessitates consideration of five stages of transmission and infection, shown in Fig. 1 . Virus-laden droplets are exhaled from an infected person with a viral load (i.e., the number concentration of pathogens in the droplets). The exhaled droplets then disperse and evaporate in the combined background of the exhaled air and ambient air. Some of the droplets or their residuals (droplet nuclei) in air are inhaled by the exposed person and deposit in the respiratory system, and finally induce infection according to the viral dose-response rate.

Fig. 1.

A schematic view of the transmission risk induced by inhalation of small droplets and droplet nuclei between the infected person and the susceptible person. In a thermally-stratified indoor environment, the ambient air density ${\rho }_a$ decreases with the height y. HA (head airway regions), TB (tracheobronchial regions) and AL (alveolar regions). The physical distancing refers to the distance between two human mouths.

2.1. Viral load in exhaled droplets

The number (${\text{N}}_{\text{p}}$) and size distribution (${\text{d}}_{\text{p}}$) of expelled droplets generated from speaking are obtained from (Duguid, 1946), which is still widely adopted today in understanding dynamics of airborne viruses or transmission model and has been repeated and confirmed by other more recent studies using modern aerosol characterization equipment (Yang et al., 2007, Chao et al., 2009). In this work, the viral load (${\text{n}}_{\text{path}}^{\text{p}}$) of three viruses, i.e., the influenza A virus (IAV), SARS-CoV-1 and HCoV-229E are located from the published literature (Gao et al., 2020, Lim et al., 2006, Lambert et al., 2008). The number of pathogens in any given expiratory droplet is therefore determined by the pathogen concentration, i.e., $V_0{n}_{\mathit{path}}^p$, where $V_0=\frac{1}{6}\pi {d_p}^3$ is the initial volume of each droplet upon exhalation. Although the droplet size varies due to evaporation, the pathogens themselves are assumed to be nonvolatile, and the number of pathogens in any droplet is assumed to be constant. The concentration of pathogens per unit volume of air is ${\text{C}}_{\text{path}}\text{=}{\text{C}}_{\text{p}}{\text{V}}_{\text{0}}{\text{n}}_{\text{path}}^{\text{p}}$, where ${\text{C}}_{\text{p}}$ is the local concentration of expiratory droplets per unit volume of air.

2.2. Droplet transport and transformation

The airflow generated by speaking is assumed to be a turbulent round jet oriented in the x-direction, as shown in Fig. 1. The state parameters on the cross-sectional plane of the expiratory jet are assumed to follow the Gaussian profiles (see Supplementary Eqs. (S1)-(S4)). The total fluxes of volume, momentum, buoyancy and excess state parameters in the turbulent jet flow are obtained through cross-sectional integrations over the jet profiles, in which the buoyancy flux is dependent on a stable density distribution of ambient air ${\rho }_a$ (y) in a stratified environment, which is determined by the temperature gradient in the vertical y-direction (Fig. 1). An integral model is formulated for the conservation equations for the flux quantities using an entrainment closure approach, and the state parameters of the jet flow can be obtained, as detailed by (Liu et al., 2019). According to (Duguid, 1946), the speaking-generated droplet size ranges from 0.3 to 1000 μm, with a large proportion of droplets smaller than 40 μm. (Wei and Li, 2015) and (Liu et al., 2020a) showed that droplets of < 50 µm can disperse closely following the exhaled airflow after being expelled. This result led to the conclusion that the short-range airborne route dominates the transmission in close contact with an infected person while speaking, in which case the droplet number concentration ${\text{C}}_{\text{p}}$ during the transport process can be directly obtained using the above jet integral model. The detailed mathematical derivation for each stage of transmission and infection is provided in the Supplementary Material.

Exhaled droplets will evaporate and become droplet nuclei while dispersing with the jet flow. The size of the droplet nucleus is a function of the initial size of the droplet, its components, RH and ambient temperature distribution (Liu et al., 2017b). Based on existing models for the exhaled droplet motion and mass and heat transfer (Wei and Li, 2015), the size variation with distancing and time of the speaking-generated droplets (<40 μm) can be obtained (see Supplementary Fig. S3). It shows that the speaking-generated droplets can evaporate totally at a short distance (<0.4 m) within 0.2 s, and the residual droplet nuclei continues to travel longer distances with the airflow in indoor environments and finally be inhaled by exposed person.

2.3. Inhalation and deposition in respiratory system

To determine the particle concentrations that are actually inhaled by the susceptible person, a breathing rate B is assumed to be constant throughout the transmission process. The deposition efficiency depends on the particle size and the region of the airway where deposition occurs (Hinds, 1999). In general, large droplets deposit in nasopharyngeal area, while small ones can reach the conducting airways and alveolar. Studies on airborne transmission indicated that infections via aerosols were most likely to originate in the lower respiratory tract, specifically the alveoli (Nicas et al., 2005). Furthermore, medical studies show that respiratory disease viruses present a clinicopathological difference in the distribution in human airways. For example, common human-derived viruses (such as HCoV-229E) are found to bound extensively to epithelial cells in the bronchi and, to a lesser degree, to alveolar cells (Shinya et al., 2006); by contrast, IAV and SARS-CoV-1 bound extensively to alveolar cells (Shinya et al., 2006, Gu and Korteweg, 2007). Because the site of airborne infection is not absolutely clear, the total deposition rate (η) of inhaled particles in HA, TB and AL regions is considered here, and calculated using the International Commission on Radiological Protection model (Hinds, 1999) (see Supplementary Fig. S4). Therefore, the number of pathogens (${\text{μ}}_{{\text{d}}_{\text{p}}}$) deposited in the respiratory system induced by the droplet of initial diameter ${\text{d}}_{\text{p}}$ during an exposure time interval t is related to the local airborne concentration of pathogens as ${{\text{μ}}_{{\text{d}}_{\text{p}}}\text{=C}}_{\text{path,}{\text{d}}_{\text{p}}}\text{ηBt}$. Since the risk of infection by pathogen-laden particles is a combination of the probabilities that one or more particles from the different diameter ranges contact a mucous membrane and causes infection, the ultimate number of deposited pathogens is $\text{μ=}{\sum }_{{\text{d}}_{\text{p}}\text{=}\text{1}}^{\text{40}}{\text{μ}}_{{\text{d}}_{\text{p}}}$.

2.4. Viral dose-response rate

Deposition of virus-laden droplets in the respiratory tract does not always result in infection, since the mucus layer could provide some level of protection against virus invasion and subsequent infection. The dose-response relation is utilized here to assess the infection risk as a function of the exposure dose (${\text{μ}}_{\text{total}}$). The model providing the best fit to the infectious dose data on the disease should be selected for infection risk assessment. Considering the current unavailable information on SARS-CoV-2 when conducting this study, we chose to reference the dose-response models for IAV, SARS-CoV-1 and HCoV-229E from existing studies.

2.5. People-to-people postures

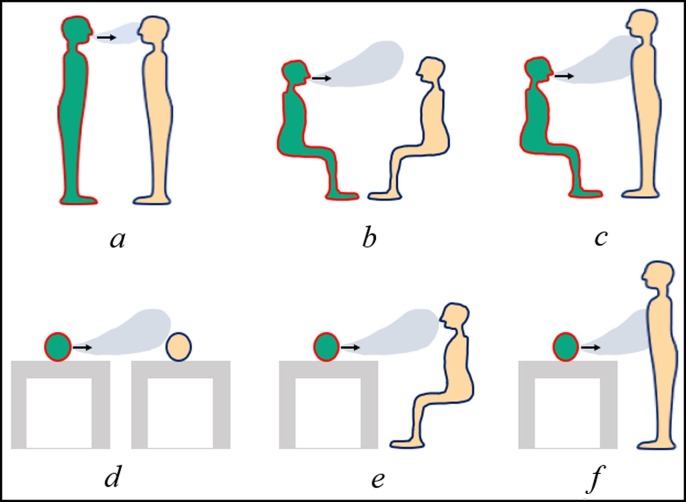
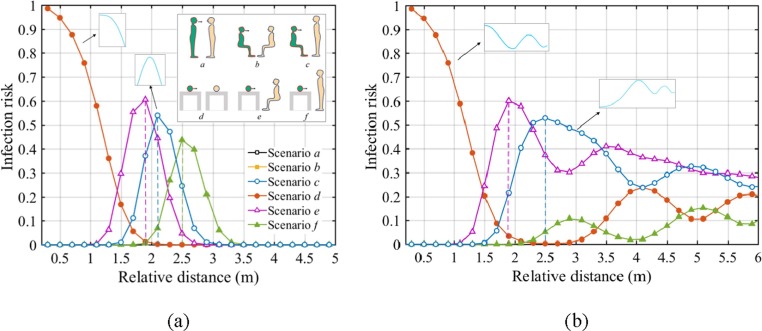
Six scenarios for common person-to-person postures in public places, such as hospital ward, waiting room, public transportations and other environments are summarized in Fig. 2 . The breathing heights are 1.75 m, 1.18 m and 0.8 m for standing, seated and lying person, respectively. Other key modelling parameters are listed in Supplementary Table S1.

Fig. 2.

Scenarios of relative postures of infected and susceptible individuals: a- standing to standing, b-seated to seated, c-seated to standing, d-lying to lying, e-lying to seated, and f-lying to standing. The infector is green, and the susceptible person is yellow. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.6. Sensitivity analysis

Sensitivity analysis of the infection-risk-based model is undertaken for two type of relative postures in the stratified environment: 1) same breathing heights between two individuals (Scenarios a, b and d); 2) different breathing heights (Scenarios c, e and f). The major input parameters considered in the sensitivity study include: (i) viral load, ${\text{n}}_{\text{path}}^{\text{drop}}$, (ii) exposure time, t, (iii) temperature gradient, dT/dy, (iv) ambient temperature, ${\text{T}}_{\text{a}}$, (v) relative humidity, RH, and (vi) breathing rate, B. A total of 6,000 Latin-hypercube samples from the 6 parameter distributions (see Supplementary Table S2) are generated and the parameter variability are propagated through Monte Carlo simulations of the model in non-uniform indoor environments. Sobol’s variance-based sensitivity analysis is conducted to quantitatively attribute the variance of the infection risk to the uncertainties or variabilities of different input parameters (Sobol, 2001).

3. Results

3.1. Influential factors for distribution of transmission probability

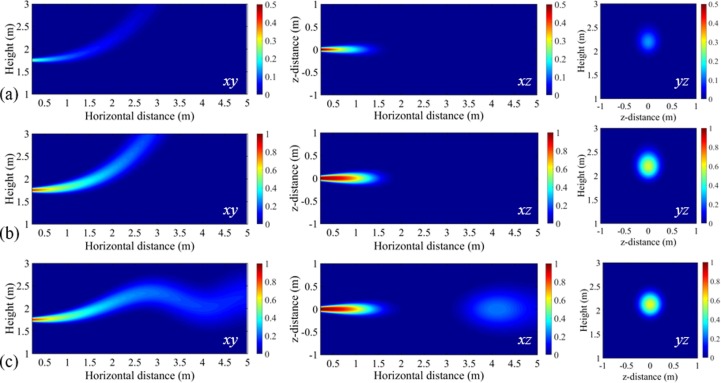
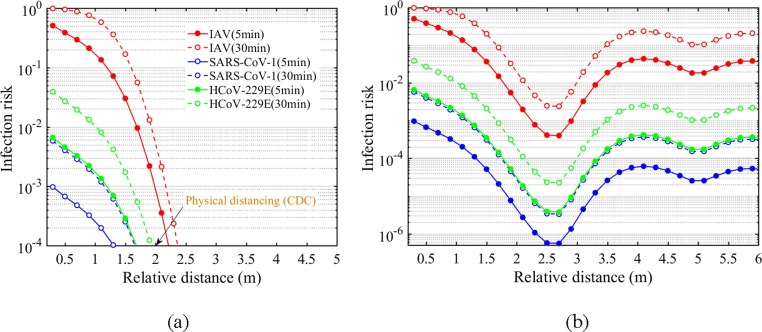
The distributions of infection risk on three cross planes (i.e., planes xy, xz and yz in Fig. 1) are calculated to investigate the influences of exposure time (5 min and 30 min) of the susceptible individual and indoor temperature distribution (dT/dy = 0 and dT/dy = 2 °C/m). The virus-laden droplets are exhaled from a standing infector, transport in air and reach the standing susceptible person. Representative contour plots of the transmission probability of IAV as a function of relative distance are presented in Fig. 3 . It shows that in each case there is a high transmission probability near the infected person (i.e., near x, y, z = 0, 1.75 m, 0), with the probability decaying at larger distances and greater heights. The exact shape of the ‘airborne infectious zone’ depends on both the exposure time and the temperature distribution of indoor air.

Fig. 3.

Contour plots of transmission probability of IAV: (a) uniform environment (dT/dy = 0), exposure time of 5 min; (b) uniform environment (dT/dy = 0), exposure time of 30 min; (c) stratified environment (dT/dy = 2 °C/m), exposure time of 30 min. Red denotes high probability and blue denotes low probability. Planes xy (z = 0), xz (y = 1.75 m), and yz (x = 2 m) are donated in Fig. 1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

With a longer exposure time, the infection risk becomes higher for the susceptible individual at the same exposure distance. In specific, as shown in the contours on yz planes at a relative distance of 2 m to the infector, the infection risk is close to be 0.6 when the susceptible person is exposed for 30 min, but only a risk of 0.3 for 5 min exposure. However, it is observed from the contours on xz planes of Fig. 3 (a) and (b) that at the breathing height (1.75 m) the transmission probability can decay to 0 within 2 m, unaffected by the exposure time. It suggests that the exposure time has an impact on the infection risk, but less affecting the transmission distance. However, in a non-uniform environment with a thermal stratification, as shown in Fig. 3 (c), the transmission probability with the distance gets a little complicated. The infection risk cannot keep decaying along the vertical height, but varying along the exhalation direction for a long distance, further than 2 m. It is more obvious to see from the contours on the xz plane that the infection risk firstly decreases to 0 within 2 m, but increasing again within 3.5–5 m due to the oscillation shape of the “infection zone” on the xy plane, i.e., under this setting, even 2 m may be too close.

3.2. Physical distancing and infection risk for two standing persons

The infection risk with distancing under Scenario a is presented in Fig. 4 . To make a comparison with the current distancing rules recommended by CDC, ambient air temperature distribution is not considered in Fig. 4 (a). It shows that the infection risk of all three viruses to an exposed person decreases monotonously with distancing, and approaches approx. 0.0001 at about 2 m, coincident with the 1–2 m physical distancing rule. However, when indoor airflow is characterized with a vertical temperature gradient, as shown in Fig. 4 (b), there is a first decrease of the infection risk within 2 m, but a second-high level rather than continuously decreasing at a distance larger than 2 m. Therefore, it seems that the current distancing rules are only applicable for the simplest airborne transmission case where the relative postures and ambient temperature distribution are ignored.

Fig. 4.

Quantified infection-risk-based physical distancing of two standing persons, with different exposure time in parentheses of the legend: (a) uniform environment (dT/dy = 0); (b) stratified environment (dT/dy = 2 °C/m).

3.3. Impact of different relative postures on infection risk

The infection risk of IAV is examined under six scenarios in Fig. 2. The calculations are conducted in the indoor environment with a temperature gradient of dT/dy = 2 °C/m, with the results in a uniform environment included here for comparisons.

The results in a well-mixed indoor environment are shown in Fig. 5 (a). The infection risk curves overlap perfectly when the infected and exposed persons are at the same breathing height (i.e., Scenarios a, b and d). Under these conditions, the infection risk shows a monotonic decrease with the distancing in a uniform environment, so the 2-m distancing rule is still effective here. However, when there is a breathing height difference between the individuals (i.e., Scenarios c, e and f, with the difference of 0.57 m, 0.38 m and 0.95 m, respectively), the infection risk shows parabolic trend with the distancing, that means, the exposed person could be more susceptible at a certain distance to the source, such as approx. 2 m under Scenarios c and e, or even 2.5 m under Scenario f. Therefore, this is a situation where relative posture become an important parameter, and the 2-m distancing could become a dangerous threshold with a high transmission probability for the susceptible people.

Fig. 5.

Risk-based physical distancing under different relative postures of the infected and susceptible people (with exposure time of 30 min): (a) uniform environment (dT/dy = 0); (b) stratified environment (dT/dy = 2 °C/m). Lines of Scenarios a, b and d overlap exactly in two figures.

When the temperature is non-uniformly distributed indoors, as shown in Fig. 5 (b), the infection risk curves also overlap exactly under the Scenarios a, b and d. However, things get a little complicated because there is a clear rebound within 3–4 m, and then the infection risk remains at a high level with oscillations for a long distance. What is worse, the existence of the breathing height difference (i.e., Scenarios c, e and f) makes the risk peak at much closer distances to the infector. It suggests that in the poorly ventilated places, the infection risk may become very high at or after 2 m rather than show a simple decrease tend with distancing. It is highly likely that the disease infection happens within a long distance to the source patient, up to several meters or room scales.

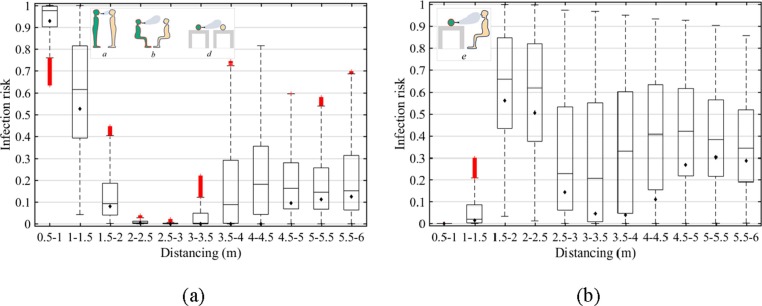
3.4. Sensitivity analysis

We obtain 11 social distancing bins at 0.5 m interval for up to 6 m distance. Considerable variability of infection risk has been observed spanning 11 social distancing bins in relation to simultaneous variation of the 6 input parameters. Fig. 6 shows the results under Scenarios a, b and d (same breathing heights, Fig. 6a), and Scenario e (with a breathing height difference of 0.38 m, Fig. 6b). The results under Scenarios c and f are shown in Supplementary Fig. S6. Overall, the simulated infection risk has a left-tail distribution for all scenarios. The variability of the transmission probability is more significant when there is a breathing height difference between exposed and infected people. In specific, the highest probability ranges within 0.86–0.95 after 1.5 m distancing in Figure (b), while only 0.22–0.82 after 3 m distancing in Fig. 6 (a). It implies a breathing height difference could make the susceptible person more likely to get infected after a 3 m distancing. However, the lowest transmission probability invariably occurs at 2–3 m distancing for the same breathing heights in Fig. 6(a) and 0.5–1 m distancing for the case of breathing height difference in Fig. 6(b), respectively, which is less sensitive to the changes of variables.

Fig. 6.

Box plots of infection risk: (a) without breathing height difference (Scenarios a, b and d); (b) with a breathing height difference of 0.38 m (Scenario e). The box indicates 1st, 2nd and 3rd quartiles. The lower whisker shows the minimum and the upper whisker shows the maximum. Mean values are indicated by the diamonds (◆). Results under Scenarios c and f can be found in Supplementary Fig. S6.

Results of Sobol’s analyses (see Supplementary Tables S3-S6) show the 6 input parameters contribute to the risk differently at various social distances, where the main effect ${\text{S}}_{\text{i}}$ indicates the proportion of output uncertainty removed by fixed parameter ${\text{X}}_{\text{i}}$. Of all 6 input parameters, RH (${\text{S}}_{\text{i}}\text{=0}$) is the least significant for the infection risk, since the speaking-generated droplets (<40 μm) evaporate quickly into droplet nuclei within a short time of 0.2 s and a short distance of 0.4 m from the infector (see Supplementary Fig. S3), being hardly affected by RH. The results are also consistent with the recent findings of (Liu et al., 2020a), i.e., RH has more impact on medium droplets, while almost unaffecting small droplets of < 40 μm and their residuals. The largest ${\text{S}}_{\text{i}}$ is determined as temperature gradient and exposure time. At 2.5–4.5 m distancing to the infector, thermal stratification is the most important contributor (accounting for approx. 45.7%-88.8%) to the variance in the infection risk, especially under Scenarios a, b, d and e with a small breathing height difference. Therefore, it is of paramount importance to take into account of indoor thermal stratification to get full picture of infection risk in indoor environment when the distance between people is within 2.5–4.5 m. At other distances, especially at 0.5–2.5 m, exposure time is considerably significant, whose ${\text{S}}_{\text{i}}$ can reach 86.2%. It means that in close proximity to the source infector, reducing the exposure time is more crucial to minimize the risk comparing with other interventions. The viral load, ambient air temperature and breathing rate are relatively less influential to the variability of the transmission probability within the range evaluated.

4. Discussion

Most existing droplet transport models for defining the physical distancing have not recognized the complexity of the transport process of expired droplets or droplet nuclei, and the resulting exposure and infection risk. Our model attempts to relax some of the assumptions in the existing models and incorporate the infection risk estimation. After a sensitivity analysis of the model, we found that the infection risk is significantly affected by indoor environmental conditions, relative postures and exposure time. The one-size-fits-all 2-m physical distancing rule seems not applicable in some realistic settings.

4.1. Droplet-physics-based versus infection-risk-based physical distancing

Traditionally, the 1–2-m rule of spatial separation based on droplet transport physics in isolation was central to infection precautions and assumed that large droplets did not travel further than 2 m. In the recent Lancet review, (Chu et al., 2020) analyzed 29 studies on droplet spread of actual case and model predictions, and suggested that the physical distancing of 1–2 m may be probably associated with a reduction in infection. The finding is consistent with the droplet-physics based model, and has been used to define exposure to the SARS-CoV-2 in the earlier studies when the virus was thought to be spread by ‘contact and droplet’ transmission only (WHO, 2020b, CDC, 2020). However, some other studies that considered the possible close-range airborne transmission route via small droplets do not actually support the 1–2-m rule of spatial separation. For example, (Xie et al., 2007) revisited the Wells’ work and found that droplets of <50 µm can travel more than 6 m for sneezing with an exhalation velocity of 50 m/s and more than 2 m for coughing at a velocity of 10 m/s. (Wei and Li, 2015) employed the discrete random walk model for particle tracking and found small droplets (<50 µm) can follow the coughing airflow easily, dispersing in the whole jet region to 4 m. Subsequently, (Ji et al., 2018) further emphasized that the small droplets can disperse with the exhaled jet flow to a long distance by numerical simulations, which cannot be neglected in accessing the infection risk within a close-range contact of people. In most of these studies prior to the current pandemic, the violent respiratory events like sneezing and coughing are the focus only because they are recognized as the manifest symptoms of respiratory diseases. With increasing evidence that the droplets from an asymptomatic individual while speaking is a likely mode of disease transmission, dispersion of speaking-generated droplets begins to get attention. That means, the disease transmission cannot neatly be separated into the dichotomy of droplet versus airborne transmission routes based on an overly simplified model. Most recently, (Jones et al., 2020) reviewed the evidence of the 2-m physical distancing and agreed with our study that the final infection risk of an exposed person is determined by multiple factors, rather than being reflected by the single and fixed physical distancing rules based only on droplet physics.

Our results suggest that a unified distancing rule of 1–2 m is not always an effective guidance of spatial separation in different epidemics, but rather may underestimate the infection risk to exposed people. In addition, prior droplet-physics based physical distancing mainly focused on the infected person, without considering the exposure time of the susceptible people. However, the Sobol’s analysis indicates that a prolonged exposure time could significantly increase the risk to a high level at a close distancing to the infection source, which can probably be linked to some clusters of cases in the outbreak of COVID-19. For example, a two-and-a-half-hour choir rehearsal with one symptomatic person led to 32 confirmed and 20 probable COVID-19 cases among the 61 singers (Hamner et al., 2020, Miller et al., 2020); a cross-infection occurred in a Chinese restaurant among three non-associated families at neighboring tables during the lunch, and all the three families occupied the restaurants for more than one hour, without no evidence of direct or indirect contact according to the video record (Li et al., 2020b). Thus, it appears that for the exposed people, keeping the 1–2 m physical distancing alone may be not enough to mitigate transmission at some conditions.

4.2. Well-mixed versus thermally-stratified indoor environment

We found that the infection risk in indoor environment is about three orders of magnitude larger than that in outdoor space with natural wind. (Zhang et al., 2020) evaluated the aerosol transmission risk for COVID-19 from South China Seafood Market to surrounding buildings and found that the outdoor infection risk by aerosol transmission rapidly decreased due to the strong dilution by the ambient air. Different from outdoor environment with sufficient wind dilution capacity, our results suggest that the indoor infection risk variability with the distancing is greatly affected by the indoor thermal stratification, especially at 2.5–4.5 m (Tables S3–S6). In a well-mixed room, the infection probability decreases to an acceptable risk (<0.0001) after 2 m, regardless of the exposure time and viral load. In this case, a physical distancing of >2 m may be effective to lower the infection risk. However, when considering the thermal stratification indoors (e.g., with DV, UFAD, DNV systems), the infection risk shows multiple peaks with distancing. It is because the exhaled airflow can be easily trapped at a lock-up layer by indoor thermal stratification and travel a long distance with some oscillations, i.e., the lock-up phenomenon reported in references (Qian et al., 2006, Liu et al., 2019). The airborne droplets and droplet nuclei carried by the airflow can finally accumulate at the lock-up layer, causing a high infection risk to the susceptible people. The physical distancing rule seems to be ineffective in such indoor environments. Our infection risk-based model also supports the early recommendation that DV should not be used in hospital environments to avoid cross infection (Qian et al., 2006). In addition, ventilation designers need to be careful with the thermal stratification in critical environments, such as the emergency Fangcang hospitals converted from gymnasiums or convention centers in the pandemic, where a thermal stratification could prevail. It should take special care to design an appropriate indoor environment or to modify existing ventilation patterns with respect to control of airborne transmission of diseases.

4.3. The importance of relative posture on infection risk

The importance of relative posture of individuals on personal exposure to exhaled aerosols has been mentioned in previous studies (Liu et al., 2019, Bjørn and Nielsen, 2002), but no further studies quantifying its relationship with infection risk. In our model, six commonly-observed relative posture scenarios based on human regular activities in real world are discussed (Fig. 2). The estimations of infection risk suggest that for two persons with the same breathing heights (e.g., standing-to-standing people talking to each other, seated-to-seated people in public transportations or waiting rooms, and lying-to-lying patients in hospital wards), a 2-m physical distancing rule could effectively reduce the infection risk when the indoor air is well mixed. However, the existing of a breathing height difference could make the exposed person riskier at 1.5–3-m distancing. For example, for a lying patient and a seated visitor, the infection risk could peak at approx. 2 m, while for a seated/lying patient and a standing healthcare worker in hospital wards, or seated-to-standing people in public transportations or waiting rooms, the infection risk could peak at a further distance of approx. 3 m. This is related to the directionality of the non-isothermal exhaled airflow to be upward and forward, causing the susceptible person with a higher breathing height to be easily exposed at a further distance. The findings are consistent with the observations of (Bjørn and Nielsen, 2002). In their full-scale experiments, the exposure concentration of the exposed manikin decreased with distance for standing-to-standing situation, while there was a higher exposure within a short distance in the case with a seated source manikin and a standing exposed manikin. In addition, our results suggest that the condition could be even worse in stratified environments, i.e., there is a continuously high level with multiple peaks of the infection risk regardless of distancing. (Liu et al. 2019) predicted the exposed concentration of susceptible people in hospital wards with thermal stratification, and found that the breathing height difference could make people more easily exposed to a high concentration within a long distance. The infection-risk-based model provide a further validation on the importance of relative postures in view of the infection risk. It suggests that special attentions should be given by the susceptible people who have relatively high breathing heights in an enclosed environment, e.g., the health care workers and visitors standing next to the lying/seated patients in hospital and the standing passengers relative to the seated passengers in public transportations.

4.4. Implication to the COVID-19 transmission

This study looks specifically at the physical distancing in relation to the transmission risk via speaking-generated airborne aerosols. The model developed here includes some major stages of infectious disease transmission, and considers the important roles of the exhalation and indoor environments under the various relative posture conditions, and is applicable to different airborne diseases carried by expiratory droplets. We focused on three key viruses, i.e., IAV, SARS-CoV-1 and HCoV-229E, because the key data of these three viruses such as viral load and dose-response models are available and have been used in other modeling studies (Watanabe et al., 2010, Halloran et al., 2012, Gao et al., 2020). Many viral kinetics of SARS-CoV-2 are now emerging (Ma et al., 2020, Zhou et al., 2021), the theoretical framework can therefore be extended to COVID-19 when the dose-response relation of SARS-CoV-2 becomes available. The infection risk due to close contact (direct/indirect) and large respiratory droplets by coughs or sneezes or droplets of saliva is not included in this study. In addition, COVID-19 transmission from asymptomatic hosts makes it critical that we develop the infection-risk-based model in view of normal speaking instead of sneezing or coughing. This work suggests that physical distancing rules at a specific distance of 1–2 m may not work in some realistic settings. Other strategies, such as good personal protection such as mask wearing and better building ventilation should be carried out along with the physical distancing rule.

Distancing is important when it is linked to decreased incidence of respiratory infectious disease (Alagoz et al., 2020, Du et al., 2020), especially via the close contact transmission. We particularly look at the short-range airborne route, and the resultant infectious dose and finally infection risk considering the corresponding dose-response relationship per virus. Although it is well recognized that more distance is better to reduce overall infection risk, there is debate on what is the safe distance threshold to make an effective use of indoor space (Wong et al., 2004, Chu et al., 2020, Tang et al., 2021). This is particularly useful information when considering the reopening strategies for various buildings after the pandemic. We hope to provide some useful evidence-based guidelines for determining such safe distance threshold.

The limitations include several assumptions built in the model e.g., the consideration of a steady state expired jet, the fixed position and gesture/posture of the two people in space, as well as the non-consideration of thermal plume around the human body and the breathing synchronization of the two people.

Funding

This work was supported by UK GCRF Rapid Response Grant (ZL), National Natural Science Foundation of China (grant number 51778128), Scientific Research Foundation of Graduate School of Southeast University (grant number YBJJ1806) (HQ) and China Scholarship Council (CSC) (FL).

CRediT authorship contribution statement

Fan Liu: Conceptualization, Methodology, Writing - original draft. Zhiwen Luo: Conceptualization, Supervision, Resources. Yuguo Li: Methodology. Xiaohong Zheng: Software. Chongyang Zhang: Methodology, Software. Hua Qian: Conceptualization, Supervision, Resources.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Xavier Querol

Appendix A. Supplementary material

The following are the Supplementary data to this article: