Spherical Deformable U-Net: Application to Cortical Surface Parcellation and Development Prediction

Abstract

Convolutional Neural Networks (CNNs) have achieved overwhelming success in learning-related problems for 2D/3D images in the Euclidean space. However, unlike in the Euclidean space, the shapes of many structures in medical imaging have an inherent spherical topology in a manifold space, e.g., the convoluted brain cortical surfaces represented by triangular meshes. There is no consistent neighborhood definition and thus no straightforward convolution/pooling operations for such cortical surface data. In this paper, leveraging the regular and hierarchical geometric structure of the resampled spherical cortical surfaces, we create the 1-ring filter on spherical cortical triangular meshes and accordingly develop convolution/pooling operations for constructing Spherical U-Net for cortical surface data. However, the regular nature of the 1-ring filter makes it inherently limited to model fixed geometric transformations. To further enhance the transformation modeling capability of Spherical U-Net, we introduce the deformable convolution and deformable pooling to cortical surface data and accordingly propose the Spherical Deformable U-Net (SDU-Net). Specifically, spherical offsets are learned to freely deform the 1-ring filter on the sphere to adaptively localize cortical structures with different sizes and shapes. We then apply the SDU-Net to two challenging and scientifically important tasks in neuroimaging: cortical surface parcellation and cortical attribute map prediction. Both applications validate the competitive performance of our approach in accuracy and computational efficiency in comparison with state-of-the-art methods.

I. Introduction

CONVOLUTIONAL Neural Networks (CNNs) based deep learning methods have been providing state-of-the-art performance for a variety of tasks in computer vision in the last few years, e.g., image classification [1], segmentation [2], detection and tracking [3], benefiting from their powerful abilities in feature learning. In biomedical image analysis, U-Net [4] and its variants have become one of the most popular and powerful network architectures for medical image segmentation [5], synthesis [6], reconstruction [7], and registration [8]. One of the reasons for the tremendous success of U-Net and its variants is the hierarchical architecture and skip connection, where features from low, middle, and high levels are integrated and thus both contextual and localization information can be captured jointly. Notably, for the regular grid format of image, feature maps can be easily pooled and upsampled, which allows CNNs, e.g., U-Net, to learn and enrich features hierarchically using different receptive fields at different resolution levels. Therefore, it is the consistent neighboring relationship in the Euclidean space providing the bases for these popular CNN architectures.

However, such relationships generally do not exist in many other data representations. For example, the shapes of many structures in medical imaging have an inherent spherical topology in manifold space represented by triangular meshes. As shown in Fig. 1, the constructed brain cortical surface represented by triangular meshes [9] typically has large inter-subject and intra-subject variations in shapes, i.e., different vertex number and inconsistent local connectivity. Leveraging the spherical topology nature of the cerebral cortex, a standard method for analyzing the complex cortex is to inflate and map the cortical surface onto a standard sphere [10] and further resample it using the icosahedron discretized sphere [11]. Since the resampled spherical surface has a consistent structure and uniform-sampled vertices, and thus can establish a consistent coordinate system for different subjects, it is widely used in neuroimaging analyses [12], [13]. However, there is still no consistent straightforward neighborhood definition across different vertices on the spherical surface and thus no convolution/transposed convolution and pooling operations are defined. Therefore, despite many advantages of CNNs in 2D/3D images, the conventional CNNs cannot be directly applicable to cortical surface data. To address these issues, in this paper, we capitalize on the consistent structure of the resampled spherical cortical surface. The motivation is that the standard spherical representation of a cortical surface is typically a uniform icosahedron discretized sphere that is generated starting from an icosahedron by hierarchically adding new vertices to the center of each edge in each triangle [11]. Therefore, based on the consistent and regular structure across subjects, we design a novel intuitive convolution filter on the sphere, termed 1-ring filter. With this new convolution filter, we then develop surface convolution, pooling, and transposed convolution in spherical space by considering the analogy between the standard filter on the 2D image grid and the 1-ring filter on the spherical surface. Accordingly, we extend the popular U-Net architecture from image domain to spherical surface domain and construct the Spherical U-Net architecture.

Fig. 1.

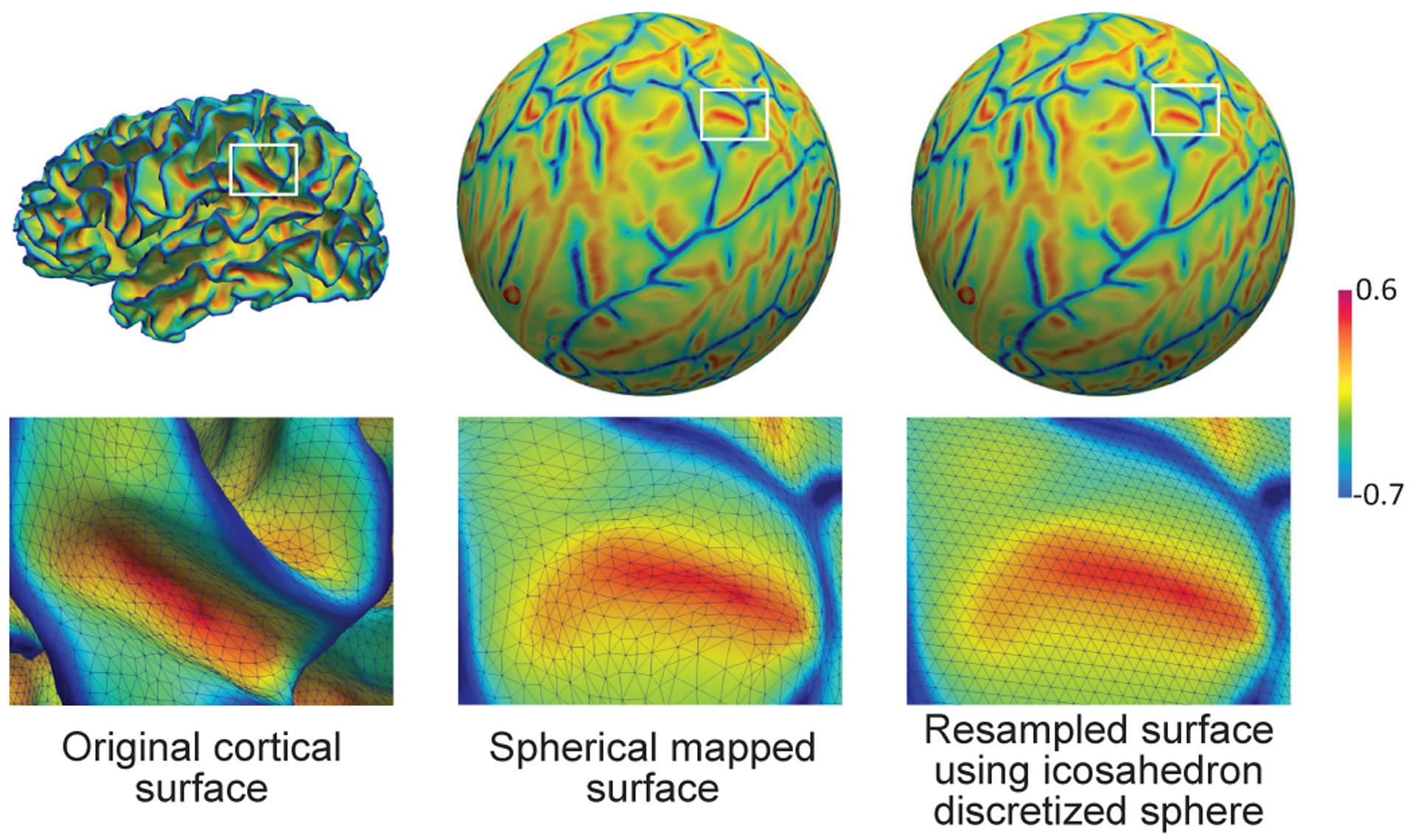
An example of the cortical surface represented by triangular meshes at different stages of neuroimaging data analysis pipeline. The surfaces are color-coded by mean curvature.

However, the Spherical U-Net constructed using the 1-ring filter are inherently limited to model large, fixed transformations [14]. As cortical folds vary greatly in shape and size, another challenge is how to accommodate and model various geometric transformations of cortical folding. This limitation comes from the fixed design of the 1-ring filter and the accordingly developed spherical convolution/pooling operations, where the 1-ring filter samples the input feature map at fixed locations for each operation. In this way, the receptive fields of all vertices in the same layer are the same, which is undesirable for high level layers that encode the semantics over spatial locations, because different locations may correspond to cortical structures with different shapes and sizes. Therefore, the adaptive determination of sampling locations and scales is crucial for cortical surface tasks. Inspired by the idea of deformable convolutional networks (DCN) [14] in Euclidean space that learns to augment the spatial sampling locations in convolution and pooling layers for different tasks, we propose to further develop the 1-ring filter as a deformable 1-ring filter for spherical convolution and pooling operations, namely spherical deformable convolution and spherical deformable pooling. They add spherical offsets to the regular 1-ring filter sampling locations, thus enabling free form deformation of the 1-ring filter for adaptively localizing cortical structures with different sizes and shapes. They are both lightweight and can readily replace their plain counterparts in Spherical U-Net, resulting in the novel Spherical Deformable U-Net (SDU-Net).

To validate our proposed methods, we focus on two challenging and important tasks in neuroimaging studies: cortical surface parcellation, which is a vertex-wise classification/segmentation problem, and cortical attribute map development prediction, which is a vertex-wise dense regression problem. Both applications validate the competitive performance of our approach in accuracy and computational efficiency in comparison with state-of-the-art methods.

II. Related Work

A. Deep Learning for Cortical Surface Analysis

There have been few attempts to apply deep learning techniques to cortical surface data. Wu et al. [15] first applied deep CNN on cortical surface parcellation. They projected intrinsic spherical surface patches into tangent spaces to form 2D image patches, and then the conventional CNN was employed to classify each patch for predicting the center vertex label, and further derived the surface parcellation map. However, this type of patch-wise classification method for segmentation tasks treats each patch independently, thus leading to lots of redundancy due to patch overlapping. Seong et al. [16] designed several convolution filters on the tangent plane so that the network can learn high level features from the hierarchical CNN architecture. Although these tangent convolution filters are effective, it introduces heavy computational burden by repeatedly re-interpolating the spherical surface to the tangent plane. Another way is taking the original cortical surface as a graph and applying graph convolutional networks (GCN). For example, MoNet [17] was employed to predict missing infant cortical surfaces in longitudinal studies [18], which showed good performance. However, it is still a patch-based method, the high-level context information across patches is less explored. Gopinath et al. [19], [20] tried to combine spectral embedding features with spatial features in GCN, such as cortical thickness used in [20] for disease prediction and sulcal depth in [19] for cortical surface parcellation. However, as a global representation, spectral features used in GCN may lose subtle local information, which cannot be obtained from spectral embedding features.

B. CNN for Spherical Data

As a kind of spherical data, the cortical surface might also be studied by recent techniques developed for spherical data in computer vision. The spherical data, such as the so-called omnidirectional images, can be represented by various discretized spheres. The commonly used one is the equirectangular projection (ERP) method, which is also known as Mercator projection in the geographical map projection. With ERP method, the sphere can be parameterized by spherical coordinates α ∈ [0, 2π) and β ∈ [0, π], and the projected images can be represented by regular grids in a Euclidean-like space with consistent neighborhood definition, and then conventional CNNs can be directly applied [21]. However, ERP representations lead to severe shape distortion in projected images due to non-uniform points on the sphere, especially near the polar regions. To reduce the distortion in ERP images and be rotation invariant in the 3D object classification task, Esteve et al. [22] and Cohen et al. [23] performed convolutions on the 3D rotation group SO(3) using Fast Fourier Transform. However, although they worked effectively on classification or regression tasks, semantic segmentation tasks were not fully addressed, especially for the learnable upsampling methods. Su and Grauman [24] proposed to increase the kernel size towards the polar regions to resolve the distortion problem on ERP images. However, in this strategy, the weights can only be shared along the latitude, resulting in a significant increase in computational and storage costs. Further, Zhao et al. [25] used distortion-aware kernels that sampled points on the tangent plane of the omnidirectional image to reduce distortions, which was similar to [16] in spherical cortical surface analysis. It is worth noting that this projection strategy [16], [25] was more like Hammer projection in the geographical map projection. However, as mentioned earlier, the kernel resampled on the tangent plane introduces an extra re-interpolation process, thus complicating the network and increasing the computational burden.

Concurrently, many researchers have found the advantages of icosahedron discretized spheres, which is like the Dymaxion map projection and has the smallest shape distortion and area irregularity among those map projections and the 5 Platonic solids [26]. Our preliminary work [27], to the best of our knowledge, was the first one to directly utilize the consistent and hierarchical structure of icosahedron discretized spheres for spherical CNNs development and apply it on cortical surface applications. Liu et al. [28] and Rao et al. [29] also used the 1-ring filter to develop convolution layers on icosahedron discretized spherical surfaces for 3D object classification and retrieval tasks. However, the opening and stretching surface implementation in [28] was more complex and computationally expensive. In [29], the 1-ring filter was only used in the pooling layer and not in the convolution layer, which obviously limits the 1-ring filter’s learning ability. Different from those methods [27]–[29] that take vertices as pixels, Lee et al. [26] had a very similar intuition that took the triangle faces as pixels and designed two kernels for two types of triangles for omnidirectional images classification and segmentation. Jiang et al. [30] used the 1-ring filter to estimate differential operators on icosahedron discretized spheres, which is then used as the convolution kernel for 3D object classification and cortical surface parcellation [31]. The main difference compared to our method is that the differential operators [30], [31] are designed to learn the global combination of the whole surface’s first and second order differentials, while our 1-ring filter learns patterns between local neighboring vertices and thus is more similar to classic convolution kernels in 2D/3D images and more suitable for extending other deep learning techniques to the cortical surface, e.g., the deformable convolution and pooling.

Another limitation of previous works [15], [16], [26], [28]–[31] is that they mainly focus on spherical convolution and pooling operations for constructing classification CNNs, resulting in a lack of effective upsampling methods in the community for omnidirectional image semantic segmentation and cortical surface parcellation tasks. There are only some simple upsampling methods that have been studied, e.g., padding the new vertices after upsampling with 0 [30], [31] or nearest vertex’s value [29]. To fill in this methodology gap, we proposed to extend several popular upsampling methods to icosahedron discretized sphere, such as linear interpolation, max-pooling indices [32] and transposed convolution. Among them, transposed convolution is an effective upsampling method and has been widely used for its learnable parameters in deep encoder-decoder CNN architectures, especially in image semantic segmentation [2], super resolution and registration [8]. Inspired by this, we extend the transposed convolution to the spherical surface based on the 1-ring filter and incorporating it in our SDU-Net generates superior performance, compared to other upsampling methods.

C. Deformable Convolutional Networks

Conventional CNNs are inherently ineffective in modeling geometric transformations. To address this issue, DCN proposed to augment the spatial sampling locations in convolution and pooling with additional offsets and learning the offsets from target tasks [14]. Hence, it can adaptively learn to model various transformations. Some works partly shared the concept in modeling geometric transformations, but only for some specific transformations known as a priori, such as scale [33] and rotation [34]. Spatial transform networks [35] was the first to directly learn the transformations from data without priori. It aims to learn a global transformation, such as affine transformation, which is then used to warp the feature map, while DCN focuses more on local, deformable transformations and without a feature warping step and thus is easier to integrate into any CNN architectures. When the offsets in the deformable convolution are fixed at some specific sparse locations, the deformable convolution turns into atrous convolution [36] that keeps the original convolution kernel’s weights at fixed sparse locations, which is a special case of DCN. Therefore, DCN is a more general CNN model that can flexibly adjust receptive field size and greatly enhance the transformation modeling capability of CNNs. It is also lightweight and easy to train and is shown effective for complex vision tasks that require dense predictions [14].

Therefore, based on the developed 1-ring filter and its corresponding convolution and pooling operation, we further propose to extend the DCN model to the spherical surface for modeling the various and unknown transformations of cortical surface data. We design specific spherical offsets on the spherical surface for 1-ring filter. The spherical deformable convolution and pooling are then implemented by weighting the features in the deformed 1-ring filter and then the SDU-Net can be constructed.

D. Contributions

In our previous work [27], which is the first of using the 1-ring filter on icosahedron discretized sphere for cortical surface applications, we designed the spherical convolution, pooling and accordingly the Spherical U-Net architecture for cortical surface parcellation and achieved promising performance. We further demonstrated its capability and effectiveness on cortical attribute map prediction [37] and harmonization [38]. This 1-ring filter and the corresponding spherical operations provide a new solution for cortical surface analysis by taking advantage of the powerful deep learning ability. However, again, it is still challenging to effectively model diverse cortical structures with different sizes and shapes. Therefore, in this paper, we extend the previously presented conference versions [27], [37] by introducing novel spherical deformable convolution/pooling operations and the SDU-Net to cortical surface applications, and also adding more technical details and expanded analyses. To summarize our contributions,

1. We demonstrate that deep learning techniques can be efficiently extended to spherical space based on the proposed 1-ring filter, including but not limited to convolution, pooling, transposed convolution, and skip connection, thus construing the Spherical U-Net.

2. We demonstrate further performance gain enabled by introducing novel spherical deformable convolution and pooling to construct the Spherical Deformable U-Net, compared to the conference version thanks to its enhanced geometric transformation modeling capability.

3. We perform comprehensive experiments on different datasets for cortical surface parcellation and attribute prediction and demonstrate consistently competitive performance and higher computational efficiency of our method compared to state-of-the-art methods.

III. Method

A. Icosahedron Discretized Spherical Surfaces

The icosahedron is one of the Platonic solids with most faces and least area irregularity and thus is most close to the sphere [26]. It has 12 vertices, 20 faces, and 30 edges (see Fig. 2, top left). From the data representation view, it is a graph with 12 vertices, and each vertex has 5 neighboring vertices. The icosahedron discretized spherical surfaces are the subdivisions of the icosahedron and can be obtained using the following expansion steps iteratively: 1) add new vertices to the center of each edge on the last level subdivision of icosahedron; 2) add new edges between every two new vertices that are in a triangle; 3) project the newly added vertices onto the sphere. Therefore, the number of vertices on the spherical surfaces are N₁ = 12, N_i+1 = 4N_i − 6, i = 1, 2, 3, … where i represents the i-th subdivision of icosahedron. As introduced earlier, the icosahedron discretized spherical surfaces are widely used in neuroimaging studies to represent the resampled cortical surface data after spherical mapping [11]. Typically, 7th or 8th subdivision of icosahedron with 40,962 or 163,842 vertices are employed to represent the subject-specific, vertex-wise cortical morphological attributes, such as sulcal depth, mean curvature, and cortical thickness, which can provide enough resolutions for the cortical surface study.

Fig. 2.

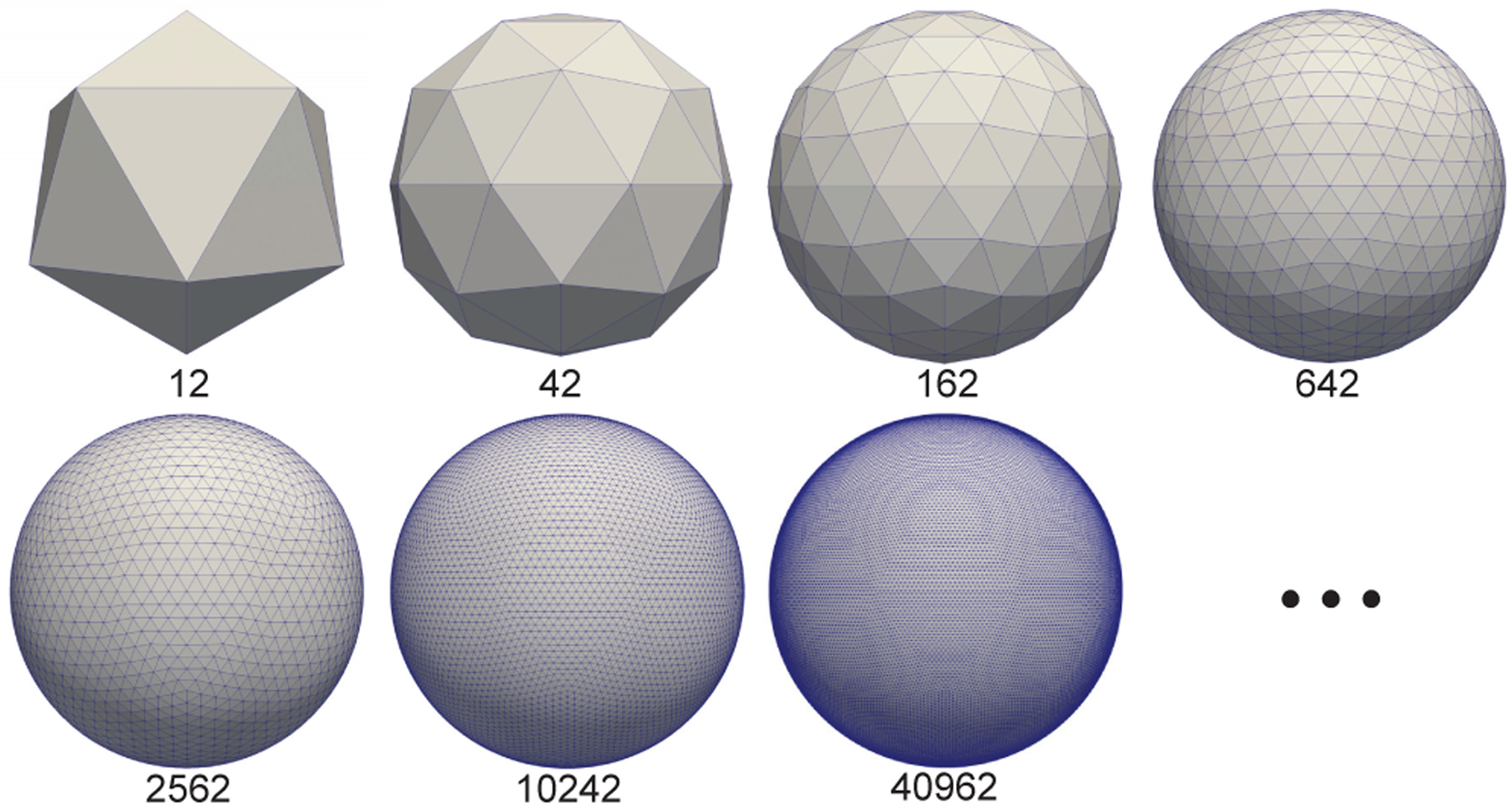
Representative icosahedron discretized spherical surfaces with sequential subdivisions. The number of vertices of each spherical surface is denoted under the surface.

B. 1-ring Filter

We define the 1-ring filter using the center vertex and its 1-hop neighboring vertices, as shown in Fig. 3 (a). After the discretization of the sphere using subdivisions of the icosahedron, we can see that each spherical surface is consistently composed of two types of vertices: 1) the original 12 vertices on the icosahedron each with only 5 1-hop neighbors; and 2) the remaining vertices each with 6 1-hop neighbors in their 1-ring filter. To make the learned pattern with the 1-ring filter more consistent and effective on the sphere, we need to define a consistent order of neighboring vertices properly. Unlike 2D images in regular grids, spherical surfaces have no clear reference direction and thus neighborhood orders become ambiguous. To overcome this issue, we propose to utilize the prior posture information. In neuroimaging, the cortical surface is generally preprocessed using a rigid alignment [39] to make the surface’s posture corresponding to the normal brain orientation when standing at origin and facing to the negative y-axis in the coordinate system. Therefore, based on the spherical cortical surface coordinate, we want the 1-ring filter azimuthally rotation equivariant/invariant.

Fig. 3.

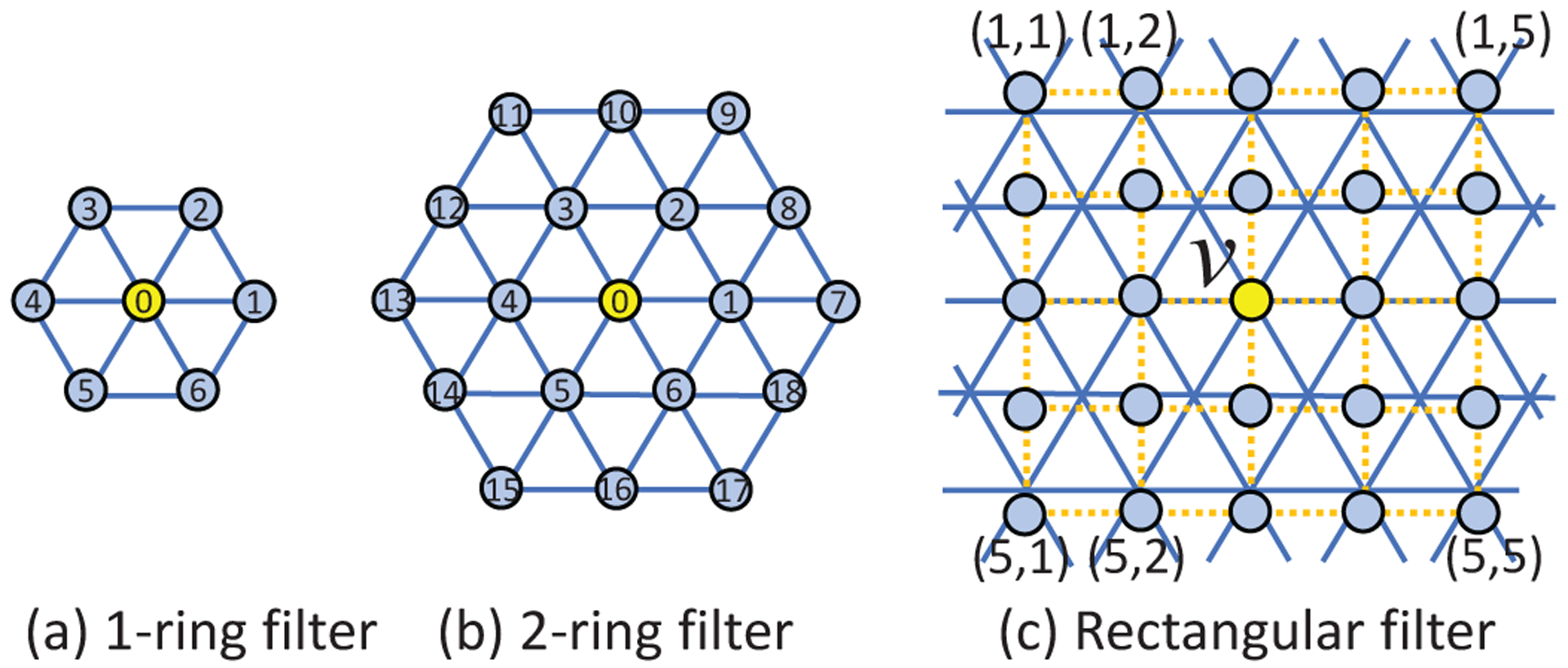
Three types of convolution filters on the icosahedron discretized spherical surfaces.

Specifically, we define the orders of neighboring vertices in the 1-ring filter as follows. As shown in Fig. 4, let v₀ be the center vertex, v_i be the neighboring vertices in the 1-ring filter, i = 1, 2, …, 5 (with 5 neighbors) or 1, 2, …, 6 (with 6 neighbors), and $T_{v_0}$ be the tangent plane at v₀. We define ${\overrightarrow{\Gamma }}_{v_0}$ to be the tangent vector at v₀ pointing along the great circle as the x-axis in $T_{v_0}$. ${\overrightarrow{\Gamma }}_{v_0}$ can be obtained by ${\overrightarrow{n}}_z\times {\overrightarrow{v}}_0$, where ${\overrightarrow{n}}_z$ is the unit normal vector of XOY plane, ${\overrightarrow{v}}_0$ is the vector from the origin O to v₀ (for the two vertices at poles, we define ${\overrightarrow{\Gamma }}_{v_0}=(1,0,0)$). Then we project vertices v_i to the tangent plane $T_{v_0}$, obtaining projected vertices $v_i^{\prime }\in T_{v_0}$. The angles θ_i between each neighboring vertex and the x-axis in tangent plane is then computed as:

$${\theta }_i=\text{arccos}\frac{{\overrightarrow{\Gamma }}_{v_0}·\left(\overrightarrow{v_i^{\prime }}-{\overrightarrow{v}}_0\right)}{\Vert {\overrightarrow{\Gamma }}_{v_0}\Vert \Vert \overrightarrow{v_i^{\prime }}-{\overrightarrow{v}}_0\Vert }.$$ (1)

By sorting θ_i, we assign indices 1–6 (1–5 for 12 original icosahedron vertices) to the neighboring vertices sequentially and index 0 to the center vertex; for the 12 vertices with only 5 neighbors, we additionally assign index 6 to the center vertex.

Fig. 4.

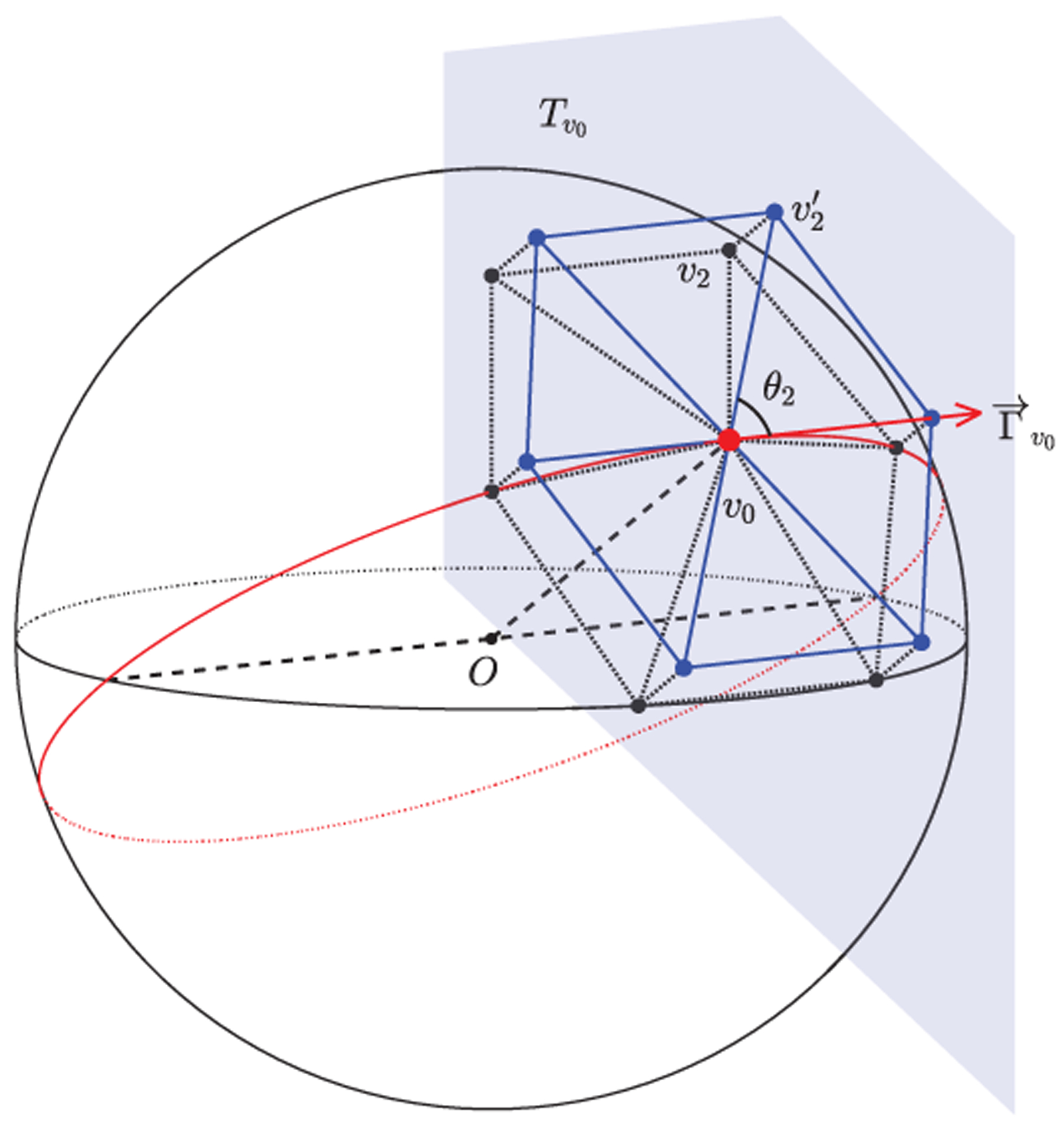
Consistent definition of 1-ring filter’s neighborhood orders. The black vertices v_i represent neighboring vertices on sphere. The blue vertices $v_i^{\prime }$ represent projected vertices onto the tangent plane of the center vertex v₀. The orders are then obtained according to θ_i.

Note that discretized sphere with perfect uniformly distributed vertices does not exist [26]. We empirically show that the 1-ring filter with our neighboring vertices orders has the desired rotation equivariant/invariant property and the gauge variance among vertices (which means the 1-ring neighborhoods’ directions or positions are not the exactly same across all vertices) can be overcome by feature learning process [26], [28], [30], [37]. It is also worth noting that in implementation, we just computed the neighboring vertices orders only once using the aforementioned approach and then stored them in the memory for later use, which thus provides us high efficiency in computation by matrix indexing.

C. Standard Convolution on Spherical Surface

With the 1-ring filter definition, spherical convolution on icosahedron discretized spherical surface can be easily formulated as a filter weighting process. As shown in Fig. 5, the 1-ring filter is employed to convolve over the whole surface with each vertex to obtain new feature maps on the spherical surface, analogously to the conventional convolution operation in 2D/3D images. The stride in 2D/3D convolution is not necessary here, because the 1-ring filter will always convolve with each vertex to obtain a new feature vector for each vertex. The padding is also not applicable here, because the convolution is on a closed sphere. The convolution layer on the spherical surface is then used to transform feature maps from one dimension to another dimension on the same level of icosahedron subdivision, and further to learn and extract high level representations by hierarchical architectures.

Fig. 5.

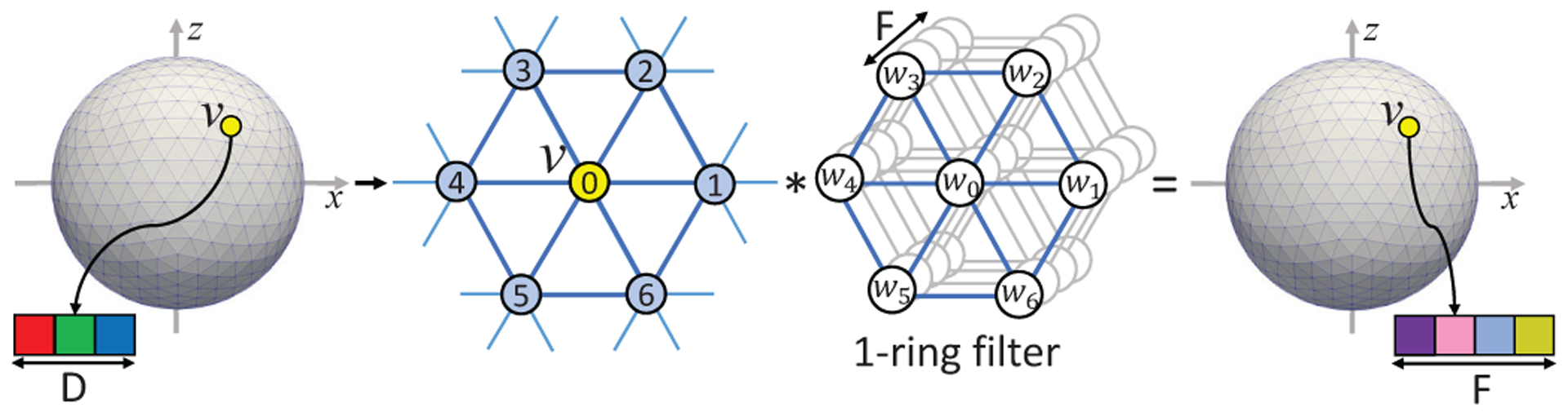
Spherical convolution operation using 1-ring filter. The convolution transfers the input feature maps with D channels to the output feature maps with F channels using F filters.

In the implementation, for each vertex v on a spherical surface with N vertices and D features map channels, we firstly extract the local patch I_v(7 × D) from the 1-ring neighborhood and reshape it into a row vector $I_v^{\prime }(1\times 7D)$ for this vertex. Then, iterating over all N vertices, we stack the first dimension to obtain the full-node filter matrix I(N × 7D) (refer to “im2col” function in MATLAB or other deep learning toolboxes). Afterward, with the desired output feature channel number F, by multiplying I with the convolution layer’s filter weight W(7D × F), the output surface feature maps O(N × F) can be obtained.

D. Standard Pooling on Spherical Surface

The pooling operation on the spherical surface has the same function as in 2D/3D images. It is used to increase the receptive field and reduce the spatial size of the representation to reduce the number of parameters and computation in the network. It is performed in reverse order of the icosahedron expansion process, which we can call the icosahedron contraction process. On an i-th icosahedron subdivision, the contraction process will first choose the center vertices that are also on the (i-1)-th subdivision and thus will still be remained after this contraction process. Then, the 1-ring filter is applied to the chosen vertices as the pooling kernel. Lastly, the edges on the (i-1)-th subdivision are re-connected. As a consequence, a pooled surface with a smaller number of vertices and fine fused features is obtained. See Fig. 6 for a better understanding.

Fig. 6.

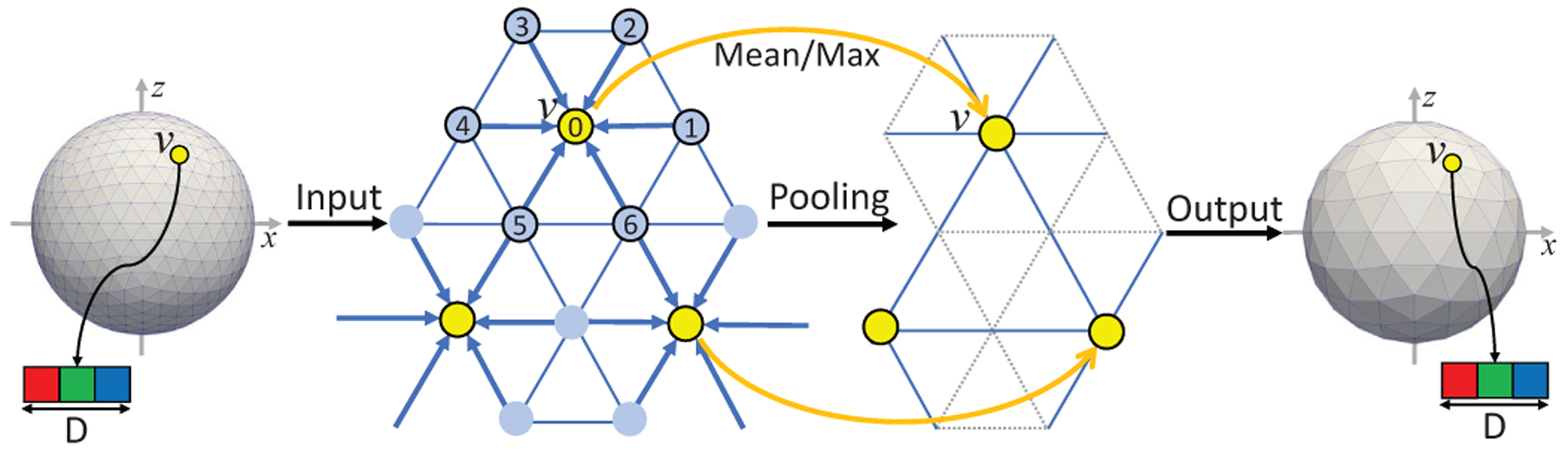
Spherical pooling operation using 1-ring filter. The input surface with i-th subdivision is pooled to (i-1)-th subdivision. The feature map channel number D is unchanged.

Similarly in implementation, we will extract the feature data I(N ×7D) for all center vertices aggregated from their 1-ring neighborhood. Then we reshape it into I′(N × D × 7). By averaging (mean pooling) or maximizing (max pooling) the 3rd dimension of I′, we can obtain the refined feature map O(N × D). Meanwhile, the number of vertices is decreased from 4N − 6 on original surfaces to N on the pooled surface.

E. Spherical Deformable Convolution and Pooling

Based on the standard spherical convolution and pooling operations, we develop the spherical deformable convolution and pooling as illustrated in Fig. 7 and Fig. 8. The spherical offsets are firstly obtained by applying a standard spherical convolution layer over the same input feature map for spherical deformable convolution or the pooled map for spherical deformable pooling. The output offset field is represented by the tangent vectors with size N × 14. Note that the tangent plane for each vertex is defined at that vertex, which means each vertex has a different tangent plane. The channel dimension 14 corresponds to 7 tangent vectors ${\left\{\overrightarrow{u_{n,i}}\right\}}_{i=1}^7$ for each vertex ${\left\{v_{n,i}\right\}}_{i=1}^7$ in the 1-ring filter at vertex v_n (i represents i-th neighborhood). Then $E_{n,i}\overrightarrow{u_{n,i}}$ maps the tangent vector from the tangent space to 3D space, where $E_{n,i}=\left[\overrightarrow{e_{n,i}^1},\overrightarrow{e_{n,i}^2}\right]$ is a 3 × 2 orthonormal basis on the tangent space at v_n,i. The deformed sampling locations ${\left\{v_{n,i}^{\prime }\right\}}_{i=1}^7$ is then defined as:

$$v_{n,i}^{\prime }=\frac{v_{n,i}+E_{n,i}\overrightarrow{u_{n,i}}}{\Vert v_{n,i}+E_{n,i}\overrightarrow{u_{n,i}}\Vert }$$ (2)

on a unit sphere. In this way, the regular 1-ring filter is deformed and augmented with additional spherical offsets $\overrightarrow{u_{n,i}}$, thus enabling adaptive learning of receptive field at different locations. Then, the cortical feature values at the deformed 1-ring filter’s sampling locations are weighted with the 1-ring filter for spherical deformable convolution, or pooled for spherical deformable pooling operation. Of note, the range that the deformed sampling locations extend to is not restricted on the tangent plane but is restricted on the sphere within the range (−π/2, +π/2) since it is finally normalized to the sphere as described in equation (2). Despite that, we find that the deformation size in practice is still within a small range, which is a reasonable deformation size even for large ROIs on cortical parcellation maps. In such a case, the deformed points on the tangent plane and sphere are very close. The simple and approximately equal relationship (equation (2)) between them can be easily learned by the network to find the actual optimal deformed sampling locations on the sphere. As $\overrightarrow{u_{n,i}}$ is typically fractional, the feature value at $v_{n,i}^{\prime }$ is computed via barycentric interpolation [40]. Finally, since all the operations are differentiable, the gradients in the network can be efficiently backpropagated to train the convolution filters for generating the output features and the offsets simultaneously.

Fig. 7.

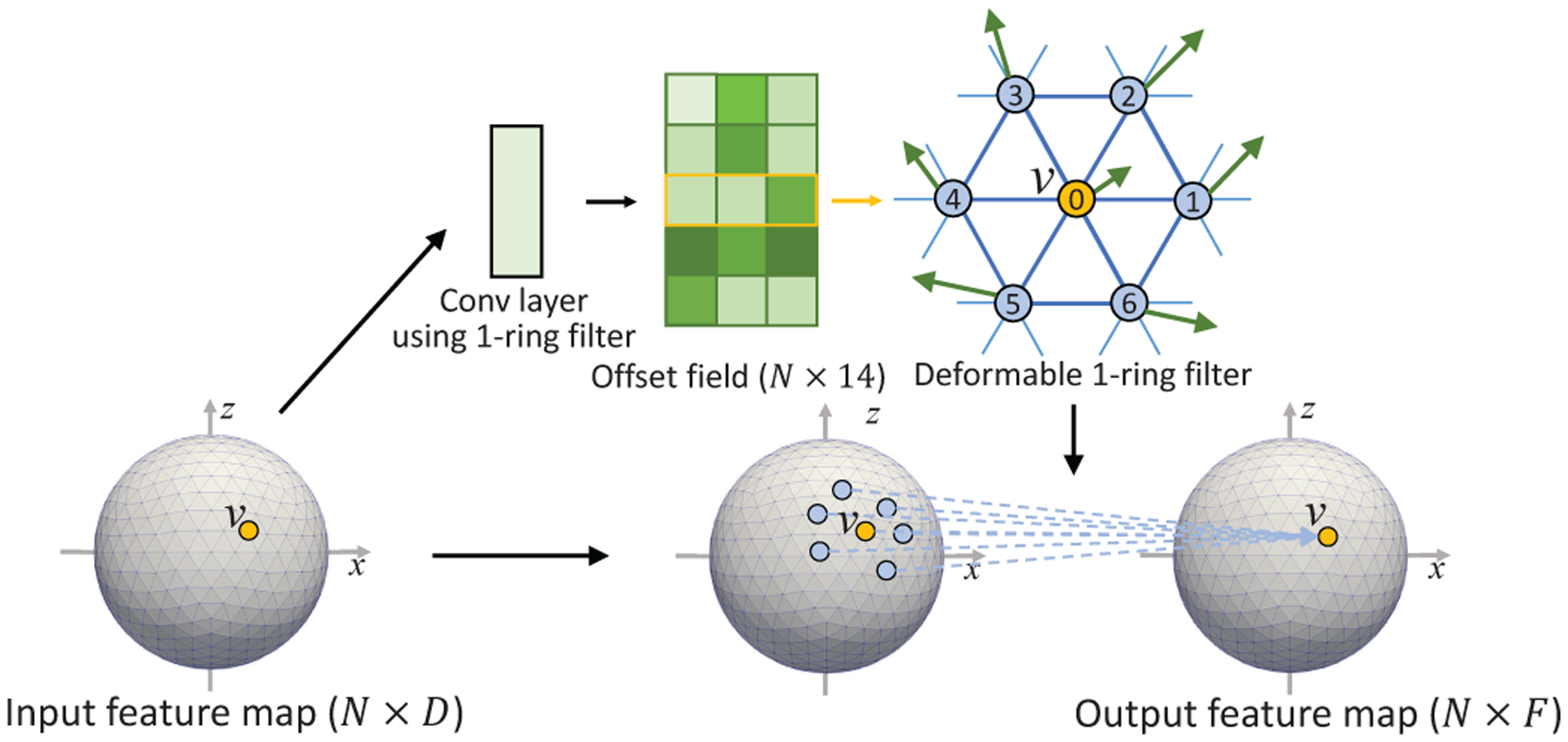
Illustration of spherical deformable convolution operation.

Fig. 8.

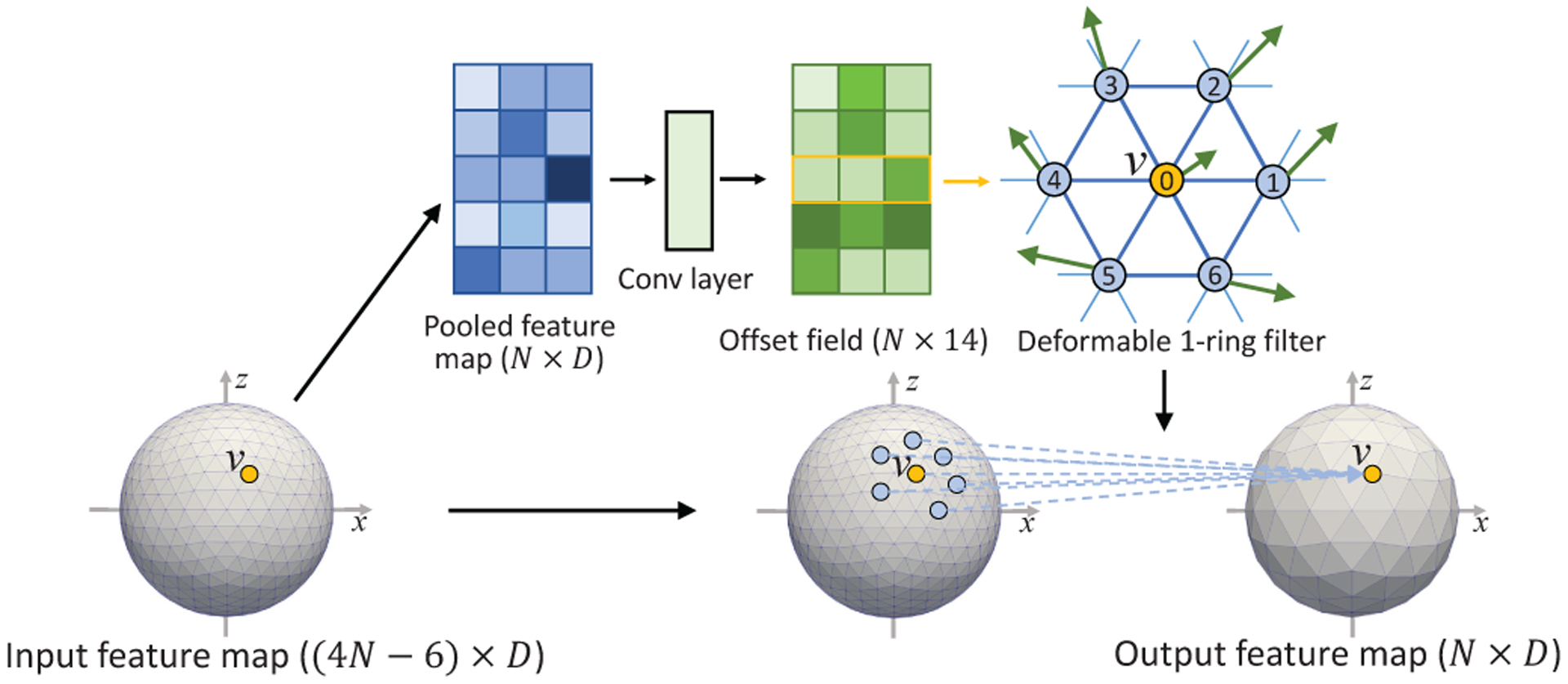
Illustration of spherical deformable pooling operation.

F. Upsampling on Spherical Surface

Upsampling on the spherical surface is used to recover the original high resolution surface from the pooled low resolution surface feature maps. Therefore, it is crucial to the construction of the decoder network in the encoder-decoder style architecture [32] for vertex-wise classification and prediction tasks. We propose to extend several popular upsampling methods to icosahedron discretized spherical surface here.

1). Linear Interpolation:

Linear Interpolation on the spherical surface follows the rule of icosahedron expansion, which is the opposite of mean-pooling operation. For each new vertex generated from the edge’s center, its feature is linearly interpolated by the two parent vertices of this edge (Fig. 9A).

Fig. 9.

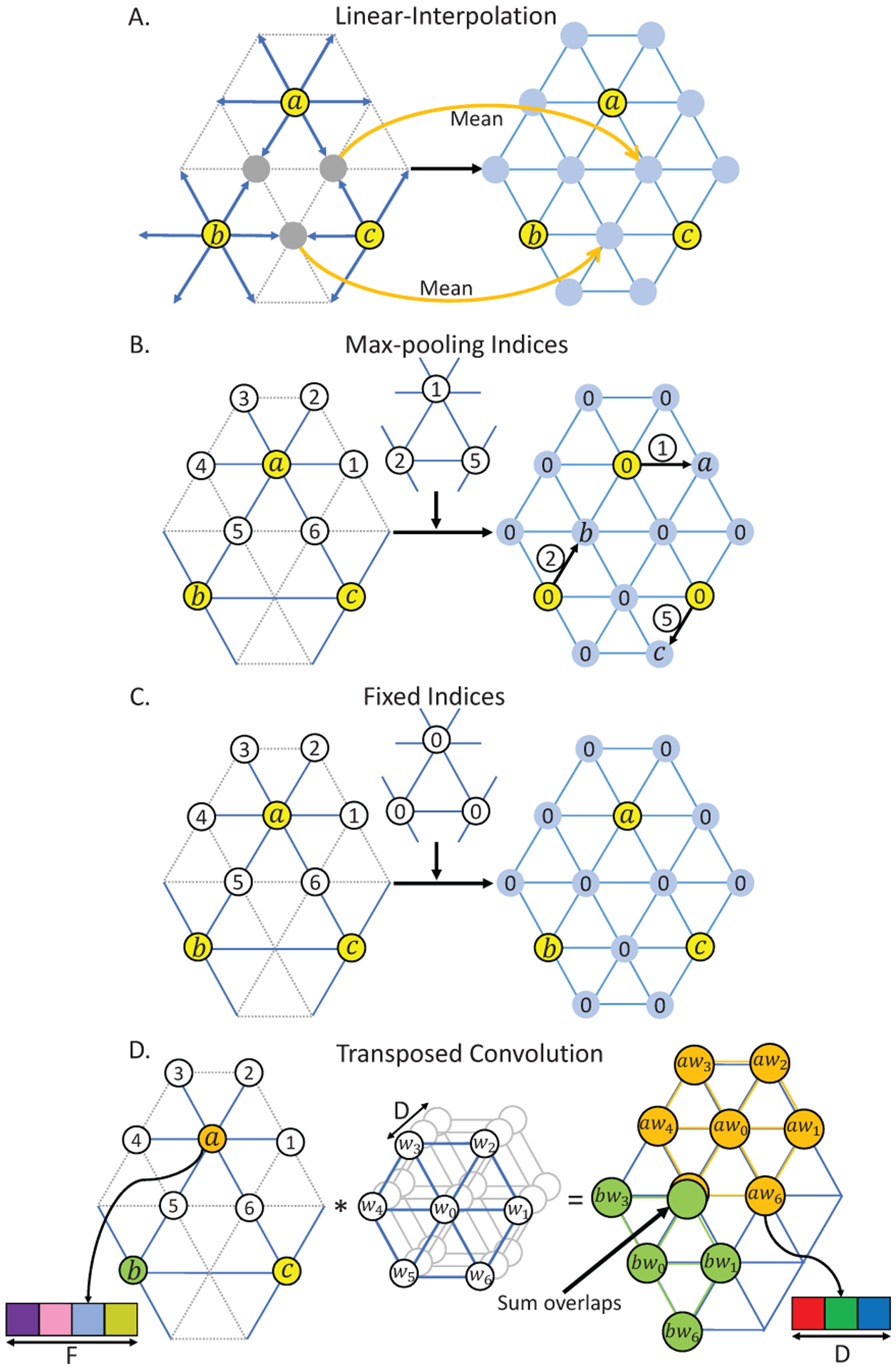
Illustration of upsampling methods on the spherical surface. A, B, and D are our methods, C is the Fixed Indices used in [30], [31]. The left input feature maps are on (i-1)-th subdivision. The right output feature maps are on i-th subdivision. In A, B, C, we used yellow to represent the vertices on (i-1)-subdivision, and blue to represent newly generated vertices on i-th subdivision. In D, we used different colors to represent three different vertices a, b, c on (i-1)-th subdivision, and other different colors to represent the data channels, which is consistent with the channel colors in Fig. 5 and Fig. 6. Then each subfigure shows how the i-th subdivision is upsampled from the (i-1)-subdivision using respective upsampling methods.

2). Max-pooling Indices:

Max-pooling Indices, introduced by SegNet [32], uses the stored pooling indices computed in the max-pooling layer of the encoder to perform nonlinear upsampling in the corresponding decoder. We have adapted this method to the spherical surface as shown in Fig. 9B. For example, vertices a, b, and c are first pooled from their 1-ring neighborhood using max-pooling indices 1, 2, and 5, respectively, in the encoder part. Then at the corresponding upsampling layer, the 1st neighbor of a, 2nd neighbor of b, and 5th neighbor of c are restored with a, b, and c’s value, respectively, and other vertices are set as 0. For better understanding and comparison, we also drew the upsampling method with Fixed Indices used in [30] as shown in Fig. 9C.

3). Transposed Convolution:

Transposed convolution is also known as fractionally-strided convolution, deconvolution or up-convolution in U-Net [4]. From the perspective of image transformation, transposed convolution first restores pixels around every pixel by sliding-window filtering over all original pixels, and then sums where restored pixels overlap (controlled by stride). Inspired by this perspective, for a spherical surface with the original feature map I (N_i × D, where N_i denotes the number of vertices on i-th icosahedron subdivision and D denotes the number of features) and the pooled feature map O (N_i−1 × F), we can restore I by first using the 1-ring filter to do transposed convolution with every vertex on the pooled surface O and then summing overlap vertices, as illustrated in Fig. 9D.

G. Spherical U-Net Architecture

With our defined operations for spherical surface convolution, pooling, and transposed convolution, it is straightforward to construct the Spherical U-Net architecture for different cortical surface applications. Once again, to enhance the transformation capability of Spherical U-Net and model various cortical structures with different sizes and shapes adaptively, we further integrate the spherical deformable convolution and pooling into it. Since both deformable operations have the same input and output as their plain versions, they can readily replace their counterparts in Spherical U-Net and therefore construct the Spherical Deformable U-Net (SDU-Net) architecture. As shown in Fig. 10, it has an encoder path and a decoder path, each with four resolution steps, indexed by i, i = 1, 2, 3, 4. The encoder is composed of 8 spherical convolution and 3 spherical pooling layers. Spherical deformable operations are applied to the first 4 convolution and all pooling layers. We experimented with different numbers of such layers and found this configuration as a good trade-off for different tasks, as reported in Table I. Then the decoder composed of repetitive spherical transposed convolution and convolution generates the results from the extracted feature maps in the encoder. In addition to the standard U-Net, before each convolution layer’s rectified linear units (ReLU) activation function, a batch normalization (BN) layer is added. At the final layer, vertex-wise filter weighting is used to map C₁-component feature vector to the desired C_out at the last layer. Note that we do not need any tiling strategy in the original U-Net [4] to allow a seamless output map, because all the data flow in our network is on a closed spherical surface. We simply double the number of feature channels after each surface pooling layer and halve the number of feature channels at each transposed convolution layer. That makes C_i+1 = C_i × 2, and N_i+1 = 4N_i − 6.

Fig. 10.

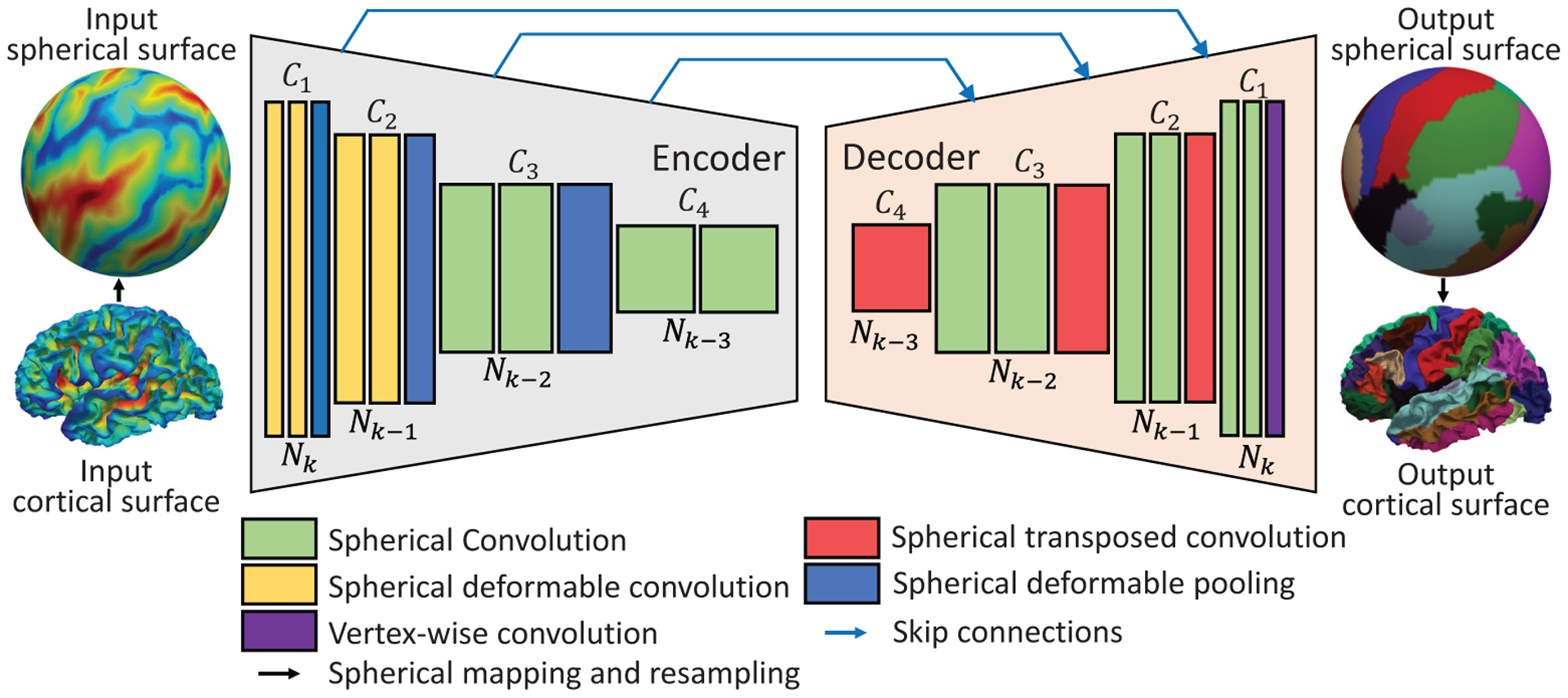
Spherical deformable U-Net architecture. The number of features C_i after each operation is denoted above the box. The number of vertices N_i is denoted below the box. N_i+1 = 4N_i − 6, C_i+1 = C_i × 2. The k in the input number of vertices N_k indicates that the input surface is on the k-th icosahedron subdivision. Typically, we use the 7-th subdivision of icosahedron with 40,962 vertices and set C₁=64.

Table I.

Results On Infant Dataset Using Spherical Deformable Operations In Different Layers In The Encoder Part Of Different Architectures

Usage of spherical deformable operations (# layers)	Spherical U-Net23	Spherical U-Net18	Spherical SegNet	Spherical FCN-8s
Baseline	92.67±1.60	92.28±1.70	89.49±3.52	91.75±1.55
2 deformable conv layers (1–2)	93.09±1.57	92.78±1.72	89.72±2.60	92.10±1.50
4 deformable conv layers (1–4)	93.15±1.40	92.85±1.57	90.04±2.19	92.15±1.59
6 deformable conv layers (1–6)	92.97±1.59	92.76±1.70	90.01±2.40	92.16±1.51
6 deformable conv layers (3–8)	93.05±1.58	92.75±1.87	90.01±2.67	92.10±1.60
Spherical deformable pooling	92.98±1.56	92.61±1.67	89.95±2.56	92.06±1.62
Spherical deformable pooling+ 4 deformable conv layers (1–4)	93.20±1.40	93.07±1.51	90.06±2.11	92.41±1.51

IV. Experiments

To validate the proposed SDU-Net on cortical surfaces, we quantify the performance on two neuroscientifically and clinically important tasks, cortical surface parcellation, and cortical attribute map development prediction during infancy. Both tasks are suffering from designing of hand-crafted features and heavy computational burden. We show that our task-agnostic and feature-agnostic SDU-Net is still effective for these different tasks. Our PyTorch implementation for all experiments is freely available.

A. Cortical Surface Parcellation

1). Experimental Setup:

Automatic and accurate parcellation of cortical surfaces into anatomically and functionally meaningful regions is of fundamental importance in human brain mapping [41]. It is essential for region localization and inter-subject comparison in region-based or network-based brain studies. Conventional registration-based methods [40]–[42] require designing of specific hand-crafted features to map the cortical shape to parcellation labels, which is time-consuming, expertise-dependent, and error-prone. Here we propose to address these issues as a semantic labeling problem using our deep learning-based SDU-Net for parcellating the entire cortical surface, where each vertex is assigned a label.

We used the NAMIC dataset [41] with 39 adult brain MR images and an infant brain MRI dataset containing 90 subjects. All the cortical surfaces in the NAMIC dataset were reconstructed using FreeSurfer [11]. The infant cortical surfaces were obtained using an infant-dedicated pipeline [43], [44]. We only focused on the left hemisphere of the brain as the right hemisphere is similar. Each vertex on the left cortical surface was coded with 3 shape attributes, i.e., the mean curvature (curv), average convexity (sulc), and sulcal depth. Basically, the mean curvature measures the cortical folding in a fine view; the average convexity measures the cortical folding in a coarse view; and the sulcal depth measures the cortical folding by combining both the coarse and fine views. These shape descriptors reflect local geometric attributes of the cortical surface, which are useful for cortical surface parcellation [45]. Each cortical surface was manually labeled into 35 gyrus-based regions by a neuroanatomist, based on the FreeSurfer parcellation protocols [45]. All surfaces were first rigidly aligned and mapped onto the spherical space and then resampled to have the same tessellation on the 7th subdivision of icosahedron with 40,962 vertices.

To better show the generalization ability, we used 60% data for training, 15% for validation, and 25% for testing (there was a 5-fold cross-validation between the 15% validation set and 60% training set). The results are then reported based on the hold-out test set using the model re-trained with the best hyper-parameters from the cross-validation on all training and validation data for each architecture. In training, we used Adam optimization algorithm with cross-entropy loss and a self-adaption strategy for updating learning rate, which reduces the learning rate by a factor of 5 once training Dice stagnates for 2 epochs. We performed data augmentation by randomly azimuthally rotating spherical surfaces 50 times. For quantitative evaluation, we measured the Dice score as in [40] averaged over all testing surfaces.

2). Baseline models:

For the cortical surface parcellation task, we used the SDU-Net architecture as shown in Fig. 10. We set C_in as 3 for 3 shape attributes, C_out as 35 for the 35 labels of parcellation, k as 7 (N_k = 40, 962) for the input icosahedron subdivision and C₁ as 32. To study the effect of the size of network parameters and overfitting, we also call the baseline model Spherical U-Net18 because of the 18 convolution layers in it and construct Spherical U-Net23 by adding one more resolution steps with 5 more convolution layers and doubling all the feature channels.

To better validate the effectiveness of the spherical deformable operations, we also integrate spherical deformable operations with other state-of-the-art CNN architectures. We note that these architectures generally consist of two stages, an encoder generating feature maps over the whole input and a task-specific decoder generating results from the encoded feature maps. Therefore, we use the same encoder as in the SDU-Net, and adopt other two state-of-the-art decoder architectures, SegNet [32] and FCN [2]. SegNet is a state-of-the-art method for semantic segmentation. Spherical SegNet is different from SDU-Net in two aspects: 1) There is no copy and concatenation path in Spherical SegNet; 2) For upsampling, Spherical SegNet uses Linear-Interpolation. FCN is another popular segmentation network. We construct Spherical FCN architecture based on the conventional FCN-8s [2], which is the best FCN variant that can combine high layer information with low layer information. The Spherical FCN-8s fuses the feature maps at different resolution levels after each pooling layer. Then, the fused feature maps are mapped to the desired output channels using a transposed convolution layer.

3). Ablation Study:

Spherical Deformable Convolution.

Table I evaluates the effect of spherical deformable convolution on different usages of deformable operations in different architectures. Dice ratio steadily improves when more deformable convolution layers are used. The improvement saturates when using 6 deformable convolution layers in the first 6 convolution layers for Spherical FCN-8s and 4 for others. In the remaining experiments, we will use 4 in the feature extraction networks. To better understand the mechanism of spherical deformable convolution, we draw the sampling locations of the 1-ring filter and deformed 1-ring filter after 3 successive convolution layers in Fig. 11. We empirically observed that the learned offsets in the successive deformable convolution layers are highly adaptive to different cortical structures.

Fig. 11.

From left to right: after three successive convolution layers, the sampling locations of trained 1-ring filter overlapped on parcellation map (i.e., fixed receptive filed with 3-ring) for two activation units (green points) on the pars orbitalis (a small ROI, top row) and paracentral lobule (a large ROI, bottom row); sampling locations of trained deformable filters on parcellation, sulc and curv maps. Note how the receptive filed is adaptively transformed for different structures.

Spherical Deformable Pooling.

As shown in Table I, using spherical deformable pooing alone already consistently improve the Dice compared to baseline models. When both spherical deformable convolution and pooling are used, significant improvements are obtained and result in the best model for all architectures.

Model Complexity and Runtime.

Table II reports the model complexity and runtime of the spherical deformable networks and their plain versions on an NVIDIA Geforce GTX2080 Ti GPU. We can see that spherical deformable operations only add a small overhead over model parameters and computation. This indicates that the performance improvement is from the capability of modeling geometric transformations, other than increasing model parameters. On the contrary, Spherical U-Net23 only achieves slightly better results while adding much more parameters and inference time. Therefore, taking the speed and usability into consideration, we take Spherical Deformable U-Net18 as our default SDU-Net model and will use it the following comparisons with other approaches.

Table II.

Model Complexity And Runtime Comparison Of Spherical Deformable Networks And Their Plain Counterparts

	Parameters (M)	Inference time (ms)
Spherical U-Net23	26.86	20.3
Spherical Deformable U-Net23	26.89	51.9
Spherical U-Net18	1.67	4.1
Spherical Deformable U-Net18	1.68	13.2
Spherical SegNet	1.37	3.5
Spherical Deformable SegNet	1.39	12.2
Spherical FCN-8s	1.01	3.0
Spherical Deformable FCN-8s	1.02	11.5

Upsampling Methods.

Besides the deformable convolution and pooling in the encoder part, we also studied different upsampling methods in the decoder part for SDU-Net, such as Fixed Indices used in [30], [31] and report the results in Table III. The results validate the superiority of spherical transposed convolution for its learnable filters and thereby effectively address the upsampling issue on spherical surfaces. We note that the advantage of the transposed convolution over other upsampling methods is not much better. This may be because, for other 3 upsampling methods, we add a regular 1-ring convolution after them for matching the number of channels, which may also improve their learning ability greatly.

Table III.

Comparison With Different Upsampling Methods For Infant Cortical Surface Parcellation

	Dice (%)
SDU-Net-Linear Interpolation	92.91±1.52
SDU-Net-Max-pooling Indices	86.69±3.74
SDU-Net-Fixed Indices	92.85±1.98
SDU-Net-Transposed Convolution	93.07±1.51

Comparison with Other Spherical CNNs.

As mentioned in Introduction, methods [21]–[23] that discretize sphere using ERP method are obviously not suitable for cortical surface applications. Therefore we only compare currently popular spherical CNNs that perform convolution directly on icosahedron discretized surfaces and present the results in Table IV. As can be seen, our SDU-Net outperforms the patch-style classification method [15] and global differential filters [30]. This indicates that our approach successfully learns the high-level representation from their neighborhood in the hierarchical architectures, which is lacking in [15], [30]. Again, note that SDU-Net outperforms our previous Spherical U-Net architecture in conference version [37]. Finally, it is also worth noting that although the 2-ring filter and rectangular patch filter in the tangent plane, as shown in Fig. 3, are also effective in feature learning, our 1-ring filter is much smaller in terms of memory storage, and lighter in terms of model size.

Table IV.

Comparison With Other Spherical Cnns On Infant Cortical Surfaces

	Dice (%)
Wu et al. [15]	87.06
Jiang et al. [30], [31]	75.15±3.09
Spherical U-Net18-Rectangular filter [16], [25], [46]	92.24±1.98
Spherical U-Net18–1 ring filter	92.28±1.70
Spherical U-Net18–2 ring filter	92.28±2.03
SDU-Net	93.07±1.51

Note that Wu et al.’s result is directly reported in their paper. Jiang et al. [30] and Parvathaneni et al. [31] are implemented using the default spherical U-Net architecture in Jiang et al.’s code. Other methods are all implemented by ourselves using the spherical convolution filter in the referred papers.

Comparison with State-of-the-art Parcellation Methods.

As previous methods [40], [41], [45] all train the classifier after registration, we further co-registered all surfaces in the NAMIC dataset using Spherical Demons [40] and resampled the surfaces before and after the registration, respectively. In order to directly compare with the results in their papers and meanwhile guarantee a hold-out set for testing, we adopted a different 4-fold cross-validation strategy that splits the data into 60% for training, 15% for validation, and 25% for testing in each fold. The final results are obtained by averaging the Dice over all testing surfaces. As shown in Table V, our SDU-Net outperforms other classifiers under the same experimental conditions and achieves better performance than the state-of-the-art Random Forest + Graph Cuts [41] method. Of note, in terms of computational complexity, our model is end-to-end and only needs about 13.2ms (Table II) for parcellating one cortical surface, while the non-DNN based methods typically need registration and additional feature extraction. Either of these two steps would need much more time. It is also worth noting that the augmentation did improve the network’s generalization ability and on the other hand validate that the required rotation invariance along the z-axis is fulfilled.

Table V.

Comparison Of Different Methods For Parcellation On Namic Dataset

	Registration	Augmentation	Features	Dice (%)
Freesurfer [45]	Yes	No	Curv, sulc, location	88.90
Spherical Demons [40]	Yes	No	Curv, sulc, inflated curv, location	89.60
Random Forest [41]	Yes	No	Curv, sulc, location	90.00
Random Forest + Graph cut [41]	Yes	No	Curv, sulc, location	90.20
SDU-Net	No	No	Curv, sulc	88.95±2.16
SDU-Net	No	Yes	Curv, sulc	89.41±1.79
SDU-Net	Yes	No	Curv, sulc, location	90.46±1.30

In the features column, location represents the spatial coordinate on the sphere. The standard deviation is across subjects. The results of other methods for comparison are reported by their papers, and they didn’t report the standard deviations.

B. Cortical Property Development Prediction

We have also applied our SDU-Net to the prediction of cortical surface attribute maps of 1-year-old brains from the corresponding neonatal (0-year-old) brains using 370 infants. Each of the involved subjects has longitudinal 0-year-old and 1-year-old brain MRI data. All infant MR images were processed using an infant-specific computational pipeline [43]. All cortical surfaces were mapped onto the spherical space, nonlinearly aligned, and further resampled using the 7th icosahedron subdivision with 40,962 vertices. Following the experimental configuration in [47], we used the sulcal depth and cortical thickness maps at birth to predict the cortical thickness map at 1 year of age. The reason to choose the cortical thickness map as the prediction target for validating our method is that cortical thickness has dynamic, region-specific, and subject-specific development and is highly related to future cognitive outcomes [48]. To have a robust prediction for the cortical thickness, we also introduced the sulcal depth as an additional channel for leveraging the relationship between sulcal depth and cortical thickness maps [49]. The validation strategy is the same as in Sec. IV-A.1 cortical surface parcellation. The evaluation metrics we adopted for the prediction performance are mean absolute error (MAE) and mean relative error (MRE).

1). Implementation Details:

Here we still consider the basic, simple architecture and training strategy to validate the effectiveness of our SDU-Net. We set C_in = 2 (representing sulcal depth and cortical thickness at birth), C_out=1 (representing cortical thickness at 1 year of age). We trained the SDU-Net using Adam and L1 loss. The reason we used L1 loss rather than L2 as L1 encourages less blurring [50]. The whole training process had 50 epochs on an NVIDIA Geforce GTX2080 Ti GPU.

2). Comparison with Feature-based Approaches:

For the feature-based approaches, we extracted 102 features for each vertex on the 0-year-old cortical surface. Same as in [47], the 1st and 2nd features are sulcal depth and cortical thickness, respectively, providing local information at each vertex. The 3rd to 102nd features are contextual features, providing rich neighboring information for each vertex, which are composed of 50 Haar-like features of sulcal depth and 50 Haar-like features of cortical thickness. The Haar-like features were extracted using the method and hyper-parameters in [47].

We then trained the following machine learning algorithms on the 102 features in a vertex-wise manner: Linear Regression, Polynomial Regression, Random Forest, and a plain 4-layer Neural Network. Linear Regression assumes that the development of cortical thickness at each vertex is linearly increased, and Polynomial Regression assumes that it has a two-order polynomial relationship with age. Random Forest is a stable and effective non-linear regression method for high dimensional data analysis, which has been proved to be the state-of-the-art method for cortical thickness prediction [47]. The 4-layer Neural Network, also called a Multi-layer Perceptron with two hidden layers, has 102, 200, 200, and 1 neurons in each layer, which is a plain and more conventional neural network without any fancy designs. Herein, each above algorithm would generate 40,962 models, each for predicting the thickness of a vertex at 1-year-old, while our Spherical U-Net just generates one model for all vertices. All the machine learning algorithms were firstly applied on randomly selected 1000 vertices using grid search (20 portions in the range from 1e-4 to 1e4 for each parameter) to find the best hyper-parameters. The parameter tuning and training process all lasted an extremely long time (1–3 days).

3). Results:

Table VI presents the results of the comparison between SDU-Net and conventional machine learning algorithms for cortical thickness map prediction. Our SDU-Net outperforms all other machine learning algorithms and our previous Spherical U-Net both in terms of MAE and MRE. While the main competitor, Random Forest is involved with complex hand-crafted features extraction step and heavy vertex-wise computational burden. Our task-agnostic and feature-agnostic SDU-Net still achieves better results, demonstrating higher effectiveness with a more lightweight design. The key factor contributing to the better performance of our method over conventional approaches is that our SDU-Net learns globally useful features effectively and automatically from the hierarchical architecture while other machine learning methods predict the attribute based on local hand-crafted features.

Table VI.

Comparison Of Different Methods On Cortical Thickness Map Prediction

Methods	MAE (mm)	MRE (%)
Linear Regression	0.3595±0.0641	14.89±3.12
Polynomial Regression	0.6067±0.0901	26.63±4.53
4-layer Neural Network	0.3665±0.0603	14.67±2.89
Random Forest [47]	0.2950±0.0394	12.42±2.01
Spherical U-Net [37]	0.2817±0.0409	11.15±1.56
SDU-Net	0.2804±0.0515	11.10±2.08

V. DISCUSSION AND CONCLUSION

In this paper, we proposed the 1-ring filter on spherical space based on the icosahedron discretized sphere for developing corresponding operations for constructing the Spherical CNNs. The 1-ring filter has a natural and intuitive definition, making it interpretable for recognizing patterns on the spherical surface. We then extended the conventional U-Net and deformable convolution/pooling to the spherical surface and construct the SDU-Nets by deploying corresponding spherical operations. Furthermore, we have shown that the SDU-Net is computationally efficient and capable of learning useful features and adaptive receptive filed for different tasks, including cortical surface parcellation and cortical attribute map development prediction. Extensive ablation studies on these two challenging tasks confirm the robustness, efficiency, and accuracy of the SDU-Net both visually and quantitatively.

Our main motivation in this paper was to design a general filter on the spherical surface that can be easily used and extended to various cortical surface tasks. Although the 1-ring filter can already provide us an efficient way to obtain high level representations from the data defined on the spherical surface manifold, it is inherently limited to model a small part of geometric transformations. Therefore, we further propose the spherical deformable 1-ring filter and spherical deformable convolution/pooling to significantly improve the network’s transformation modeling capability, instead of expensive data collection and augmentation, especially in medical imaging. In this way, cortical surface analysis can be benefited and facilitated by the prosperous deep learning techniques more efficiently. From this point of view, there are a lot of potential directions and applications to be explored. Some interesting future work may include extending CycleGAN [51] and its variants to harmonize cortical feature maps across multiple scanners, ResNet [52] to help classify and find biomarkers for brain disorders, and VoxelMorph framework [8] to cortical surface for faster surface registration.

One limitation of our work is that the reference direction we defined on the sphere only guarantees the azimuthally rotation invariance and does not strictly guarantee invariance for other rotations, which means the same pattern can be detected when spheres are rotated along the z-axis and may not be detected when spheres are rotated across the z-axis. Therefore, it may lead to distortions in the learned features in polar regions. It is still acceptable and can be overcome for supervised learning using big data with its ground truth, such as the cortical surface parcellation and attribute map prediction. However, when facing unsupervised learning, this design needs to be reconsidered and some specific modifications may be necessary to fulfill the rotation invariant requirements.

Finally, our SDU-Net presented here is a general model and not limited to a particular cortical feature or analysis task. It may be also useful in other genus 0 organs and computer vision tasks. It provides a valuable tool for research studies involving deep learning-related cortical surface-based tasks and thus can help better study and understand brain development, aging, and disorders. Our code is freely available at https://www.nitrc.org/projects/infantsurfparc/.