Labeling Vertebrae with Two-dimensional Reformations of Multidetector CT Images: An Adversarial Approach for Incorporating Prior Knowledge of Spine Anatomy

Abstract

Purpose

To use and test a labeling algorithm that operates on two-dimensional reformations, rather than three-dimensional data to locate and identify vertebrae.

Materials and Methods

The authors improved the Btrfly Net, a fully convolutional network architecture described by Sekuboyina et al, which works on sagittal and coronal maximum intensity projections (MIPs) and augmented it with two additional components: spine localization and adversarial a priori learning. Furthermore, two variants of adversarial training schemes that incorporated the anatomic a priori knowledge into the Btrfly Net were explored. The superiority of the proposed approach for labeling vertebrae on three datasets was investigated: a public benchmarking dataset of 302 CT scans and two in-house datasets with a total of 238 CT scans. The Wilcoxon signed rank test was employed to compute the statistical significance of the improvement in performance observed with various architectural components in the authors’ approach.

Results

On the public dataset, the authors’ approach using the described Btrfly Net with energy-based prior encoding (Btrfly_pe-eb) network performed as well as current state-of-the-art methods, achieving a statistically significant (P < .001) vertebrae identification rate of 88.5% ± 0.2 (standard deviation) and localization distances of less than 7 mm. On the in-house datasets that had a higher interscan data variability, an identification rate of 85.1% ± 1.2 was obtained.

Conclusion

An identification performance comparable to existing three-dimensional approaches was achieved when labeling vertebrae on two-dimensional MIPs. The performance was further improved using the proposed adversarial training regimen that effectively enforced local spine a priori knowledge during training. Spine localization increased the generalizability of our approach by homogenizing the content in the MIPs.

Supplemental material is available for this article.

© RSNA, 2020

Summary

The proposed fully convolutional network architecture, Btrfly Net with energy-based prior encoding, was trained to learn the a priori knowledge of the spine’s shape on two-dimensional maximum intensity projections to locate and identify vertebrae at a rate comparable to that of prior methods that operated in three dimensions.

Key Points

• ■ Three-dimensional labeling of vertebrae using two-dimensional sagittal and coronal maximum intensity projections resulted in a computationally lighter but high-performing pipeline when processed using a butterfly-shaped fully convolutional network.

• ■ Employing spine localization as a preprocessing stage enabled the proposed approach to be applicable to scans of any field of view, including complete vertebrae, thus increasing its generalizability to a clinical setting.

• ■ Enforcing anatomic a priori knowledge (in the form of the vertebral arrangement) onto the labeling network using so-called adversarial learning improved the vertebrae identification rate to greater than 88% on a public benchmarking dataset.

Introduction

Spine CT is a commonly performed imaging procedure. In this study, we focused on labeling the vertebrae, which is the task of both locating and identifying the cervical, thoracic, lumbar, and sacral vertebrae in a regular spine CT scan. Labeling the vertebrae has immediate diagnostic consequences. Vertebral landmarks help identify scoliosis, pathologic lordosis, and kyphosis, for example. From a modeling perspective, labeling simplifies the downstream tasks of intervertebral disk segmentation and vertebral segmentation.

Previous approaches to labeling fell into one of two broad categories: the traditional model-based approaches and the relatively recent learning-based approaches. Model-based approaches such as those of Schmidt et al (1), Klinder et al (2), and Ma and Lu (3) used a priori information on the spine structure, such as statistical shape models or atlases. Due to their extensive reliance on a priori information, the generalizability of these approaches was limited. From a machine learning perspective, approaches have existed, ranging from regression forest models working on context features in Glocker et al (4), Glocker et al (5), and Suzani et al (6); a combination of convolutional neural networks and random forest models in Chen et al (7); and three-dimensional (3D) fully convolutional networks in Yang et al (8), followed by recurrent neural networks in Yang et al (9) and Liao et al (10). Most of these approaches work on full 3D multidetector CT scans. Recently, an approach achieved a higher labeling performance by working on two-dimensional (2D) maximum intensity projections (MIPs) using an architecture termed Btrfly Net, which was first proposed by Sekuboyina et al (11).

In this study, we improved on the Btrfly architecture and extended it with a spine localization module, thus making the combination more generalizable. Concurrently, inspired by the generative adversarial learning domain, we investigated an a priori learning module that enforced the spine’s anatomic a priori knowledge (ie, prior) onto the Btrfly network. Earlier approaches were aimed at prior learning, such as those of Ravishankar et al (12) and Oktay et al (13). Typically, such approaches consist of two networks, with one primary network solving a task (eg, segmentation) and use of a secondary pretrained network that learns the shape of interest and either “corrects” the primary network’s prediction (12) or “enforces” it on the primary network (13). Our network was similar to these approaches in that it includes two components: a labeling network and an adversary as the secondary network. However, Btrfly Net was fundamentally different in the training and inference processes compared with the previous work (12,13). First, the adversary required no pretraining because it was trained along with the labeling network by penalizing it if the labels deviated from the ground truth distribution. Second, since the adversarial loss was used to update directly the weight of the Btrfly net, the adversary was no longer needed during inference.

Thus, our hypothesis was that by incorporating a spine localization stage before vertebral labeling and then using adversarial learning on an anatomic prior and enforcing it onto the Btrfly network, the labeling performance would be improved while also making the setup generalizable to clinical routines. We describe the use of the prior-encoded Btrfly variant for improved vertebrae identification and labeling compared with the original Btrfly Net. Furthermore, we validate this network for vertebrae labeling on in-house data, supporting its use in a clinical diagnostic setting.

Materials and Methods

Study Datasets

We worked with two datasets: (a) a public benchmarking dataset and (b) a collection of two in-house datasets. The Computational Spine Imaging (CSI) workshop during the 2014 Medical Image Computing and Computer Assisted Intervention conference by the Department of Radiology at the University of Washington released a public benchmarking dataset, called CSI_label. It consists of 302 spine-focused (ie, tightly cropped) CT scans (of which 242 are for training and 60 are for testing) that include fractures, scans with and without contrast material enhancement, abnormal curvatures, and nearly 150 scans comprising postoperative cases with metal implants. The dataset has a mean voxel spacing of approximately 2 × 0.35 × 0.35 mm³ in the craniocaudal × left-right × anteroposterior directions and a mean dimension of (318 ± 131) × (172 ± 24) × (172 ± 24) at 1-mm³ isotropic resolution. Vertebrae centroids have been manually annotated as described by Glocker et al (5).

Our two in-house datasets consisted of 238 CT scans in total (178 for training and 60 for testing, with fivefold cross validation). It is a collection of examinations of healthy and abnormal spines (eg, osteoporosis, vertebral fractures, degeneration, and scoliosis) of patients 30–80 years old, collected for two previously published retrospective studies (14,15). Ethics approval was obtained from the local ethics committee of the faculty of medicine of the Technical University of Munich for both studies. Because of the retrospective nature of these studies, the need for informed consent was waived. In the study published in 2017, Valentinitsch et al (14) established a normative atlas of the thoracolumbar spine in healthy patients using nonenhanced CT scans collected between 2005 and 2014. In the study published in 2019, Valentinitsch et al (15) investigated texture analysis techniques for diagnosis of opportunistic osteoporosis using contrast material–enhanced CT scans collected from February 2007 to February 2008. For both studies, cases with metastasis and metal implants were excluded as they would change vertebral texture as well as biomechanical behavior and thus interfere with fracture prediction. These exclusion criteria are based on the older studies and not on the current study we report on here. In this study, we used 65 non–contrast-enhanced scans from Valentinitsch et al (14) and 173 contrast-enhanced scans from Valentinitsch et al (15). Overall, approximately 20% of the dataset (46 scans) included parts of the rib cage, where 92 patients had fractured vertebrae. Annotations of the vertebrae were automatically derived from available segmentations, performed with an automated algorithm based on shape model matching (2). They were verified by one radiologist (J.S.K.), with more than 15 years of experience in spine imaging, and corrected where necessary.

CT Imaging

All CT scans were performed with either a 256–detector row (Philips Medical Systems, Best, the Netherlands) or a 128–detector row (Siemens Healthineers, Erlangen, Germany) CT scanner and reconstructed using an edge-enhancing kernel. All scans were acquired with 120 kVp and an adaptive tube load. All patients received intravenous contrast material (Iomeron 400; Bracco, Konstanz, Germany) with a delay of 70 seconds, a flow rate of 3 mL/sec, and a body weight–dependent dose between 80 and 100 mL. The mean voxel size of the dataset is approximately 0.7 × 2.75 × 0.7 mm³ in the craniocaudal × left-right × anteroposterior directions with a mean size of (565 ± 111) × (123 ± 58) × (401 ± 140) mm³.

Spine Localization as a Preprocessing Stage

For efficiently handling data with diverse fields of view, localizing the spine was an important step that improved the 2D projections on which all subsequent vertebrae labeling stages relied. For localizing the spine, a 3D fully convolutional neural network was employed to regress Gaussian heat maps centered at the vertebrae, followed by extracting a bounding box around the spine. This stage operated at very low resolution (4-mm isotropic), employing a lightweight, fully convolutional U-network. The network architecture is described in Figure E1 (supplement). Figure 1a shows examples of the predicted heat maps and the extracted bounding boxes. With this spine localization stage, we were able to extract a localized MIP, which is an MIP across only those sections that contain the spine. Localized MIP projections gave an unoccluded view of the spine (Fig 1b).

Figure 1a:

Spine localization and its necessity illustrated on a data sample from the in-house dataset. (a) Ground truth and predicted localization maps along with extracted bounding boxes (blue = actual, green = predicted), plotted on sagittal and coronal sections of a CT scan. (b) A naive maximum intensity projection (MIP) of a scan shows the rib cage completely occluding the spine (left). This can be handled by extracting a localized MIP of the same scan using the bounding box of the localized spine (right).

Figure 1b:

Spine localization and its necessity illustrated on a data sample from the in-house dataset. (a) Ground truth and predicted localization maps along with extracted bounding boxes (blue = actual, green = predicted), plotted on sagittal and coronal sections of a CT scan. (b) A naive maximum intensity projection (MIP) of a scan shows the rib cage completely occluding the spine (left). This can be handled by extracting a localized MIP of the same scan using the bounding box of the localized spine (right).

Vertebrae Labeling with the Btrfly Net

Networks working in 3D are computationally intensive owing to their features vectors being of O (N³), where N is one of the scan dimensions. As an alternative to working in a computationally demanding 3D domain, Sekuboyina et al (11) proposed working with 2D sagittal and coronal MIPs by proposing a butterfly-shaped architecture, Btrfly Net. As the Btrfly Net processes 2D data, its feature dimensionality is limited to O (N²). This reduction in requirement of computational resources allows the design of deeper 2D networks with more convolutional layers leading to higher receptive fields. In this study, we used an improved version of the Btrfly Net. Most importantly, we work with scans at 2-mm isotropic resolution, consequently increasing the receptive field and the representational capacity of the Btrfly Net (Fig E2 [supplement]).

Adversarial Enforcement of the Shape of the Spine onto Btrfly Net

Human anatomy usually follows certain structural rules; thus, anatomic nomenclature has strong tacit assumptions (or priors). For example, in the spine, vertebra L2 is almost always caudal to L1 and cranial to L3. Enabling a network to learn such priors results in anatomically consistent predictions. In our case, a secondary network or discriminator (D), which was trained along with the primary Btrfly Net, learned the spine’s shape and forced the Btrfly Net’s predictions to respect this shape. In Sekuboyina et al (11), an energy-based (EB) autoencoder was used as a discriminator (EB-D). In this study, we improved the architecture of the EB-D and compared it with a purely encoding, Wasserstein distance–based discriminator (W-D). (16). The combination of the Btrfly Net and EB-D was referred to as Btrfly_pe-eb (denoting energy-based prior encoding) and that of the Btrfly Net and W-D was referred to as Btrfly_pe-w (for Wasserstein distance–based prior encoding). The architectures, the cost functions, and the adversarial training details of both the improved EB-D and proposed W-D are described in Appendix E1 (supplement). Note that EB-D is a fully convolutional network and has a receptive field covering only a fixed part of the spine irrespective of the input scan dimension. On the other hand, W-D has a receptive field covering the full image owing to the dense connections in the architecture. We refer to these two receptive fields as local and global, respectively, and investigate the difference in their behavior.

Inference

Our algorithm included two components—spine localization and vertebrae labeling—as illustrated in Figure 2. Given a multidetector CT scan, the localization stage predicts a heat map (and a bounding box) indicating the location of the spine from which localized MIPs can be extracted and passed to the labeling stage. Each arm of the Btrfly Net labels the sagittal and coronal projections, which are then fused by outer product to obtain the 3D vertebral locations. Note that the role of the discriminators ends with adversarial enforcement of the spine prior onto the Btrfly Network during the training stage and are not a part of the inference path. The improvement in performance due to various components of our approach was assessed using a Wilcoxon signed rank test assuming independence across scans.

Figure 2:

An overview of our labeling approach. Also illustrated is the spine localization stage, which is, in some cases, necessary for our approach to be generalizable to any clinical CT scan including complete vertebrae. 3D = three-dimensional, 2D = two-dimensional.

Performance Evaluation of Spine and Vertebral Detection

Spine localization.—The performance of the localization stage is evaluated with two metrics defined as: (a) intersection over union between the actual and predicted bounding boxes and (b) detection rate, where a detection was successful if the corresponding intersection over union was greater than 50%. It was observed that this overlap suffices for our task of filtering out the obstructions.

Vertebrae labeling.—The labeling performance was evaluated using metrics defined in Glocker et al (4) and Sekuboyina et al (11), namely, identification rate, localization distance, precision, and recall. A vertebra was correctly “identified” if the predicted vertebral location was the closest point to the ground truth location and was less than 20 mm away from it. The distance of this prediction was then recorded as the localization distance. Precision and recall values were used to quantify the relevance of the predictions (eg, accurately labeling all vertebrae in the scan vs labeling a vertebra that was not present in the scan).

Statistical Analysis

Since the test sets are large with 60 scans each for the public and in-house datasets, we employed the nonparametric Wilcoxon signed rank test for validating the statistical significance of the improvement in various performance measures due to our architectural modifications. These modifications included the fusion of the sagittal and coronal views in the Btrfly Net and the inclusion of prior-encoding components in Btrfly_pe-w and Btrfly_pe-eb Nets.

Results

Successful Spine Localization within the CSI_label and In-House Datasets

Localizing the spine at CT is a relatively simple task owing to the higher attenuation (measured in Hounsfield units) of the bone. The network only needs to isolate the spine from the rest of the skeletal structure. Table 1 records the performance of this stage on the two datasets in use. We obtained a mean intersection over union greater than 75% on both datasets. A detection rate of 100% on CSI_label and 97% on the in-house dataset indicated a successful localization of the spine in all the cases. Note that a complete failure of localization might not be detrimental as it would result only in an occluded MIP. Labeling such a projection could be handled in the subsequent stages with appropriate augmentation if the failure rate is minimal.

Table 1:

Performance of the Spine Localization Stage

Btrfly Network Variants, Btrfly_pe-eb and Btrfly_pe-w, Perform Refined Vertebrae Labeling Compared with the Original Btrfly Network

We evaluated the vertebrae labeling performance in two stages: (a) On the public CSI_label dataset, we evaluated the performance of the stand-alone labeling component and compared it with prior work (Tables 2, 3) and (b) on the in-house dataset, we deployed the combination of localization and labeling to evaluate the contribution of localizing the spine (Table 4). To be agnostic to initialization, and since the train-test split is official, we reported the mean performance over three runs of training with independent initializations on the public dataset, while we performed a fivefold cross-validation on the in-house dataset to compensate for any dataset bias. All the improvements in the performance due to our contributions are statistically significant (P < .05) according to the Wilcoxon signed rank test.

Table 2:

Performance Comparison of Our Approach with Prior Work

Table 3:

Precision and Recall Analysis

Table 4:

Contribution of Spine Localization

Contribution of Btrfly architecture.—To validate the importance of combining the views and processing them in the Btrfly Net, we compared its performance to a network setup working individually on the coronal and sagittal views without any such fusion of views. This setup was denoted by “Cor+Sag”. The architecture of each of these networks was similar to one arm of the Btrfly Net without the fusion of views. Due to this architectural modification, an increase of 1% in the identification rate was observed between Cor+Sag Net and Btrfly Net, as reported in Table 2.

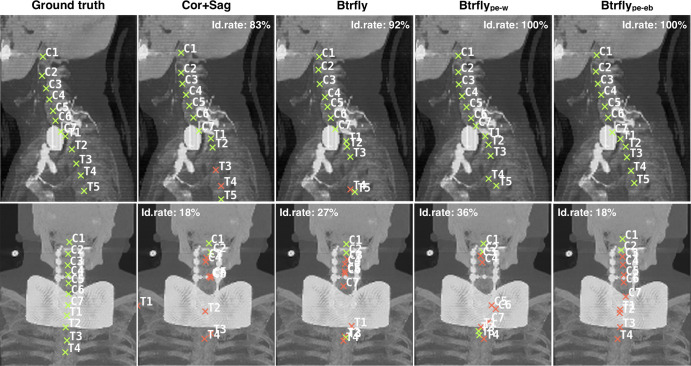
Effect of adversarial encoding.—Enforcing prior information into the Btrfly Net’s training resulted in a 1% to 2% improvement in the identification rate. We observed that the performance of Btrfly_pe-eb was marginally superior to that of Btrfly_pe-w (Table 2). This can be explained by the distinction between the locally encoding Btrfly_pe-eb and a globally acting Btrfly_pe-w. This difference in encoding also explains the high variance of the identification rate of Btrfly_pe-w (standard deviation of 0.2 [Btrfly_pe-eb] vs 1.2 [Btrfly_pe-w]). A qualitative comparison of the three variants in our experiments is shown in Figure 3. The top row shows a use-case with successful labeling, and the bottom row shows an interesting failure use-case where the labeling fails due to the presence of an obstruction along the coronal view.

Figure 3:

Qualitative comparison of our network architectures shows two cases from the public dataset with one successful labeling (top, sagittal view) and one unsuccessful labeling (bottom, coronal view). The Cor+Sag and Btrfly Nets label mostly in the presence of spatial information. However, the energy-based prior encoding Btrfly Net (Btrfly_pe-eb) and Wasserstein distance–based prior encoding Btrfly Net (Btrfly_pe-w) hallucinate prospective vertebral labels despite no image information (labels on shaded gray area on coronal view). In addition, Btrfly_pe-eb tries to retain the order of vertebral labels. Cor+Sag = coronal plus sagittal. Id. rate = identification rate.

Precision and recall.—A Gaussian image predicted for any vertebra was counted as a final label if the response was higher than a threshold. Thus, the threshold controls the false-positive and true-positive label predictions of the network. Figure 4 shows a precision-recall curve generated by varying the threshold between 0 and 0.8 in steps of 0.1, while Table 3 records the performance at the F1-optimal threshold. Despite not choosing a recall-optimistic threshold, our networks performed comparably well at an optimal-F1 threshold. Notice the overarching nature of Btrfly_pe-eb over others at all thresholds.

Figure 4:

Precision-recall curve with F1 isolines shows the effect of the threshold during inference. For any threshold, Btrfly_pe-eb offers a better trade between precision and recall. Cor+Sag = coronal plus sagittal, Btrfly (pe-eb) = Btrfly Net with energy-based prior encoding, Btrfly (pe-w) = Btrfly Net with Wasserstein distance–based prior encoding.

Rigorous evaluation with respect to identification rate.—As defined in Glocker et al (4), a vertebra was accurately identified if it was the closest to the ground truth and less than 20 mm away. We denote this distance threshold as d_th. However, a d_th of 20 mm is a weak requirement; for example, in the case of cervical vertebrae, which are quite close to one another, predicting the current vertebra’s landmark on the adjacent vertebra might not be penalized. Demonstrating the spatial precision of our localization, we performed a breakdown test with respect to the identification rates by varying d_th between 5 mm and 30 mm in steps of 5 mm. Figure 5 shows the regionwise performance curves obtained for this variation across our setups. Notice the reasonably stable behavior of the curves until d_th = 10 mm.

Figure 5:

Regionwise variation of identification rates (Id.rates) (y-axis) for different values of the distance threshold (d_th) (x-axis) considered as a positive identification. Btrfly (pe-eb) = Btrfly Net with energy-based prior encoding, Btrfly (pe-w) = Btrfly Net with Wasserstein distance–based prior encoding, Cor+Sag = coronal plus sagittal.

Labeling with improved projections.—The performance of the Btrfly_pe-eb architecture (chosen because of its superior performance) on naive MIPs with that of localized MIPs on the in-house dataset is shown in Table 4. Observe an inferior identification rate and high localization distances with naive MIPs due to the lack of visible vertebrae (Fig 6). However, localized MIPs from the spine’s bounding box result in approximately a 4% gain in identification rate.

Figure 6:

Localized (Loc) maximum intensity projection (MIP) and a naive MIP from the same scan from the in-house dataset using the Btrfly_pe-eb network. Observe occlusions in naive MIP and the lack thereof in the localized MIP, resulting in an improved labeling performance. Btrfly (pe-eb) = Btrfly Net with energy-based prior encoding, Id. rate = identification rate.

Discussion

We proposed a generalizable pipeline to localize and identify vertebrae on multidetector CT scans that operates on appropriate 2D projections, unlike prior studies whose authors worked with 3D scans. Specifically, we incorporated an improved version of the Btrfly architecture in combination with a spine localization and a prior-learning stage.

The performance of the localization stage, with intersection over unions greater than 75%, shows that detecting the spine is an easier task. The network localized the spine better in the public dataset when compared with the in-house dataset. This can be attributed to the composition of the datasets: CSI_label is predominantly composed of thoracolumbar reformations with a uniform axial field of view centered around the spine, while the in-house dataset has a higher variety of scans in terms of axial and coronal fields of view. For the same reason, localizing the spine and extracting MIPs only across the sections containing the spine showed an improvement in labeling performance on the in-house dataset from 81% with naive MIPs to 85% (Table 4) with localized MIPs. Such an improvement was not observed for scans from CSI_label due to their relatively uniform fields of view. For the in-house dataset, the improvement can be attributed to the resulting homogeneity in the appearance of the MIPs owing to the localization irrespective of the scan content in the anteroposterior and lateral directions. Such data homogenization also resulted in a more stable learning.

In the module responsible for vertebral labeling, our algorithm contained two principle architectural components: (a) Fusion of the sagittal and coronal MIPs (using the Btrfly net) and (b) incorporation of anatomic prior information using the adversarial discriminators. This architecture, when trained end-to-end, resulted in an identification rate of 88% and localization distances of 6 mm (Table 2) on the public dataset, outperforming prior state-of-the-art methods (7,8,10). The effectiveness of these architectural components can be analyzed in three stages: First, a setup working purely on 2D MIPs (Cor+Sag) readily outperformed the naive 3D fully convolutional network proposed by Yang et al (8). This was mainly due to the depth of our setup, which can be afforded due to lesser computational load in 2D. Second, fusing the coronal and sagittal views increased the identification rate by approximately 1%. This can be attributed to two reasons: (a) one view now gets access to the key points in the other view, and (b) the combination of views causes the predictions of the Btrfly net to be spatially consistent between views. Third, the Btrfly net’s predictions were made to respect an anatomic prior using adversarial discriminators (EB-D or W-D) as a proxy to the postprocessing steps usually employed. For example, Yang et al (8) used a learned dictionary of vertebral centroids to correct a new prediction, and Yang et al (9) and Liao et al (10) used a pretrained recurrent neural network enforcing the vertebrae’s sequence to the prediction. Substituting these secondary steps, our Btrfly net was trained adversarially. The second network in our case (the adversary) was neither pretrained nor required during inference. The adversary provided a higher loss when the Btrfly network’s prediction did not conform to a normal spine structure. This enforced the anatomic prior directly onto the Btrfly Net during training. On one of the cross-validation data splits of the in-house dataset, our method achieved a 100% vertebra identification in 34 of the 60 test scans. Moreover, of the remaining 26 scans, seven scans had only one vertebra misidentified and two scans had only two vertebrae misidentified.

Delving deeper into prior learning, EB-D, whose receptive field covered a fixed part of a spine irrespective of the input field of view, enforced the spine’s structure locally. In contrast, W-D enforced a global spine prior since the dense layers in it resulted in the receptive field covering the entire input scan. Note that adversarial learning in any form improved the identification rate by 1% to 2%. However, Btrfly_pe-eb marginally outperformed Btrfly_pe-w. This can be attributed to the fact that a local prior is easier to learn than a global one. Since spine multidetector CT scans have highly varying fields of view, accurately learning a global prior was nontrivial for W-D. In the case of EB-D, the receptive field always covered approximately three vertebrae in the lumbar region (and more elsewhere). Since these subregions are relatively similar across scans, it was relatively easier for EB-D to learn and enforce a local prior. This can also be observed in a lower standard deviation in the identification rate of Btrfly_pe-eb across initializations, indicating a more stable performance.

This study has certain limitations stemming from design choices that need further investigation. First, concerning the proposed approach, the optimality of MIPs for labeling requires further study to ascertain cases in which they would break down. From the evaluations performed in this study, it seems to accurately label scoliotic spines, spines with metallic insertions, and spines with fractures, and so forth. However, an organized analysis is lacking. Second, the independent training of the localization stage weakens our approach’s “end-to-end trainable” feature. Moreover, the labeling performance depends on the accuracy of localization. When trained until convergence, localization seems to be accurate enough to aid the subsequent labeling stage. However, the robustness of the labeling stage to errors in spine localization is yet to be ascertained. Finally, our study is retrospective, and the computations have been performed on graphical processing units, where a forward pass takes less than 10 seconds. However, even if our model is lighter than its contemporaries, it is demanding for a regular CPU and takes approximately 1 minute per scan. Hence, an effort toward further making the setup lighter is of interest. Finally, consistent with the labels of CSI_label, we only considered 24 labels for C1-L5 and did not account for segmentation anomalies, such as L6, or transitional vertebrae, such as a lumbarized S1 vertebra.

Our study presents a simple, efficient algorithm for labeling vertebrae by arguing for processing the spine scans in two dimensions using an appropriate network architecture. Localizing the spine before labeling and forcing the labeling network to respect the spine’s anatomic shape during prediction further improved the labeling performance. The entire setup is computationally lighter than its counterparts in the literature, which is a step toward real-time clinical deployment.