Pattern formation and polarity sorting of driven actin filaments on lipid membranes

Significance

Pattern formation processes in active systems give rise to a plethora of collective structures. Predicting how the emergent structures depend on the microscopic interactions between the moving agents remains a challenge. By introducing a high-density actin gliding assay on a fluid membrane, we demonstrate the emergence of polar structures in a regime of nematic binary interactions dominated by steric repulsion. The transition from a microscopic nematic symmetry to a macroscopic polar structure is linked to microscopic polarity sorting mechanisms, including accumulation in wedge-like topological defects. Our results should be instrumental for a better understanding of pattern formation and polarity sorting processes in active matter.

Abstract

Collective motion of active matter is ubiquitously observed, ranging from propelled colloids to flocks of bird, and often features the formation of complex structures composed of agents moving coherently. However, it remains extremely challenging to predict emergent patterns from the binary interaction between agents, especially as only a limited number of interaction regimes have been experimentally observed so far. Here, we introduce an actin gliding assay coupled to a supported lipid bilayer, whose fluidity forces the interaction between self-propelled filaments to be dominated by steric repulsion. This results in filaments stopping upon binary collisions and eventually aligning nematically. Such a binary interaction rule results at high densities in the emergence of dynamic collectively moving structures including clusters, vortices, and streams of filaments. Despite the microscopic interaction having a nematic symmetry, the emergent structures are found to be polar, with filaments collectively moving in the same direction. This is due to polar biases introduced by the stopping upon collision, both on the individual filaments scale as well as on the scale of collective structures. In this context, positive half-charged topological defects turn out to be a most efficient trapping and polarity sorting conformation.

Collective motion of active matter is ubiquitous, with observations ranging from flocks of birds (1) and schools of fish (2) to propelled colloids (3). The interactions between agents in such systems lead to the formation of complex structures including clusters, swirls, or lanes of agents moving coherently (4). The structure of the emerging patterns strongly depends on both the agents’ shape and their velocity alignment mechanism. A particular case is that of elongated microscopic particles that translate along their major axis in a quasi-two-dimensional environment and only interact upon collision (5, 6). In the context of cytoskeletal systems, gliding actin filaments or microtubules propelled by molecular motors are found to be able to readily crawl over each other and only retain a weak level of alignment upon binary collisions, which eventually leads at high densities to a diverse set of patterns (7). Such resulting patterns are found to be strongly dependent on this weak microscopic alignment interaction, and therefore, even slightly tuning it causes the system to switch between polar and nematic phases, separated by a coexistence regime (8, 9). Observed structures in cytoskeletal systems with weak to moderate interactions include nematic lanes, polar waves, and vortices (10–12). Conversely, pattern formation in systems of elongated bacteria or granular matter is often based on hard interactions with a strong steric component (13–18). In this repulsion-dominated regime, particles are unable to crawl over each other and must stop upon collision. In the limiting case of spherical self-propelled particles, this kind of steric interaction can lead to a stable phase separation between stuck and moving particles, the so-called motility induced phase separation (MIPS) (19). On the other hand, in the case of elongated particles, steric effects can still act as velocity aligning mechanisms. As orientation mismatches are unstable, particles end up aligning and this leads to flocking behavior rather than to phase separation (5, 20–25). This latter case, in which strong steric constraints dominate binary interactions but alignment is still present, is poorly understood, and how modeling has to be extended to account for the emergent collective behavior of elongated, flexible agents with volume exclusion also remains still under debate (26–30). This is partly due to the lack of microscopic experimental systems allowing to explore this regime. Semiflexible cytoskeletal filaments would be the best candidate, but their volume exclusion is usually too weak. However, having them propelled by motors immobilized on a fluid membrane would be a promising route to bridge this experimental gap (31).

Here, we enforce a steric repulsion-dominated interaction, leading to alignment between actin filaments by coupling myosin motors to a fluid-supported lipid bilayer. Because of the slippage of the motors on the membrane, the force propelling the filaments is too weak to enable filaments to crawl over each other and thus effectively implements a repulsion-dominated regime, with filaments stopping upon collisions. Eventually, however, because of the thermal fluctuations of their tips, filaments can align and resume motion. The experimental realization of such a microscopic binary interaction, based on volume exclusion, enables us to observe and quantify the resulting pattern formation process in a system of active semiflexible filaments. We then first characterize the interaction at the single filament scale, showing that it leads to nematic alignment. As the filaments’ density is increased, patterns of collective motion emerge, ranging from clusters to thick streams and vortices. Despite the nematic collision rule, we find the emerging structures to be locally polar. The repulsion-dominated interaction indeed introduces a polar bias not only due to the tendency of active filaments or clusters to keep moving together after a polar collision but also by forcing filaments with similar orientation to stop and accumulate when encountering an obstacle. In particular, at high densities, such an interaction leads to the formation of transient local +1/2 topological defects, which act as wedges and, therefore, effectively trap and polarity-sort motile filaments. We interpret this trapping mechanism as an analog of MIPS for elongated self-propelled particles.

Results

Binary Interactions Have Nematic Symmetry.

The actin gliding assay (32, 33) has been used to study the collective behavior of elongated filaments at high density (34, 35). Here, we bind biotinylated heavy meromyosin (HMM) motors via streptavidin to a supported lipid bilayer (SLB) containing 0.5% M/M biotinylated lipids (36) (Materials and Methods). The molecular motors are thus free to move on the fluid bilayer. The SLB’s lateral diffusion coefficient was found to be D = (3.4 ± 0.15) μm²/s (mean + SD, n = 14), as measured by fluorescence recovery after photobleaching (FRAP) according to refs. 31, 37 (SI Appendix, Fig. S1 and Movie S1). Successively, a mixture containing small phalloidin-stabilized fluorescent actin filaments (mean length L ∼2 µm, geometrical aspect ratio of ∼1:200) at a given concentration is incubated for 5 min. The incubation step is performed in ATP-free conditions to allow filaments to bind to the motors in the rigor state. A total of 0.2% methylcellulose is also present in the chamber to increase the motors’ processivity (8) but in a concentration low enough to avoid bundling or substantial filament–filament interaction (38). Finally, ATP as a fuel is added to the observation chamber and the surface of the sample is observed by total internal reflection fluorescence (TIRF) microscopy. In these conditions the system is active for at least 2 h.

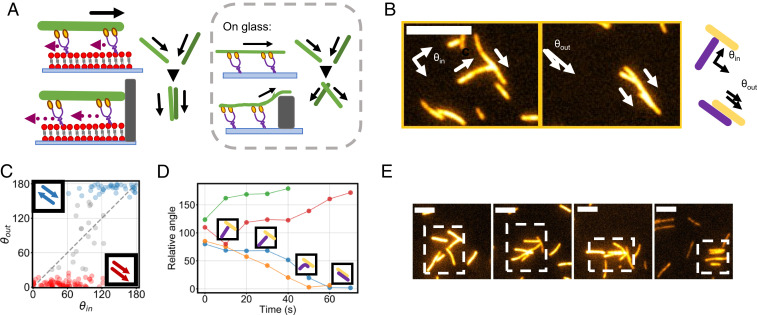
To monitor the motion of individual actin filaments, we first incubated only a small amount (10 nM) of filaments and obtained a final surface concentration of ρ ∼0.08 filaments/μm² measured right after ATP addition. Freely moving filaments have a speed of ∼150 nm/s (Movie S2), which is one order of magnitude slower than observed in a regular HMM motility assays on glass surface (1 to 5 µm/s) (35, 39, 40). This is due to the fact that motors are bound to a fluid bilayer, and thus, slippage of motors in the membrane limits their efficiency in transmitting force to the filaments. For the same reason, the motors’ ability to push filaments against a load is hindered (Fig. 1A) (31). In the case of a side collision between two driven filaments, we observe that the one, which has its direction of motion obstructed by the second one, does not glide over it. Instead, it stops until either the other filament moves away and thereby the obstacle is removed or until, thanks to the filaments’ flexibility, both filaments become aligned by fluctuations in the filaments’ tip and can move again (Fig. 1B and Movie S3). The net effect in individual collisions is thus an effective alignment. It occurs over ∼30 to 60 s (Fig. 1D), and its outcome has a dependency on the angle between filaments at which the collision takes place. We measured the angle between the filaments’ directions of motion both right before (θ_in) and right after (θ_out) collision occurs (Materials and Methods). We found that in 90% of the cases the final angle is either ∼0° or 180°, with collisions at small (large) angles (i.e., θ_in < 90° [θ_in > 90°]) resulting in a final angle of θ_out ∼0° (θ_out ∼180°) (Fig. 1C). Thus, on average, alignment can be either polar, with filaments moving together after having collided, or antipolar, with filaments moving in opposite directions. Collisions happening at a perpendicular angle result in a perfectly nematic response of the outgoing angles. Only a fraction (∼5%) of the collisions, mostly occurring between perpendicular filaments, does not lead to an alignment as the obstacle glides away too soon. While right after antipolar collisions the filaments glide in different directions, the tendency of filaments to move together for a prolonged time when colliding polarly introduces an asymmetry at the binary collision level, which stabilizes polar pairs with respect to antipolar ones (5). Additionally, as filaments stop upon collision, it is possible that multiple filaments aggregate transiently against the same obstacle. As all such filaments are oriented in the same direction, this further increases the tendency toward the formation of transient polar order (Fig. 1E). Thus, despite the microscopic nematic symmetry of the binary interaction, the steric repulsion between filaments together with the stopping behavior introduces a tendency toward polar alignment, especially in multiparticle collisions, which is absent in the standard actin gliding assay.

Fig. 1.

Microscopic interaction between filaments. (A) Schematics of the system. Contrary to what happens on glass, motors on a supported membrane are incapable of pushing filaments against an obstacle as they slip on the membrane. On glass, conversely, colliding filaments can overcome obstacles and crawl over each other. (B) Example of a collision between filaments on a membrane resulting in alignment in roughly a minute. (Scale bar, 5 μm). The Inset shows a schematic of the collision and of the incoming angle θ_in and the outcoming angle θ_out. (C) Outcoming angle (θ_out) of collisions between filaments as a function of the incoming angle (θ_in). The dashed line indicates the case of no interaction. Red indicates collisions resulting in polar alignment and blue antipolar. (D) Angles between four different colliding filaments as a function of time. Insets show different phases of the collision: because of volume exclusion, filaments stop, fluctuate, and eventually align, either polarly or anti-polarly. (E) Example of a multifilament collision leading to polarity sorting. Filaments acting as an obstacle also act as accumulation sites. As all filaments accumulating are oriented in the same direction, this introduces a polar bias in the system. (Scale bar, 2 μm).

Emergence of Polar Order at Low Filament Densities.

We then increased the surface concentration of filaments. At any concentration, transient alignment of filaments is observed. After increasing the surface density of filaments to about ρ ∼ 0.18 filaments/μm², clusters of filaments moving together appeared. This concentration is about two order of magnitudes lower than the critical density for ordering of 5 filaments/μm² determined in high-density motility assay on glass (35). Thus, in the repulsion-dominated alignment regime, collisions of a small number of filaments are already sufficient to account for the emergence of local order. By multiplying the surface density ρ of filaments times the squared mean length L of the filaments, one obtains the dimensionless parameter ρ$L^2$, indicating the scaled number density (41, 42). While for ρ$L^2\hspace{1em}$ ∼0.32 (ρ ∼0.08 filaments/μm²), no clustering is visible (Movie S2), at ρ$L^2$ ∼0.72 (ρ ∼0.18 filaments/μm²), filaments already aggregate (Fig. 2A). Such a value is much lower than the Onsager threshold of ρ$L^2$ ∼4.7 for the isotropic–nematic transition (43, 44) of passive filaments, indicating that activity lowers the aggregation threshold in this regime. These values are comparable with the clustering threshold found by simulations of propelled rods (41, 42, 45, 46) and experiments with bacteria (14), despite the actin filaments here having a much bigger aspect ratio.

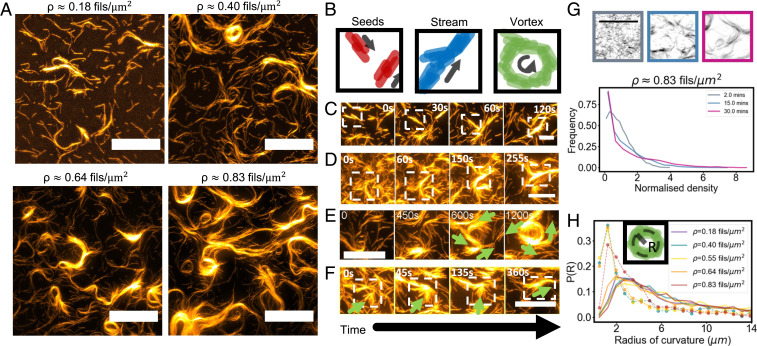
Fig. 2.

Formation of streams and vortices at different surface densities. (A) Structures forming at different surface densities ρ of filaments. (Scale bars, 20 μm.) (B) Schematic representations of seeds composed of a few filaments, of an elongated stream composed of several filaments, and of a vortex. (C–E) Close-up of different structures forming. Seeds can merge together (C, ρ ∼0.4 filaments/μm²), and the merging of seeds can result in stream formation (D, ρ ∼0.83 filaments/μm²) or vortex formation (E, ρ ∼0.64 filaments/μm²). Green arrows indicate the local direction of motion. (F) Filaments and seeds stop against a transient obstacle for about 2 min, and additional filaments with the same orientation further accumulate in place. As the obstacle glides away, a thicker stream has formed composed of filaments moving in the same direction (Scale bars in C–F, 10 μm.) (G) Snapshots of the system at ρ ∼0.83 filaments/μm² for different times and corresponding density histogram showing cluster formation over time. A normalized density of one indicates the isotropic phase. (Scale bar, 10 μm.) (H) Histogram of the local radius of curvature R of streams (solid lines) and vortices (dashed lines with circles) at different densities. The Inset shows a schematic of the radius of curvature for a vortex.

We further increased the surface density of filaments to ρ ∼0.40, 0.55, 0.64, and 0.83 filaments/μm² (ρ$L^2$ ∼1.6, 2.2, 2.56, and 3.32), which resulted in increasingly stable collective patterns (Fig. 2A and Movies S4 and S5). We also note here that such surface densities roughly correspond to a 0.8 to 1.7% surface area coverage.

We further observed that successive individual collisions between filaments lead to the formation, at short times, of small polar clusters or “seeds”, composed of a few filaments moving in the same direction (Fig. 2B). Depending on the local concentration, these can either disassemble or act as seeds for the further alignment of colliding filaments (Fig. 2C). Being composed of filaments, seeds follow the same dynamics (i.e., they stop and align upon collision). As seeds colliding at small angles (<90°) often exit the collision polarly oriented, they have the tendency to travel together and form longer-lived structures. During such collisions, seeds are temporarily immobile and can act as obstacles for other filaments, which then accumulate locally.

Ultimately, successive merging events lead to the formation of dynamic streams of filaments, which are elongated structures composed of motile filaments (Fig. 2D and Movie S6). Already at ρ ∼0.18 filaments/μm², most seeds are stable enough to result in the formation of short streams, while at ρ ∼0.40 filaments/μm² and above (ρ$L^2>$1.60), streams are longer and persistent in time, again confirming a transition to stable order in the range (ρ$L^2=1-2$) predicted$\hspace{1em}$by simulations of propelled rods (41, 45).

This is further characterized by plotting the histogram of the local density over time (Fig. 2G and Materials and Methods). A transition is visible at concentration higher than ρ ∼0.08 filaments/μm² from an initially uniform state to a final state in which big areas of the sample are devoid of filaments, whereas the tails of the distribution expand toward higher values. Long tails are already present at ρ ∼0.18 filaments/μm², and the effect is more pronounced as the surface density is increased (SI Appendix, Fig. S2).

Streams move and change shape and direction over time. They can also merge further, giving rise to either a thicker stream or to two adjacent streams of filaments moving in opposite directions. Depending on the surface density, streams can also bend or merge into a vortex (Fig. 2E and Movie S6), or they can disassemble again into smaller streams. As the bulk density is further increased, streams become thicker, longer, and more persistent in time. By comparing the transverse intensity profile of individual filaments with that of streams, we estimate the thickness of streams in terms of the number of filaments (SI Appendix, Fig. S2). While at ρ ∼0.07 filaments/μm², filaments move individually, with only transient clusters composed of 2 to 3 filaments appearing, the average number of filaments in a stream increases as the surface density increases, with streams composed of up to 100 aligned filaments at ρ ∼0.83 filaments/μm². Streams thus get thicker and longer (SI Appendix, Figs. S3 and S4) and disassemble less frequently. At the same time, isolated seeds become less favorable. At all concentrations, individual filaments can also be observed leaving and joining streams or moving freely in low density areas. Seeds keep forming, but if the concentration is high enough, they ultimately either disassemble or join a stream. Erosion and accretion of streams can only happen on the sides, as filaments flowing inside the stream are trapped by neighboring filaments. The steric component of the interaction here also plays a role in impeding that streams cross each other, forcing them to either stop or merge upon contact. For this reason, vortices, when formed by a stream that loops on itself, can be particularly persistent in time, as filaments composing it are trapped in their own loop. Vortices are observed with radii 1.5 to 8 µm (and thus with a circumference of 10 to 50 µm), which is much longer than the average filament’s size of 2 µm. This rules out that vortices are stabilized by longer individual filaments, as previously observed in simulations of filaments (47) and bacterial systems (48). It rather indicates that vortices are formed by streams and seeds colliding and merging, as previously observed in simulations of semiflexible filaments with hard repulsion (26), and that they are always composed by multiple filaments. Vortices are thus, due to the repulsion-dominated interaction that allows filaments to form structures, longer than their individual size.

To further understand the formation of collective structures, we computed the histogram of curvature radii, separately for vortices and streams, at different surface densities (Fig. 2H and Materials and Methods). The distributions appear similar for all densities, with the mean curvature radius only slightly increasing with the density. Vortices appear to be able to bend more than streams and thus can have a smaller radius of curvature, suggesting that highly bent streams often end up in a vortex. Additionally, as no vortex is observed with a mean radius below 1.5 µm, we conclude that vortices can start forming only when the streams’ length is comparable to the minimum vortex circumference (∼10 µm) or enough streams and seeds are present that can loop on each other. No vortices are indeed observed at ρ ∼0.18 filaments/μm², when only a few such long streams are present (SI Appendix, Fig. S3), while they appear at ρ ∼0.40 filaments/μm² and increase in number at higher densities (Fig. 2A).

At higher densities, most of the filaments are eventually part of a dense structure, either a stream or a vortex. The filaments, as well as the formed structures, are all still mobile with a frequent exchange of the filaments with the surrounding less dense phase. The speed of filaments inside streams and vortices in the absence of obstacles is around 50 nm/s and thus only weakly affected by the local density. All observed collective structures (seeds, streams, and vortices), being composed of filaments incapable of crawling over each other, still stop upon collision with an obstacle. Several events of stopping, aggregating, and then moving as a coherent polar structure are observed also at the level of seeds and streams (Fig. 2 C, D, and F). As a result of such polar bias because of stopping, structures are composed of polarly moving filaments (see Fig. 4).

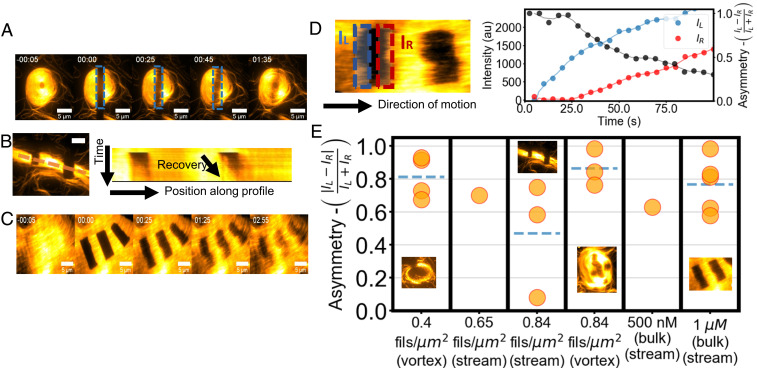
Fig. 4.

FRAP experiments reveal the polarity of streams and vortices. (A) Example of bleaching and recovery of a vortex at ρ ∼ 0.83 filaments/μm². Time 0 is right after bleaching. (B) Bleaching and kymograph of recovery along the dashed line for a stream at ρ ∼0.83 filaments/μm². Total time is 100 s. (C) Bleaching and recovery of a stream at 1 μm actin. Time 0 is right after bleaching. (Scale bars in A–C, 10 μm.) (D) Schematics and example of the polarity measurement. Two opposite regions of the bleached area along the filaments’ direction of motion are recorded independently over time (red and blue curves) to compute the polarity parameter P (black curve). The lag in the recovery of the red region indicates polar motion. (E) Plot of the polarity parameter $P=\frac{|I_L-I_R|}{I_L+I_R}\hspace{1em}$for different structures at different densities, showing recovery starting from one side. Streams and vortices are analyzed separately. Dashed lines indicate a mean value. The Inset shows examples of the FRAP experiments.

Emergence of Polar Order at High Filament Densities.

In order to reach even higher surface densities, another set of experiments is performed in which actin is added directly together with ATP and progressively sedimented on the motor-coated SLB by 0.2% methylcellulose. This allows for experiments with higher actin bulk concentration (up to 1 µM). By these means, filaments sediment, move, and align progressively over time, allowing higher surface concentrations (higher than ρ = 5 filaments/μm², corresponding to ∼10% area coverage). Similar to lower densities, thick streams form, and filaments are still motile within them. Because of the higher density, streams are now more persistent and can, after formation, act as an obstacle for filaments traveling in the transverse direction, which then start stopping upon collision because of the repulsion-dominated interaction. Additional filaments stopping in the same position lead to a local accumulation of filaments, which hinder each other’s transverse motion. Local bends in streams are particularly efficient in trapping filaments, acting as a wedge-shaped trap (49).

The accumulation of filaments in areas where the motility is low because of an obstacle causes the depletion of isolated freely moving filaments, which end up either flowing in a stream or being trapped. This results in big portions of space being depleted from filaments (Fig. 3A and Movie S7). Where filaments have been trapped by a perpendicularly moving stream, a local mismatch in the orientation of filaments is present, which resembles that of a classical +1/2 defect (50, 51) (Fig. 3B). As filaments cannot crawl over each other, the conformation of a +1/2 defect acts as a “nematic wedge,” which stops filaments and traps them, as both their forward and lateral motion is prevented, causing an up-concentration of filaments in the core of the defect. Defects of an opposite charge (−1/2 charge defects) are also present in approximately the same quantity as positively charged defects. However, differently from the case of positive defects, the conformation resulting in −1/2 defects does not enforce density up-concentration as they do not trap filaments (Fig. 3B and Movie S8) and the core of the defect is devoid of filaments (52).

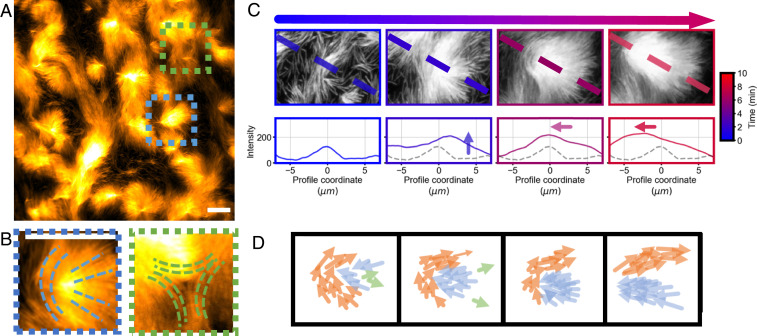
Fig. 3.

Formation of nematic wedges at high filaments’ density. (A) Structures forming at 1 μm bulk actin. (B) Close-up of locally forming +1/2 (Left) and −1/2 (Right) topological defects. The local alignment of filaments is also shown, with a mismatch present in the core of the defect. Positive defects up-concentrate filaments, whereas negative ones are empty. (C) Formation of a comet-like stream emerging from a +1/2 defect. The intensity profile along the dashed line is also plotted, showing the accumulation and then motion of the comet. Gray profile is the profile at the initial time as a reference. (D) Scheme of the nematic wedge-based polarity sorting. If a wedge is formed by a preexisting stream (orange), filaments (blue) get trapped inside it unable to escape and accumulate, forming locally a +1/2 defect. Filaments with opposite polarity (green) are able to escape. Thus, the polarity of filaments is locally sorted. When the obstacle is removed, filaments are now free to move again and form a comet-like stream. (Scale bars in A–C, 10 μm.)

Unlike defects in a two-dimensional nematic system (50, 51, 53), defects in different regions of space do not interact or merge, as they are not part of a same nematic layer that fully covers the surface. They instead independently form in locally dense regions, separated from one another by the low-density phase and thus can also independently dissolve when filaments are able to leave the region (Movie S7).

Negative defects eventually dissolve as filaments glide away along the sides of the defect. Positive wedge-like defects also eventually dissolve. However, they can still affect the further behavior of this system. Once the stream previously acting as an obstacle flows away, the wedge-like obstacle disappears, and filaments are free to move again. Looking at the intensity profile along the defect axis over time, one can indeed notice both a first phase of accumulation of filaments in the presence of a barrier and a second one in which the defect coherently moves as the barrier vanishes (Fig. 3 C and D). Since only filaments oriented in one direction had been trapped in the nematic wedge, as it dissolves it gives rise to a comet-like stream of filaments, a thick polar stream that moves persistently. As they arise from a +1/2 defect, filaments inside such a stream conserve a comet-looking alignment pattern. These streams move and can merge into other streams or get stuck again if they meet further obstacles.

Thus, nematic wedges act as a polarity sorting mechanism, whose origin is in the steric interaction between individual filaments, enforcing the tendency to be trapped in convex structures (5, 49, 54, 55), and in the topological structure of +1/2 defect, in the case of short actin filaments, which favors accumulation. As a consequence, streams forming in the high-density case are thick (more than 10 µm) and strongly polar, with most filaments traveling in the same direction (Fig. 4C).

Polarity of Observed Patterns.

At all densities, streams and vortices appear to be mostly composed of filaments moving in the same direction. To investigate the polar nature of the filaments’ direction of motion, we perform FRAP experiments in which an area of the sample is bleached and then observe the recovery of the fluorescence intensity (Fig. 4 A–C and Movies S9 and S10). When bleaching an area inside a stream, both at intermediate and high density, a recovery starting only from one side can be observed, indicating the polar motion of the filaments (56). We monitor this by measuring the asymmetry of the fluorescence recovery $P=\frac{|I_L-I_R|}{I_L+I_R}$, where $I_R$ and $I_L$ are the mean fluorescent intensities on opposite sides of the bleached area (Fig. 4D) averaged over the first 25 s after bleaching. Only one side of the area is expected to recover if the motion of the filaments is in a uniform direction ($P=1$), whereas a symmetric recovery would be the result if the motion within the structures is nematic (P ∼ 0). At all tested densities, we find values of P above zero. Streams are, indeed, found to be polar, despite the nematic nature of the binary interactions (Fig. 4D). At lower densities (up to ρ ∼0.83 filaments/μm²), we measured P ∼0.6 for streams, indicating polar motion of the filaments within them. The formation of parallel streams flowing in opposite directions next to each other can also be observed, leading to symmetric recovery (P ∼0) of the intensity if both parallel streams are included in the bleached region and to higher values of P otherwise. Vortices appear to be composed of filaments that mostly move coherently, even at lower densities (P ∼0.6 to 0.8). As the density is increased, streams too become noticeably composed of filaments, mostly moving in the same direction. Streams emerging from +1/2 defects also clearly move in a single direction with elevated values of P (P ∼0.8 to 0.9).

We attribute the fact that polar structures arise from a nematic microscopic interaction to the polar bias, introduced by the repulsion-dominated interaction, in particular to the stopping of filaments against transient obstacles. While alignment is nematic on the individual filaments’ scale, steric repulsion favors accumulation of filaments oriented in the same direction, thus polar sorting them (Figs. 1D and 2F). We note that the nematic wedge mechanism we described is particularly effective in enforcing local polar order by trapping filaments according to their orientation (Fig. 3).

Discussion

In summary, our experimental system shows that semiflexible filaments with hard volume exclusion interaction and alignment self-organize into locally polar phases. The observed structures arise from the interplay of filaments’ flexibility, thermal fluctuations, and a microscopic interaction preventing filaments from crawling over each other. Here, the membrane does not act as an immobile momentum sink during collision, which is usually assumed in the simulation of self-propelled rods and motivated in most experimental setups (5, 20), but rather, momentum is transferred to the lipid bilayer (31). This effectively limits the filaments’ ability to push upon collisions and leads to the sterically enforced stopping of filaments upon collisions and successive alignment. Stopping also plays a role in the accumulation of filaments in the presence of obstacles and, thus, in their polarity sorting. This allows breaking the microscopic nematic symmetry and is at the base of the formation of polar streams and vortices, which are different from those observed for driven actin filaments on hard substrates (7–9) and reminiscent of microtubules systems with slightly stronger steric interactions (10–12, 57). Simulations of flexible filaments with volume exclusion (26, 29, 30, 47, 58) also result in similar vortexes and stream-like structures, as observed here. The impossibility for filaments on a membrane to push may be the underlying reason for the higher stability of the observed polar phases compared to previous predictions in the context of self-propelled rod theory (20, 59–61). In some of these cases, topological defects were also observed but found to be unstable due to the accumulation of elastic energy. In the present experiments, however, orientational mismatches appear to be more stable due to the fluidity of the substrate, which can adsorb any excess stress.

Additionally, topological defects, already well studied in the context of active nematics (24, 51, 62–66), play a role not only in the accumulation of particles (52, 67) but also in shaping the dynamics. We find indeed that +1/2 topological defects act as “nematic wedges,” a particularly effective polarity-sorting mechanism. This hints that the shape of topological defects, dictated by the filaments’ mechanical properties (53), can have further importance in the self-organization of active systems composed of semiflexible filaments, even in contexts different from that of active nematics. The trapping in the self-organized nematic wedges resembles the collective trapping phase transition observed for motile polar granular particles by the presence of a V-shaped micropatterns (54, 55). This links the presented pattern formation to the phenomenon of MIPS for elongated objects (27, 58), with the main difference that the trapping of particles is not directly related to the local density but rather to the local nematic order.

Taken together, these observations constitute a step forward in the comprehension of the behavior of elongated active matter, starting from its microscopic interactions and from the constraints present on their alignment. Additionally, the ability to observe pattern formation on a fluid substrate has biological implications. The fluidity of the substrate is already known to influence the mechanical properties of two-dimensional bacterial and yeast colonies (66, 68). In the context of the cytoskeleton, understanding how a fluid substrate, possibly crowded by obstacles, influences collective activity is instrumental to understand the governing self-organization processes in the formation of the cell cortex and the possibility of force generation by membrane-bound motors (69–76).

Materials and Methods

Buffers.

Assay Buffer (A Buffer) is 25 mM Imidazole (pH 7.4), 4 mM MgCl2, 25 mM KCl, and 1 mM EGTA. One mM DTT and 2 mM ATP are added right before use.

F25 Buffer is 50 mM Tris (pH 7.5), 2 mM MgCl2, 0.5 mM ATP, 0.2 mM CaCl2, and 25 mM KCl. A total of 1 mM DTT is added right before use.

Proteins and Reagents.

Actin and skeletal muscle myosin were purified from rabbit skeletal muscle. No rabbits were directly involved in the study. Monomeric actin was stored at 4 °C in G-Buffer (2 mM Tris, 0.2 mM ATP, 0.2 mM CaCl2, 0.2 mM DTT, and 0.005% NaN3 at pH 8.0). HMMs were prepared by dialyzing ground rabbit skeletal muscle against the Myosin-buffer (0.6 M KCl, 10 mM KH₂PO₄, and 2 mM DTT) at 4 °C (77). Gelsolin was purified from adult bovine serum (Sigma Aldrich) (SI Appendix). Alexa Fluor 488 phalloidin, dark phalloidin, and streptavidin are purchased from Thermo Fisher. Lipids (Egg PC, DSPE-PEG [2000] Biotin, Texas Red DHPE) are purchased from Avanti.

Preparation of Glass Slides.

Glass slides and coverslips (Roth) are sonicated for 20 min in a 3-M NaOH solution and then rinsed five times with double-distilled water. Afterward, they are etched for 2 min in Piranha solution (2:1 sulphuric acid: hydrogen peroxide) and then rinsed in distilled water, in which they are stored. We stress that Piranha solution should be handled with care. After cleaning, slides and coverslips are used within a week. Right before formation of the membrane, an ∼50-µl observation chamber is made using a stack of three parafilm stripes as spacer.

Formation of a Supported Lipid Bilayer.

SLBs are formed according to previous protocols (31, 38). Briefly, a 20-mM solution of lipids (99.5% Egg PC and 0.5% DSPE-PEG [2000]-biotin) in chloroform is dried under a nitrogen stream and left in a vacuum chamber for at least 1 h in order to evaporate the solvent. When the labeling of the lipids was necessary, a small amount (0.05%) of Texas Red DHPE (Avanti) was added to the mix. The resulting lipid film is then resuspended to 2 mM in phosphate-buffered saline (PBS) (pH 7.4), sonicated for 30 min, and then extruded 10 times (using an Avanti Mini Extruder with 10-mm filter supports and a 100-nm pore Whatman membrane) in order to obtain small unilamellar vesicles (SUVs). SUVs are then incubated for 10 min inside the observation chamber and washed with at least a 10-fold volume of PBS, then with a twofold volume of A Buffer. SUVs are stored on ice and used within a week.

Preparation of the Assay.

Actin filaments are obtained by incubating for 45 min at room temperature 20 µM G-Actin in F25 Buffer together with 50 nM Gelsolin and 10 µM labeled phalloidin.

Enzymatically inactive bHMM heads are eliminated by centrifuging 2 µM of HMM with 10 µM of prepolymerized phalloidin-stabilized F-Actin (1:2 phalloidin:G-Actin ratio) in saturating ATP conditions (2 mM in A Buffer) at 4 °C, 120,000 × g for 30 min. Afterward, HMM is incubated on ice with streptavidin in a 1:1 ratio in A Buffer.

To bind motors to the membrane, 200 nM of streptavidin–bHMM clusters in A Buffer are incubated in the observation chamber for 5 min and then rinsed.

Before the start of the experiment the desired actin concentration is incubated in A Buffer for 5 min together with 0.2% methylcellulose in the observation chamber, then rinsed with A Buffer. To start the experiment, 2 mM ATP and 0.2% methylcellulose in A Buffer is inserted in the chamber. To avoid oxidation damage, 2 mg Glucose-oxidase (Sigma) and 0.5 mg Catalase (Fluka) with glucose are also present. After sealing the chamber with vacuum grease, it is put on the microscope and observed. Images are acquired with a TIRF microscope (Leica DMi8 with Infinity Scanner using a 100× TIRF objective).

Filament Count and Collision Statistics.

The density of filaments is computed by manually counting the number of filaments in at least five independent square regions of side 5 µm, when the filaments’ distribution is still uniform in space. To measure the incoming and outcoming angle of binary collisions, the orientation of each filaments is defined by their velocity. Orientations are measured from the raw data with Fiji’s line selection. The difference between the two orientations, shifted in a (0, 180) interval, is then plotted. Only collisions lasting more than 15 s are analyzed, and the orientation of the filaments is computed right before collision and either after the two filaments are clearly detached or, in the case of persistent alignment, after they have been in contact at least 10 s.

Analysis of Streams’ and Vortices’ Curvature.

Streams and vortices are manually selected with a segmented line with Fiji. To compute the local curvature, a spline fit with a two-pixel interval is performed to the selected line and the best fitting radius is computed by a Python script, considering at each point the five closest points for the fit. The same line selections are used to compute the length distribution of streams by integrating the geometric distance between points of the spline fits.

Histogram of Densities.

To estimate the local density and compute its distribution, images are first preprocessed with a Gaussian filter to eliminate background intensity, and then, an automated thresholding algorithm is applied to set the background to zero. Images are normalized by the total integrated intensity, which is assumed to be proportional to the total density and thus should be kept constant. Finally, the intensity of the image is integrated inside regions of size 4.8 × 4.8 µm, each separated from the other by 2.4 µm. The distribution of such values is then computed.

FRAP Experiments.

To measure the diffusion coefficient of the supported membrane, we use the method from refs. 31, 37. Briefly, a rectangular-shaped region is bleached, and the recovery of fluorescence intensity is monitored. To correct for additional bleaching during recovery, the intensity is divided by that of a reference region outside the bleached area. The recovery curve is fit with a Python script using the function suggested in ref. 37. A total of 14 different experiments are performed on two different bilayers. In the case of FRAP experiments for the actin system, the experiment is carried out using Leica’s infinity scanner. Again, a region of the desired shape is bleached, and recovery is observed. The region is arbitrarily chosen to match the shape of the stream of filaments. In this case, recovery is measured for two opposite regions along the filaments’ direction of motion and the maximum values from the first few frames are used in order to quantify the polarity (56).

Data Availability.

The movies and scripts data have been deposited in Zenodo (DOI: 10.5281/zenodo.3983553).