Network motifs involving both competition and facilitation predict biodiversity in alpine plant communities

Significance

Biodiversity is driven by complex associations among species, but ecologists often look only at competitive or facilitative interactions either independently or only for few species at a time. Using a large dataset of mountain ecosystems encompassing more than 2,000 species across the globe, we analyze the prevalence and importance of both positive and negative associations among plants. Our findings indicate that facilitation and competition between plant species must be studied together in order to explain biodiversity change.

Abstract

Biological diversity depends on multiple, cooccurring ecological interactions. However, most studies focus on one interaction type at a time, leaving community ecologists unsure of how positive and negative associations among species combine to influence biodiversity patterns. Using surveys of plant populations in alpine communities worldwide, we explore patterns of positive and negative associations among triads of species (modules) and their relationship to local biodiversity. Three modules, each incorporating both positive and negative associations, were overrepresented, thus acting as "network motifs." Furthermore, the overrepresentation of these network motifs is positively linked to species diversity globally. A theoretical model illustrates that these network motifs, based on competition between facilitated species or facilitation between inferior competitors, increase local persistence. Our findings suggest that the interplay of competition and facilitation is crucial for maintaining biodiversity.

Identifying the processes that maintain natural biodiversity is a longstanding goal of ecology (1–4). Theoretical and empirical explanations of coexistence in plant communities have largely proceeded along two parallel lines: one focused on competition (5–7) and the other on facilitation (8–10). Regarding the former, recent theoretical models highlight the role of intransitive competition in preventing individual plant species from excluding inferior competitors (7, 11). Regarding the latter, studies have shown that key plant species (ecosystem engineers) can support many other species through the amelioration of local environmental conditions, a process widely referred to as direct facilitation (12–15). However, focusing on either competition or facilitation independently may be inadequate for fully understanding species coexistence. In fact, the balance between positive and negative effects plays a crucial role in regulating nutrient flow and driving population and community response to environmental change (2, 13).

There is substantial evidence indicating that both competition and facilitation occur simultaneously within the same communities (16, 17). For instance, facilitated species may compete against one another (18), or species can facilitate each other in ways that outcompete other species (19, 20). Yet, because facilitation and competition are rarely considered together at the community level, we have little understanding of the degree to which the interplay of competition and facilitation affects biodiversity. A recent empirical study found that the overall frequency of positive and negative associations between plant species was only weakly correlated to plant diversity in drylands (21). It is unknown, however, whether it is the combination of positive and negative associations at fine spatial scales (orders of centimeters) that matters for biodiversity maintenance. This expectation is consistent with theoretical evidence on the impact of network modules on community dynamics (22).

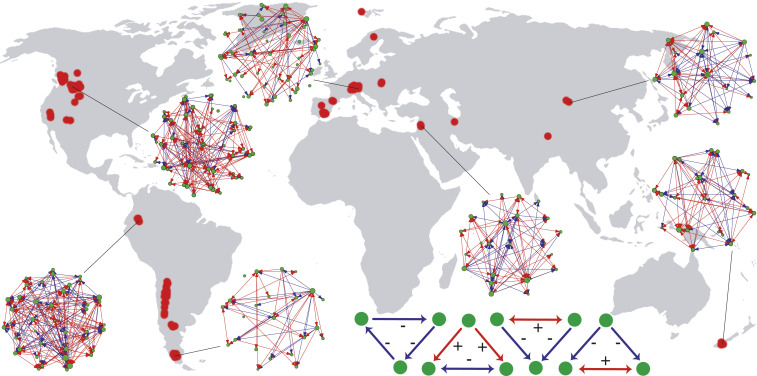
Here, we explore the prevalence and importance of community-level positive and negative associations among species in a global set of alpine plant communities. We analyzed whole-community population data (abundance of individuals per species) for 166 alpine plant communities at 83 sites worldwide (10) (Fig. 1). The dataset includes 2,252 plant species and more than 13,000 observations. Within the dataset, microhabitats with and without ecosystem engineers (an average of 81 paired plots per site) are treated separately (10, 14). We inferred positive and negative associations among all plant species using a Bayesian model in which the expected population size of a species is the sum of proportional changes in the population size of all other species (ref. 23; see Materials and Methods).

Fig. 1.

Global map of alpine plant networks studied here. Red dots on the map indicate the spatial location of the networks, with a few networks plotted for reference. In the networks, green dots represent plant species, and blue and red arrows represent negative- and positive species associations, respectively. Dot size is proportional to species abundance. The four network modules analyzed here are represented at the bottom of the figure, from left to right: intransitive competition, facilitation-driven competition, and competition-driven facilitation 1 and 2.

According to Abrams (24) and Wootton (25), and following the plant ecology literature (12, 15), network interactions derived from species associations are defined according to long-term effects measured on population size. In general, it is hard to infer interactions from association data alone (20, 26). Still, we have confidence that inferred categorical associations are indicative of the long-term outcome of species interactions to a large extent because: 1) alpine plant communities are relatively simple and spatial patterns closely reflect the net effects of plant–plant interactions (8, 12, 15, 27); 2) population data (number of plants per species) were collected at a fine spatial scale on the order of centimeters, where direct interactions take place (4, 8, 12), minimizing the influence of environmental heterogeneity and maximizing the imprint of direct neighbor effects (17, 27); 3) each network was built for each microhabitat at each site, with species growing in the same homogeneous environmental conditions (temperature, soil, aridity, etc.) (10), thus excluding spatial gradients that might mask or confound the correct inference of interactions from plant–plant associations (26); 4) we used high-resolution community data (as opposed to presence/absence data) that allow us to derive robust estimates of plant associations (28), as demonstrated in the sensitivity analysis (SI Appendix, Data and Code); 5) in addition to having highly resolved local communities, the survey was also replicated on a global scale, which allows us to generalize our findings since patterns are observed over a broad range of environmental and biogeographic contexts, from tropical to arctic latitudes (Fig. 1); and 6) inference was carried out with a Bayesian model that describes association strengths among plants with a similar power to existing models of plant fecundity and growth (5). This includes joint-posterior distributions of parameters, which allows us to infer associations among many species at the community level (23, 28).

Results and Discussion

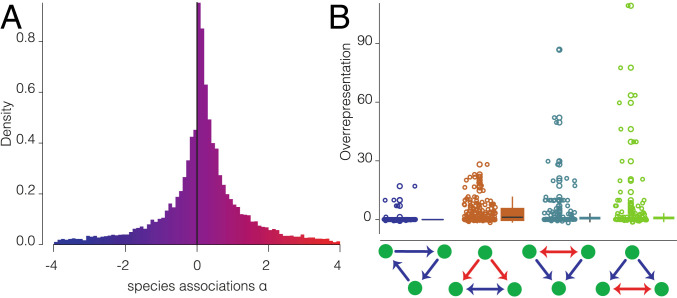
We found that the distribution of species associations ${\alpha }_{ij}$ across alpine plant communities is neither consistently positive, nor negative (mean = 0.028, 95% CI = −0.063–0.115) (Fig. 2A and SI Appendix, Fig. S1 and Table S1). In agreement with previous studies (17–21), these findings confirm that both positive and negative associations frequently cooccur within the same communities. Also, we found that biodiversity was explained by neither the median values of species associations ${\alpha }_{ij}$ (mean = 0.138, 95% CI = −0.153–0.432), nor the frequency of positive over negative associations (mean = 0.034, 95% CI = −0.050–0.117; see Materials and Methods). Although we observed a positive association of biodiversity with network connectance (mean = 0.440, 95% CI = 0.163–0.715), these results reflect previously noted limitations of certain macroscopic network properties for predicting biodiversity (21). This highlights the need to examine finer-scale patterns of species associations among more than two species.

Fig. 2.

Positive and negative species associations and overrepresentation of network modules. (A) The density distribution (y axis) of pairwise species associations ${\alpha }_{ij}$ (x axis) across the networks. (B) Overrepresentation (z score, y axis) of the four modules studied here (x axis). Data points, median lines, and quartiles are shown. While intransitive competition does not occur more often than expected by chance, the other three modules involving both facilitation and competition are overrepresented and can therefore be considered as network motifs.

Therefore, we next assessed whether particular modules involving positive and negative associations within species triads were more prevalent than expected by chance in our networks. We focused on network modules comprising three species for comparison with the well-known module representing intransitive competition (Fig. 1). Among all possible combinations of three-way positive and negative associations, we focused on four ecologically relevant network modules with a putative ecological interest and relevance in our system: 1) intransitive competition (A→⁻B, B→⁻C, C→⁻A), when net direct competitive effects cannot be linearly ranked, leading to even competitive dominance (3, 7, 11); 2) facilitation-driven competition (A→⁺B, A→⁺C, ⁻B↔⁻C), when one species facilitates two other species that compete with each other (e.g., through direct facilitation by ecosystem engineers and juxtaposition of subordinate plants that compete with each other) (18); 3) competition-driven facilitation 1 (⁺B↔⁺C, B→⁻A, C→⁻A), when two species outcompete a third one facilitating each other (e.g., through cooperation via shared symbionts to exclude a competitor) (2); and 4) competition-driven facilitation 2 (⁺B↔⁺C, A→⁻B, A→⁻C), when one species outcompetes two others that facilitate each other (e.g., through the competitive exclusion from favorable assemblages of two species that cooperate when in more stressful conditions) (20).

Network modules that occur more frequently than expected by chance are referred to as network motifs and can be seen as the basic building blocks of complex networks (29–32). In line with our approach, the concept of network motifs has been extended to modules involving both antagonistic and mutualistic interactions (31). We identified motifs by measuring the departure of observed module frequency from chance expectations given by randomized plant communities and calculating standard z scores and empirical P values (29, 30; see Materials and Methods). Note that we randomized the original community-matrix data and then calculated the expected module frequency on the resulting networks (SI Appendix). This procedure is more robust than randomizing observed networks since it randomizes the actual data, i.e., the distribution of plants across each site, that are at the root of the inference process. Results remain qualitatively the same when using two alternative null models (SI Appendix, Table S5).

Our analyses indicate that intransitive competition did not occur more frequently than expected by chance [z = −0.24 ± 0.85 (mean ± SE); Fig. 2B], being overrepresented in only 3% of communities. Intransitive competition, therefore, appears to be rare in these plant communities. This pattern conflicts with theoretical predictions (3, 11) and observations (21), but is consistent with empirical results (33). A potential explanation for this divergence from theoretical expectations is that models focusing on intransitivity have assumed that all species interact exclusively via competitive interactions. Instead, our empirical findings suggest that real-world plant networks are characterized by the interplay between competition and facilitation (Fig. 2B and SI Appendix, Table S2). Indeed, facilitation-driven competition, and competition-driven facilitation 1 and 2 are overrepresented globally (z = 3.23 ± 0.85, 2.64 ± 0.85, 3.06 ± 0.85, respectively), being more frequent than expected by chance in at least 34% of the communities. These analyses reveal that network motifs incorporating both positive and negative associations prevail in alpine plant communities worldwide.

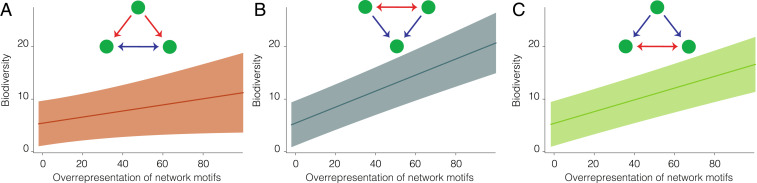
We next explored the extent to which particular network modules—including the network motifs identified by our previous analyses, along with intransitivity—explain global-scale variation in biodiversity. To accomplish this, we employed a hierarchical model that assessed the statistical association between biodiversity and the overrepresentation of network modules, after considering the effects of environmental conditions and general network descriptors (see Materials and Methods and SI Appendix). We found that all three network motifs that include both positive and negative associations predict biodiversity patterns globally, as increasing module overrepresentation is consistently associated with greater diversity (Fig. 3 and SI Appendix, Table S3). Furthermore, the strength and direction of such relationships is consistent over a wide range of environmental conditions (SI Appendix, Fig. S3). In contrast, we found that intransitive competition is not associated with biodiversity (SI Appendix, Table S3). In summary, intransitive competition showed no relationship with biodiversity, whereas network motifs including both competition and facilitation were positively associated with biodiversity. These findings suggest that the complex interplay of positive and negative effects may support high levels of biodiversity in alpine plant communities worldwide.

Fig. 3.

Biodiversity is associated with network motifs across alpine plant communities worldwide. (A–C) Relationship between biodiversity (average number of species per plot over a community, y axis) and overrepresentation of the three network motifs combining both positive and negative associations (z score, x axis). The figure shows estimated trends and 95% CI

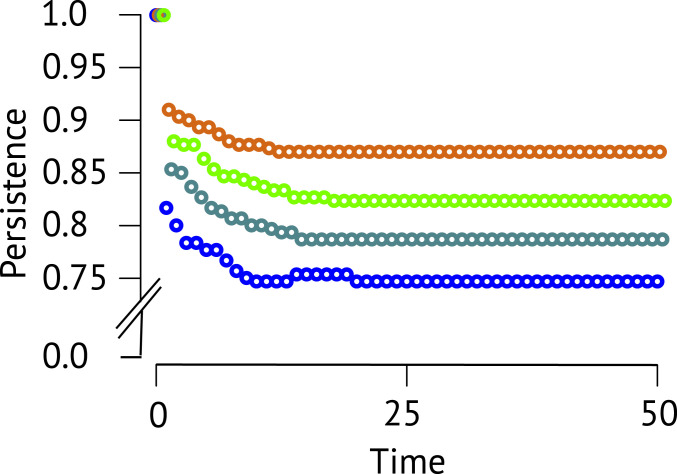
To shed more light on whether such motifs are directly contributing to greater biodiversity, as opposed to simply being correlated with it, we next investigated the role of network motifs in increasing species persistence. We used a theoretical model of community dynamics (6, 22, 24; see Materials and Methods) that phenomenologically describes positive and negative direct effects within the examined three-species modules on species persistence, measured as the fraction of species remaining at the end of a simulation timestep. We found that species persistence differed significantly among the four modules (Fig. 4 and SI Appendix, Table S4). Specifically, persistence was the highest for facilitation-driven competition (90% on average) and competition-driven facilitation 2 (85%), intermediate for competition-driven facilitation 1 (80%), and the lowest for intransitive competition (75%). The results of this model thus match the observed empirical patterns, reproducing the relationships between biodiversity and network motifs that include both competition and facilitation. This matching also suggests that the assumption of overall associations, estimated as long-term effects on population size at fine spatial scale, reflecting direct interactions is valid. Furthermore, our results provide evidence that, compared to intransitive competition, the combination of positive and negative effects most enhances community persistence. The current model represents a first, basic theoretical approach to understand the consistency and plausibility of our empirical results, which shall encourage the exploration of more complex dynamics.

Fig. 4.

Effects of network modules on local persistence. Mean persistence values (y axis) over time (x axis) are shown for each module (blue for intransitive competition, red for facilitation-driven competition, green for competition-driven facilitation 1, and yellow for competition-driven facilitation 2).

Taken together, these findings suggest that modules based exclusively on competitive interactions are neither widespread nor important in alpine communities worldwide. Instead, modules including both facilitation and competition prevail in these communities, supporting biodiversity and promoting species persistence and coexistence locally. We suggest that competition between facilitated species and facilitation between inferior competitors can stabilize plant communities. For instance, as with facilitation by perennial ecosystem engineers of annual subordinate plants (12, 18, 19), competition among facilitated plants may keep the system stable by setting an upper boundary to the growth of subordinate plants. Such regulation may prevent facilitated species to outcompete their facilitator. Analogously, facilitation among outcompeted plants may boost the populations of these otherwise excluded species.

It is important to note that the nonprevalence of intransitive modules, in which at least one generally inferior competitor outcompetes a generally superior competitor, does not imply the absence of other “indirect” competitive or facilitative processes. “Indirect modification” of interactions by ecosystem engineers can lead to substantially altered competitive outcomes and community organization (34). Furthermore, strong indirect interactions among facilitated species can only occur when these species reach high enough densities (19), and unlike in other systems, high plant density may rarely occur in examined alpine environments. Importantly, our network modules included only plants, overlooking the potential impact of other antagonistic and mutualistic partners. Although herbivory tends to be less important in patchy alpine vegetation than in closed grasslands at lower elevations (35), future studies should include other interaction types such as herbivory and pollination (36), and examine other biomes to assess how general are our results for other systems.

Measuring interactions among plants is challenging (3, 5, 20), particularly those among all species in communities occurring in slow-growing mountain ecosystems. As such, our study relied on correlations among plant populations at a centimeter scale, rather than interactions estimated through experiments. Experimenting with all possible combinations of species in pairs and triads was not feasible. Nevertheless, we maximized the utility of available data by fitting state-of-the-art inference models to a detailed, large, and global dataset on cooccurring populations at a remarkably fine spatial scale. This allowed us reconstructing plant association networks at the community level from local to global scales. Furthermore, fully defining an interaction is not always straightforward (24), particularly in plant communities (15). Nevertheless, measuring long-term effects on population sizes, such as we did, can overcome these limitations since: 1) plant–plant interactions do not involve the absolute transfer of matter and energy between partners, but result in relative effects on individuals and populations (12); 2) long-term effects provide a comprehensive picture on the persistence of real-world plant communities compared to many independent measurements of disparate mechanisms (15), superseding the context dependency of specific mechanism outcomes that vary in the short term (24); and 3) long-term population effects allow identifying global patterns and synthetizing over a broad range of environmental and biogeographic contexts.

In conclusion, our results support the hypothesis that the interplay between facilitation and competition can have an important role in the maintenance of biodiversity. Our study suggests that supporting groups of species that leverage the balance between competition and facilitation can be a valuable solution for promoting local persistence and mitigating species loss. This is particularly relevant for mountain ecosystems as they are facing fast changes in biodiversity (1). As many other natural and social systems involve both cooperative and antagonistic interactions among many interconnected members, these findings may prompt exploration of similar patterns and processes in fields beyond plant community ecology.

Materials and Methods

Study Sites.

Alpine plant communities were studied at 83 sites worldwide (10, 14, 37). We focused on patchy vegetation dominated by cushion plants that commonly function as ecosystem engineers by ameliorating local environmental conditions and thus facilitating other species (12). We adopted the following standardized sampling protocol. We recorded the number of adult individuals of each vascular plant species following a paired-plot design, where a plot consists of a single ecosystem engineer and an adjacent open plot of equal size randomly selected. At each site, the environment is relatively uniform within each microhabitat (14). Therefore, each plot within a community represents a different realization of the community assembly process (10, 27). The number of paired plots per site was on average 81 (±3 SE), with a minimum of 30. Average plot size at a site ranged from 137.3 cm² to 9,463.9 cm². At each site, plots were randomly distributed over an area of 500 m × 500 m. Rarefaction curves reached an asymptote at most sites, indicating that the composition of species assemblages was fully captured (10). Climate data of temperature and aridity were obtained from Worldclim (38). The variable temperature was the summer mean air temperature. The variable aridity was the ratio between average summer temperature and average total precipitation.

Species Associations.

For each study site, we considered abundance data of plant species occurring within ecosystem engineers and in adjacent open microhabitats separately (10, 14, 37). Thus, ecosystem engineers were solely considered as a microhabitat type in the subsequent analysis. Since experimental assessments of all possible combinations of plant interactions in a community context are not feasible, spatial patterns of species associations represent a good proxy for species interactions, provided the right spatial scale is met and individual-based data are measured (10–18, 20). Other microscale differences may have contributed to spatial patterns, including priority effects and minute differences in soil water content and disturbance.

We quantified species associations with a multivariate regression model of species abundances. Specifically, we used a Bayesian Poisson generalized linear model (bayesglm function in arm R package) (23, 28) based on plant abundance. We selected this inference model given: 1) its descriptive power of species interactions among plants, similarly to models of plant fecundity and growth (4, 5); 2) its predictive power of species performances across ecological communities (23); 3) it includes joint-posterior distributions of parameters, allowing us to incorporate communitywide processes and infer associations among many species at the community level (28); 4) the log-link function of the Poisson model avoids fitting negative species abundances when associations are negative; and that 5) it alleviates the problem of multiple testing since Bayesian inference, by not relying on P values and statistical significance but rather on posterior intervals, does not overestimate effect sizes and makes fewer claims with confidence than a frequentist approach (39).

In this inference model, the overall population size of species in a community is taken from a Poisson distribution. The abundance of a target species is a function of the abundances of all its neighboring plant species occurring in the community across all samples. The generalized linear model form allowed us estimating plant–plant associations ${\alpha }_{ij}$ as per capita effect on population size of neighboring species j on target species i across all species in the community. In other words, the parameter ${\alpha }_{ij}$ represents fine-scale proportional change in abundance of a target species i relative to changes in abundance of neighboring species j within the same microhabitat. This ${\alpha }_{ij}$ parameter reflects the definition of long-term effects on population size (24).

We retained only ${\alpha }_{ij}$ whose Bayesian Credible Interval excludes zero with a probability of 0.95. These species associations ${\alpha }_{ij}$ higher or lower than zero were then categorized as positive or negative network interactions from species j to i, respectively. As default prior for the parameters, we used a t-Student distribution with mean zero and one degree of freedom. Such a distribution has larger tails than a Gaussian one, thus allowing for stronger positive and negative parameters, and it is built on previous evidence of plant interactions in various ecosystems (3–5, 8). We retained ${\alpha }_{ij}$ for communities with at least five species (n = 162), for a total of 9,736 species associations.

To check the robustness of our approach, we ran a sensitivity analysis comparing this Bayesian Poisson framework to four additional frameworks (SI Appendix, Data and Code). Results show that neither the estimated magnitudes and signs of parameters nor the structure of the networks change across the dataset when: 1) individual plots are left out of analysis (SI Appendix, Fig. S4); 2) fitting a different distribution (e.g., negative binomial instead of Poisson) and changing the model (e.g., zero-inflated models) (SI Appendix, Fig. S5); 3) removing rare species (SI Appendix, Fig. S5); 4) changing the 95% CI cutoff to 90% (SI Appendix, Fig. S6). These additional analyses produce very similar networks to our original networks (SI Appendix, Fig. S4), and therefore yield no qualitative difference in our results and conclusions.

Network Motifs.

We built species networks composed of V_s plant species and E_αij directed associations between species i and j over S species in each community. Species associations E_αij were described by directed interactions taking values of 1, −1, 0, if retained α_ij was higher than, lower than, or equal to zero, respectively. These E_αij values thus correspond to positive, neutral, and negative associations between species in each network.

We quantified the frequency of four network modules formed by the associations among three species: 1) intransitive competition (A→⁻B, B→⁻C, C→⁻A) by using the triad census function in igraph R package (40); 2) facilitation-driven competition (A→⁺B, A→⁺C, ⁻B↔⁻C) by searching for a species j that had a positive association with two species i which had a reciprocal negative association with each other (SI Appendix, Data and Code); 3) competition-driven facilitation 1 (⁺B↔⁺C, B→⁻A, C→⁻A) and competition-driven facilitation 2 (⁺B↔⁺C, A→⁻B, A→⁻C) by searching for two species j that had a reciprocal positive association and both had a negative associations with a third species i (SI Appendix, Data and Code). In addition, nine other network modules involving three species associations were explored too: intransitive facilitation (A→⁺B, B→⁺C, C→⁺A), module 6 (A→⁺B, A→⁻C, B→⁻C), module 7 (A→⁻B, B→⁺C, A→⁻C), facilitation cascade (A→⁺B, B→⁺C, A→⁺C), dominance (A→⁻B, A→⁻C, B⁻↔⁻C), codominance (A→⁻B, C→⁻B A⁻↔⁻C), quasiintransitive competition (A→⁻B, B→⁻C, A⁻↔⁻C), complete competition (A⁻↔⁻B, B⁻↔⁻C, A⁻↔⁻C), and quasicomplete competition (A→⁻B, B⁻↔⁻C, A⁻↔⁻C). However, these nine latter modules were overrepresented in 3.7, 23.5, 17.9, 30.9, 20.4, 9.9, 6.8, 5.6, and 9.3% of communities, respectively, less than the former modules that we originally explored (with the exception of intransitive competition).

To assess whether network modules are overrepresented relative to chance, thus acting as network motifs (29), we randomized the original plant community data and repeated the same calculations for estimating species associations and building the resulting random networks. We randomized each community matrix (i.e., species × plot) using a well-established null model in community ecology (r00_ind in ref. 32). This randomization uses a quantitative shuffle method that preserves both species occurrence and overall species abundance while randomizing individuals among plots. This null model first transforms the quantitative matrix into binary, randomizes species distribution across the matrix while preserving the number of plots occupied, and finally randomly assigns species density per plot while preserving the overall abundance (41). We also tested two additional randomizations by keeping species relative abundance constant (c0_ind in ref. 41) and keeping both species relative abundance and plot density constant (vaznull in ref. 42). Results of biodiversity response to module overrepresentation remain qualitatively the same (SI Appendix, Table S5).

Then, we calculated the overrepresentation of network modules by means of the standard z score$=\frac{\left(obs-\overline{exp}\right)}{sd\left(exp\right)},$ where the number of each observed network module obs is compared with the mean and SD of the same type of module across 99 random networks (29). We also estimated the significance of observed patterns as P value $=1-\raisebox{1ex}{${{\displaystyle \sum }}_i^{sim}I[obs>exp]$}\!\left/ \!\raisebox{-1ex}{$sim+1$}\right.,$ where $I\left[obs>exp\right]$ is an indicator function that equals 1 if the observed module frequency was greater than the random value and 0 otherwise across 99 simulations plus one empirical value.

Statistical Analysis.

We used mixed-effects models (43) to test: 1) the distribution (mean and variance, two separate models) of pairwise species associations ${\alpha }_{ij}$ across environmental conditions (temperature, aridity, and habitat) (SI Appendix, Fig. S1 and Table S1); 2) the overrepresentation of network modules across environmental conditions (SI Appendix, Fig. S2 and Table S2); 3) the relative importance of network modules for biodiversity after considering effects of environmental conditions (temperature, aridity, and habitat) and general network descriptors (median species associations ${\alpha }_{ij}$, connectance, and frequency of positive over negative associations). Sites were included as random effects. Biodiversity was calculated as the mean number of species per plot across each community (10, 14). Connectance was calculated as $c=L/(S\times \left(S-1\right)),$ where L is the number of $E_{{\alpha }_{ij}}$ species associations in a community composed of S species. For discontinuity in the distributions of variables, temperature was classified as low ($temp\le 18\mathrm{℃}$), medium ($18\mathrm{℃}<temp\le 26\mathrm{℃}$), and high ($temp>26\mathrm{℃}$); aridity was classified as low ($arid\le 0.2\mathrm{℃}{\text{*H}}_2{\text{Omm}}^{-1}$), medium ($0.2\mathrm{℃}{\text{*H}}_2{\text{Omm}}^{-1}<arid\le 0.5$), and high ($arid>0.5\mathrm{℃}{\text{*H}}_2{\text{Omm}}^{-1}$). We used least-square means (44) for comparisons between treatment levels.

Dynamic.

To explore the role of network modules for biodiversity maintenance we used a phenomenological model of community dynamics. We considered modules in isolation using the following network matrices:

$$\text{intransitive}\hspace{0.17em}\text{competition}=\left[\begin{array}{ccc}0& -1& 0\\ 0& 0& -1\\ -1& 0& 0\end{array}\right];$$

$$\text{facilitation}-\text{mediated}\hspace{0.17em}\text{competition}=\left[\begin{array}{ccc}0& 0& 0\\ 1& 0& -1\\ 1& -1& 0\end{array}\right];$$

$$\text{competition}-\text{mediated}\hspace{0.17em}\text{facilitation}\hspace{0.17em}\text{type}\hspace{0.17em}1=\left[\begin{array}{ccc}0& -1& -1\\ 0& 0& 1\\ 0& 1& 0\end{array}\right];$$

$$\text{competition}-\text{mediated}\hspace{0.17em}\text{facilitation}\hspace{0.17em}\text{type}\hspace{0.17em}2=\left[\begin{array}{ccc}0& 0& 0\\ -1& 0& 1\\ -1& 1& 0\end{array}\right],$$

where $1$ and $-1$ indicate net positive and negative effects between species, respectively.

We then simulated community dynamics using a system of ordinary differential equations derived from a multispecies generalized Lotka–Volterra model (6, 13, 22, 24). This formalism phenomenologically describes changes in the abundance $N_i$ of species $i$ due to the presence of other species j in a community composed of $S$ species as:

$$\frac{\text{d}{N}_i}{\text{d}t}=N_i\left(r_i+{\displaystyle \sum }_{j=1}^S{A}_{ij}{N}_j\right),$$

where $A_{ij}$ is the rescaled per capita effect of species $j$ on $i$, with $A_{ij}=$ ${\alpha }_{ij}{r}_i/K_i$, where ${\alpha }_{ij}$ is the interaction strength, $r_i$ is the intrinsic growth rate of species $i$, and $K_i$ is the carrying capacity of species $i$. Parameters were randomly assigned as follows: off-diagonal entries ${\alpha }_{ij}$ (with $i\ne j$) of the matrix were sampled from the empirically observed distribution of ${\alpha }_{ij}$ values (Fig. 2A), with ${\alpha }_{ij}\in \left[-4,4\right]$; $r_i$ was sampled from a normal distribution with mean 0.5 and SD 0.1, truncated between 0.1 and 1; $K_i$ was sampled from a normal distribution with mean 5 and SD 1, truncated between 1 and 10. These values resemble the slow growth and low cover of alpine plants; initial conditions $N_0$ were set to 1; intraspecific interactions (diagonal entries ${\alpha }_{ii}$) were set to a constant −3. All simulations were run to 50 model timesteps.

We generated 100 random network modules for each type. For the numerical integration, we used Hindmarsh’s solver (45). We used generalized additive models (46) to analyze the effects of network modules on local persistence, calculated as the fraction of species that survive within each module at each timestep; time was included as a smooth function. Analyses were performed in R (47). Future studies shall address species-rich network dynamics incorporating physical disturbance, dispersal limitation with a competition—colonization tradeoff in metacommunity dynamics, and density-dependent crowding effects. Models should also consider that alpine plants are not simply consumers of resources but enrich soil organic matter and nutrients as well as physically stabilize the substrate.

Data Availability.

All study data are included in the article and/or supporting information.