Significance
Many organs have densely packed cells divided in subpopulations that display coherent and spatially differentiated behavior. Using yeast cells packed in a microfluidic device, constructed to mimic an organ structure with peripheral blood flow, we show that cells coupled via diffusion of metabolites can lead to spatially differentiated subpopulations with temporally synchronized behavior. A detailed mathematical model for each yeast cell simulated in its precise architectural location within the microfluidic system correctly predicts the cells’ behavior as a function of an external stress solution. Our results provide us with a mechanistic understanding of this system and indicate how a relatively simple mechanism can underlie a yet poorly understood cellular differentiation process.
Keywords: cell–cell communication, synchronization waves, glycolytic oscillations
Abstract
Many organs have internal structures with spatially differentiated and sometimes temporally synchronized groups of cells. The mechanisms leading to such differentiation and coordination are not well understood. Here we design a diffusion-limited microfluidic system to mimic a multicellular organ structure with peripheral blood flow and test whether a group of individually oscillating yeast cells could form subpopulations of spatially differentiated and temporally synchronized cells. Upon substrate addition, the dynamic response at single-cell level shows glycolytic oscillations, leading to wave fronts traveling through the monolayered population and to synchronized communities at well-defined positions in the cell chamber. A detailed mechanistic model with the architectural structure of the flow chamber incorporated successfully predicts the spatial-temporal experimental data, and allows for a molecular understanding of the observed phenomena. The intricate interplay of intracellular biochemical reaction networks leading to the oscillations, combined with intercellular communication via metabolic intermediates and fluid dynamics of the reaction chamber, is responsible for the generation of the subpopulations of synchronized cells. This mechanism, as analyzed from the model simulations, is experimentally tested using different concentrations of cyanide stress solutions. The results are reproducible and stable, despite cellular heterogeneity, and the spontaneous community development is reminiscent of a zoned cell differentiation often observed in multicellular organs.
In early studies on synchronized glycolytic oscillations of yeast populations, acetaldehyde (ACA) was proposed as the intercellular chemical mediator (1). ACA is a metabolite either produced by the yeast cells themselves (2) or externally supplied (3) and needs to be constrained at intermediate concentrations for effective communication. This is possible by working at high biomass concentrations, to keep ACA above a lower threshold level, combined with the addition of cyanide (), which binds ACA, to keep ACA below an upper threshold level. By local addition of glucose (GLC), macroscopic glycolytic synchronization waves can be induced (4–6) but not resolved at the single-cell level. Only recently, single-cell analysis has been achieved by using fixed cells on coated microscope slides (7, 8) and in alginate microparticles (9). While these approaches manage to obtain biochemical information at the single-cell level, their limited control on the environment prevents a full characterization of the interactions between the cells. Recently, we have used microfluidics to precisely control the flow fields and chemical concentrations surrounding yeast cells. This has permitted us to externally entrain the oscillations of single yeast cells by the periodic injection of ACA or (10, 11). However, the flow present in these microfluidic systems removes cell secretions, including the ACA mediator required to achieve cell–cell communication. While such an approach is important to study oscillations in isolated cells, it prevents studying the process leading to synchronization, which is dependent on intercellular communication. Similar balancing between flow and intercellular communication is necessary for the coordinated functioning of multicellular organs, where zonal differentiation into different cell types coexists with a peripheral blood flow. In recent years, microfluidic systems have been successfully applied in so-called organ-on-chip initiatives, where a well-defined environment with controlled convection terms and shearing forces enable differentiation of three-dimensional (3D) tissue (12, 13).
Here we implement a custom-designed diffusion-limited microfluidic chamber to host a mesoscopic cell culture. Such a design represents a wide range of diffusion-dependent human organs, i.e., the liver, kidneys, or pancreatic tissue. While controlling the extracellular environment to trigger the oscillatory behavior, we acquire biochemical information from every single cell. We observe glycolytic synchronization waves and, by employing tools from graph theory, identify the emergence of coupled subpopulations. By integrating a mechanistic model that incorporates the physical geometry and hydrodynamic conditions in the microfluidic chamber as well as the detailed biochemical intracellular reactions (11, 14, 15), we analyze how the diffusion and reaction of intercellular metabolites couple the oscillation phases of neighboring cells. This coupling leads to the appearance of waves and subpopulations. The mechanistic understanding of the spatiotemporal behavior of the model organism gives insights into the possible role of cellular synchronization in collective cell behavior, as observed, for example, in insulin secretion regulation (16–18).
Results
Glycolytic Oscillations in a Microfluidic Environment.
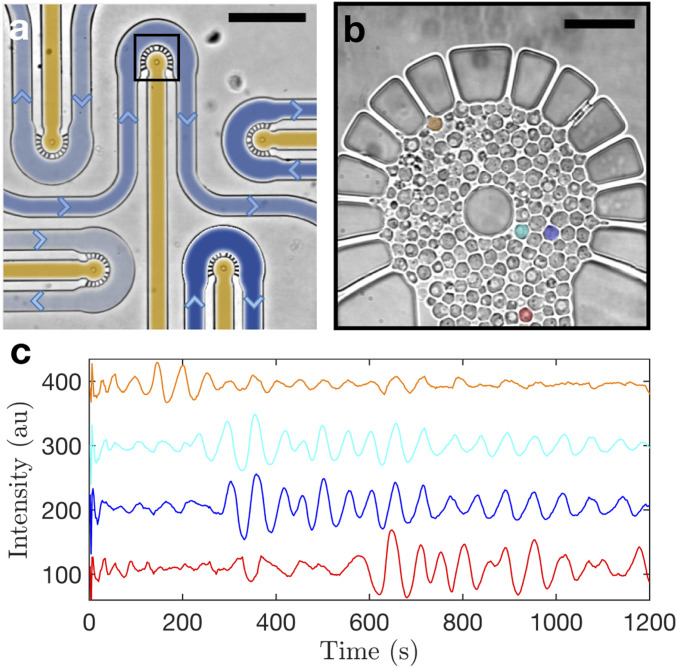
We designed a microfluidic environment to trigger and track glycolytic oscillations in an array of yeast cells (Saccharomyces cerevisiae) with single-cell resolution (Materials and Methods). Fig. 1A shows an image of the microfluidic chip with five chambers, one of which is highlighted by the black box and zoomed in on in Fig. 1B. The use of a single microfluidic device with multiple chambers permits us to load cells from a single batch and expose them to a range of stress solution concentrations in parallel, thus avoiding artifacts that might arise when performing experiments sequentially due to confounding factors such as cell storing time. As shown in Fig. 1A, each cell chamber has an inlet channel (shaded in yellow), which we use to load the yeast cells into the chamber, and a perfusion channel (shaded in blue), which we use to expose the cells to a GLC and solution with various concentrations of (indicated by the different shades of blue). Importantly, the perfusion occurs by diffusion in quasi-static flow conditions through a series of diffusion apertures between the perfusion channel and the cell chamber, as can be seen in Fig. 1B. In this diffusion-limited cell chamber, the ACA produced by the cells is not washed away by convection and can mediate the cell–cell interactions.
Fig. 1.
Glycolytic oscillations are affected by cell position in the microfluidic chamber. (A) Yeast cells from a single batch culture are loaded through the yellow-shaded inlet channels of the diffusion chambers. They are then exposed to GLC and different concentrations of (weighted blue shades) and NADH autofluorescence signals are detected in individual cells. The length bar is 200 m. (B) Zoom-in of a loaded cell chamber highlighting four representative individual cells at different locations. The length bar is 20 m. (C) For illustration purposes, the processed time series of the NADH concentration at the representative cells color-coded in B is shown to exemplify the influence of location on the metabolic signals. The data correspond to a 12 mM exposure case, and the intensity of the signals is shifted along the y axis for visualization purposes. The amplitude bursts of the representative NADH signals at different time points indicate relative delays between cells located in the upper and lower parts of the chamber. The strong oscillations start from about 100 s in the orange cell, while the cyan and blue cells start around 300 s, and finally, the red cell at the bottom of the chamber starts approximately at 500 s.
Fig. 1B zooms in on a loaded cell chamber where the single yeast cells can be clearly seen. We grow, harvest, and starve the yeast cells to obtain a strong oscillatory behavior in response to GLC addition (Cell Preparation). The cells are loaded at a controlled density in all cell chambers using a precision multisyringe pump. Afterward, we inject the stress solutions containing 40 mM GLC with 8, 12, 16, 20, or 24 mM using a second multisyringe pump. We provide a constant stress solution supply for 20 min; during this time, GLC and diffuse into the cell chambers through the diffusion apertures and are progressively consumed by the cells leading to an initial concentration gradient that decreases over time. GLC consumption is linked to the production of reduced nicotinamide adenine dinucleotide (NADH), an intermediate metabolite, which can be detected on an individual cell basis due to its autofluorescence (Materials and Methods and SI Appendix, Movie S1). These measurements can be used to track other coupled metabolite signals such as ACA (11).
Depending on the cells’ position in the chamber, they start to oscillate at different times. To illustrate this time delay between the metabolic signals across the chamber, NADH time series of four representative cells in a 12 mM case are shown in Fig. 1C. The orange cell is located next to a diffusion aperture and starts to show oscillations with a transient increase in the amplitude about 100 s after the stress solution injection; the cyan and blue cells are located farther away from the diffusion apertures, and they display sustained oscillations with an amplitude increase at about 300 s; and the red cell is even farther away from the diffusion apertures, and its strong oscillations appear only after about 500 s. The fluctuations of these NADH signals reflect the periodicity of the glycolytic metabolic cycles. The signal amplitude is affected by the local concentration (1, 15, 19, 20), which follows the diffusion gradient away from the diffusion apertures: the amplitude of the orange cell signal is smaller than those of the cyan and blue cells, which in turn are smaller than that of the red cell.
Finally, local synchronization between cells occurs because of their secretion and exchange of ACA, which determines the local cell–cell coupling (14, 15). For example, the cyan and blue cells are close to each other, and thus, their signals are highly synchronized for the whole duration of the experiment. For the 12 mM case in Fig. 1B, all cells are induced to transient oscillatory states where the oscillation intervals and amplitude strength depend on the cell location in the chamber. This is due to the and ACA concentration exposure of the cells, as previously reported (10).
Cell–cell synchronization.
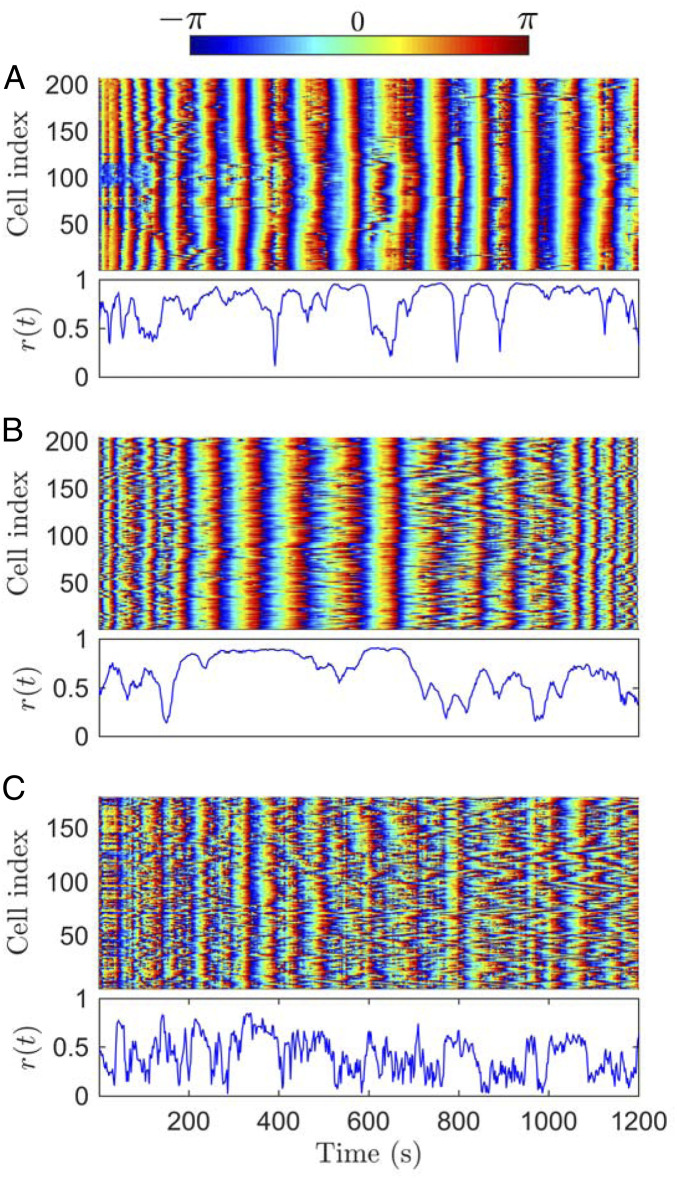
For the synchronization analysis of the NADH signals, we extract instantaneous phases of the discrete Hilbert transforms of the time series (color-coded phase plots in Fig. 2). From these phases we calculate the time-dependent order parameter (21) (Materials and Methods). The order parameter quantifies the degree of synchronization and is normalized between 0 and 1, where a value of 1 means that the entire cell array oscillates in phase (lower plot in each of the panels of Fig. 2).
Fig. 2.
Coupling between the glycolytic signals of the single cells. Instantaneous phases (– to ) of the NADH autofluorescent signals for all cells (Top) and normalized order parameter (Bottom) when glycolytic oscillations in yeast cells are triggered using (A) 12, (B) 16, and (C) 20 mM combined with 40 mM GLC. (A and B) At 12 and 16 mM concentrations, the instantaneous cell phases feature global patterns across the cell array corresponding to . The closer the order parameter to 1, the higher the temporal cell synchronization, while a lower order parameter describes cell desynchronization. (C) At high concentrations, this synchronization is lost, reflected in the low values of the order parameter. Each panel shows a representative example from in total five experiments (see SI Appendix, Figs. S3–S7, for the repeat experiments).
When the concentration of in the stress solution is sufficiently high (12 mM [Fig. 2A] and 16 mM [Fig. 2B]), the majority of the cells exhibit sustained oscillatory behavior and synchronization, which is shown by the fact that describes intervals very close to 1. In both cases, features some minima, which reflect temporary incoherent behavior between the oscillating cells.
At higher concentrations (e.g., 20 mM ; Fig. 2C), the cells still oscillate, but the phase plot does not show any global synchronization between them, which is reflected in the fact that is consistently smaller than 1 and fluctuates for the whole duration of the experiment. Under these conditions, the higher rate of binding to cyanide lowers the CA concentration, which leads to a decrease in the coupling between the cells, disrupting the synchronization. The results for the 8 and 24 mM experiments are shown in SI Appendix, Fig. S2, and four additional repeat experiments are shown in SI Appendix, Figs. S3–S7.
Synchronization Communities.
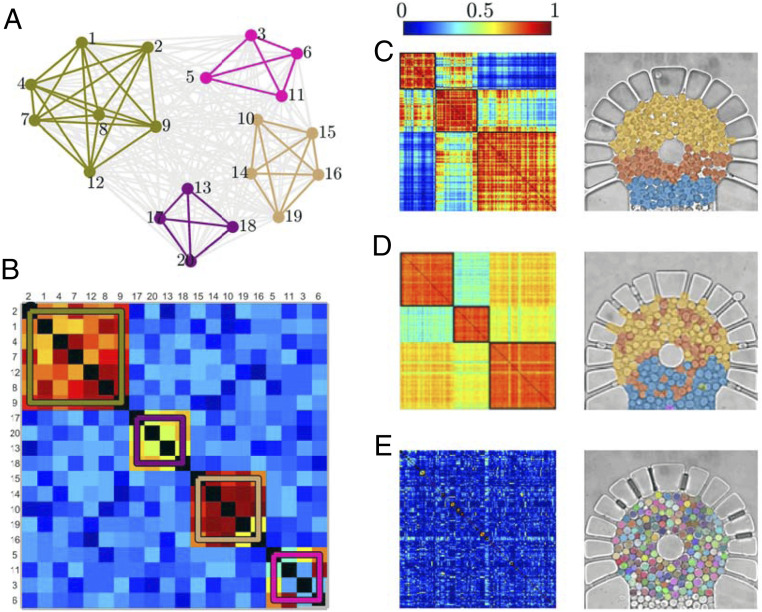
To test for the existence of locally synchronized communities within the population, we make use of graph theory and community analysis (Graph Construction and Community Analysis). Using a technique that is commonly employed in studying connectivity between brain regions (22), we determine the coupling strength between cells based on the degree of synchrony in their glycolytic signals. The resulting graph can be represented as a series of nodes (cells, each one tagged with a number used for identification purposes) and edges (correlation) (Fig. 3A) or, more conveniently for analysis purposes, as an adjacency matrix (Fig. 3B). The latter is a square matrix where each entry represents the strength of the connection between the nodes corresponding to its row and column indices.
Fig. 3.
Synchronization communities. (A) In a functional graph analysis, the signal correlation between different nodes provides a measure of the strength of connectivity between them. In the resulting graph, it is possible to identify communities of nodes (colored subgraphs) that are well connected with each other but poorly connected to nodes belonging to different communities. (B) Such community structure is reflected in the adjacency matrix representing the graph. Note that the order of the nodes has been rearranged to more clearly highlight the community structure. (C–E) Similarly, from the NADH autofluorescent signals of the cells (each tagged with a number used for identification purposes), we construct adjacency matrices and overlay the resulting communities on the images of the corresponding cell arrays for (C) 12, (D) 16, and (E) 20 mM . The figure shows a representative example from five experiments (see SI Appendix, Figs. S3–S7, for the repeat experiments).
A graph can be divided into communities so that the nodes within each community are more strongly connected with each other than with the rest of the graph. We identify the communities using the Louvain algorithm (23). For example, we show the color-coded communities on the schematic of the graph in Fig. 3A and on the adjacency matrix in Fig. 3B.
Fig. 3 C–E show the adjacency matrices and the corresponding communities overlaid on the cell images for cell arrays exposed to different concentrations. When exposed to 12 mM (Fig. 3C), three well-defined communities form. The community in yellow covering half of the circular chamber is radially exposed to the stress solution through the diffusion apertures. Hence, these cells experience simultaneous triggering of the oscillations. The community in red is triggered by the resulting concentration of the stress solution that passes through the yellow community and the lateral diffusion apertures. Consequently, the oscillations appear with a delay with respect to those of the yellow community. Finally, the cells in blue are not directly exposed to the diffusion apertures. This community shows the longest delay and will be exposed to lower concentrations of GLC and than the two prior communities. Each of the communities remains synchronized due to the local exchange of ACA.
When the concentration is increased to 16 mM (Fig. 3D), the boundaries between the communities become less defined. The yellow community (top half) forms similarly to the 12 mM scenario. However, a second community (red) appears with scattered cells at different locations in the top half of the cell chamber. At 16 mM , the higher rate of binding of ACA to leads to a lower ACA concentration, which reduces the coupling between the cells. With a less defined boundary, a third community (blue) appears where cells are not exposed to diffusion apertures.
At 20 mM (Fig. 3E), the coupling between the cells is reduced even more, resulting in uncorrelated behavior, and the community structure breaks down. SI Appendix, Figs. S3–S7, show the community structures for the repeat experiments, where the overall spatial distribution is consistent for each concentration.
Glycolytic Synchronization Waves.
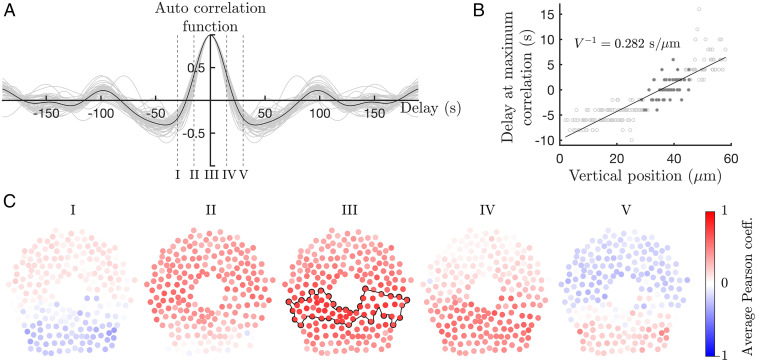
SI Appendix, Movie S1, shows the NADH autofluorescence spatiotemporal distribution across the cell array. To obtain a temporal description of the arising glycolytic wave, we calculate the autocorrelation function of every NADH signal within a community of cells identified with the modularity analysis. The gray lines in Fig. 4A show the autocorrelation curves of the individual cells and the black line their mean value for the community located in the middle region of a cell array exposed to 12 mM (dark gray in Fig. 4B and outlined by the black line in Fig. 4C). The indicated time interval contains three periods of oscillation at a fixed position, revealing the inherent frequency of the glycolytic oscillation. Then, we characterize the traveling wave by calculating the delayed cross-correlation between the NADH signals in one community of cells and the rest of the cell array (Graph Construction and Community Analysis).
Fig. 4.
Temporal and spatial propagation of a glycolytic synchronization wave. (A) The autocorrelation function of a single community (outlined by the black line in C, III), shows the temporal description of oscillatory behavior at a specific region in the chamber exposed to 12 mM . The gray lines show the autocorrelation functions of each cell in the community, and the black line is their average. (B) The linear behavior of the delays at maximum correlation with respect to the second community (dark gray) as a function of the vertical position of the cells (top to bottom), confirms the spatial evolution of a traveling wave. Furthermore, the slope of the linear fit corresponds to the inverse of the wave velocity, where 3.5 m/s. (C) The spatiotemporal evolution can be displayed using the average delayed and normalized cross-correlations between the second community of synchronized cells (enclosed with black line) and every cell present in the chamber (red circles) for a cell array exposed to 12 mM . The delayed Pearson correlations are calculated with delays from –20 to +20 s (indicated by I to V in A) and feature a series of maxima that propagate from top to bottom. The shape of this glycolytic wave depends on the chemical diffusion profiles of stress solution and secreted metabolites, and it is influenced by the geometrical constraints of the device. See also SI Appendix, Movie S4.
The resulting wave describes the transition between the communities as a function of their relative delays, giving a phase relation between them. Fig. 4B shows the delay at maximum correlation as a function of the vertical position of the individual cells (top to bottom). The linear behavior of this relation portrays a constant velocity, 3.5 m/s, of the wave propagating down the chamber. Fig. 4C shows five specific frames of the spatiotemporal evolution in a cell array exposed to 12 mM . SI Appendix, Figs. S8–S9, show the corresponding results for communities 1 and 3 (top and bottom), respectively, when a cell array is exposed to 12 mM . The high values of the normalized cross-correlations (dark red) travel from the region mostly exposed to the diffusion apertures, to the region containing the cells farther away from the direct exposure to the stress solution. The transition from a minimum in a community average correlation (Fig. 4C, I) to the next minimum (Fig. 4C, V) gives the spatial description of a traveling wave across the chamber as a function of the relative delay.
Due to the cell heterogeneity and the discrete nature of the cell monolayer, local cell–cell interactions show small variations in the wave front shape. However, the overall synchronization wave can be tracked despite these deviations. For more detailed description of the wave propagation, the transition between intermediate delay values can be seen in SI Appendix, Movie S4.
Simulations.
We simulate a 2D array of cells with the same structure as the experimental one. We calculate the time-dependent concentrations of GLC, , ACA, and ethanol (ETOH) (SI Appendix, Movie S2) together with all of the intracellular metabolites.
To test the ACA coupling, we use a previously published detailed enzyme mechanistic model (15) to simulate glycolysis in each cell as a set of ordinary differential equations. Transport and diffusion of extracellular metabolites are simulated using partial differential equations with the physical characteristics of the microfluidic chamber determining the boundary conditions (Numerical Simulations). We then extract the glycolytic signals (NADH concentration) for each cell and analyze them as in the experimental data (Synchronization Analysis and Graph Construction and Community Analysis). SI Appendix, Fig. S1, shows the NADH instantaneous phase distribution and the community structure for the simulated cases of 20, 24, and 28 mM . As the concentration is increased in the cell chamber, the communities show less defined boundaries, in good agreement with the experimental data (Fig. 3), albeit that slightly higher cyanide concentrations are used in the simulations. concentrations of 24 and 28 mM induce transient oscillations leading to a steady state (SI Appendix, Fig. S1 B and C).
The simulated time-dependent ACA distributions for external and internal concentrations (SI Appendix, Movie S2) reflect an adaptation to traveling waves. The initial oscillations display uncorrelated behavior that gradually transforms to periodic propagation across the cell array. To have a quantitative comparison with the experiments that displays a clear wave formation, the wave velocity was extracted for the 12 mM case (m/s) (SI Appendix, Fig. S10)). The simulation results are in good agreement with the experimental results although wave fronts in the simulations show a more continuous profile than is observed in the experimental data. This is most likely due to an incomplete capture of cellular heterogeneity in the model.
The high external GLC concentration supply (40 mM) induces a fast diffusion until homogeneous covering of the complete monolayer (SI Appendix, Movie S3). In contrast, the diffusion of shows a quasi-constant distribution profile to which the ACA wave front shapes adapt. The periodic fluctuations given by the external ACA and reaction show negligible influence on the levels as it has a much higher absolute concentration.
Discussion
We studied the coupling between individually oscillating cells in yeast at a single-cell level. First, we detected the single-cell metabolic responses from yeast cells in a microfluidic device, designed to resemble a diffusion-based mechanism in human organs. Second, we identified synchronized communities and tracked the synchronization waves using graph theory. Third, the underlying mechanism for cell–cell communication was tested in a validated mechanistic model for individually oscillating yeast cells, where each glycolytic network is linked to the architecture and physics of the microfluidic system.
The implemented microfluidic device permits us to control the concentration of extracellular chemicals required to trigger glycolytic oscillations, ensuring a constant supply of GLC and by direct diffusion. After addition of the stress solution, the start of oscillations in individual cells is dependent on their position in the cell chamber. The spatiotemporal distribution of the concentration influences the overall degree of synchronization, which is reflected in the time evolution of the extracted instantaneous phases and order parameter. Furthermore, even in the presence of low overall values of synchronization, there can be communities of cells that are synchronized at the local level, which we have identified using graph theory analysis. In addition, we have shown that the lateral metabolic coupling between individual cells can induce metabolic synchronization waves.
In ref. 11, it was demonstrated, through experimental observation and analyses using a detailed mechanistic model, that single oscillating cells can adapt their phases to external ACA signals. These signals are transduced through the system of cofactors that regulates the activity of phosphofructokinase and leads to a phase shift to allow synchronization. For globally coupled diffusion-reaction oscillators, cluster patterns (24) can be used to describe the behavior of such a system. When combined with diffusion, cluster patterns also display zones of identical behavior but still rely on global coupling. In our system, as the concentration of the coupling agent is regulated by the glycolytic cycle, the entrainment of the oscillation phase propagates across the chamber. Therefore, the coupling mechanism presented herein can be described by a traveling wave. In addition, our findings corroborate the observations of previous studies on macroscopic glycolytic waves (4–6, 25) and explain these waves in terms of metabolic coupling between individually oscillating cells. However, the wave velocity discrepancies between our study and these population-level experiments can be attributed to the distinct hydrodynamic conditions influencing ACA and transport during the experimental procedures. Here we show that the spatiotemporal dynamics of synchronization waves in a population are well described by the detailed mechanistic model (constrained to the physical conditions of the cells in the microfluidic chamber) showing that the proposed ACA coupling between the cells is sufficient for the observed collective behavior. The presented numerical simulations describe how synchronized cell communities can exist in complex arrangements and architectures resembling organs and lead to function-based zonation. The simulations give a general description of the mechanism behind synchronization and community structure formation between single cells. The obtained wave velocities from the simulations are in good agreement with the experimental analysis, even though they do not replicate exactly the results observed in the heterogeneous conditions present in the experimental scenario. This is also reflected on the slight spatial deviations in the synchronized subpopulation arrangement.
The combination of detailed mechanistic models at single-cell level, with the experimental analyses of collective synchronized responses at the population level, can also be used for studying the spatiotemporal dynamics present in coordinated organ functions, such as in insulin production by pancreatic cells (16, 26–29). In such a cell system, the coordination of synchronized cells is vital for the required pulsatile insulin secretion. Furthermore, the presented analysis can be applied to other biological systems that display synchronization of individual oscillators, e.g., wave propagation in the heart leading to muscle contraction and synchronized oscillatory phenomena in groups of neurons.
Materials and Methods
Microfluidic Device Design and Fabrication.
Each chamber where the cells are loaded (diameter 55 m, height 5 m; Fig. 1B) is surrounded by a series of diffusion apertures (width 2 m). These diffusion apertures are connected to a perfusion channel (width 65 m; weighted blue shades in Fig. 1A), where the stress solution flows through inlet and outlet channels (width 50 m). A cylindrical pillar (diameter 10 m) is placed at the center of the chamber to prevent the chamber ceiling from bending. The dimensions of the chamber, diffusion apertures, and central cylindrical pillars were optimized through numerical simulations and experiments. The chamber dimensions (diameter, height, and perfusion aperture width) had to 1) encompass enough cells to enable tracking entrained behavior and wave propagation, 2) ensure a monolayer to limit cell communication to lateral interactions, and 3) provide sufficient diffusion-based perfusion of the cell population avoiding mechanical stress. The function of the pillar is to uphold the cell chamber, fulfilling the microfluidic structure aspect ratio. The cylindrical geometry of the pillar and its location is intended to ensure symmetry in the diffusion profile.
Silicon molding masters are fabricated using photolithography. A negative photoresist (SU-8 3005; MicroChem Corp.) is spin-coated (3,500 rpm, 30 s), soft-baked (2 min at C; 3 min at C), UV-exposed (15 mW for 10 s [Suss MicroTec SE] under HardContact pressure mode), postexposure-baked (3 min at C; 4 min at C), and developed (2 min, SU-8 developer mr-Dev 600; Micro resist technology GmbH).
For the molding procedure, we have followed the established procedure described in ref. 30. Briefly, polydimethylsiloxane (PDMS) is homogeneously mixed with a curing agent (Sylgard 184 Silicone Elastomer Kit; Dow Corning Corp.) in a 15:1 ratio. The mixture is degassed using a vacuum dessicator (30 min), poured onto the master, and baked (3 h at C). The resulting PDMS structure is covalently bonded to a cover glass (thickness no. 1 [0.13 to 0.16 mm], 45 60 mm, HECH990/6045, VWR) using oxygen plasma (40 s, PDC-32G; Harric Plasma).
Cell Preparation.
The yeast cell strain used in the experiments is S. cerevisiae X2180. Cell cultures were grown from single colonies following the same protocol used in refs. 31, 32. The cells are grown in a carbon source medium containing 10 g GLC, 6.7 g yeast nitrogen base (YNB), and 100 mM of potassium phthalate at pH 5. The suspensions are cultured in a rotary shaker at C until GLC depletion in the media. To achieve the diauxic shift (GLC starved and switched to a slower exponential growth), the cells are washed and starved in 100 mM potassium phosphate (pH 6.8) for 3 more hours in the rotary shaker at C. Finally, in order to maintain the cells in the diauxic shift, they are washed and stored at C until the experiments. After filling the chamber, the loaded cells cover no more than 50 m of the cell inlet below the field of view (corresponding to about 210 cells). This is achieved by injecting a cell solution with an optical density 4 at 600 nm using a flow rate of 50 nL min−1 for 1 min. A longer injection time, or at a higher rate, can force the cells through the diffusion apertures.
Experimental Procedure.
Cells are loaded into the five cell chambers using 250 L glass syringes connected via polytetrafluoroethylene tubing (inner diameter 0.012 in.; Cole-Parmer). In order to obtain equal cell densities, the cell solution is introduced via equal length microfluidic paths and flow rates (40 nL/min) until the cell chambers are filled. After cell loading, the experiment is initiated with the injection of 40 mM GLC and 8, 12, 16, and 24 mM stress solutions, which circulate in the perfusion channel surrounding around each cell chamber at 25 nL . These concentration values were chosen based on previous studies (15). It was shown that variations in GLC concentrations, as long as they remain above 20 mM, do not have a significant effect on the oscillatory signal in a flow-based exposure. In the same study it was reported that concentrations above 5 mM and below 20 mM are required for sustained glycolytic oscillations in single cells. Once the yeast cells are loaded into the microfluidic chamber and the experiment starts, the cells’ metabolism is induced to an anaerobic fermentation state due to the exposure, producing as a fermentation product. The perfusion flow remains constant for the 20 min corresponding to the complete experimental acquisition. The cell loading and stress injection are performed using a precision multisyringe pump (CMA 400; CMA Microdialysis). The presence of captured air bubbles in the diffusion channels is permeated through the PDMS and dissolved once the fluid pumps are started and does not affect the substrate perfusion.
Signal Acquisition and Conditioning.
Image acquisition is performed using an inverted microscope (DMi 6000B; Leica Microsystems) with a 100, NA = 1.33 oil-immersion objective in an epifluorescence configuration. In order to measure the NADH autofluorescence intensity fluctuations, a 350/54 excitation filter and a 415/64 emission filter (DAPI set) are used together with a 15-W mercury short-arc reflector lamp (EL6000; Leica Microsystems) (33). An Electron Multiplying Charge-Coupled Device camera (C9100-12; Hamamatsu Photonics) is used with an exposure time of 400 ms. Images are acquired every 2 s for a total period of 20 min using an automatized illumination, positioning, and acquisition routine programmed using OpenLaboratory (PerkinElmer).
The time series for the individual cells are obtained from the NADH autofluorescence images. For each cell and frame, the average intensity of cell is computed over the region of interest corresponding to the cell area. Using MATLAB, a background signal and a running average of 55 data points are subtracted from the signal to reduce noise and short-term fluctuations.
Synchronization Analysis.
Starting from the glycolythic signals , the phase of cell is calculated as
| [1] |
where is the Hilbert transform of evaluated with the MATLAB built-in function. These data are shown in Fig. 2 and SI Appendix, Fig. S1 A–C, for the experimental and simulated signals, respectively.
To evaluate synchronization, as standardized in previous works (8, 10), the time-dependent order parameter is obtained from the expression
| [2] |
where is the number of cells in the cell chamber and is the instant phase for each yeast cell. The order parameter is normalized between 0 and 1. When is large, the individual cells’ phases are synchronized; when is small, there is high heterogeneity in the individual cell phases (34, 35). The degree of synchrony is characterized with values from 0 to 1 where low order parameter translates into high heterogeneity in the instant phases.
Graph Construction and Community Analysis.
By using graph theory, all of the oscillating cells are considered as nodes of a network with connections weighted by the correlation of their signals. Synchronization distribution can then be characterized in terms of the formation of cell communities showing higher coherence in their signals.
The community structure algorithms aim to optimize the modularity, a measure of the quality of the community division of the network. In short, modularity measures the density of the connections within a community and compares it with what it would be in a given random network. The more positive modularity indicates a better division of the network into communities (22).The Louvain algorithm approaches the problem of modularity maximization by iteratively grouping single nodes into communities (23). It starts by assigning each node in the network to a separate community. By changing the community participation of a node and its neighbors, it optimizes the modularity locally throughout the network. This results in having some community structure in the network. In the second step, these communities become nodes, and the first step of local modularity maximization is reapplied. These two steps are repeated until the maximum modularity is obtained and there are no changes in modularity values with any new iteration. Finally, the community organization of the step with maximal modularity is taken to be the real and final community of the network.
By setting a threshold in the correlation coefficient of 0.7, subgroups of cells showing synchronized behavior are obtained for the different concentration ratios in the stress solution. The functions to perform this process are adapted from the MATLAB-based software BRAPH (BRain Analysis using graPH theory) (22). A correlation adjacency matrix weighted with the correlation coefficients can be constructed by rearranging the node indices in subgroups showing higher connectivity. The indices assigned to each community can then be mapped based on their original location in the cell array and display the community spatial distribution.
To map the spatial distribution of the phase in form of wave fronts propagating across the cell array, the average correlation coefficient is calculated between each cell signal and a reference synchronization community at different delays. The Pearson correlations are calculated using the MATLAB build-in function corr.
Numerical Simulations.
The numerical simulations combine a kinetic model for single-cell glycolysis (14) with the geometrical and hydrodynamical conditions given by the cell arrangement in the microfluidic chip. The flow velocity field and the concentration gradients through the device are calculated using the finite-element based interpolation software COMSOL Multiphysics (COMSOL Inc.). The device geometry is defined with no-slip boundary conditions, and the nodes for the numerical interpolation are generated using the extra fine, physics controlled mesh mode. The fluid inside the device design is considered as Newtonian and incompressible, which obeys the Navier–Stokes equation for the stationary case:
| [3] |
where u is the flow velocity, f represents body force densities—which are negligible for this case—and the constants and are the density and dynamic viscosity, respectively, corresponding to water at room temperature; finally, p represents the pressure (36). The density and dynamic viscosity of the fluid is considered as the predefined for water by the software. To simulate the chemical transport and distribution, the time-dependent concentration gradients are calculated in order to follow diffusion across the cell chamber. The relation describing the process is given by the convection-diffusion equation:
| [4] |
Here is the concentration, and is the diffusion coefficient. The stress solution contained GLC and with diffusion coefficients of 6.7 /s and 20.7 /s, respectively. In addition, the concentration gradients are calculated for the time-dependent secretions of ETOH and ACA from the cells, with diffusion coefficients of 1.15 /s and 1.3 /s, respectively. Initial concentrations in the chamber are defined with the minimum values required to guarantee the oscillatory state of all of the cells (31), with 5 mM , 9 mM GLC, 1 mM ACA, and 1x mM ETOH.
A total of 210 circular boundaries are defined with sizes in the range of yeast cells at different ages—between 4 and 10 m—and are distributed inside the chamber design in a dense monolayer to emulate the experimental conditions. Global definitions of the membrane diffusion coefficients are assigned for ETOH, ACA, and with values of 5.88 /s, 5.87 /s, and 5.88 /s, respectively. On the other hand, diffusion coefficients inside the cells are defined high enough (1 /s) to consider the chemical concentrations to be homogenous and obtain single values for each cell geometry. The kinetic model previously described for individual cells in a microfluidic device (11, 14, 31, 37) is implemented to calculate the metabolite concentrations inside the cells as well as the secretions of ACA and ETOH in the chamber. For these calculations, the GLC and total exposure is defined by the convection-diffusion equation in combination with the lactonitrile formation from the reaction of with ACA (1, 38). The initial concentrations inside the cells are defined with a global initial intracellular GLC level of 3 mM and a heterogeneity of 10 different values of initial , ACA and ETOH. Similarly, 10 different initial values are assigned for all of the metabolites taking place in the ordinary differential equations along the metabolic pathway. The reaction rates taking place inside the cells are defined for each of the circular domains for GLC, , ACA, and ETOH (for details on all of the rate equations, see the interactive online model in https://jjj.bio.vu.nl/models/gustavsson5/simulate/). The resulting concentrations are tracked in time by individual probes inside each cell and in the extracellular media. Note that in the simulations the initial phase only is set individually while the whole cell array attains the same frequency. Furthermore, the level of heterogeneity is also much lower as only the cell sizes (in terms of diffusion rates) are varied and not the intracellular kinetic parameters.
Supplementary Material
Acknowledgments
We acknowledge the financial assistance from the Department of Science and Technology/National Research Foundation in South Africa, particularly for funding the South African Research Chairs Initiative (grant NRF-SARCHI-82813 to J.L.S.) and for grant 116298 (to D.D.v.N.), the Swedish Research Council (grant 2015-04014 to M.G., grant 2015-04155 to C.B.A., and grant 2017-04828 to B.M.), the Carl Trygger foundation for Scientific Research (grant CTS 16:157 to M.G. and grant CTS 13:38 to C.B.A.), and the European Research Council (grant ERC-StG 677511 to G.V.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2010075118/-/DCSupplemental.
Data Availability.
All study data are included in the article and SI Appendix.
References
- 1.Betz A., Becker J. U., Phase dependent phase shifts induced by pyruvate and acetaldehyde in oscillating NADH of yeast cells. J. Interdiscip. Cycle Res. 6, 167–173 (1975). [Google Scholar]
- 2.Richard P., Bakker B. M., Teusink B., Van Dam K., Westerhoff H. V., Acetaldehyde mediates the synchronization of sustained glycolytic oscillations in populations of yeast cells. Eur. J. Biochem. 235, 238–241 (1996). [DOI] [PubMed] [Google Scholar]
- 3.Danø S., Madsen M. F., Sørensen P. G., Quantitative characterization of cell synchronization in yeast. Proc. Natl. Acad. Sci. U.S.A. 104, 12732–12736 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jacobsen H., Busse H., Havsteen B., Spontaneous spatio-temporal organization in yeast cell suspension. J. Cell Sci. 43, 367–377 (1980). [DOI] [PubMed] [Google Scholar]
- 5.Bolyó J., Mair T., Kuncová G., Hauser M. J., Spatiotemporal dynamics of glycolytic waves provides new insights into the interactions between immobilized yeast cells and gels. Biophys. Chem. 153, 54–60 (2010). [DOI] [PubMed] [Google Scholar]
- 6.Schütze J., Mair T., Hauser M. J., Falcke M., Wolf J., Metabolic synchronization by traveling waves in yeast cell layers. Biophys. J. 100, 809–813 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Weber A., Prokazov Y., Zuschratter W., Hauser M. J. B., Desynchronisation of glycolytic oscillations in yeast cell populations. PloS One 7, e43276 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Weber A., Prokazov Y., Zuschratter W., Hauser M. J. B., “From synchronised to desynchronised glycolytic oscillations in individual yeast cells” in Complexity and Synergetics, Müller S. C., Plath P. J., Radons G., Fuchs A., Eds. (Springer International Publishing, Cham, 2018), pp. 239–254. [Google Scholar]
- 9.Amemiya T., et al. , Collective and individual glycolytic oscillations in yeast cells encapsulated in alginate microparticles. Chaos 25, 064606 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Gustavsson A. K., Adiels C. B., Mehlig B., Goksör M., Entrainment of heterogeneous glycolytic oscillations in single cells. Sci. Rep. 5, 9404 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.van Niekerk D., et al. , Phosphofructokinase controls the acetaldehyde induced phase shift in isolated yeast glycolytic oscillators. Biochem. J. 476, 353–363 (2019). [DOI] [PubMed] [Google Scholar]
- 12.Banaeiyan A. A., et al. , Design and fabrication of a scalable liver-lobule-on-a-chip microphysiological platform. Biofabrication 9, 015014 (2017). [DOI] [PubMed] [Google Scholar]
- 13.Glieberman A. L., et al. , Synchronized stimulation and continuous insulin sensing in a microfluidic human islet on a chip designed for scalable manufacturing. Lab Chip 19, 2993–3010 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.du Preez F. B., van Niekerk D. D., Kooi B., Rohwer J. M., Snoep J. L., From steady-state to synchronized yeast glycolytic oscillations I: Model construction. FEBS J. 279, 2810–2822 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Gustavsson A. K., et al. , Allosteric regulation of phosphofructokinase controls the emergence of glycolytic oscillations in isolated yeast cells. FEBS J. 281, 2784–2793 (2014). [DOI] [PubMed] [Google Scholar]
- 16.Merrins M. J., Van Dyke A. R., Mapp A. K., Rizzo M. A., Satin L. S., Direct measurements of oscillatory glycolysis in pancreatic islet -cells using novel fluorescence resonance energy transfer (FRET) biosensors for pyruvate kinase M2 activity. J. Biol. Chem. 288, 33312–33322 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.O’Rahilly S., Turner R. C., Matthews D. R., Impaired pulsatile secretion of insulin in relatives of patients with non-insulin-dependent diabetes. N. Engl. J. Med. 318, 1225–1230 (1988). [DOI] [PubMed] [Google Scholar]
- 18.Matveyenko A. V., et al. , Pulsatile portal vein insulin delivery enhances hepatic insulin action and signaling. Diabetes 61, 2269–2279 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hynne F., Dano S., Sorensen P. G., Full-scale model of glycolysis in saccharomyces cerevisiae. Biophys. Chem. 94, 121–163 (2001). [DOI] [PubMed] [Google Scholar]
- 20.Gustavsson A. K., Adiels C. B., Goksör M., “Induction of sustained glycolytic oscillations in single yeast cells using microfluidics and optical tweezers” in Optical Trapping and Optical Micromanipulation IX, Dholakia K., Spalding G. C., Eds. (International Society for Optics and Photonics, SPIE, 2012), vol. 8458, pp. 140–146. [Google Scholar]
- 21.Strogatz S. H., From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Phys. Nonlinear Phenom. 143, 1–20 (2000). [Google Scholar]
- 22.Mijalkov M., Kakaei E., Pereira J. B., Westman E., Volpe G., BRAPH: A graph theory software for the analysis of brain connectivity. PloS One 12, e0178798 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Blondel V. D., Guillaume J. L., Lambiotte R., Lefebvre E., Fast unfolding of communities in large networks. J. Stat. Mech. Theor. Exp. 2008, P10008 (2008). [Google Scholar]
- 24.Falcke M., Engel H., Neufeld M., Cluster formation, standing waves, and stripe patterns in oscillatory active media with local and global coupling. Phys. Rev. E 52, 763–771 (1995). [DOI] [PubMed] [Google Scholar]
- 25.Schütze J., Wolf J., Spatio-temporal dynamics of glycolysis in cell layers. A mathematical model. Biosystems 99, 104–108 (2010). [DOI] [PubMed] [Google Scholar]
- 26.Suzuki T., Kanamori T., Inouye S., Quantitative visualization of synchronized insulin secretion from 3D-cultured cells. Biochem. Biophys. Res. Commun. 486, 886–892 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Chou H. F., Berman N., Ipp E., Oscillations of lactate released from islets of langerhans: Evidence for oscillatory glycolysis in beta-cells. Am. J. Physiol. Endocrinol. Metabol. 262, E800–E805 (1992). [DOI] [PubMed] [Google Scholar]
- 28.Tornheim K., Are metabolic oscillations responsible for normal oscillatory insulin secretion? Diabetes 46, 1375–1380 (1997). [DOI] [PubMed] [Google Scholar]
- 29.Bertram R., Sherman A., Satin L. S., Metabolic and electrical oscillations: Partners in controlling pulsatile insulin secretion. Am. J. Physiol. Endocrinol. Metab. 293, E890–900 (2007). [DOI] [PubMed] [Google Scholar]
- 30.Sott K., Eriksson E., Goksor M., Acquisition of single cell data in an optical microscope. Lab Chip 2, 151–166 (2009). [Google Scholar]
- 31.Poulsen A. K., Petersen M. Ø., Olsen L. F., Single cell studies and simulation of cell–cell interactions using oscillating glycolysis in yeast cells. Biophys. Chem. 125, 275–280 (2007). [DOI] [PubMed] [Google Scholar]
- 32.Richard P., Teusink B., Westerhoff H. V., van Dam K., Around the growth phase transition S. cerevisiae’s make-up favours sustained oscillations of intracellular metabolites. Fed. Eur. Biochem. Soc. Lett. 318, 80–82 (1993). [DOI] [PubMed] [Google Scholar]
- 33.Patterson G. H., Knobel S. M., Arkhammar P., Thastrup O., Piston D. W., Separation of the glucose-stimulated cytoplasmic and mitochondrial NAD(P)H responses in pancreatic islet cells. Proc. Natl. Acad. Sci. U.S.A. 97, 5203–5207 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kuramoto Y., “Self-entrainment of a population of coupled non-linear oscillators” in International Symposium on Mathematical Problems in Theoretical Physics, Araki H., Ed. (Springer, Berlin, 1975), pp. 420–422. [Google Scholar]
- 35.Shinomoto S., Kuramoto Y., Phase transitions in active rotator systems. Prog. Theor. Phys. 75, 1105–1110 (1986). [Google Scholar]
- 36.Tabeling P., Introduction to Microfluidics (Oxford University Press, New York, 2005). [Google Scholar]
- 37.Gustavsson A. K., et al. , Sustained glycolytic oscillations in individual isolated yeast cells. FEBS J. 279, 2837–2847 (2012). [DOI] [PubMed] [Google Scholar]
- 38.Yates W., Heider R., The dissociation of lactonitrile in aqueous solution. J. Am. Chem. Soc. 74, 4153–4155 (1952). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix.